69  ANOVA ad una via

“The agricultural analogy is for [ANOVA] what the barnyard is to the city child—a romantic but inefficient source of fundamental concepts.”

– David Bakan, The Test of Significance in Psychological Research (1966)

Introduzione

Nel Capitolo 66 ci siamo concentrati sul confronto tra due gruppi utilizzando una regressione lineare con variabili dummy. Questo approccio ci ha permesso di modellare in modo semplice l’effetto di un fattore binario e di stimare con incertezza l’ampiezza della differenza. Ora estendiamo quella logica al caso in cui il fattore abbia più di due livelli.

Questo passaggio ci introduce al cuore dell’ANOVA a una via, che non è altro che un modello lineare con un fattore categoriale a \(k\) livelli. In questo contesto, ci interessa capire quanta variabilità nei dati può essere attribuita alle differenze tra gruppi, e quanto invece rimane all’interno dei gruppi stessi. Come sempre in questo manuale, manterremo una lettura orientata all’incertezza e alla variabilità intra- e inter-individuale, trattando l’inferenza come uno strumento per quantificare la credibilità delle ipotesi.

Panoramica del capitolo

  • Fare inferenza sulla media di un campione.
  • Trovare le distribuzioni a posteriori usando brms.
  • Verificare il modello usando i pp-check plots.
  • Leggere il capitolo Geocentric models di Statistical rethinking (McElreath, 2020).
here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, bayestestR, brms, emmeans)

69.1 Codifica del modello con variabili dummy

Supponiamo un esperimento con tre gruppi. Per rappresentare questo fattore all’interno di un modello lineare, usiamo due variabili dummy e consideriamo il terzo gruppo come riferimento implicito. Il modello assume la forma:

\[ Y_i = \alpha + \gamma_1 D_{i1} + \gamma_2 D_{i2} + \varepsilon_i \tag{69.1}\]

dove:

  • \(\alpha\) è l’intercetta del modello,
  • \(\gamma_1\) e \(\gamma_2\) sono i coefficienti associati alle variabili dummy,
  • \(D_{i1}\) e \(D_{i2}\) indicano l’appartenenza dell’osservazione \(i\) ai gruppi 1 e 2, rispettivamente,
  • \(\varepsilon_i\) è l’errore aleatorio.

La codifica delle dummy è la seguente:

\[ \begin{array}{c|cc} \text{Gruppo} & D_{1} & D_{2} \\ \hline 1 & 1 & 0 \\ 2 & 0 & 1 \\ 3 & 0 & 0 \end{array} \tag{69.2}\]

69.1.1 Interpretazione dei parametri

Con questa codifica, possiamo esprimere le medie di ciascun gruppo come:

\[ \begin{aligned} \mu_1 &= \alpha + \gamma_1 \\ \mu_2 &= \alpha + \gamma_2 \\ \mu_3 &= \alpha \end{aligned} \]

Da cui otteniamo:

\[ \alpha = \mu_3, \quad \gamma_1 = \mu_1 - \mu_3, \quad \gamma_2 = \mu_2 - \mu_3. \]

Quindi:

  • \(\alpha\): media del gruppo 3 (riferimento),
  • \(\gamma_1\): quanto il gruppo 1 si discosta da \(\mu_3\),
  • \(\gamma_2\): quanto il gruppo 2 si discosta da \(\mu_3\).

In un’ottica bayesiana, questi coefficienti possono essere pensati come distribuzioni: esprimono quanto crediamo che ciascuna differenza sia plausibile, date le osservazioni. Passiamo ora a una simulazione.

69.2 Simulazione

Simuliamo un esperimento con tre condizioni: controllo, psicoterapia1 e psicoterapia2. Ogni gruppo ha una media diversa ma la stessa deviazione standard. Ci interessa modellare la variabilità tra le condizioni e interpretare le differenze in modo probabilistico.

set.seed(123)

n <- 30  # numero di osservazioni per gruppo
# Medie di ciascun gruppo
mean_control <- 30
mean_psico1  <- 25
mean_psico2  <- 20
# Deviazione standard comune
sd_value <- 5

# Generazione dei dati
controllo     <- rnorm(n, mean_control, sd_value)
psicoterapia1 <- rnorm(n, mean_psico1,  sd_value)
psicoterapia2 <- rnorm(n, mean_psico2,  sd_value)

# Creazione del data frame
df <- data.frame(
  condizione = rep(c("controllo", "psicoterapia1", "psicoterapia2"), each = n),
  punteggio  = c(controllo, psicoterapia1, psicoterapia2)
)

df |> head()
#>   condizione punteggio
#> 1  controllo     27.20
#> 2  controllo     28.85
#> 3  controllo     37.79
#> 4  controllo     30.35
#> 5  controllo     30.65
#> 6  controllo     38.58

69.2.1 Esplorazione iniziale

Visualizziamo le distribuzioni dei punteggi:

ggplot(df, aes(x = condizione, y = punteggio, fill = condizione)) +
  geom_violin(trim = FALSE) +
  geom_boxplot(width = 0.2, outlier.shape = NA) +
  labs(
    title = "Distribuzione dei punteggi di depressione per gruppo",
    x = "Condizione sperimentale",
    y = "Punteggio di depressione"
  ) +
  theme(legend.position = "none")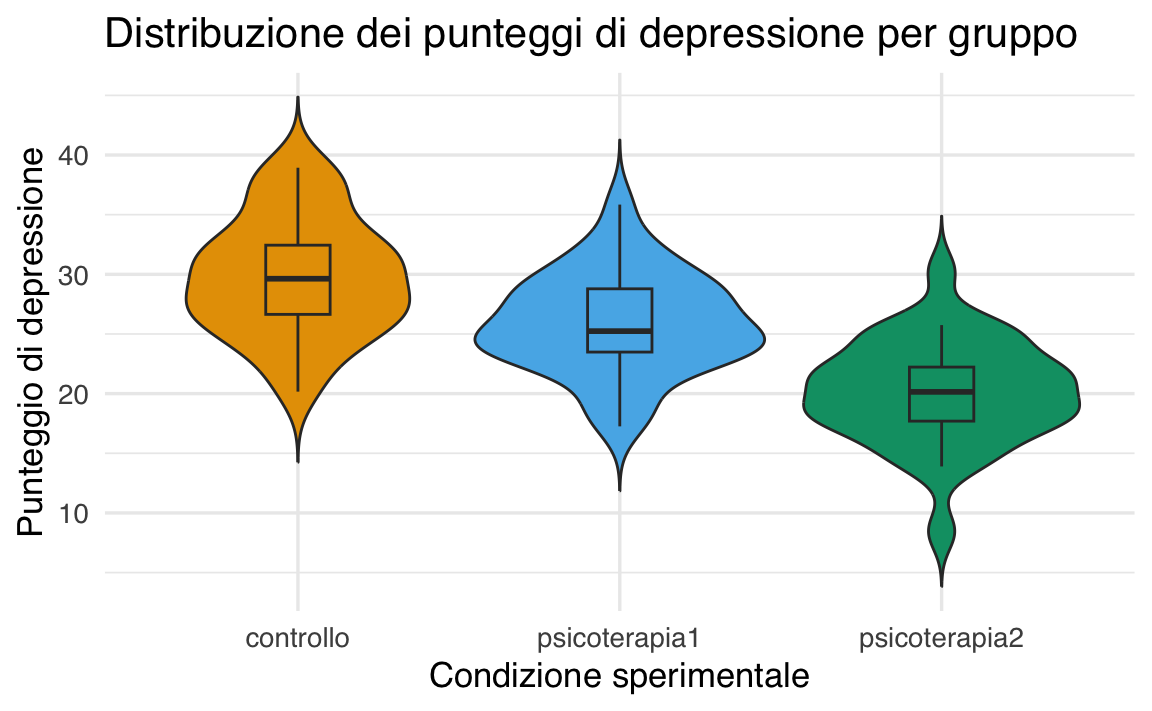

Calcoliamo media e deviazione standard per ogni gruppo:

df |> 
  group_by(condizione) |> 
  summarize(
    media = mean(punteggio),
    sd = sd(punteggio)
  )
#> # A tibble: 3 × 3
#>   condizione    media    sd
#>   <chr>         <dbl> <dbl>
#> 1 controllo      29.8  4.91
#> 2 psicoterapia1  25.9  4.18
#> 3 psicoterapia2  20.1  4.35

69.3 Modello lineare con variabili dummy

Convertiamo condizione in fattore e definiamo controllo come categoria di riferimento:

df$condizione <- factor(df$condizione)
df$condizione <- relevel(df$condizione, ref = "controllo")
contrasts(df$condizione)
#>               psicoterapia1 psicoterapia2
#> controllo                 0             0
#> psicoterapia1             1             0
#> psicoterapia2             0             1

Il modello di regressione con le variabili dummy sarà:

\[ Y_i = \beta_0 + \beta_1 \cdot \text{psicoterapia1}_i + \beta_2 \cdot \text{psicoterapia2}_i + \varepsilon_i, \]

dove:

  • \(\beta_0\) è la media del gruppo di controllo;
  • \(\beta_1\) e \(\beta_2\) sono le differenze tra le rispettive psicoterapie e il gruppo di controllo.

69.3.1 Stima del modello

Eseguiamo una prima analisi usando il metodo di massima verosimiglianza:

fm1 <- lm(punteggio ~ condizione, data = df)
summary(fm1)
#> 
#> Call:
#> lm(formula = punteggio ~ condizione, data = df)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -11.668  -2.620  -0.183   2.681  10.128 
#> 
#> Coefficients:
#>                         Estimate Std. Error t value Pr(>|t|)
#> (Intercept)               29.764      0.819   36.33  < 2e-16
#> condizionepsicoterapia1   -3.873      1.159   -3.34   0.0012
#> condizionepsicoterapia2   -9.642      1.159   -8.32  1.1e-12
#> 
#> Residual standard error: 4.49 on 87 degrees of freedom
#> Multiple R-squared:  0.446,  Adjusted R-squared:  0.434 
#> F-statistic: 35.1 on 2 and 87 DF,  p-value: 6.75e-12

Verifica delle medie e differenze tra i gruppi:

out <- tapply(df$punteggio, df$condizione, mean)
out[2] - out[1]  # psicoterapia1 - controllo
#> psicoterapia1 
#>        -3.873
out[3] - out[1]  # psicoterapia2 - controllo
#> psicoterapia2 
#>        -9.642

69.4 Contrasti personalizzati

I contrasti ci permettono di andare oltre il test globale e formulare ipotesi teoriche mirate. Ad esempio:

  • la media del gruppo controllo è diversa dalla media delle due psicoterapie?
  • le due psicoterapie differiscono tra loro?

A questo fine, specifichiamo la seguente matrice dei contrasti:

my_contrasts <- matrix(c(
  0.6667,  0,     # controllo
 -0.3333,  0.5,   # psicoterapia1
 -0.3333, -0.5    # psicoterapia2
), ncol = 2, byrow = TRUE)

colnames(my_contrasts) <- c("Ctrl_vs_PsicoMean", "P1_vs_P2")
rownames(my_contrasts) <- c("controllo", "psicoterapia1", "psicoterapia2")

contrasts(df$condizione) <- my_contrasts

Adattiamo il modello:

mod_custom <- lm(punteggio ~ condizione, data = df)

Esaminiamo i coefficienti:

summary(mod_custom)
#> 
#> Call:
#> lm(formula = punteggio ~ condizione, data = df)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -11.668  -2.620  -0.183   2.681  10.128 
#> 
#> Coefficients:
#>                             Estimate Std. Error t value Pr(>|t|)
#> (Intercept)                   25.259      0.473   53.40  < 2e-16
#> condizioneCtrl_vs_PsicoMean    6.758      1.003    6.73  1.7e-09
#> condizioneP1_vs_P2             5.770      1.159    4.98  3.2e-06
#> 
#> Residual standard error: 4.49 on 87 degrees of freedom
#> Multiple R-squared:  0.446,  Adjusted R-squared:  0.434 
#> F-statistic: 35.1 on 2 and 87 DF,  p-value: 6.75e-12

Interpretazione dei coefficienti:

  • Intercetta: non rappresenta più una singola media, ma una combinazione lineare dei gruppi.
  • Ctrl_vs_PsicoMean: confronta la media di controllo con la media combinata delle due psicoterapie.
  • P1_vs_P2: differenza tra le due psicoterapie.

Verifica manuale:

# Controllo - media delle psicoterapie
out[1] - (out[2] + out[3]) / 2
#> controllo 
#>     6.758
# Psicoterapia1 - Psicoterapia2
out[2] - out[3]
#> psicoterapia1 
#>          5.77

69.5 Estensione bayesiana con brms e emmeans

Usiamo ora il modello bayesiano:

mod <- brm(punteggio ~ condizione, data = df, backend = "cmdstanr")
summary(mod)
#>  Family: gaussian 
#>   Links: mu = identity; sigma = identity 
#> Formula: punteggio ~ condizione 
#>    Data: df (Number of observations: 90) 
#>   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 4000
#> 
#> Regression Coefficients:
#>                             Estimate Est.Error l-95% CI u-95% CI Rhat
#> Intercept                      25.26      0.48    24.33    26.15 1.00
#> condizioneCtrl_vs_PsicoMean     6.78      1.04     4.73     8.85 1.00
#> condizioneP1_vs_P2              5.76      1.16     3.49     8.08 1.00
#>                             Bulk_ESS Tail_ESS
#> Intercept                       4321     2937
#> condizioneCtrl_vs_PsicoMean     4260     2964
#> condizioneP1_vs_P2              4598     2785
#> 
#> Further Distributional Parameters:
#>       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma     4.54      0.34     3.93     5.26 1.00     4287     3279
#> 
#> Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Le medie marginali e i confronti possono essere ottenuti con il pacchetto emmeans:

em <- emmeans(mod, specs = "condizione")
em
#>  condizione    emmean lower.HPD upper.HPD
#>  controllo       29.8      28.1      31.4
#>  psicoterapia1   25.9      24.3      27.5
#>  psicoterapia2   20.1      18.4      21.7
#> 
#> Point estimate displayed: median 
#> HPD interval probability: 0.95

Confronti tra gruppi:

pairs(em)  # confronti a coppie
#>  contrast                      estimate lower.HPD upper.HPD
#>  controllo - psicoterapia1         3.90      1.70      6.21
#>  controllo - psicoterapia2         9.65      7.31     12.03
#>  psicoterapia1 - psicoterapia2     5.75      3.57      8.14
#> 
#> Point estimate displayed: median 
#> HPD interval probability: 0.95

Contrasti personalizzati:

my_list <- list(
  "Ctrl_vs_PsicoMean" = c(
    "controllo" = 1, "psicoterapia1" = -0.5, "psicoterapia2" = -0.5
  ),
  "P1_vs_P2" = c(
    "controllo" = 0, "psicoterapia1" = 1, "psicoterapia2" = -1
  )
)
contrast(em, method = my_list)
#>  contrast          estimate lower.HPD upper.HPD
#>  Ctrl_vs_PsicoMean     6.77      4.77      8.88
#>  P1_vs_P2              5.75      3.57      8.14
#> 
#> Point estimate displayed: median 
#> HPD interval probability: 0.95
# Visualizzazione
plot(em)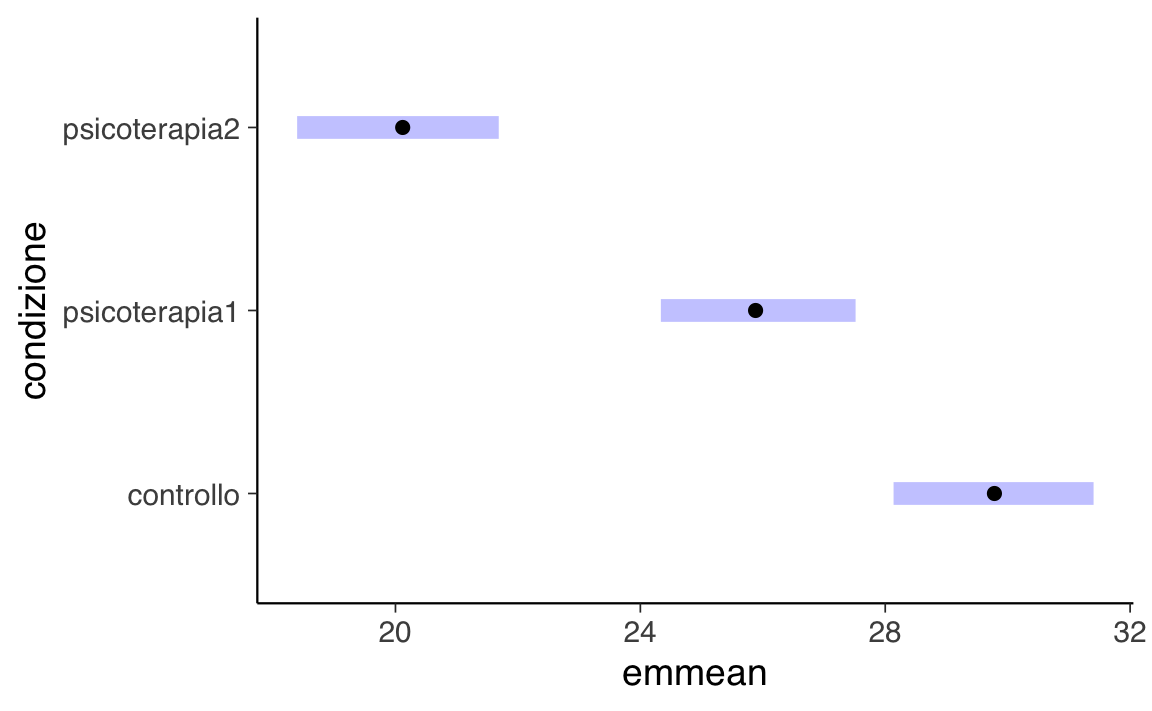

Riflessioni conclusive

Ecco una proposta rivista delle Riflessioni conclusive, che integra il riferimento storico a Fisher e la riflessione critica di McArdle sull’uso dell’ANOVA in psicologia:

Riflessioni conclusive

L’ANOVA a una via rappresenta un punto di passaggio fondamentale nella storia della statistica. Fisher la introdusse negli anni ’20 per risolvere problemi molto concreti di agricoltura sperimentale: ad esempio, confrontare le rese di diversi fertilizzanti su parcelle di terreno, in cui le variabili erano chiaramente definite e osservabili. In questo contesto, l’ANOVA si rivelò uno strumento elegante per separare la variabilità “tra trattamenti” dalla variabilità “entro trattamenti”.

In psicologia, tuttavia, il quadro è radicalmente diverso. Come ha osservato ripetutamente John J. McArdle (ad es. McArdle, 1994), i nostri oggetti di studio sono in larga misura costrutti latenti — ansia, depressione, intelligenza — che non possono essere osservati direttamente come la crescita di una pianta o il peso di un raccolto. Applicare in modo acritico tecniche nate per l’agricoltura rischia quindi di ridurre la complessità dei fenomeni psicologici a semplici confronti tra medie di punteggi osservati.

Questo non significa che l’ANOVA non abbia avuto (e non abbia tuttora) un ruolo didattico e applicativo importante: il modello lineare sottostante resta una base utile per introdurre la logica del confronto tra gruppi. Tuttavia, per affrontare in modo adeguato i problemi della psicologia contemporanea, è spesso più appropriato ricorrere a tecniche che modellano esplicitamente la natura latente delle variabili, come l’analisi fattoriale o i modelli a equazioni strutturali. Questi approcci permettono di connettere in modo più diretto le osservazioni empiriche ai costrutti teorici che ci interessano davvero.

In sintesi, l’ANOVA è uno strumento storico e concettualmente utile, ma deve essere vista come un trampolino: una tappa di apprendimento che prepara all’uso di modelli più adatti a catturare la complessità dei dati psicologici.

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] emmeans_1.11.2        bayestestR_0.16.1     cmdstanr_0.9.0       
#>  [4] pillar_1.11.0         tinytable_0.11.0      patchwork_1.3.1      
#>  [7] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.13.0     
#> [10] ggplot2_3.5.2         reliabilitydiag_0.2.1 priorsense_1.1.0     
#> [13] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [16] StanHeaders_2.32.10   brms_2.22.0           Rcpp_1.1.0           
#> [19] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [22] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [25] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [28] here_1.0.1           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3        inline_0.3.21        sandwich_3.1-1      
#>  [4] rlang_1.1.6          magrittr_2.0.3       multcomp_1.4-28     
#>  [7] snakecase_0.11.1     compiler_4.5.1       reshape2_1.4.4      
#> [10] systemfonts_1.2.3    vctrs_0.6.5          stringr_1.5.1       
#> [13] pkgconfig_2.0.3      arrayhelpers_1.1-0   fastmap_1.2.0       
#> [16] backports_1.5.0      labeling_0.4.3       utf8_1.2.6          
#> [19] rmarkdown_2.29       ps_1.9.1             ragg_1.4.0          
#> [22] purrr_1.1.0          xfun_0.52            cachem_1.1.0        
#> [25] jsonlite_2.0.0       broom_1.0.9          parallel_4.5.1      
#> [28] R6_2.6.1             stringi_1.8.7        RColorBrewer_1.1-3  
#> [31] lubridate_1.9.4      estimability_1.5.1   knitr_1.50          
#> [34] zoo_1.8-14           pacman_0.5.1         Matrix_1.7-3        
#> [37] splines_4.5.1        timechange_0.3.0     tidyselect_1.2.1    
#> [40] abind_1.4-8          yaml_2.3.10          codetools_0.2-20    
#> [43] curl_6.4.0           processx_3.8.6       pkgbuild_1.4.8      
#> [46] plyr_1.8.9           lattice_0.22-7       withr_3.0.2         
#> [49] bridgesampling_1.1-2 coda_0.19-4.1        evaluate_1.0.4      
#> [52] survival_3.8-3       RcppParallel_5.1.10  tensorA_0.36.2.1    
#> [55] checkmate_2.3.2      stats4_4.5.1         insight_1.3.1       
#> [58] distributional_0.5.0 generics_0.1.4       rprojroot_2.1.0     
#> [61] rstantools_2.4.0     scales_1.4.0         xtable_1.8-4        
#> [64] glue_1.8.0           tools_4.5.1          data.table_1.17.8   
#> [67] mvtnorm_1.3-3        grid_4.5.1           QuickJSR_1.8.0      
#> [70] colorspace_2.1-1     nlme_3.1-168         cli_3.6.5           
#> [73] textshaping_1.0.1    svUnit_1.0.6         Brobdingnag_1.2-9   
#> [76] V8_6.0.5             gtable_0.3.6         digest_0.6.37       
#> [79] TH.data_1.1-3        htmlwidgets_1.6.4    farver_2.1.2        
#> [82] memoise_2.0.1        htmltools_0.5.8.1    lifecycle_1.0.4     
#> [85] MASS_7.3-65

Bibliografia

McArdle, J. J. (1994). Structural factor analysis experiments with incomplete data. Multivariate Behavioral Research, 29(4), 409–454. https://doi.org/10.1207/s15327906mbr2904_5
McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2nd Edition). CRC Press.