52 Distribuzione predittiva a posteriori

In questo capitolo imparerai a:

utilizzare la distribuzione predittiva a posteriori per fare previsioni sui dati futuri, incorporando sia l’incertezza sui parametri del modello sia la variabilità intrinseca del processo generativo.
comprendere il ruolo della distribuzione predittiva a posteriori nel verificare la coerenza del modello bayesiano rispetto ai dati osservati.
applicare il concetto di distribuzione predittiva a posteriori al caso beta-binomiale per un’analisi pratica e intuitiva.

Prerequisiti

Leggere il capitolo Posterior Inference & Prediction di Bayes Rules!.
Consultare Bayesian statistics and modelling (Schoot et al., 2021).

Preparazione del Notebook

here::here("code", "_common.R") |> 
  source()

Introduzione

Nell’inferenza bayesiana non ci interessa soltanto stimare i parametri di un modello (ad esempio, la probabilità \(p\) di successo in un compito con esiti binomiali). Un obiettivo altrettanto importante è prevedere dati futuri, sulla base di ciò che abbiamo già osservato. La distribuzione predittiva a posteriori serve proprio a questo: combina

l’incertezza sui parametri, descritta dalla distribuzione a posteriori,
la variabilità intrinseca del processo che genera i dati futuri.

In parole semplici, la distribuzione predittiva a posteriori ci dice quali risultati futuri sono plausibili, dati i dati osservati e il modello che utilizziamo per interpretarli.

52.1 Definizione formale

Supponiamo di avere dati osservati \(y = {y_1, y_2, \ldots, y_n}\), generati da un modello che dipende da un parametro ignoto \(\theta\). Questo parametro può rappresentare, a seconda del caso, una probabilità, una media, o un coefficiente di regressione.

La conoscenza iniziale su \(\theta\) è descritta da una distribuzione a priori \(p(\theta)\). Dopo aver osservato i dati, aggiorniamo tale conoscenza attraverso la formula di Bayes, ottenendo la distribuzione a posteriori:

\[ p(\theta \mid y) = \frac{p(y \mid \theta)\, p(\theta)}{p(y)} , \]

dove:

\(p(\theta \mid y)\) è la distribuzione a posteriori: rappresenta ciò che sappiamo su \(\theta\) dopo i dati.
\(p(y \mid \theta)\) è la verosimiglianza: quanto i dati osservati sono compatibili con un certo valore di \(\theta\).
\(p(\theta)\) è la distribuzione a priori.
\(p(y)\) è l’evidenza, cioè la probabilità totale dei dati, calcolata come

\[ p(y) = \int p(y \mid \theta) p(\theta)\, d\theta . \]

Ora vogliamo prevedere un nuovo dato, \(\tilde{y}\). In questo caso ci serve la distribuzione predittiva a posteriori \(p(\tilde{y} \mid y)\).

52.1.1 Che cos’è \(\tilde{y}\)?

È un dato futuro o non ancora osservato.
Per esempio, se \(y\) rappresenta il numero di successi in una serie di lanci di moneta, \(\tilde{y}\) può rappresentare i successi in una nuova serie di lanci.

52.1.2 Che cos’è \(p(\tilde{y} \mid \theta)\)?

È la probabilità di osservare \(\tilde{y}\) se sapessimo che il parametro del modello è proprio \(\theta\).
Nell’esempio binomiale, corrisponde alla probabilità di ottenere \(\tilde{y}\) successi su \(n_{\text{new}}\) prove, dato che la probabilità di successo è \(\theta\).

52.1.3 Come combinare \(p(\tilde{y} \mid \theta)\) e \(p(\theta \mid y)\)

Poiché non conosciamo il vero valore di \(\theta\), consideriamo tutti i valori possibili, pesandoli in base alla loro plausibilità a posteriori. Questo porta alla formula fondamentale:

\[ p(\tilde{y} \mid y) = \int p(\tilde{y} \mid \theta)\, p(\theta \mid y)\, d\theta . \tag{52.1}\]

52.1.4 Interpretazione

La distribuzione predittiva a posteriori \(p(\tilde{y} \mid y)\) rappresenta la miglior stima possibile della probabilità di un dato futuro: tiene conto sia dell’incertezza sui parametri sia della variabilità del fenomeno stesso.

52.2 Caso discreto

Se \(\theta\) può assumere un numero finito di valori, l’integrale si riduce a una somma:

\[ p(\tilde{y} \mid y) = \sum_{\theta} p(\tilde{y} \mid \theta)\, p(\theta \mid y). \tag{52.2}\]

Questo approccio è particolarmente utile nei modelli discreti o quando lavoriamo con approssimazioni basate su campioni finiti di valori di \(\theta\) (ad esempio, i campioni MCMC).

52.3 Il caso Beta–Binomiale

Consideriamo un esperimento binomiale: lanciamo una moneta \(n\) volte e osserviamo il numero di successi \(y\) (ad esempio, il numero di teste). In ottica bayesiana, l’analisi segue tre passaggi fondamentali:

Distribuzione a priori Prima di osservare i dati, esprimiamo le nostre conoscenze (o incertezze) sulla probabilità di successo \(p\). Una scelta comune è la distribuzione Beta(\(\alpha, \beta\)), perché è definita sull’intervallo \([0,1]\) e molto flessibile:
- \(\alpha\) si può interpretare come un numero “fittizio” di successi già osservati;
- \(\beta\) come un numero “fittizio” di insuccessi.
In questo modo, la prior sintetizza eventuali conoscenze pregresse sotto forma di “dati immaginari”.
Distribuzione a posteriori Dopo aver osservato \(y\) successi su \(n\) prove, aggiorniamo la prior con i dati tramite la regola di Bayes. Poiché la Beta è coniugata alla Binomiale, la distribuzione a posteriori ha ancora forma Beta, con parametri aggiornati:

\[ \alpha_{\text{post}} = \alpha_{\text{prior}} + y, \quad \beta_{\text{post}} = \beta_{\text{prior}} + (n - y). \]

Questa distribuzione descrive ciò che sappiamo su \(p\) dopo aver osservato i dati.
Distribuzione predittiva a posteriori Se vogliamo prevedere il numero di successi futuri \(y_{\text{new}}\) in un nuovo esperimento con \(n_{\text{new}}\) prove, dobbiamo combinare:
- l’incertezza residua su \(p\), descritta dalla distribuzione a posteriori;
- la variabilità del processo binomiale per le nuove osservazioni.
In pratica:
- estraiamo \(p \sim \text{Beta}(\alpha_{\text{post}}, \beta_{\text{post}})\);
- generiamo \(y_{\text{new}} \sim \text{Binomiale}(n_{\text{new}}, p)\).
Questo procedimento produce la distribuzione predittiva a posteriori, che integra entrambe le fonti di incertezza.

52.4 Un esempio numerico

52.4.1 Parametri osservati e prior

Dati: \(y = 70\) successi su \(n = 100\) prove.
Prior: Beta(2, 2), debolmente informativa, con leggera preferenza per valori di \(p\) vicini a 0.5.

52.4.2 Distribuzione a posteriori

Aggiornando la prior:

\[ \alpha_{\text{post}} = 2 + 70 = 72, \quad \beta_{\text{post}} = 2 + (100 - 70) = 32. \]

La distribuzione a posteriori è quindi \(p \sim \text{Beta}(72, 32)\), centrata attorno a \(p \approx 0.7\).

52.4.3 Simulazione predittiva

Supponiamo di voler prevedere \(y_{\text{new}}\) su \(n_{\text{new}} = 10\) prove:

set.seed(123)

# Dati osservati
y <- 70
n <- 100

# Prior
alpha_prior <- 2
beta_prior <- 2

# Posterior
alpha_post <- alpha_prior + y
beta_post <- beta_prior + (n - y)

# Campioni da p|y ~ Beta(72, 32)
p_samples <- rbeta(1000, alpha_post, beta_post)

# Simulazione di successi futuri
y_preds <- rbinom(1000, size = 10, prob = p_samples)

# Proporzioni di successi
prop_preds <- y_preds / 10

52.4.4 Spiegazione del codice

1. Distribuzione a posteriori di \(p\).

alpha_post <- alpha_prior + y
beta_post <- beta_prior + (n - y)
p_samples <- rbeta(1000, alpha_post, beta_post)

Qui calcoliamo la distribuzione a posteriori di \(p\): \(p \mid y \sim \text{Beta}(72, 32)\). Con rbeta(1000, 72, 32) estraiamo 1000 campioni da questa distribuzione: ognuno rappresenta un valore plausibile della probabilità di successo \(p\), pesato implicitamente dalla distribuzione a posteriori. In altre parole, stiamo implementando il concetto: non conosciamo il vero \(p\), ma lo trattiamo come una variabile aleatoria distribuita secondo la posterior.

2. Distribuzione predittiva di nuovi dati.

y_preds <- rbinom(1000, size = 10, prob = p_samples)

Per ogni valore di \(p\) campionato dalla posterior, simuliamo un nuovo esperimento con 10 prove (rbinom). Questa parte del codice riflette l’integrale teorico della distribuzione predittiva:

\[ p(\tilde{y} \mid y) = \int p(\tilde{y} \mid p)\, p(p \mid y)\, dp . \]

In pratica, invece di calcolare l’integrale, lo approssimiamo con simulazioni:

per ciascun \(p\) plausibile (estratto dalla posterior),
generiamo un possibile esito futuro \(\tilde{y}\),
ripetiamo il processo tante volte.

Così otteniamo un campione dalla distribuzione predittiva a posteriori.

3. Proporzioni di successi.

prop_preds <- y_preds / 10

Convertiamo i conteggi di successi in proporzioni: ogni valore rappresenta un possibile esito futuro, considerando sia l’incertezza su \(p\) sia la variabilità intrinseca del processo binomiale.

4. Legame con l’idea teorica.

L’idea era:

“Poiché non conosciamo il vero valore di \(p\), consideriamo tutti i valori possibili, pesandoli in base alla loro plausibilità a posteriori.”

Il codice fa esattamente questo:

con rbeta() campioniamo valori plausibili di \(p\) dalla distribuzione a posteriori (il “peso” viene dal fatto che valori più probabili vengono campionati più spesso);
con rbinom() generiamo i dati futuri \(\tilde{y}\) per ognuno di questi valori.

Il risultato (prop_preds) è un insieme di possibili esiti futuri che incorpora entrambe le fonti di incertezza:

l’incertezza residua sul parametro \(p\) (posterior),
la variabilità del processo binomiale (dati futuri).

52.4.5 Visualizzazione

Distribuzione a priori:

curve(dbeta(x, alpha_prior, beta_prior), from = 0, to = 1,
      main = "Distribuzione a Priori", col = "blue", lwd = 2, ylab = "Densità")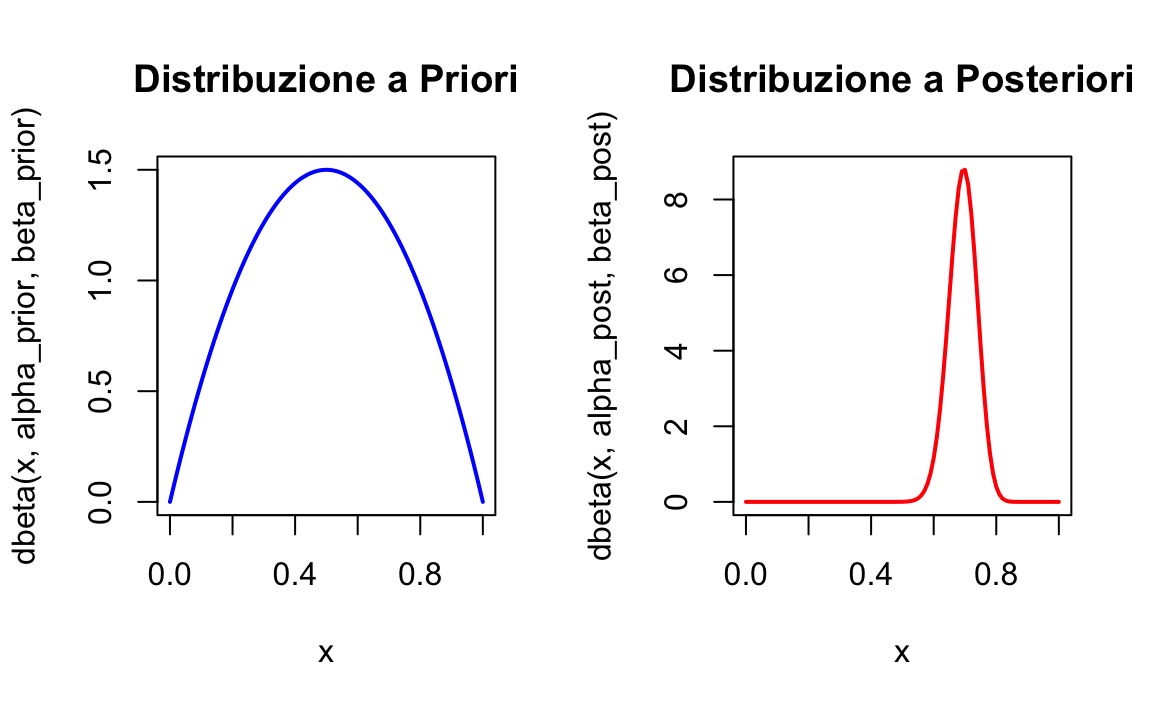

Distribuzione a posteriori:

curve(dbeta(x, alpha_post, beta_post), from = 0, to = 1,
      main = "Distribuzione a Posteriori", col = "red", lwd = 2, ylab = "Densità")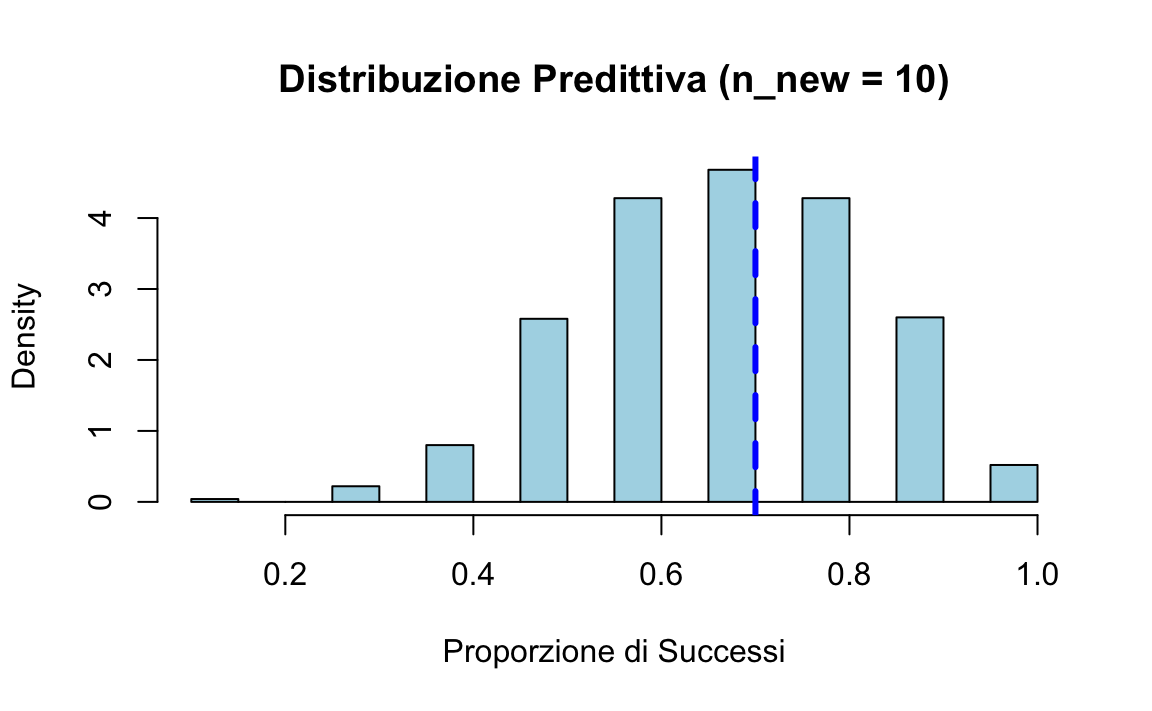

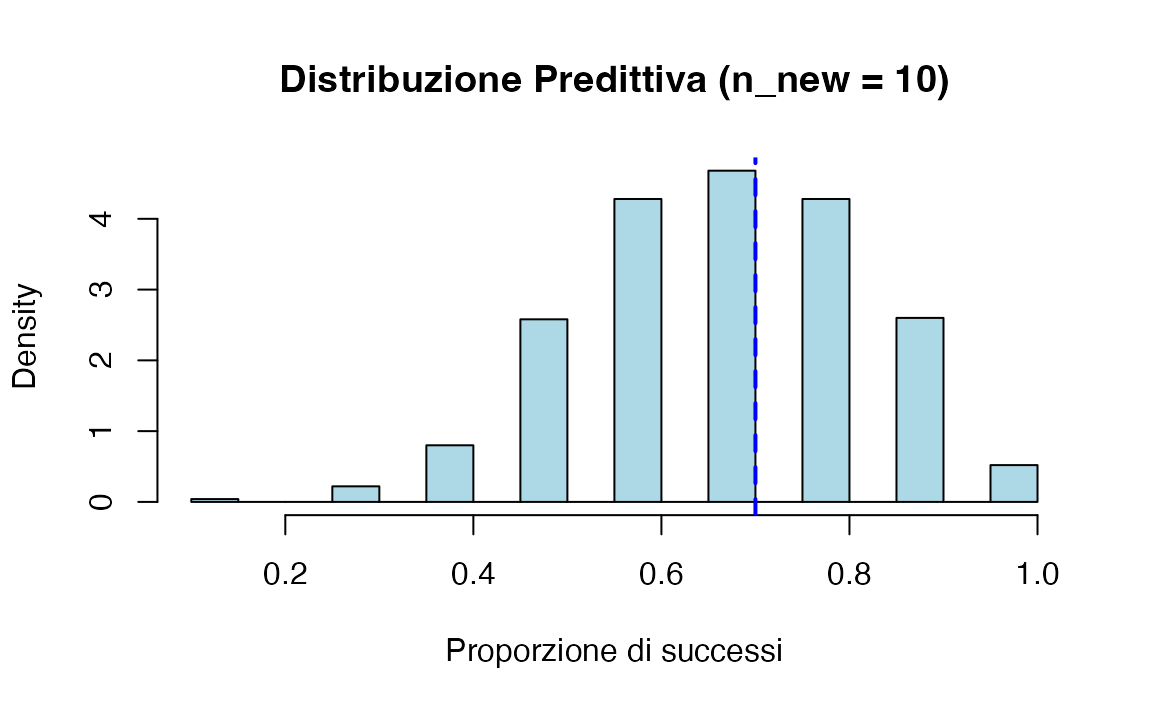
Distribuzione predittiva per \(n_{\text{new}} = 10\):

hist(prop_preds, breaks = 20, col = "lightblue", freq = FALSE,
     main = "Distribuzione Predittiva (n_new = 10)",
     xlab = "Proporzione di successi")
abline(v = y/n, col = "blue", lwd = 2, lty = 2)

52.4.6 Interpretazione

La distribuzione a posteriori \(p \sim \text{Beta}(72, 32)\) è stretta attorno a 0.7, riflettendo l’elevata informazione contenuta nei 100 lanci osservati.
La distribuzione predittiva per \(n_{\text{new}} = 10\) è invece più ampia: la ridotta numerosità introduce ulteriore variabilità oltre all’incertezza residua su \(p\).
L’istogramma mostra che i valori più probabili per la proporzione futura oscillano intorno a 0.7, ma con maggiore dispersione.

La distribuzione predittiva a posteriori consente di verificare se il modello è in grado di generare dati simili a quelli osservati.

Nel nostro caso, la proporzione osservata (\(0.7\)) cade vicino al centro della distribuzione predittiva: ciò indica che il modello riproduce bene i dati e può essere utilizzato con fiducia per fare previsioni.

Il fatto che la distribuzione predittiva a posteriori rappresenti accuratamente la proporzione osservata può sembrare ovvio nel caso presente. Questo avviene perché stiamo lavorando con un modello semplice e ben specificato, utilizzato qui con l’intento di chiarire la logica del concetto di distribuzione predittiva a posteriori. Tuttavia, nei modelli più complessi, tipici delle indagini psicologiche, la corrispondenza tra i dati osservati e quelli predetti dal modello non può mai essere data per scontata. È essenziale verificarla attraverso la distribuzione predittiva a posteriori.

Se i dati osservati non sono ben rappresentati dalla distribuzione predittiva a posteriori, ciò indica che il modello non è adeguato a spiegare i dati e necessita di revisione. Questo processo di verifica non solo garantisce la coerenza del modello con i dati disponibili, ma consente anche di identificare eventuali aree problematiche nella specificazione del modello, come prior inappropriati o assunzioni non realistiche. In definitiva, il confronto tra i dati osservati e quelli predetti è un passo fondamentale per la validazione di modelli complessi in contesti psicologici e scientifici.

Riflessioni conclusive

La distribuzione predittiva a posteriori è il fulcro dell’inferenza bayesiana, non solo per la sua capacità di generare previsioni robuste sui dati futuri, ma soprattutto perché integra intrinsecamente l’incertezza sui parametri del modello con la variabilità stocastica del processo. Questa sintesi di incertezze offre un quadro probabilistico completo, superando la mera stima puntuale dei parametri e fornendo una base solida per il confronto diretto tra le aspettative del modello e le evidenze empiriche.

Nel flusso di lavoro bayesiano, la distribuzione predittiva a posteriori si rivela indispensabile per la valutazione del modello. Attraverso i controlli predittivi a posteriori, permette di identificare sistematicamente le discrepanze tra i dati osservati e quelli simulati dal modello. Questi controlli non sono semplici verifiche, ma strumenti diagnostici cruciali: rivelano problemi di specificazione del modello, la non adeguatezza delle distribuzioni a priori scelte e orientano attivamente il processo iterativo di revisione e miglioramento del modello.

Il caso beta-binomiale ha illustrato con chiarezza come un’incertezza sui parametri (rappresentata dalla distribuzione beta) si traduca in previsioni probabilistiche per eventi futuri (i successi binomiali). L’esempio ha evidenziato come le previsioni non richiedano assunzioni restrittive o non realistiche, ma emergano direttamente dalla propagazione dell’incertezza. Questo approccio non solo quantifica rigorosamente l’incertezza, ma facilita anche la comunicazione trasparente e l’interpretabilità delle previsioni.

In sintesi, la distribuzione predittiva a posteriori è l’elemento che salda l’inferenza parametrica all’analisi predittiva empirica nella modellazione bayesiana. Essa garantisce che il processo inferenziale sia non solo più affidabile e interpretabile, ma anche intrinsecamente più applicabile a scenari complessi del mondo reale, fornendo un ponte essenziale tra la teoria del modello e la sua utilità pratica.

Esercizi

Problemi

Consideriamo i dati della SWLS somministrata a un campione di studenti, ottenendo per ciascuno uno score complessivo. Per semplicità, vogliamo “dichiarare positivo” lo studente se il punteggio SWLS supera una determinata soglia (ad esempio, 20 su 35). In questo modo otteniamo una variabile dicotomica (0/1), che useremo come “successo” in un modello binomiale.

Dati e conteggio dei successi
- Carica il dataset con le risposte SWLS.
- Costruisci la variabile binaria (ad esempio SWLS_dich) che vale 1 se lo score ≥ 20, e 0 altrimenti.
- Calcola il numero di successi (numero di persone che superano la soglia) e il numero totale di osservazioni (N).
Modello beta-binomiale (approccio manuale via simulazione)
- Specifica una distribuzione Beta(a, b) come prior per la probabilità di successo \(p\). Scegli una coppia \((a, b)\) relativamente poco informativa, ad esempio (2,2) o (1,1).
- Osservando \(y\) successi su \(n\) soggetti, aggiorna i parametri a posteriori: \[ a_{\text{post}} = a + y, \quad b_{\text{post}} = b + (n - y). \]
- Simula un gran numero di campioni di \(p\) dalla distribuzione Beta\(\bigl(a_{\text{post}},\, b_{\text{post}}\bigr)\).
- Per ciascun campione di \(p\), genera un valore \(\tilde{y}\) da una Binomiale\(\bigl(n_{\text{new}}, p\bigr)\), dove \(n_{\text{new}}\) è la dimensione di un ipotetico nuovo campione (che puoi scegliere, ad esempio, uguale a \(n\) oppure un valore diverso). Otterrai così una posterior predictive distribution per \(\tilde{y}\).
- Infine, calcola statistiche descrittive (media, varianza, intervalli) e/o disegna un istogramma di \(\tilde{y}\) o della proporzione \(\tilde{y}/n_{\text{new}}\).

Replicare con brms

Usa il pacchetto brms per costruire un modello binomiale. Per esempio:

library(brms)

# Crea un data frame con la variabile dicotomica
df_binom <- data.frame(
  successes = y,    # conteggio dei successi
  failures  = n - y
)

# Modello binomiale con prior Beta(a,b) approssimato tramite logit
fit_brms <- brm(
  bf(successes | trials(n) ~ 1), 
  data = df_binom,
  family = binomial(link = "logit"),
  prior = c(
    prior(beta(2, 2), class = "Intercept", dpar = "mu") 
    # NOTA: la specifica di una "beta(2,2)" diretta sull'intercetta
    # è un'approssimazione, tipicamente serve passare a una scala logit.
    # In brms, di solito si usa prior su scale normali dell'intercetta.
  ),
  seed = 123
)

(Le specifiche del prior potrebbero richiedere una formulazione differente se vuoi rispettare esattamente la corrispondenza con Beta(a,b). In ogni caso, l’idea è mostrare come definire un prior e costruire un modello binomiale con brms.)

Verifica la convergenza e poi estrai la posterior predictive distribution con le funzioni di brms:
```
pp_check(fit_brms, nsamples = 100)
```
Questo ti mostrerà come i dati predetti dal modello (in termini di binomiale) si confrontano con i dati osservati.

Confronto e interpretazione
- Metti a confronto i risultati della simulazione “manuale” (Beta-Binomial) e quelli ottenuti con brms. Noterai che le distribuzioni predittive dovrebbero essere coerenti, se hai impostato un prior per brms simile a quello del modello Beta-Binomiale.
- Discuti brevemente se la distribuzione predittiva a posteriori acquisita è plausibile rispetto ai dati osservati. Ad esempio, la probabilità di osservare \(\tilde{y}\) simile a \(y\) dovrebbe essere relativamente alta se il modello è appropriato.
- Se vuoi, puoi cambiare \(n_{\text{new}}\) (es. previsione su 200 soggetti futuri) per vedere come la variabilità della previsione si “ridimensiona” o cresce a seconda della taglia del campione.

Soluzioni

Costruzione del dataset

Se la SWLS varia tra 5 e 35, e la soglia è 20, puoi fare:

df$SWLS_dich <- ifelse(df$SWLS_score >= 20, 1, 0)
y <- sum(df$SWLS_dich)
n <- nrow(df)

Approccio Beta-Binomial manuale

Prior: \((a, b) = (2, 2)\)
Posterior: \((a_{\text{post}}, b_{\text{post}}) = (2 + y,\, 2 + n - y)\).

Generazione dei campioni:

N_sim <- 2000
p_post <- rbeta(N_sim, a_post, b_post)
y_pred <- rbinom(N_sim, size = n_new, prob = p_post)

# Se preferisci la proporzione futura:
prop_pred <- y_pred / n_new

Statistiche:

mean_p <- mean(p_post) # media a posteriori di p
quantile_p <- quantile(p_post, c(0.025, 0.975))  

mean_prop_pred <- mean(prop_pred)
quantile_prop_pred <- quantile(prop_pred, c(0.025, 0.975))

Grafici (istogramma e densità):

hist(prop_pred, freq=FALSE, col='lightblue',
     main='Posterior Predictive Distribution: prop. di successi')

Modello con brms

Usa la sintassi di una binomiale con offset o con trials(n).

Specifica un prior che approssimi Beta(2,2) sullo scale logit, ad esempio:

# Beta(2,2) ha media ~ 0.5, varianza relativamente ampia.
# Approssimandola su scala logit ~ normal(0, 2.2) 
# (valore indicativo: la normal(0, 2) su logit copre un intervallo ampio).

prior_approx <- prior(normal(0, 2), class = "Intercept")

Esegui pp_check(fit_brms) e interpreta.

Interpretazione
- Se la soglia scelta per la SWLS cattura un “buon livello di soddisfazione”, potresti aspettarti una certa % di successi.
- Se i dati futuri simulati sono coerenti con i dati reali — ad esempio, la media di \(\tilde{y}\) è vicina a \(y\) — allora il modello sembra descrivere bene la realtà. Altrimenti, potresti rivedere la soglia o la specifica del prior.

L’elemento chiave è che la distribuzione predittiva a posteriori (posterior predictive distribution) non si limita a considerare un solo valore di \(p\), bensì campiona molteplici valori plausibili (dalla posterior), e per ciascuno simula un potenziale outcome. Così facendo, si riflette pienamente l’incertezza residua sul parametro e l’aleatorietà del processo binomiale.

Informazioni sull’ambiente di sviluppo

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] pillar_1.11.0         tinytable_0.11.0      patchwork_1.3.1      
#>  [4] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.13.0     
#>  [7] ggplot2_3.5.2         reliabilitydiag_0.2.1 priorsense_1.1.0     
#> [10] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [13] StanHeaders_2.32.10   brms_2.22.0           Rcpp_1.1.0           
#> [16] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [19] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [22] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [25] here_1.0.1           
#> 
#> loaded via a namespace (and not attached):
#>  [1] svUnit_1.0.6         tidyselect_1.2.1     farver_2.1.2        
#>  [4] fastmap_1.2.0        TH.data_1.1-3        tensorA_0.36.2.1    
#>  [7] digest_0.6.37        timechange_0.3.0     estimability_1.5.1  
#> [10] lifecycle_1.0.4      survival_3.8-3       magrittr_2.0.3      
#> [13] compiler_4.5.1       rlang_1.1.6          tools_4.5.1         
#> [16] knitr_1.50           bridgesampling_1.1-2 htmlwidgets_1.6.4   
#> [19] curl_6.4.0           pkgbuild_1.4.8       RColorBrewer_1.1-3  
#> [22] abind_1.4-8          multcomp_1.4-28      withr_3.0.2         
#> [25] purrr_1.1.0          grid_4.5.1           stats4_4.5.1        
#> [28] colorspace_2.1-1     xtable_1.8-4         inline_0.3.21       
#> [31] emmeans_1.11.2       scales_1.4.0         MASS_7.3-65         
#> [34] cli_3.6.5            mvtnorm_1.3-3        rmarkdown_2.29      
#> [37] ragg_1.4.0           generics_0.1.4       RcppParallel_5.1.10 
#> [40] cachem_1.1.0         stringr_1.5.1        splines_4.5.1       
#> [43] parallel_4.5.1       vctrs_0.6.5          V8_6.0.5            
#> [46] Matrix_1.7-3         sandwich_3.1-1       jsonlite_2.0.0      
#> [49] arrayhelpers_1.1-0   systemfonts_1.2.3    glue_1.8.0          
#> [52] codetools_0.2-20     distributional_0.5.0 lubridate_1.9.4     
#> [55] stringi_1.8.7        gtable_0.3.6         QuickJSR_1.8.0      
#> [58] htmltools_0.5.8.1    Brobdingnag_1.2-9    R6_2.6.1            
#> [61] textshaping_1.0.1    rprojroot_2.1.0      evaluate_1.0.4      
#> [64] lattice_0.22-7       backports_1.5.0      memoise_2.0.1       
#> [67] broom_1.0.9          snakecase_0.11.1     rstantools_2.4.0    
#> [70] coda_0.19-4.1        gridExtra_2.3        nlme_3.1-168        
#> [73] checkmate_2.3.2      xfun_0.52            zoo_1.8-14          
#> [76] pkgconfig_2.0.3

Bibliografia

Schoot, R. van de, Depaoli, S., King, R., Kramer, B., Märtens, K., Tadesse, M. G., Vannucci, M., Gelman, A., Veen, D., Willemsen, J., et al. (2021). Bayesian statistics and modelling. Nature Reviews Methods Primers, 1(1), 1.