37  Caso continuo

In questo capitolo imparerai a

• estendere i concetti di probabilità congiunta, marginale e condizionale alle variabili continue, utilizzando gli integrali.

Prerequisiti

• Leggere il capitolo Joint Distributions (Chan & Kroese, 2025).
• Leggere il capitolo Joint Distributions (Blitzstein & Hwang, 2019).

Preparazione del Notebook

here::here("code", "_common.R") |>
  source()

pacman::p_load(MASS, viridis, ggExtra)

37.1 Introduzione

Immaginate di voler studiare la relazione tra due caratteristiche psicologiche, ad esempio:

• livello di ansia (da 20 a 80 punti su una scala analogica visiva);
• prestazione cognitiva (da 0 a 100 punti su un test di memoria in cui sono possibili punteggi frazionari).

Queste variabili sono chiamate continue perché possono assumere qualsiasi valore all’interno di certi intervalli, e non solo valori specifici come accade con le variabili discrete (es. numero di risposte corrette a un quiz).

Quando consideriamo contemporaneamente due variabili continue, parliamo di densità di probabilità congiunta. Questa ci permette di visualizzare e analizzare come le due variabili tendono a manifestarsi insieme.

37.2 La Densità Congiunta Continua come una Mappa Termica

Per capire meglio, immaginate la densità congiunta come una mappa termica (heatplot) in cui:

• l’asse orizzontale (asse X) rappresenta il livello di ansia (0-100);
• l’asse verticale (asse Y) rappresenta la prestazione cognitiva (0-100);
• le zone più calde indicano combinazioni più frequenti e dunque più probabili.

# Parametri
mu <- c(30, 70)
sigma_x <- 10
sigma_y <- 15
rho <- -0.7

# Matrice di covarianza
Sigma <- matrix(
  c(
    sigma_x^2, rho * sigma_x * sigma_y,
    rho * sigma_x * sigma_y, sigma_y^2
  ),
  nrow = 2
)

# Generiamo 500 osservazioni casuali
set.seed(123)
dati <- as.data.frame(mvrnorm(500, mu, Sigma))
colnames(dati) <- c("Ansia", "Prestazione")

# Grafico con mappa termica della densità congiunta e punti
grafico <- ggplot(
  dati, aes(x = Ansia, y = Prestazione)
) +
  stat_density_2d(
    aes(fill = ..density..),
    geom = "raster", contour = FALSE
  ) +
  scale_fill_viridis(option = "viridis") +
  geom_density_2d(
    color = "black", linewidth = 0.5, linetype = "dotted"
  ) +
  geom_point(alpha = 0.3, size = 0.8) +
  labs(
    title = "Mappa termica\ndella densità congiunta",
    x = "Punteggio Ansia",
    y = "Punteggio Prestazione Cognitiva"
  )

# Aggiungere grafici marginali delle densità
grafico_finale <- ggMarginal(
  grafico,
  type = "density",
  fill = "lightblue", color = "black"
)

# Visualizza il grafico
grafico_finale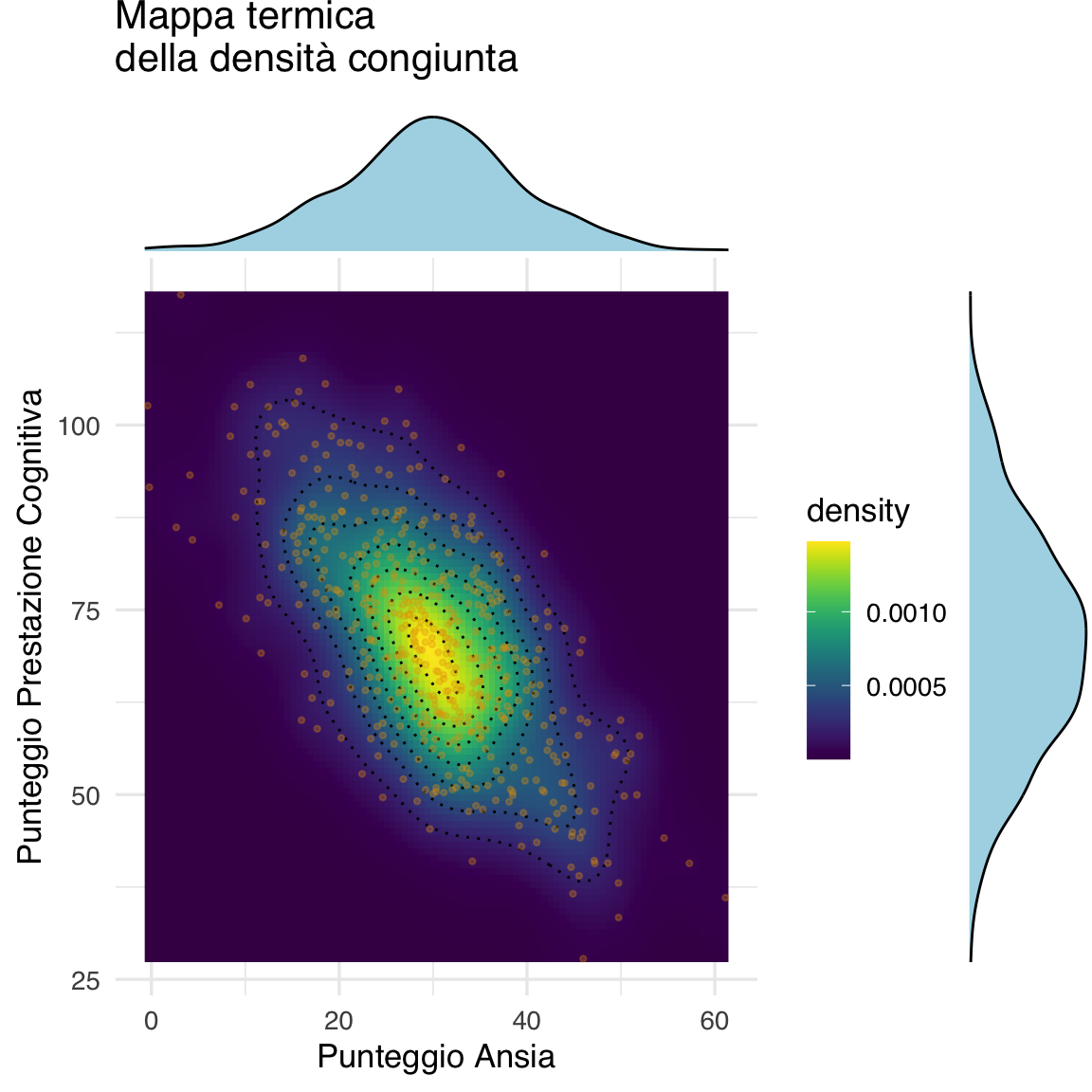

Sulla mappa termica la zona più calda è intorno a “ansia = 30” e “prestazione = 70”. Questo significa che la maggior parte dei soggetti mostra un livello di ansia relativamente bassa e tende a mostrare una prestazione cognitiva relativamente alta. Tuttavia, all’aumentare dell’ansia, la prestazione cognitiva tende a diminuire (Eysenck et al., 2007).

37.3 Come Interpretare la Probabilità?

Quando lavoriamo con variabili continue, non possiamo semplicemente contare le combinazioni come nel caso discreto (ad esempio, lanci di un dado). Invece, misuriamo la probabilità calcolando l’area della regione interessata sulla nostra mappa termica:

• la probabilità che l’ansia sia tra 50 e 55, e la prestazione tra 30 e 50, è rappresentata dall’area della regione corrispondente nella mappa termica;
• gli integrali (strumenti matematici per calcolare aree) sono semplicemente un modo preciso per fare questa operazione.

37.4 Densità Marginale: Proiettare la Mappa su un Asse

La densità marginale descrive come si distribuisce una singola variabile, prescindendo completamente dall’altra. Possiamo immaginare questo processo come la proiezione della mappa termica su uno degli assi, ottenendo così un’ombra o una proiezione dell’intera distribuzione:

• proiettando tutti i valori sull’asse dell’ansia, si ottiene la densità marginale dell’ansia;
• proiettando tutti i valori sull’asse della prestazione, si ottiene la densità marginale della prestazione.

Queste proiezioni rivelano la distribuzione di ciascuna variabile considerata isolatamente. Nella figura a cui si fa riferimento, le distribuzioni marginali sono state elaborate utilizzando in modo indipendente i dati relativi a ciascuna variabile, senza considerare le loro interrelazioni.

Infatti, i colori più caldi nella mappa termica indicano zone con maggiore densità di osservazioni. Quando proiettiamo questi valori su un asse, otteniamo una curva di densità che rappresenta la distribuzione della variabile. Le aree dove la curva raggiunge valori più alti corrispondono ai valori più frequenti della variabile nella popolazione studiata.

37.5 Densità Condizionale: Fette della Mappa Termica

La densità condizionale risponde alla domanda: “Se osservo persone con un determinato punteggio di prestazione cognitiva (ad esempio 40 punti), qual è la distribuzione dell’ansia tra queste persone?”

• Immaginate di prendere una fetta verticale della mappa termica in corrispondenza della prestazione = 40 punti. Questa fetta mostra la distribuzione dell’ansia soltanto tra coloro che hanno esattamente quella prestazione cognitiva.
• Per rendere questa distribuzione coerente, normalizziamo (cioè “aggiustiamo”) la fetta rispetto alla probabilità complessiva della prestazione a quel livello.

Questa fetta verticale con i suoi vari colori (più caldi dove c’è maggiore densità) può essere convertita in una curva di densità che mostra come si distribuisce l’ansia specificamente per le persone con quel determinato livello di prestazione cognitiva. Il processo di normalizzazione assicura che l’area sotto questa curva di densità condizionale sia uguale a 1, consentendo confronti tra diverse condizioni.

37.6 Perché Tutto Questo è Importante?

La densità congiunta ci permette di identificare relazioni complesse e non lineari tra variabili psicologiche che potrebbero rimanere nascoste con analisi più semplici. Nel nostro esempio:

• potremmo scoprire varie tipologie di relazioni tra ansia e prestazione cognitiva:

  • una relazione negativa lineare (maggiore ansia associata a minore prestazione cognitiva);
  • relazioni curvilinee (come la relazione a U rovesciata della legge di Yerkes-Dodson);
  • pattern bimodali dove l’ansia elevata si associa sia a prestazioni molto basse che molto alte, suggerendo l’esistenza di diversi sottogruppi nella popolazione studiata;
  • cluster o addensamenti che indicano tipologie specifiche di individui con particolari combinazioni di ansia e prestazione;

• analizzare solo le densità marginali (cioè ciascuna variabile separatamente) ci farebbe perdere queste informazioni cruciali sulle interrelazioni tra le variabili, portando potenzialmente a conclusioni incomplete o fuorvianti;

• le densità condizionali ci permettono di esaminare come una variabile si comporta in presenza di specifici valori dell’altra, rivelando dipendenze contestuali che arricchiscono la nostra comprensione dei fenomeni psicologici.

37.7 Riflessioni Conclusive

I concetti di densità congiunta, marginale e condizionale ci permettono di esplorare con chiarezza e precisione come variabili psicologiche continue interagiscono fra loro. Comprendere queste densità ci aiuta a individuare relazioni complesse, come quelle che spesso emergono nello studio di fenomeni psicologici reali. Sebbene il passaggio dalle variabili discrete a quelle continue richieda strumenti matematici diversi (integrali anziché somme), l’intuizione e il significato concettuale di queste misure rimangono invariati. In questo modo, la logica che avete imparato nel caso discreto vi sarà sempre utile anche per affrontare fenomeni continui, più realistici e comuni in psicologia.

37.8 Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.3.2
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] ggExtra_0.10.1    viridis_0.6.5     viridisLite_0.4.2 MASS_7.3-65      
#>  [5] thematic_0.1.6    MetBrewer_0.2.0   ggokabeito_0.1.0  see_0.11.0       
#>  [9] gridExtra_2.3     patchwork_1.3.0   bayesplot_1.11.1  psych_2.5.3      
#> [13] scales_1.3.0      markdown_2.0      knitr_1.50        lubridate_1.9.4  
#> [17] forcats_1.0.0     stringr_1.5.1     dplyr_1.1.4       purrr_1.0.4      
#> [21] readr_2.1.5       tidyr_1.3.1       tibble_3.2.1      ggplot2_3.5.1    
#> [25] tidyverse_2.0.0   rio_1.2.3         here_1.0.1       
#> 
#> loaded via a namespace (and not attached):
#>  [1] gtable_0.3.6      xfun_0.51         htmlwidgets_1.6.4 lattice_0.22-6   
#>  [5] tzdb_0.5.0        vctrs_0.6.5       tools_4.4.2       generics_0.1.3   
#>  [9] parallel_4.4.2    pacman_0.5.1      pkgconfig_2.0.3   lifecycle_1.0.4  
#> [13] compiler_4.4.2    farver_2.1.2      munsell_0.5.1     mnormt_2.1.1     
#> [17] httpuv_1.6.15     htmltools_0.5.8.1 pillar_1.10.1     later_1.4.1      
#> [21] mime_0.13         nlme_3.1-167      tidyselect_1.2.1  digest_0.6.37    
#> [25] stringi_1.8.4     labeling_0.4.3    rprojroot_2.0.4   fastmap_1.2.0    
#> [29] grid_4.4.2        colorspace_2.1-1  cli_3.6.4         magrittr_2.0.3   
#> [33] withr_3.0.2       promises_1.3.2    timechange_0.3.0  rmarkdown_2.29   
#> [37] hms_1.1.3         shiny_1.10.0      evaluate_1.0.3    miniUI_0.1.1.1   
#> [41] rlang_1.1.5       isoband_0.2.7     Rcpp_1.0.14       xtable_1.8-4     
#> [45] glue_1.8.0        rstudioapi_0.17.1 jsonlite_1.9.1    R6_2.6.1

Bibliografia

Blitzstein, J. K., & Hwang, J. (2019). Introduction to probability. CRC Press.

Chan, J. C. C., & Kroese, D. P. (2025). Statistical Modeling and Computation (2ª ed.). Springer.

Eysenck, M. W., Derakshan, N., Santos, R., & Calvo, M. G. (2007). Anxiety and cognitive performance: attentional control theory. Emotion, 7(2), 336–353.