82  Errori di segno e errori di grandezza

In questo capitolo imparerai a
  • Relazione tra crisi della replicabilità e approccio frequentista.
  • Limiti della significatività statistica.
  • Errori di grandezza e errori di segno.
  • Utilizzo dell’approccio bayesiano per ottenere stime più precise e affidabili.
Prerequisiti
  • Leggere Horoscopes. Alla luce degli approfondimenti forniti in questo corso, questo capitolo di McElreath (2020) dovrebbe assumere un significato diverso rispetto a quando è stato letto all’inizio del corso.
Preparazione del Notebook 
here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(tidyr)

82.1 Introduzione

In questo capitolo analizzeremo la relazione tra la crisi della replicabilità e le procedure decisionali statistiche proprie dell’approccio frequentista. In particolare, approfondiremo gli errori di tipo M (magnitude) e di tipo S (sign), discussi da Loken & Gelman (2017), e il loro impatto sulla validità dei risultati scientifici.

Domande Iniziali

Prima di esplorare le simulazioni e i risultati discussi in questo capitolo, prova a riflettere sulle seguenti domande. Ti invitiamo a formulare delle ipotesi sui risultati delle simulazioni prima di leggere le spiegazioni:

  1. Se si effettuano molteplici studi su un effetto molto piccolo utilizzando campioni di dimensioni ridotte, cosa pensi che accadrà ai risultati pubblicati che ottengono significatività statistica? Saranno accurati rispetto alla vera grandezza dell’effetto?
  2. In uno scenario in cui non esiste alcuna differenza tra due gruppi, quanto spesso credi che un test t fornisca un risultato statisticamente significativo che verrà pubblicato? Quali fattori potrebbero influenzare questa probabilità?
  3. Supponiamo che in una serie di esperimenti alcuni studi trovino effetti significativi e altri no. Quale pensi sia la tendenza degli studi pubblicati rispetto a quelli non pubblicati? Quale impatto può avere questa tendenza sulla percezione della realtà scientifica?
  4. Se dovessi valutare la replicabilità di uno studio basato sulla significatività statistica, quali problemi potresti incontrare se l’effetto sottostante è molto piccolo?

Tieni a mente le tue risposte mentre esplori le simulazioni presentate in questo capitolo. Alla fine del capitolo, confronteremo le previsioni con i risultati effettivi.

82.2 Il Filtro della Significatività Statistica

Nel ?sec-crisis abbiamo esplorato come la pratica scientifica contemporanea sia spesso compromessa da casi di frode, principalmente a causa delle significative implicazioni economiche legate alla pubblicazione su riviste scientifiche di alto prestigio. Questo fenomeno è spesso sottovalutato, poiché le riviste tendono a essere riluttanti nel riconoscere la necessità di correzioni o ritrattazioni degli articoli già pubblicati.

La frode scientifica rappresenta una minaccia evidente alla riproducibilità dei risultati, un pilastro fondamentale del metodo scientifico. Tuttavia, le difficoltà nel replicare i risultati pubblicati non sono attribuibili esclusivamente a frodi o a “pratiche di ricerca disoneste” (Nelson et al., 2018). Un problema intrinseco risiede nel metodo statistico ampiamente adottato dai ricercatori: l’approccio del test di ipotesi nulla e della significatività statistica di stampo fisheriano. Secondo questo metodo, i risultati che non raggiungono la soglia di “significatività statistica” vengono scartati, mentre quelli che la superano sono considerati credibili, basandosi esclusivamente su questo criterio (Wagenmakers et al., 2008).

Tuttavia, l’idea che la significatività statistica sia un filtro affidabile per distinguere i risultati di ricerca “validi” da quelli “non validi” è fondamentalmente errata. Numerose evidenze dimostrano i limiti di questo approccio. Per approfondire questa problematica, esamineremo lo studio di Loken & Gelman (2017), che mette in luce la relazione tra la crisi della replicabilità e le procedure decisionali statistiche dell’approccio frequentista.

Uno dei principali problemi evidenziati da Loken & Gelman (2017) è che, in contesti di ricerca complessi, la significatività statistica fornisce prove molto deboli riguardo al segno (sign) o all’entità (magnitude) degli effetti sottostanti. In altre parole, il raggiungimento della significatività statistica non garantisce né la rilevanza né la consistenza dei risultati ottenuti. Questo solleva seri dubbi sull’affidabilità di tale criterio come unico strumento per valutare la validità delle scoperte scientifiche.

82.3 Errori di tipo M e S

Per illustrare le implicazioni del processo decisionale basato sulla significatività statistica, Loken & Gelman (2017) hanno condotto una simulazione. In questa simulazione, hanno considerato uno scenario di ricerca ipotetico in cui era presente un effetto reale, sebbene molto debole, difficilmente rilevabile senza un ampio volume di dati. Utilizzando l’approccio frequentista, hanno cercato di identificare questo effetto valutando la significatività statistica.

I risultati della simulazione hanno mostrato che, anche in presenza di un effetto reale (seppur debole), l’approccio frequentista riusciva a rilevare un effetto statisticamente significativo solo in una piccola percentuale dei casi. Inoltre, quando un effetto significativo veniva individuato, la stima della sua grandezza risultava altamente imprecisa e instabile.

In sintesi, la significatività statistica fornisce un’indicazione generica sulla presenza o assenza di un effetto, ma non offre informazioni affidabili sulla sua entità o replicabilità. Questo problema è particolarmente rilevante in campi come la psicologia e le scienze sociali, dove gli studi spesso si basano su campioni di dimensioni ridotte e gli effetti osservati tendono a essere modesti. In tali contesti, l’approccio frequentista rischia di produrre prove deboli e instabili, compromettendo la replicabilità e l’affidabilità dei risultati.

82.3.1 Simulazione semplificata

Riproduciamo qui, in forma semplificata, la simulazione condotta da Loken & Gelman (2017). Iniziamo importando le librerie necessarie.

Consideriamo due campioni casuali indipendenti di dimensioni \(n_1 = 20\) e \(n_2 = 25\), estratti rispettivamente dalle distribuzioni normali \(\mathcal{N}(102, 10)\) e \(\mathcal{N}(100, 10)\). La dimensione effettiva dell’effetto (\(d\)) per la differenza tra le medie dei due campioni è calcolata utilizzando la formula:

\[ d = \frac{\bar{y}_1 - \bar{y}_2}{s_p}, \]

dove \(\bar{y}_1\) e \(\bar{y}_2\) rappresentano le medie campionarie dei due gruppi, e \(s_p\) è la deviazione standard combinata, definita come:

\[ s_p = \sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}}. \]

In questo caso specifico, la dimensione effettiva dell’effetto risulta molto piccola, indicando che la differenza osservata tra le medie dei due gruppi non ha una rilevanza pratica significativa. Ciò suggerisce che la distinzione tra i due gruppi, seppur statisticamente rilevabile, non ha un impatto sostanziale in contesti reali.

# Parametri
mu_1 <- 102  # Media del primo gruppo
mu_2 <- 100  # Media del secondo gruppo
sigma <- 10  # Deviazione standard comune
n1 <- 20     # Numero di osservazioni nel primo gruppo
n2 <- 25     # Numero di osservazioni nel secondo gruppo

# Calcolo della differenza media
mean_difference <- abs(mu_1 - mu_2)

# Calcolo della deviazione standard pooled
pooled_sd <- sqrt(((n1 - 1) * sigma^2 + (n2 - 1) * sigma^2) / (n1 + n2 - 2))

# Calcolo di Cohen's d
cohen_d <- mean_difference / pooled_sd

# Output del risultato
cat("Dimensione dell'effetto (Cohen's d):", cohen_d, "\n")
#> Dimensione dell'effetto (Cohen's d): 0.2

Esaminiamo ora le conclusioni che emergerebbero applicando l’approccio frequentista e la sua procedura di decisione statistica in questo contesto. Supponiamo di condurre una simulazione in cui vengono estratti due campioni: il primo composto da 20 osservazioni provenienti dalla prima popolazione e il secondo da 25 osservazioni provenienti dalla seconda popolazione. Successivamente, applichiamo il test \(t\) di Student per confrontare le medie dei due gruppi.

Nell’ambito dell’approccio frequentista, il valore-\(p\) ottenuto dal test determina la decisione statistica. Se il valore-\(p\) è superiore a 0.05, i risultati vengono considerati non significativi e, di conseguenza, scartati. Al contrario, se il valore-\(p\) è inferiore a 0.05, il risultato è ritenuto “pubblicabile” e si conclude che esiste una differenza statisticamente significativa tra i due gruppi.

Per valutare in modo approfondito le conclusioni derivate da questa procedura, è necessario ripetere l’intero processo per un numero elevato di iterazioni, ad esempio 50.000 volte. Ciò significa che, in ciascuna iterazione, vengono estratti nuovi campioni, viene calcolato il test \(t\) di Student e viene determinato il corrispondente valore-\(p\). Ripetendo questo processo su larga scala, è possibile ottenere una distribuzione completa dei risultati, che consente di analizzare la frequenza con cui si ottengono risultati significativi e la stabilità delle stime prodotte dall’approccio frequentista in questo contesto.

# Parametri
n_samples <- 50000
mu_1 <- 102
mu_2 <- 100
sigma <- 10
n1 <- 20
n2 <- 25

# Inizializzazione del risultato
res <- c()

# Simulazioni
set.seed(123)  # Per la riproducibilità
for (i in 1:n_samples) {
  # Generazione dei campioni casuali
  y1 <- rnorm(n1, mean = mu_1, sd = sigma)
  y2 <- rnorm(n2, mean = mu_2, sd = sigma)
  
  # Calcolo della dimensione dell'effetto
  y1bar <- mean(y1)
  y2bar <- mean(y2)
  v1 <- var(y1)
  v2 <- var(y2)
  s <- sqrt(((n1 - 1) * v1 + (n2 - 1) * v2) / (n1 + n2 - 2))
  efsize <- (y1bar - y2bar) / s
  
  # Calcolo del valore p
  t_test <- t.test(y1, y2, var.equal = TRUE)
  
  # Salvataggio della dimensione dell'effetto solo per risultati "statisticamente significativi"
  if (t_test$p.value < 0.05) {
    res <- c(res, efsize)
  }
}
res_df <- data.frame(effect_size = res)

ggplot(res_df, aes(x = effect_size)) +
  geom_histogram(bins = 20, fill = "blue", color = "black", alpha = 0.7) +
  geom_vline(
    xintercept = 0.2, color = "red", linetype = "dashed", 
    size = 1.2, label = "True Effect Size") +
  labs(
    x = "Effect Size",
    y = "Frequency",
    title = "Histogram of Effect Sizes for\n'Statistically Significant' Results"
  )

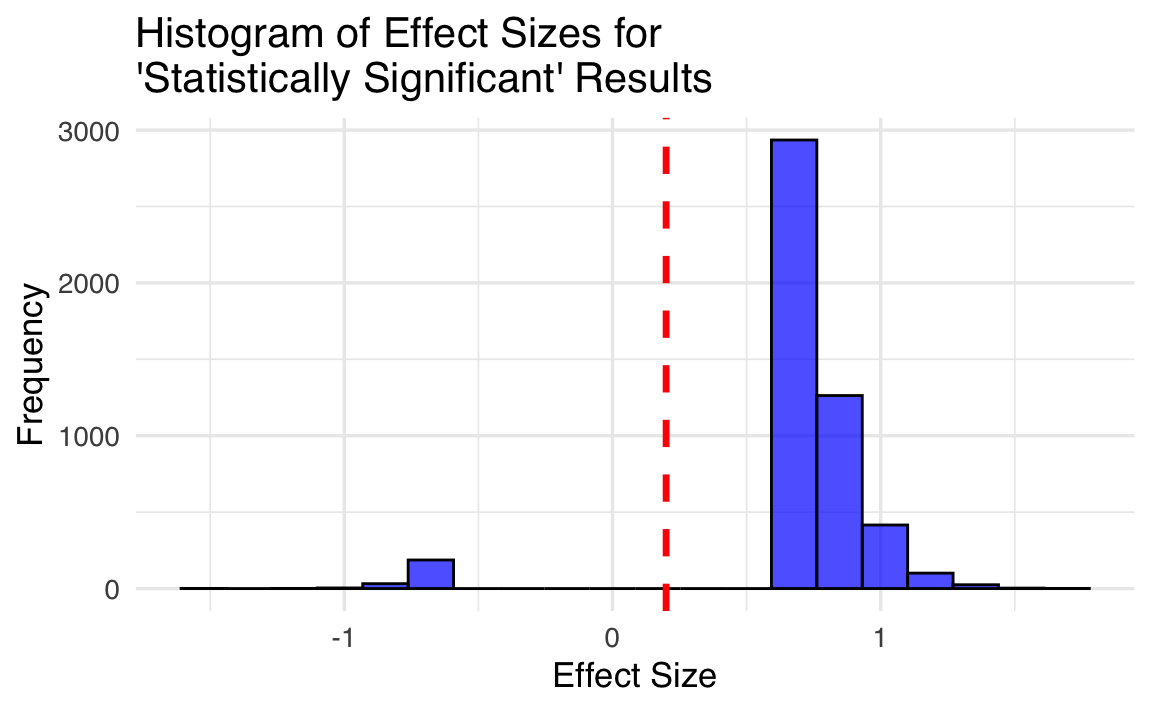
Come evidenziato da Loken & Gelman (2017), l’applicazione dell’approccio frequentista nella procedura di decisione statistica può condurre a due tipi di errori rilevanti. Il primo, noto come errore di magnitude (grandezza), si manifesta quando i risultati pubblicati tendono a sovrastimare la reale entità dell’effetto. Nella simulazione condotta, nonostante la vera grandezza dell’effetto fosse modesta (0.2), la media della grandezza dell’effetto per i risultati classificati come “statisticamente significativi” era circa 0.8, suggerendo un effetto di entità “ampia”. Questo indica una distorsione sistematica verso stime esagerate.

Il secondo errore, chiamato errore di segno, si verifica quando, a causa della variabilità campionaria, la direzione dell’effetto viene stimata in modo errato. In tali casi, il ricercatore potrebbe erroneamente concludere che \(\mu_2 > \mu_1\), quando in realtà non è così. È importante sottolineare che, anche in queste situazioni, la grandezza assoluta dell’effetto risulta sovrastimata.

Un aspetto degno di nota è che queste conclusioni rimarrebbero valide anche se si considerasse l’intervallo di confidenza per la differenza tra le medie. In sintesi, l’approccio frequentista introduce un errore sistematico nella stima della grandezza dell’effetto, che rappresenta la quantità più rilevante per il ricercatore. In alcuni casi, può persino portare a errori nella determinazione della direzione dell’effetto, compromettendo ulteriormente l’affidabilità delle conclusioni scientifiche.

82.4 Riflessioni Conclusive

In conclusione, l’approccio frequentista non rappresenta un metodo affidabile per valutare i risultati della ricerca e determinarne l’attendibilità o la necessità di scartarli (Gelman & Carlin, 2014; Loken & Gelman, 2017). Questa mancanza di affidabilità è dovuta all’introduzione di errori sistematici nella stima della grandezza degli effetti, che in alcuni casi possono persino portare a errori nella direzione dell’effetto stesso. Alla luce di queste criticità, non sembrano esserci motivi validi per continuare a fare affidamento su questo approccio.

Al contrario, l’adozione dell’approccio bayesiano sembra offrire una soluzione più precisa e affidabile per l’analisi dei dati di ricerca. Questo metodo valuta la probabilità delle ipotesi alla luce dei dati osservati, evitando gli errori intrinseci dell’approccio frequentista e fornendo una base più solida per prendere decisioni informate sulla validità dei risultati. In questo modo, l’approccio bayesiano si presenta come un’alternativa più robusta e scientificamente rigorosa.

Ora confrontiamo le previsioni con i risultati ottenuti dalle simulazioni:

  1. Sovrastima della grandezza dell’effetto: I risultati pubblicati tendono a essere selezionati sulla base della significatività statistica, il che porta a una sovrastima sistematica della grandezza dell’effetto rispetto alla realtà. Questo fenomeno, noto come errore di tipo M (magnitude), si verifica perché solo gli effetti con valori estremi (per caso) superano la soglia di significatività statistica e vengono pubblicati.

  2. Falsi positivi e loro frequenza: In uno scenario in cui non esiste alcuna differenza tra i due gruppi (cioè la vera differenza è zero), il test t ha fornito risultati statisticamente significativi nel 5% dei casi, come previsto dalla soglia di α = 0.05. Tuttavia, la selezione dei risultati pubblicati amplifica questo problema, rendendo più probabile che i lettori incontrino falsi positivi nella letteratura scientifica.

  3. Bias nella pubblicazione: Gli studi che riportano risultati significativi hanno maggiore probabilità di essere pubblicati rispetto a quelli che non trovano un effetto significativo. Questo porta a un effetto distorsivo nella letteratura scientifica, in cui i risultati pubblicati tendono a sovrastimare l’effetto reale. Il “filtro della significatività statistica” crea una percezione distorta della realtà scientifica, poiché gli effetti nulli o piccoli tendono a essere sottorappresentati nella letteratura.

  4. Replicabilità e significatività statistica: Gli studi con effetti piccoli e campioni ridotti sono particolarmente vulnerabili al fallimento della replicazione. Anche quando un effetto reale esiste, la probabilità di ottenerne una stima precisa è bassa, e la replicazione potrebbe risultare in un valore non significativo, generando confusione nella comunità scientifica.

Considerazioni Finali

Le simulazioni evidenziano come la significatività statistica, utilizzata come criterio per la pubblicazione, contribuisca a un bias nella selezione dei risultati, distorcendo la percezione della realtà scientifica. Questo fenomeno, noto come “filtro della significatività statistica”, è una delle cause principali della crisi della replicabilità, poiché induce i ricercatori e i lettori a sovrastimare la grandezza e la presenza di effetti studiati.

Per affrontare queste problematiche, approcci alternativi, come quelli bayesiani, possono offrire soluzioni più robuste, permettendo una valutazione più affidabile delle ipotesi alla luce dei dati osservati.

Esercizi

  1. Perché la significatività statistica non è un criterio affidabile per valutare la validità dei risultati scientifici?
  2. Spiega il concetto di “filtro della significatività statistica” e il suo impatto sulla pubblicazione dei risultati.
  3. Qual è la differenza tra errore di tipo M e errore di tipo S? Come influenzano l’interpretazione dei risultati?
  4. Perché i risultati pubblicati tendono a sovrastimare la grandezza dell’effetto rispetto alla realtà?
  5. Quali sono le conseguenze della pubblicazione selettiva dei risultati per la replicabilità degli studi?
  6. Perché gli studi con campioni di piccole dimensioni sono più vulnerabili a errori nella stima della grandezza dell’effetto?
  7. In che modo la selezione dei risultati pubblicati altera la percezione della forza degli effetti studiati?
  8. Perché un test frequentista può portare a una falsa conclusione sulla direzione di un effetto?
  9. Quali sono le principali differenze tra l’approccio frequentista e quello bayesiano nella valutazione della significatività di un effetto?
  10. In che modo l’approccio bayesiano può ridurre il rischio di errori dovuti alla selezione dei risultati basata sulla significatività statistica?

  1. La significatività statistica non garantisce la validità di un risultato perché dipende dalla dimensione del campione e da soglie arbitrarie (come p < 0.05). Inoltre, non misura la rilevanza pratica di un effetto, ma solo la probabilità che i dati osservati siano ottenuti sotto l’ipotesi nulla.

  2. Il “filtro della significatività statistica” si riferisce alla tendenza a pubblicare solo risultati con p < 0.05, tralasciando studi con risultati non significativi. Questo porta a una distorsione nella letteratura scientifica e a una sovrastima della forza degli effetti riportati.

  3. Errore di tipo M (Magnitude) indica la sovrastima della grandezza dell’effetto nei risultati pubblicati, mentre errore di tipo S (Sign) si riferisce all’errata determinazione della direzione dell’effetto. Questi errori si verificano perché solo gli effetti più estremi tendono a superare il filtro della significatività statistica.

  4. I risultati pubblicati tendono a sovrastimare la grandezza dell’effetto perché solo gli effetti più grandi (anche per pura casualità) superano la soglia di significatività statistica e vengono pubblicati, mentre quelli più piccoli restano inediti.

  5. La pubblicazione selettiva riduce la replicabilità perché introduce una distorsione sistematica nei risultati disponibili. Le repliche spesso non trovano effetti altrettanto grandi o significativi, creando instabilità nella conoscenza scientifica.

  6. I campioni piccoli aumentano la variabilità delle stime dell’effetto, rendendo più probabile che un risultato significativo sia solo un’oscillazione casuale dei dati piuttosto che un vero effetto replicabile.

  7. La selezione dei risultati pubblicati altera la percezione della forza degli effetti perché induce i lettori a credere che gli effetti siano più forti e consistenti di quanto non siano realmente.

  8. Un test frequentista può portare a una falsa conclusione sulla direzione dell’effetto perché, in campioni piccoli, le stime dell’effetto possono essere fortemente influenzate dal rumore, portando a interpretazioni errate.

  9. L’approccio frequentista si basa sul valore-p e sulla soglia di significatività, mentre l’approccio bayesiano utilizza la probabilità a posteriori per aggiornare la credibilità delle ipotesi alla luce dei dati osservati. Il metodo bayesiano permette inferenze più flessibili e robuste.

  10. L’approccio bayesiano riduce il rischio di errori dovuti alla selezione dei risultati perché non si basa su una soglia arbitraria di significatività, ma fornisce un quadro probabilistico della forza dell’effetto, evitando distorsioni dovute alla pubblicazione selettiva.

In questo esercizio simuleremo più esperimenti, ognuno con 15 osservazioni, per comprendere come il filtro della significatività statistica possa distorcere le nostre conclusioni sugli effetti osservati.

Obiettivo

  • Comprendere come l’approccio frequentista possa portare a stime errate dell’effetto reale.
  • Esplorare gli errori di tipo M (magnitude) e S (sign), derivanti dal filtro della significatività statistica.

Struttura dell’esercizio

  1. Simuliamo esperimenti in cui il vero effetto tra due gruppi è piccolo (Cohen’s d = 0.2). Consideriamo i dati SWLS e due popolazioni che differiscono nel modo indicato. Ipotizziamo che le due popolazioni SWLS siano normali.
  2. Estraiamo 15 osservazioni per gruppo.
  3. Usiamo un test t per verificare se la differenza tra i gruppi è significativa.
  4. Registriamo solo i risultati con p < 0.05, calcolando la distribuzione degli effetti significativi.
  5. Valutiamo se la stima dell’effetto nei risultati pubblicabili è gonfiata rispetto al vero effetto.
  6. Contiamo i casi in cui il segno dell’effetto è invertito.
# Librerie necessarie
library(ggplot2)

# Impostazioni della simulazione
set.seed(42)         # Per la riproducibilità
n_sims <- 50000      # Numero di simulazioni
n_per_group <- 15    # Numero di osservazioni per gruppo
true_d <- 0.2        # Vero effetto (Cohen's d)
swls_mean <- 25      # Media ipotizzata per il primo gruppo
swls_sd <- 5         # Deviazione standard ipotizzata per la SWLS

# Calcolo della media del secondo gruppo sulla base di Cohen's d
swls_mean_2 <- swls_mean + true_d * swls_sd

# Inizializziamo i vettori per registrare i risultati
effect_sizes <- c()
false_sign_count <- 0

# Simulazioni
for (i in 1:n_sims) {
  # Generazione dei due gruppi da distribuzioni normali
  group1 <- rnorm(n_per_group, mean = swls_mean, sd = swls_sd)
  group2 <- rnorm(n_per_group, mean = swls_mean_2, sd = swls_sd)
  
  # Calcolo della dimensione dell'effetto (Cohen's d)
  mean_diff <- mean(group2) - mean(group1)
  pooled_sd <- sqrt(((n_per_group - 1) * var(group1) + (n_per_group - 1) * var(group2)) / (2 * n_per_group - 2))
  d_estimated <- mean_diff / pooled_sd
  
  # Test t per confrontare le medie
  t_test <- t.test(group1, group2, var.equal = TRUE)
  
  # Consideriamo solo i risultati statisticamente significativi
  if (t_test$p.value < 0.05) {
    effect_sizes <- c(effect_sizes, d_estimated)
    
    # Conta i casi in cui il segno è invertito
    if (d_estimated < 0) {
      false_sign_count <- false_sign_count + 1
    }
  }
}

# Creazione di un dataframe per la visualizzazione
res_df <- data.frame(effect_size = effect_sizes)

# Istogramma della dimensione dell'effetto tra i risultati "significativi"
ggplot(res_df, aes(x = effect_size)) +
  geom_histogram(bins = 30, fill = "blue", color = "black", alpha = 0.7) +
  geom_vline(xintercept = true_d, color = "red", linetype = "dashed", size = 1.2) +
  labs(
    x = "Dimensione dell'effetto stimata",
    y = "Frequenza",
    title = "Distribuzione degli effetti significativi (SWLS)"
  ) +
  theme_minimal()

# Output di sintesi
cat("Numero di risultati statisticamente significativi:", length(effect_sizes), "\n")
cat("Media della dimensione dell'effetto tra i risultati pubblicati:", mean(effect_sizes), "\n")
cat("Numero di risultati con segno invertito:", false_sign_count, "\n")
cat("Proporzione di risultati con segno invertito:", false_sign_count / length(effect_sizes), "\n")

Interpretazione dei Risultati

  1. Errore di tipo M (Magnitude): La media degli effetti stimati nei risultati pubblicati sarà molto più grande di 0.2 (il vero effetto), dimostrando come il filtro della significatività tenda a sovrastimare gli effetti reali.
  2. Errore di tipo S (Sign): Una percentuale dei risultati pubblicabili mostrerà effetti nella direzione sbagliata (d < 0), dimostrando che il processo decisionale basato su p < 0.05 può portare a conclusioni errate.
  3. Visualizzazione: L’istogramma mostrerà che la distribuzione degli effetti significativi è spostata rispetto al vero effetto (linea rossa tratteggiata).

Domande di discussione:

  1. Perché la stima dell’effetto è gonfiata nei risultati pubblicabili?
  2. Come cambia la situazione aumentando il numero di osservazioni per gruppo?
  3. Quali strategie alternative potrebbero ridurre questi errori?

Approfondimento:

  • Ripetere l’esperimento con n_per_group = 50 e osservare se l’errore di tipo M diminuisce.
  • Confrontare questo approccio con un’analisi Bayesiana per evidenziare il ruolo dell’inferenza basata su probabilità posteriori.

Conclusione

Questo esercizio mostra chiaramente i problemi dell’approccio frequentista basato su p < 0.05, evidenziando i limiti dell’uso della significatività statistica come filtro decisionale.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] thematic_0.1.6   MetBrewer_0.2.0  ggokabeito_0.1.0 see_0.11.0      
#>  [5] gridExtra_2.3    patchwork_1.3.0  bayesplot_1.12.0 psych_2.5.3     
#>  [9] scales_1.4.0     markdown_2.0     knitr_1.50       lubridate_1.9.4 
#> [13] forcats_1.0.0    stringr_1.5.1    dplyr_1.1.4      purrr_1.0.4     
#> [17] readr_2.1.5      tidyr_1.3.1      tibble_3.2.1     ggplot2_3.5.2   
#> [21] tidyverse_2.0.0  rio_1.2.3        here_1.0.1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] generics_0.1.4     stringi_1.8.7      lattice_0.22-7    
#>  [4] hms_1.1.3          digest_0.6.37      magrittr_2.0.3    
#>  [7] evaluate_1.0.3     grid_4.5.0         timechange_0.3.0  
#> [10] RColorBrewer_1.1-3 fastmap_1.2.0      rprojroot_2.0.4   
#> [13] jsonlite_2.0.0     mnormt_2.1.1       cli_3.6.5         
#> [16] rlang_1.1.6        withr_3.0.2        yaml_2.3.10       
#> [19] tools_4.5.0        parallel_4.5.0     tzdb_0.5.0        
#> [22] pacman_0.5.1       vctrs_0.6.5        R6_2.6.1          
#> [25] lifecycle_1.0.4    htmlwidgets_1.6.4  pkgconfig_2.0.3   
#> [28] pillar_1.10.2      gtable_0.3.6       glue_1.8.0        
#> [31] xfun_0.52          tidyselect_1.2.1   rstudioapi_0.17.1 
#> [34] farver_2.1.2       htmltools_0.5.8.1  nlme_3.1-168      
#> [37] labeling_0.4.3     rmarkdown_2.29     compiler_4.5.0

Bibliografia

Gelman, A., & Carlin, J. (2014). Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors. Perspectives on Psychological Science, 9(6), 641–651.
Loken, E., & Gelman, A. (2017). Measurement Error and the Replication Crisis. Science, 355(6325), 584–585.
McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2nd Edition). CRC Press.
Nelson, L. D., Simmons, J., & Simonsohn, U. (2018). Psychology’s renaissance. Annual review of psychology, 69(1), 511–534.
Wagenmakers, E.-J., Lee, M., Lodewyckx, T., & Iverson, G. J. (2008). Bayesian versus frequentist inference. Bayesian evaluation of informative hypotheses, 181–207.