67  Pianificazione della dimensione campionaria

In questo capitolo imparerai a
  • progettare e implementare simulazioni bayesiane per la determinazione della dimensione campionaria.
Prerequisiti
  • Consultare Regression and Other Stories (Gelman et al., 2021).
  • Prestare particolare attenzione al capitolo 16, “Design and sample size decisions”, che offrono una guida dettagliata al tema del potere statistico frequentista che spesso genera aspettative irrealistiche sulla rilevabilità degli effetti e conduce alla progettazione di studi con elevata variabilità e scarso valore informativo.
Preparazione del Notebook 
here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(mice, brms, cmdstanr)

67.1 Introduzione

Nel contesto bayesiano, l’obiettivo principale non è verificare un’ipotesi nulla, ma stimare con quanta incertezza possiamo affermare che un effetto ha una certa ampiezza pratica. Questo approccio è particolarmente rilevante in psicologia, dove l’importanza di un risultato raramente si esaurisce nella sua “significatività statistica”.

Tuttavia, nella pratica scientifica è ancora diffuso l’uso della potenza frequentista. Per completezza, in questo capitolo presentiamo sia la formula classica per la potenza in un confronto tra due medie, sia una sua controparte bayesiana basata su simulazione. Il nostro scopo è mostrare come un approccio bayesiano orientato alla stima e alla simulazione possa offrire strumenti più flessibili, informativi e utili alla pianificazione degli studi.

67.2 L’approccio frequentista

Nel framework frequentista, la potenza è definita come la probabilità, calcolata prima che uno studio venga condotto, che un determinato test statistico produca un p-value inferiore a una soglia prestabilita (tipicamente 0,05), dato un effetto reale ipotizzato.

Il calcolo della potenza richiede:

  • una stima della dimensione dell’effetto atteso,
  • una stima della variabilità nei dati (deviazione standard),
  • una decisione sulla soglia di significatività,
  • e infine un calcolo (o simulazione) della probabilità che il p-value sia < 0.05.

Si sconsiglia in genere di condurre studi con potenza bassa, perché hanno una bassa probabilità di produrre risultati “significativi”. Tuttavia, questo ragionamento non considera che il concetto stesso di significatività può essere fuorviante: anche quando un test ha potenza dell’80%, ciò non garantisce che l’effetto stimato sia preciso o utile.

67.2.1 La maledizione del vincitore

Uno studio con bassa potenza può produrre risultati statisticamente significativi che sono ingannevoli. In presenza di molto rumore, gli effetti significativi osservati tendono a essere:

  • esagerati (errore di tipo \(M\), magnitude),
  • sbagliati nel segno (errore di tipo \(S\), sign).

In altre parole, anche quando uno studio riesce a “scoprire” un effetto, la stima ottenuta può essere gravemente distorta. Questa è una delle ragioni principali per cui molti risultati pubblicati si rivelano non replicabili (Gelman & Carlin, 2014).

67.3 Un esempio concreto

Per rendere il confronto più chiaro, usiamo un esempio con gli stessi dati in entrambi gli approcci:

  • differenza vera tra le medie: \(\Delta = 5\);
  • deviazione standard comune: \(\sigma = 10\);
  • dimensione del campione: \(n = 64\) per gruppo;
  • effetto standardizzato: Cohen’s d = 0.5

67.4 Analisi frequentista: dimensione del campione per potenza dell’80%

Per stimare la dimensione del campione necessaria a ottenere una potenza dell’80% in un confronto tra due gruppi indipendenti (con varianza uguale), possiamo usare la funzione power.t.test() disponibile in R.

Nel nostro esempio ipotizziamo:

  • una differenza attesa tra i gruppi pari a \(\Delta = 5\),
  • una deviazione standard comune pari a \(\sigma = 10\),
  • un test bilaterale con livello di significatività \(\alpha = 0.05\).

67.4.1 Calcolo in R

# Calcolo della dimensione campionaria necessaria per 80% di potenza
power.t.test(
  delta = 5,        # differenza attesa tra le medie
  sd    = 10,       # deviazione standard
  power = 0.8,      # potenza desiderata
  sig.level = 0.05, # livello di significatività
  type = "two.sample",
  alternative = "two.sided"
)
#> 
#>      Two-sample t test power calculation 
#> 
#>               n = 63.77
#>           delta = 5
#>              sd = 10
#>       sig.level = 0.05
#>           power = 0.8
#>     alternative = two.sided
#> 
#> NOTE: n is number in *each* group

Il risultato indica che sono necessari circa 64 partecipanti per gruppo per ottenere l’80% di potenza con questi parametri. Tuttavia, come vedremo nella sezione successiva, questo valore non garantisce necessariamente che la stima dell’effetto sarà sufficientemente precisa o utile dal punto di vista decisionale. L’analisi bayesiana ci offrirà uno strumento più flessibile per valutare l’informatività del disegno proposto.

67.5 Analisi bayesiana: informatività a posteriori

Nell’approccio bayesiano, non ci si chiede se l’effetto è “significativo” rispetto a una soglia arbitraria, ma quanto è informativo il risultato per prendere decisioni pratiche. In questo contesto, pianificare uno studio significa domandarsi:

“Con quanti dati il mio modello bayesiano riuscirà a fornire una stima sufficientemente precisa e utile dell’effetto?”

Per rispondere, possiamo stabilire dei criteri di informatività che riflettano le esigenze del nostro problema. Due criteri possibili sono:

  1. l’intervallo di credibilità all’89% per Cohen’s d ha larghezza ≤ 0.4 (criterio di precisione);
  2. la probabilità a posteriori che d > 0.3 è ≥ 90% (criterio di utilità pratica).

67.5.1 Simulazione generativa di uno studio

Per verificare se un disegno sperimentale con \(n = 64\) per gruppo soddisfa questi criteri, possiamo simulare uno studio 100 volte, ogni volta:

  • generando nuovi dati,
  • stimando un modello bayesiano,
  • valutando se il risultato è sufficientemente informativo.

Di seguito definiamo la funzione sim_once() che esegue una singola simulazione.

# Funzione per standardizzare su scala z
standardise <- function(x) (x - mean(x)) / sd(x)

# Una singola simulazione bayesiana di uno studio
sim_once <- function(n = 64, mu0 = 100, delta = 5, sigma = 10) {

  # 1. Generazione dei dati
  y0 <- rnorm(n, mu0, sigma)         # gruppo controllo
  y1 <- rnorm(n, mu0 + delta, sigma) # gruppo trattamento

  # 2. Standardizzazione
  dat <- tibble(score = standardise(c(y0, y1)),
                group = factor(rep(c("ctrl", "trt"), each = n)))

  # 3. Stima del modello bayesiano
  fit <- brm(score ~ group,
             data = dat,
             backend = "cmdstanr",
             chains = 2, iter = 1000, warmup = 500,
             refresh = 0, silent = 0,
             prior = c(
               prior(normal(0, 2), class = "b"),
               prior(exponential(2), class = "sigma")
             ))

  # 4. Estrazione dei campioni posteriori e calcolo di Cohen's d
  post <- as_draws_df(fit)
  d_smp <- post$b_grouptrt / post$sigma

  # 5. Output: due indici di informatività
  tibble(
    CIw89  = diff(quantile(d_smp, c(.055, .945))),  # larghezza IC 89%
    p_gt03 = mean(d_smp > 0.3)                      # P(d > 0.3)
  )
}

Ecco cosa succede passo passo:

  1. Simulazione dei dati
  y0 <- rnorm(n, mu0, sigma)
  y1 <- rnorm(n, mu0 + delta, sigma)

  • Si generano due gruppi di n = 64 osservazioni:

    • Il gruppo di controllo ha media mu0 = 100.
    • Il gruppo trattamento ha media aumentata di delta = 5.
    • Entrambi i gruppi hanno la stessa variabilità (sigma = 10).

  • In pratica: simula un esperimento in cui il trattamento ha un effetto medio di 5 unità.

  1. Standardizzazione dei dati
  score = standardise(c(y0, y1))

  • Le osservazioni dei due gruppi vengono unite e standardizzate (portate su scala z): media = 0, deviazione standard = 1.

  • Questo serve a:

    • rendere i dati comparabili tra simulazioni,
    • semplificare l’interpretazione dei risultati (si lavora su scala standardizzata).
  1. Creazione del dataset
  dat <- tibble(score = ..., group = ...)

  • Si crea una tabella con le variabili:

    • score: i dati standardizzati
    • group: un’etichetta che indica se il dato appartiene al gruppo controllo (ctrl) o trattamento (trt).
  1. Stima del modello bayesiano
  fit <- brm(score ~ group, ...)

  • Si stima un modello bayesiano con brms, dove:

    • la variabile score è prevista dalla variabile group,
    • si usano priori debolmente informativi su effetto (b) e variabilità (sigma).

  • Il coefficiente b_grouptrt stima la differenza media tra i gruppi (sulla scala standardizzata).

  1. Estrazione dei campioni posteriori
  post <- as_draws_df(fit)
  d_smp <- post$b_grouptrt / post$sigma
  • Si estraggono i campioni dalla distribuzione a posteriori.
  • Si calcola Cohen’s d a posteriori dividendo l’effetto stimato per la deviazione standard stimata: d_smp.
  1. Output: due indicatori di informatività
  tibble(
    CIw89  = diff(quantile(d_smp, c(.055, .945))),
    p_gt03 = mean(d_smp > 0.3)
  )
  • CIw89: larghezza dell’intervallo di credibilità all’89% → misura di precisione.
  • p_gt03: proporzione dei campioni a posteriori in cui d > 0.3 → misura di utilità pratica.

In sintesi, ogni volta che chiami sim_once():

  • simuli un nuovo dataset realistico;
  • stimi l’effetto del trattamento con un modello bayesiano;
  • misuri quanto è preciso e informativo il risultato.

Questa funzione è il mattone fondamentale per la simulazione generativa di uno studio: ti permette di verificare, ad esempio, se con n = 64 per gruppo riesci a stimare d in modo sufficientemente utile.

67.5.2 Esecuzione della simulazione

Simuliamo 100 studi indipendenti con n = 64 per gruppo:

set.seed(123)
res <- bind_rows(replicate(100, sim_once(), simplify = FALSE))

Esaminiamo i risultati della simulazione:

resum <- summarise(res,
  mean_CI   = mean(CIw89),
  sd_CI     = sd(CIw89),
  prop_good = mean(p_gt03 >= 0.9)
)
print(resum)
#> # A tibble: 1 × 3
#>   mean_CI  sd_CI prop_good
#>     <dbl>  <dbl>     <dbl>
#> 1   0.569 0.0206      0.35

67.5.3 Visualizzazione dei risultati

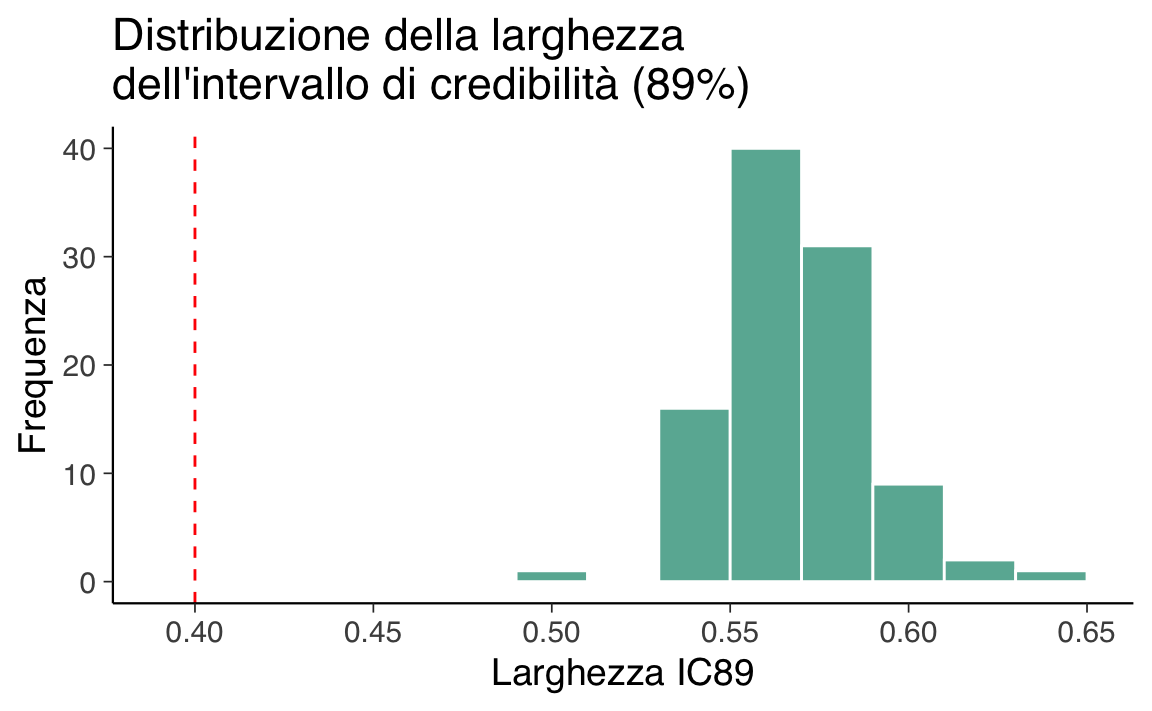
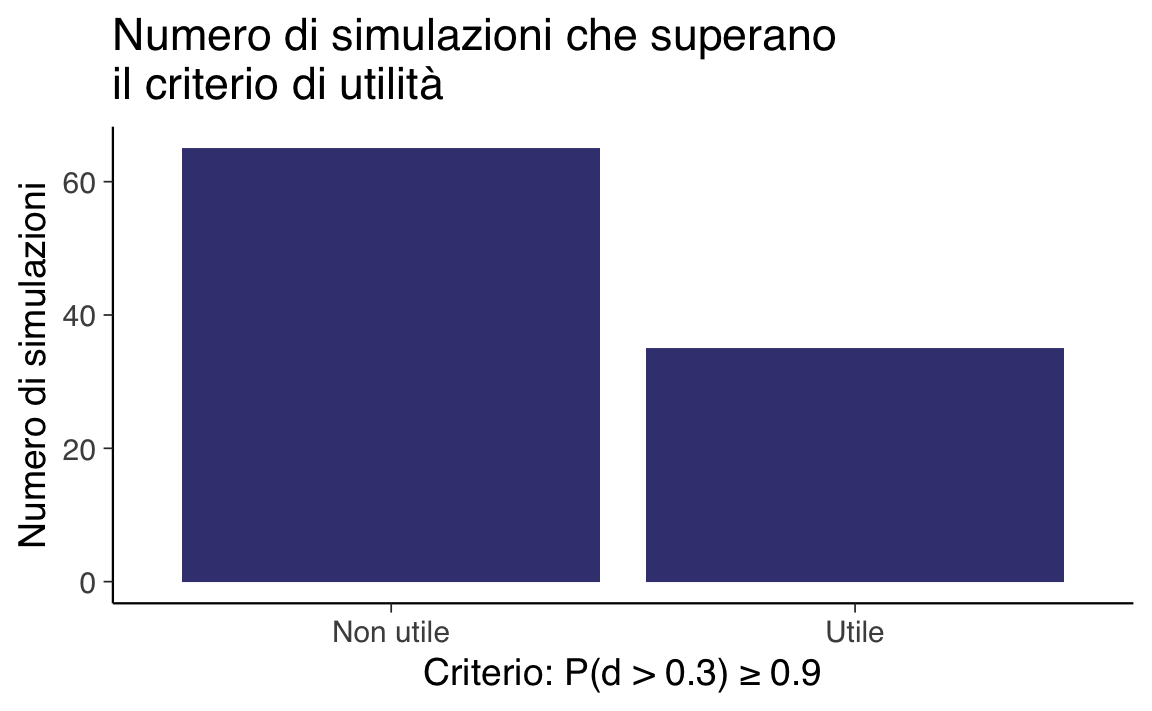
Il primo grafico mostra la distribuzione delle larghezze degli intervalli di credibilità all’89%, evidenziando quante simulazioni superano la soglia di 0.4. Il secondo mostra quante simulazioni soddisfano il criterio di utilità.

# Grafico 1: distribuzione della larghezza IC89
ggplot(res, aes(x = CIw89)) +
  geom_histogram(binwidth = 0.02, fill = "#69b3a2", color = "white") +
  geom_vline(xintercept = 0.4, linetype = "dashed", color = "red") +
  labs(
    title = "Distribuzione della larghezza\ndell'intervallo di credibilità (89%)",
    x = "Larghezza IC89",
    y = "Frequenza"
  ) 

# Grafico 2: classificazione delle simulazioni utili/non utili
ggplot(res, aes(x = p_gt03 >= 0.9)) +
  geom_bar(fill = "#404080") +
  scale_x_discrete(labels = c("FALSE" = "Non utile", "TRUE" = "Utile")) +
  labs(
    title = "Numero di simulazioni che superano\nil criterio di utilità",
    x = "Criterio: P(d > 0.3) ≥ 0.9",
    y = "Numero di simulazioni"
  )

67.5.4 Interpretazione dei risultati

  • mean_CI rappresenta la larghezza media dell’intervallo di credibilità all’89%. Nel nostro caso è circa 0.569, quindi troppo ampio per considerare la stima precisa.
  • prop_good è la proporzione di simulazioni in cui l’evidenza a favore di un effetto pratico d > 0.3 supera il 90%. Con prop_good = 0.1, solo 1 simulazione su 10 soddisfa questo criterio.

Conclusione: con n = 64 per gruppo, lo studio simulato è sottodimensionato: raramente produce una stima precisa e utile. Serve un campione più grande (es. n = 80 o n = 100) per raggiungere criteri più severi di informatività.

67.5.5 Confronto con la potenza frequentista

Secondo l’approccio frequentista, n = 64 per gruppo garantisce circa 80% di potenza per d = 0.5. Ma la simulazione bayesiana mostra che:

  • l’intervallo di credibilità risulta troppo ampio (≈ 0.57);
  • l’evidenza utile (P(d > 0.3) ≥ 0.9) si verifica solo nel 10% dei casi.

Questo evidenzia i limiti della potenza come unico criterio per pianificare gli studi. Anche uno studio “con potenza adeguata” potrebbe produrre risultati imprecisi o non praticabili, e contribuire agli errori di tipo M (esagerazione della stima) o S (errore nel segno dell’effetto).

In sintesi, pianificare uno studio non significa garantire il p < .05, ma garantire che la stima sia abbastanza precisa e utile per informare decisioni.

67.6 Riflessioni Conclusive

  • L’approccio bayesiano consente di valutare in modo più trasparente quanto i risultati previsti saranno precisi e utili.
  • Anche se un disegno ha potenza dell’80%, potrebbe non produrre stime sufficientemente informative.
  • La simulazione bayesiana è uno strumento efficace per esplorare scenari realistici prima di raccogliere dati.

Buona pratica: non fermarti al calcolo della potenza. Definisci criteri di utilità, simula gli studi e verifica se i dati attesi permetteranno davvero di rispondere alla tua domanda.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] cmdstanr_0.9.0   brms_2.22.0      Rcpp_1.0.14      mice_3.17.0     
#>  [5] thematic_0.1.6   MetBrewer_0.2.0  ggokabeito_0.1.0 see_0.11.0      
#>  [9] gridExtra_2.3    patchwork_1.3.0  bayesplot_1.12.0 psych_2.5.3     
#> [13] scales_1.4.0     markdown_2.0     knitr_1.50       lubridate_1.9.4 
#> [17] forcats_1.0.0    stringr_1.5.1    dplyr_1.1.4      purrr_1.0.4     
#> [21] readr_2.1.5      tidyr_1.3.1      tibble_3.2.1     ggplot2_3.5.2   
#> [25] tidyverse_2.0.0  rio_1.2.3        here_1.0.1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] Rdpack_2.6.4         mnormt_2.1.1         inline_0.3.21       
#>  [4] rlang_1.1.6          magrittr_2.0.3       matrixStats_1.5.0   
#>  [7] compiler_4.5.0       loo_2.8.0            vctrs_0.6.5         
#> [10] pkgconfig_2.0.3      shape_1.4.6.1        fastmap_1.2.0       
#> [13] backports_1.5.0      labeling_0.4.3       rmarkdown_2.29      
#> [16] tzdb_0.5.0           ps_1.9.1             nloptr_2.2.1        
#> [19] xfun_0.52            glmnet_4.1-8         jomo_2.7-6          
#> [22] jsonlite_2.0.0       pan_1.9              broom_1.0.8         
#> [25] parallel_4.5.0       R6_2.6.1             StanHeaders_2.32.10 
#> [28] stringi_1.8.7        RColorBrewer_1.1-3   boot_1.3-31         
#> [31] rpart_4.1.24         estimability_1.5.1   rstan_2.32.7        
#> [34] iterators_1.0.14     pacman_0.5.1         Matrix_1.7-3        
#> [37] splines_4.5.0        nnet_7.3-20          timechange_0.3.0    
#> [40] tidyselect_1.2.1     rstudioapi_0.17.1    abind_1.4-8         
#> [43] yaml_2.3.10          codetools_0.2-20     curl_6.2.2          
#> [46] processx_3.8.6       pkgbuild_1.4.7       lattice_0.22-7      
#> [49] withr_3.0.2          bridgesampling_1.1-2 posterior_1.6.1     
#> [52] coda_0.19-4.1        evaluate_1.0.3       survival_3.8-3      
#> [55] RcppParallel_5.1.10  pillar_1.10.2        tensorA_0.36.2.1    
#> [58] stats4_4.5.0         checkmate_2.3.2      foreach_1.5.2       
#> [61] reformulas_0.4.1     distributional_0.5.0 generics_0.1.4      
#> [64] rprojroot_2.0.4      hms_1.1.3            rstantools_2.4.0    
#> [67] minqa_1.2.8          xtable_1.8-4         glue_1.8.0          
#> [70] emmeans_1.11.1       tools_4.5.0          data.table_1.17.2   
#> [73] lme4_1.1-37          mvtnorm_1.3-3        grid_4.5.0          
#> [76] QuickJSR_1.7.0       rbibutils_2.3        colorspace_2.1-1    
#> [79] nlme_3.1-168         cli_3.6.5            Brobdingnag_1.2-9   
#> [82] V8_6.0.3             gtable_0.3.6         digest_0.6.37       
#> [85] htmlwidgets_1.6.4    farver_2.1.2         htmltools_0.5.8.1   
#> [88] lifecycle_1.0.4      mitml_0.4-5          MASS_7.3-65

Bibliografia

Gelman, A., & Carlin, J. (2014). Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors. Perspectives on Psychological Science, 9(6), 641–651.
Gelman, A., Hill, J., & Vehtari, A. (2021). Regression and other stories. Cambridge University Press.