72  Stime, stimatori e parametri

In questo capitolo imparerai a
  • Comprendere il concetto di distribuzione campionaria.
  • Familiarizzare con le proprietà della distribuzione campionaria della media dei campioni.
  • Comprendere il teorema del limite centrale.
  • Acquisire conoscenze sulle proprietà della distribuzione campionaria della varianza.
Prerequisiti
Preparazione del Notebook 
here::here("code", "_common.R") |> 
  source()

72.1 Introduzione

In questo capitolo, ci concentreremo sul concetto di distribuzione campionaria, uno dei pilastri dell’inferenza statistica frequentista. La distribuzione campionaria descrive come le stime dei parametri della popolazione, come la media o la varianza, variano da campione a campione. Essa permette di stabilire proprietà probabilistiche delle stime campionarie, come la loro media e varianza, che sono fondamentali per costruire intervalli di confidenza e condurre test di ipotesi, strumenti essenziali dell’inferenza statistica frequentista.

Domande introduttive

Prima di iniziare a esplorare il concetto di distribuzione campionaria e il suo ruolo nell’inferenza statistica, considera le seguenti domande. Prova a formulare una risposta intuitiva basata sulle tue conoscenze attuali prima di procedere con la lettura del capitolo. Le simulazioni che seguiranno ti aiuteranno a confermare o rivedere le tue risposte.

  1. Se estraiamo ripetutamente campioni casuali dalla stessa popolazione e calcoliamo la loro media, come saranno distribuite queste medie campionarie rispetto alla media della popolazione?

  2. Supponiamo di estrarre campioni di dimensione \(n=2\) da una popolazione. L’insieme delle medie campionarie sarà più concentrato intorno alla media della popolazione rispetto ai valori individuali della popolazione stessa?

  3. Quale relazione esiste tra la dimensione del campione \(n\) e la variabilità delle medie campionarie? In altre parole, se aumentiamo la dimensione del campione, cosa succede alla dispersione della distribuzione campionaria?

  4. La distribuzione campionaria della media campionaria sarà sempre normale? Quali fattori influenzano la sua forma?

  5. La media della distribuzione campionaria coincide sempre con la media della popolazione? E la sua varianza è maggiore o minore rispetto alla varianza della popolazione?

  6. Supponiamo di estrarre piccoli campioni da una popolazione che ha una distribuzione fortemente asimmetrica. Quale forma avrà la distribuzione delle medie campionarie per piccoli campioni? E per campioni più grandi?

72.2 Stime, stimatori e parametri

Dopo aver esplorato il contesto culturale del frequentismo nel capitolo precedente, ci spostiamo ora su un piano strettamente statistico per introdurre il concetto di stima statistica.

Quando si analizzano i dati, l’obiettivo è spesso quello di ottenere informazioni su una caratteristica della popolazione. Tuttavia, nella maggior parte dei casi, si ha accesso solo a un campione di osservazioni. La quantità sconosciuta che vogliamo stimare viene chiamata parametro, mentre il valore che calcoliamo dal campione per approssimare questo parametro è la stima. La formula o il procedimento matematico che utilizziamo per ottenere la stima è detto stimatore. Formalmente, uno stimatore è una funzione dei dati osservati utilizzata per produrre una stima di un parametro.

In altre parole, quando analizziamo un campione, cerchiamo di inferire proprietà della popolazione da cui il campione è tratto. Il parametro rappresenta una misura di queste proprietà, ma raramente può essere calcolato direttamente sulla popolazione intera. Pertanto, utilizziamo le osservazioni campionarie per ottenere una stima del parametro. La stima è quindi un’approssimazione del valore del parametro basata sui dati raccolti, mentre lo stimatore è la regola matematica o statistica che la produce.

È importante sottolineare che le stime non coincidono necessariamente con il vero valore del parametro, poiché sono soggette a incertezza dovuta alla variabilità del campionamento. In questo capitolo esamineremo come l’approccio frequentista quantifica questa incertezza e come possiamo utilizzare tale quantificazione per trarre conclusioni affidabili sui parametri di interesse.

72.3 Distribuzione campionaria

Nell’inferenza frequentista applicata alla psicologia, il parametro di maggiore interesse è spesso la media della popolazione—si veda anche la discussione nella Sezione 19.9.1. In questo capitolo esploreremo come la media di un campione casuale possa essere utilizzata per stimare la media \(\mu\) di una popolazione. Per valutare l’incertezza associata a questa stima, introdurremo il concetto di distribuzione campionaria, un principio fondamentale dell’approccio frequentista.

Per chiarire questa idea, inizieremo con un esempio basato su una popolazione finita di piccole dimensioni, pur consapevoli che le proprietà illustrate si estendono anche a popolazioni di dimensioni maggiori.

72.3.1 Esempio introduttivo

Consideriamo la seguente popolazione:

x <- c(2, 4.5, 5, 5.5)
x
#> [1] 2.0 4.5 5.0 5.5

Questi valori potrebbero rappresentare il tempo di reazione (in secondi) di quattro partecipanti a un esperimento di decisione rapida, in cui devono identificare il colore di uno stimolo visivo. In questo caso, l’intera popolazione è costituita da tutti i partecipanti disponibili per lo studio, ad esempio se l’esperimento è stato condotto in un piccolo gruppo di persone selezionate per caratteristiche specifiche, come quattro gemelli monozigoti in uno studio sulle differenze cognitive intra-familiari.

L’istogramma sottostante rappresenta la distribuzione di frequenza della popolazione:

# Creazione del dataframe
df <- data.frame(Valori = c(2, 4.5, 5, 5.5))

# Istogramma con ggplot2
ggplot(df, aes(x = Valori)) +
  geom_histogram(bins = 5, aes(y = after_stat(density)), fill = "lightblue", color = "black") +
  labs(title = "Distribuzione della popolazione", x = "Valori", y = "Densità")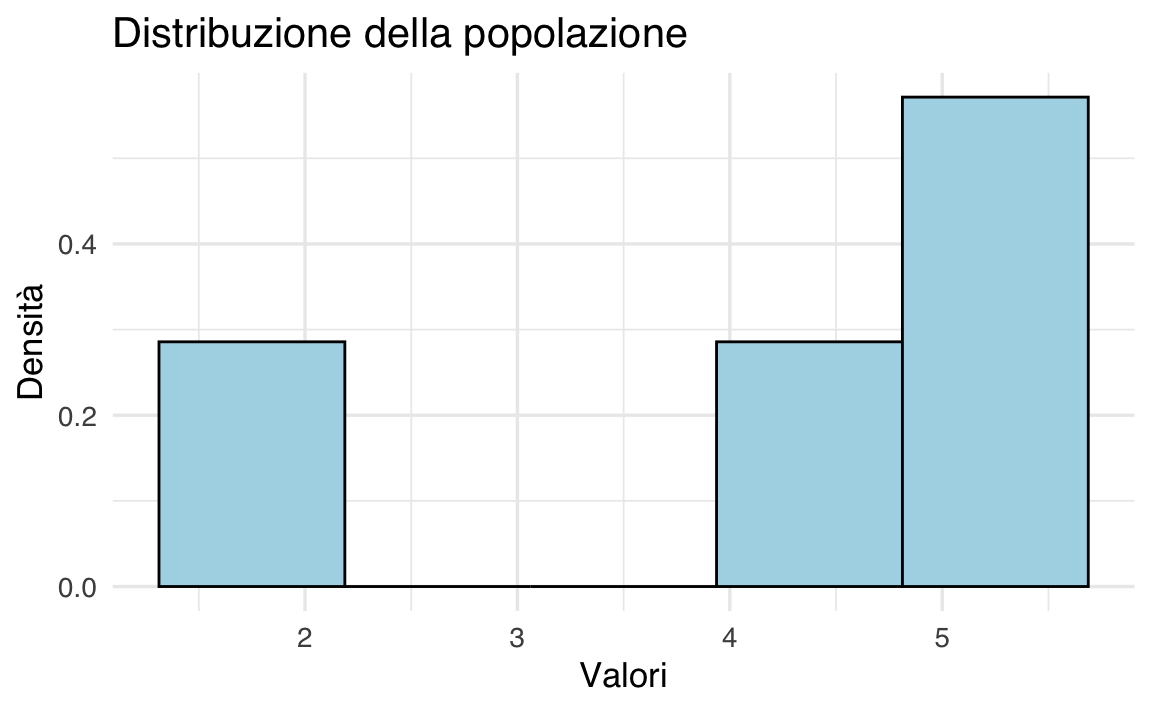

Calcoliamo la media e la varianza della popolazione:

mean(x)  # Media
#> [1] 4.25
var(x)   # Varianza
#> [1] 2.417

72.3.2 Campionamento

Consideriamo ora tutti i possibili campioni di dimensione \(n = 2\) che possiamo estrarre dalla popolazione. Poiché ogni valore può essere selezionato indipendentemente in entrambe le posizioni del campione, il numero totale di combinazioni possibili si ottiene con il calcolo combinatorio:

\[ \text{Numero totale di campioni} = k^n , \]

dove \(k\) è la dimensione della popolazione e \(n\) è la dimensione del campione. Nel nostro caso, con \(k = 4\) e \(n = 2\), otteniamo:

\[ 4^2 = 16 . \]

Possiamo generare esplicitamente queste combinazioni con il seguente codice:

samples <- expand.grid(x, x)
samples
#>    Var1 Var2
#> 1   2.0  2.0
#> 2   4.5  2.0
#> 3   5.0  2.0
#> 4   5.5  2.0
#> 5   2.0  4.5
#> 6   4.5  4.5
#> 7   5.0  4.5
#> 8   5.5  4.5
#> 9   2.0  5.0
#> 10  4.5  5.0
#> 11  5.0  5.0
#> 12  5.5  5.0
#> 13  2.0  5.5
#> 14  4.5  5.5
#> 15  5.0  5.5
#> 16  5.5  5.5

Ogni riga rappresenta un campione possibile. Confermiamo il numero totale di campioni con:

nrow(samples)
#> [1] 16

Ora calcoliamo la media di ciascun campione, ottenendo la distribuzione campionaria delle medie per \(n = 2\):

sample_means <- rowMeans(samples)
sample_means
#>  [1] 2.00 3.25 3.50 3.75 3.25 4.50 4.75 5.00 3.50 4.75 5.00 5.25 3.75 5.00
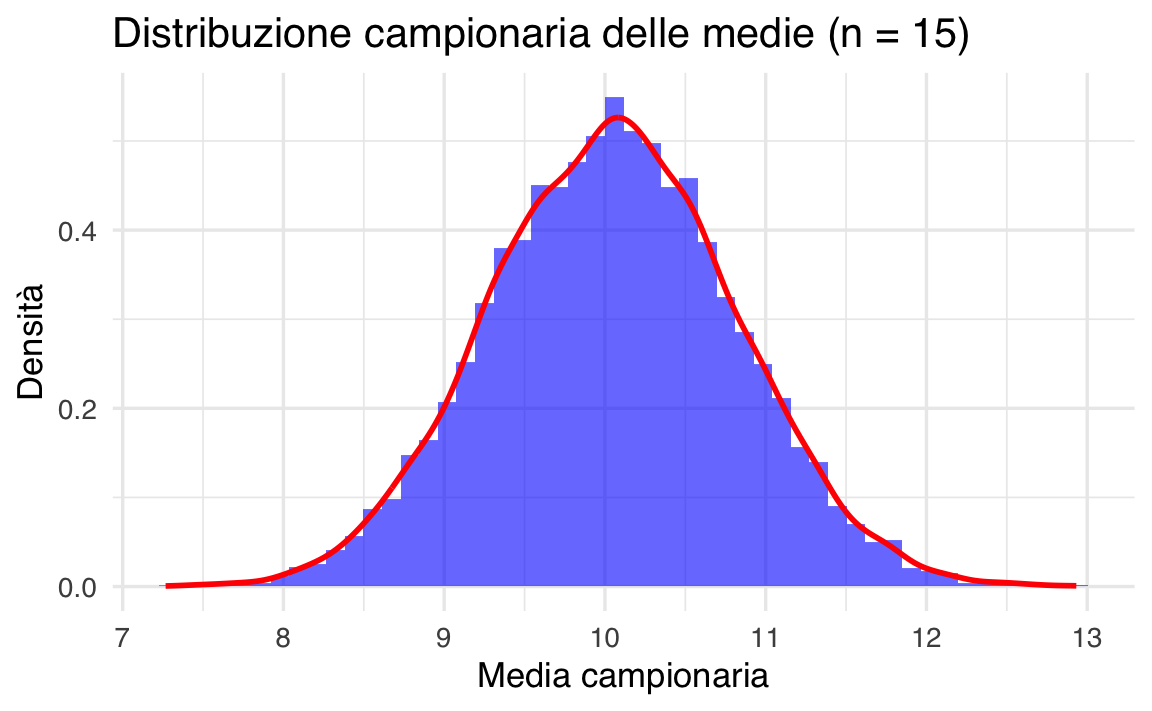
#> [15] 5.25 5.50

Questa distribuzione campionaria mostra tutte le possibili medie che possiamo ottenere estraendo campioni casuali di dimensione 2 dalla popolazione. Si tratta di un concetto fondamentale in inferenza statistica frequentista, poiché la distribuzione delle medie campionarie diventa progressivamente più simmetrica e concentrata attorno alla media della popolazione man mano che \(n\) aumenta, come previsto dal teorema del limite centrale.

72.3.3 Visualizzazione della distribuzione campionaria

Possiamo visualizzare la distribuzione campionaria delle medie con un istogramma:

# Creazione del dataframe
df <- data.frame(Valori = sample_means)

# Istogramma con ggplot2
ggplot(df, aes(x = Valori)) +
  geom_histogram(bins = 5, aes(y = after_stat(density)), fill = "lightblue", color = "black") +
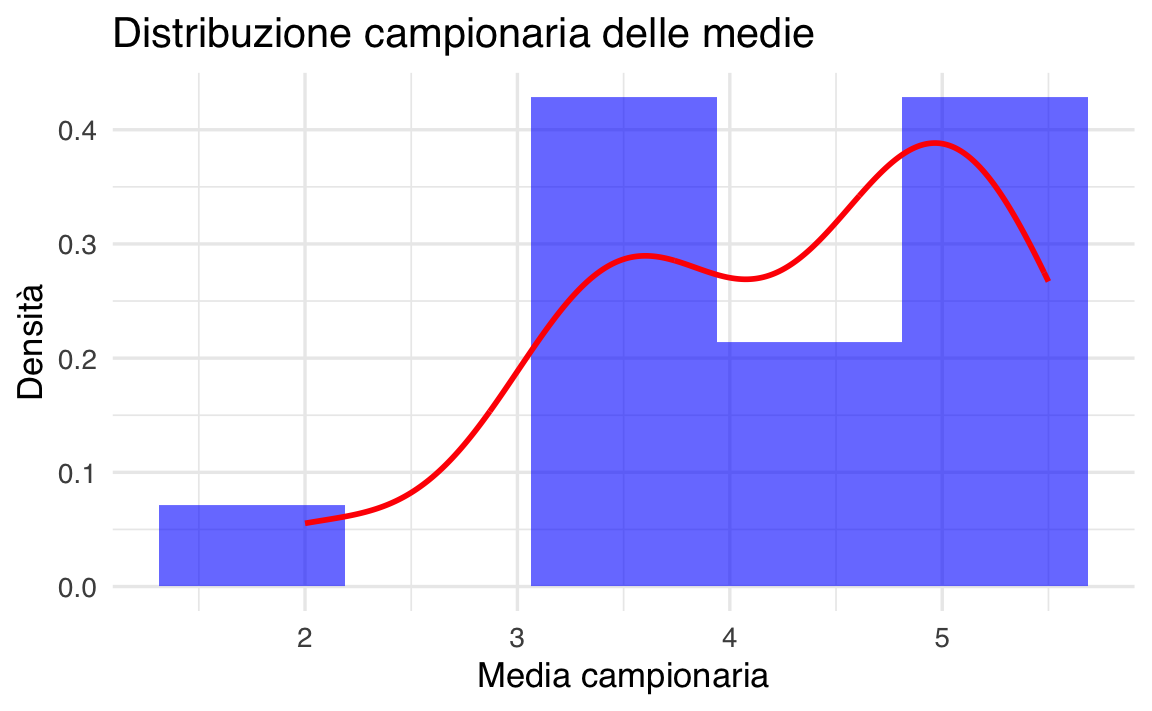
  labs(title = "Distribuzione campionaria delle medie (n = 2)", x = "Media campionaria", y = "Densità")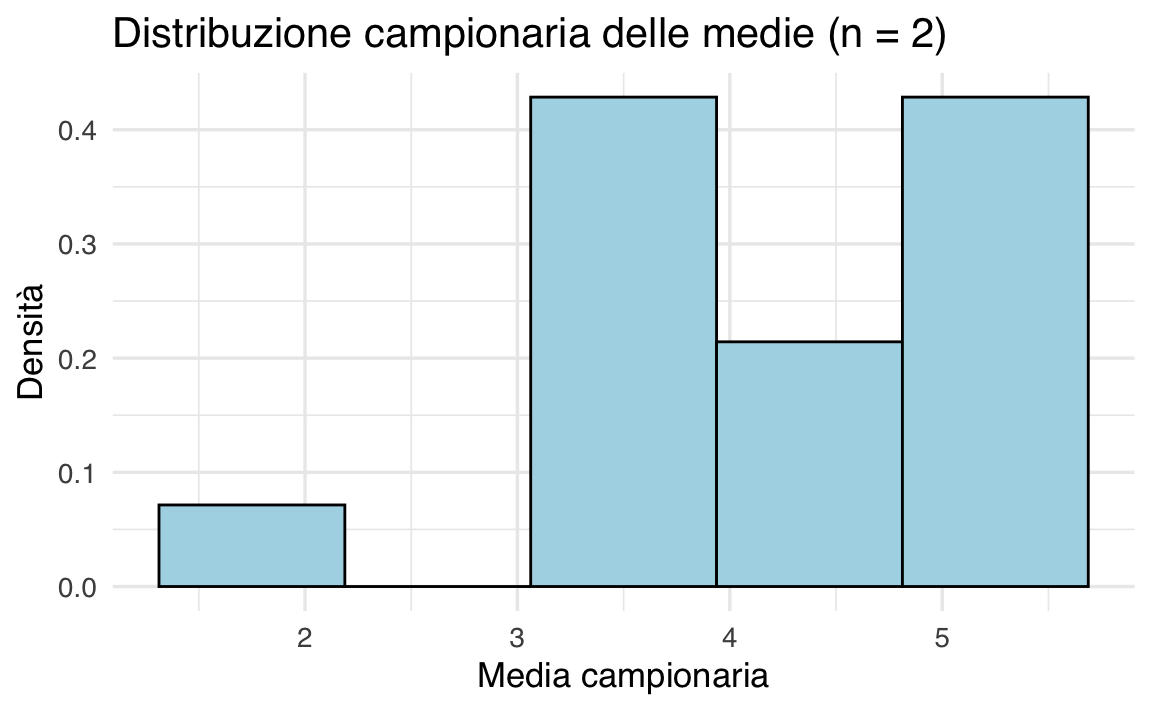

L’istogramma mostra come le medie campionarie non siano distribuite uniformemente, ma seguano una struttura precisa determinata dalla distribuzione dei valori originali della popolazione. Con un numero maggiore di osservazioni per campione (\(n\) più grande), la distribuzione campionaria delle medie tende a diventare più stretta e simmetrica attorno alla media della popolazione, illustrando così il principio alla base dell’inferenza statistica frequentista.

72.3.4 Verifiche teoriche

72.3.4.1 Media della distribuzione campionaria

Secondo la teoria statistica, la media della distribuzione campionaria deve coincidere con la media della popolazione. Questo implica che, se prendiamo la media di tutti i campioni possibili di una certa dimensione, il valore risultante sarà uguale alla media della popolazione stessa. Possiamo verificarlo con il seguente calcolo:

mean(x)  # Media della popolazione
#> [1] 4.25
mean(sample_means)  # Media della distribuzione campionaria
#> [1] 4.25

72.3.4.2 Varianza della distribuzione campionaria

Un altro risultato importante è che la varianza della distribuzione campionaria delle medie è inferiore alla varianza della popolazione. In particolare, la teoria prevede che sia pari alla varianza della popolazione divisa per la dimensione del campione \(n\):

\[ \mathbb{V}(\bar{X}) = \frac{\sigma^2}{n} \]

Poiché in questo caso \(n = 2\), confrontiamo la varianza teorica con quella empirica:

# Funzione per calcolare la varianza senza la correzione di Bessel
variance <- function(x) {
  mean((x - mean(x))^2)
}
variance(x) / 2  # Varianza teorica
#> [1] 0.9062
variance(sample_means)  # Varianza empirica
#> [1] 0.9062

Osserviamo che la varianza delle medie campionarie è inferiore alla varianza della popolazione, confermando che le medie campionarie mostrano meno variabilità rispetto alle singole osservazioni.

72.3.5 Esempio di campione osservato

Per comprendere meglio questi concetti, consideriamo un singolo campione, ad esempio:

observed_sample <- c(5, 5.5)
observed_sample
#> [1] 5.0 5.5

Calcoliamo la sua media e deviazione standard:

mean(observed_sample)  # Media del campione
#> [1] 5.25
sqrt(variance(observed_sample))  # Deviazione standard del campione
#> [1] 0.25

Ora confrontiamo questi valori con quelli della popolazione:

mean(x)  # Media della popolazione
#> [1] 4.25
sqrt(variance(x))  # Deviazione standard della popolazione
#> [1] 1.346

Osserviamo che la media del campione si avvicina a quella della popolazione, ma non coincide necessariamente con essa. Questo è del tutto normale: ogni campione rappresenta solo una porzione della popolazione e la sua media può variare leggermente a seconda delle osservazioni selezionate.

Per quanto riguarda la deviazione standard, in questo caso specifico risulta inferiore a quella della popolazione. Tuttavia, in generale, la dispersione di un singolo campione può essere maggiore o minore rispetto a quella della popolazione, poiché dipende dalla variabilità casuale delle osservazioni estratte. Proprio per questo motivo, per trarre inferenze affidabili sulla popolazione, è più utile considerare la distribuzione campionaria delle medie piuttosto che un singolo campione isolato.

Questo esempio illustra bene il principio della stima campionaria: mentre un singolo campione fornisce un’informazione parziale, l’analisi di molteplici campioni consente di ottenere una stima più precisa e stabile della media della popolazione, riducendo l’incertezza e migliorando l’affidabilità dell’inferenza statistica.

72.3.6 La Simulazione Illustra Due Principi

Dalla simulazione emergono due principi fondamentali dell’inferenza statistica:

  1. La media della distribuzione campionaria coincide con la media della popolazione. Questo implica che se estraiamo molteplici campioni di dimensione \(n\) e calcoliamo la loro media, il valore atteso della media campionaria sarà uguale alla media della popolazione \(\mu\). Formalmente:

    \[ \mathbb{E}(\bar{X}_n) = \mu . \]

    Questo risultato conferma che la media campionaria è uno stimatore non distorto della media della popolazione.

  2. La varianza della distribuzione campionaria è minore della varianza della popolazione. Questo riflette il fatto che le medie campionarie tendono a essere più stabili rispetto alle singole osservazioni. La relazione teorica che descrive questa proprietà è:

    \[ \mathbb{V}(\bar{X}) = \frac{\sigma^2}{n} . \]

    Ciò significa che, aumentando la dimensione del campione \(n\), la variabilità delle medie campionarie si riduce, rendendo la stima della media della popolazione più precisa. Questo concetto è alla base della teoria del teorema centrale del limite, che diventa sempre più evidente con campioni di dimensioni maggiori.

Dato un campione casuale di \(n\) osservazioni \(X_1, X_2, \dots, X_n\) estratte da una popolazione con media \(\mu\) e varianza \(\sigma^2\), la media campionaria è definita come:

\[ \bar{X}_n = \frac{1}{n} \sum_{i=1}^{n} X_i . \]

Utilizziamo la linearità dell’operatore di aspettativa:

\[ \mathbb{E}(\bar{X}_n) = \mathbb{E} \left( \frac{1}{n} \sum_{i=1}^{n} X_i \right) . \]

Per la proprietà della linearità dell’aspettativa, possiamo portare fuori il fattore costante \(\frac{1}{n}\):

\[ \mathbb{E}(\bar{X}_n) = \frac{1}{n} \sum_{i=1}^{n} \mathbb{E}(X_i) . \]

Poiché ogni \(X_i\) proviene dalla stessa popolazione, ha la stessa aspettativa \(\mathbb{E}(X_i) = \mu\), quindi:

\[ \mathbb{E}(\bar{X}_n) = \frac{1}{n} \sum_{i=1}^{n} \mu . \]

Sommando \(n\) volte \(\mu\), otteniamo:

\[ \mathbb{E}(\bar{X}_n) = \frac{1}{n} (n \mu) = \mu . \]

In conclusione, abbiamo dimostrato che:

\[ \mathbb{E}(\bar{X}_n) = \mu . \]

Questo significa che la media campionaria \(\bar{X}_n\) è uno stimatore corretto (non distorto) della media della popolazione \(\mu\), poiché il suo valore atteso coincide esattamente con la quantità che vogliamo stimare.

Sia \(X_1, X_2, \dots, X_n\) un campione casuale di \(n\) osservazioni indipendenti estratte da una popolazione con media \(\mu\) e varianza \(\sigma^2\). La media campionaria è definita come:

\[ \bar{X} = \frac{1}{n} \sum_{i=1}^n X_i. \]

Per definizione, la varianza di \(\bar{X}\) è:

\[ \mathbb{V}(\bar{X}) = \mathbb{V}\left(\frac{1}{n} \sum_{i=1}^n X_i\right). \]

Poiché una costante moltiplicata da una variabile aleatoria può essere “estratta” dalla varianza, otteniamo:

\[ \mathbb{V}(\bar{X}) = \frac{1}{n^2} \mathbb{V}\left(\sum_{i=1}^n X_i\right). \]

Ora dobbiamo calcolare \(\mathbb{V}\left(\sum_{i=1}^n X_i\right)\). Le variabili \(X_1, X_2, \dots, X_n\) sono indipendenti, quindi la varianza della somma è la somma delle varianze:

\[ \mathbb{V}\left(\sum_{i=1}^n X_i\right) = \sum_{i=1}^n \mathbb{V}(X_i). \]

Poiché tutte le variabili \(X_i\) hanno la stessa varianza \(\sigma^2\):

\[ \mathbb{V}\left(\sum_{i=1}^n X_i\right) = n \sigma^2. \]

Sostituendo nella formula precedente, otteniamo:

\[ \mathbb{V}(\bar{X}) = \frac{1}{n^2} \cdot n \sigma^2 = \frac{\sigma^2}{n}. \]

In generale, dunque, per un campione di ampiezza \(n\), vale la relazione \(\mathbb{V}(\bar{X}) = \frac{\sigma^2}{n}\).

72.4 Proprietà della distribuzione campionaria

Una caratteristica fondamentale della distribuzione campionaria riguarda la sua forma e il modo in cui dipende dalla distribuzione della popolazione da cui vengono estratti i campioni. Possiamo distinguere due casi principali:

  • Se la popolazione segue una distribuzione normale, allora anche la distribuzione delle medie campionarie sarà normalmente distribuita, indipendentemente dalla dimensione del campione \(n\). Questo significa che, anche con campioni molto piccoli, la media campionaria manterrà la stessa forma della distribuzione originale.

  • Se la popolazione non segue una distribuzione normale, entra in gioco il teorema centrale del limite. Questo teorema afferma che, man mano che la dimensione del campione \(n\) aumenta, la distribuzione delle medie campionarie tenderà comunque a una distribuzione normale, indipendentemente dalla forma della distribuzione di partenza. In pratica, per campioni sufficientemente grandi, possiamo approssimare la distribuzione delle medie campionarie con una normale, anche se la popolazione da cui provengono i dati è asimmetrica o non gaussiana.

Queste proprietà sono fondamentali nell’inferenza statistica frequentista: permettono di stimare e testare parametri della popolazione utilizzando campioni, facilitando l’applicazione di strumenti basati sulla distribuzione normale, come gli intervalli di confidenza e i test di ipotesi.

72.5 Teorema del Limite Centrale

Esaminiamo ora più in dettaglio il Teorema del Limite Centrale (TLC). Nel 1812, Pierre-Simon Laplace dimostrò il TLC, che afferma che la somma (o la media) di una sequenza di variabili casuali indipendenti e identicamente distribuite (i.i.d.) tende a distribuirsi secondo una distribuzione Normale (o Gaussiana), al crescere della dimensione del campione. Inoltre, il TLC specifica i parametri della distribuzione Normale risultante in base ai valori attesi e alle varianze delle variabili casuali sommate.

Teorema 72.1 Si consideri una sequenza di variabili aleatorie indipendenti e identicamente distribuite (i.i.d.) \(Y_1, Y_2, \dots, Y_n\), con valore atteso \(\mathbb{E}(Y_i) = \mu\) e deviazione standard \(\text{SD}(Y_i) = \sigma.\) Si definisca una nuova variabile casuale come la media campionaria:

\[ Z = \frac{1}{n} \sum_{i=1}^n Y_i. \]

Al tendere di \(n\) all’infinito (\(n \rightarrow \infty\)), la distribuzione di \(Z\) converge a una distribuzione Normale con valore atteso \(\mu\) e deviazione standard \(\frac{\sigma}{\sqrt{n}}\):

\[ Z \sim \mathcal{N}\left(\mu, \, \frac{\sigma}{\sqrt{n}} \right). \]

In altre parole, la densità di probabilità di \(Z\) tende a:

\[ p_Z(z) \rightarrow \mathcal{N}\left(z \ \Bigg| \ \mu, \, \frac{\sigma}{\sqrt{n}} \right). \]

Il TLC può essere generalizzato anche a variabili casuali che non sono identicamente distribuite, purché siano indipendenti e abbiano valori attesi e varianze finite. Questo teorema spiega perché molti fenomeni naturali, come l’altezza degli adulti o il peso di una popolazione, tendono a seguire una distribuzione Normale. Infatti, tali fenomeni sono spesso il risultato di una combinazione di numerosi effetti additivi e indipendenti, ciascuno dei quali contribuisce in modo relativamente piccolo. Indipendentemente dalla distribuzione individuale di ciascun effetto, la loro somma (o media) tende a distribuirsi in modo Normale. Questa è la ragione per cui la distribuzione Normale fornisce una buona approssimazione per la distribuzione di molti fenomeni osservati in natura.

72.5.1 Illustrazione del Teorema del Limite Centrale (TLC)

Per comprendere il Teorema del Limite Centrale (TLC), consideriamo una popolazione iniziale che segue una distribuzione fortemente asimmetrica: la distribuzione Beta(2,1), caratterizzata da una forte asimmetria positiva.

# Parametri della distribuzione Beta
a <- 2
b <- 1

# Genera valori per la distribuzione Beta
x <- seq(0, 1, length.out = 1000)  # Valori tra 0 e 1
y <- dbeta(x, shape1 = a, shape2 = b)  # Densità della distribuzione Beta

# Crea un dataframe per qplot
data <- data.frame(x = x, y = y)

# Grafico con qplot
qplot(x, y, data = data, geom = "line", 
      main = "Distribuzione Beta(2, 1)", 
      xlab = "x", 
      ylab = "Densità")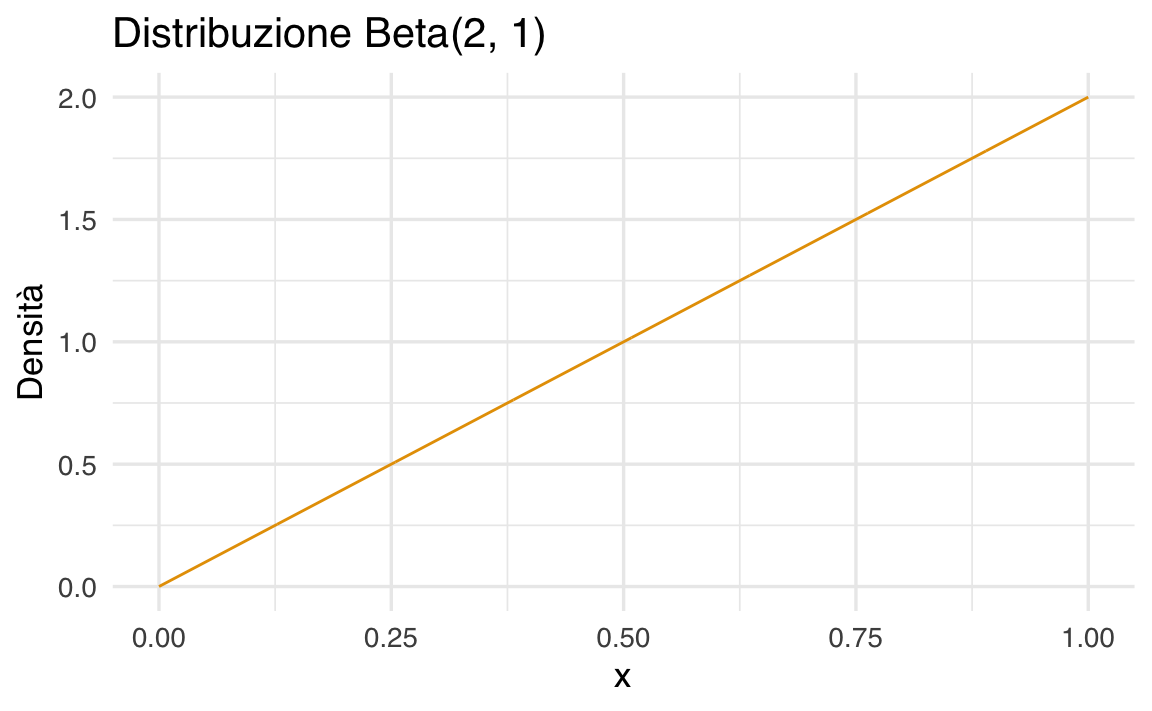

Estrarremo più volte campioni casuali di ampiezza \(n\) da questa popolazione e calcoleremo le medie campionarie. Il TLC prevede che, all’aumentare della dimensione del campione, la distribuzione delle medie campionarie tenda a una distribuzione normale, indipendentemente dalla forma della popolazione di partenza.

Per verificare questa proprietà, definiamo una funzione che genera campioni, calcola le medie e visualizza la loro distribuzione campionaria per diversi valori di \(n\):

# Parametri della distribuzione Beta
alpha <- 2
beta <- 1

# Funzione per simulare e visualizzare la distribuzione campionaria
plot_samples <- function(n) {
  # Media e deviazione standard della distribuzione Beta
  mu <- alpha / (alpha + beta)
  sigma <- sqrt(alpha * beta / ((alpha + beta)^2 * (alpha + beta + 1)))
  
  # Generazione di 50.000 campioni casuali di dimensione n
  sample_means <- replicate(50000, mean(rbeta(n, alpha, beta)))
  
  # Creazione del dataframe
  df <- data.frame(MediaCampionaria = sample_means)
  
  # Creazione del grafico con ggplot2
  ggplot(df, aes(x = MediaCampionaria)) +
    geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "lightblue", color = "black") +
    stat_function(fun = dnorm, args = list(mean = mu, sd = sigma / sqrt(n)), color = "black", lwd = 1.2) +
    labs(title = paste("Distribuzione campionaria per n =", n),
         x = "Media campionaria",
         y = "Densità") +
    theme_minimal()
}

72.5.1.1 Visualizzazione della convergenza alla normalità

Analizziamo l’effetto della dimensione del campione sulle medie campionarie:

  1. Campioni di ampiezza \(n = 1\)

    Se \(n = 1\), la distribuzione campionaria coincide esattamente con la distribuzione della popolazione di partenza, che in questo caso è fortemente asimmetrica:

    plot_samples(1)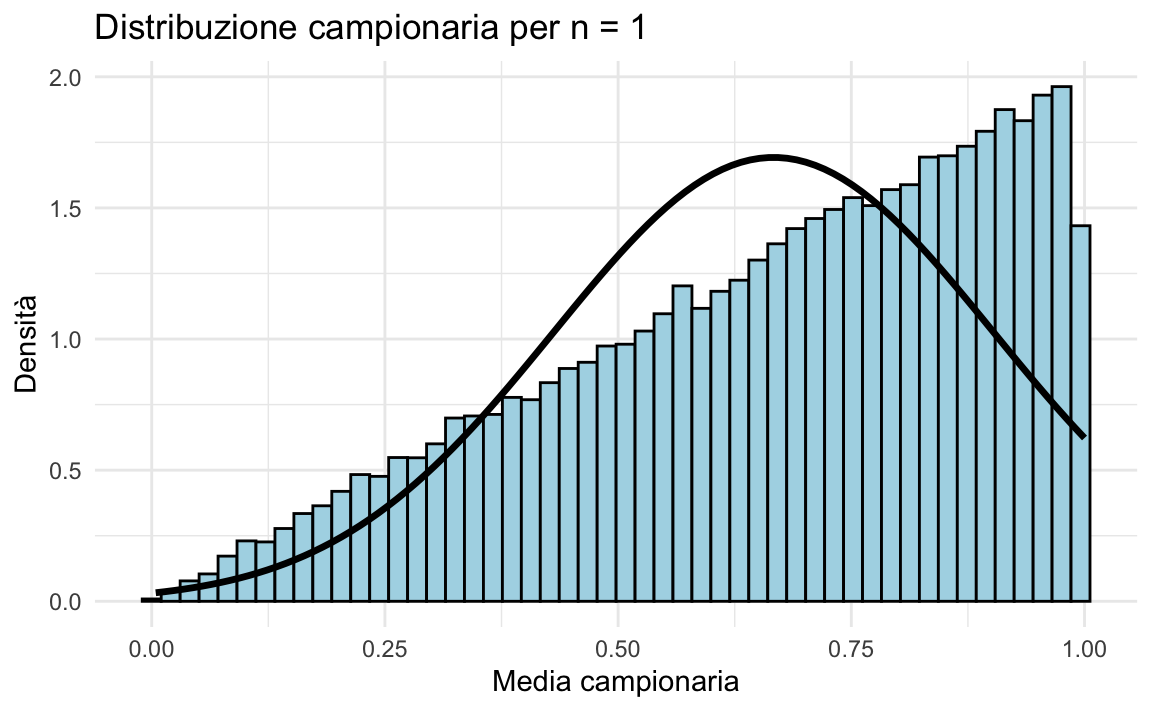

  2. Campioni di ampiezza \(n = 2\)

    Con \(n = 2\), la distribuzione delle medie campionarie inizia a perdere parte della sua asimmetria:

    plot_samples(2)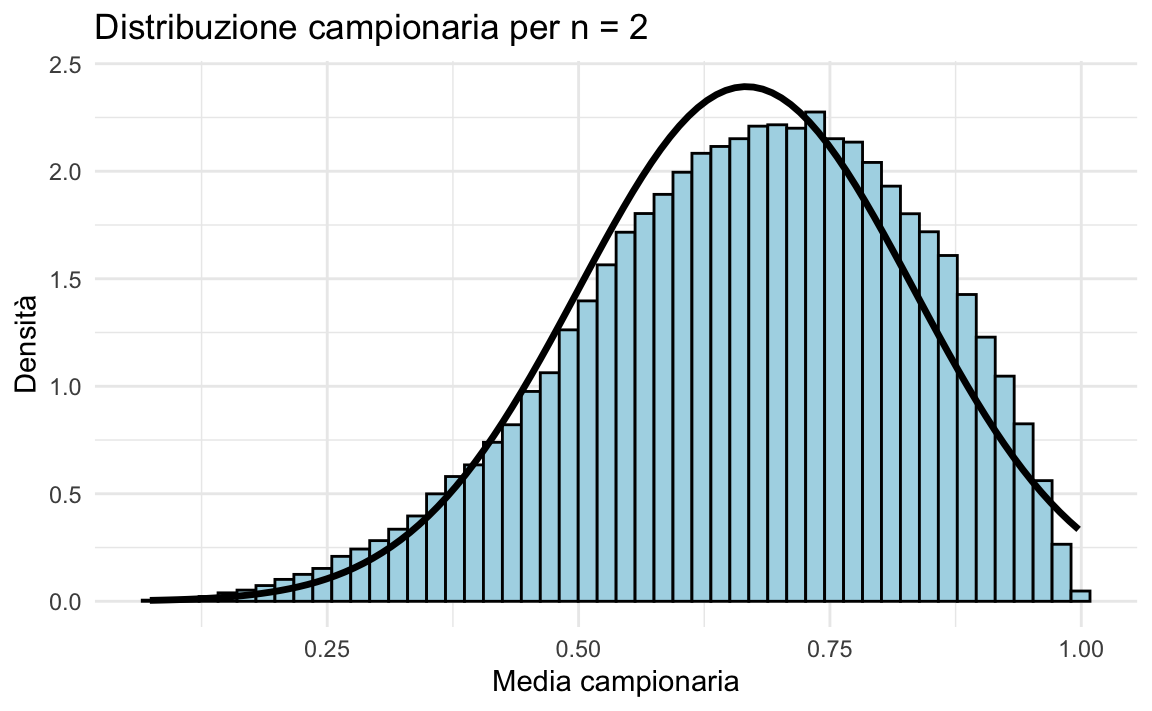

  3. Campioni di ampiezza \(n = 4\)

    Per \(n = 4\), la distribuzione delle medie campionarie diventa più simmetrica e tende già a una forma più vicina a quella normale:

    plot_samples(4)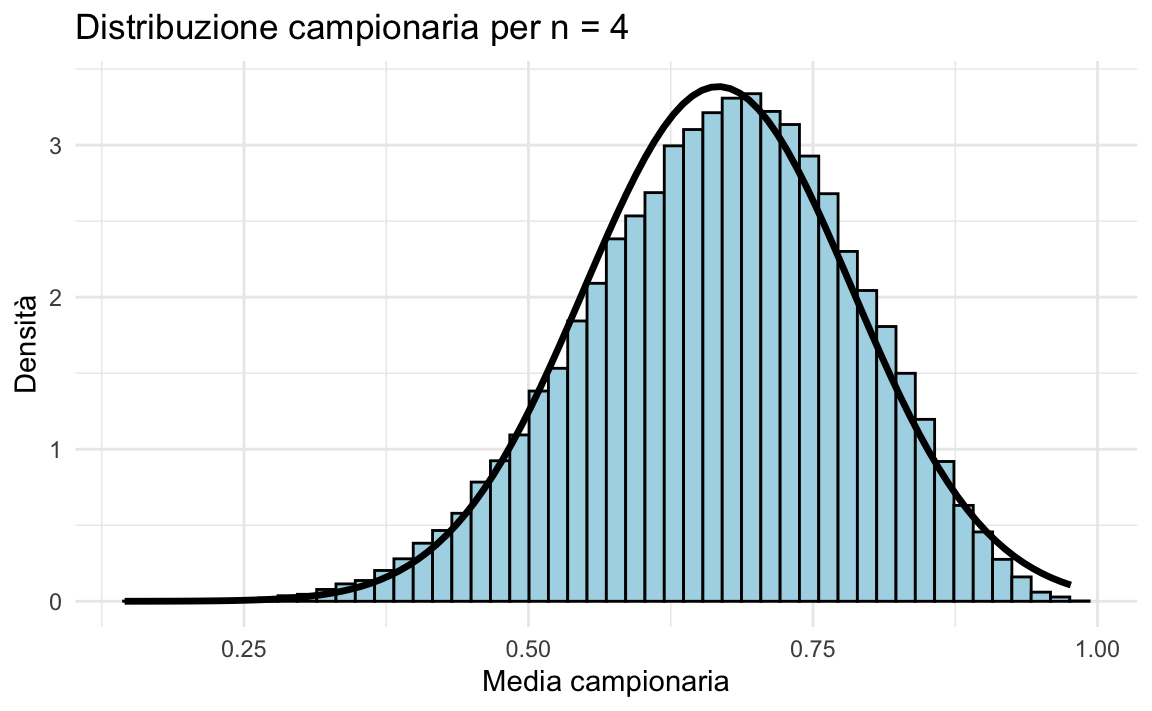

  4. Campioni di ampiezza \(n = 30\)

    Quando \(n\) diventa sufficientemente grande (ad esempio \(n = 30\)), la distribuzione campionaria delle medie è praticamente indistinguibile da una normale:

    plot_samples(30)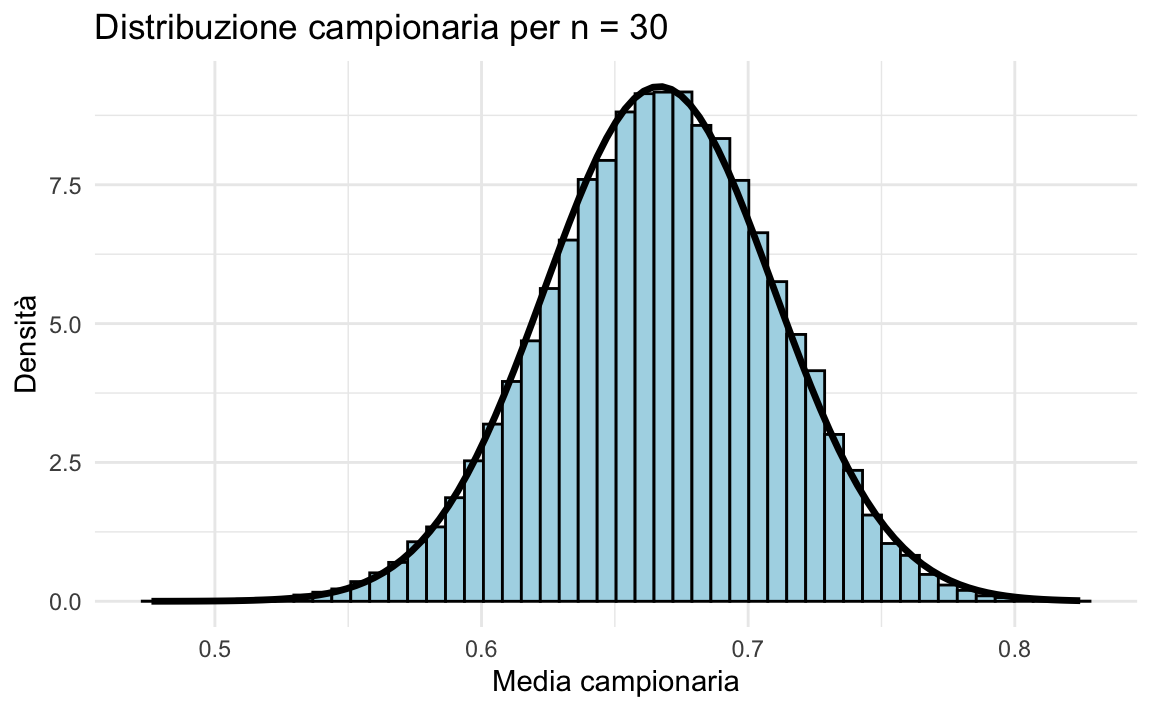

72.5.1.2 Conclusione

Il Teorema del Limite Centrale (TLC) afferma che, indipendentemente dalla forma della distribuzione della popolazione:

  • Se la dimensione del campione è sufficientemente grande, la distribuzione delle medie campionarie \(\bar{X}\) sarà approssimativamente normale, anche se la popolazione di partenza non lo è.

  • La distribuzione delle medie campionarie avrà media uguale a quella della popolazione \(\mu\) e deviazione standard pari a:

    \[ \bar{X} \sim \mathcal{N}(\mu, \sigma / \sqrt{n}) \]

    dove \(\sigma\) è la deviazione standard della popolazione e \(n\) è la dimensione del campione.

72.5.2 Implicazioni

  1. Normalità emergente
    Il TLC giustifica l’uso della distribuzione normale in molte applicazioni statistiche, anche quando i dati originali non seguono una distribuzione normale.

  2. Errore standard e precisione delle stime
    Il TLC fornisce una formula esplicita per calcolare l’errore standard \(\sigma / \sqrt{n}\), che quantifica l’incertezza associata alla media campionaria. All’aumentare di \(n\), l’errore standard diminuisce, migliorando la precisione della stima della media della popolazione.

Questa proprietà è alla base di molte tecniche statistiche, come gli intervalli di confidenza e i test di ipotesi, che assumono la normalità della distribuzione campionaria delle medie anche quando la popolazione di partenza non è normale.

72.5.3 Applicazioni in psicologia

Molti fenomeni psicologici che misuriamo (ad esempio, il QI come media di molte abilità cognitive) derivano dalla media di più variabili, e quindi seguono la distribuzione normale grazie al TLC. Questo spiega perché la distribuzione normale appare così frequentemente nei dati sperimentali di psicologia e in molte altre discipline scientifiche.

72.6 Distribuzioni campionarie di altre statistiche

Abbiamo già analizzato la distribuzione campionaria della media dei campioni. Tuttavia, è possibile costruire distribuzioni campionarie per altre statistiche campionarie. Ad esempio, consideriamo la distribuzione campionaria del valore massimo e della varianza.

72.6.1 Distribuzione campionaria del valore massimo

Supponiamo di avere una popolazione normalmente distribuita con media \(\mu = 100\) e deviazione standard \(\sigma = 15\). Generiamo 10.000 campioni casuali di ampiezza \(n = 5\) e calcoliamo il valore massimo per ogni campione.

72.6.1.1 Simulazione e visualizzazione

set.seed(123)  # Per risultati riproducibili

# Parametri della distribuzione
mu <- 100
sigma <- 15

# Simulazione: calcolo del valore massimo per ciascun campione
n_samples <- 10000
sample_maxes <- replicate(
  n_samples, 
  max(rnorm(5, mean = mu, sd = sigma))
)

# Creazione del dataframe
df <- data.frame(ValoreMassimo = sample_maxes)

# Istogramma con ggplot2
ggplot(df, aes(x = ValoreMassimo)) +
  geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "lightblue", color = "black") +
  stat_function(fun = dnorm, args = list(mean = mu, sd = sigma), color = "black", lwd = 1.2) +
  labs(title = "Distribuzione campionaria del valore massimo",
       x = "Valore massimo",
       y = "Densità")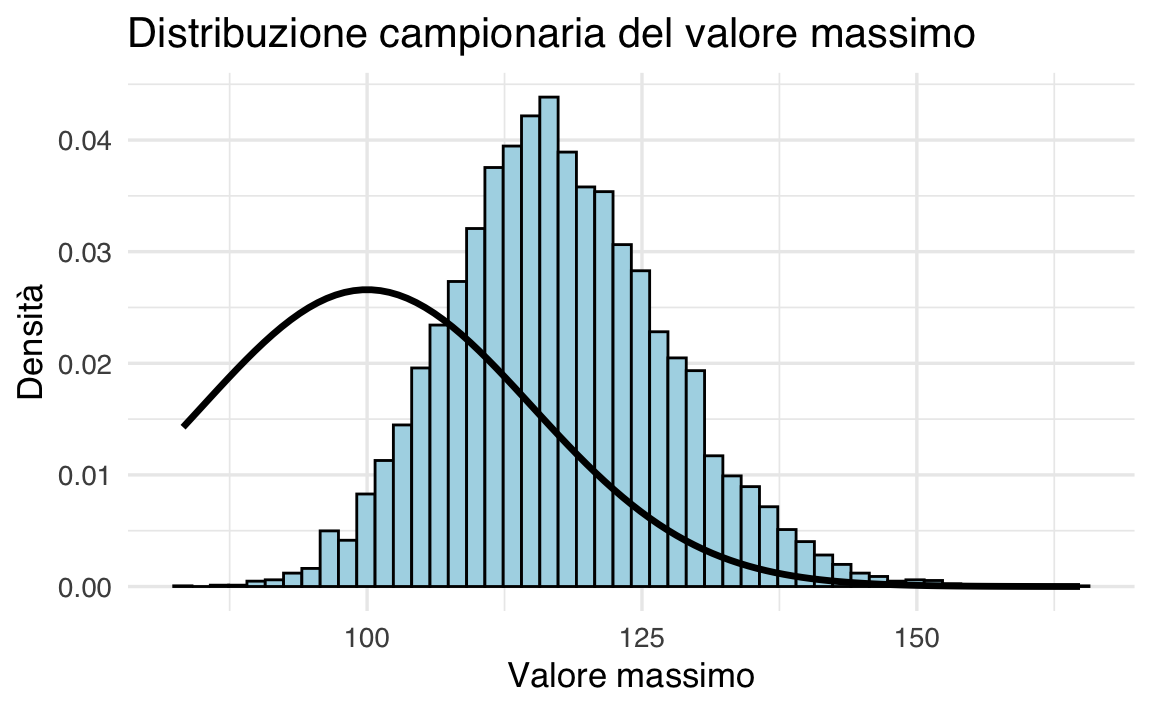

Osserviamo che il valore atteso della distribuzione campionaria del massimo è maggiore della media della popolazione \(\mu\).

72.6.2 Distribuzione campionaria della varianza

Un’altra statistica interessante è la varianza campionaria. La formula della varianza campionaria, basata sulla statistica descrittiva, è:

\[ S^2 = \frac{\sum_{i=1}^n (Y_i - \bar{Y})^2}{n}. \]

Calcoliamo la distribuzione campionaria della varianza per campioni di ampiezza \(n = 5\).

72.6.2.1 Simulazione e visualizzazione

set.seed(123)

# Parametri della distribuzione
mu <- 100
sigma <- 15
n_samples <- 10000

# Funzione per calcolare la varianza senza la correzione di Bessel
variance <- function(x) {
  mean((x - mean(x))^2)  # Divisione per n invece di (n-1)
}

# Simulazione: calcolo della varianza per ciascun campione
sample_vars <- replicate(
  n_samples, 
  variance(rnorm(5, mean = mu, sd = sigma))
)

# Creazione del dataframe
df <- data.frame(Varianza = sample_vars)

# Istogramma con ggplot2
ggplot(df, aes(x = Varianza)) +
  geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "lightblue", color = "black") +
  labs(title = "Distribuzione campionaria della varianza",
       x = "Varianza",
       y = "Densità")

# Media empirica della varianza campionaria
mean(sample_vars)
#> [1] 180.7

Sappiamo che la varianza della popolazione è \(\sigma^2 = 15^2 = 225\). Tuttavia, il valore medio empirico delle varianze campionarie calcolate con \(S^2\) risulta minore di 225. Questo avviene perché lo stimatore \(S^2\) è distorto.

72.6.3 Correzione della distorsione

Per eliminare la distorsione, utilizziamo il seguente stimatore della varianza della popolazione:

\[ s^2 = \frac{\sum_{i=1}^n (Y_i - \bar{Y})^2}{n-1}. \]

72.6.3.1 Verifica con simulazione

set.seed(123)

# Simulazione: calcolo della varianza con la correzione
sample_vars_unbiased <- replicate(
  n_samples, 
  var(rnorm(5, mean = mu, sd = sigma))
)

# Creazione del dataframe
df <- data.frame(Varianza = sample_vars_unbiased)

# Istogramma con ggplot2
ggplot(df, aes(x = Varianza)) +
  geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "lightblue", color = "black") +
  labs(title = "Distribuzione campionaria della varianza (corretta)",
       x = "Varianza",
       y = "Densità")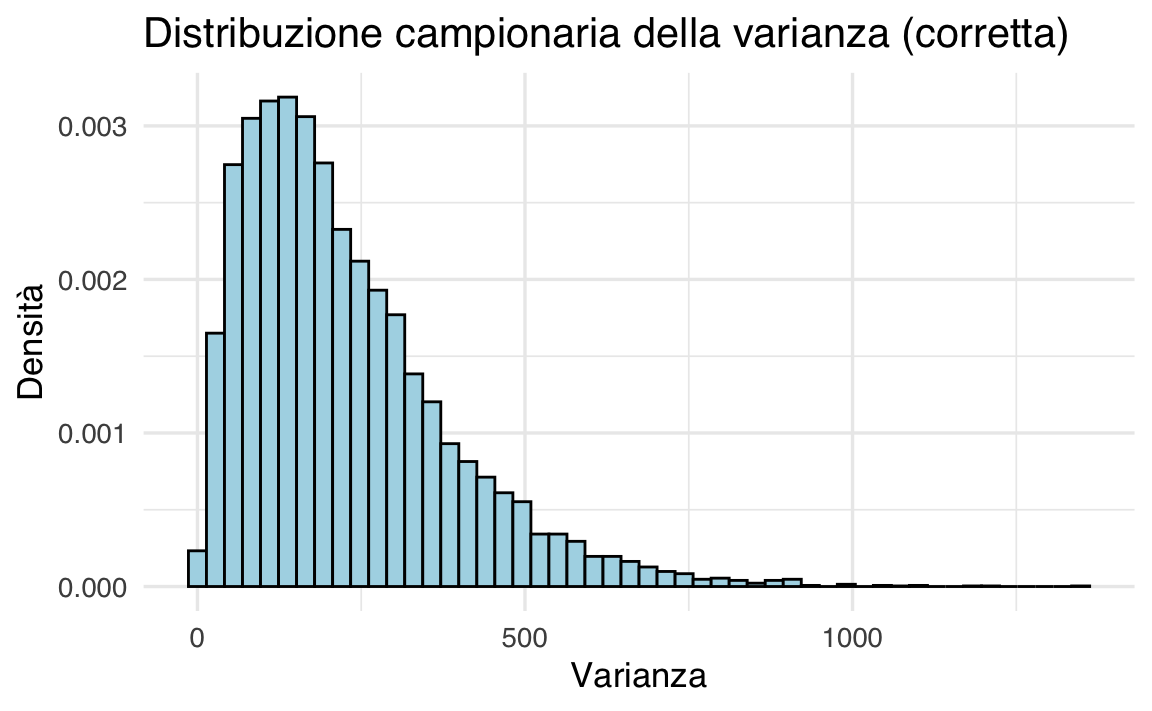

# Media empirica della varianza corretta
mean(sample_vars_unbiased)
#> [1] 225.8

Con questo stimatore, la media della distribuzione campionaria coincide con la varianza reale della popolazione \(\sigma^2 = 225\).

In conclusione:

  1. La distribuzione campionaria del massimo mostra che il valore massimo dei campioni è, in media, maggiore della media della popolazione.
  2. La varianza campionaria non corretta (\(S^2\)) è uno stimatore distorto, poiché il suo valore atteso non coincide con la varianza della popolazione.
  3. Lo stimatore corretto \(s^2\), che utilizza il divisore \(n - 1\), elimina la distorsione e fornisce una stima non distorta della varianza della popolazione.

In generale, uno stimatore è considerato non distorto quando il valore atteso delle sue stime coincide con il valore reale del parametro. Nel caso della media campionaria e della varianza corretta, entrambi gli stimatori sono non distorti.

72.7 Riflessioni Conclusive

In generale, i parametri della popolazione sono sconosciuti, ma possiamo stimarli utilizzando le informazioni del campione. Di seguito viene presentata una tabella che riassume i simboli comuni utilizzati per indicare le quantità note e sconosciute nel contesto dell’inferenza statistica. Questo ci aiuterà a tenere traccia di ciò che sappiamo e ciò che non sappiamo.

Simbolo Nome È qualcosa che conosciamo?
\(s\) Deviazione standard del campione Sì, la calcoliamo dai dati grezzi
\(\sigma\) Deviazione standard della popolazione No, tranne in casi particolari o nelle simulazioni
\(\hat{\sigma}\) Stima della deviazione standard della popolazione Sì, ma non è uguale a \(\sigma\)
\(s^2\) Varianza del campione Sì, la calcoliamo dai dati grezzi
\(\sigma^2\) Varianza della popolazione No, tranne in casi particolari o nelle simulazioni
\(\hat{\sigma}^2\) Stima della varianza della popolazione Sì, ma non è uguale a \(\sigma^2\)


Utilizzando le informazioni di un campione casuale di ampiezza \(n\):

  • La stima migliore che possiamo ottenere per la media \(\mu\) della popolazione è la media del campione \(\bar{Y}\).
  • La stima migliore che possiamo ottenere per la varianza \(\sigma^2\) della popolazione è:

\[ \hat{\sigma}^2 = \frac{1}{n-1} \sum_{i=1}^n (Y_i - \bar{Y})^2. \]

Dopo aver esplorato il concetto di distribuzione campionaria attraverso simulazioni ed esempi pratici, possiamo ora confrontare le nostre risposte intuitive con quanto appreso:

  1. Le medie campionarie tendono a distribuirsi intorno alla media della popolazione, con una variabilità che dipende dalla dimensione del campione.

  2. Sì, le medie campionarie sono meno disperse rispetto ai singoli valori della popolazione, il che significa che forniscono una stima più stabile della media della popolazione.

  3. All’aumentare di \(n\), la distribuzione campionaria delle medie diventa più stretta, ossia la variabilità delle medie campionarie si riduce. La varianza della distribuzione campionaria è pari a \(\sigma^2 / n\), dove \(\sigma^2\) è la varianza della popolazione.

  4. No, la distribuzione campionaria della media è normale solo se la popolazione di partenza è normale o se la dimensione del campione è sufficientemente grande (Teorema del Limite Centrale).

  5. Sì, la media della distribuzione campionaria coincide con la media della popolazione. Tuttavia, la varianza della distribuzione campionaria è inferiore alla varianza della popolazione, poiché viene divisa per la dimensione del campione (\(n\)).

  6. Per campioni piccoli, la distribuzione delle medie campionarie somiglierà alla distribuzione della popolazione originale. Se la popolazione è fortemente asimmetrica, anche la distribuzione campionaria per piccoli campioni sarà asimmetrica. Tuttavia, aumentando \(n\), la distribuzione delle medie campionarie tenderà a una normale, indipendentemente dalla forma della popolazione di partenza.

Esercizi

Parte 1: Popolazione di Piccole Dimensioni Si consideri una popolazione con i seguenti valori:

\[ x = \{2, 4.5, 5, 5.5\} \]

  1. Calcolare la media e la varianza della popolazione.
  2. Estrarre tutti i possibili campioni di ampiezza \(n = 2\) con ripetizione e calcolare la media di ciascun campione.
  3. Rappresentare graficamente la distribuzione campionaria delle medie.
  4. Calcolare la probabilità che la media campionaria sia inferiore a 3:
    • Esattamente, utilizzando la distribuzione campionaria.
    • Approssimativamente, assumendo una distribuzione normale se il campione fosse sufficientemente grande.

Parte 2: Popolazione di Grandi Dimensioni

Si consideri ora una popolazione più grande, generata da una distribuzione normale con media \(\mu = 10\) e deviazione standard \(\sigma = 3\).

  1. Generare una popolazione di 1000 osservazioni.
  2. Calcolare la media e la varianza della popolazione.
  3. Estrarre 10.000 campioni casuali di ampiezza \(n = 15\) e calcolare la media campionaria per ciascun campione.
  4. Rappresentare graficamente la distribuzione campionaria delle medie.
  5. Calcolare la probabilità che la media campionaria sia inferiore a 9:
    • Esattamente, utilizzando la distribuzione campionaria.
    • Approssimativamente, utilizzando la distribuzione normale.

Obiettivo: Verificare sperimentalmente le proprietà della distribuzione campionaria della media e confrontare i risultati con le previsioni teoriche fornite dal Teorema del Limite Centrale.

Proprietà della Distribuzione Campionaria della Media

  1. Media: La media della distribuzione campionaria coincide con la media della popolazione:

  2. Varianza: La varianza della distribuzione campionaria è pari alla varianza della popolazione divisa per la dimensione del campione:

  3. Forma:

  • Se la popolazione segue una distribuzione normale, anche la distribuzione campionaria della media sarà normale.
  • Se la popolazione non è normale, il Teorema del Limite Centrale garantisce che la distribuzione campionaria della media sarà approssimativamente normale per campioni di dimensioni sufficientemente grandi (\(n \geq 30\)).

Definiamo una popolazione e calcoliamo i parametri:

# Popolazione
x <- c(2, 4.5, 5, 5.5)
mean(x)  # Media della popolazione
#> [1] 4.25
var(x)   # Varianza della popolazione
#> [1] 2.417

Estrarre tutti i possibili campioni di ampiezza \(n = 2\) e calcolare la media di ciascun campione:

# Tutti i campioni di ampiezza 2
samples <- expand.grid(x, x)
sample_means <- rowMeans(samples)

# Visualizzare la distribuzione campionaria
df <- data.frame(sample_means = sample_means)

ggplot(df, aes(x = sample_means)) +
  geom_histogram(aes(y = after_stat(density)), bins = 5, fill = "blue", alpha = 0.6) +
  geom_density(color = "red", size = 1) +
  labs(
    title = "Distribuzione campionaria delle medie",
    x = "Media campionaria",
    y = "Densità"
  )

Calcoliamo la probabilità che, all’interno della distribuzione campionaria, la media del campione sia minore di 3. Troviamo il valore esatto nella simulazione. Approssimiamo il valore esatto con il valore atteso se il campione fosse sufficientemente grande da poter assumere una distribuzione campionaria normale:

# Probabilità esatta dalla distribuzione campionaria
exact_probability <- mean(sample_means < 3)
exact_probability
#> [1] 0.0625

# Approssimazione tramite distribuzione normale
mu <- mean(x)  # Media della popolazione
sigma <- sqrt(var(x) / 2)  # Deviazione standard della distribuzione campionaria
approx_probability <- pnorm(3, mean = mu, sd = sigma)
approx_probability
#> [1] 0.1277

Ripetiamo ora l’esempio, mantenendo la stessa struttura della simulazione, ma considerando una popolazione più grande tale per cui si possa estrarre un campione di ampiezza 15:

# Nuova popolazione
set.seed(123)
x_large <- rnorm(1000, mean = 10, sd = 3)  # Popolazione più grande
mean(x_large)  # Media della popolazione
#> [1] 10.05
var(x_large)   # Varianza della popolazione
#> [1] 8.851

# Estrazione di campioni di ampiezza 15
samples_large <- replicate(10000, mean(sample(x_large, size = 15)))

# Creazione del data frame per ggplot2
df_large <- data.frame(sample_means = samples_large)

# Visualizzazione con ggplot2
ggplot(df_large, aes(x = sample_means)) +
  geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "blue", alpha = 0.6) +
  geom_density(color = "red", size = 1) +
  labs(
    title = "Distribuzione campionaria delle medie (n = 15)",
    x = "Media campionaria",
    y = "Densità"
  )

# Probabilità esatta dalla simulazione
exact_probability_large <- mean(samples_large < 9)
exact_probability_large
#> [1] 0.0834
# Approssimazione tramite distribuzione normale
mu_large <- mean(x_large)
sigma_large <- sqrt(var(x_large) / 15)
approx_probability_large <- pnorm(9, mean = mu_large, sd = sigma_large)
approx_probability_large
#> [1] 0.08616

Distribuzione Campionaria della Differenza tra Medie

L’obiettivo di questo esercizio è esplorare le proprietà della distribuzione campionaria della differenza tra medie campionarie, analizzando sia il caso di popolazioni finite di piccole dimensioni sia il caso di popolazioni più grandi, con distribuzioni normali.

Esercizio 1: Simulazione con Popolazioni di Piccole Dimensioni

Consideriamo due popolazioni finite composte da un numero limitato di elementi:

  • Popolazione 1: \(x_1 = \{2, 4.5, 5, 6\}\)
  • Popolazione 2: \(x_2 = \{3, 3.5, 4, 7\}\)

72.7.0.1 Compiti:

  1. Calcolo dei parametri delle popolazioni:
    • Determinare la media e la varianza di entrambe le popolazioni.
  2. Estrazione di campioni:
    • Estrarre tutti i possibili campioni di ampiezza \(n = 2\) con ripetizione da entrambe le popolazioni.
    • Calcolare la media campionaria di ciascun campione.
  3. Distribuzione campionaria della differenza tra le medie:
    • Calcolare la differenza tra le medie di tutti i possibili campioni ottenuti dalle due popolazioni.
    • Rappresentare graficamente la distribuzione della differenza tra le medie.
  4. Probabilità della differenza tra le medie:
    • Calcolare la probabilità che la differenza tra le medie campionarie sia maggiore di 1.

Esercizio 2: Simulazione con Popolazioni di Grande Dimensione

Consideriamo ora due popolazioni più grandi, distribuite normalmente:

  • Popolazione 1: \(X_1 \sim N(10, 4^2)\) (media = 10, deviazione standard = 4)
  • Popolazione 2: \(X_2 \sim N(8, 3^2)\) (media = 8, deviazione standard = 3)

Compiti:

  1. Generazione delle popolazioni:
    • Creare due popolazioni casuali di 10.000 osservazioni ciascuna, distribuite normalmente.
  2. Estrazione di campioni:
    • Estrarre 10.000 campioni casuali di ampiezza \(n_1 = 15\) dalla prima popolazione e \(n_2 = 20\) dalla seconda popolazione.
    • Calcolare la media di ciascun campione.
  3. Distribuzione campionaria della differenza tra le medie:
    • Calcolare la differenza tra le medie campionarie ottenute dalle due popolazioni.
    • Rappresentare graficamente la distribuzione della differenza tra le medie.
  4. Probabilità della differenza tra le medie:
    • Calcolare la probabilità che la differenza tra le medie campionarie sia maggiore di 2 in due modi:
      • Metodo empirico: utilizzando la distribuzione ottenuta nella simulazione.
      • Metodo teorico: approssimando la distribuzione con una normale e calcolando la probabilità con la formula teorica della varianza della differenza tra le medie.

Domande di Discussione

  1. Come cambia la forma della distribuzione campionaria al variare delle dimensioni dei campioni \(n_1\) e \(n_2\)?
  2. La probabilità stimata tramite simulazione coincide con quella calcolata utilizzando l’approssimazione normale? Perché?
  3. Cosa accadrebbe alla distribuzione campionaria se le popolazioni originali non fossero normali? Quale sarebbe il ruolo del Teorema del Limite Centrale?

Esercizio 1: Simulazione con Popolazioni di Piccola Dimensione

Supponiamo di avere due popolazioni finite definite come segue:

  • Popolazione 1: \(x_1 = \{2, 4.5, 5, 6\}\)
  • Popolazione 2: \(x_2 = \{3, 3.5, 4, 7\}\)
  1. Calcola le medie e le varianze delle due popolazioni:
# Popolazione 1
x1 <- c(2, 4.5, 5, 6)
mean(x1)  # Media di x1
#> [1] 4.375
var(x1)   # Varianza di x1
#> [1] 2.896
# Popolazione 2
x2 <- c(3, 3.5, 4, 7)
mean(x2)  # Media di x2
#> [1] 4.375
var(x2)   # Varianza di x2
#> [1] 3.229
  1. Estrai tutti i possibili campioni di ampiezza \(n = 2\) da entrambe le popolazioni:
# Tutti i campioni di ampiezza 2
samples1 <- expand.grid(x1, x1)
samples2 <- expand.grid(x2, x2)

# Medie campionarie
sample_means1 <- rowMeans(samples1)
sample_means2 <- rowMeans(samples2)
  1. Calcola la differenza tra le medie campionarie di ciascuna combinazione di campioni:
# Differenze tra le medie campionarie
sample_diff <- as.vector(outer(sample_means1, sample_means2, "-"))
  1. Visualizza la distribuzione campionaria della differenza tra le medie:
# Istogramma della differenza tra medie campionarie

# Creazione del data frame per ggplot2
df_diff <- data.frame(sample_diff = sample_diff)

# Visualizzazione con ggplot2
ggplot(df_diff, aes(x = sample_diff)) +
  geom_histogram(aes(y = after_stat(density)), bins = 10, fill = "blue", alpha = 0.6) +
  geom_density(color = "red", size = 1) +
  labs(
    title = "Distribuzione campionaria della differenza tra medie",
    x = "Differenza campionaria",
    y = "Densità"
  )

  1. Calcola la probabilità che la differenza campionaria sia maggiore di 1:
# Probabilità esatta dalla distribuzione campionaria
exact_probability <- mean(sample_diff > 1)
exact_probability
#> [1] 0.2656

Esercizio 2: Simulazione con Popolazioni di Grande Dimensione

Ora considera due popolazioni più grandi con distribuzioni normali:

  • Popolazione 1: \(X_1 \sim N(10, 4^2)\)
  • Popolazione 2: \(X_2 \sim N(8, 3^2)\)
  1. Genera due popolazioni casuali:
set.seed(123)
pop1 <- rnorm(10000, mean = 10, sd = 4)
pop2 <- rnorm(10000, mean = 8, sd = 3)
  1. Estrai 10.000 campioni casuali di ampiezza \(n_1 = 15\) e \(n_2 = 20\) rispettivamente:
# Estrazione di campioni e calcolo delle medie
sample_means1 <- replicate(10000, mean(sample(pop1, size = 15)))
sample_means2 <- replicate(10000, mean(sample(pop2, size = 20)))
  1. Calcola la differenza tra le medie campionarie:
# Differenze tra medie campionarie
sample_diff_large <- sample_means1 - sample_means2
  1. Visualizza la distribuzione campionaria della differenza tra le medie:
# Istogramma della distribuzione campionaria

# Creazione del data frame per ggplot2
df_diff_large <- data.frame(sample_diff = sample_diff_large)

# Visualizzazione con ggplot2
ggplot(df_diff_large, aes(x = sample_diff)) +
  geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "blue", alpha = 0.6) +
  geom_density(color = "red", size = 1) +
  labs(
    title = "Distribuzione campionaria della differenza tra medie (n1 = 15, n2 = 20)",
    x = "Differenza campionaria",
    y = "Densità"
  )

  1. Calcola la probabilità che la differenza campionaria sia maggiore di 2 utilizzando:

    • la simulazione;
    • l’approssimazione normale.
# Probabilità esatta
exact_probability_large <- mean(sample_diff_large > 2)
exact_probability_large
#> [1] 0.505
# Approssimazione normale
mu_diff <- 10 - 8  # Differenza tra le medie delle popolazioni
sigma_diff <- sqrt(4^2 / 15 + 3^2 / 20)  # Deviazione standard della differenza
approx_probability_large <- 1 - pnorm(2, mean = mu_diff, sd = sigma_diff)
approx_probability_large
#> [1] 0.5

Domande di Discussione.

  1. Come cambia la forma della distribuzione campionaria al variare delle dimensioni campionarie \(n_1\) e \(n_2\)?
  2. La probabilità calcolata tramite simulazione coincide con quella calcolata tramite approssimazione normale? Perché?
  3. Cosa accadrebbe alla distribuzione campionaria se le popolazioni originali non fossero normali?

Problema: Distribuzione Campionaria di una Proporzione

L’obiettivo di questo esercizio è esplorare la distribuzione campionaria di una proporzione campionaria \(\hat{p}\) e verificare l’applicabilità dell’approssimazione normale per grandi dimensioni campionarie, come previsto dal Teorema del Limite Centrale.

Situazione

Supponiamo di avere una popolazione infinita in cui ciascun individuo può appartenere a una di due categorie: “successo” (codificato come 1) o “insuccesso” (codificato come 0). La probabilità di successo nella popolazione è data da \(p = 0.6\).

Compiti

  1. Definizione della popolazione e dei parametri:
    • La popolazione ha una proporzione di successi pari a \(p = 0.6\).
    • La deviazione standard teorica della distribuzione campionaria della proporzione è calcolata come:
      \[ \text{SD}(\hat{p}) = \sqrt{\frac{p(1 - p)}{n}} \]
    • Si fissi una dimensione campionaria pari a \(n = 100\).
  2. Simulazione di campioni:
    • Generare 10.000 campioni casuali di ampiezza \(n = 100\).
    • Per ogni campione, calcolare la proporzione campionaria \(\hat{p}\), cioè la frazione di successi nel campione.
  3. Distribuzione campionaria delle proporzioni:
    • Rappresentare graficamente la distribuzione delle proporzioni campionarie con un istogramma.
    • Sovrapporre la distribuzione normale teorica \(N(p, \text{SD}(\hat{p}))\) per confrontare l’andamento empirico con quello teorico.
  4. Analisi della distribuzione:
    • Valutare se la distribuzione campionaria ottenuta rispetta l’approssimazione normale.
    • Riflettere su come la dimensione del campione e il valore di \(p\) influenzano questa approssimazione.

Domande di Discussione

  1. La distribuzione campionaria delle proporzioni \(\hat{p}\) sembra approssimarsi a una distribuzione normale? Perché?
  2. Cosa accadrebbe se la dimensione del campione fosse più piccola, ad esempio \(n = 30\)?
  3. Se la probabilità di successo \(p\) fosse molto vicina a 0 o 1, l’approssimazione normale sarebbe ancora valida? Perché?

La distribuzione campionaria di una proporzione descrive come la proporzione campionaria (\(\hat{p}\)) varia tra campioni di una popolazione. Per campioni grandi, il Teorema del Limite Centrale garantisce che la distribuzione campionaria di \(\hat{p}\) può essere approssimata con una distribuzione normale.

  1. Supponiamo una popolazione infinita in cui la probabilità di successo (\(p\)) è \(p = 0.6\). Scegli una dimensione campionaria \(n = 100\).
  2. Simula 10.000 campioni casuali di ampiezza \(n\) e calcola le proporzioni campionarie (\(\hat{p}\)).
  3. Confronta l’istogramma delle proporzioni campionarie con la distribuzione normale teorica approssimativa.
# Parametri della popolazione
p <- 0.6  # Probabilità di successo nella popolazione
n <- 100  # Dimensione del campione

# Simulazione di 10.000 campioni
set.seed(123)
sample_props <- replicate(10000, mean(rbinom(n, size = 1, prob = p)))

# Creazione di un data frame per ggplot2
df_props <- data.frame(sample_props = sample_props)

# Parametri della distribuzione normale teorica
mean_theoretical <- p
sd_theoretical <- sqrt(p * (1 - p) / n)

# Visualizzazione con ggplot2
ggplot(df_props, aes(x = sample_props)) +
  geom_histogram(aes(y = after_stat(density)), bins = 40, fill = "blue", alpha = 0.6) +
  stat_function(
    fun = dnorm,
    args = list(mean = mean_theoretical, sd = sd_theoretical),
    color = "red",
    size = 1
  ) +
  labs(
    title = "Distribuzione campionaria di una proporzione (n = 100)",
    x = "Proporzione campionaria (\u0302p)",
    y = "Densità"
  )

  1. Popolazione e parametri:
    • La popolazione è definita da \(p = 0.6\).
    • La deviazione standard teorica della distribuzione campionaria è calcolata come \(\text{SD}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\).
  2. Simulazione:
    • Per ogni campione, i successi (\(0\) o \(1\)) sono generati con rbinom, e la proporzione campionaria \(\hat{p}\) è calcolata come media.
  3. Grafico:
    • L’istogramma delle proporzioni campionarie è sovrapposto alla curva normale teorica (\(N(p, \text{SD}(\hat{p}))\)).

Domande di Discussione.

  1. La distribuzione campionaria di \(\hat{p}\) sembra approssimarsi a una distribuzione normale? Perché?
  2. Cosa accadrebbe se \(n\) fosse più piccolo (es. \(n = 30\))?
  3. Se \(p\) fosse più vicino a \(0\) o \(1\), l’approssimazione normale sarebbe ancora valida? Spiega.

Problema: Distribuzione Campionaria della Differenza tra Due Proporzioni

L’obiettivo di questo esercizio è esplorare la distribuzione campionaria della differenza tra due proporzioni campionarie, \(\hat{p}_1 - \hat{p}_2\), ottenute da due campioni indipendenti estratti da popolazioni diverse. Per campioni sufficientemente grandi, il Teorema del Limite Centrale garantisce che la distribuzione di \(\hat{p}_1 - \hat{p}_2\) può essere approssimata con una distribuzione normale.

Situazione

Abbiamo due popolazioni con proporzioni di successo diverse:

  • Popolazione 1 ha una proporzione di successo \(p_1 = 0.6\).
  • Popolazione 2 ha una proporzione di successo \(p_2 = 0.4\).

Vogliamo studiare il comportamento della distribuzione campionaria della differenza tra le proporzioni campionarie quando preleviamo campioni indipendenti da ciascuna popolazione.

Compiti

  1. Definizione delle popolazioni e dei parametri:
    • La proporzione di successi nelle due popolazioni è \(p_1 = 0.6\) e \(p_2 = 0.4\).
    • Entrambi i campioni hanno dimensione \(n_1 = n_2 = 150\).
    • La deviazione standard teorica della distribuzione campionaria della differenza tra proporzioni è calcolata come: \[ \text{SD}(\hat{p}_1 - \hat{p}_2) = \sqrt{\frac{p_1 (1-p_1)}{n_1} + \frac{p_2 (1-p_2)}{n_2}} \]
  2. Simulazione di campioni:
    • Generare 10.000 campioni indipendenti di ampiezza \(n_1 = 150\) dalla prima popolazione e \(n_2 = 150\) dalla seconda popolazione.
    • Calcolare la proporzione campionaria \(\hat{p}_1\) e \(\hat{p}_2\) per ciascun campione.
    • Calcolare la differenza tra le proporzioni campionarie.
  3. Distribuzione campionaria della differenza tra le proporzioni:
    • Rappresentare graficamente la distribuzione di \(\hat{p}_1 - \hat{p}_2\) con un istogramma.
    • Sovrapporre la distribuzione normale teorica \(N(p_1 - p_2, \text{SD}(\hat{p}_1 - \hat{p}_2))\) per confrontare l’andamento empirico con quello teorico.
  4. Calcolo della probabilità che la differenza tra proporzioni sia maggiore di un valore specifico:
    • Metodo empirico: calcolare la proporzione di campioni in cui \(\hat{p}_1 - \hat{p}_2 > 0.1\).
    • Metodo teorico: utilizzare la distribuzione normale approssimata per stimare la probabilità che \(\hat{p}_1 - \hat{p}_2 > 0.1\).

Domande di Discussione

  1. L’approssimazione normale è valida in questo caso? Perché?
  2. Come cambierebbe la distribuzione campionaria se la dimensione del campione \(n_1\) o \(n_2\) fosse più piccola?
  3. Se i valori di \(p_1\) o \(p_2\) fossero più vicini a 0 o 1, come cambierebbe la probabilità calcolata e l’accuratezza dell’approssimazione normale?

La distribuzione campionaria della differenza tra due proporzioni (\(\hat{p}_1 - \hat{p}_2\)) descrive come la differenza tra le proporzioni campionarie varia tra due campioni indipendenti estratti da due popolazioni.

Per campioni grandi, il Teorema del Limite Centrale garantisce che \(\hat{p}_1 - \hat{p}_2\) segue approssimativamente una distribuzione normale con media e varianza calcolate dalle proporzioni della popolazione.

Obiettivo:

  1. Simulare due popolazioni con proporzioni \(p_1\) e \(p_2\).
  2. Estrarre campioni indipendenti da ciascuna popolazione.
  3. Calcolare la distribuzione campionaria di \(\hat{p}_1 - \hat{p}_2\).
  4. Calcolare la probabilità che la differenza campionaria sia maggiore di un valore specifico (es. \(0.1\)).

Parametri del Problema:

  • Popolazione 1: \(p_1 = 0.6\)
  • Popolazione 2: \(p_2 = 0.4\)
  • Dimensione campionaria: \(n_1 = n_2 = 150\)
  • Valore specifico: \(0.1\) 
# Parametri delle due popolazioni
p1 <- 0.6  # Proporzione di successi nella Popolazione 1
p2 <- 0.4  # Proporzione di successi nella Popolazione 2
n1 <- 150  # Dimensione campionaria per la Popolazione 1
n2 <- 150  # Dimensione campionaria per la Popolazione 2

# Simulazione di 10.000 campioni indipendenti
set.seed(123)
sample_p1 <- replicate(10000, mean(rbinom(n1, size = 1, prob = p1)))
sample_p2 <- replicate(10000, mean(rbinom(n2, size = 1, prob = p2)))

# Calcolo della differenza tra proporzioni campionarie
sample_diff <- sample_p1 - sample_p2

# Parametri teorici della distribuzione normale approssimata
mean_diff <- p1 - p2
sd_diff <- sqrt((p1 * (1 - p1) / n1) + (p2 * (1 - p2) / n2))

# Creazione del data frame per ggplot2
df_diff <- data.frame(sample_diff = sample_diff)

# Visualizzazione con ggplot2
ggplot(df_diff, aes(x = sample_diff)) +
  geom_histogram(
    aes(y = after_stat(density)), bins = 40, fill = "blue", alpha = 0.6
  ) +
  stat_function(
    fun = dnorm,
    args = list(mean = mean_diff, sd = sd_diff),
    color = "red",
    size = 1
  ) +
  labs(
    title = "Distribuzione campionaria della differenza tra proporzioni",
    x = "Differenza campionaria (p1 - p2)",
    y = "Densità"
  )

# Calcolo della probabilità che la differenza sia maggiore di 0.1
exact_probability <- mean(sample_diff > 0.1)
exact_probability
#> [1] 0.9599
# Approssimazione tramite distribuzione normale
approx_probability <- 1 - pnorm(0.1, mean = mean_diff, sd = sd_diff)
approx_probability
#> [1] 0.9615
  1. Parametri delle popolazioni:
    • Due popolazioni con proporzioni \(p_1 = 0.6\) e \(p_2 = 0.4\).
    • Dimensioni campionarie \(n_1 = n_2 = 150\).
  2. Simulazione:
    • Per ogni campione, i successi (\(0\) o \(1\)) sono generati con rbinom.
    • Calcoliamo le proporzioni campionarie e la differenza tra di esse.
  3. Distribuzione teorica:
    • Media teorica: \(p_1 - p_2\).
    • Deviazione standard teorica: \(\sqrt{\frac{p_1 (1-p_1)}{n_1} + \frac{p_2 (1-p_2)}{n_2}}\).
  4. Visualizzazione:
    • Un istogramma di \(\hat{p}_1 - \hat{p}_2\) sovrapposto alla curva della distribuzione normale teorica.
  5. Calcolo della probabilità:
    • Probabilità esatta dalla simulazione: proporzione di \(\hat{p}_1 - \hat{p}_2 > 0.1\).
    • Probabilità approssimata dalla distribuzione normale.

Domande di Discussione.

  1. L’approssimazione normale è valida in questo caso? Perché?
  2. Come cambierebbe la distribuzione campionaria se \(n_1\) o \(n_2\) fossero più piccoli?
  3. Come influenzerebbe la probabilità calcolata un valore \(p_1\) o \(p_2\) più vicino a \(0\) o \(1\)?

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] thematic_0.1.7   MetBrewer_0.2.0  ggokabeito_0.1.0 see_0.11.0      
#>  [5] gridExtra_2.3    patchwork_1.3.0  bayesplot_1.13.0 psych_2.5.3     
#>  [9] scales_1.4.0     markdown_2.0     knitr_1.50       lubridate_1.9.4 
#> [13] forcats_1.0.0    stringr_1.5.1    dplyr_1.1.4      purrr_1.0.4     
#> [17] readr_2.1.5      tidyr_1.3.1      tibble_3.3.0     ggplot2_3.5.2   
#> [21] tidyverse_2.0.0  rio_1.2.3        here_1.0.1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] generics_0.1.4     stringi_1.8.7      lattice_0.22-7    
#>  [4] hms_1.1.3          digest_0.6.37      magrittr_2.0.3    
#>  [7] evaluate_1.0.4     grid_4.5.0         timechange_0.3.0  
#> [10] RColorBrewer_1.1-3 fastmap_1.2.0      rprojroot_2.0.4   
#> [13] jsonlite_2.0.0     mnormt_2.1.1       cli_3.6.5         
#> [16] rlang_1.1.6        withr_3.0.2        tools_4.5.0       
#> [19] parallel_4.5.0     tzdb_0.5.0         pacman_0.5.1      
#> [22] vctrs_0.6.5        R6_2.6.1           lifecycle_1.0.4   
#> [25] htmlwidgets_1.6.4  pkgconfig_2.0.3    pillar_1.10.2     
#> [28] gtable_0.3.6       glue_1.8.0         xfun_0.52         
#> [31] tidyselect_1.2.1   rstudioapi_0.17.1  farver_2.1.2      
#> [34] htmltools_0.5.8.1  nlme_3.1-168       labeling_0.4.3    
#> [37] rmarkdown_2.29     compiler_4.5.0