27 La Probabilità come misura della certezza razionale: un’interpretazione Bayesiana
- comprendere le nozioni di misura e distribuzione di probabilità, seguendo l’approccio presentato da Michael Betancourt.
- Leggere il capitolo Probability and counting del testo di Blitzstein & Hwang (2019).
- Leggere il Appendice G dell’Appendice.
- Leggere il Appendice H dell’Appendice.
27.1 Introduzione
Nel Capitolo 26 abbiamo introdotto il concetto di probabilità come una funzione che soddisfa gli assiomi di Kolmogorov:
- Non-negatività e normalizzazione: \(0 \leq P(A) \leq 1\) per ogni evento \(A\), con \(P(\Omega) = 1\).
- Additività numerabile: Per una successione di eventi disgiunti \(\{A_i\}\), \[ P\Bigl(\bigcup_{i} A_i\Bigr) = \sum_{i} P(A_i) . \]
Sebbene questa formalizzazione matematica sia essenziale, rimane aperta una questione fondamentale: qual è il significato intrinseco dei valori numerici che chiamiamo “probabilità”? Questo interrogativo ha alimentato un secolare dibattito filosofico che esploreremo in questo capitolo attraverso la lente dell’interpretazione bayesiana.
Adotteremo una prospettiva in cui la probabilità non descrive frequenze osservabili, bensì quantifica il grado di convinzione razionale di un agente epistemico. In questa visione soggettivista, la probabilità diventa una misura normativa di come dovremmo allocare la nostra certezza totale (normalizzata a 1) tra proposizioni mutualmente esclusive ed esaustive.
Per rendere operativo questo framework, seguiremo la trattazione proposta da Michael Betancourt. Ci concentreremo qui sull’interpretazione della probabilità come distribuzione della nostra certezza soggettiva.
27.2 Distribuzione della Certezza Soggettiva sugli Elementi
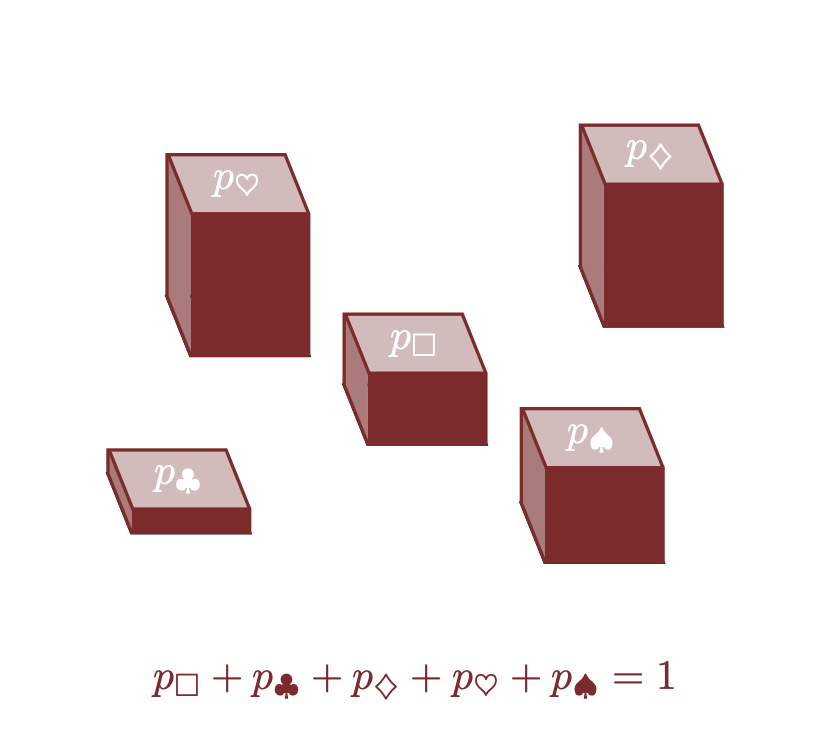
In un approccio bayesiano, la probabilità rappresenta il grado di certezza soggettiva che attribuiamo al verificarsi di un certo evento. Immaginiamo di possedere una certezza totale pari a 1, che corrisponde alla nostra convinzione complessiva che, tra tutti gli esiti possibili, qualcosa avverrà. Questa certezza totale deve essere ripartita tra i diversi eventi.
Consideriamo il seguente spazio campionario discreto:
\[ X = \{\Box, \clubsuit, \diamondsuit, \heartsuit, \spadesuit\}. \]
Ad ogni elemento \(x_n \in X\) associamo un valore \(p_n \geq 0\), interpretato come la frazione della nostra certezza totale che assegnamo a quell’evento. Poiché la certezza complessiva è 1, la somma dei valori deve essere:
\[ p_{\Box} + p_{\clubsuit} + p_{\diamondsuit} + p_{\heartsuit} + p_{\spadesuit} = 1. \]
Questa collezione \(\{ p_{\Box}, p_{\clubsuit}, p_{\diamondsuit}, p_{\heartsuit}, p_{\spadesuit} \}\), in cui ciascun valore è compreso tra 0 e 1, è quella che chiamiamo distribuzione di probabilità. Ogni \(p_n\) esprime il grado di certezza (in termini relativi) che attribuiamo all’evento corrispondente a \(x_n\).
Questa visione ci permette di passare da una certezza assoluta (1) a una distribuzione in cui la certezza è divisa in porzioni proporzionali tra i vari eventi. Per esempio, se siamo particolarmente convinti che l’evento \(\Box\) si verifichi, potremmo assegnargli un valore alto, mentre a un evento meno probabile corrisponderà un valore più basso.
27.3 Distribuzione della Certezza Sugli Sottoinsiemi
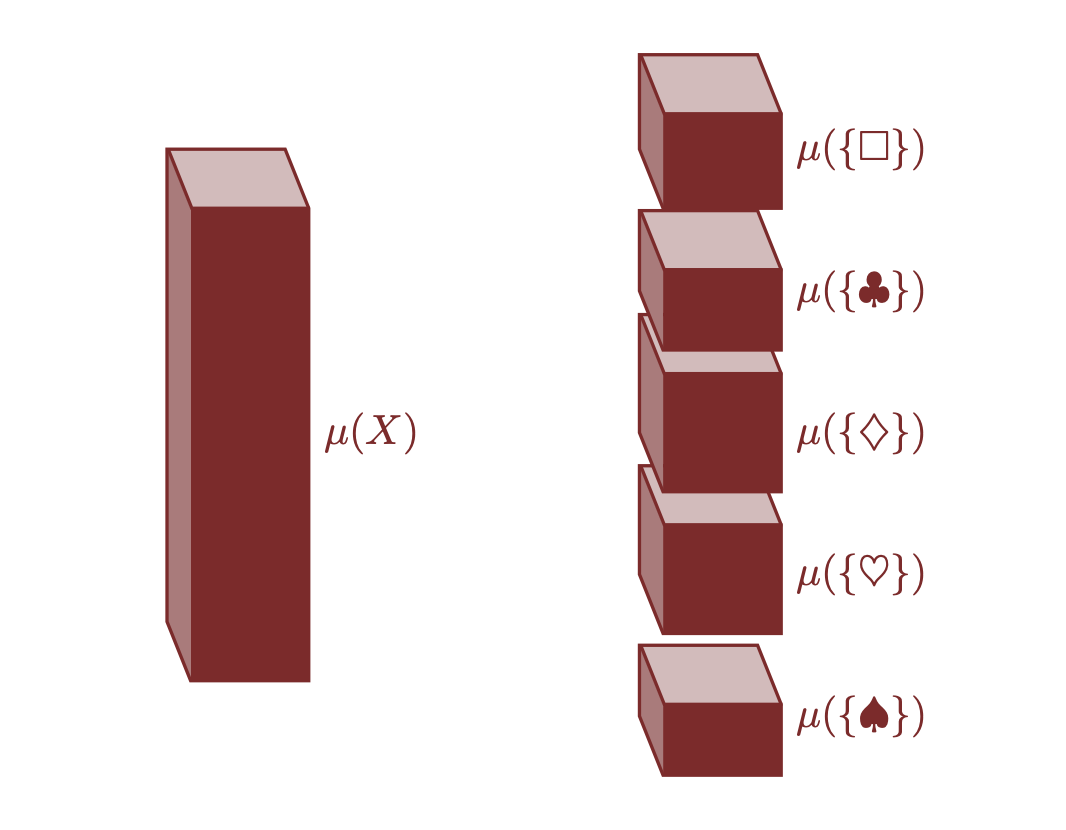
Una volta che abbiamo assegnato un grado di certezza soggettiva a ciascun elemento di \(X\), possiamo estendere questa assegnazione a qualsiasi sottoinsieme di \(X\). In altre parole, se ad ogni elemento \(x_n \in X\) assegniamo la probabilità (cioè, il grado di certezza) \(p_n\), la certezza complessiva che un sottoinsieme \(\mathsf{x} \subset X\) si realizzi è data dalla somma dei gradi di certezza dei suoi elementi:
\[ P(\mathsf{x}) = \sum_{x_n \in \mathsf{x}} p_n. \]
Per costruzione, valgono le seguenti proprietà:
La certezza associata all’insieme vuoto è zero:
\[ P(\emptyset) = 0. \]
La certezza associata all’intero spazio campionario è 1:
\[ P(X) = \sum_{n} p_n = 1. \]
Queste proprietà sono in linea con l’idea che la nostra certezza totale (pari a 1) venga completamente distribuita tra tutti gli eventi possibili.
27.3.1 Additività
Se un sottoinsieme può essere suddiviso in parti che non si sovrappongono, il grado di certezza dell’intero sottoinsieme è la somma dei gradi di certezza delle parti. Ad esempio, se \(\mathsf{x}_1\) e \(\mathsf{x}_2\) sono sottoinsiemi disgiunti (cioè, non hanno elementi in comune), allora:
\[ P(\mathsf{x}_1 \cup \mathsf{x}_2) = P(\mathsf{x}_1) + P(\mathsf{x}_2). \]
In particolare, se \(\mathsf{x}\) è un sottoinsieme di \(X\), il complemento \(\mathsf{x}^c\) (cioè, tutti gli elementi non in \(\mathsf{x}\)) è disgiunto da \(\mathsf{x}\) e la loro unione dà \(X\). Quindi:
\[ P(\mathsf{x}) + P(\mathsf{x}^c) = 1 \quad \Longrightarrow \quad P(\mathsf{x}^c) = 1 - P(\mathsf{x}). \]
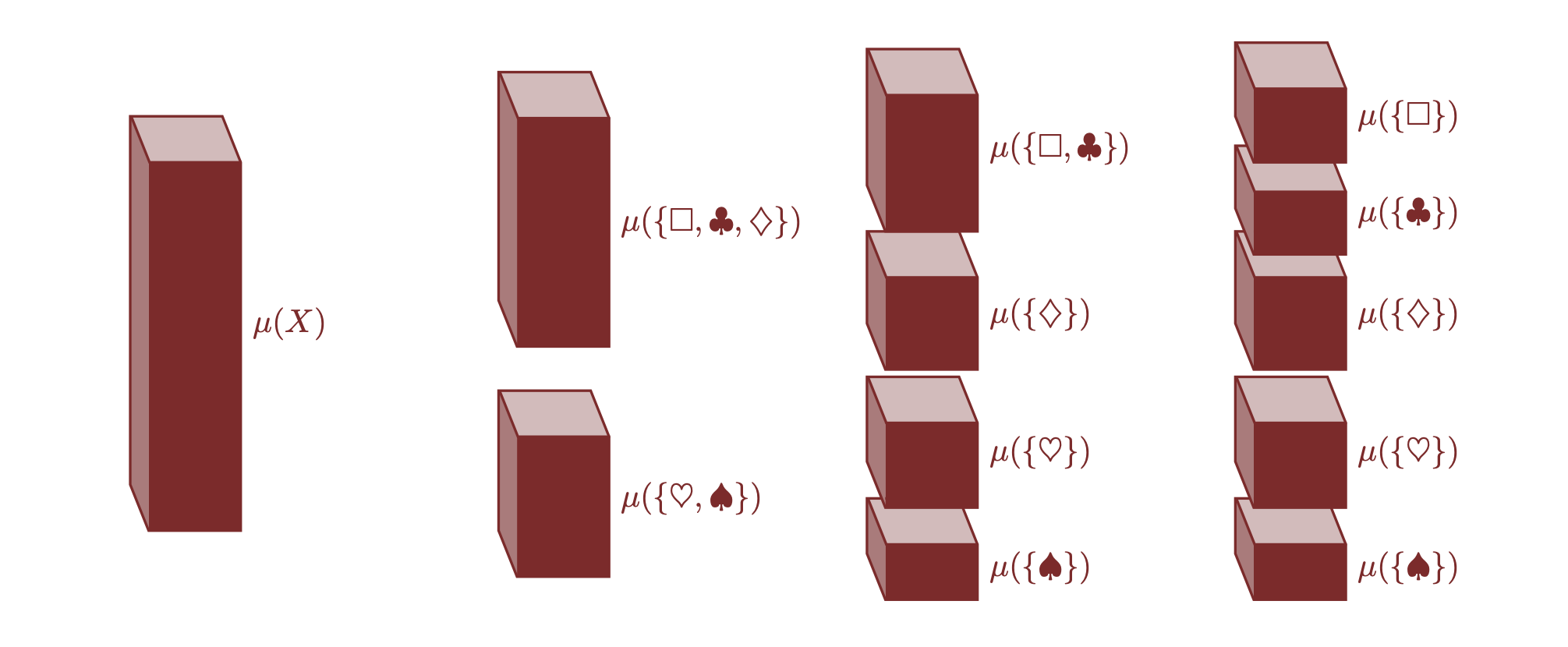
27.3.2 Sovrapposizione di Sottoinsiemi
Quando due sottoinsiemi si sovrappongono, la certezza degli elementi comuni viene conteggiata in entrambe le somme. Per chiarire, consideriamo:
- \(\mathsf{x}_1 = \{\Box, \heartsuit\}\),
- \(\mathsf{x}_2 = \{\Box, \spadesuit\}\).
Allora:
La certezza di \(\mathsf{x}_1\) è \(P(\mathsf{x}_1) = p_{\Box} + p_{\heartsuit}\).
La certezza di \(\mathsf{x}_2\) è \(P(\mathsf{x}_2) = p_{\Box} + p_{\spadesuit}\).
L’intersezione è \(\mathsf{x}_1 \cap \mathsf{x}_2 = \{\Box\}\), con certezza \(p_{\Box}\).
L’unione è \(\mathsf{x}_1 \cup \mathsf{x}_2 = \{\Box, \heartsuit, \spadesuit\}\), con certezza
\[ P(\mathsf{x}_1 \cup \mathsf{x}_2) = p_{\Box} + p_{\heartsuit} + p_{\spadesuit}. \]
Notiamo che:
\[ P(\mathsf{x}_1) + P(\mathsf{x}_2) = P(\mathsf{x}_1 \cup \mathsf{x}_2) + p_{\Box} = P(\mathsf{x}_1 \cup \mathsf{x}_2) + P(\mathsf{x}_1 \cap \mathsf{x}_2). \]
Questo è un esempio del principio di inclusione-esclusione, che garantisce che non contiamo più volte la certezza degli elementi comuni.
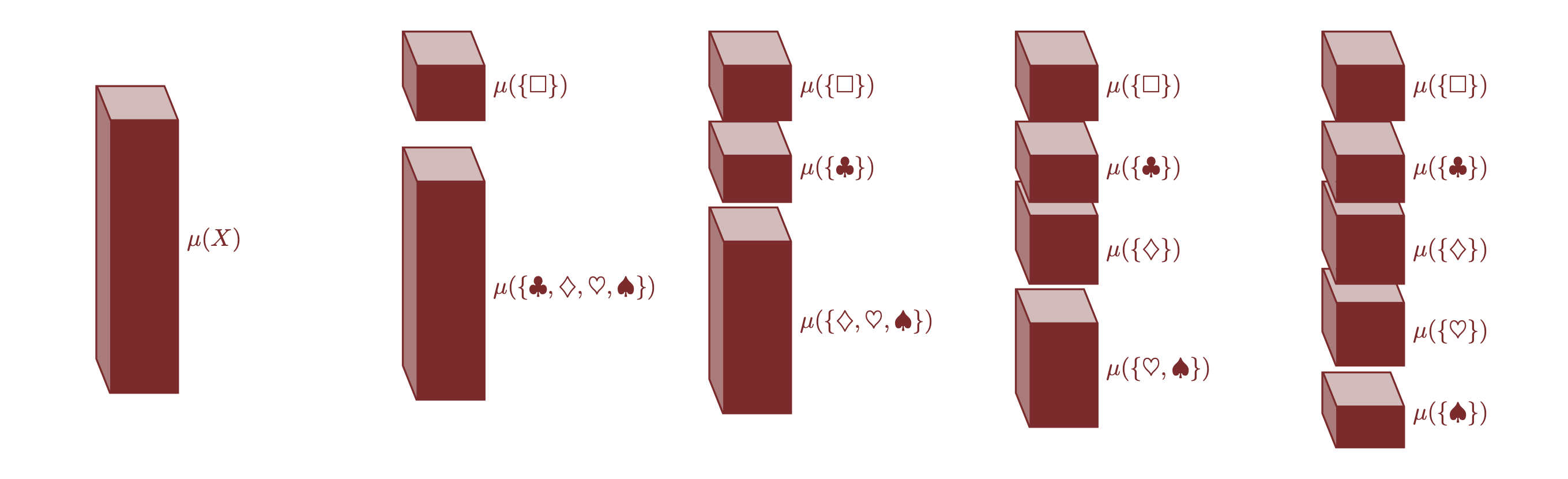
27.4 Costruzione delle Distribuzioni di Certezza
Esistono diversi modi per “costruire” una distribuzione di certezza (cioè, una distribuzione di probabilità) su uno spazio finito \(X\):
Distribuzione globale:
Possiamo assegnare simultaneamente il grado di certezza a tutti gli elementi di \(X\). In questo approccio si specifica direttamente la distribuzione \(\{p(x_n)\}\) per ciascun \(x_n \in X\), in modo tale che\[ \sum_{x_n \in X} p(x_n) = 1. \]
Figura 27.2: Le misure possono essere costruite specificando le allocazioni degli elementi individuali tutte insieme. Distribuzione locale:
Possiamo assegnare il grado di certezza a ciascun elemento uno alla volta, procedendo in maniera sequenziale. Questo metodo ci permette di “costruire” la distribuzione gradualmente, concentrandoci su un elemento alla volta.
Figura 27.3: Le misure possono essere costruite specificando le allocazioni degli elementi individuali uno alla volta. Distribuzione iterativa:
Un altro metodo consiste nel suddividere lo spazio campionario in sottoinsiemi disgiunti, assegnare ad ognuno un certo grado di certezza, e poi ripartire iterativamente la certezza all’interno di ciascun sottoinsieme fino a raggiungere gli elementi individuali.
Figura 27.4: Le misure possono essere costruite allocando la misura totale a sottoinsiemi disgiunti e poi raffinando iterativamente tale allocazione a sottoinsiemi sempre più piccoli.
Questa flessibilità consente di adattare l’approccio alle esigenze specifiche del problema in esame.
27.5 Riflessioni Conclusive
L’interpretazione della probabilità come grado di certezza soggettiva ci offre un modo intuitivo per ragionare su eventi incerti. La nostra certezza totale, pari a 1, viene distribuita tra i vari possibili esiti secondo una distribuzione di probabilità:
\[ \{p_1, p_2, \dots, p_N\} \quad \text{con} \quad 0 \leq p_n \leq 1 \quad \text{e} \quad \sum_{n=1}^{N} p_n = 1. \]
Ogni valore \(p_n\) rappresenta la frazione della nostra certezza che attribuiamo all’evento corrispondente a \(x_n\). Questo approccio è particolarmente utile nella statistica bayesiana, dove le probabilità vengono interpretate non come frequenze oggettive, ma come gradi di convinzione soggettivi basati sulle informazioni a nostra disposizione.
Esercizi
Dal testo di Blitzstein & Hwang (2019), svolgere i seguenti esercizi: 1.4.3, 1.4.4, 1.4.5, 1.4.6, 1.4.9, 1.4.12, 1.4.13.