64  Zucchero sintattico

In questo capitolo imparerai a

• utilizzare brm per costruire e adattare modelli;
• analizzare i risultati con brm.

Prerequisiti

• Leggere Navigating the Bayes maze: The psychologist’s guide to Bayesian statistics, a hands-on tutorial with R code (Alter et al., 2025).
• Consultare The brms Book: Applied Bayesian Regression Modelling Using R and Stan.

Preparazione del Notebook

here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, posterior, cmdstanr, tidybayes)

64.1 Introduzione

I modelli lineari sono così ampiamente utilizzati che sono stati sviluppati appositamente una sintassi, dei metodi e delle librerie per la regressione. Una di queste librerie è brms (Bayesian Regression Models using Stan), già introdotta nel Capitolo 63. brms è un pacchetto R progettato per adattare modelli gerarchici generalizzati lineari (di cui il modello lineare bivariato è un caso particolare), utilizzando una sintassi simile a quella presente nei pacchetti R, come lm, lme4, nlme, rstanarm. brms si basa su Stan, ma offre un’API di livello superiore.

In questo capitolo esploreremo in maniera dettagliata come condurre un’analisi di regressione utilizzando brms invece di Stan.

64.2 Interfaccia brms

Per fare un esempio, applicheremo il modello di regressione bivariato alla relazione tra altezza e peso. I dati contenuti nel file Howell_18.csv sono parte di un censimento parziale della popolazione !Kung San dell’area di Dobe, raccolti tramite interviste condotte da Nancy Howell alla fine degli anni ’60 (McElreath, 2020). I !Kung San sono una delle popolazioni di raccoglitori-cacciatori più conosciute del ventesimo secolo e sono stati oggetto di numerosi studi antropologici. In questa analisi, consideriamo un sottocampione di dati relativi alla popolazione adulta (di età superiore ai 18 anni).

Importiamo i dati contenuti nel file Howell_18.csv.

df <- rio::import(here::here("data", "Howell_18.csv"))

df |> 
  head()
#>   height weight age male
#> 1  151.8  47.83  63    1
#> 2  139.7  36.49  63    0
#> 3  136.5  31.86  65    0
#> 4  156.8  53.04  41    1
#> 5  145.4  41.28  51    0
#> 6  163.8  62.99  35    1

Generiamo un diagramma a dispersione tra le variabili height (altezza) e weight (peso):

ggplot(df, aes(x = weight, y = height)) +
  geom_point() +  
  labs(x = "Weight", y = "Height")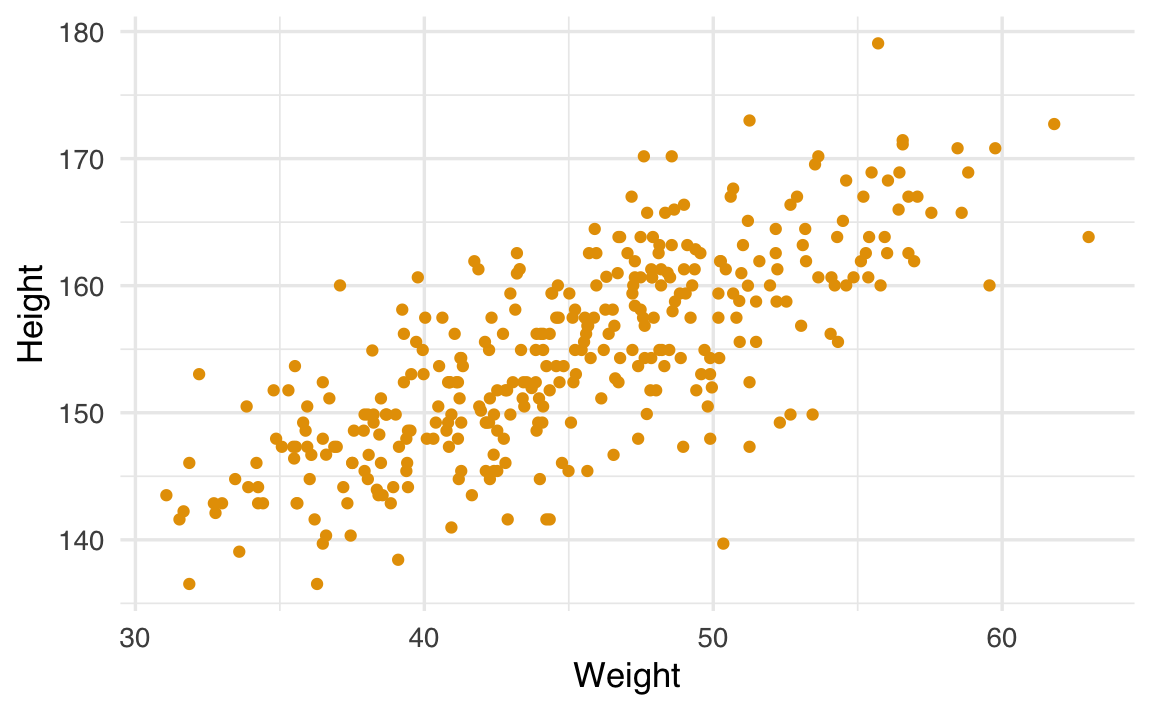 

brms si concentra sui modelli di regressione, e questa specializzazione permette di adottare una sintassi più semplice, conosciuta come sintassi di Wilkinson (Wilkinson & Rogers, 1973).

Ad esempio, il modello \(y = \alpha + \beta x + \varepsilon\) si implementa come segue:

a_model = brm(y ∼ 1 + x, data = df)

Nella sintassi di Wilkinson, il simbolo tilde (∼) separa la variabile dipendente (a sinistra) dalle variabili indipendenti (a destra). In questo caso, stiamo specificando solo la media (\(\mu\)) della \(y\).

brms assume di default che la distribuzione di verosimiglianza sia gaussiana, ma è possibile modificarla tramite l’argomento family.

La notazione 1 si riferisce all’intercetta. L’intercetta viene inclusa di default. Per cui il modello precedente si può anche scrivere, in maniera equivalente, come

a_model = brm(y ∼ x, data = df)

Se desideriaamo escludere l’intercetta dal modello, possiamo farlo in questo modo

no_intercept_model = brm(y ∼ 0 + x, data = df)

oppure in questo modo

no_intercept_model = brm(y ∼ -1 + x, data = df)

Per includere ulteriori variabili nel modello, possiamo procedere così:

model_2 = brm("y ∼ x + z", data)

brms consente anche di includere effetti a livello di gruppo (gerarchici). Ad esempio, se desideriamo un modello ad effetti misti nel quale abbiamo un effetto diverso di \(x\) in ciascun gruppo g, possiamo usare la seguente sintassi:

model_h = brm(y ∼ x + z + (x | g), data = df)

La sintassi di Wilkinson non specifica le distribuzioni a priori, ma solo come le variabili dipendenti e indipendenti sono collegate. brms definirà automaticamente delle distribuzioni a priori debolmente informative per noi, rendendo superflua la loro definizione esplicita. Tuttavia, se preferiamo avere un maggiore controllo, possiamo specificarle manualmente, come vedremo in seguito.

64.2.1 Centrare le Variabili

Per interpretare più facilmente l’intercetta, centriamo la variabile weight rispetto alla media del campione:

df$weight_c <- df$weight - mean(df$weight)

Ora, l’intercetta (\(\alpha\)) rappresenterà l’altezza media quando il peso corrisponde alla media del campione.

Adattiamo un modello lineare con la variabile weight centrata e esaminiamo i risultati:

fit_1 = brm(
  bf(height ~ 1 + weight_c, center = FALSE), 
  data = df, 
  backend = "cmdstanr", 
  silent = 0
)

Utilizzando center = FALSE nel modello Bayesiano garantiamo che il centraggio venga mantenuto e non applicato nuovamente da brms.

L’argomento backend = "cmdstanr" indica a brms di usare cmdstan per il campionamento, al posto di Stan che è l’impostazione predefinita. Poiché in questo insegnamento utilizzeremo cmdstan, è essenziale specificare questo backend.

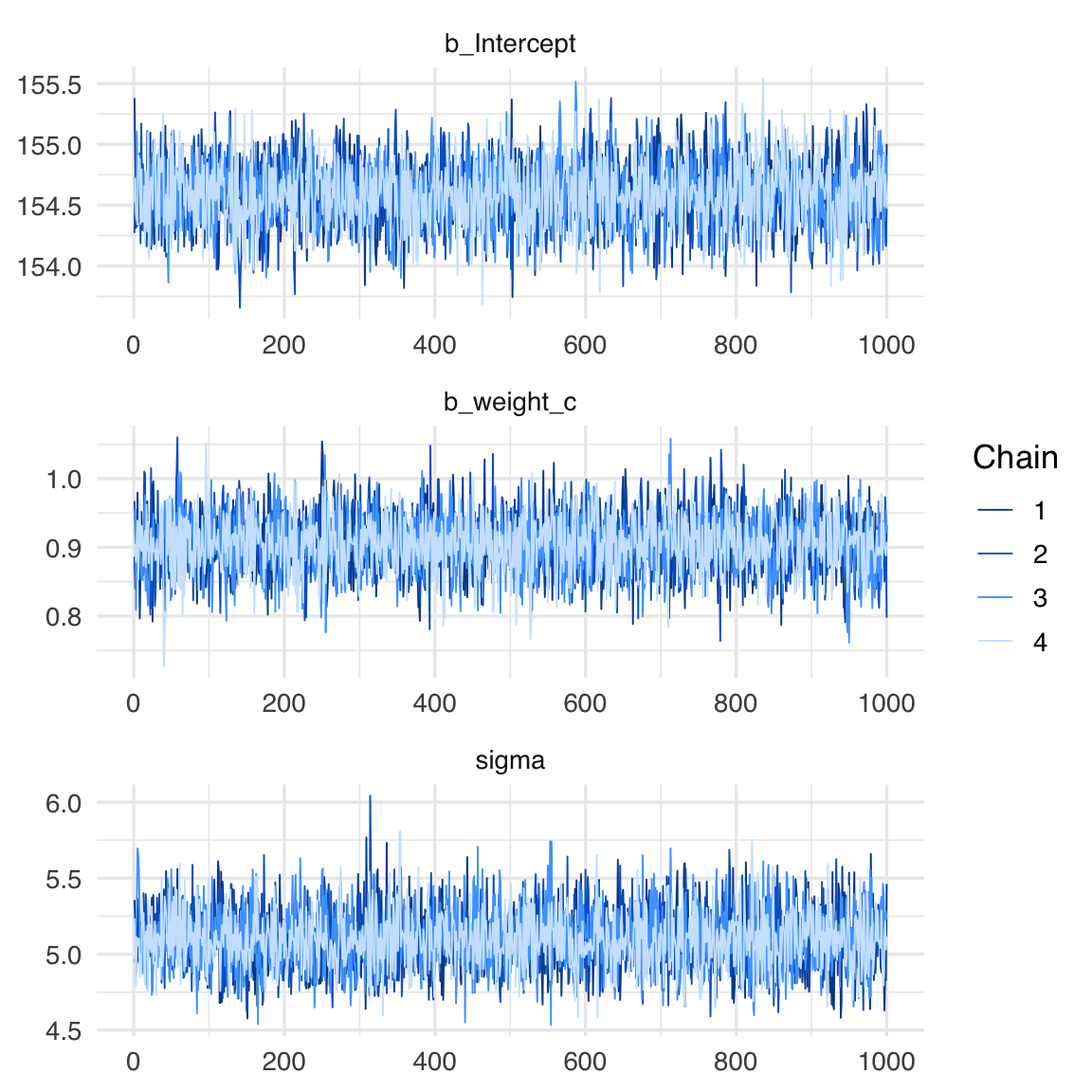
Le tracce dei parametri si ottengono nel modo seguente:

mcmc_trace(
  fit_1, 
  pars = c("b_Intercept", "b_weight_c", "sigma"),
  facet_args = list(nrow = 3)
)

summary(fit_1)
#>  Family: gaussian 
#>   Links: mu = identity; sigma = identity 
#> Formula: height ~ 1 + weight_c 
#>    Data: df (Number of observations: 352) 
#>   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 4000
#> 
#> Regression Coefficients:
#>           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept   154.59      0.27   154.06   155.11 1.00     3947     2871
#> weight_c      0.91      0.04     0.82     0.99 1.00     3945     2996
#> 
#> Further Distributional Parameters:
#>       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma     5.10      0.20     4.74     5.51 1.00     4902     3275
#> 
#> Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

La stima dell’intercetta \(\alpha\) = 154.60 suggerisce che, per le persone con un peso corrispondente al valore medio del campione analizzato, l’altezza prevista è di 154.60 cm.

Possiamo confrontare i risultati ottenuti da brm() con quelli prodotti dall’approccio frequentista:

fit_2 <- lm(height ~ 1 + weight_c, data = df)

summary(fit_2)
#> 
#> Call:
#> lm(formula = height ~ 1 + weight_c, data = df)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -19.746  -2.884   0.022   3.142  14.774 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)
#> (Intercept)  154.597      0.271   570.2   <2e-16
#> weight_c       0.905      0.042    21.5   <2e-16
#> 
#> Residual standard error: 5.09 on 350 degrees of freedom
#> Multiple R-squared:  0.57,   Adjusted R-squared:  0.568 
#> F-statistic:  463 on 1 and 350 DF,  p-value: <2e-16

L’uso di prior debolmente informativi fa in modo che i risultati dei due approcci siano praticamente equivalenti.

64.3 Visualizzazione dei Risultati

Per comprendere visivamente la relazione stimata tra peso e altezza nel nostro modello bayesiano, utilizziamo la funzione conditional_effects:

conditional_effects(fit_1, effects = "weight_c")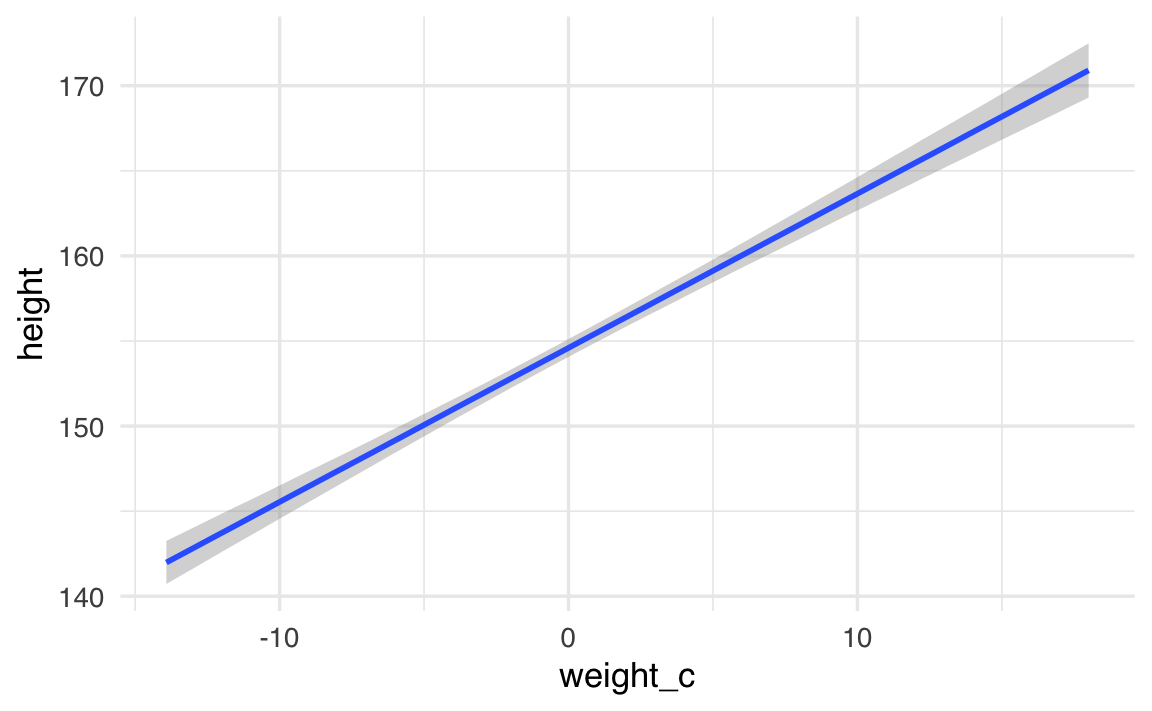

Il grafico generato fornisce una rappresentazione completa della relazione stimata:

• Linea centrale (media posteriore): rappresenta la stima più probabile dell’altezza per ciascun valore del peso centrato.
• Area colorata (intervallo di credibilità): mostra l’intervallo di densità più alta (HDI) al 95%, indicando l’incertezza attorno alla stima centrale.

È possibile adattare il livello di incertezza mostrato modificando l’argomento prob:

# Visualizzazione con intervallo di credibilità all'89%
conditional_effects(fit_1, effects = "weight_c", prob = 0.89)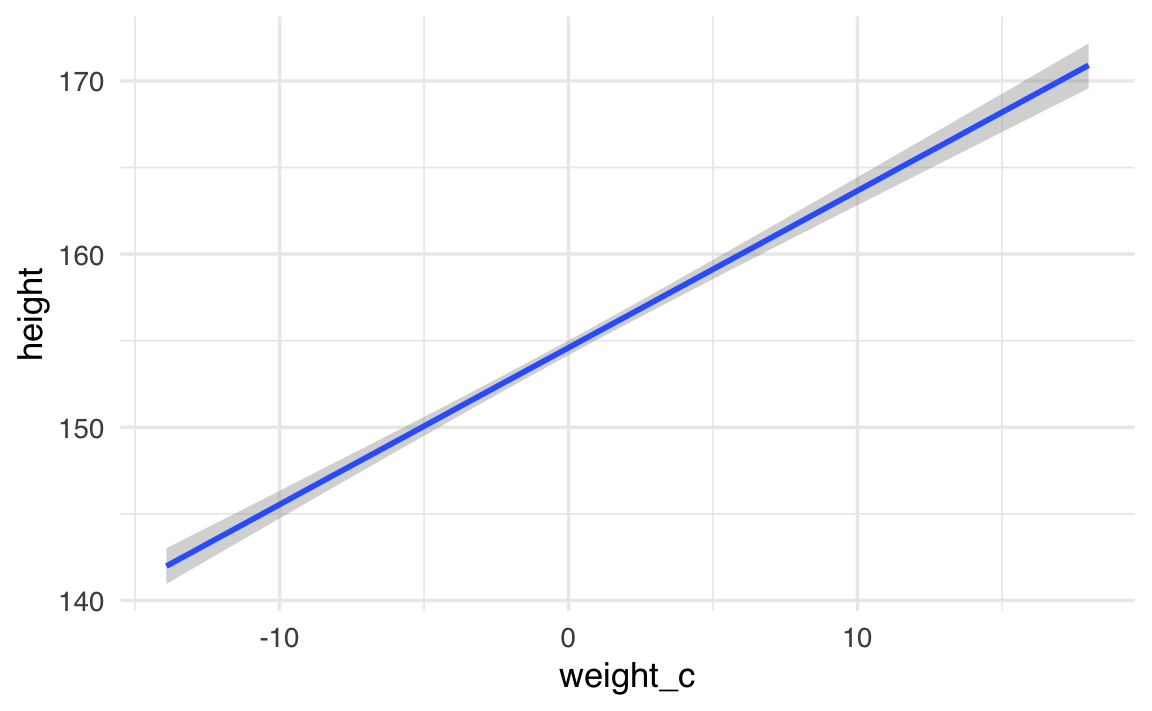

Ridurre il valore di prob (es. a 0.80 o 0.50) produce un intervallo più stretto, mentre aumentarlo (es. a 0.99) amplia l’area di incertezza visualizzata.

64.3.1 Interpretazione Pratica del Grafico

Nel grafico:

• il punto dove la linea attraversa weight_c = 0 corrisponde all’altezza prevista per un individuo con peso medio (poiché abbiamo centrato la variabile);
• la pendenza della linea indica quanto ci aspettiamo che l’altezza aumenti per ogni kg di peso aggiuntivo;
• la larghezza dell’intervallo di credibilità indica la nostra certezza sulle stime: più stretto l’intervallo, maggiore la certezza.

64.4 Due Tipi di Incertezza nei Modelli Bayesiani

Immaginiamo di voler capire come il peso (variabile X) sia collegato all’altezza (variabile Y) in un gruppo di persone. Con un modello bayesiano ottieniamo due tipi distinti di informazioni incerte:

Che cosa stiamo stimando?	Come si chiama l’incertezza?	Che intervallo disegniamo?
La media “vera” dell’altezza per ogni valore di peso	Incertezza del parametro (o dell’effetto medio)	Intervallo di credibilità (credibility/credible interval)
La singola osservazione futura (quanto sarà alta la prossima persona di quel peso)	Incertezza predittiva	Intervallo di predizione (prediction interval)

64.4.1 Incertezza del parametro – «Quanto stiamo sbagliando la linea media?»

• Che cosa fa il codice

  conditional_effects(fit_1, effects = "weight_c")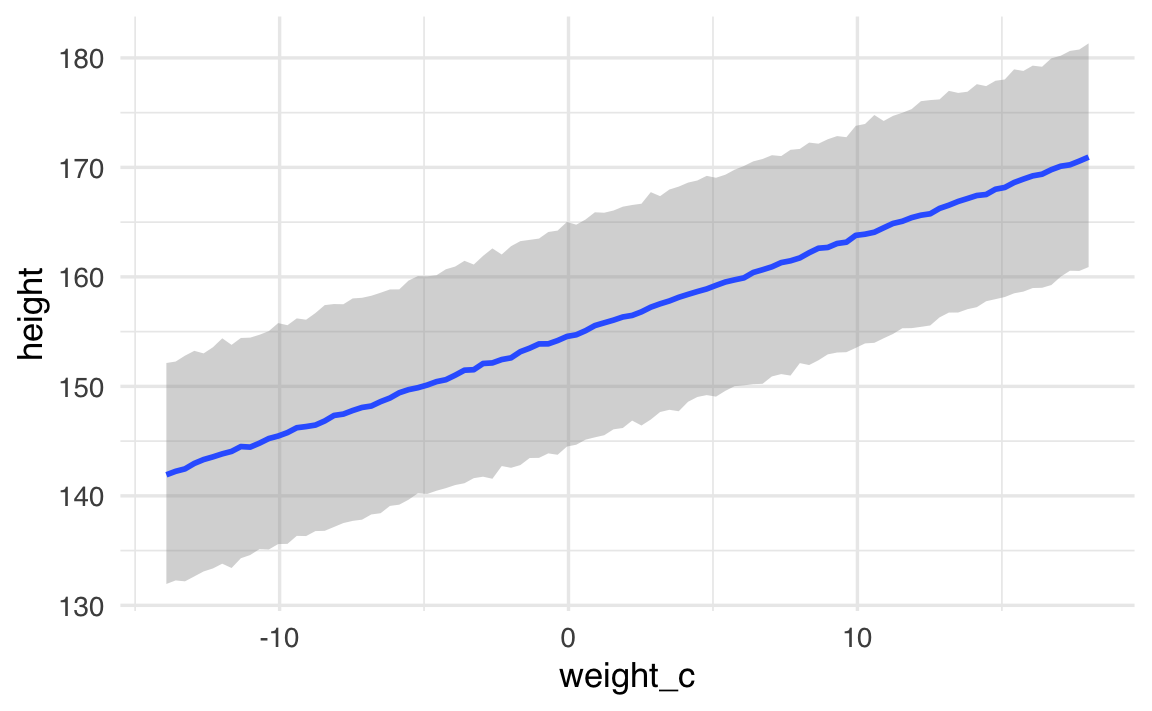

  

  • Disegna la linea di regressione (in pratica: la media stimata dell’altezza per ogni peso).
    
  • Aggiunge intorno una fascia stretta: è l’intervallo di credibilità al 95 %.
    

• Come leggerla

  • Se la fascia copre, ad esempio, da 170 cm a 172 cm per un peso di 70 kg, significa che “con il 95 % di probabilità la vera media dell’altezza per quel peso sta lì dentro”.
    
  • Non dice nulla sul fatto che le persone individuali possano essere molto più basse o molto più alte.

Metafora veloce
Pensa a tirare freccette: la freccia media cade vicino al centro, ma ogni singola freccia può andare ovunque sul bersaglio. L’intervallo di credibilità descrive la posizione del centro.

64.4.2 Incertezza predittiva – «Quanto potrebbe variare la prossima persona?»

• Che cosa fa il codice

  conditional_effects(fit_1, effects = "weight_c", method = "predict")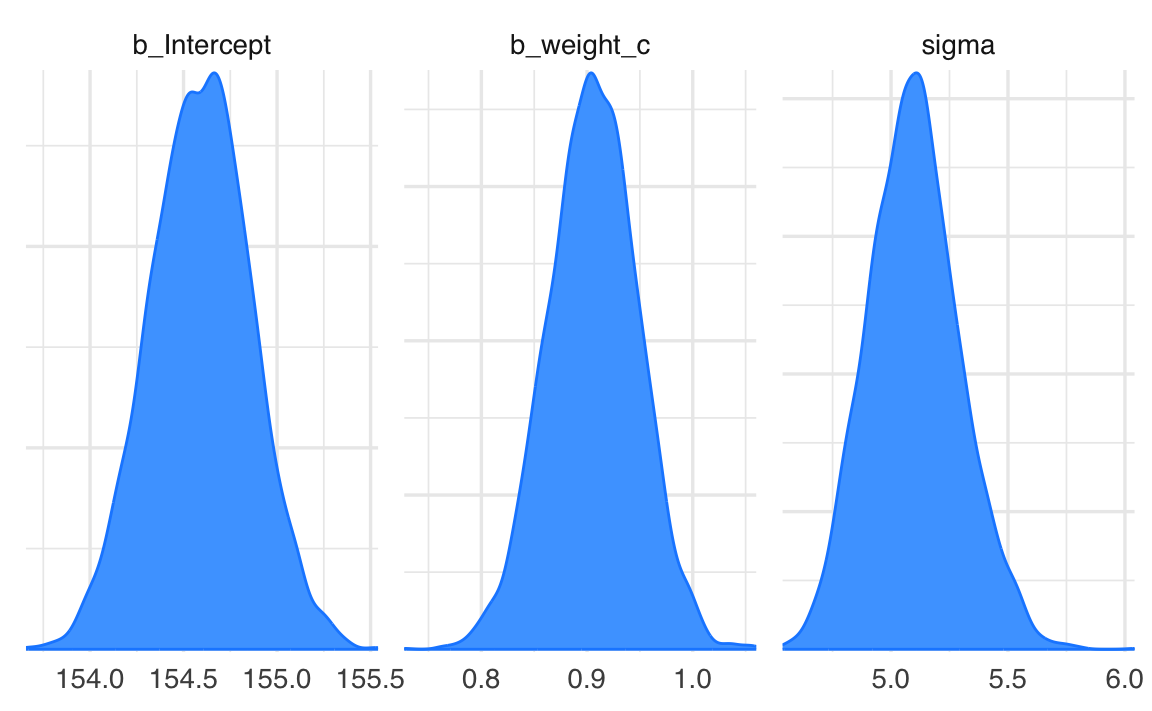

  

  • Ripropone la stessa linea media.
    
  • Disegna però una fascia molto più larga: l’intervallo di predizione.
    

• Perché è più largo

  • Contiene le due fonti di variabilità:
    1. Incertezza sulla linea media (come sopra).
       
    2. Variabilità residua: le differenze naturali tra persone di uguale peso (chi è più muscoloso, chi ha ossa più leggere ecc.).

Metafora veloce
Ora guardi non il centro del bersaglio, ma l’intero disco dove ogni freccia potrebbe atterrare. Quell’area è molto più grande.

64.4.3 Quando usare l’una o l’altra fascia?

Obiettivo della tua domanda	Funzione da usare	Che fascia guardare
Capire l’effetto medio (es. “quanto cresce in media l’altezza al crescere di 1 kg?”)	conditional_effects(...)	Intervallo di credibilità
Fare previsioni su nuovi casi (es. “quanto sarà alta Maria che pesa 70 kg?”)	conditional_effects(..., method = "predict")	Intervallo di predizione

64.4.4 Riepilogo

1. Credibilità = incertezza sul parametro medio → fascia stretta perché stiamo stimando solo la retta di regressione.
   
2. Predizione = incertezza su osservazioni future → fascia larga perché somma l’incertezza della retta + la variabilità individuale.
   
3. Scegliamo la visualizzazione che risponde alla nostra domanda: “qual è la media?” (credibilità) o “dove cadrà il prossimo dato?” (predizione).

In sintesi, la differenza principale sta nell’inclusione o meno della variabilità residua. La visualizzazione predittiva è più onesta riguardo alla nostra capacità di fare previsioni per singole osservazioni, mentre quella standard è più adatta per comprendere la relazione generale tra le variabili.

64.5 Distribuzione a Posteriori dei Parametri

Per esaminare la distribuzione a posteriori dei parametri usiamo la funzione mcmc_plot():

mcmc_plot(fit_1, type = "dens")

Esaminiamo in maggiori dettagli il sommario numerico dei parametri stimati:

draws <- posterior::as_draws(fit_1, variable = "^b_", regex = TRUE)
posterior::summarise_draws(draws, "mean", "sd", "mcse_mean", "mcse_sd")
#> # A tibble: 2 × 5
#>   variable       mean     sd mcse_mean  mcse_sd
#>   <chr>         <dbl>  <dbl>     <dbl>    <dbl>
#> 1 b_Intercept 155.    0.269   0.00428  0.00391 
#> 2 b_weight_c    0.906 0.0423  0.000675 0.000681

Utilizziamo la funzione as_draws() che trasforma un oggetto R in un formato compatibile con posterior. Gli argomenti variable = "^b_" e regex = TRUEconsentono di selezionare solo i parametri il cui nome inizia con b_: nel nostro caso saranno l’intercetta e la pendenza del modello di regressione lineare.

Successivamente usiamo la funzione summarise_draws() con gli argomenti specificati per un sommario della distribuzione a posteriori dei parametri prescelti.

64.5.1 Spiegazione di mcse_mean e mcse_sd

I valori mcse_mean e mcse_sd sono le Monte Carlo Standard Errors (errori standard Monte Carlo) per la stima della media (mean) e della deviazione standard (sd), rispettivamente. Questi valori quantificano l’incertezza associata al processo di campionamento effettuato durante l’analisi bayesiana, in particolare quando si utilizzano algoritmi Monte Carlo come MCMC (Markov Chain Monte Carlo).

64.5.1.1 mcse_mean

• Rappresenta l’errore standard Monte Carlo per la stima della media.
• Indica quanto la media stimata (\(\text{mean}\)) potrebbe variare a causa della finitezza dei campioni generati dall’algoritmo MCMC.
• Un valore di mcse_mean basso rispetto alla deviazione standard (\(\text{sd}\)) suggerisce che il numero di campioni generati è sufficiente per ottenere una stima accurata della media.

64.5.1.2 mcse_sd

• Rappresenta l’errore standard Monte Carlo per la stima della deviazione standard.
• Indica quanto potrebbe variare la stima della deviazione standard (\(\text{sd}\)) a causa del numero finito di campioni generati.
• Anche qui, un valore basso di mcse_sd rispetto alla sd suggerisce che l’incertezza introdotta dal campionamento è trascurabile.

64.5.2 Come interpretarli?

• Proporzione rispetto alla sd:
  • mcse_mean e mcse_sd dovrebbero essere molto più piccoli rispetto ai rispettivi parametri (mean e sd), idealmente almeno un ordine di grandezza inferiore.
  • Ad esempio, per b_Intercept, mcse_mean = 0.0044 è molto più piccolo rispetto a sd = 0.2695, indicando che la stima della media è robusta.
• Indicazione della qualità del campionamento:
  • Valori alti di mcse_mean o mcse_sd rispetto alla sd potrebbero indicare che il numero di iterazioni MCMC non è sufficiente, che le catene non sono ben mescolate o che ci sono problemi di convergenza.

In sintesi, mcse_mean e mcse_sd sono utili per valutare l’affidabilità delle stime derivate dal campionamento Monte Carlo. Se questi valori sono bassi, possiamo essere confidenti che il numero di campioni è sufficiente per rappresentare accuratamente la distribuzione a posteriori.

64.6 Specificare i Priors

Se vogliamo personalizzare i priors, possiamo utilizzare la funzione get_prior per esplorare quelli predefiniti:

get_prior(height ~ 1 + weight_c, data = df)
#>                     prior     class     coef group resp dpar nlpar lb ub
#>  student_t(3, 154.3, 8.5) Intercept                                     
#>                    (flat)         b                                     
#>                    (flat)         b weight_c                            
#>      student_t(3, 0, 8.5)     sigma                                 0   
#>        source
#>       default
#>       default
#>  (vectorized)
#>       default

1. prior: descrive il prior predefinito assegnato a ciascun parametro del modello. Ad esempio:
   • student_t(3, 154.3, 8.5): prior t di Student per l’intercetta con 3 gradi di libertà, una media di 154.3, e una scala di 8.5.
   • (flat): prior piatto (non informativo) per i coefficienti delle variabili predittive, come \(b\) e \(b_{weight_c}\).
   • student_t(3, 0, 8.5): prior t di Student per il parametro \(\sigma\) (deviazione standard residua), centrato su 0 con una scala di 8.5.
2. class: identifica la classe di parametro a cui il prior si applica:
   • Intercept: prior per l’intercetta (\(\alpha\)).
   • b: prior per i coefficienti delle variabili predittive (\(\beta\)).
   • sigma: prior per il parametro della deviazione standard residua (\(\sigma\)).
3. coef: specifica a quale predittore si riferisce il prior, se applicabile. Ad esempio:
   • Vuoto per l’intercetta (poiché non dipende da un predittore specifico).
   • weight_c per il coefficiente relativo al predittore weight_c.
4. lb e ub: rappresentano rispettivamente i limiti inferiori (lower bound) e superiori (upper bound) per il prior, se specificati. Ad esempio:
   • Per sigma, il limite inferiore è \(0\), dato che la deviazione standard non può essere negativa.
5. source: indica l’origine del prior. Se il prior è predefinito (default), il valore sarà default. Se un prior è specificato manualmente dall’utente, sarà indicato come tale.

Ora impostiamo priors espliciti e adattiamo un nuovo modello:

prior_guassian <-
  brms::prior(normal(160, 10), class = "b", coef = "Intercept") +
  brms::prior(normal(0, 5), class = "b", coef = "weight_c") +
  brms::prior(cauchy(0, 5), class = "sigma")

Si noti l’uso di brms::prior(). Questa notazione specifica esplicitamente che stiamo utilizzando la funzione prior() propria del pacchetto brms, evitando potenziali conflitti con funzioni omonime presenti in altre librerie caricate.

fit_2 = brm(
  bf(height ~ 1 + weight_c, center = FALSE), 
  prior = prior_guassian,
  data = df, 
  backend = "cmdstanr", 
  silent = 0
)

Otteniamo un sommario numerico dei parametri stimati:

draws <- posterior::as_draws(fit_2, variable = "^b_", regex = TRUE)
posterior::summarise_draws(draws, "mean", "sd", "mcse_mean", "mcse_sd")
#> # A tibble: 2 × 5
#>   variable       mean     sd mcse_mean  mcse_sd
#>   <chr>         <dbl>  <dbl>     <dbl>    <dbl>
#> 1 b_Intercept 155.    0.273   0.00425  0.00409 
#> 2 b_weight_c    0.905 0.0428  0.000703 0.000678

I prior che abbiamo specificato non cambiano in maniera rilevante la soluzione a posteriori.

64.7 Predizioni Predittive a Posteriori

Un aspetto fondamentale nella valutazione di un modello statistico, sia frequentista che bayesiano, è verificare quanto bene i dati osservati siano rappresentati dalle predizioni del modello. Tuttavia, l’approccio e l’interpretazione differiscono tra i due paradigmi.

64.7.1 Confronto Frequentista

Nel caso frequentista, si confrontano i valori predetti dal modello, \(\hat{y} = \hat{\alpha} + \hat{\beta}x\), con i dati osservati. Questo confronto si basa sull’analisi di:

• la vicinanza della retta di regressione stimata ai dati osservati;
• l’eventuale presenza di pattern nei dati che si discostano da un andamento lineare;
• la variazione della dispersione dei valori di \(y\) rispetto a \(x\) (ad esempio, per verificare l’ipotesi di omoschedasticità).

64.7.2 Approccio Bayesiano

Nell’approccio bayesiano, si eseguono le stesse verifiche di base, ma l’analisi si arricchisce attraverso l’uso delle Predizioni Predittive a Posteriori (Posterior Predictive Checks, PPCs). Questo metodo consente di confrontare i dati osservati con dati simulati dal modello, utilizzando l’incertezza stimata nelle distribuzioni a posteriori dei parametri.

64.7.3 Costruzione delle Predizioni Predittive a Posteriori

Nel caso di un modello bivariato, il processo per generare un grafico delle Predizioni Predittive a Posteriori è il seguente:

1. Dati osservati: Si parte dall’istogramma lisciato dei dati osservati, che rappresenta la distribuzione empirica di \(y\).

2. Simulazione di dati predetti:

   • Si estrae un campione casuale di valori \(\alpha'\), \(\beta'\), e \(\sigma'\) dalle distribuzioni a posteriori dei parametri (\(\alpha\), \(\beta\), e \(\sigma\)).
   • Usando questi valori, si calcolano dati simulati da una distribuzione normale: \[ y_{\text{sim}} \sim \mathcal{N}(\alpha' + \beta'x, \sigma') \] dove \(x\) sono i valori predittori osservati.

3. Creazione di istogrammi: Per ogni campione simulato, si costruisce un istogramma lisciato che rappresenta la distribuzione predetta dal modello.

4. Ripetizione: Il processo viene ripetuto più volte, generando molti istogrammi lisciati.

5. Confronto: Tutti gli istogrammi predetti vengono sovrapposti all’istogramma dei dati osservati. Questo consente di confrontare visivamente la capacità del modello di rappresentare la distribuzione dei dati.

64.7.4 Interpretazione

• Buona corrispondenza: Se gli istogrammi lisciati dei dati simulati si sovrappongono bene all’istogramma dei dati osservati, significa che il modello è in grado di rappresentare adeguatamente il campione corrente.
• Discrepanze: Se vi sono discrepanze sistematiche (ad esempio, picchi o code mancanti nei dati predetti rispetto agli osservati), ciò indica che il modello potrebbe non essere adeguato o che vi sono aspetti dei dati non catturati dal modello.

L’approccio delle Predizioni Predittive a Posteriori è particolarmente potente perché:

• integra l’incertezza nei parametri del modello;
• permette di verificare non solo la bontà di adattamento complessiva, ma anche specifici aspetti delle distribuzioni predette;
• è visivo e intuitivo, facilitando l’identificazione di discrepanze tra modello e dati.

In conclusione, le Predizioni Predittive a Posteriori forniscono un modo robusto per valutare l’adeguatezza di un modello bayesiano rispetto ai dati osservati. Se il modello riproduce bene la distribuzione dei dati osservati, si può concludere che è adatto almeno per il campione corrente. In caso contrario, potrebbe essere necessario rivedere le specifiche del modello, come i priors o la struttura delle variabili.

Verifichiamo dunque le predizioni del modello confrontandole con i dati osservati del campione corrente:

pp_check(fit_2)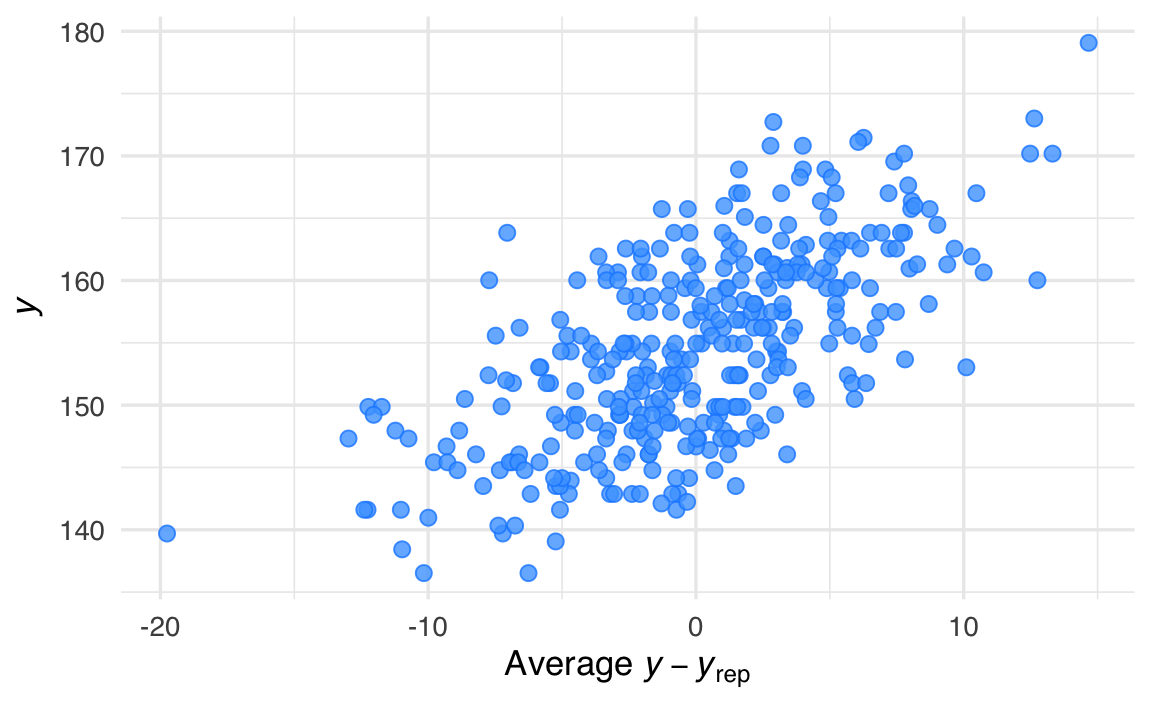

Nel caso presente, vi è una buona corrispondenza tra i dati simulati dal modello e i dati osservati.

Il grafico seguente analizza gli errori del modello rispetto alla retta di regressione stimata.

pp_check(fit_1, type = "error_scatter_avg")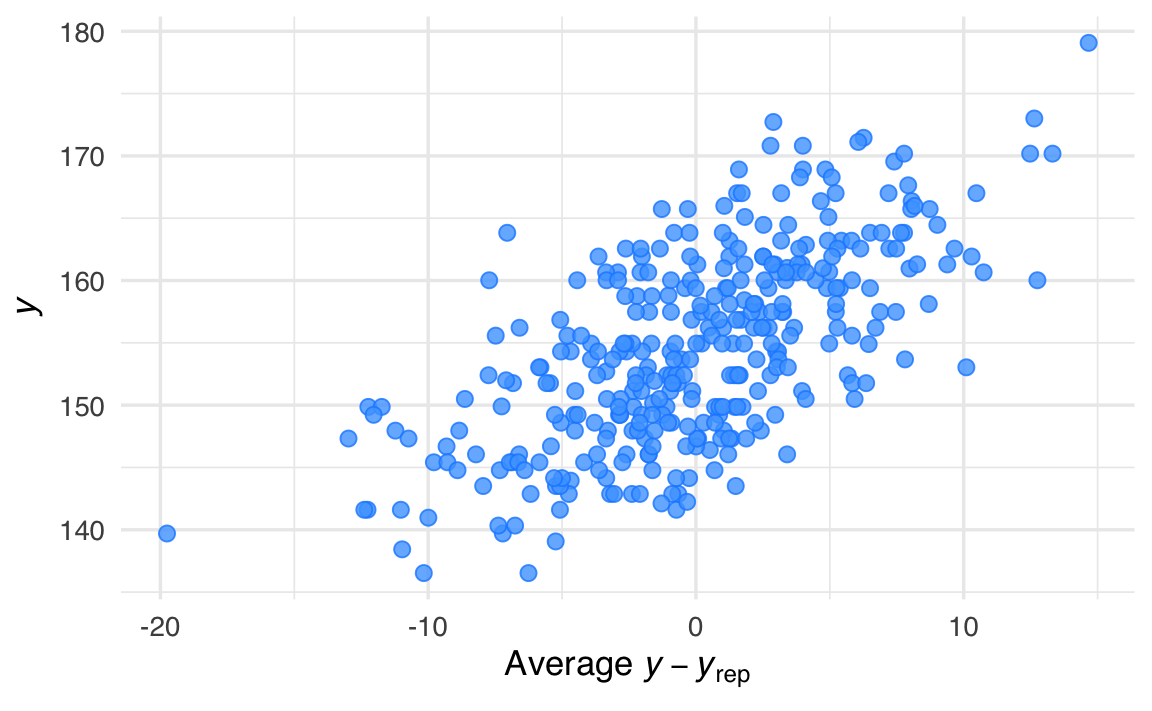

Questo comando utilizza la funzione pp_check() per produrre un grafico che mostra i residui bayesiani, ovvero le differenze tra i dati osservati e quelli predetti dal modello. Nel tipo specifico di grafico scelto ("error_scatter_avg"), i residui sono rappresentati rispetto ai valori predetti, consentendo di valutare visivamente se sono distribuiti in modo uniforme.

Dal grafico, si osserva che i residui bayesiani appaiono distribuiti in modo omogeneo rispetto alla retta di regressione (che non è direttamente mostrata nel grafico). Questo suggerisce che:

• Il modello cattura correttamente la relazione tra la variabile predittiva e la variabile di risposta.
• Non ci sono pattern sistematici nei residui, come deviazioni non lineari o variazioni della dispersione (eteroschedasticità).

Se fossero presenti pattern evidenti nei residui (ad esempio, una struttura curva o una variazione sistematica della dispersione), ciò indicherebbe che il modello potrebbe non essere adeguato, richiedendo una rivalutazione della sua struttura (ad esempio, aggiungendo termini non lineari o trasformando le variabili).

64.8 Regressione Robusta

In questa sezione introduciamo la regressione robusta. Lo scopo è quello di mostrare quanto sia facile modificare il modello definito da brm per specificare una diversa distribuzione degli errori. Questo non è possibile nel caso dell’approccio frequentista.

I modelli robusti sono utili in presenza di outlier. Ad esempio, introduciamo un outlier nei dati:

df_outlier <- df
df_outlier$height[1] <- 400
df_outlier$weight_c[1] <- -25

df_outlier |> 
  ggplot(aes(x = weight_c, y = height)) +
    geom_point() +  
    labs(x = "Weight", y = "Height")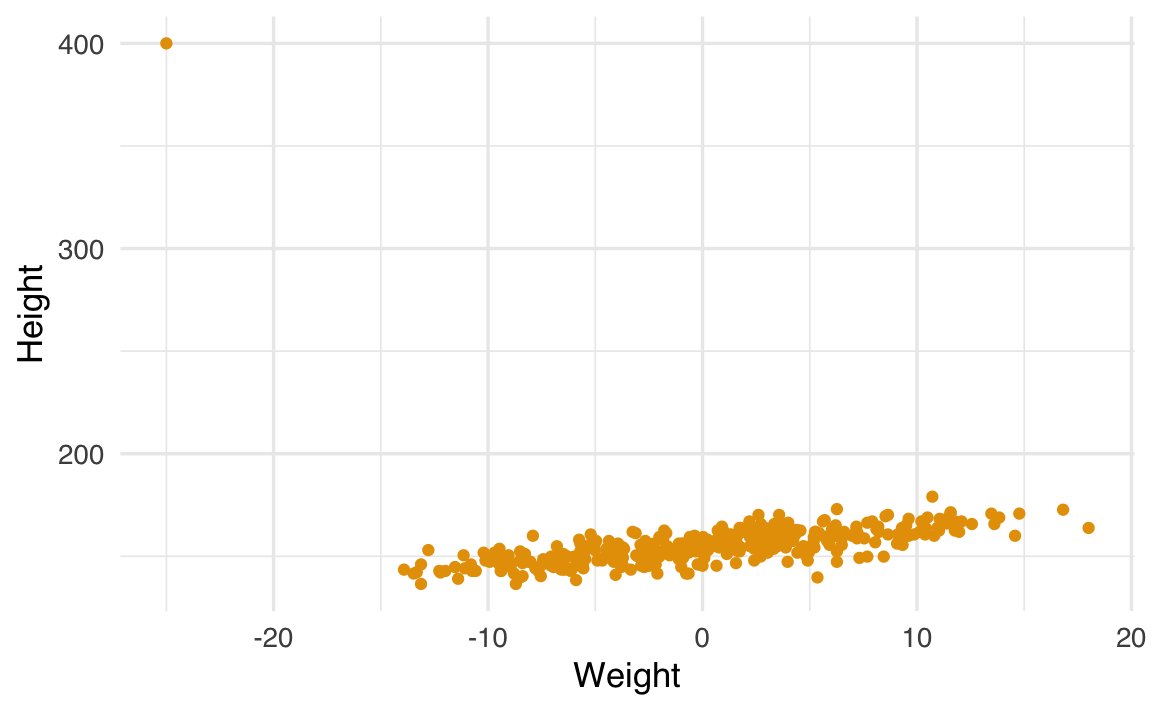 

Notiamo come la presenza di un solo outlier introduce una distorsione nei risultati:

fit_3 = brm(
  bf(height ~ 1 + weight_c, center = FALSE), 
  prior = prior_guassian,
  data = df_outlier, 
  backend = "cmdstanr", 
  silent = 0
)

draws <- posterior::as_draws(fit_3, variable = "^b_", regex = TRUE)
posterior::summarise_draws(draws, "mean", "sd", "mcse_mean", "mcse_sd")
#> # A tibble: 2 × 5
#>   variable       mean    sd mcse_mean mcse_sd
#>   <chr>         <dbl> <dbl>     <dbl>   <dbl>
#> 1 b_Intercept 155.    0.795   0.0116  0.0122 
#> 2 b_weight_c    0.466 0.123   0.00183 0.00192

Senza il valore outlier, la stima di beta è circa 0.9.

Adattiamo ora un modello robusto utilizzando una distribuzione \(t\) di Student:

fit_4 = brm(
  bf(height ~ 1 + weight_c, center = FALSE), 
  prior = prior_guassian,
  family = student(),
  data = df_outlier, 
  backend = "cmdstanr", 
  silent = 0
)

I risultati mostrano che il modello \(t\) è meno influenzato dagli outlier rispetto al modello gaussiano.

draws <- posterior::as_draws(fit_4, variable = "^b_", regex = TRUE)
posterior::summarise_draws(draws, "mean", "sd", "mcse_mean", "mcse_sd")
#> # A tibble: 2 × 5
#>   variable       mean     sd mcse_mean  mcse_sd
#>   <chr>         <dbl>  <dbl>     <dbl>    <dbl>
#> 1 b_Intercept 155.    0.256   0.00413  0.00410 
#> 2 b_weight_c    0.928 0.0392  0.000654 0.000634

Il parametro \(\nu\) della \(t\) di Student viene stimato dal modello. Nel caso presente

draws <- posterior::as_draws(fit_4, variable = "nu")
posterior::summarise_draws(draws, "mean", "sd", "mcse_mean", "mcse_sd")
#> # A tibble: 1 × 5
#>   variable  mean    sd mcse_mean mcse_sd
#>   <chr>    <dbl> <dbl>     <dbl>   <dbl>
#> 1 nu        4.24 0.825    0.0147  0.0146

Con un parametro \(\nu=4\), la distribuzione \(t\) di Student presenta code molto più pesanti rispetto a una gaussiana. Questo la rende più robusta nel gestire la presenza di outliers rispetto al modello gaussiano.

64.9 Indice di Determinazione Bayesiano

Con il pacchetto brms, possiamo calcolare il Bayes \(R^2\), che rappresenta l’equivalente bayesiano del classico indice di determinazione \(R^2\). Questo indice quantifica la proporzione di varianza spiegata dal modello, tenendo conto dell’incertezza intrinseca delle stime bayesiane.

Il comando per calcolarlo è:

bayes_R2(fit_2)
#>    Estimate Est.Error   Q2.5  Q97.5
#> R2    0.568   0.02331 0.5198 0.6085

Il comando restituisce un tibble (una tabella ordinata) con le seguenti informazioni:

• Estimate: La stima media del Bayes \(R^2\), cioè la proporzione di varianza spiegata dal modello, basata sulle distribuzioni a posteriori dei parametri.
• Est.Error: L’errore standard associato alla stima del \(R^2\).
• Q2.5 e Q97.5: I limiti inferiore e superiore dell’intervallo di credibilità al 95% per il Bayes \(R^2\). Questi valori indicano l’incertezza sul \(R^2\), riflettendo la distribuzione a posteriori.

Nel caso presente

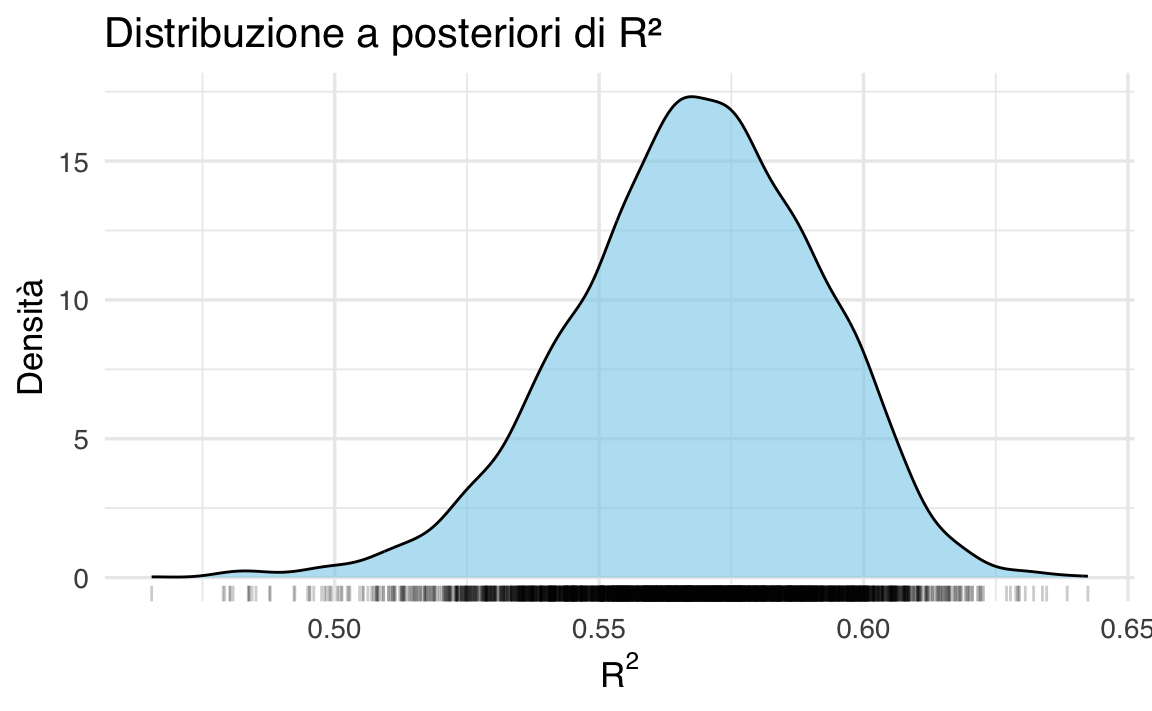
• Stima del \(R^2\): Il modello spiega in media circa il 57% della varianza osservata nella variabile dipendente.
• Errore Standard: L’incertezza sulla stima è relativamente bassa (±0.02).
• Intervallo di Credibilità: C’è un 95% di probabilità che il vero valore del \(R^2\) si trovi tra 0.52 e 0.61.

64.9.1 Differenze rispetto al Frequentista \(R^2\)

1. Incertezza: Il Bayes \(R^2\) include un’intera distribuzione a posteriori, permettendo di rappresentare l’incertezza attraverso l’intervallo di credibilità. Questo non è possibile con il \(R^2\) frequentista, che fornisce una stima puntuale.
2. Priors: Il Bayes \(R^2\) è influenzato dai priors scelti per i parametri del modello, il che consente una maggiore flessibilità e incorpora conoscenze preesistenti.

In conclusione, il Bayes \(R^2\) è uno strumento potente per valutare l’adattamento di un modello bayesiano, permettendo di quantificare non solo la proporzione di varianza spiegata, ma anche l’incertezza associata alla stima.

r2_draws <- bayes_R2(fit_2, summary = FALSE)

r2_df <- data.frame(R2 = as.numeric(r2_draws))

ggplot(r2_df, aes(x = R2)) +
  geom_density(fill = "skyblue", alpha = 0.6) +
  geom_rug(alpha = 0.2) +
  labs(
    title = "Distribuzione a posteriori di R²",
    x = expression(R^2),
    y = "Densità"
  ) 

round(quantile(r2_df$R2, probs = c(.025, .5, .975)), 3)
#>  2.5%   50% 97.5% 
#> 0.520 0.569 0.609

Lo stesso risultato si ottiene con la funzione mcmc_areas() di bayesplot:

mcmc_areas(r2_draws, prob = 0.95) +
  ggtitle("Posterior di R² (area = 95% CI)")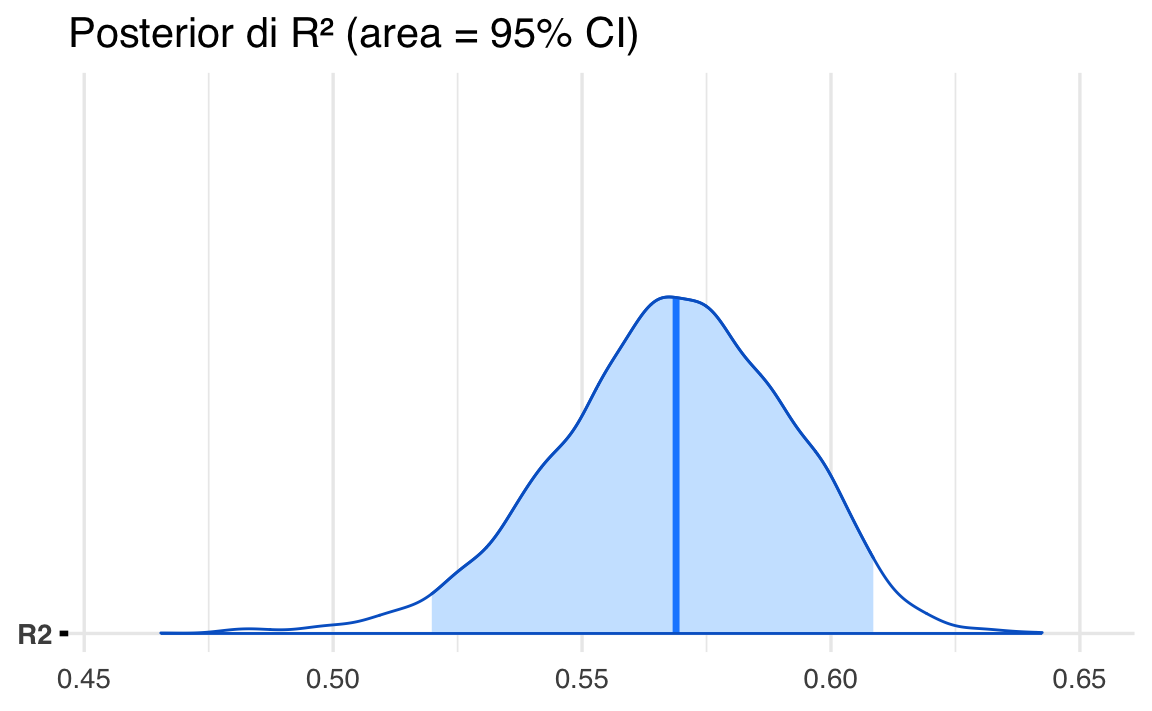

64.10 Approfondimento sulla manipolazione della distribuzione a posteriori con brms

Di seguito illustriamo come accedere e manipolare i campioni generati dal modello bayesiano in brms. Supponiamo di aver costruito un modello lineare semplice, dove vogliamo predire la variabile height in funzione di weight_c:

fit_2 = brm(
  bf(height ~ 1 + weight_c, center = FALSE), 
  prior = prior_guassian,
  data = df, 
  backend = "cmdstanr", 
  silent = 0
)

Una volta che il modello è stato adattato e abbiamo ottenuto l’oggetto fit_2, possiamo estrarre le draws (ossia i campioni) della distribuzione a posteriori tramite la funzione as_draws():

posterior_2 <- as_draws(fit_2)

L’oggetto posterior_2 ottenuto è di tipo draws (una struttura definita dal pacchetto posterior), che internamente può essere rappresentato come una lista o un array in cui sono memorizzati i campioni MCMC:

str(posterior_2)
#> List of 4
#>  $ 1:List of 5
#>   ..$ b_Intercept: num [1:1000] 154 154 155 154 154 ...
#>   ..$ b_weight_c : num [1:1000] 0.955 0.95 0.962 0.969 0.905 ...
#>   ..$ sigma      : num [1:1000] 5.42 5.31 5.54 5.4 5.22 ...
#>   ..$ lprior     : num [1:1000] -8.76 -8.75 -8.78 -8.76 -8.72 ...
#>   ..$ lp__       : num [1:1000] -1080 -1080 -1081 -1081 -1078 ...
#>  $ 2:List of 5
#>   ..$ b_Intercept: num [1:1000] 155 155 154 154 154 ...
#>   ..$ b_weight_c : num [1:1000] 0.922 0.804 0.933 0.933 0.925 ...
#>   ..$ sigma      : num [1:1000] 4.88 5.11 5 5 5.2 ...
#>   ..$ lprior     : num [1:1000] -8.61 -8.67 -8.67 -8.67 -8.75 ...
#>   ..$ lp__       : num [1:1000] -1082 -1081 -1078 -1078 -1082 ...
#>  $ 3:List of 5
#>   ..$ b_Intercept: num [1:1000] 154 154 154 155 155 ...
#>   ..$ b_weight_c : num [1:1000] 0.841 0.87 0.861 0.976 0.97 ...
#>   ..$ sigma      : num [1:1000] 5.2 5.08 5.06 5.17 5.31 ...
#>   ..$ lprior     : num [1:1000] -8.71 -8.7 -8.68 -8.69 -8.71 ...
#>   ..$ lp__       : num [1:1000] -1080 -1079 -1079 -1080 -1081 ...
#>  $ 4:List of 5
#>   ..$ b_Intercept: num [1:1000] 154 155 154 155 154 ...
#>   ..$ b_weight_c : num [1:1000] 0.821 0.981 0.863 0.933 0.954 ...
#>   ..$ sigma      : num [1:1000] 5.04 5.15 5.2 5.13 5 ...
#>   ..$ lprior     : num [1:1000] -8.69 -8.69 -8.72 -8.68 -8.68 ...
#>   ..$ lp__       : num [1:1000] -1081 -1080 -1079 -1079 -1079 ...
#>  - attr(*, "class")= chr [1:3] "draws_list" "draws" "list"

Questa ispezione ci permette di vedere che l’oggetto contiene le catene e i parametri campionati.

Possiamo estrarre i nomi dei parametri del modello dall’oggetto creato da brm() nel modo seguente:

variables(fit_2)
#> [1] "b_Intercept" "b_weight_c"  "sigma"       "lprior"      "lp__"

Nel nostro esempio, siamo interessati al coefficiente di regressione associato a weight_c, che in brms è etichettato come b_weight_c. Per semplificare la manipolazione e l’analisi, possiamo servirci di tidybayes, un pacchetto che fornisce funzioni utili per trasformare i campioni in formati “tidy”.

b_slope_draws <- posterior_2 |> 
  spread_draws(b_weight_c)

La funzione spread_draws() estrae e “srotola” le draw dei parametri in un tibble, che risulta più comodo da esplorare:

head(b_slope_draws)
#> # A tibble: 6 × 4
#>   .chain .iteration .draw b_weight_c
#>    <int>      <int> <int>      <dbl>
#> 1      1          1     1      0.955
#> 2      1          2     2      0.950
#> 3      1          3     3      0.962
#> 4      1          4     4      0.969
#> 5      1          5     5      0.905
#> 6      1          6     6      0.888

In questo modo, ogni riga corrisponde a un singolo campione della catena MCMC, per quel parametro.

Una volta estratti i campioni del parametro di interesse (qui b_weight_c), possiamo calcolare facilmente statistiche come quantili e medie:

quantile(b_slope_draws$b_weight_c, probs = c(0.03, 0.50, 0.97))
#>     3%    50%    97% 
#> 0.8263 0.9037 0.9839

mean(b_slope_draws$b_weight_c)
#> [1] 0.9047

• I quantili a 0.03, 0.50 e 0.97 forniscono, rispettivamente, un limite inferiore al 94% (0.03–0.97), la mediana a posteriori (0.50) e un limite superiore.
  
• La funzione mean() restituisce la media a posteriori del coefficiente, un’altra statistica utile per la stima puntuale.

Per comprendere meglio la forma della distribuzione a posteriori, è buona prassi tracciarne la densità. Con tidyverse e tidybayes, possiamo creare un grafico elegante in poche righe:

tibble(beta = b_slope_draws$b_weight_c) %>%
  ggplot(aes(x = beta)) +
  stat_halfeye(fill = "skyblue", alpha = 0.6) +
  labs(
    title = "Distribuzione a posteriori di β (b_weight_c)",
    x = "Valore di β",
    y = "Densità a posteriori"
  )

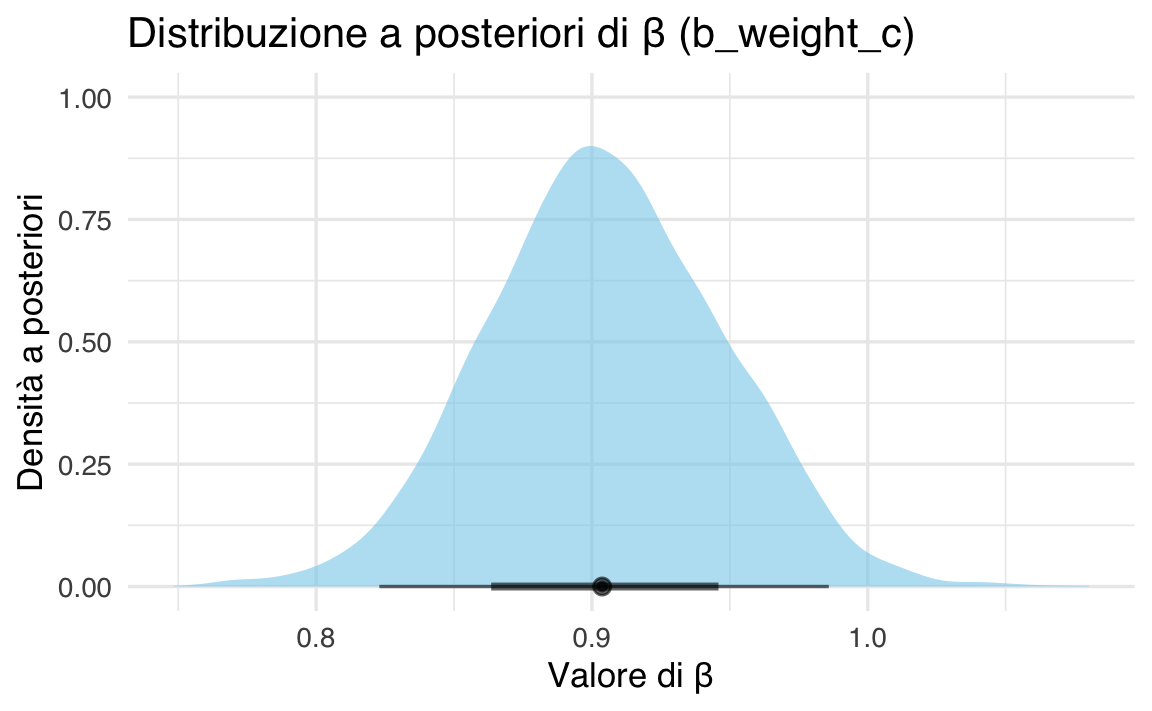
• stat_halfeye() mostra la densità stimata dei campioni, evidenziando in modo intuitivo i valori più probabili.
  
• Il colore e l’alpha permettono di personalizzare l’aspetto del grafico.

In sintesi, utilizzando l’oggetto restituito da brm() e la funzione as_draws(), possiamo estrarre i campioni della distribuzione a posteriori e analizzare:

• statistiche di sintesi, come media, mediana e quantili;
• distribuzioni di densità, per una visualizzazione più immediata della variabilità e della forma della distribuzione a posteriori di un parametro.

La combinazione di posterior, tidybayes e tidyverse rende l’intero flusso di lavoro — dall’estrazione dei campioni fino alla creazione di grafici e statistiche — semplice e flessibile.

64.11 Riflessioni Conclusive

Questo capitolo ha mostrato come utilizzare brms per costruire e interpretare modelli lineari, evidenziando le sue capacità di gestione dei priors, diagnostica e modellizzazione robusta. Grazie alla sua semplicità e flessibilità, brms rappresenta un potente strumento per l’inferenza bayesiana.

Problemi

1. Modello base
   Importa il dataset Howell_18.csv, filtra gli individui di età ≥ 18 anni e adatta un modello bayesiano lineare height ∼ weight usando brm(). Visualizza il sommario.

2. Centraggio del predittore
   Calcola la variabile centrata weight_c e adatta il modello height ∼ weight_c. Confronta l’intercetta (b_Intercept) con quella del modello non centrato. Spiega la differenza.

3. Specificazione dei prior
   Usa get_prior() per recuperare i prior di default, poi definisci manualmente prior debolmente informativi:

   • Intercept ∼ Normal(150, 20)
   • weight_c ∼ Normal(0, 10)
   • sigma ∼ Cauchy(0, 5)

   Adatta il modello con questi prior e confronta le stime a posteriori con quelle del modello con prior di default.

4. Predizioni predittive a posteriori
   Per il modello con prior personalizzati:

   • Esegui pp_check() per la densità e per l’errore medio (type = "error_scatter_avg").
   • Descrivi brevemente cosa mostrano i due grafici.

5. Modello robusto
   Introduci un outlier modificando il primo record: imposta height = 400.

   • Adatta prima un modello gaussiano e poi uno robusto con family = student().
   • Confronta le stime di b_weight_c nei due modelli e discuti l’impatto dell’outlier.

Soluzioni

1. Modello base

   library(brms)
   df <- rio::import("data/Howell_18.csv")
   df_adults <- subset(df, age >= 18)
   fit_base <- brm(height ~ weight, data = df_adults, backend = "cmdstanr")
   summary(fit_base)

2. Centraggio del predittore

   df_adults$weight_c <- df_adults$weight - mean(df_adults$weight)
   fit_centered <- brm(height ~ weight_c, data = df_adults, backend = "cmdstanr")
   summary(fit_centered)

   • Il b_Intercept nel modello non centrato è l’altezza prevista per peso = 0 (non interpretabile realisticamente).
     
   • Nel modello centrato, l’intercetta rappresenta l’altezza media alla media del peso del campione.

3. Specificazione dei prior

   get_prior(height ~ weight_c, data = df_adults)
   
   priors_custom <- c(
     prior(normal(150, 20), class = "b", coef = "Intercept"),
     prior(normal(0, 10), class = "b", coef = "weight_c"),
     prior(cauchy(0, 5), class = "sigma")
   )
   fit_priors <- brm(
     height ~ weight_c,
     data = df_adults,
     prior = priors_custom,
     backend = "cmdstanr"
   )
   summary(fit_priors)

   • Le stime a posteriori rimangono simili, ma i prior personalizzati influenzano leggermente l’incertezza.

4. Predizioni predittive a posteriori

   pp_check(fit_priors)
   pp_check(fit_priors, type = "error_scatter_avg")

   • Il grafico di densità mostra se la distribuzione simulata riproduce quella osservata.
     
   • Il grafico degli errori media evidenzia eventuali pattern sistematici nei residui.

5. Modello robusto

   df_out <- df_adults
   df_out$height[1] <- 400
   fit_gauss <- brm(height ~ weight_c, data = df_out, backend = "cmdstanr")
   fit_student <- brm(height ~ weight_c, family = student(),
                      data = df_out, backend = "cmdstanr")
   summary(fit_gauss)$fixed["weight_c", ]
   summary(fit_student)$fixed["weight_c", ]

   • Il modello gaussiano vede una variazione marcata di b_weight_c a causa dell’outlier.
     
   • Il modello Student stima un coefficiente più vicino al valore senza outlier, dimostrando robustezza.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.4.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] tidybayes_3.0.7  cmdstanr_0.9.0   posterior_1.6.1  brms_2.22.0     
#>  [5] Rcpp_1.0.14      thematic_0.1.6   MetBrewer_0.2.0  ggokabeito_0.1.0
#>  [9] see_0.11.0       gridExtra_2.3    patchwork_1.3.0  bayesplot_1.12.0
#> [13] psych_2.5.3      scales_1.4.0     markdown_2.0     knitr_1.50      
#> [17] lubridate_1.9.4  forcats_1.0.0    stringr_1.5.1    dplyr_1.1.4     
#> [21] purrr_1.0.4      readr_2.1.5      tidyr_1.3.1      tibble_3.2.1    
#> [25] ggplot2_3.5.2    tidyverse_2.0.0  rio_1.2.3        here_1.0.1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] tidyselect_1.2.1     svUnit_1.0.6         farver_2.1.2        
#>  [4] loo_2.8.0            R.utils_2.13.0       fastmap_1.2.0       
#>  [7] tensorA_0.36.2.1     pacman_0.5.1         digest_0.6.37       
#> [10] timechange_0.3.0     lifecycle_1.0.4      StanHeaders_2.32.10 
#> [13] processx_3.8.6       magrittr_2.0.3       compiler_4.5.0      
#> [16] rlang_1.1.6          tools_4.5.0          utf8_1.2.4          
#> [19] yaml_2.3.10          data.table_1.17.0    labeling_0.4.3      
#> [22] bridgesampling_1.1-2 htmlwidgets_1.6.4    curl_6.2.2          
#> [25] pkgbuild_1.4.7       mnormt_2.1.1         plyr_1.8.9          
#> [28] RColorBrewer_1.1-3   abind_1.4-8          withr_3.0.2         
#> [31] R.oo_1.27.0          stats4_4.5.0         grid_4.5.0          
#> [34] colorspace_2.1-1     inline_0.3.21        ggridges_0.5.6      
#> [37] cli_3.6.5            mvtnorm_1.3-3        rmarkdown_2.29      
#> [40] generics_0.1.3       RcppParallel_5.1.10  rstudioapi_0.17.1   
#> [43] reshape2_1.4.4       tzdb_0.5.0           rstan_2.32.7        
#> [46] parallel_4.5.0       matrixStats_1.5.0    vctrs_0.6.5         
#> [49] V8_6.0.3             Matrix_1.7-3         jsonlite_2.0.0      
#> [52] hms_1.1.3            arrayhelpers_1.1-0   ggdist_3.3.3        
#> [55] glue_1.8.0           codetools_0.2-20     ps_1.9.1            
#> [58] distributional_0.5.0 stringi_1.8.7        gtable_0.3.6        
#> [61] QuickJSR_1.7.0       pillar_1.10.2        htmltools_0.5.8.1   
#> [64] Brobdingnag_1.2-9    R6_2.6.1             rprojroot_2.0.4     
#> [67] evaluate_1.0.3       lattice_0.22-7       R.methodsS3_1.8.2   
#> [70] backports_1.5.0      rstantools_2.4.0     coda_0.19-4.1       
#> [73] nlme_3.1-168         checkmate_2.3.2      xfun_0.52           
#> [76] pkgconfig_2.0.3

Bibliografia

Alter, U., Too, M. A., & Cribbie, R. A. (2025). Navigating the Bayes maze: The psychologist’s guide to Bayesian statistics, a hands-on tutorial with R code. International Journal of Psychology, 60(1), e13271.

McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2nd Edition). CRC Press.

Wilkinson, G., & Rogers, C. (1973). Symbolic description of factorial models for analysis of variance. Journal of the Royal Statistical Society Series C: Applied Statistics, 22(3), 392–399.