31  Proprietà delle variabili casuali

“If I expect a or b, and have an equal chance of gaining either of them, my Expectation is worth \((a+b)/2\).”

— Christiaan Huygens, De ratiociniis in ludo aleae (1657).

Introduzione

È spesso molto utile sintetizzare la distribuzione di una variabile casuale attraverso indicatori caratteristici. Questi indicatori consentono di cogliere le principali proprietà della distribuzione, come la posizione centrale (ovvero il “baricentro”) e la variabilità (ossia la dispersione attorno al centro). In questo modo, è possibile ottenere una descrizione sintetica e significativa della distribuzione di probabilità della variabile casuale.

In questo capitolo, introdurremo i concetti fondamentali di valore atteso e varianza di una variabile casuale, che sono strumenti essenziali per comprendere e riassumere le proprietà di una distribuzione probabilistica.

Panoramica del capitolo

• Concetti di valore atteso e varianza per variabili casuali discrete.
• Proprietà del valore atteso e della varianza.
• Valore atteso e varianza per variabili casuali continue.
• Utilizzare R per calcolare valore atteso e varianza.

---

Prerequisiti

Per affrontare al meglio questo capitolo, assicurati di avere familiarità con i seguenti argomenti:

• È fondamentale aver letto la sezione Appendice I.
• Si consiglia la lettura del capitolo Expectation in Schervish & DeGroot (2014).

Preparazione del Notebook

here::here("code", "_common.R") |> 
  source()

31.1 Tendenza centrale

Quando vogliamo comprendere il comportamento tipico di una variabile casuale, ci interessa spesso determinare il suo “valore tipico”. Tuttavia, questa nozione può essere interpretata in diversi modi:

• Media: La somma dei valori divisa per il numero dei valori.
• Mediana: Il valore centrale della distribuzione, quando i dati sono ordinati in senso crescente o decrescente.
• Moda: Il valore che si verifica con maggiore frequenza.

Ad esempio, per il set di valori \(\{3, 1, 4, 1, 5\}\), la media è \(\frac{3+1+4+1+5}{5} = 2.8\), la mediana è 3, e la moda è 1. Tuttavia, quando ci occupiamo di variabili casuali, anziché di semplici sequenze di numeri, diventa necessario chiarire cosa intendiamo per “valore tipico” in questo contesto. Questo ci porta alla definizione formale del valore atteso.

31.2 Valore atteso

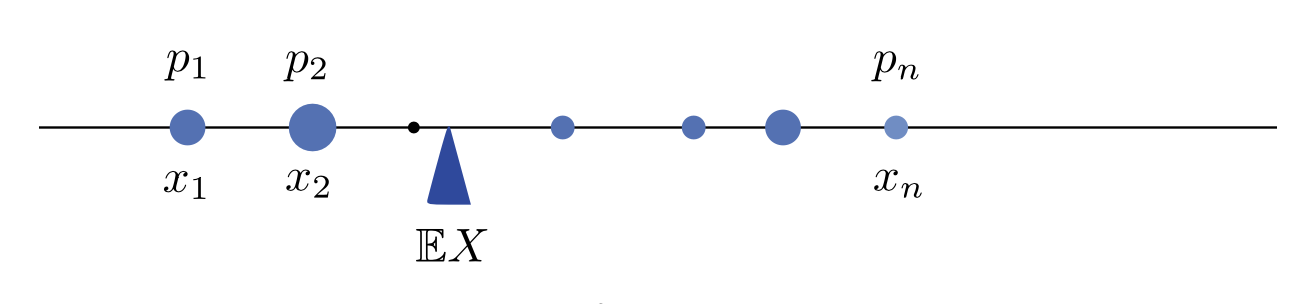
Definizione 31.1 Sia \(X\) una variabile casuale discreta che assume i valori \(x_1, \dots, x_n\) con probabilità \(P(X = x_i) = p(x_i)\). Il valore atteso di \(X\), denotato con \(\mathbb{E}(X)\), è definito come:

\[ \mathbb{E}(X) = \sum_{i=1}^n x_i \cdot p(x_i). \]

In altre parole, il valore atteso (noto anche come speranza matematica o aspettazione) di una variabile casuale è la somma di tutti i valori che la variabile può assumere, ciascuno ponderato dalla probabilità con cui esso si verifica.

Esercizio

Calcoliamo il valore atteso della variabile casuale \(X\) corrispondente al lancio di una moneta equilibrata, dove testa corrisponde a \(X = 1\) e croce corrisponde a \(X = 0\):

\[ \mathbb{E}(X) = \sum_{i=1}^{2} x_i \cdot P(x_i) = 0 \cdot \frac{1}{2} + 1 \cdot \frac{1}{2} = 0.5. \]

Esercizio

Calcoliamo il valore atteso della variabile casuale \(X\) che rappresenta la somma dei punti ottenuti dal lancio di due dadi equilibrati a sei facce.

La variabile casuale \(X\) può assumere i seguenti valori:

\[ \{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}. \]

La probabilità associata a ciascun valore è data dalla distribuzione di massa di probabilità. Ad esempio, il valore \(X = 2\) si ottiene solo se entrambi i dadi mostrano 1, quindi ha probabilità:

\[ P(X = 2) = \frac{1}{36}. \]

Analogamente, \(X = 7\) può essere ottenuto con sei combinazioni diverse: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1), quindi:

\[ P(X = 7) = \frac{6}{36}. \]

La distribuzione di massa di probabilità completa è:

\[ P(X) = \left\{\frac{1}{36}, \frac{2}{36}, \frac{3}{36}, \frac{4}{36}, \frac{5}{36}, \frac{6}{36}, \frac{5}{36}, \frac{4}{36}, \frac{3}{36}, \frac{2}{36}, \frac{1}{36}\right\}. \]

Il valore atteso \(\mathbb{E}[X]\) è definito come:

\[ \mathbb{E}[X] = \sum_{x} x \cdot P(X = x). \]

Applicando questa formula:

\[ \mathbb{E}[X] = 2 \cdot \frac{1}{36} + 3 \cdot \frac{2}{36} + 4 \cdot \frac{3}{36} + \cdots + 12 \cdot \frac{1}{36} = 7. \]

Ecco come calcolarlo utilizzando R:

# Valori di X e le loro probabilità
valori <- 2:12
prob <- c(1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1) / 36

# Calcolo del valore atteso
valore_atteso <- sum(valori * prob)
valore_atteso
#> [1] 7

Il risultato sarà: \[ \mathbb{E}[X] = 7. \]

Per rappresentare graficamente la distribuzione di massa di probabilità:

# Creazione di un data frame
dati <- data.frame(Valore = valori, Probabilità = prob)

# Plot
ggplot(dati, aes(x = Valore, y = Probabilità)) +
  geom_col(fill = "lightblue") +
  labs(
    title = "Distribuzione di Massa di Probabilità per X",
    x = "Valore della Somma (X)",
    y = "Probabilità"
  ) 

Nel suo Ars conjectandi, Bernoulli introduce la nozione di valore atteso con le seguenti parole:

il termine “aspettativa” non deve essere inteso nel suo significato comune […], bensì come la speranza di ottenere il meglio diminuita dalla paura di ottenere il peggio. Pertanto, il valore della nostra aspettativa rappresenta sempre qualcosa di intermedio tra il meglio che possiamo sperare e il peggio che possiamo temere (Hacking, 2006).

In termini moderni, questa intuizione può essere rappresentata in modo più chiaro attraverso una simulazione. Possiamo affermare, infatti, che il valore atteso di una variabile casuale corrisponde alla media aritmetica di un gran numero di realizzazioni indipendenti della variabile stessa.

Esercizio

Per fare un esempio concreto, consideriamo nuovamente il caso del lancio di due dadi bilanciati a sei facce, dove la variabile casuale \(X\) rappresenta la “somma dei due dadi”. Simuliamo un numero elevato di realizzazioni indipendenti di \(X\).

set.seed(123)  
x_samples <- sample(valori, size = 1e6, replace = TRUE, prob = prob)

L’istruzione sample(x, size = 1e6, replace = TRUE, prob = px)) utilizza R per generare un array di 1.000.000 di elementi (specificato dal parametro size), selezionati casualmente dall’array x secondo le probabilità specificate nell’array px.

Quando il numero di realizzazioni indipendenti è sufficientemente grande, la media aritmetica dei campioni generati si avvicina al valore atteso della variabile casuale:

mean(x_samples)
#> [1] 6.998

Questo risultato conferma che il valore atteso \(\mathbb{E}[X] = 7\) rappresenta la somma media dei punti ottenuti nel lancio di due dadi equilibrati su un numero elevato di prove. Anche se ogni singola somma può variare tra 2 e 12, in media ci aspettiamo una somma di 7.

L’aspettativa può anche essere interpretata come un centro di massa. Immagina che delle masse puntiformi con pesi \(p_1, p_2, \dots, p_n\) siano posizionate alle posizioni \(x_1, x_2, \dots, x_n\) sulla retta reale. Il centro di massa—il punto in cui i pesi sono bilanciati—è dato da:

\[ \text{centro di massa} = x_1 p_1 + x_2 p_2 + \dots + x_n p_n, \]

che corrisponde esattamente all’aspettativa della variabile discreta \(X\), che assume valori \(x_1, \dots, x_n\) con probabilità \(p_1, \dots, p_n\). Una conseguenza ovvia di questa interpretazione è che, per una funzione di densità di probabilità (pdf) simmetrica, l’aspettativa coincide con il punto di simmetria (a patto che l’aspettativa esista).

Figura 31.1: L’aspettativa come centro di massa (figura tratta da Chan & Kroese, 2025).

31.2.1 Proprietà del valore atteso

Una delle proprietà più importanti del valore atteso è la sua linearità: il valore atteso della somma di due variabili casuali è uguale alla somma dei loro rispettivi valori attesi:

\[ \mathbb{E}(X + Y) = \mathbb{E}(X) + \mathbb{E}(Y). \tag{31.1}\]

Questa proprietà, espressa dalla formula sopra, è intuitiva quando \(X\) e \(Y\) sono variabili casuali indipendenti, ma è valida anche nel caso in cui \(X\) e \(Y\) siano correlate.

Inoltre, se moltiplichiamo una variabile casuale per una costante \(c\), il valore atteso del prodotto è uguale alla costante moltiplicata per il valore atteso della variabile casuale:

\[ \mathbb{E}(cY) = c \mathbb{E}(Y). \tag{31.2}\]

Questa proprietà ci dice che una costante può essere “estratta” dall’operatore di valore atteso, e si applica a qualunque numero di variabili casuali.

Un’altra proprietà significativa riguarda il prodotto di variabili casuali indipendenti. Se \(X\) e \(Y\) sono indipendenti, allora il valore atteso del loro prodotto è uguale al prodotto dei loro valori attesi:

\[ \mathbb{E}(XY) = \mathbb{E}(X) \mathbb{E}(Y). \tag{31.3}\]

Infine, consideriamo la media aritmetica \(\bar{X} = \frac{X_1 + \ldots + X_n}{n}\) di \(n\) variabili casuali indipendenti con la stessa distribuzione e con valore atteso \(\mu\). Il valore atteso della media aritmetica è:

\[ \mathbb{E}(\bar{X}) = \frac{1}{n} \left(\mathbb{E}(X_1) + \dots + \mathbb{E}(X_n)\right) = \frac{1}{n} \cdot n \cdot \mathbb{E}(X) = \mu. \]

Questo risultato conferma che la media aritmetica di un campione di variabili casuali indipendenti ha lo stesso valore atteso della distribuzione originaria, rendendo il valore atteso uno strumento cruciale per l’analisi statistica e probabilistica.

Esercizio

Consideriamo il seguente esperimento casuale. Sia \(Y\) il numero che si ottiene dal lancio di un dado equilibrato a sei facce e \(Y\) il numero di teste prodotto dal lancio di una moneta equilibrata (0 oppure 1). Troviamo il valore atteso di \(X+Y\).

Per risolvere il problema iniziamo a costruire lo spazio campione dell’esperimento casuale.

\(x /\ y\)	1	2	3	4	5	6
0	(0, 1)	(0, 2)	(0, 3)	(0, 4)	(0, 5)	(0, 6)
1	(1, 1)	(1, 2)	(1, 3)	(1, 4)	(1, 5)	(1, 6)

ovvero

\(x /\ y\)	1	2	3	4	5	6
0	1	2	3	4	5	6
1	2	3	4	5	6	7

Il risultato del lancio del dado è indipendente dal risultato del lancio della moneta. Pertanto, ciascun evento elementare dello spazio campione avrà la stessa probabilità di verificarsi, ovvero \(P(\omega) = \frac{1}{12}\). Il valore atteso di \(X+Y\) è dunque uguale a:

\[ \mathbb{E}(X+Y) = 1 \cdot \frac{1}{12} + 2 \cdot \frac{1}{12} + \dots + 7 \cdot \frac{1}{12} = 4.0. \]

Si ottiene lo stesso risultato usando l’Equazione 31.1:

\[ \mathbb{E}(X+Y) = \mathbb{E}(X) + E(Y) = 3.5 + 0.5 = 4.0. \]

Esercizio

Svolgiamo ora l’esercizio in R

coin <- 0:1  # Valori della moneta: testa (0) e croce (1)
die <- 1:6   # Valori del dado: da 1 a 6

# Creazione del campione come combinazione di valori (moneta, dado)
sample <- expand.grid(coin = coin, die = die)
print(sample)
#>    coin die
#> 1     0   1
#> 2     1   1
#> 3     0   2
#> 4     1   2
#> 5     0   3
#> 6     1   3
#> 7     0   4
#> 8     1   4
#> 9     0   5
#> 10    1   5
#> 11    0   6
#> 12    1   6

px <- numeric()  # Vettore per memorizzare le probabilità

for (i in 1:7) {
  # Filtrare le combinazioni in cui la somma è uguale a 'i'
  event <- subset(sample, coin + die == i)
  # Calcolare la probabilità
  prob <- nrow(event) / nrow(sample)
  px <- c(px, prob)
  
  # Stampare la probabilità
  cat(sprintf("P(X + Y = %d) = %d / %d\n", i, nrow(event), nrow(sample)))
}
#> P(X + Y = 1) = 1 / 12
#> P(X + Y = 2) = 2 / 12
#> P(X + Y = 3) = 2 / 12
#> P(X + Y = 4) = 2 / 12
#> P(X + Y = 5) = 2 / 12
#> P(X + Y = 6) = 2 / 12
#> P(X + Y = 7) = 1 / 12

x <- 1:7  # Valori della variabile casuale (somma di moneta e dado)
expected_value <- sum(x * px)
expected_value
#> [1] 4

Esercizio

Consideriamo le variabili casuali \(X\) e \(Y\) definite nel caso del lancio di tre monete equilibrate, dove \(X\) conta il numero delle teste nei tre lanci e \(Y\) conta il numero delle teste al primo lancio. Si calcoli il valore atteso di \(Z = X \cdot Y\).

La distribuzione di probabilità congiunta \(P(X, Y)\) è fornita nella tabella seguente.

\(x /\ y\)	0	1	\(p(Y)\)
0	1/8	0	1/8
1	2/8	1/8	3/8
2	1/8	2/8	3/8
3	0	1/8	1/8
\(p(y)\)	4/8	4/8	1.0

Il calcolo del valore atteso di \(XY\) si riduce a

\[ \mathbb{E}(Z) = 1 \cdot \frac{1}{8} + 2 \cdot \frac{2}{8} + 3 \cdot \frac{1}{8} = 1.0. \]

Si noti che le variabili casuali \(Y\) e \(Y\) non sono indipendenti. Dunque non possiamo usare l’Equazione 31.3. Infatti, il valore atteso di \(X\) è

\[ \mathbb{E}(X) = 1 \cdot \frac{3}{8} + 2 \cdot \frac{3}{8} + 3 \cdot \frac{1}{8} = 1.5 \]

e il valore atteso di \(Y\) è

\[ \mathbb{E}(Y) = 0 \cdot \frac{4}{8} + 1 \cdot \frac{4}{8} = 0.5. \]

Perciò

\[ 1.5 \cdot 0.5 \neq 1.0. \]

31.2.2 Valore atteso di una variabile casuale continua

Nel caso di una variabile casuale continua \(X\), il valore atteso è definito come:

\[ \mathbb{E}(X) = \int_{-\infty}^{+\infty} x \cdot p(x) \, \mathrm{d}x. \]

Anche in questo contesto, il valore atteso rappresenta una media ponderata dei valori di \(x\), dove ogni possibile valore di \(x\) è ponderato in base alla densità di probabilità \(p(x)\).

L’integrale può essere interpretato analogamente a una somma continua, in cui \(x\) rappresenta la posizione delle barre infinitamente strette di un istogramma, e \(p(x)\) rappresenta l’altezza di tali barre. La notazione \(\int_{-\infty}^{+\infty}\) indica che si sta sommando il contributo di ogni valore possibile di \(x\) lungo l’intero asse reale.

Questa interpretazione rende chiaro come l’integrale calcoli una somma ponderata che si estende su tutti i possibili valori di \(x\), fornendo una misura centrale della distribuzione della variabile casuale continua. Per ulteriori dettagli sulla notazione dell’integrale, si veda l’?sec-calculus.

31.2.2.1 Moda

Un’altra misura di tendenza centrale delle variabili casuali continue è la moda. La moda di \(Y\) individua il valore \(y\) più plausibile, ovvero il valore \(y\) che massimizza la funzione di densità \(p(y)\):

\[ Mo(Y) = \text{argmax}_y p(y). \tag{31.4}\]

La notazione \(\text{argmax}_y p(y)\) significa: il valore \(y\) tale per cui la funzione \(p(y)\) assume il suo valore massimo.

31.3 Varianza

Dopo il valore atteso, la seconda proprietà più importante di una variabile casuale è la varianza.

Definizione 31.2 Se \(X\) è una variabile casuale discreta con distribuzione \(p(x)\), la varianza di \(X\), denotata con \(\mathbb{V}(X)\), è definita come:

\[ \mathbb{V}(X) = \mathbb{E}\Big[\big(X - \mathbb{E}(X)\big)^2\Big]. \tag{31.5}\]

In altre parole, la varianza misura la deviazione media quadratica dei valori della variabile rispetto alla sua media. Se denotiamo il valore atteso di \(X\) con \(\mu = \mathbb{E}(X)\), la varianza \(\mathbb{V}(X)\) diventa il valore atteso di \((X - \mu)^2\).

La varianza rappresenta una misura della “dispersione” dei valori di \(X\) intorno al suo valore atteso. Quando calcoliamo la varianza, stiamo effettivamente misurando quanto i valori di \(X\) tendono a differire dalla media \(\mu\).

Per capire meglio, consideriamo la variabile casuale \(X - \mathbb{E}(X)\), detta scarto o deviazione dalla media. Questa variabile rappresenta le “distanze” tra i valori di \(X\) e il valore atteso \(\mathbb{E}(X)\). Tuttavia, poiché lo scarto può essere positivo o negativo, la media dello scarto è sempre zero, il che lo rende inadatto a quantificare la dispersione.

Per risolvere questo problema, eleviamo al quadrato gli scarti, ottenendo \((X - \mathbb{E}(X))^2\), che rende tutte le deviazioni positive. La varianza è quindi la media di questi scarti al quadrato, fornendo una misura efficace della dispersione complessiva dei valori di \(X\) rispetto alla sua media.

Questo concetto è fondamentale per comprendere la variabilità di una distribuzione e per applicare strumenti statistici che richiedono una conoscenza approfondita della distribuzione dei dati.

Esercizio

Posta \(S\) uguale alla somma dei punti ottenuti nel lancio di due dadi equilibrati, si calcoli la varianza di \(S\).

La variabile casuale \(S\) ha la seguente distribuzione di probabilità:

\(s\)	2	3	4	5	6	7	8	9	10	11	12
\(P(S = s)\)	\(\frac{1}{36}\)	\(\frac{2}{36}\)	\(\frac{3}{36}\)	\(\frac{4}{36}\)	\(\frac{5}{36}\)	\(\frac{6}{36}\)	\(\frac{5}{36}\)	\(\frac{4}{36}\)	\(\frac{3}{36}\)	\(\frac{2}{36}\)	\(\frac{1}{36}\)

Essendo \(\mathbb{E}(S) = 7\), la varianza diventa

\[ \begin{aligned} \mathbb{V}(S) &= \sum \left(s - \mathbb{E}(S)\right)^2 \cdot P(s) \notag\\ &= (2 - 7)^2 \cdot \frac{1}{36} + (3-7)^2 \cdot \frac{3}{36} + \dots + (12 - 7)^2 \cdot \frac{1}{36} \notag\\ &= 5.8333.\notag \end{aligned} \]

Esercizio

Svolgiamo l’esercizio in R

# Definire i valori di x e le loro probabilità px
x <- 2:12
px <- c(
  1 / 36, 2 / 36, 3 / 36, 4 / 36, 5 / 36, 6 / 36,
  5 / 36, 4 / 36, 3 / 36, 2 / 36, 1 / 36
)

# Calcolare il valore atteso
ex <- sum(x * px)
ex
#> [1] 7

Applichiamo l’Equazione 31.5:

# Calcolo della varianza utilizzando la definizione
variance <- sum((x - ex)^2 * px)
variance
#> [1] 5.833

Usiamo la funzione var() di rv_discrete:

# Calcolo della varianza con pesi
variance_check <- weighted.mean((x - ex)^2, w = px)
variance_check
#> [1] 5.833

31.3.1 Formula alternativa per la varianza

La varianza di una variabile casuale \(X\), indicata come \(\mathbb{V}(X)\), misura la dispersione dei valori attorno alla media. La definizione classica è:

\[ \mathbb{V}(X) = \mathbb{E}\Big[\big(X - \mathbb{E}(X)\big)^2\Big]. \]

Esiste però una formula alternativa che semplifica il calcolo.

Dimostrazione.

1. Espansione del quadrato
   Consideriamo la varianza, definita come \(\mathbb{V}(X) = \mathbb{E}\big[(X - \mathbb{E}(X))^2\big]\).
   Espandiamo il quadrato \((X - \mathbb{E}(X))^2\) utilizzando la regola \((a - b)^2 = a^2 - 2ab + b^2\): \[ (X - \mathbb{E}(X))^2 = X^2 - 2\,X\,\mathbb{E}(X) + \big(\mathbb{E}(X)\big)^2. \]

2. Applicazione dell’aspettativa
   Applichiamo \(\mathbb{E}[\cdot]\) a ciascun termine, ricordando che l’aspettativa è un operatore lineare: \[ \mathbb{E}\big[(X - \mathbb{E}(X))^2\big] = \mathbb{E}\big[X^2\big] \;-\; 2 \,\mathbb{E}\big[X\,\mathbb{E}(X)\big] \;+\; \mathbb{E}\big[\big(\mathbb{E}(X)\big)^2\big]. \]

3. Gestione dei termini costanti
   L’aspettativa \(\mathbb{E}(X)\) è una costante (indipendente da \(X\)). Indichiamola con \(\mu\). Quindi:

   • \(\mathbb{E}(X^2)\) resta com’è.
   • \(\mathbb{E}[X \cdot \mu] = \mu \, \mathbb{E}[X] = \mu \cdot \mu = \mu^2\).
   • \(\mathbb{E}\big(\mu^2\big) = \mu^2\).

4. Sostituzione e semplificazione
   Rimpiazzando i risultati nel secondo passaggio si ottiene: \[ \mathbb{E}(X^2) \;-\; 2\,\mu^2 \;+\; \mu^2 \;=\; \mathbb{E}(X^2) - \mu^2. \]
   Poiché \(\mu = \mathbb{E}(X)\), la varianza può quindi essere scritta come:

   \[ \boxed{ \mathbb{V}(X) = \mathbb{E}(X^2) \;-\; \bigl(\mathbb{E}(X)\bigr)^2. } \tag{31.6}\]

Questa forma risulta molto utile per ragioni di efficienza computazionale: invece di calcolare gli scarti \((X - \mu)\) per ogni osservazione, è sufficiente trovare \(\mathbb{E}(X^2)\) e poi sottrarre \(\mu^2\). In tal modo si riducono i passaggi intermedi e, di conseguenza, si minimizzano gli errori pratici. Inoltre, nelle dimostrazioni che richiedono manipolazioni algebriche – come quelle tipiche della Teoria Classica dei Test – questa espressione semplifica notevolmente le trasformazioni.

Esercizio

Consideriamo la variabile casuale \(X\) che corrisponde al numero di teste che si osservano nel lancio di una moneta truccata con probabilità di testa uguale a 0.8. Si trovi la varianza di \(Y\).

Il valore atteso di \(X\) è

\[ \mathbb{E}(X) = 0 \cdot 0.2 + 1 \cdot 0.8 = 0.8. \]

Usando la formula tradizionale della varianza otteniamo:

\[ \mathbb{V}(X) = (0 - 0.8)^2 \cdot 0.2 + (1 - 0.8)^2 \cdot 0.8 = 0.16. \]

Lo stesso risultato si trova con la formula alternativa della varianza. Il valore atteso di \(X^2\) è

\[ \mathbb{E}(X^2) = 0^2 \cdot 0.2 + 1^2 \cdot 0.8 = 0.8. \]

e la varianza diventa

\[ \mathbb{V}(X) = \mathbb{E}(X^2) - \big(\mathbb{E}(Y) \big)^2 = 0.8 - 0.8^2 = 0.16. \]

Esercizio

Svolgiamo l’esercizio in R:

# Definire i valori di x e le probabilità px
x <- c(0, 1)
px <- c(0.2, 0.8)

# Calcolare il risultato
result <- sum(x^2 * px) - (sum(x * px))^2
result
#> [1] 0.16

31.3.2 Proprietà

Segno della varianza. La varianza di una variabile aleatoria non è mai negativa, ed è zero solamente quando la variabile assume un solo valore.

Invarianza per traslazione. La varianza è invariante per traslazione, che lascia fisse le distanze dalla media, e cambia quadraticamente per riscalamento:

\[ \mathbb{V}(a + bX) = b^2\mathbb{V}(X). \]

Dimostrazione. Iniziamo a scrivere

\[ (aX+b)-{\mathbb{E}}[aX+b]=aX+b-a{\mathbb{E}}[X]-b=a(X-{\mathbb {E}}[X]). \]

Quindi

\[ \sigma _{{aX+b}}^{2}={\mathbb{E}}[a^{2}(X-{\mathbb {E}}[X])^{2}]=a^{2}\sigma _{X}^{2}. \]

Esaminiamo una dimostrazione numerica.

# Definire i valori di x
x <- c(2, 1, 4, 7)

# Calcolare y
y <- 100 + 2 * x

# Verificare la relazione tra le varianze
result <- var(y) == 2^2 * var(x)
result
#> [1] TRUE

Varianza della somma di due variabili indipendenti. La varianza della somma di due variabili indipendenti o anche solo incorrelate è pari alla somma delle loro varianze:

\[ \mathbb{V}(X+Y) = \mathbb{V}(X) + \mathbb{V}(Y). \]

Dimostrazione. Se \(\mathbb{E}(X) = \mathbb{E}(Y) = 0\), allora \(\mathbb{E}(X+Y) = 0\) e

\[\mathbb{V}(X+Y) = \mathbb{E}((X+Y)^2) = \mathbb{E}(X^2) + 2 \mathbb{E}(XY) + \mathbb{E}(Y^2).\]

Siccome le variabili sono indipendenti risulta \(\mathbb{E}(XY) = \mathbb{E}(X)\mathbb{E}(Y) = 0\).

Varianza della differenza di due variabili indipendenti. La varianza della differenza di due variabili indipendenti è pari alla somma delle loro varianze:

\[ \mathbb{V}(X-Y) = \mathbb{V}(X) + \mathbb{V}(Y). \]

Dimostrazione.

\[ \mathbb{V}(X-Y) = \mathbb{V}(X +(-Y)) = \mathbb{V}(X) + \mathbb{V}(-Y) = \mathbb{V}(X) + \mathbb{V}(Y). \]

Varianza della somma di due variabili non indipendenti. Se \(X\) e \(Y\) non sono indipendenti, la formula viene corretta dalla loro covarianza:

\[ \mathbb{V}(X+Y) = \mathbb{V}(X) + \mathbb{V}(Y) + 2 Cov(X,Y), \]

dove \(Cov(X,Y) = \mathbb{E}(XY) - \mathbb{E}(X)\mathbb{E}(Y)\).

Una dimostrazione numerica di questo principio è fornita sotto.

# Definire i valori di x e y
x <- c(2, 1, 4, 7)
y <- c(1, 3, 5, 11)

# Calcolare la varianza di x + y con ddof = 0
var_x_y <- mean((x + y - mean(x + y))^2)
var_x_y
#> [1] 35.25

# Definire i valori di x e y
x <- c(2, 1, 4, 7)
y <- c(1, 3, 5, 11)

# Calcolo della varianza combinata
result <- mean((x - mean(x))^2) + 
          mean((y - mean(y))^2) + 
          2 * cov(x, y) * (length(x) - 1) / length(x)
result
#> [1] 35.25

Varianza della media di variabili indipendenti. La media aritmetica \(\textstyle {\bar {X}}={\frac {X_{1}+\ldots +X_{n}}{n}}\) di \(n\) variabili casuali indipendenti aventi la medesima distribuzione, ha varianza

\[ \mathbb{V}(\bar{X}) = \frac{1}{n^2} \mathbb{V}(X_1)+ \dots \mathbb{V}(X_n) = \frac{1}{n^2} n \mathbb{V}(X) = \frac{1}{n} \mathbb{V}(X). \]

Esercizio

Il principio precedente è illustrato dalla seguente simulazione.

# Creare la popolazione
set.seed(123)  # Per riproducibilità
population <- rnorm(10000, mean = 50, sd = 10)

# Definire dimensione del campione e numero di campioni
sample_size <- 30
num_samples <- 100000

# Creare un vettore per memorizzare le medie campionarie
sample_means <- numeric(num_samples)

# Generare i campioni e calcolare le medie
for (i in 1:num_samples) {
  sample <- sample(population, size = sample_size, replace = TRUE)
  sample_means[i] <- mean(sample)
}

# Calcolare la varianza delle medie campionarie
sampling_dist_mean_var <- var(sample_means) * ((num_samples - 1) / num_samples)  # ddof = 0
sampling_dist_mean_var
#> [1] 3.331

Il valore teorico della varianza della distribuzione campionaria della media è

10^2 / 30
#> [1] 3.333

31.3.3 Varianza di una variabile casuale continua

Per una variabile casuale continua \(X\), la varianza è definita come:

\[ \mathbb{V}(X) = \int_{-\infty}^{+\infty} \large[x - \mathbb{E}(X)\large]^2 p(x) \,\operatorname {d}\!x. \tag{31.7}\]

Analogamente al caso discreto, la varianza di una variabile casuale continua \(X\) una misura della dispersione, ovvero la “distanza” media quadratica attesa dei valori \(x\) rispetto alla loro media \(\mathbb{E}(X)\). In altre parole, la varianza quantifica quanto i valori della variabile casuale si discostano tipicamente dal loro valore medio.

31.3.4 Deviazione standard

Quando si lavora con le varianze, i valori sono elevati al quadrato, il che può rendere i numeri significativamente più grandi (o più piccoli) rispetto ai dati originali. Per riportare questi valori all’unità di misura della scala originale, si prende la radice quadrata della varianza. Il risultato ottenuto è chiamato deviazione standard ed è comunemente indicato con la lettera greca \(\sigma\).

Definizione 31.3 La deviazione standard, o scarto quadratico medio, è definita come la radice quadrata della varianza:

\[ \sigma_X = \sqrt{\mathbb{V}(X)}. \tag{31.8}\]

Come nella statistica descrittiva, la deviazione standard di una variabile casuale fornisce una misura della dispersione, ossia la “distanza” tipica o prevista dei valori \(x\) rispetto alla loro media.

Esercizio

Per i dadi equilibrati dell’esempio precedente, la deviazione standard della variabile casuale \(S\) è pari a \(\sqrt{5.833} = 2.415\). Questo valore indica quanto i risultati della somma dei due dadi tendono a variare attorno alla loro media.

31.4 Standardizzazione

Definizione 31.4 Data una variabile casuale \(X\), si dice variabile standardizzata di \(X\) l’espressione

\[ Z = \frac{X - \mathbb{E}(X)}{\sigma_X}. \tag{31.9}\]

Solitamente, una variabile standardizzata viene denotata con la lettera \(Z\).

31.5 Il teorema di Chebyshev

Il Teorema di Chebyshev ci permette di stimare la probabilità che una variabile aleatoria si discosti dal suo valore atteso (media) di una certa quantità. In altre parole, ci fornisce un limite superiore alla probabilità che una variabile aleatoria assuma valori “estremi”.

Il teorema di Chebyshev afferma che, per qualsiasi variabile aleatoria X con media E(X) e varianza Var(X), e per qualsiasi numero reale k > 0, si ha:

\[ P(\mid X - E(X)\mid \geq k \sigma) \leq 1/k^2, \tag{31.10}\]

dove:

• \(P(\mid X - E(X)\mid \geq k \sigma)\) è la probabilità che lo scarto assoluto tra X e la sua media sia maggiore o uguale a k volte la deviazione standard (σ).
• σ è la radice quadrata della varianza, ovvero la deviazione standard.

Cosa ci dice questo teorema?

• Limite superiore: Il teorema ci fornisce un limite superiore alla probabilità che una variabile aleatoria si discosti dalla sua media di più di k deviazioni standard.
• Qualsiasi distribuzione: La bellezza di questo teorema è che vale per qualsiasi distribuzione di probabilità, a patto che la media e la varianza esistano.
• Utilizzo: Il teorema di Chebyshev è molto utile quando non conosciamo la distribuzione esatta di una variabile aleatoria, ma conosciamo la sua media e la sua varianza.

In sintesi, il teorema di Chebyshev ci fornisce un limite superiore alla probabilità che una variabile aleatoria si discosti dalla sua media di una certa quantità, in base alla sua varianza. Il teorema di Chebyshev ci permette quindi di fare inferenze sulla distribuzione di una variabile aleatoria anche quando abbiamo informazioni limitate.

Esercizio

Supponiamo di avere una variabile aleatoria \(X\) con media 100 e varianza 25. Vogliamo stimare la probabilità che \(X\) assuma valori al di fuori dell’intervallo [90, 110].

In questo caso, \(k\) = 2 (poiché 10 è uguale a 2 volte la deviazione standard, che è 5). Applicando il teorema di Chebyshev, otteniamo:

\[ P(\mid X - 100 \mid \geq 10) \leq \left( \frac{1}{2} \right)^2 = 0.25 \]

Quindi, possiamo affermare con certezza che al massimo il 25% dei valori di X saranno al di fuori dell’intervallo [90, 110].

31.6 Momenti di variabili casuali

Definizione 31.5 Si chiama momento di ordine \(q\) di una v.c. \(X\), dotata di densità \(p(x)\), la quantità

\[ \mathbb{E}(X^q) = \int_{-\infty}^{+\infty} x^q p(x) \; dx. \tag{31.11}\]

Se \(X\) è una v.c. discreta, i suoi momenti valgono:

\[ \mathbb{E}(X^q) = \sum_i x_i^q P(x_i), \tag{31.12}\]

dove:

• \(E(X^q)\) rappresenta il valore atteso di \(X\) elevato alla \(q\)-esima potenza.
• \(x_i\) sono i possibili valori della variabile discreta.
• \(P(x_i)\) è la probabilità associata a ciascun valore discreto.

I momenti sono parametri statistici che forniscono informazioni importanti sulle caratteristiche di una variabile casuale. Tra questi, i più noti e utilizzati sono:

1. Il momento del primo ordine (\(q\) = 1): corrisponde al valore atteso (o media) della variabile casuale \(X\).
2. Il momento del secondo ordine (\(q\) = 2): quando calcolato rispetto alla media, corrisponde alla varianza.

Per i momenti di ordine superiore al primo, è comune calcolarli rispetto al valore medio di \(X\). Questo si ottiene applicando una traslazione: \(x_0 = x − \mathbb{E}(X)\), dove \(x_0\) rappresenta lo scarto dalla media. In particolare, il momento centrale del secondo ordine, calcolato con questa traslazione, corrisponde alla definizione di varianza.

Esercizio

In R, possiamo calcolare il valore atteso e la varianza di variabili casuali discrete utilizzando vettori di valori e probabilità.

Consideriamo una variabile casuale \(X\) che rappresenta i valori ottenuti dal lancio di un dado non equilibrato, con valori possibili da 0 a 6, e con la seguente distribuzione di massa di probabilità: 0.1, 0.2, 0.3, 0.1, 0.1, 0.0, 0.2.

Iniziamo a definire un vettore che contiene i valori della v.c.:

x <- 0:6
print(x)
#> [1] 0 1 2 3 4 5 6

Il vettore px conterrà le probabilità associate ai valori x:

px <- c(0.1, 0.2, 0.3, 0.1, 0.1, 0.0, 0.2)
print(px)
#> [1] 0.1 0.2 0.3 0.1 0.1 0.0 0.2

Controlliamo che la somma sia 1:

sum(px)
#> [1] 1

Calcoliamo il valore atteso di \(X\) implementando la formula del valore atteso utilizzando i vettori x e px:

x_ev <- sum(x * px)
x_ev
#> [1] 2.7

Calcoliamo la varianza di \(X\) usando i vettori x e px:

x_var <- sum((x - x_ev)^2 * px)
x_var
#> [1] 3.81

Calcoliamo la deviazione standard di \(X\) prendendo la radice quadrata della varianza:

x_sd <- sqrt(x_var)
x_sd
#> [1] 1.952

Per rappresentare graficamente la distribuzione di massa, possiamo usare ggplot2:

df <- data.frame(x = x, pmf = px)
ggplot(df, aes(x = x, y = pmf)) +
  geom_point(color = "#832F2B", size = 3) +
  geom_segment(aes(xend = x, yend = 0), linewidth = 1) +
  labs(title = "Distribuzione di massa di probabilità", 
       x = "Valori", y = "Probabilità")

Questo codice calcola il valore atteso, la varianza e la deviazione standard di una variabile casuale discreta e rappresenta graficamente la distribuzione di massa, tutto in R.

Esercizio

Un esempio pratico dell’uso del valore atteso e della varianza in psicologia è rappresentato dagli studi sulla memoria episodica, in particolare attraverso il paradigma sperimentale delle risposte “Remember-Know”. Questo paradigma permette di esplorare come le persone riconoscano eventi passati, distinguendo tra ricordi dettagliati e semplici sensazioni di familiarità.

Il Paradigma “Remember-Know”

In un tipico esperimento di memoria episodica:

1. Ai partecipanti viene presentata una lista di stimoli (es. parole o immagini).
2. Dopo un intervallo di tempo, viene mostrata una nuova lista contenente elementi precedentemente visti (old) e elementi nuovi (new).
   
3. Per ogni stimolo old riconosciuto, i soggetti devono specificare se:
   • Remember (R): Ricordano consapevolmente dettagli contestuali dell’episodio di encoding (es. “Ricordo che questa parola era scritta in rosso”).
   • Know (K): Avvertono familiarità con lo stimolo, ma senza accesso a dettagli specifici (es. “Sembra conosciuto, ma non so perché”).
     
   • Miss: Non riconoscono lo stimolo.

La variabile in gioco è quindi categorica e discreta, con tre possibili esiti per gli stimoli old: {R, K, Miss}.

Modelli Teorici e Previsioni Statistiche

Due importanti teorie cercano di spiegare come avviene questo riconoscimento:

Teoria del Processo Unico (Strength Theory) (e.g., Wixted & Mickes, 2010)

• Ipotesi centrale:
  C’è una sola dimensione continua (la “forza mnemonica”) che determina il tipo di risposta.
  • Le risposte Remember derivano da tracce molto forti, quelle Know da tracce di forza intermedia, e i Miss da tracce troppo deboli.
• Implicazioni statistiche: molte risposte Know, meno risposte Remember, bassa varianza.

Teoria del Doppio Processo (Dual-Process) (e.g., Yonelinas, 2002)

• Ipotesi centrale:
  Ci sono due processi indipendenti:
  1. Recollection (R): Processo qualitativo e binario (presente/assente), legato al ricordo consapevole di dettagli contestuali.
     
  2. Familiarità (K): Processo continuo, basato su una sensazione generica di familiarità.
• Implicazioni statistiche: numero simile di risposte Remember e Know, alta varianza.

Qui entrano in gioco i concetti statistici: ogni teoria formula previsioni diverse sul valore atteso (es. proporzione attesa di risposte R o K) e sulla varianza (dispersione dei dati attorno a questi valori). Confrontando le osservazioni sperimentali con le aspettative teoriche, è possibile testare quale modello sia più coerente con i dati empirici, illustrando come strumenti probabilistici possano chiarire meccanismi cognitivi complessi.

Confronto Statistico: Previsioni Teoriche

Per confrontare quantitativamente le previsioni dei due modelli, consideriamo un esperimento ipotetico con 100 stimoli old. Assegniamo punteggi numerici alle categorie di risposta per trasformarle in una variabile discreta, facilitando il calcolo di valore atteso e varianza:

• Remember (R) = 2
  
• Know (K) = 1
  
• Miss = 0

Questa codifica riflette l’intensità mnemonica associata a ciascuna risposta, permettendo di quantificare le differenze teoriche tra i modelli.

1. Modello Single-Process (Forza continua)

Secondo questa teoria, la distribuzione attesa delle risposte è:

Categoria	R	K	Miss
% Prevista	25%	60%	15%

Calcoli statistici:
- Valore atteso (media ponderata):
\[ E(X) = (2 \cdot 0.25) + (1 \cdot 0.60) + (0 \cdot 0.15) = 1.10 \]
- Varianza (dispersione attorno alla media):
\[ \begin{aligned} Var(X) &= (2-1.10)^2 \cdot 0.25 + (1-1.10)^2 \cdot 0.60 + (0-1.10)^2 \cdot 0.15 \\ &= 0.2025 + 0.006 + 0.1815 = 0.39 \end{aligned} \]

2. Modello Dual-Process (Recollection e Familiarità)

La teoria prevede una distribuzione basata su due meccanismi indipendenti:

Categoria	R	K	Miss
% Prevista	40%	40%	20%

Calcoli statistici:
- Valore atteso:
\[ E(X) = (2 \cdot 0.40) + (1 \cdot 0.40) + (0 \cdot 0.20) = 1.20 \]
- Varianza:
\[ \begin{aligned} Var(X) &= (2-1.20)^2 \cdot 0.40 + (1-1.20)^2 \cdot 0.40 + (0-1.20)^2 \cdot 0.20 \\ &= 0.256 + 0.016 + 0.288 = 0.56 \end{aligned} \]

Sintesi del Confronto

I due modelli generano previsioni distinte, riassunte nella tabella seguente:

Modello	Valore Atteso	Varianza	Interpretazione
Single-Process	1.10	0.39	Media più bassa, varianza ridotta (distribuzione concentrata attorno a K).
Dual-Process	1.20	0.56	Media più alta, varianza elevata (effetto della miscela tra due processi).

• Valore atteso: Il modello dual-process predice una media superiore, coerente con la maggiore proporzione attesa di risposte Remember.
  
• Varianza: La differenza nella dispersione (0.39 vs. 0.56) riflette l’eterogeneità introdotta dalla separazione tra recollection e familiarità nel modello duale.

Applicazione a Dati Empirici

Supponiamo ora di aver raccolto dati reali da 100 soggetti che hanno prodotto questa distribuzione:

R	K	Miss
38%	42%	20%

Calcoliamo il valore atteso e la varianza empiriche:

\[ E(X) = 2 \cdot 0.38 + 1 \cdot 0.42 + 0 \cdot 0.20 = 1.18 \]

\[ Var(X) = (2-1.18)^2 \cdot 0.38 + (1-1.18)^2 \cdot 0.42 + (0-1.18)^2 \cdot 0.20 = 0.55 \]

Risultati:

Dati	Valore Atteso	Varianza
Empirici	1.18	0.55

Confrontando questi risultati con le previsioni teoriche, notiamo che i dati empirici si avvicinano molto più al modello dual-process (valore atteso: 1.20 vs. 1.18; varianza: 0.56 vs. 0.55).

Implicazioni Psicologiche e Cliniche

• Teoriche: Il confronto tra distribuzioni osservate e teoriche, usando valore atteso e varianza, consente di identificare quale teoria cognitiva spieghi meglio i dati.

• Cliniche: In contesti clinici (es. valutazione di deficit cognitivi), questo approccio consente di identificare se un paziente mostra un profilo riconducibile a un danno selettivo della recollection (R ↓) o della familiarità (K ↓).

Questo framework illustra come strumenti probabilistici di base possano tradurre ipotesi psicologiche complesse in predizioni quantitative verificabili, avanzando la comprensione dei meccanismi cognitivi.

Riflessioni conclusive

In conclusione, i concetti di valore atteso e varianza sono fondamentali per comprendere il comportamento delle variabili casuali. Il valore atteso fornisce una misura centrale, rappresentando il “valore tipico” che ci si aspetta di osservare, mentre la varianza quantifica la dispersione dei valori attorno a questa media, offrendo una visione più completa della distribuzione. Questi strumenti sono essenziali per l’analisi e la modellizzazione statistica, fornendo le basi per valutare e interpretare la variabilità nei fenomeni aleatori.

Problemi 1

Esercizio 1: Calcolo del Valore Atteso per Variabili Discrete

Utilizzando i dati raccolti dagli studenti sulla SWLS, calcola il valore atteso della soddisfazione con la vita (\(X\)). Organizza i dati come nell’esempio seguente e interpretalo come se fosse la distribuzione di probabilità nella popolazione:

SWLS Score	Probabilità \(P(X)\)
5	0.05
10	0.10
15	0.20
20	0.30
25	0.20
30	0.10
35	0.05

1. Calcola il valore atteso di \(X\), \(\mathbb{E}(X)\).
2. Interpreta il risultato ottenuto.

Esercizio 2: Varianza e Deviazione Standard

Data la stessa distribuzione della SWLS utilizzata nell’esercizio precedente:

1. Calcola la varianza \(\mathbb{V}(X)\).
2. Calcola la deviazione standard \(\sigma_X\).
3. Commenta il significato della dispersione dei valori rispetto alla media.

Esercizio 3: Proprietà del Valore Atteso

Utilizzando la distribuzione della LSNS-6:

1. Definisci una nuova variabile casuale \(Y = 2X + 3\).
2. Calcola il valore atteso di \(Y\), \(\mathbb{E}(Y)\), utilizzando la linearità dell’operatore di aspettazione.
3. Verifica il risultato calcolando direttamente \(\mathbb{E}(Y)\) dalla distribuzione di probabilità di \(Y\).

Utilizza una distribuzione della LSNS-6 organizzata come segue (sostituisci i valori presenti con quelli del campione):

LSNS-6 Score	Probabilità \(P(Y)\)
5	0.10
10	0.15
15	0.25
20	0.25
25	0.15
30	0.10

Esercizio 4: Applicazione del Teorema di Chebyshev

Sia la soddisfazione con la vita (SWLS) distribuita con media \(\mu = 3.2\) e deviazione standard \(\sigma = 0.8\).

1. Usa il teorema di Chebyshev per trovare un limite superiore alla probabilità che un valore di SWLS sia oltre due deviazioni standard dalla media.
2. Confronta questo risultato con la probabilità empirica calcolata utilizzando i dati raccolti.

Esercizio 5: Standardizzazione e Distribuzione Normale

# Definizione dei dati osservati della LSNS-6 (sostituisci con i dati reali se disponibili)
lsns6_scores <- c(5, 8, 10, 12, 15, 18, 20, 22, 25, 28)

# Parametri della distribuzione
mu <- 12   # Media della LSNS-6
sigma <- 4  # Deviazione standard della LSNS-6

# Standardizzazione dei valori osservati
z_scores <- (lsns6_scores - mu) / sigma

# Creazione dell'istogramma della distribuzione standardizzata
hist(z_scores, 
     breaks = 10, 
     col = "lightblue", 
     main = "Istogramma della distribuzione standardizzata di LSNS-6", 
     xlab = "Z-score", 
     ylab = "Frequenza",
     probability = TRUE)

# Sovrapposizione della curva normale standard
curve(dnorm(x, mean = 0, sd = 1), col = "red", lwd = 2, add = TRUE)

1. Standardizzazione: La trasformazione dei punteggi della LSNS-6 in Z-score permette di esprimere ogni valore in termini di deviazioni standard rispetto alla media. Un valore \(Z = 1\) significa che il punteggio di LSNS-6 è una deviazione standard sopra la media, mentre \(Z = -1\) significa che è una deviazione standard sotto la media.

2. Istogramma della distribuzione standardizzata: Il grafico mostra la distribuzione dei punteggi standardizzati. Se la distribuzione originale è simile a una normale, l’istogramma dei punteggi standardizzati dovrebbe assomigliare a una distribuzione normale standard.

3. Confronto con la distribuzione normale standard: La curva rossa rappresenta la densità di una normale standard (\(\mathcal{N}(0,1)\)). Se i dati sono approssimativamente normali, l’istogramma dei punteggi standardizzati dovrebbe seguire la forma della curva normale standard. Differenze marcate potrebbero indicare asimmetria o curtosi anomale nella distribuzione dei punteggi LSNS-6.

Soluzioni 1

Esercizio 1: Calcolo del Valore Atteso della SWLS

La Satisfaction With Life Scale (SWLS) è composta da 5 item, ciascuno valutato su una scala Likert da 1 a 7. Supponiamo di avere la seguente distribuzione di probabilità per il punteggio totale della SWLS basata su un campione di studenti:

SWLS Score	Probabilità \(P(X)\)
5	0.05
10	0.10
15	0.20
20	0.30
25	0.20
30	0.10
35	0.05

Domanda:
Calcola il valore atteso \(\mathbb{E}[X]\) del punteggio SWLS.

Soluzione: Il valore atteso si calcola come:

\[ \mathbb{E}[X] = \sum x_i P(x_i) \]

Calcoliamo in R:

# Definizione dei valori SWLS e delle probabilità
swls_scores <- c(5, 10, 15, 20, 25, 30, 35)
prob_swls <- c(0.05, 0.10, 0.20, 0.30, 0.20, 0.10, 0.05)

# Calcolo del valore atteso
expected_swls <- sum(swls_scores * prob_swls)
expected_swls

Risultato:
\[ \mathbb{E}[X] = 20 \]

Il valore atteso rappresenta la media teorica della soddisfazione con la vita nella popolazione, assumendo che la distribuzione dei punteggi SWLS segua esattamente le probabilità fornite. In altre parole, se prendessimo un numero molto grande di individui con questa distribuzione di probabilità, il punteggio medio atteso sarebbe 20. Questo suggerisce che, nella popolazione considerata, il livello medio di soddisfazione con la vita si colloca al centro della scala SWLS.

Esercizio 2: Calcolo della Varianza e Deviazione Standard della SWLS

# Definizione dei dati
swls_scores <- c(5, 10, 15, 20, 25, 30, 35)
probabilities <- c(0.05, 0.10, 0.20, 0.30, 0.20, 0.10, 0.05)

# Calcolo del valore atteso (media attesa)
expected_value <- sum(swls_scores * probabilities)

# Calcolo della varianza
variance <- sum((swls_scores - expected_value)^2 * probabilities)

# Calcolo della deviazione standard
std_deviation <- sqrt(variance)

# Stampa dei risultati
cat("Valore atteso (E[X]):", expected_value, "\n")
cat("Varianza (Var[X]):", variance, "\n")
cat("Deviazione standard (σ_X):", std_deviation, "\n")

• Varianza: Misura la dispersione dei punteggi SWLS rispetto alla media attesa. Se la varianza è alta, significa che i punteggi sono molto variabili; se è bassa, significa che i punteggi sono più concentrati attorno al valore atteso.
• Deviazione standard: È la radice quadrata della varianza e ha la stessa unità di misura dei dati originali. Fornisce un’indicazione della dispersione media dei punteggi rispetto alla media.

Se la deviazione standard è elevata, significa che nella popolazione ci sono sia individui con livelli di soddisfazione molto bassi sia individui con livelli molto alti. Se è bassa, i punteggi sono più omogenei intorno alla media.

Esercizio 3: Calcolo del Valore Atteso della Scala della Rete Sociale di Lubben (LSNS-6)

# Definizione dei dati della LSNS-6
lsns_scores <- c(5, 10, 15, 20, 25, 30)
probabilities <- c(0.10, 0.15, 0.25, 0.25, 0.15, 0.10)

# Definizione della trasformazione della variabile casuale Y = 2X + 3
y_values <- 2 * lsns_scores + 3

# Calcolo del valore atteso di X
expected_x <- sum(lsns_scores * probabilities)

# Utilizzo della linearità dell'operatore di aspettazione: E[Y] = 2E[X] + 3
expected_y_from_x <- 2 * expected_x + 3

# Calcolo diretto del valore atteso di Y
expected_y_direct <- sum(y_values * probabilities)

# Stampa dei risultati
cat("Valore atteso di X (E[X]):", expected_x, "\n")
cat("Valore atteso di Y calcolato con la linearità (E[Y] = 2E[X] + 3):", expected_y_from_x, "\n")
cat("Valore atteso di Y calcolato direttamente dalla distribuzione di probabilità di Y:", expected_y_direct, "\n")

1. Linearità dell’operatore di aspettazione: Questo principio afferma che se una variabile casuale \(X\) viene trasformata linearmente in \(Y = aX + b\), allora il valore atteso di \(Y\) è dato da:

   \[ \mathbb{E}(Y) = a \mathbb{E}(X) + b \]

   Questo semplifica il calcolo senza dover ridefinire una nuova distribuzione di probabilità.

2. Verifica del risultato: Dopo aver calcolato \(\mathbb{E}(Y)\) con la proprietà di linearità, lo confrontiamo con il calcolo diretto utilizzando la distribuzione trasformata. Se i due valori coincidono, confermiamo che la proprietà di linearità è rispettata.

3. Significato pratico: La trasformazione lineare di una variabile casuale può rappresentare un’operazione reale come la conversione di punteggi da una scala all’altra. Il valore atteso si comporta linearmente, il che è utile per interpretare trasformazioni senza dover ricalcolare completamente la distribuzione.

Esercizio 4: Probabilità secondo il Teorema di Chebyshev

Il Teorema di Chebyshev afferma che per qualsiasi distribuzione, la probabilità che un valore sia oltre \(k\) deviazioni standard dalla media è al massimo:

\[ P(|X - \mu| \geq k\sigma) \leq \frac{1}{k^2} \]

Sostituendo \(k = 2\):

\[ P(|X - 3.2| \geq 2 \cdot 0.8) \leq \frac{1}{2^2} = \frac{1}{4} = 0.25 \]

Quindi, il Teorema di Chebyshev fornisce un limite superiore del 25% alla probabilità che un valore di SWLS sia oltre due deviazioni standard dalla media.

Per confrontare questo risultato con la probabilità empirica, è necessaro usare i dati raccolti sulla SWLS.

Esercizio 5: Standardizzazione del Punteggio LSNS-6

Domanda:
Standardizza il punteggio LSNS-6 trasformandolo nella variabile standardizzata \(Z\).

\[ Z = \frac{Y - \mathbb{E}(Y)}{\sigma_Y} \]

Soluzione: Calcoliamo in R:

# Standardizzazione dei punteggi LSNS-6
z_lsns <- (lsns_scores - expected_lsns) / sd_lsns
z_lsns

Risultato:

LSNS-6 Score	Z-Score
5	-2.23
10	-1.34
15	-0.45
20	0.45
25	1.34
30	2.23

Problemi 2

Esercizio 6: Personalizzazione degli Interventi Basati sulla Probabilità Condizionata

Uno psicologo scolastico vuole identificare quali studenti potrebbero trarre maggiore beneficio da un programma di supporto psicologico. Dalla letteratura, si sa che la probabilità di avere livelli bassi di soddisfazione con la vita (SWLS ≤ 15) è più alta tra gli studenti che riportano elevati livelli di stress accademico.

Dai dati raccolti su un campione di studenti:

• \(P(\text{SWLS} \leq 15) = 0.35\)
• \(P(\text{Stress Alto}) = 0.40\)
• \(P(\text{SWLS} \leq 15 \mid \text{Stress Alto}) = 0.60\)

Domanda Se uno studente è scelto a caso, qual è la probabilità che abbia un alto livello di stress dato che il suo punteggio SWLS è ≤ 15?

Esercizio 7: Prevedere il Successo di un Intervento Psicologico Uno psicologo clinico sta valutando l’efficacia di un intervento sulla riduzione dell’ansia. Ha raccolto i dati di 100 pazienti e ha osservato che il miglioramento medio nei punteggi di ansia (misurati con DASS-21) è di 5 punti con una deviazione standard di 2.5.

Supponiamo che il miglioramento sia una variabile aleatoria normale con media 5 e deviazione standard 2.5.

Domanda Qual è la probabilità che un paziente scelto a caso migliori di almeno 7 punti?

Esercizio 8: Allocazione Ottimale delle Risorse in un Programma di Prevenzione Uno psicologo organizza un programma di sensibilizzazione sulla salute mentale in diverse scuole. Ha raccolto dati sulla frequenza con cui gli studenti si rivolgono allo sportello di ascolto, con la seguente distribuzione:

Numero di Visite	Probabilità
0	0.40
1	0.30
2	0.15
3+	0.15

Domanda Se lo psicologo ha risorse per organizzare colloqui individuali solo per il 30% degli studenti, quale soglia può usare per selezionare gli studenti più bisognosi in base alla distribuzione delle visite?

Esercizio 9: Misurare la Variabilità della Risposta a un Trattamento Uno psicologo somministra un trattamento per la depressione e misura la variazione nei punteggi di depressione su un campione di pazienti prima e dopo l’intervento.

Le variazioni seguono questa distribuzione:

Δ Punteggio DASS-21	Probabilità
-10	0.10
-5	0.20
0	0.40
+5	0.20
+10	0.10

Domanda Qual è la deviazione standard della variazione nei punteggi di depressione?

Esercizio 10: Probabilità di un Fallimento in un Programma di Sensibilizzazione Uno psicologo organizza un programma per ridurre il pregiudizio sulla salute mentale. Dai dati precedenti, la probabilità di successo di ogni evento di sensibilizzazione è del 70%. Se organizza 5 eventi indipendenti, qual è la probabilità che almeno 1 fallisca?

Soluzioni 2

Esercizio 6: Personalizzazione degli Interventi Basati sulla Probabilità Condizionata

Utilizziamo la formula della probabilità condizionata:

\[ P(\text{Stress Alto} \mid \text{SWLS} \leq 15) = \frac{P(\text{SWLS} \leq 15 \mid \text{Stress Alto}) P(\text{Stress Alto})}{P(\text{SWLS} \leq 15)} \]

Calcoliamo in R:

p_swls_low <- 0.35
p_stress_high <- 0.40
p_swls_given_stress <- 0.60

p_stress_given_swls <- (p_swls_given_stress * p_stress_high) / p_swls_low
p_stress_given_swls

Risultato Lo psicologo può usare questa informazione per identificare studenti con alta probabilità di avere stress elevato, anche se non hanno segnalato direttamente il problema, e offrire supporto mirato.

Esercizio 7: Prevedere il Successo di un Intervento Psicologico

Usiamo la normalizzazione:

\[ Z = \frac{X - \mu}{\sigma} \]

e calcoliamo la probabilità corrispondente:

mean_improvement <- 5
sd_improvement <- 2.5
threshold <- 7

p_improve_7 <- 1 - pnorm(threshold, mean = mean_improvement, sd = sd_improvement)
p_improve_7

Risultato Questo aiuta lo psicologo a comunicare ai pazienti la probabilità di ottenere miglioramenti significativi e ad adattare le aspettative dell’intervento.

Esercizio 8: Allocazione Ottimale delle Risorse in un Programma di Prevenzione

Soluzione Calcoliamo la probabilità cumulativa:

visits <- c(0, 1, 2, 3)
probabilities <- c(0.40, 0.30, 0.15, 0.15)
cumulative_prob <- cumsum(probabilities)

# Determinare la soglia per il 30% più bisognoso
threshold <- visits[min(which(cumulative_prob >= 0.70))]
threshold

Risultato Lo psicologo può decidere di offrire supporto prioritario a studenti con almeno 2 visite, massimizzando l’impatto con risorse limitate.

Esercizio 9: Misurare la Variabilità della Risposta a un Trattamento

Soluzione Calcoliamo la varianza e la deviazione standard:

score_changes <- c(-10, -5, 0, 5, 10)
probabilities <- c(0.10, 0.20, 0.40, 0.20, 0.10)

# Media attesa
expected_change <- sum(score_changes * probabilities)

# Varianza
variance_change <- sum((score_changes - expected_change)^2 * probabilities)

# Deviazione standard
sd_change <- sqrt(variance_change)
sd_change

Risultato Se la deviazione standard è grande, significa che l’effetto del trattamento è molto variabile e potrebbero essere necessarie strategie personalizzate.

Esercizio 10: Probabilità di un Fallimento in un Programma di Sensibilizzazione

Usiamo la distribuzione binomiale:

p_success <- 0.70
n_events <- 5

p_failure_at_least_one <- 1 - dbinom(5, n_events, p_success)
p_failure_at_least_one

Risultato Lo psicologo può pianificare strategie di miglioramento sapendo la probabilità di un fallimento.

Problemi 3

Esercizio 3

Consiglio gli esercizi di base disponibili nella seguente pagina web.

Informazioni sull’ambiente di sviluppo

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.6.1
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Zagreb
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] pillar_1.11.0         tinytable_0.11.0      patchwork_1.3.1      
#>  [4] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.13.0     
#>  [7] ggplot2_3.5.2         reliabilitydiag_0.2.1 priorsense_1.1.0     
#> [10] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [13] StanHeaders_2.32.10   brms_2.22.0           Rcpp_1.1.0           
#> [16] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [19] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [22] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [25] here_1.0.1           
#> 
#> loaded via a namespace (and not attached):
#>  [1] svUnit_1.0.6         tidyselect_1.2.1     farver_2.1.2        
#>  [4] fastmap_1.2.0        TH.data_1.1-3        tensorA_0.36.2.1    
#>  [7] digest_0.6.37        timechange_0.3.0     estimability_1.5.1  
#> [10] lifecycle_1.0.4      survival_3.8-3       magrittr_2.0.3      
#> [13] compiler_4.5.1       rlang_1.1.6          tools_4.5.1         
#> [16] knitr_1.50           labeling_0.4.3       bridgesampling_1.1-2
#> [19] htmlwidgets_1.6.4    curl_6.4.0           pkgbuild_1.4.8      
#> [22] RColorBrewer_1.1-3   abind_1.4-8          multcomp_1.4-28     
#> [25] withr_3.0.2          purrr_1.1.0          grid_4.5.1          
#> [28] stats4_4.5.1         colorspace_2.1-1     xtable_1.8-4        
#> [31] inline_0.3.21        emmeans_1.11.2       scales_1.4.0        
#> [34] MASS_7.3-65          cli_3.6.5            mvtnorm_1.3-3       
#> [37] rmarkdown_2.29       ragg_1.4.0           generics_0.1.4      
#> [40] RcppParallel_5.1.10  cachem_1.1.0         stringr_1.5.1       
#> [43] splines_4.5.1        parallel_4.5.1       vctrs_0.6.5         
#> [46] V8_6.0.5             Matrix_1.7-3         sandwich_3.1-1      
#> [49] jsonlite_2.0.0       arrayhelpers_1.1-0   systemfonts_1.2.3   
#> [52] glue_1.8.0           codetools_0.2-20     distributional_0.5.0
#> [55] lubridate_1.9.4      stringi_1.8.7        gtable_0.3.6        
#> [58] QuickJSR_1.8.0       htmltools_0.5.8.1    Brobdingnag_1.2-9   
#> [61] R6_2.6.1             textshaping_1.0.1    rprojroot_2.1.0     
#> [64] evaluate_1.0.4       lattice_0.22-7       backports_1.5.0     
#> [67] memoise_2.0.1        broom_1.0.9          snakecase_0.11.1    
#> [70] rstantools_2.4.0     coda_0.19-4.1        gridExtra_2.3       
#> [73] nlme_3.1-168         checkmate_2.3.2      xfun_0.52           
#> [76] zoo_1.8-14           pkgconfig_2.0.3

Bibliografia

Chan, J. C. C., & Kroese, D. P. (2025). Statistical Modeling and Computation (2ª ed.). Springer.

Hacking, I. (2006). The emergence of probability: A philosophical study of early ideas about probability, induction and statistical inference. Cambridge University Press.

Schervish, M. J., & DeGroot, M. H. (2014). Probability and statistics (Vol. 563). Pearson Education London, UK:

Wixted, J. T., & Mickes, L. (2010). A continuous dual-process model of remember/know judgments. Psychological Review, 117(4), 1025–1054.

Yonelinas, A. P. (2002). The nature of recollection and familiarity: A review of 30 years of research. Journal of Memory and Language, 46(3), 441–517.