here::here("code", "_common.R") |>
source()
# Funzione per il calcolo dei termini della divergenza KL
kl_terms <- function(p, q) {
stopifnot(length(p) == length(q))
non_zero <- p > 0 & q > 0
p <- p[non_zero]
q <- q[non_zero]
term <- p * log2(p / q)
data.frame(x = seq_along(p), p = p, q = q, term = term)
}
# Funzione compatta per il valore totale
kl_divergence <- function(p, q) {
sum(kl_terms(p, q)$term)
}
# Entropia vera (in bit)
entropy <- function(p) {
p <- p[p > 0]
-sum(p * log2(p))
}
# Entropia incrociata (in bit)
cross_entropy <- function(p, q) {
non_zero <- p > 0 & q > 0
p <- p[non_zero]
q <- q[non_zero]
-sum(p * log2(q))
}76 La divergenza di Kullback-Leibler
“La divergenza di Kullback-Leibler non è una vera e propria distanza, ma una misura di informazione relativa. È il prezzo che paghiamo in termini di informazione quando sostituiamo la distribuzione ‘vera’ con una sua approssimazione.”
– Christopher M. Bishop, Autore di “Pattern Recognition and Machine Learning”
Introduzione
Nel capitolo precedente abbiamo introdotto l’entropia come misura dell’incertezza di una distribuzione di probabilità. Ora facciamo un passo avanti: invece di misurare l’incertezza di una sola distribuzione, vogliamo misurare quanto una distribuzione differisce da un’altra. Uno strumento cruciale per rispondere a questa domanda è la divergenza di Kullback-Leibler (Kullback & Leibler, 1951), spesso abbreviata come divergenza KL (\(D_{\text{KL}}\)). Essa misura quanto si perde in precisione o efficienza se si utilizza un modello errato per descrivere la realtà.
Panoramica del capitolo
- Cos’è la divergenza KL e da dove nasce.
- Come si collega al concetto di entropia.
- Perché è utile nella scelta tra modelli statistici.
- Come calcolarla e interpretarla, anche con esempi in R.
76.1 La generalizzabilità dei modelli e il metodo scientifico
Uno degli obiettivi fondamentali della scienza è la generalizzabilità: un buon modello non deve spiegare solo i dati che abbiamo già, ma anche prevedere correttamente nuovi dati che potremmo raccogliere in futuro. Un modello troppo semplice rischia di sotto-adattarsi ai dati (underfitting), perdendo informazioni importanti; uno troppo complesso rischia di sovra-adattarsi (overfitting), confondendo il rumore casuale con segnali reali. Il problema della generalizzabilità è quindi centrale nel metodo scientifico: vogliamo modelli abbastanza flessibili da catturare i pattern reali, ma non così flessibili da adattarsi anche a variazioni casuali.
Nell’approccio bayesiano, come osserva McElreath (2020), la scelta di un modello implica trovare un equilibrio tra due esigenze:
- accuratezza predittiva – il modello deve produrre previsioni affidabili sui dati futuri;
- controllo della complessità – il modello non deve introdurre più complessità di quanta ne richieda il fenomeno studiato.
Questo principio è vicino a quello noto come rasoio di Occam: tra due modelli che spiegano altrettanto bene i dati, preferiamo quello più semplice. La differenza è che, in ambito bayesiano, questa preferenza non è solo una regola intuitiva, ma può essere formalizzata in termini quantitativi, misurando quanta “informazione in più” dobbiamo spendere quando il nostro modello si discosta dalla realtà. Questa misura è data dalla divergenza di Kullback–Leibler, che vedremo nel seguito.
76.2 L’entropia relativa
Nel Capitolo 75 abbiamo visto che l’entropia \(H(P)\) misura la lunghezza media del codice più efficiente per descrivere una distribuzione di probabilità \(P\). Ora estendiamo il ragionamento al confronto tra due distribuzioni:
- \(P\) = distribuzione vera dei dati, cioè quella che genera realmente gli eventi;
- \(Q\) = distribuzione approssimata, cioè quella fornita dal modello.
La divergenza di Kullback–Leibler, \(D_{\text{KL}}(P \parallel Q)\), risponde alla seguente domanda:
in media, quanta informazione in più dobbiamo spendere se usiamo \(Q\) invece di \(P\) per descrivere i dati?
Dal punto di vista della codifica, questa quantità rappresenta l’aumento medio della lunghezza del codice quando si usa un modello impreciso.
76.2.1 Definizione formale
Per una variabile casuale discreta \(X\):
\[ D_{\text{KL}}(P \parallel Q) = \sum_x p(x) \log_2 \frac{p(x)}{q(x)} \tag{76.1}\]
che può essere riscritta come:
\[ D_{\text{KL}}(P \parallel Q) = \sum_x p(x) \left[ \log_2 p(x) - \log_2 q(x) \right]. \tag{76.2}\]
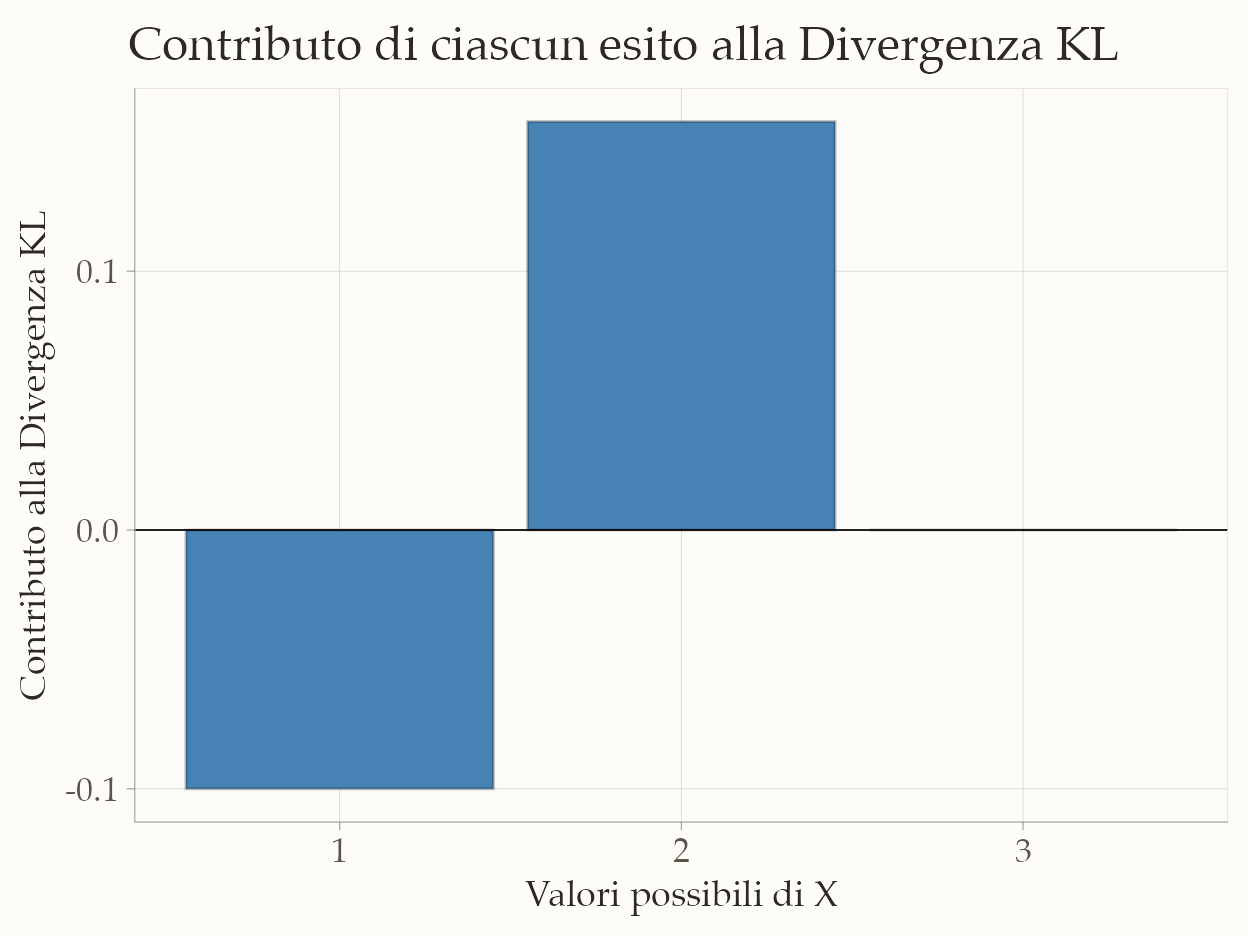
Questa forma mette in evidenza un’interpretazione intuitiva:
- \(\log_2 p(x)\) è l’informazione (in bit) associata all’esito \(x\) secondo la distribuzione vera \(P\);
- \(\log_2 q(x)\) è l’informazione associata allo stesso esito secondo il modello \(Q\);
- la differenza \(\log_2 p(x) - \log_2 q(x)\) indica, per quell’esito, quanto il modello \(Q\) sottostima o sovrastima la sorpresa rispetto a \(P\);
- moltiplicando per \(p(x)\) e sommando su tutti gli esiti otteniamo una media ponderata (pesata in base a quanto l’esito è probabile nella realtà).
In sintesi, \(D_{\text{KL}}(P \parallel Q)\) è la perdita media di efficienza quando descriviamo la variabile \(X\) con la distribuzione approssimata \(Q\) invece che con la distribuzione vera \(P\).
Se \(P = Q\) la divergenza è 0, perché non vi è alcuna perdita. Quanto più \(Q\) si discosta da \(P\), tanto più grande sarà la divergenza, segnalando un “costo informativo” maggiore.
Esempio: Divergenza KL (2)
Supponiamo che la variabile casuale \(X\) possa assumere tre valori: x = 1, 2, 3.
- Distribuzione vera (\(P\)): \([0.1, \ 0.6, \ 0.3]\)
- Distribuzione approssimata (\(Q\)): \([0.2, \ 0.5, \ 0.3]\)
Calcoliamo la divergenza KL secondo la formula ?eq-kl-def:
# Calcolo dei contributi per ciascun esito
df_kl_terms <- kl_terms(P, Q)
print(df_kl_terms)
#> x p q term
#> 1 1 0.1 0.2 -0.1000
#> 2 2 0.6 0.5 0.1578
#> 3 3 0.3 0.3 0.0000# Visualizzazione dei contributi
ggplot(df_kl_terms, aes(x = factor(x), y = term)) +
geom_col(fill = "steelblue") +
geom_hline(yintercept = 0, color = "black", linewidth = 0.3) +
labs(
x = "Valori possibili di X",
y = "Contributo alla Divergenza KL",
title = "Contributo di ciascun esito alla Divergenza KL"
)
Infine, sommiamo i contributi per ottenere la divergenza totale:
Interpretazione
- Esito 1 (\(p=0.1\), \(q=0.2\)) – Il modello \(Q\) sovrastima un evento raro. Il contributo alla divergenza è negativo, ma l’impatto è ridotto perché l’evento è poco probabile nella realtà (\(p\) piccolo).
- Esito 2 (\(p=0.6\), \(q=0.5\)) – Il modello sottostima l’evento più frequente. Poiché \(p\) è alto, questa sottostima ha un peso maggiore nella media ponderata, generando il contributo positivo più grande.
- Esito 3 (\(p=0.3\), \(q=0.3\)) – Qui il modello è perfetto: \(p(x) = q(x)\), quindi il contributo alla divergenza è zero.
Il valore complessivo di \(D_{\text{KL}}\) è la somma di questi contributi: rappresenta la perdita media di efficienza (in bit per evento) quando si usa \(Q\) al posto di \(P\).
In questo caso, il risultato indica che usare \(Q\) comporta una leggera inefficienza: la codifica o le previsioni richiedono, in media, un po’ più informazione di quanto sarebbe necessario usando la distribuzione vera.
76.2.2 Legame con l’entropia e l’entropia incrociata
La divergenza di Kullback–Leibler può essere riscritta come differenza tra entropia incrociata e entropia vera:
\[ D_{\text{KL}}(P \parallel Q) = H(P, Q) - H(P), \tag{76.3}\]
dove:
- \(H(P)\) è l’entropia della distribuzione vera \(P\) (incertezza media/lunghezza media del codice ottimale quando conosciamo la distribuzione corretta);
- \(H(P, Q)\) è l’entropia incrociata, cioè l’incertezza media se codifichiamo dati generati da \(P\) utilizzando un codice ottimizzato per \(Q\):
\[ H(P, Q) = -\sum_x p(x)\log_2 q(x). \tag{76.4}\]
Intuizione. Con questa forma, \(D_{\text{KL}}\) è la sorpresa extra media (o costo informativo in bit per evento) che paghiamo quando usiamo il modello approssimato \(Q\) al posto della distribuzione vera \(P\). Poiché \(H(P)\) non dipende dal modello, minimizzare \(D_{\text{KL}}\) equivale a minimizzare \(H(P,Q)\).
76.2.3 Interpretazione della divergenza KL
La divergenza \(D_{\text{KL}}(P \parallel Q)\) misura l’inefficienza media che si introduce quando si usa la distribuzione \(Q\) per descrivere dati che in realtà seguono \(P\). In termini informativi, rappresenta il costo aggiuntivo di sorpresa: quanti bit in più, in media, servono per codificare gli eventi generati da \(P\) se utilizziamo un codice ottimizzato per \(Q\) invece che per \(P\).
Questa quantità:
- è sempre non negativa: il modello vero (\(P\)) non può mai essere peggiore, in media, del modello approssimato (\(Q\));
- è asimmetrica: \(D_{\text{KL}}(P \parallel Q) \neq D\_{\text{KL}}(Q \parallel P)\). L’ordine è importante: invertire \(P\) e \(Q\) cambia il significato della misura, perché cambia quale distribuzione stiamo trattando come “vera”.
Per questo motivo, la divergenza KL non è una “distanza” in senso geometrico, ma una misura direzionale di perdita di informazione o di inefficienza di codifica.
76.2.4 Proprietà fondamentali della divergenza KL
Non-negatività: \(D_{\text{KL}}(P \parallel Q) \geq 0\) per ogni coppia di distribuzioni \(P\) e \(Q\). Il valore minimo (0) si ottiene se e solo se \(P = Q\).
Asimmetria: \(D_{\text{KL}}(P \parallel Q) \neq D\_{\text{KL}}(Q \parallel P)\) in generale. Non soddisfa quindi le proprietà di una distanza simmetrica.
-
Unità di misura: dipende dalla base del logaritmo:
- base 2 → misura in bit;
- base \(e\) → misura in nat (unità naturale di informazione).
76.3 Uso della divergenza \(D_{\text{KL}}\) nella selezione di modelli
In teoria, la selezione del modello consiste nello scegliere il modello \(Q\) che minimizza la divergenza dalla distribuzione vera \(P\):
\[ \text{Modello ottimale} = \arg\min_Q D_{\text{KL}}(P \parallel Q). \]
In altre parole, il modello ideale è quello che si avvicina di più a \(P\) e quindi riduce al minimo la perdita media di informazione quando lo usiamo per descrivere i dati.
Problema: nella pratica, \(P\) è sconosciuta — non possiamo osservare direttamente la distribuzione vera che ha generato i dati. Di conseguenza, non possiamo calcolare \(D_{\text{KL}}\) in modo esatto.
76.3.1 Come procedere nella pratica
Anche se \(P\) è ignota, possiamo comunque confrontare modelli in termini di divergenza KL sfruttando il legame con l’entropia incrociata \(H(P,Q)\). Infatti, ricordiamo che:
\[ D_{\text{KL}}(P \parallel Q) = H(P,Q) - H(P). \]
L’entropia \(H(P)\) non dipende dal modello \(Q\): è una costante rispetto al confronto tra modelli. Se prendiamo la differenza di divergenza KL tra due modelli \(Q_1\) e \(Q_2\), questa costante si annulla:
\[ D_{\text{KL}}(P \parallel Q_1) - D_{\text{KL}}(P \parallel Q_2) = H(P,Q_1) - H(P,Q_2). \tag{76.5}\]
Quindi, per confrontare modelli non serve conoscere \(H(P)\): basta confrontare le loro entropie incrociate \(H(P,Q)\), che dipendono solo da \(Q\) e che possono essere stimate dai dati.
Nel prossimo capitolo vedremo due strumenti dell’approccio bayesiano che stimano proprio \(H(P,Q)\) (o, più precisamente, il suo opposto \(-H(P,Q)\)):
- Leave-One-Out Cross-Validation (LOO-CV) – valuta quanto bene il modello predice dati non usati nella stima;
- Expected Log Predictive Density (ELPD) – fornisce la stima della qualità predittiva media del modello.
Questi metodi permettono di confrontare modelli in termini di differenza di divergenza KL, avvicinandoci così alla scelta del modello che, tra quelli considerati, è più vicino alla distribuzione vera \(P\).
Riflessioni conclusive
In questo capitolo abbiamo approfondito un concetto fondamentale della teoria dell’informazione: la divergenza di Kullback–Leibler. Nata in origine per valutare l’efficienza dei codici di trasmissione, la D-KL è oggi uno strumento essenziale anche nella statistica moderna, perché misura in modo preciso quanto una distribuzione di probabilità approssimata \(Q\) (cioè un modello) si discosti dalla distribuzione vera \(P\) che genera i dati.
Abbiamo visto che la D-KL può essere interpretata come:
- perdita media di informazione quando si usa \(Q\) invece di \(P\);
- eccesso di sorpresa o inefficienza di codifica introdotta da un modello imperfetto;
- differenza tra entropia incrociata e entropia vera, il che rende possibile stimarla indirettamente.
Questo legame con l’entropia incrociata è cruciale: sebbene \(P\) non sia nota e la D-KL non possa essere calcolata in valore assoluto, possiamo confrontare modelli stimando le differenze di D-KL, perché la componente costante \(H(P)\) si annulla nel confronto.
Nel prossimo capitolo ci concentreremo proprio su come effettuare questi confronti in pratica. Vedremo come strumenti come la Leave-One-Out Cross-Validation (LOO-CV) e l’Expected Log Predictive Density (ELPD) permettano di stimare la capacità predittiva dei modelli e di identificare quello che, tra le alternative considerate, è il più vicino alla distribuzione vera dei dati.
Esercizi
Esercizio 76.1 Cosideriamo due distribuzioni di probabilità discrete, \(p\) e \(q\):
p <- c(0.2, 0.5, 0.3)
q <- c(0.1, 0.2, 0.7)Si calcoli l’entropia di \(p\), l’entropia incrociata tra \(p\) e \(q\), la divergenza di Kullback-Leibler da \(p\) a \(q\).
Si consideri q = c(0.2, 0.55, 0.25) e si calcoli di nuovo a divergenza di Kullback-Leibler da \(p\) a \(q\). Si confronti con il risultato precedente e si interpreti.
Esercizio 76.2 Sia \(p\) una distribuzione binomiale di parametri \(\theta = 0.2\) e \(n = 5\). Sia \(q_1\) una approssimazione a \(p\): q1 = c(0.46, 0.42, 0.10, 0.01, 0.01). Sia \(q_2\) una distribuzione uniforme: q2 <- rep(0.2, 5). Si calcoli la divergenza \(\mathbb{KL}\) di \(q_1\) da \(p\) e da \(q_2\) da \(p\) e si interpretino i risultati.
Bibliografia
Kullback, S., & Leibler, R. A. (1951). On information and sufficiency. The Annals of Mathematical Statistics, 22(1), 79–86.
McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2nd Edition). CRC Press.