here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(HDInterval, lubridate, brms, bayesplot, tidybayes)70 Modello di Poisson
70.1 Introduzione
In questo capitolo percorriamo l’intero processo che porta dall’idea di contare un evento raro – le sparatorie fatali da parte della polizia statunitense – alla stima del suo tasso medio annuo attraverso un modello di Poisson implementato con il pacchetto brms. Per contestualizzare il fenomeno si suggerisce di leggere l’articolo Racial Disparities in Police Use of Deadly Force Against Unarmed Individuals Persist After Appropriately Benchmarking Shooting Data on Violent Crime Rates (Ross et al., 2021). Non è obbligatorio per seguire il capitolo, ma fornisce lo sfondo sociale e metodologico dei dati che stiamo per analizzare.
70.2 Perché un modello di Poisson?
Quando il fenomeno di interesse è un conteggio – per esempio il numero di incidenti, diagnosi o, come nel nostro caso, sparatorie in un anno – la distribuzione di Poisson è spesso una scelta naturale. Questa distribuzione è definita da un solo parametro, \(\lambda\), che rappresenta la media (e varianza) del conteggio. In altre parole, se conosci \(\lambda\) conosci già la forma completa della distribuzione.
Per non appesantire la lettura ricordiamo qui solo l’essenziale: se \(Y\) è il numero di eventi osservati in un certo intervallo di tempo, dire che
\[ Y \sim \text{Poisson}(\lambda) \]
significa che la probabilità di osservare esattamente \(k\) eventi è
\[ P(Y = k) = \frac{e^{-\lambda}\, \lambda^{k}}{k!}, \quad k = 0,1,2,\dots \]
70.3 Come brms codifica \(\lambda\)
Il pacchetto brms, così come la maggior parte dei software di regressione, non stima \(\lambda\) direttamente. Per garantire che il tasso rimanga positivo adotta un link logaritmico: all’interno del modello viene quindi stimata la quantità
\[ \eta = \log(\lambda). \]
Nel caso più semplice, senza predittori, brms utilizza un solo coefficiente, l’intercetta b_Intercept, che è proprio l’equivalente di \(\eta\). Una volta ottenuti i campioni posteriori di b_Intercept è sufficiente applicare l’esponenziale per tornare sul piano di \(\lambda\):
lambda <- exp(b_Intercept) # trasforma log-lambda in lambdaOgni volta che in questo capitolo nomineremo “campioni di \(\lambda\)” sottintenderemo che abbiamo già eseguito questa trasformazione.
70.4 La domanda di ricerca
Grazie all’archivio pubblico del Washington Post disponiamo di tutti i casi di sparatorie fatali accadute negli Stati Uniti dal 2015 in poi. L’interesse è stimare quante se ne verificano in media in un anno e descrivere l’incertezza associata a tale stima.
70.5 Importiamo e prepariamo i dati
url <- "https://raw.githubusercontent.com/washingtonpost/data-police-shootings/master/v2/fatal-police-shootings-data.csv"
raw <- read.csv(url, stringsAsFactors = FALSE)
raw$date <- as.Date(raw$date)
raw$year <- lubridate::year(raw$date)
# Escludiamo il 2025 perché l’anno è ancora in corso e i dati sarebbero incompleti
shootings <- subset(raw, year < 2025)
df <- shootings %>%
dplyr::count(year, name = "events")head(df)
#> year events
#> 1 2015 995
#> 2 2016 959
#> 3 2017 984
#> 4 2018 992
#> 5 2019 993
#> 6 2020 1021A questo punto abbiamo una tabella df con due colonne: year, che va dal 2015 al 2024, ed events, che contiene il numero di sparatorie registrate in ciascun anno.
70.6 Specificare la Distribuzione a Priori
Prima di osservare i dati vogliamo dichiarare che, secondo la nostra conoscenza precedente, un intervallo plausibile per \(\lambda\) va grosso modo da 400 a 900 casi l’anno, con media attorno a 600. Per ottenere una distribuzione lognormale con queste caratteristiche possiamo lavorare sulla scala logaritmica e scegliere normal(6.4, 0.3). Il valore 6.4 è infatti il logaritmo naturale di 600; la deviazione 0.3 produce l’ampiezza desiderata dell’intervallo. In brms la specifica è molto compatta:
prior_lambda <- prior(normal(6.4, 0.3), class = "Intercept")70.7 Adattare il modello in brms
Il cuore dell’analisi si riduce a poche righe, perché il linguaggio di brms è pensato per assomigliare alla formula syntax di lm:
m0 <- brm(
events ~ 1, # ~1 indica solo l’intercetta
family = poisson(), # distribuzione di errore
data = df,
prior = prior_lambda,
iter = 3000,
warmup = 1000,
chains = 4,
seed = 123,
backend = "cmdstanr"
)Il comando produce più di quattromila campioni posteriori (\(1000\) di warm‑up per ciascuna delle quattro catene + \(2000\) validi) dell’intercetta logaritmica. Le diagnosi di convergenza – \(\hat R\) vicino a 1, effective sample size buona – sono riportate da summary(m0).
70.8 Dalla scala log a \(\lambda\)
Per passare dalla stima di b_Intercept alla stima di \(\lambda\) basta eseguire l’esponenziale sui campioni posteriori. Usando tidybayes l’operazione è quasi in linguaggio naturale:
posterior_lambda <- m0 |>
spread_draws(b_Intercept) |>
mutate(lambda = exp(b_Intercept))
posterior_lambda |>
median_qi(lambda, .width = 0.94)
#> # A tibble: 1 × 6
#> lambda .lower .upper .width .point .interval
#> <dbl> <dbl> <dbl> <dbl> <chr> <chr>
#> 1 1043. 1023. 1062. 0.94 median qiL’output ci dice che il valore più credibile di \(\lambda\) è intorno a 1043 casi l’anno, con un intervallo di credibilità al 94 % che va all’incirca da 1023 a 1062.
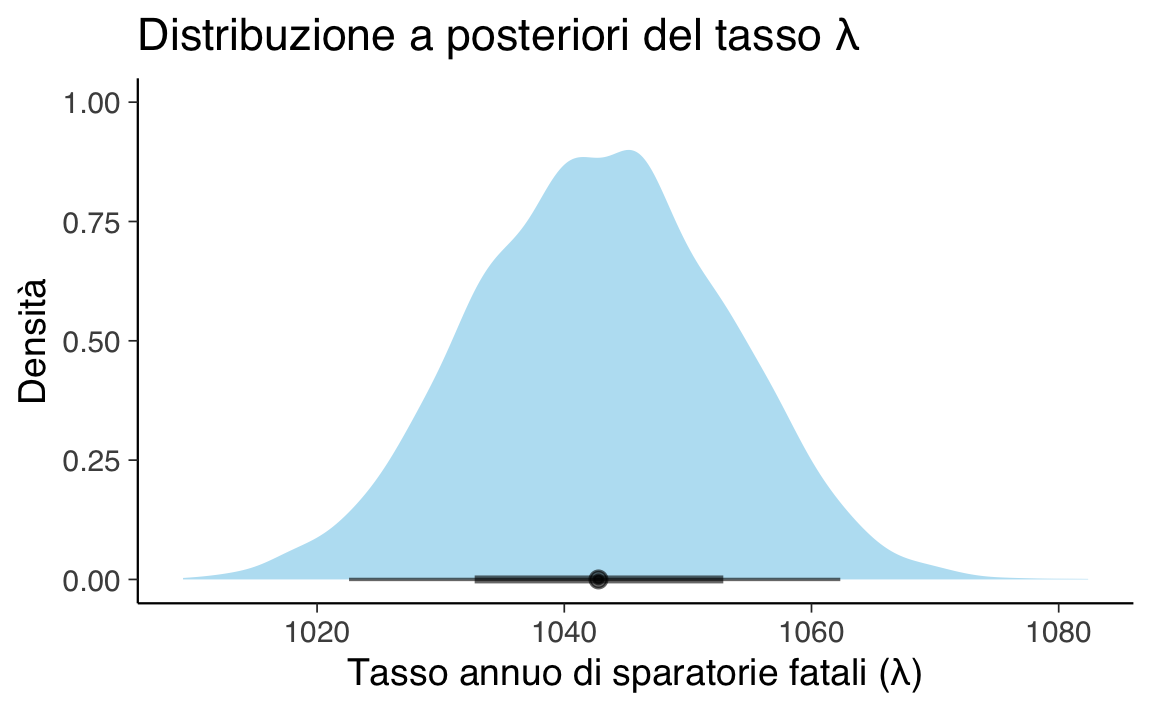
70.9 Visualizzare la distribuzione a posteriori
Un grafico spesso vale più di mille numeri. Con ggplot2 e il tema che abbiamo impostato all’inizio la figura è pronta in tre righe:
posterior_lambda |>
ggplot(aes(x = lambda)) +
stat_halfeye(fill = "skyblue", alpha = 0.6) +
labs(
title = "Distribuzione a posteriori del tasso λ",
x = "Tasso annuo di sparatorie fatali (λ)",
y = "Densità"
)
L’area più scura al centro dell’half‑eye mette in evidenza l’intervallo più denso del 50 %; l’intera “pena” laterale dell’arco rappresenta invece il 94 %.
70.10 Un’estensione: confronto tra gruppi
Finora abbiamo trattato tutte le sparatorie fatali come se provenissero da un’unica popolazione. Una domanda molto concreta, invece, è se il tasso di vittime disarmate differisce tra persone classificate come bianche (codice W nel dataset) e tutte le altre. Per rispondere ci basta duplicare lo schema già usato: al posto di un solo tasso medio (λ) ne stimiamo due, uno per ciascun gruppo.
70.10.1 Costruire il dataset
Il primo passo è filtrare le righe che ci interessano (vittime disarmate) e poi contare, per ogni anno, quante di queste vittime appartengono a ciascun gruppo. Il codice qui sotto svolge tutto il lavoro di preparazione in un’unica catena di operazioni:
url <- "https://raw.githubusercontent.com/washingtonpost/data-police-shootings/master/v2/fatal-police-shootings-data.csv"
df_groups <- read.csv(url, stringsAsFactors = FALSE) |>
dplyr::mutate(
date = as.Date(date),
year = lubridate::year(date),
group = dplyr::if_else(race == "W", "White", "NonWhite")
) |>
dplyr::filter(year < 2025, armed_with == "unarmed") |>
dplyr::count(year, group, name = "events")In df_groups ogni riga è l’abbinamento tra un anno e un gruppo, con il relativo conteggio di vittime disarmate.
70.10.2 Specificare il modello
La formula events ~ 0 + group dice a brms di rinunciare a un’intercetta comune e di stimarne una diversa per ogni valore di group. Poiché l’intercetta è, in scala logaritmica, il nostro parametro centrale, otteniamo due log‑tassi distinti.
Per la prior partiamo dall’idea che, in ciascun gruppo, potremmo aspettarci circa trenta vittime disarmate l’anno ma con incertezza ampia. Lavorando nella scala log questo si traduce in una distribuzione Normale con media 3.4 e deviazione 0.3 applicata indistintamente alle due intercette:
prior_race <- prior(normal(3.4, 0.3), class = "b")Il modello completo è ora immediato:
m_groups <- brm(
events ~ 0 + group,
family = poisson(),
data = df_groups,
prior = prior_race,
iter = 3000, warmup = 1000, chains = 4,
backend = "cmdstanr", seed = 123
)70.10.3 Dal log‑tasso al tasso annuale
Dopo aver controllato che tutti gli indicatori di convergenza (in particolare R‑hat) siano a posto, trasformiamo i campioni posteriori con l’esponenziale così da tornare alla scala dei tassi veri e propri:
Con tidybayes riassumiamo in una riga le quantità d’interesse, usando ad esempio un intervallo di credibilità al 94 %:
post |>
median_qi(lambda_White, lambda_NonWhite, diff_lambda, .width = 0.94)
#> # A tibble: 1 × 12
#> lambda_White lambda_White.lower lambda_White.upper lambda_NonWhite
#> <dbl> <dbl> <dbl> <dbl>
#> 1 22.5 19.9 25.4 34.1
#> lambda_NonWhite.lower lambda_NonWhite.upper diff_lambda diff_lambda.lower
#> <dbl> <dbl> <dbl> <dbl>
#> 1 30.9 37.6 11.6 7.21
#> diff_lambda.upper .width .point .interval
#> <dbl> <dbl> <chr> <chr>
#> 1 16.0 0.94 median qiNe risulta che il gruppo NonWhite registra in media circa 12 vittime disarmate in più l’anno rispetto al gruppo White; l’intero intervallo di credibilità rimane sopra lo zero, perciò l’ipotesi di un tasso maggiore fra le persone non bianche è fortemente supportata dai dati.
Con due soli cambiamenti – la variabile group nella formula e una prior ragionevole per ciascun gruppo – abbiamo esteso il modello di Poisson a una comparazione fra categorie. Tutto il resto resta identico: link logaritmico, diagnostica delle catene, trasformazione a valle dei campioni. Una volta compreso questo meccanismo, aggiungere ulteriori gruppi o predittori diventa un esercizio di routine.
70.11 Riflessioni Conclusive
Il modello di Poisson con prior informativa e link logaritmico è un punto di partenza potente e relativamente semplice per modellare conteggi. L’implementazione in brms riduce la complessità sintattica al minimo, ma non per questo dobbiamo tralasciare di capire cosa accade dietro le quinte:
- \(\lambda\) è il vero protagonista, ma viene stimato indirettamente tramite la sua trasformazione logaritmica.
- La scelta della prior su
b_Interceptva fatta nella scala log, pensando però a cosa significa nella scala originale. - Una volta compreso il passaggio dall’intercetta logaritmica al tasso \(\lambda\), è possibile arricchire il modello con più predittori, sapendo esattamente come trasformare il modello.
Esercizi
Informazioni sull’Ambiente di Sviluppo
sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C/UTF-8/C/C/C/C
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] tidybayes_3.0.7 brms_2.22.0 Rcpp_1.0.14 HDInterval_0.2.4
#> [5] thematic_0.1.7 MetBrewer_0.2.0 ggokabeito_0.1.0 see_0.11.0
#> [9] gridExtra_2.3 patchwork_1.3.0 bayesplot_1.13.0 psych_2.5.3
#> [13] scales_1.4.0 markdown_2.0 knitr_1.50 lubridate_1.9.4
#> [17] forcats_1.0.0 stringr_1.5.1 dplyr_1.1.4 purrr_1.0.4
#> [21] readr_2.1.5 tidyr_1.3.1 tibble_3.3.0 ggplot2_3.5.2
#> [25] tidyverse_2.0.0 rio_1.2.3 here_1.0.1
#>
#> loaded via a namespace (and not attached):
#> [1] mnormt_2.1.1 inline_0.3.21 sandwich_3.1-1
#> [4] rlang_1.1.6 magrittr_2.0.3 multcomp_1.4-28
#> [7] matrixStats_1.5.0 compiler_4.5.0 loo_2.8.0
#> [10] vctrs_0.6.5 pkgconfig_2.0.3 arrayhelpers_1.1-0
#> [13] fastmap_1.2.0 backports_1.5.0 labeling_0.4.3
#> [16] utf8_1.2.6 cmdstanr_0.9.0 rmarkdown_2.29
#> [19] tzdb_0.5.0 ps_1.9.1 xfun_0.52
#> [22] jsonlite_2.0.0 parallel_4.5.0 R6_2.6.1
#> [25] stringi_1.8.7 RColorBrewer_1.1-3 StanHeaders_2.32.10
#> [28] estimability_1.5.1 rstan_2.32.7 zoo_1.8-14
#> [31] pacman_0.5.1 Matrix_1.7-3 splines_4.5.0
#> [34] timechange_0.3.0 tidyselect_1.2.1 rstudioapi_0.17.1
#> [37] abind_1.4-8 yaml_2.3.10 codetools_0.2-20
#> [40] curl_6.3.0 processx_3.8.6 pkgbuild_1.4.8
#> [43] lattice_0.22-7 withr_3.0.2 bridgesampling_1.1-2
#> [46] posterior_1.6.1 coda_0.19-4.1 evaluate_1.0.4
#> [49] survival_3.8-3 RcppParallel_5.1.10 ggdist_3.3.3
#> [52] pillar_1.10.2 tensorA_0.36.2.1 checkmate_2.3.2
#> [55] stats4_4.5.0 distributional_0.5.0 generics_0.1.4
#> [58] rprojroot_2.0.4 hms_1.1.3 rstantools_2.4.0
#> [61] xtable_1.8-4 glue_1.8.0 emmeans_1.11.1
#> [64] tools_4.5.0 data.table_1.17.6 mvtnorm_1.3-3
#> [67] grid_4.5.0 QuickJSR_1.8.0 colorspace_2.1-1
#> [70] nlme_3.1-168 cli_3.6.5 svUnit_1.0.6
#> [73] Brobdingnag_1.2-9 V8_6.0.4 gtable_0.3.6
#> [76] digest_0.6.37 TH.data_1.1-3 htmlwidgets_1.6.4
#> [79] farver_2.1.2 htmltools_0.5.8.1 lifecycle_1.0.4
#> [82] MASS_7.3-65Bibliografia
Downey, A. B. (2021). Think Bayes. " O’Reilly Media, Inc.".
Ross, C. T., Winterhalder, B., & McElreath, R. (2021). Racial disparities in police use of deadly force against unarmed individuals persist after appropriately benchmarking shooting data on violent crime rates. Social Psychological and Personality Science, 12(3), 323–332.