here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(cmdstanr, posterior, bayestestR, brms, emmeans,
loo, bridgesampling)67 ANOVA ad due vie
67.1 Introduzione
L’ANOVA a due vie estende il modello dell’ANOVA a una via alla situazione in cui la variabile dipendente è influenzata da due fattori distinti, ciascuno con due o più livelli. Questa estensione consente di analizzare non solo gli effetti principali di ciascun fattore, ma anche l’interazione tra i due.
67.1.1 Medie di popolazione in una classificazione a due vie
Supponiamo di conoscere le medie di popolazione per ciascuna combinazione dei livelli dei due fattori. La struttura può essere rappresentata in una tabella come la seguente:
| \(C_1\) | \(C_2\) | \(\dots\) | \(C_c\) | Media riga | |
|---|---|---|---|---|---|
| \(R_1\) | \(\mu_{11}\) | \(\mu_{12}\) | \(\dots\) | \(\mu_{1c}\) | \(\mu_{1\cdot}\) |
| \(R_2\) | \(\mu_{21}\) | \(\mu_{22}\) | \(\dots\) | \(\mu_{2c}\) | \(\mu_{2\cdot}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\ddots\) | \(\vdots\) | \(\vdots\) |
| \(R_r\) | \(\mu_{r1}\) | \(\mu_{r2}\) | \(\dots\) | \(\mu_{rc}\) | \(\mu_{r\cdot}\) |
| Media colonna | \(\mu_{\cdot 1}\) | \(\mu_{\cdot 2}\) | \(\dots\) | \(\mu_{\cdot c}\) | \(\mu_{\cdot\cdot}\) |
dove:
- \(µ_{jk}\) è la media della cella per il livello \(j\) del fattore R e \(k\) del fattore C.
- \(µ_{j:}\) è la media marginale per la riga \(j\).
- \(µ_{:k}\) è la media marginale per la colonna \(k\).
- \(µ_{::}\) è la media complessiva.
67.1.2 Effetti principali e interazione
Se non c’è interazione tra i due fattori, la differenza tra livelli di un fattore è costante a prescindere dal livello dell’altro fattore. In altre parole, le differenze tra medie di cella si riflettono esattamente nelle differenze tra le medie marginali.
Ad esempio, se il fattore R non interagisce con il fattore C, allora:
\[ µ_{j1} - µ_{j'1} = µ_{j2} - µ_{j'2} = ... = µ_{j:} - µ_{j':} \]
Quando i profili delle medie sono paralleli, l’assenza di interazione è facilmente visibile. L’interazione si manifesta quando le differenze tra livelli di un fattore variano al variare dell’altro fattore.
L’interazione è simmetrica: se R interagisce con C, allora C interagisce con R. Se invece non vi è interazione, gli effetti principali dei fattori corrispondono alle differenze tra le rispettive medie marginali.
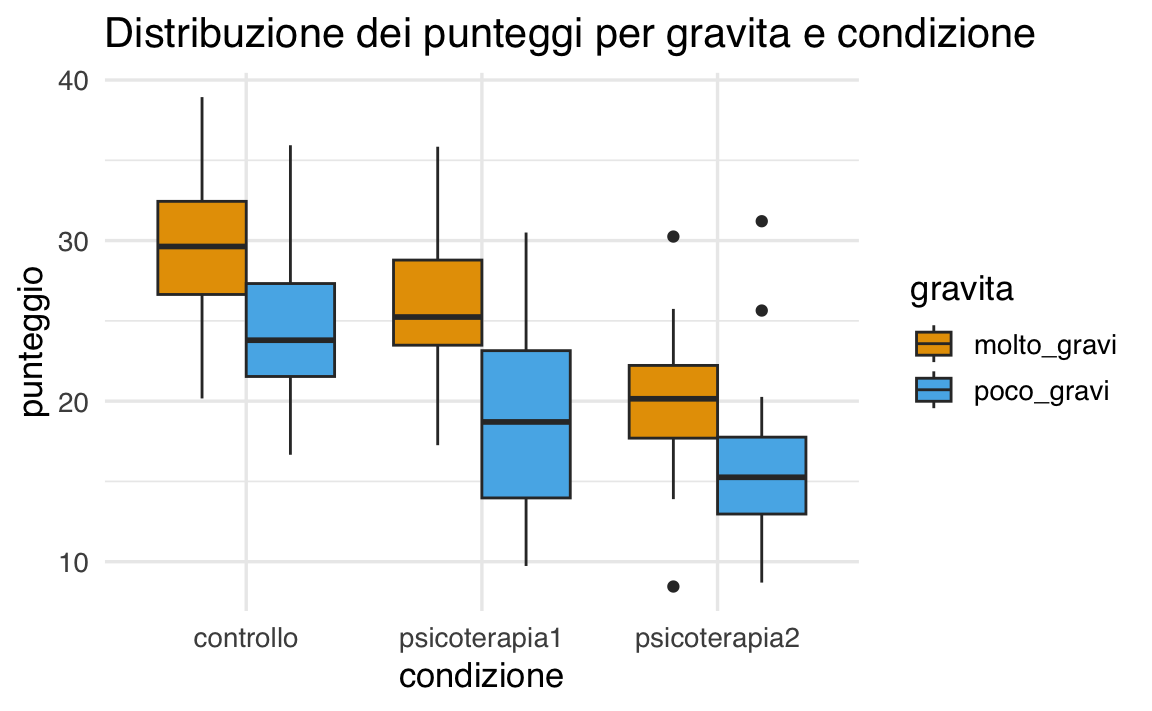
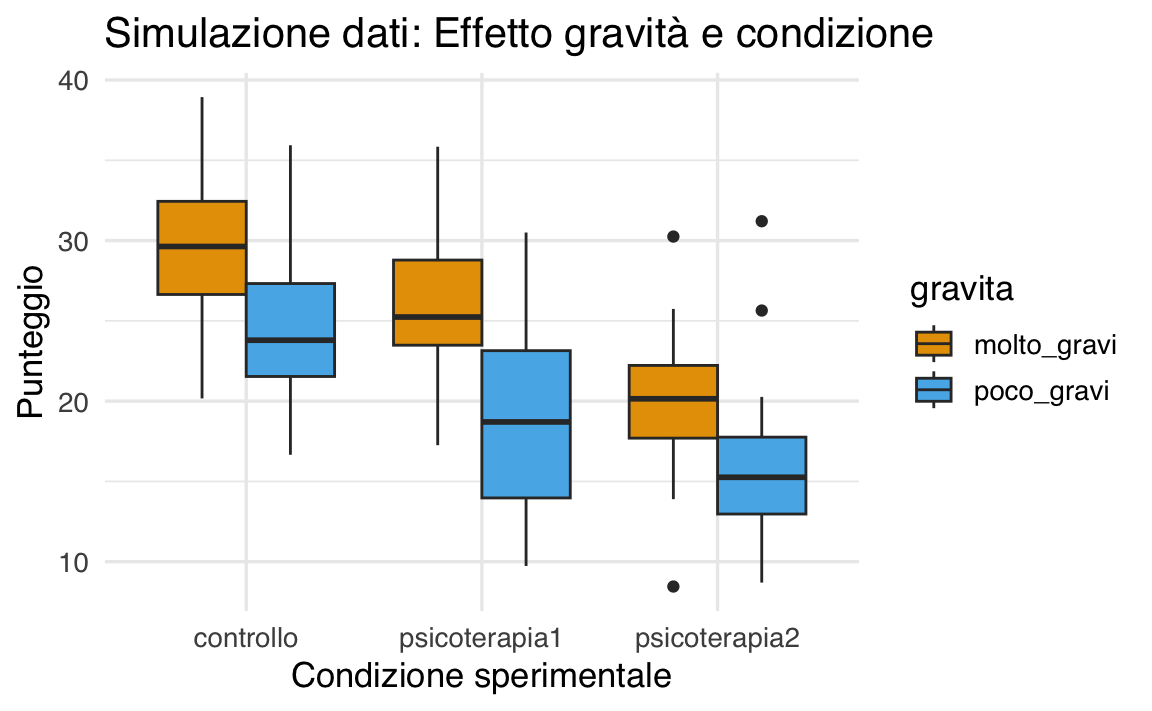
67.2 Simulazione
Simuliamo ora un dataset che rispecchi una struttura a due vie. Consideriamo:
- fattore 1:
condizione(controllo, psicoterapia1, psicoterapia2) - fattore 2:
gravita(molto_gravi, poco_gravi)
Impostiamo le medie di cella in modo che riflettano sia effetti principali sia un’interazione.
set.seed(123)
n <- 30
condizione <- c("controllo", "psicoterapia1", "psicoterapia2")
gravita <- c("molto_gravi", "poco_gravi")
sd_value <- 5
mean_table <- matrix(
c(30, 25, 20,
25, 20, 15),
nrow = 2, byrow = TRUE
)
df <- data.frame()
for (i in seq_along(gravita)) {
for (j in seq_along(condizione)) {
media <- mean_table[i, j]
dati <- rnorm(n, mean = media, sd = sd_value)
df <- rbind(df, data.frame(
gravita = gravita[i],
condizione = condizione[j],
punteggio = dati
))
}
}Visualizziamo i dati:
ggplot(df, aes(x = condizione, y = punteggio, fill = gravita)) +
geom_boxplot(position = position_dodge()) +
labs(title = "Distribuzione dei punteggi per gravita e condizione")
67.3 Modellazione Bayesiana
Adattiamo ai dati un modello che includa interazione:
mod <- brm(punteggio ~ gravita * condizione, data = df, backend = "cmdstanr")Esploriamo gli effetti condizionati:
conditional_effects(mod, "condizione:gravita")
67.4 Confronto tra Modelli
Confrontiamo due modelli:
-
mod: con interazione -
mod1: solo con effetti principali
mod1 <- brm(punteggio ~ gravita + condizione, data = df, backend = "cmdstanr")67.4.1 LOO (Leave-One-Out Cross Validation)
loo_mod <- loo(mod)
loo_mod1 <- loo(mod1)
loo_compare(loo_mod, loo_mod1)
#> elpd_diff se_diff
#> mod1 0.0 0.0
#> mod -0.7 1.5Interpretazione:
- se
elpd_diffè piccolo rispetto ase_diff, la differenza non è sostanziale; - il modello più semplice è preferibile se non vi è evidenza chiara a favore dell’interazione.
67.5 Conclusione
L’ANOVA a due vie permette di esaminare sia gli effetti separati di due fattori sia la loro interazione. La modellazione bayesiana, combinata con il confronto tramite LOO, offre un approccio potente per valutare quale struttura descrive meglio i dati. Se l’interazione non migliora la predizione in modo credibile, è preferibile adottare il modello più parsimonioso.
Informazioni sull’Ambiente di Sviluppo
sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C/UTF-8/C/C/C/C
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] bridgesampling_1.1-2 loo_2.8.0 emmeans_1.11.1
#> [4] brms_2.22.0 Rcpp_1.0.14 bayestestR_0.16.0
#> [7] posterior_1.6.1 cmdstanr_0.9.0 thematic_0.1.7
#> [10] MetBrewer_0.2.0 ggokabeito_0.1.0 see_0.11.0
#> [13] gridExtra_2.3 patchwork_1.3.0 bayesplot_1.13.0
#> [16] psych_2.5.3 scales_1.4.0 markdown_2.0
#> [19] knitr_1.50 lubridate_1.9.4 forcats_1.0.0
#> [22] stringr_1.5.1 dplyr_1.1.4 purrr_1.0.4
#> [25] readr_2.1.5 tidyr_1.3.1 tibble_3.3.0
#> [28] ggplot2_3.5.2 tidyverse_2.0.0 rio_1.2.3
#> [31] here_1.0.1
#>
#> loaded via a namespace (and not attached):
#> [1] tidyselect_1.2.1 farver_2.1.2 fastmap_1.2.0
#> [4] TH.data_1.1-3 tensorA_0.36.2.1 pacman_0.5.1
#> [7] digest_0.6.37 timechange_0.3.0 estimability_1.5.1
#> [10] lifecycle_1.0.4 StanHeaders_2.32.10 survival_3.8-3
#> [13] processx_3.8.6 magrittr_2.0.3 compiler_4.5.0
#> [16] rlang_1.1.6 tools_4.5.0 yaml_2.3.10
#> [19] data.table_1.17.6 labeling_0.4.3 htmlwidgets_1.6.4
#> [22] curl_6.3.0 pkgbuild_1.4.8 mnormt_2.1.1
#> [25] RColorBrewer_1.1-3 abind_1.4-8 multcomp_1.4-28
#> [28] withr_3.0.2 stats4_4.5.0 grid_4.5.0
#> [31] colorspace_2.1-1 inline_0.3.21 xtable_1.8-4
#> [34] MASS_7.3-65 insight_1.3.0 cli_3.6.5
#> [37] mvtnorm_1.3-3 rmarkdown_2.29 generics_0.1.4
#> [40] RcppParallel_5.1.10 rstudioapi_0.17.1 tzdb_0.5.0
#> [43] rstan_2.32.7 splines_4.5.0 parallel_4.5.0
#> [46] matrixStats_1.5.0 vctrs_0.6.5 V8_6.0.4
#> [49] Matrix_1.7-3 sandwich_3.1-1 jsonlite_2.0.0
#> [52] hms_1.1.3 glue_1.8.0 codetools_0.2-20
#> [55] ps_1.9.1 distributional_0.5.0 stringi_1.8.7
#> [58] gtable_0.3.6 QuickJSR_1.8.0 pillar_1.10.2
#> [61] htmltools_0.5.8.1 Brobdingnag_1.2-9 R6_2.6.1
#> [64] rprojroot_2.0.4 evaluate_1.0.4 lattice_0.22-7
#> [67] backports_1.5.0 rstantools_2.4.0 coda_0.19-4.1
#> [70] nlme_3.1-168 checkmate_2.3.2 xfun_0.52
#> [73] zoo_1.8-14 pkgconfig_2.0.3Bibliografia
Johnson, A. A., Ott, M., & Dogucu, M. (2022). Bayes Rules! An Introduction to Bayesian Modeling with R. CRC Press.