here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(ggbeeswarm, dslabs, gridExtra)20 Introduzione alla distribuzione normale
Introduzione
In questo capitolo forniremo un primo sguardo alla distribuzione normale, che sarà trattata in modo più approfondito nel Capitolo 40. Introduciamo la distribuzione normale a questo punto poiché essa spiega in modo chiaro perché, in molte analisi, media e deviazione standard siano impiegate come principali descrittori di una distribuzione.
20.1 La distribuzione normale
Nel Capitolo 17, abbiamo visto come gli istogrammi e i grafici di densità forniscano utili riassunti visivi di una distribuzione. In questo capitolo, ci chiediamo se sia possibile riassumere una distribuzione in modo ancora più sintetico. Spesso si fa riferimento a media e deviazione standard come statistiche riassuntive fondamentali: in sostanza, un riassunto in due numeri. Per comprendere appieno il ruolo di questi valori, dobbiamo prima capire come è definita la distribuzione normale.
La distribuzione normale, nota anche come curva a campana o distribuzione gaussiana, è uno dei concetti matematici più conosciuti (si veda il Capitolo 40). Uno dei motivi della sua fama è che numerose variabili nella realtà seguono, almeno approssimativamente, una distribuzione normale. Esempi includono le vincite nel gioco d’azzardo, l’altezza e il peso delle persone, la pressione sanguigna, i punteggi di alcuni test standardizzati e gli errori di misura negli esperimenti. I motivi matematici e probabilistici di queste approssimazioni verranno discussi in seguito; qui ci concentreremo sul come la distribuzione normale aiuti a riassumere i dati.
Anziché partire da dati empirici, la distribuzione normale si definisce tramite una formula matematica. Per un intervallo generico \((a,b)\), la proporzione di valori che cade in tale intervallo si ottiene mediante:
\[ \text{Pr}(a < x \leq b) \;=\; \int_a^b \frac{1}{\sqrt{2\pi}\,\sigma} \, e^{-\tfrac12\,\bigl(\tfrac{x - \mu}{\sigma}\bigr)^2}\, dx . \tag{20.1}\]
Non è necessario memorizzare o padroneggiare i dettagli di questa formula, ma è importante sapere che la distribuzione normale è completamente determinata da due soli parametri: \(\mu\) e \(\sigma\). Gli altri simboli nella formula (\(\pi\), \(e\), \(a\), \(b\)) rappresentano costanti matematiche o gli estremi dell’intervallo. In particolare, \(\mu\) è il valore medio (o media) e \(\sigma\) è la deviazione standard.
Questa distribuzione è simmetrica, centrata sulla media \(\mu\), e la maggior parte dei valori (circa il 95%) si trova entro 2 deviazioni standard dalla media, cioè nell’intervallo \(\mu \pm 2\sigma\). Ecco un esempio di come appare la distribuzione normale quando \(\mu = 0\) e \(\sigma = 1\):
m <- 0; s <- 1
norm_dist <- tibble(x = seq(-4, 4, length.out = 50)*s + m) |>
mutate(density = dnorm(x, m, s))
norm_dist |>
ggplot(aes(x, density)) + geom_line()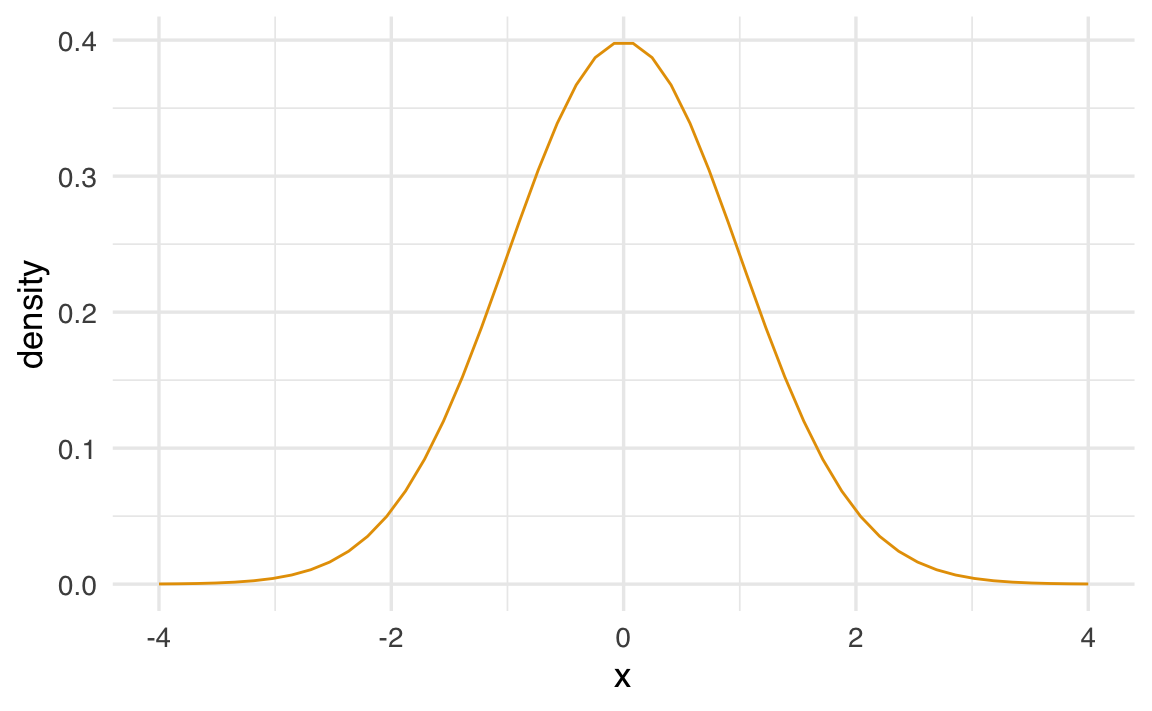
Il fatto che la distribuzione sia descritta da due parametri implica che, se un insieme di dati reali si approssima bene a una distribuzione normale, due soli numeri (media e deviazione standard) possono fornire un riassunto sintetico della distribuzione. Vediamo ora come si calcolano, in pratica, questi due parametri per una lista di valori arbitraria.
Supponiamo di avere un vettore x che contiene una serie di valori numerici. Abbiamo visto come, in R, la media si trova come:
e la deviazione standard è:
La deviazione standard si può interpretare come la distanza media dei valori dalla loro media.
20.1.1 Un esempio con i dati di altezza
Per calcolare media e deviazione standard dell’altezza maschile in un dataset, ipotizziamo che il vettore heights$height contenga le altezze di alcuni individui, mentre heights$sex contenga il genere corrispondente. Se vogliamo estrarre solo i valori relativi ai maschi, possiamo scrivere:
index <- heights$sex == "Male"
x <- heights$height[index]Quindi usiamo le funzioni predefinite di R:
Possiamo ora mettere a confronto la curva di densità osservata dei dati (in blu) con quella teorica (in nero) della distribuzione normale con media e deviazione standard stimate:
norm_dist <- tibble(
x = seq(-4, 4, length.out = 50)*s + m) |>
mutate(density = dnorm(x, m, s))
heights |>
dplyr::filter(sex == "Male") |>
ggplot(aes(height)) +
geom_density(fill = "lightblue") +
geom_line(aes(x, density), linewidth=1.5, data = norm_dist)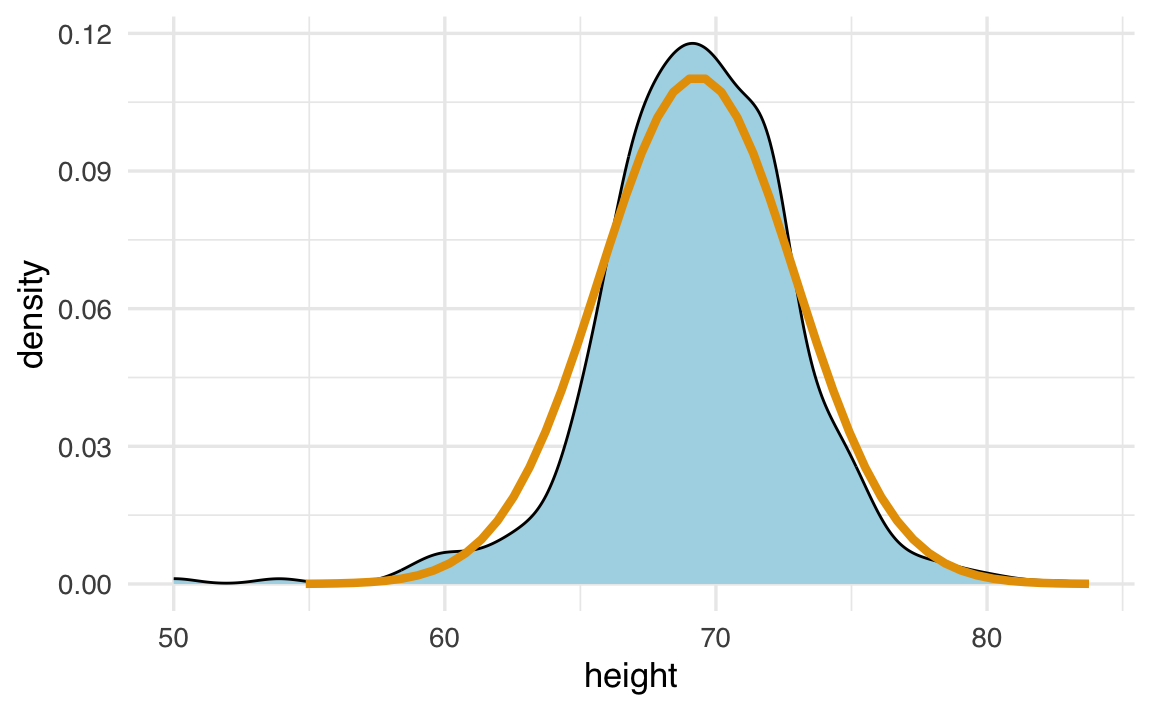
Come si vede, la curva normale fornisce una buona approssimazione per i dati sull’altezza maschile. Vedremo ora come verificare l’aderenza di una distribuzione ai dati, osservando le proporzioni di valori entro intervalli specifici.
20.2 Unità standard
Per i dati che seguono (o quasi) una distribuzione normale, è molto comodo utilizzare le cosiddette unità standard (Standard Units). Un valore \(x\) viene convertito in unità standard tramite la formula:
\[ z = \frac{x - m}{s} , \]
dove \(m\) e \(s\) sono la media e la deviazione standard della distribuzione. Questa trasformazione ci dice di quante deviazioni standard un particolare valore si discosta dalla media. Ad esempio, se \(z=0\), il valore \(x\) corrisponde esattamente alla media; se \(z = 2\), il valore \(x\) si trova a due deviazioni standard sopra la media; se \(z = -2\), a due deviazioni standard sotto la media, e così via.
In R, possiamo calcolare le unità standard con la funzione:
z <- scale(x) |> as.numeric()
head(z)
#> [1] 1.5744 0.1898 -0.3641 1.2975 -2.3026 -0.6410Se vogliamo sapere, ad esempio, quale frazione di individui si trova entro 2 deviazioni standard dalla media (cioè \(|z| < 2\)), basta scrivere:
Vedremo, in molti casi, un valore intorno al 95%, in linea con quanto previsto dalla distribuzione normale. Per confermare la bontà dell’approssimazione, si usano spesso i grafici quantile-quantile, detti anche qqplot.
20.3 Grafici quantile-quantile (qqplot)
Un modo sistematico per verificare quanto la distribuzione normale descriva bene i dati osservati consiste nel confrontare i quantili empirici con quelli teorici di una normale. Se i due insiemi di quantili sono molto simili, abbiamo un’ulteriore conferma dell’aderenza alla normalità.
- La funzione di ripartizione della distribuzione normale standard si indica spesso con \(\Phi(x)\). Ad esempio, \(\Phi(-1.96) \approx 0.025\) e \(\Phi(1.96) \approx 0.975\).
- L’inversa di \(\Phi\), indicata come \(\Phi^{-1}(p)\), ci dà il quantile corrispondente a una determinata probabilità \(p\). In R,
pnormcalcola \(\Phi(x)\) eqnormcalcola \(\Phi^{-1}(p)\). Di default,pnormeqnormsi riferiscono alla normale standard (media 0, deviazione standard 1), ma possiamo specificare valori diversi di media e deviazione standard tramite gli argomentimeanesd.
Per ottenere il quantile empirico da un vettore di dati in R, possiamo usare la funzione quantile. Ad esempio, se abbiamo un vettore x, il quantile associato alla probabilità \(p\) è il valore \(q\) per il quale mean(x <= q) = p.
Ecco lo schema logico per costruire un qqplot:
- Definiamo un vettore di proporzioni \(p_1, p_2, \dots, p_m\).
- Calcoliamo i relativi quantili empirici dei nostri dati \(\{q_1, \dots, q_m\}\) usando
quantile(x, p_i).
- Calcoliamo i quantili teorici della normale (con la stessa media e la stessa deviazione standard dei dati) usando
qnorm(p_i, mean, sd).
- Rappresentiamo i punti \((\text{quantile teorico}, \text{quantile empirico})\). Se i dati sono davvero normali, tali punti si disporranno approssimativamente lungo la retta diagonale
y = x.
Esempio in R:
p <- seq(0.05, 0.95, 0.05)
sample_quantiles <- quantile(x, p)
theoretical_quantiles <- qnorm(p, mean = mean(x), sd = sd(x))
qplot(theoretical_quantiles, sample_quantiles) + geom_abline()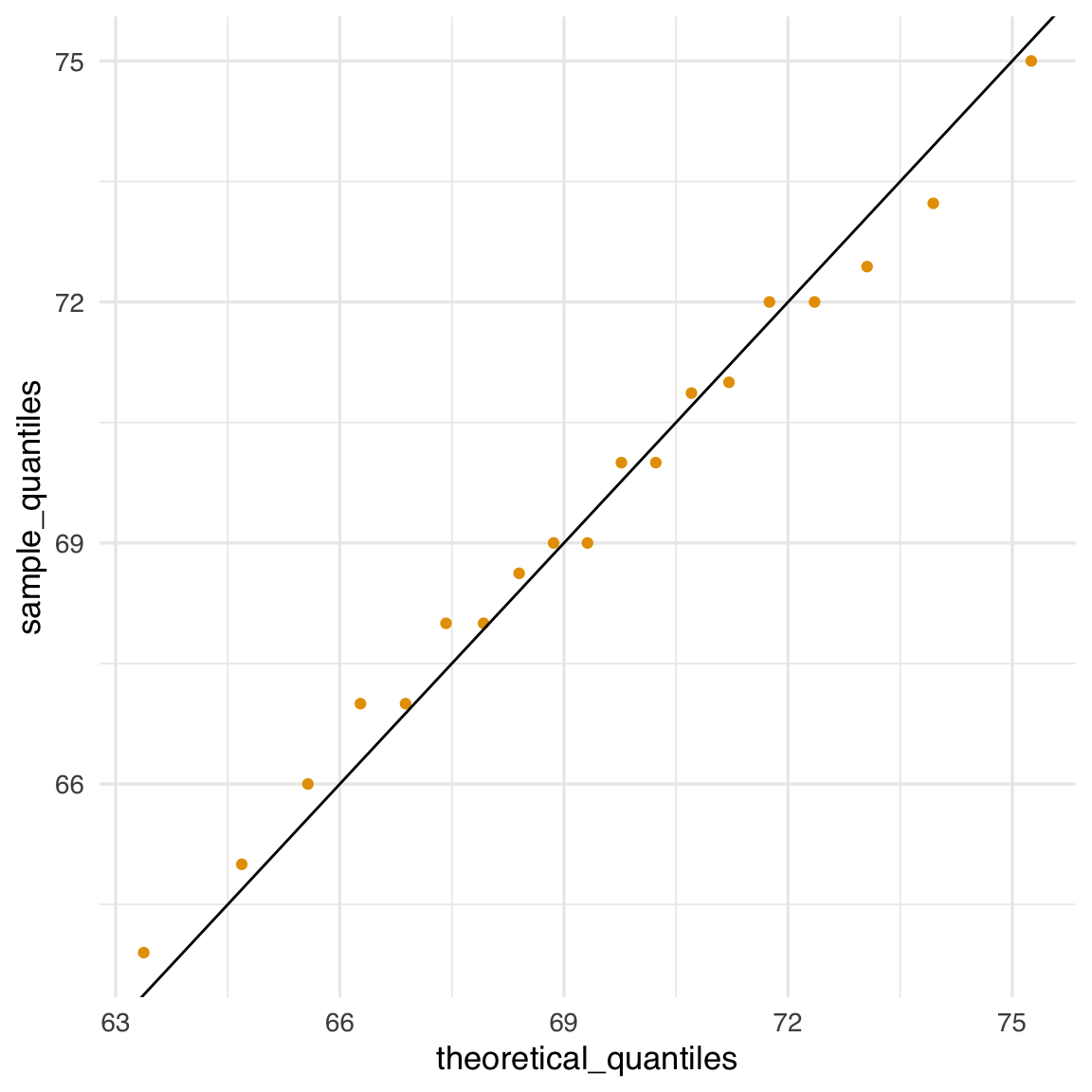
Se però abbiamo già convertito in unità standard (quindi \(\mu = 0\) e \(\sigma = 1\)), il confronto si semplifica:
sample_quantiles <- quantile(z, p)
theoretical_quantiles <- qnorm(p)
qplot(theoretical_quantiles, sample_quantiles) + geom_abline()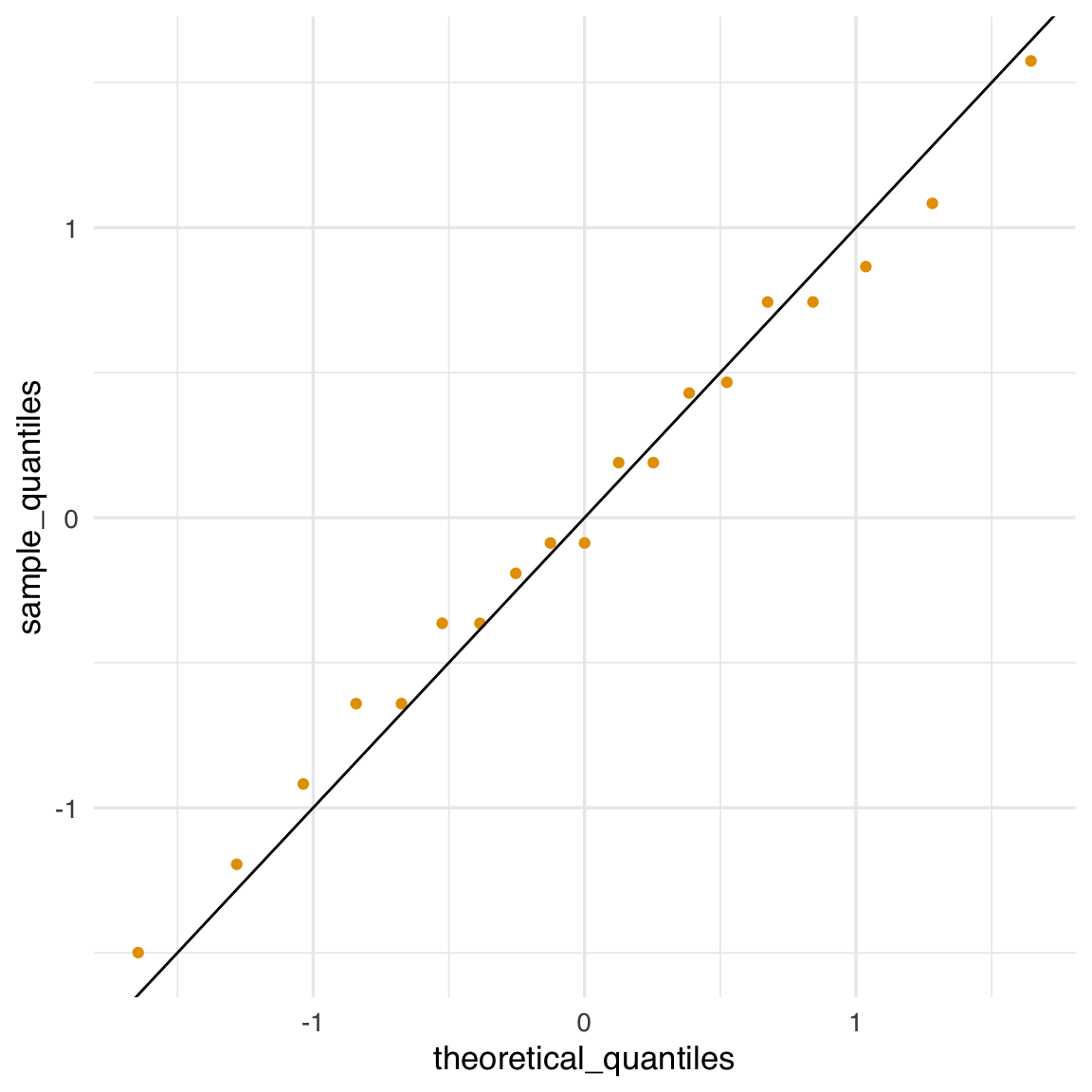
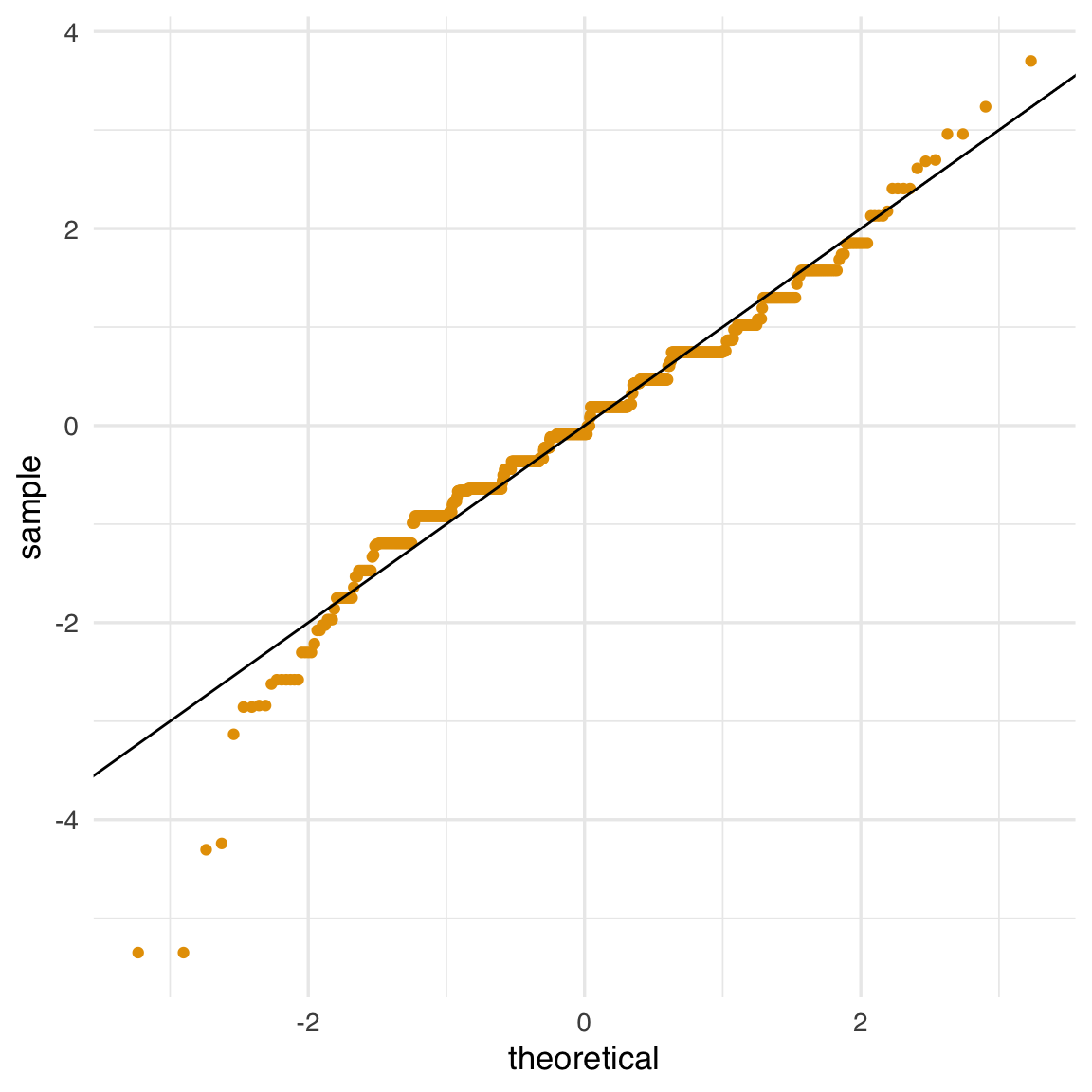
In pratica, per creare rapidamente un qqplot si usa spesso ggplot2 con la geometria geom_qq:
Come abbiamo sottolineato, se i punti nel qqplot si dispongono lungo una retta, significa che la distribuzione dei dati è in accordo con la distribuzione teorica considerata (in questo caso, la normale). I qqplot possono essere usati anche per confrontare qualsiasi coppia di distribuzioni, non solo dati e normale teorica.
Questo indica che l’approssimazione normale è accurata per il gruppo maschile (nel nostro dataset).
20.4 Media e Deviazione Standard come Statistiche Descrittive della Distribuzione
La media e la deviazione standard sono due delle statistiche più comunemente utilizzate per descrivere la distribuzione di un insieme di dati. Queste misure sono particolarmente utili quando i dati seguono una distribuzione normale. In questo caso, la media e la deviazione standard contengono tutte le informazioni necessarie per caratterizzare completamente la forma della distribuzione.
20.4.1 Distribuzione Normale e Statistiche Descrittive
La distribuzione normale è definita dalla sua media (\(\mu\)) e dalla sua deviazione standard (\(\sigma\)). La formula della densità di probabilità della distribuzione normale è data dall’Equazione 20.1. Questa formula mostra che, conoscendo solo \(\mu\) e \(\sigma\), possiamo ricostruire l’intera curva di densità. Pertanto, se i dati empirici sono ben approssimati da una distribuzione normale, la media e la deviazione standard sono sufficienti per descrivere la distribuzione.
Supponiamo di avere un dataset che segue una distribuzione normale con media 50 e deviazione standard 10. Possiamo generare dati casuali e visualizzare la curva di densità in R:
# Generiamo dati da una distribuzione normale
set.seed(123)
dati <- rnorm(1000, mean = 50, sd = 10)
# Calcoliamo media e deviazione standard
media <- mean(dati)
deviazione_standard <- sd(dati)
# Visualizziamo la curva di densità
ggplot(data.frame(dati), aes(x = dati)) +
geom_density(fill = "lightblue") +
geom_vline(xintercept = media, color = "red", linetype = "dashed") +
labs(title = "Curva di Densità di una Distribuzione Normale",
x = "Valori",
y = "Densità") +
annotate("text", x = media + 5, y = 0.03, label = paste("Media =", round(media, 2)), color = "red") +
annotate("text", x = media + 5, y = 0.025, label = paste("Deviazione Standard =", round(deviazione_standard, 2)), color = "blue")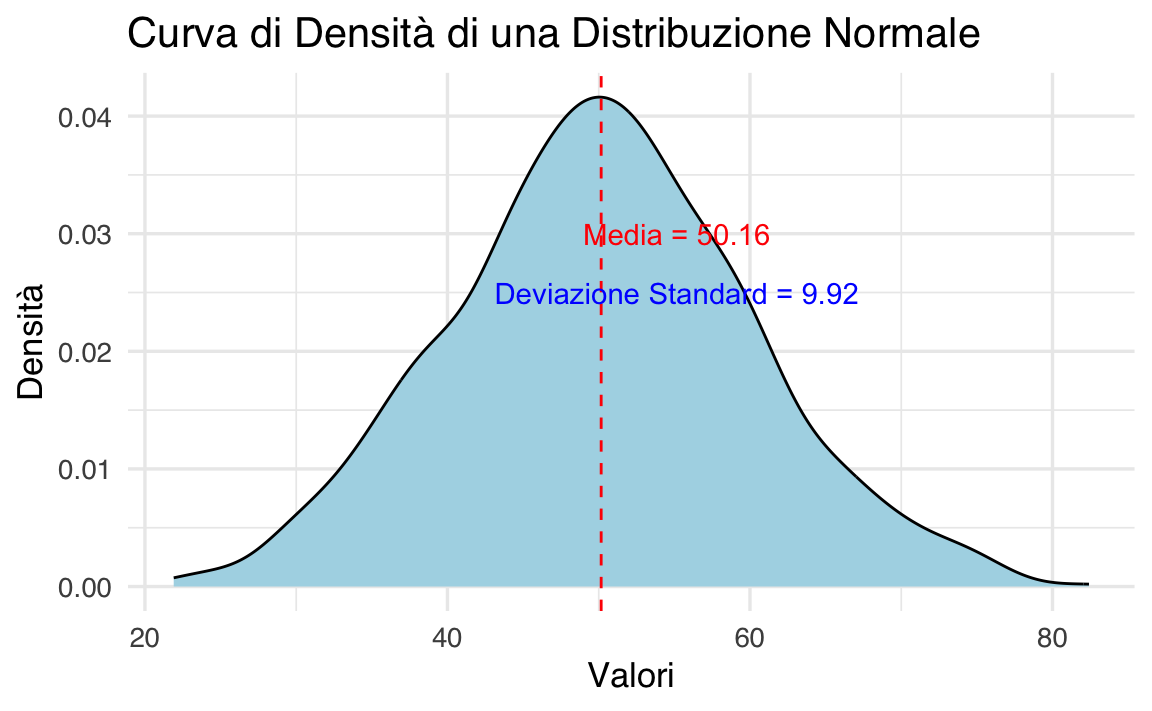
In questo esempio:
- La curva di densità è centrata attorno alla media (\(\mu = 50\)).
- La deviazione standard (\(\sigma = 10\)) determina la dispersione dei dati attorno alla media.
20.4.2 Quando Media e Deviazione Standard Non Sono Sufficienti
Sebbene media e deviazione standard siano strumenti estremamente utili per descrivere distribuzioni normali, non sempre bastano a cogliere tutte le caratteristiche di un insieme di dati. In particolare, ci sono situazioni in cui la forma della distribuzione rende necessario ricorrere a misure aggiuntive. Di seguito presentiamo alcuni casi tipici.
-
Distribuzioni Asimmetriche
Una distribuzione si dice asimmetrica (o skewed) quando una coda è più “estesa” dell’altra.- Se la coda più lunga è a destra, la distribuzione è asimmetrica positiva (o a destra).
- Se la coda più lunga è a sinistra, la distribuzione è asimmetrica negativa (o a sinistra).
In queste circostanze, la media tende a spostarsi verso la coda più lunga, mentre la mediana rimane più stabile e rappresentativa del valore centrale.
- Se la coda più lunga è a destra, la distribuzione è asimmetrica positiva (o a destra).
Distribuzioni Multimodali
Una distribuzione è multimodale quando presenta più picchi (o “modi”). Ciò significa che i dati si concentrano attorno a più di un valore, formando veri e propri sotto-gruppi. In questi casi, media e deviazione standard possono risultare poco significative, poiché non colgono la presenza di più poli di concentrazione.-
Kurtosi
La kurtosi descrive quanto una distribuzione sia “appuntita” o “piatta” rispetto a una normale.-
Alta kurtosi indica picchi molto accentuati e code più lunghe, con una maggiore probabilità di valori estremi.
- Bassa kurtosi segnala una forma più appiattita, con code ridotte e meno outlier.
-
Alta kurtosi indica picchi molto accentuati e code più lunghe, con una maggiore probabilità di valori estremi.
Quando le distribuzioni mostrano una di queste peculiarità, altre statistiche possono rivelarsi più informative:
- La mediana, insensibile ai valori estremi, fornisce una descrizione più robusta del centro.
- I quartili, e in particolare l’intervallo interquartile, danno un’idea della dispersione principale trascurando le code.
- L’indice di asimmetria (skewness) misura il grado di sbilanciamento della distribuzione.
- L’indice di curtosi (kurtosis) quantifica la “pesantezza” delle code.
Nel seguente esempio, generiamo dati da una distribuzione esponenziale, notoriamente asimmetrica:
# Generiamo dati da una distribuzione esponenziale
set.seed(123)
dati_esponenziali <- rexp(1000, rate = 0.5)
# Calcoliamo media e deviazione standard
media_esp <- mean(dati_esponenziali)
deviazione_standard_esp <- sd(dati_esponenziali)
# Visualizziamo la curva di densità
ggplot(data.frame(dati_esponenziali), aes(x = dati_esponenziali)) +
geom_density(fill = "#F8766D", alpha = 0.6) +
geom_vline(xintercept = media_esp, color = "red", linetype = "dashed") +
labs(title = "Curva di Densità di una Distribuzione Esponenziale",
x = "Valori",
y = "Densità") +
annotate("text", x = media_esp + 1, y = 0.2,
label = paste("Media =", round(media_esp, 2)),
color = "red") +
annotate("text", x = media_esp + 1, y = 0.18,
label = paste("Deviazione Standard =", round(deviazione_standard_esp, 2)),
color = "blue")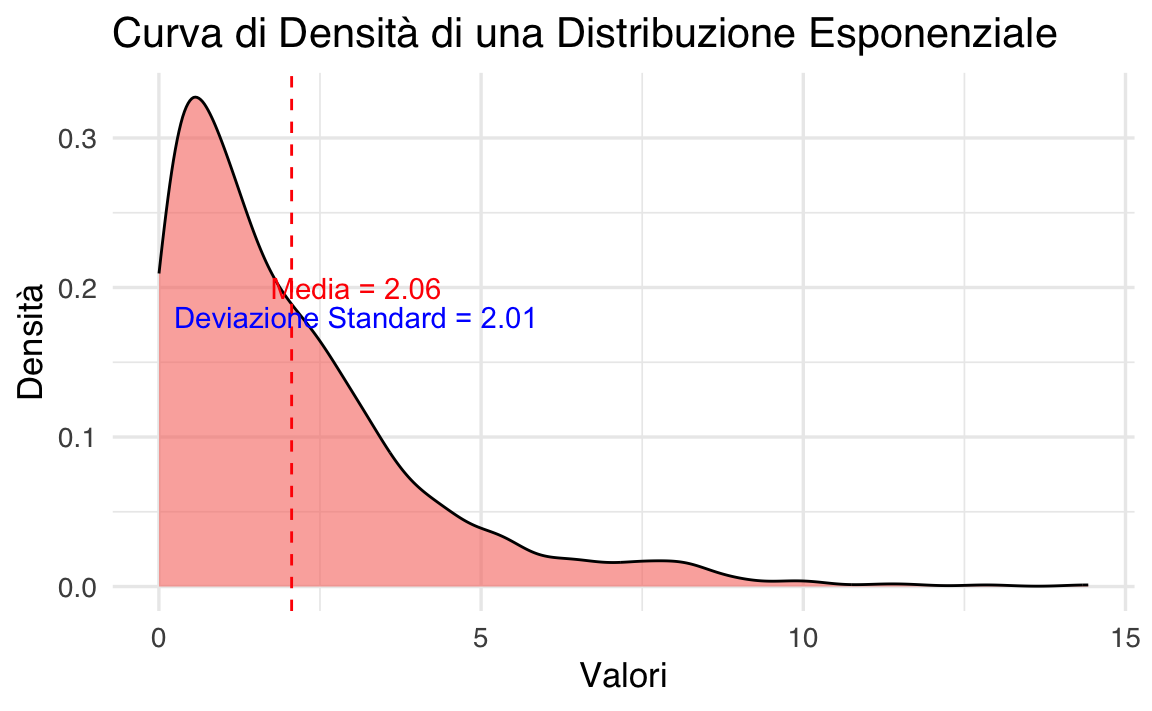
L’istogramma (o la densità) mostra chiaramente una coda lunga a destra, con molti valori piccoli e pochi valori grandi. In questo contesto:
- La media tende a seguire la coda, diventando meno rappresentativa del “centro”.
- La deviazione standard non descrive in modo efficace la variabilità, perché non considera adeguatamente la forte asimmetria.
Misure alternative, come la mediana e i quartili, forniscono informazioni più affidabili:
# Calcoliamo mediana e quartili
mediana <- median(dati_esponenziali)
quartili <- quantile(dati_esponenziali, probs = c(0.25, 0.75))
cat("Mediana:", mediana, "\n")
#> Mediana: 1.462
cat("Primo Quartile (Q1):", quartili[1], "\n")
#> Primo Quartile (Q1): 0.6134
cat("Terzo Quartile (Q3):", quartili[2], "\n")
#> Terzo Quartile (Q3): 2.853In conclusione, quando i dati non presentano una forma vicina alla normalità (ad esempio perché asimmetrici, multimodali o con kurtosi anomala), media e deviazione standard possono risultare fuorvianti o poco utili. In questi casi, è fondamentale adottare misure alternative o complementari (mediana, quartili, skewness, kurtosis) per ottenere una descrizione più accurata della distribuzione.
20.5 Riflessioni Conclusive
In questo capitolo, abbiamo esplorato alcuni concetti fondamentali per l’analisi dei dati e consolidato le basi per un’interpretazione più approfondita delle distribuzioni. In particolare, abbiamo:
- Studiato la distribuzione normale, una delle distribuzioni più importanti in statistica, e compreso perché la media e la deviazione standard siano parametri cruciali per descriverla. Questi indicatori ci permettono di riassumere in modo efficace le caratteristiche centrali e la variabilità dei dati.
- Imparato a standardizzare i dati convertendoli in unità standard (z-score), il che ci consente di confrontare variabili con scale diverse o di valutare quanto un dato specifico si discosti dalla media in termini di deviazioni standard.
- Introdotto il grafico quantile-quantile (QQ-plot), uno strumento visivo prezioso per verificare se i nostri dati seguono una distribuzione normale. Attraverso il QQ-plot, possiamo confrontare i quantili empirici dei nostri dati con quelli teorici della distribuzione normale, identificando eventuali deviazioni.
Gli strumenti descritti in questo capitolo rappresentano il primo passo essenziale nell’analisi esplorativa dei dati. Essi ci aiutano a formulare ipotesi solide e a riconoscere potenziali problemi o caratteristiche peculiari dei dati prima di applicare metodi statistici più avanzati, che approfondiremo nei prossimi capitoli.
L’analisi esplorativa, combinando grafici intuitivi e statistiche descrittive appropriate, riveste quindi un ruolo fondamentale nel processo analitico. Essa non solo ci aiuta a comprendere meglio la natura dei dati, ma ci fornisce anche una base solida su cui costruire conclusioni statistiche attendibili e informate.
20.6 Esercizi
Informazioni sull’Ambiente di Sviluppo
sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.1
#>
#> locale:
#> [1] C/UTF-8/C/C/C/C
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] dslabs_0.8.0 ggbeeswarm_0.7.2 thematic_0.1.7 MetBrewer_0.2.0
#> [5] ggokabeito_0.1.0 see_0.11.0 gridExtra_2.3 patchwork_1.3.0
#> [9] bayesplot_1.13.0 psych_2.5.3 scales_1.4.0 markdown_2.0
#> [13] knitr_1.50 lubridate_1.9.4 forcats_1.0.0 stringr_1.5.1
#> [17] dplyr_1.1.4 purrr_1.0.4 readr_2.1.5 tidyr_1.3.1
#> [21] tibble_3.3.0 ggplot2_3.5.2 tidyverse_2.0.0 rio_1.2.3
#> [25] here_1.0.1
#>
#> loaded via a namespace (and not attached):
#> [1] generics_0.1.4 stringi_1.8.7 lattice_0.22-7
#> [4] hms_1.1.3 digest_0.6.37 magrittr_2.0.3
#> [7] evaluate_1.0.4 grid_4.5.0 timechange_0.3.0
#> [10] RColorBrewer_1.1-3 fastmap_1.2.0 rprojroot_2.0.4
#> [13] jsonlite_2.0.0 mnormt_2.1.1 cli_3.6.5
#> [16] rlang_1.1.6 withr_3.0.2 tools_4.5.0
#> [19] parallel_4.5.0 tzdb_0.5.0 pacman_0.5.1
#> [22] vctrs_0.6.5 R6_2.6.1 lifecycle_1.0.4
#> [25] htmlwidgets_1.6.4 vipor_0.4.7 beeswarm_0.4.0
#> [28] pkgconfig_2.0.3 pillar_1.10.2 gtable_0.3.6
#> [31] glue_1.8.0 xfun_0.52 tidyselect_1.2.1
#> [34] rstudioapi_0.17.1 farver_2.1.2 htmltools_0.5.8.1
#> [37] nlme_3.1-168 labeling_0.4.3 rmarkdown_2.29
#> [40] compiler_4.5.0Bibliografia
Irizarry, R. A. (2024). Introduction to Data Science: Data Wrangling and Visualization with R. CRC Press.