here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, cmdstanr, posterior, brms, bayestestR, insight)
conflicts_prefer(dplyr::count)72 Confronto tra due proporzioni con la regressione logistica
“In clinical research, many of the most important questions reduce to comparing two proportions: who improves, and who does not.”
– Robert Rosenthal, Meta-Analytic Procedures for Social Research (1991)
Introduzione
Immaginiamo di voler stabilire se due gruppi di persone hanno la stessa probabilità di ottenere un certo risultato, ad esempio la guarigione dopo un trattamento o il superamento di un esame con due diversi metodi di studio. In questi casi l’esito è binario: ogni individuo può avere successo o insuccesso, sì o no, guarito o non guarito. Per analizzare dati di questo tipo possiamo ricorrere alla regressione logistica, un modello che permette di stimare l’effetto del gruppo di appartenenza sulla probabilità di successo.
Quando i due gruppi sono distinti e indipendenti, il confronto si riduce a una regressione logistica molto semplice, in cui compare un solo predittore binario. In un approccio bayesiano ciò significa che possiamo esprimere in modo esplicito le nostre ipotesi iniziali attraverso distribuzioni a priori e ottenere, come risultato dell’analisi, non un singolo numero ma una distribuzione a posteriori che descrive l’intera gamma dei valori plausibili per i parametri.
Panoramica del capitolo
- Comprendere il confronto tra due proporzioni come caso base della regressione logistica.
- Tradurre i coefficienti logit in probabilità, differenza di rischio, odds ratio e risk ratio.
- Stimare i parametri con approccio bayesiano tramite
brms.
- Interpretare le distribuzioni posteriori e l’incertezza delle stime.
- Eseguire controlli predittivi e visualizzare i risultati.
72.1 Perché usare la regressione logistica per confrontare due proporzioni
Confrontare due proporzioni significa chiedersi se la probabilità di successo osservata in un gruppo differisce da quella osservata nell’altro. Se nel gruppo 0 registriamo \(x_0\) successi su \(n_0\) prove e nel gruppo 1 osserviamo \(x_1\) successi su \(n_1\) prove, le proporzioni vere possono essere indicate con \(\theta_0\) e \(\theta_1\). La differenza tra le due proporzioni, \(\Delta = \theta_1 - \theta_0\), fornisce una misura diretta del divario. Un altro indice spesso utilizzato è l’odds ratio, che confronta il rapporto tra successi e insuccessi in ciascun gruppo.
La regressione logistica permette di formalizzare questa idea. Se indichiamo con \(D_i\) una variabile che assume valore zero per gli individui del gruppo di riferimento e valore uno per gli individui del gruppo di confronto, possiamo scrivere il modello come
\[ y_i \sim \text{Bernoulli}(p_i), \qquad \text{logit}(p_i) = \alpha + \gamma D_i . \]
In questo contesto, l’intercetta \(\alpha\) rappresenta i log-odds del gruppo di riferimento, mentre il coefficiente \(\gamma\) esprime la differenza di log-odds fra i due gruppi, cioè il logaritmo dell’odds ratio. L’esponenziale di \(\gamma\) fornisce infatti l’odds ratio vero e proprio.
Questo schema mostra che confrontare due proporzioni equivale a stimare una regressione logistica con un unico predittore dummy, con il vantaggio di ottenere risultati coerenti con modelli più complessi e di poter passare facilmente da una scala all’altra, dalle probabilità agli odds, fino alle differenze o ai rapporti di rischio. In un quadro bayesiano, questo confronto si arricchisce ulteriormente perché le stime vengono fornite sotto forma di distribuzioni a posteriori, permettendo di esprimere direttamente l’incertezza su ciascuna quantità di interesse.
72.2 Un esempio concreto
Un’applicazione particolarmente chiara di queste idee si trova nello studio di Banerjee et al. (2025), che ha confrontato le abilità matematiche di due gruppi di bambini in India: da un lato quelli che lavoravano nei mercati di Kolkata e Delhi, dall’altro quelli che frequentavano la scuola senza lavorare. Lo scopo era verificare se le competenze sviluppate nel lavoro quotidiano, come dare il resto o sommare i prezzi, si trasferissero al contesto scolastico e se, viceversa, l’addestramento scolastico potesse essere utile nei problemi pratici del mercato. I risultati hanno mostrato che i bambini lavoratori erano molto abili nei problemi concreti, ma meno preparati in quelli astratti, mentre gli scolarizzati presentavano lo schema opposto.
Consideriamo i dati relativi ai problemi astratti. Tra i bambini lavoratori si sono registrati 670 successi su 1488 prove, pari a una proporzione di circa 0.45. Tra i bambini scolarizzati i successi sono stati 320 su 542, cioè circa 0.59. La situazione è ancora più marcata nei problemi di mercato: i bambini lavoratori hanno ottenuto 134 successi su 373 prove, pari a 0.36, mentre i bambini scolarizzati hanno risolto solo 3 problemi su 271, cioè appena lo 0.01.
# Successi e denominatori
x_work <- 670 ; n_work <- 1488
x_non <- 320 ; n_non <- 542
# Tabella aggregata per il modello binomiale
dat_a <- tibble(
count = c(x_non, x_work), # ordine: riferimento (non-working), poi working
tot = c(n_non, n_work),
group = factor(c("non-working", "working"),
levels = c("non-working", "working"))
)
dat_a
#> # A tibble: 2 × 3
#> count tot group
#> <dbl> <dbl> <fct>
#> 1 320 542 non-working
#> 2 670 1488 working72.3 Un rapido controllo
Prima di impostare il modello bayesiano, può essere utile calcolare in chiave frequentista la differenza osservata fra le due proporzioni, insieme a un intervallo di confidenza. Questo non fa parte del nostro approccio principale, ma consente di verificare che i dati siano coerenti con quelli riportati in letteratura e ci offre un punto di riferimento preliminare.
p_non <- x_non / n_non
p_work <- x_work / n_work
rd_obs <- p_non - p_work
alpha <- 0.05
se_ci <- sqrt(p_non*(1-p_non)/n_non + p_work*(1-p_work)/n_work)
z_crit <- qnorm(1 - alpha/2)
ci_rd <- c(rd_obs - z_crit*se_ci, rd_obs + z_crit*se_ci)
sprintf("Differenza osservata (non-working - working): %.3f (95%% CI: [%.2f, %.2f])",
rd_obs, ci_rd[1], ci_rd[2])
#> [1] "Differenza osservata (non-working - working): 0.140 (95% CI: [0.09, 0.19])"Questo rapido controllo conferma che i bambini scolarizzati hanno una proporzione di risposte corrette maggiore rispetto ai bambini lavoratori nei problemi astratti, come già segnalato dagli autori dello studio.
72.4 Modello bayesiano con regressione logistica
Passiamo ora al modello bayesiano. Usiamo il pacchetto brms con backend cmdstanr, in continuità con i capitoli precedenti. Per impostare il modello binomiale con esito aggregato, specifichiamo dei prior debolmente informativi sulla scala logit:
priors <- c(
prior(normal(0, 2.5), class = "Intercept"),
prior(normal(0, 2.5), class = "b")
)La stima viene quindi effettuata sul numero di successi in ciascun gruppo, tenendo conto del numero totale di prove, con la variabile categoriale group che distingue fra bambini scolarizzati e bambini lavoratori. Nel gruppo di riferimento, definito come “non-working”, l’intercetta del modello rappresenta i log-odds di successo, mentre il coefficiente associato al predittore misura lo scarto di log-odds del gruppo “working”.
Dopo aver impostato il modello, procediamo alla stima con brms. I dati vengono trattati in forma aggregata, specificando il numero di successi e di prove per ciascun gruppo. Usiamo la famiglia binomiale, fissiamo i prior debolmente informativi sulla scala logit, e chiediamo al campionatore MCMC di esplorare lo spazio dei parametri.
fit_a <- brm(
count | trials(tot) ~ group,
data = dat_a,
family = binomial(),
prior = priors,
backend = "cmdstanr",
seed = 1234,
iter = 4000, chains = 4, cores = 4,
sample_prior = "yes",
refresh = 0
)Un primo sguardo ai risultati con summary(fit_a) ci mostra i coefficienti stimati sulla scala logit. Tuttavia, per comprendere appieno il significato psicologico e applicativo di questi numeri, è utile trasformarli nelle quantità di maggiore interesse: le probabilità di successo nei due gruppi, la loro differenza, e i rapporti che le mettono a confronto.
summary(fit_a)
#> Family: binomial
#> Links: mu = logit
#> Formula: count | trials(tot) ~ group
#> Data: dat_a (Number of observations: 2)
#> Draws: 4 chains, each with iter = 4000; warmup = 2000; thin = 1;
#> total post-warmup draws = 8000
#>
#> Regression Coefficients:
#> Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept 0.37 0.09 0.20 0.54 1.00 3230 3722
#> groupworking -0.57 0.10 -0.77 -0.37 1.00 3929 3843
#>
#> Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).A partire dall’intercetta otteniamo la probabilità dei bambini scolarizzati (gruppo di riferimento), mentre aggiungendo il coefficiente della variabile dummy otteniamo la probabilità del gruppo dei bambini lavoratori. La differenza fra le due probabilità definisce la risk difference. Il coefficiente della dummy, espresso come esponenziale, corrisponde invece all’odds ratio. Infine, il rapporto fra le probabilità fornisce il risk ratio.
Riepilogando i valori medi e gli intervalli credibili, possiamo osservare direttamente le stime per ciascuna quantità.
post_summary <- tibble(
quantity = c("p_ref (non-working)", "p_work (working)", "RD (work - ref)", "OR", "RR"),
mean = c(mean(post$p_ref), mean(post$p_work), mean(post$RD), mean(post$OR), mean(post$RR)),
q2.5 = c(quantile(post$p_ref, .025), quantile(post$p_work, .025), quantile(post$RD, .025),
quantile(post$OR, .025), quantile(post$RR, .025)),
q97.5 = c(quantile(post$p_ref, .975), quantile(post$p_work, .975), quantile(post$RD, .975),
quantile(post$OR, .975), quantile(post$RR, .975))
)
post_summary
#> # A tibble: 5 × 4
#> quantity mean q2.5 q97.5
#> <chr> <dbl> <dbl> <dbl>
#> 1 p_ref (non-working) 0.591 0.550 0.632
#> 2 p_work (working) 0.450 0.425 0.476
#> 3 RD (work - ref) -0.141 -0.188 -0.0918
#> 4 OR 0.569 0.465 0.692
#> 5 RR 0.763 0.698 0.834Per avere un’impressione immediata della direzione degli effetti, possiamo calcolare le probabilità posteriori che le quantità di interesse siano minori o maggiori di valori soglia. In particolare, ci chiediamo con quale probabilità la proporzione dei bambini lavoratori superi quella degli scolarizzati, oppure la differenza di rischio sia negativa, o ancora l’odds ratio e il risk ratio siano inferiori a uno.
Gli intervalli credibili confermano e quantificano l’incertezza. La probabilità stimata di successo per i bambini scolarizzati ha un intervallo al 95% che si colloca attorno a valori medio-alti, mentre quella dei bambini lavoratori si concentra su valori più bassi. L’intervallo credibile della differenza di rischio è per lo più negativo, suggerendo una minore probabilità di successo nel gruppo dei lavoratori. Lo stesso vale per l’odds ratio, con valori che tendono a collocarsi stabilmente al di sotto dell’unità.
hdi_p_ref <- bayestestR::hdi(post$p_ref, ci = 0.95)
hdi_p_work <- bayestestR::hdi(post$p_work, ci = 0.95)
hdi_RD_89 <- bayestestR::hdi(post$RD, ci = 0.89)
hdi_OR_95 <- bayestestR::hdi(post$OR, ci = 0.95)
list(
`95% HDI p_ref` = hdi_p_ref,
`95% HDI p_work` = hdi_p_work,
`89% HDI RD` = hdi_RD_89,
`95% HDI OR` = hdi_OR_95
)
#> $`95% HDI p_ref`
#> 95% HDI: [0.55, 0.63]
#>
#> $`95% HDI p_work`
#> 95% HDI: [0.43, 0.48]
#>
#> $`89% HDI RD`
#> 89% HDI: [-0.18, -0.10]
#>
#> $`95% HDI OR`
#> 95% HDI: [0.46, 0.69]Interpretare questi risultati significa tradurre le diverse scale. Le proporzioni forniscono una misura intuitiva: nei dati considerati, la probabilità di successo dei bambini scolarizzati si aggira intorno al 59 per cento, mentre quella dei bambini lavoratori è più vicina al 45 per cento. La differenza di rischio, cioè lo scarto fra le due proporzioni, risulta negativa e conferma un divario a sfavore dei lavoratori. L’odds ratio esprime lo stesso fenomeno su un’altra scala: un valore inferiore a uno indica che gli odds di successo dei lavoratori sono più bassi di quelli degli scolarizzati. Il risk ratio, infine, mostra che la probabilità di successo dei lavoratori corrisponde solo a una frazione di quella degli scolarizzati.
Tutte queste trasformazioni raccontano la stessa storia con linguaggi diversi, e lo fanno in modo coerente con quanto osservato nei dati grezzi. Il vantaggio del modello bayesiano è che non ci limita a un’unica stima puntuale, ma ci offre distribuzioni posteriori complete che quantificano l’incertezza e permettono di rispondere a domande probabilistiche dirette, come “quanto è probabile che la differenza di proporzioni sia negativa?” oppure “quanto è probabile che l’odds ratio sia minore di uno?”.
Questo capitolo si collega direttamente alla discussione precedente sull’odds ratio. In quel caso avevamo stimato l’indice in modo diretto, come parametro principale di un modello. Qui, invece, vediamo come lo stesso odds ratio emerga naturalmente come trasformazione del coefficiente logit in una regressione con variabile dummy. Le due prospettive non sono in contrasto, ma si integrano: la regressione logistica fornisce un quadro generale dal quale si derivano OR, RR e RD, mentre l’analisi bayesiana dell’odds ratio ci ha mostrato come sia possibile focalizzarsi in modo mirato su un singolo parametro di interesse.
72.5 Un secondo esempio: i problemi di mercato
Riprendiamo ora i dati relativi ai problemi di mercato. Qui le differenze tra i due gruppi diventano ancora più evidenti. I bambini lavoratori hanno risolto correttamente 134 problemi su 373, con una proporzione di circa 0.36. I bambini scolarizzati, invece, hanno risposto correttamente solo 3 volte su 271, con una proporzione che sfiora lo zero, appena 0.01. Questo scenario rappresenta una situazione di forte divario, opposta a quella vista nei problemi astratti.
# Dati per i problemi di mercato
x_work_m <- 134 ; n_work_m <- 373
x_non_m <- 3 ; n_non_m <- 271
dat_m <- tibble(
count = c(x_non_m, x_work_m),
tot = c(n_non_m, n_work_m),
group = factor(c("non-working", "working"),
levels = c("non-working", "working"))
)
dat_m
#> # A tibble: 2 × 3
#> count tot group
#> <dbl> <dbl> <fct>
#> 1 3 271 non-working
#> 2 134 373 workingImpostiamo lo stesso modello bayesiano, mantenendo la struttura logistica con dummy di gruppo.
fit_m <- brm(
count | trials(tot) ~ group,
data = dat_m,
family = binomial(),
prior = priors,
backend = "cmdstanr",
seed = 1234,
iter = 4000, chains = 4, cores = 4,
sample_prior = "yes",
refresh = 0
)Dopo la stima, estraiamo nuovamente le quantità di interesse: le probabilità nei due gruppi, la loro differenza, l’odds ratio e il risk ratio.
post_m <- as_draws_df(fit_m) %>%
mutate(
p_ref = plogis(b_Intercept),
p_work = plogis(b_Intercept + b_groupworking),
RD = p_work - p_ref,
OR = exp(b_groupworking),
RR = p_work / p_ref
)
post_summary_m <- tibble(
quantity = c("p_ref (non-working)", "p_work (working)", "RD (work - ref)", "OR", "RR"),
mean = c(mean(post_m$p_ref), mean(post_m$p_work), mean(post_m$RD), mean(post_m$OR), mean(post_m$RR)),
q2.5 = c(quantile(post_m$p_ref, .025), quantile(post_m$p_work, .025), quantile(post_m$RD, .025),
quantile(post_m$OR, .025), quantile(post_m$RR, .025)),
q97.5 = c(quantile(post_m$p_ref, .975), quantile(post_m$p_work, .975), quantile(post_m$RD, .975),
quantile(post_m$OR, .975), quantile(post_m$RR, .975))
)
post_summary_m
#> # A tibble: 5 × 4
#> quantity mean q2.5 q97.5
#> <chr> <dbl> <dbl> <dbl>
#> 1 p_ref (non-working) 0.0141 0.00393 0.0312
#> 2 p_work (working) 0.358 0.310 0.408
#> 3 RD (work - ref) 0.344 0.295 0.396
#> 4 OR 51.8 17.0 143.
#> 5 RR 33.4 11.3 91.3Le stime posteriori raccontano una storia molto chiara. La probabilità di successo per i bambini scolarizzati è praticamente nulla, con un intervallo credibile che resta vicino allo zero. Per i bambini lavoratori, invece, la probabilità si colloca intorno al 36 per cento. La differenza di rischio è quindi nettamente positiva e l’odds ratio assume valori molto superiori a uno, indicando un vantaggio marcato dei lavoratori.
Per rendere ancora più evidente la forza dell’effetto, possiamo calcolare la probabilità a posteriori che la proporzione dei lavoratori sia superiore a quella degli scolarizzati, oppure che la differenza di rischio e l’odds ratio siano strettamente positivi.
In questo caso le probabilità posteriori sono praticamente pari a uno, cioè la certezza che i bambini lavoratori abbiano prestazioni migliori nei problemi di mercato.
72.6 Confronto fra i due scenari
Mettendo insieme i due esempi — problemi astratti e problemi di mercato — si ottiene un quadro coerente con le ipotesi teoriche dello studio. Nei problemi astratti, tipici dell’ambiente scolastico, i bambini scolarizzati mostrano una probabilità di successo più elevata rispetto ai lavoratori. Nei problemi di mercato, invece, il risultato si ribalta: i bambini che hanno esperienza diretta nelle attività quotidiane del lavoro sono nettamente più preparati, mentre gli scolarizzati faticano.
La regressione logistica in chiave bayesiana ci permette di quantificare entrambi gli scenari con la stessa cornice concettuale. Le differenze non vengono solo osservate nei dati grezzi, ma diventano stime probabilistiche con intervalli credibili che riflettono l’incertezza. È particolarmente utile osservare come le diverse scale (proporzioni, differenza di rischio, odds ratio, risk ratio) restituiscano sempre la stessa conclusione, ciascuna con il proprio linguaggio: più intuitivo nel caso delle proporzioni, più compatto e comparabile in quello dell’odds ratio.
Questa analisi illustra bene il vantaggio di un modello unificato. Con un’unica struttura logistica possiamo descrivere scenari molto diversi, da un divario moderato a uno estremo, e tradurre i risultati su scale diverse a seconda delle esigenze interpretative.
72.7 Visualizzazione dei risultati
Per rendere più intuitiva l’interpretazione, possiamo rappresentare graficamente le distribuzioni posteriori.
72.7.1 Differenza di rischio (RD)
Nel primo grafico vediamo le distribuzioni posteriori della risk difference nei due scenari. Nel caso dei problemi astratti, la distribuzione si concentra su valori negativi, indicando un vantaggio per i bambini scolarizzati. Nei problemi di mercato, al contrario, la distribuzione si colloca interamente su valori positivi, con un vantaggio netto per i bambini lavoratori.
post_RD <- bind_rows(
post %>% select(RD) %>% mutate(scenario = "Problemi astratti"),
post_m %>% select(RD) %>% mutate(scenario = "Problemi di mercato")
)
ggplot(post_RD, aes(x = RD, fill = scenario)) +
geom_density(alpha = 0.5) +
geom_vline(xintercept = 0, linetype = "dashed") +
facet_wrap(~scenario, ncol = 1, scales = "free_y") +
labs(
title = "Distribuzioni posteriori della differenza di rischio (RD)",
x = "RD = p_work - p_non",
y = "Densità"
) 
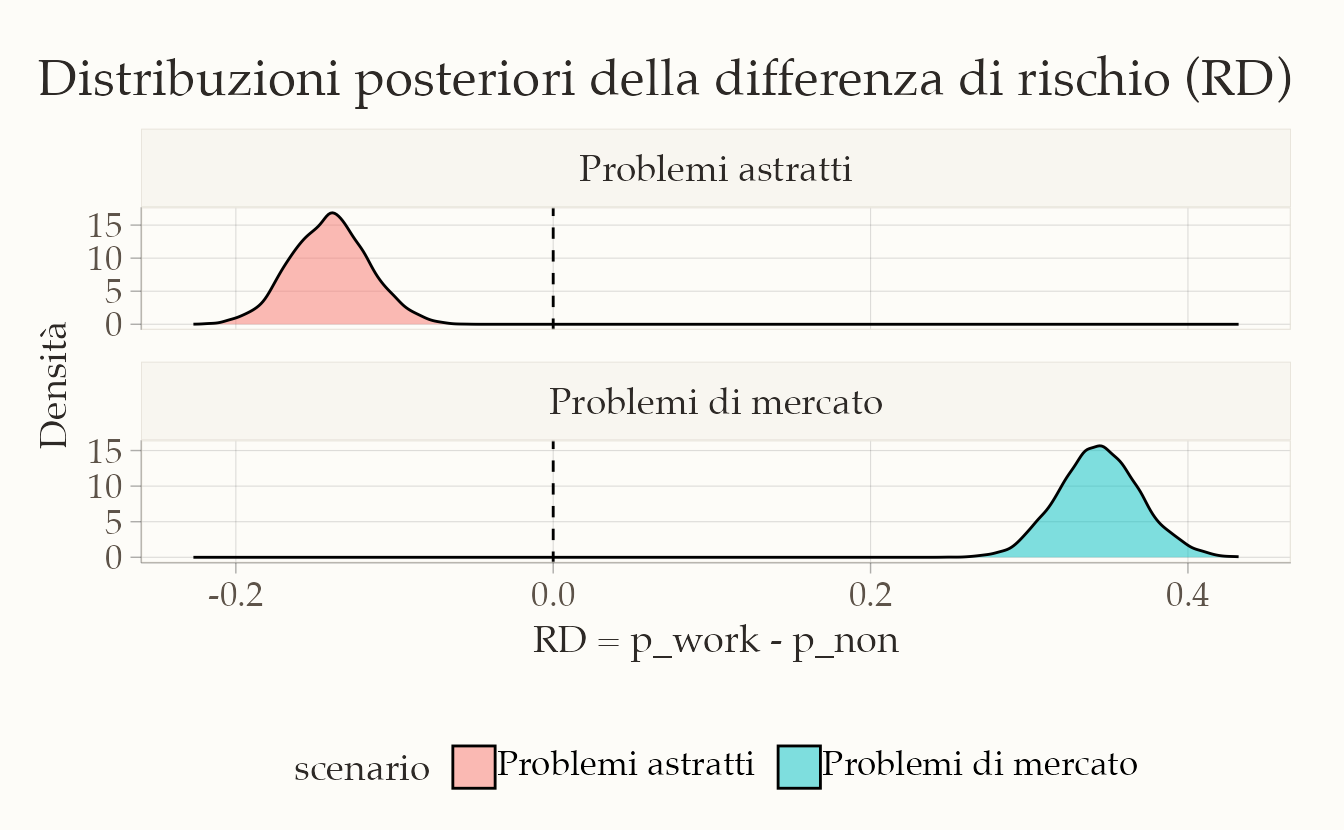
72.7.2 Odds ratio (OR)
Un secondo grafico mostra le distribuzioni posteriori dell’odds ratio. Nei problemi astratti, la distribuzione è concentrata al di sotto di 1, evidenziando odds più bassi per i bambini lavoratori. Nei problemi di mercato, l’odds ratio risulta al contrario molto più grande di 1, segnalando un vantaggio consistente per i lavoratori.
post_OR <- bind_rows(
post %>% select(OR) %>% mutate(scenario = "Problemi astratti"),
post_m %>% select(OR) %>% mutate(scenario = "Problemi di mercato")
)
ggplot(post_OR, aes(x = OR, fill = scenario)) +
geom_density(alpha = 0.5) +
geom_vline(xintercept = 1, linetype = "dashed") +
facet_wrap(~scenario, ncol = 1, scales = "free_y") +
scale_x_continuous(trans = "log", breaks = c(0.1, 0.5, 1, 2, 5, 10, 50)) +
labs(
title = "Distribuzioni posteriori dell’odds ratio (OR)",
x = "Odds ratio (scala log)",
y = "Densità"
) 
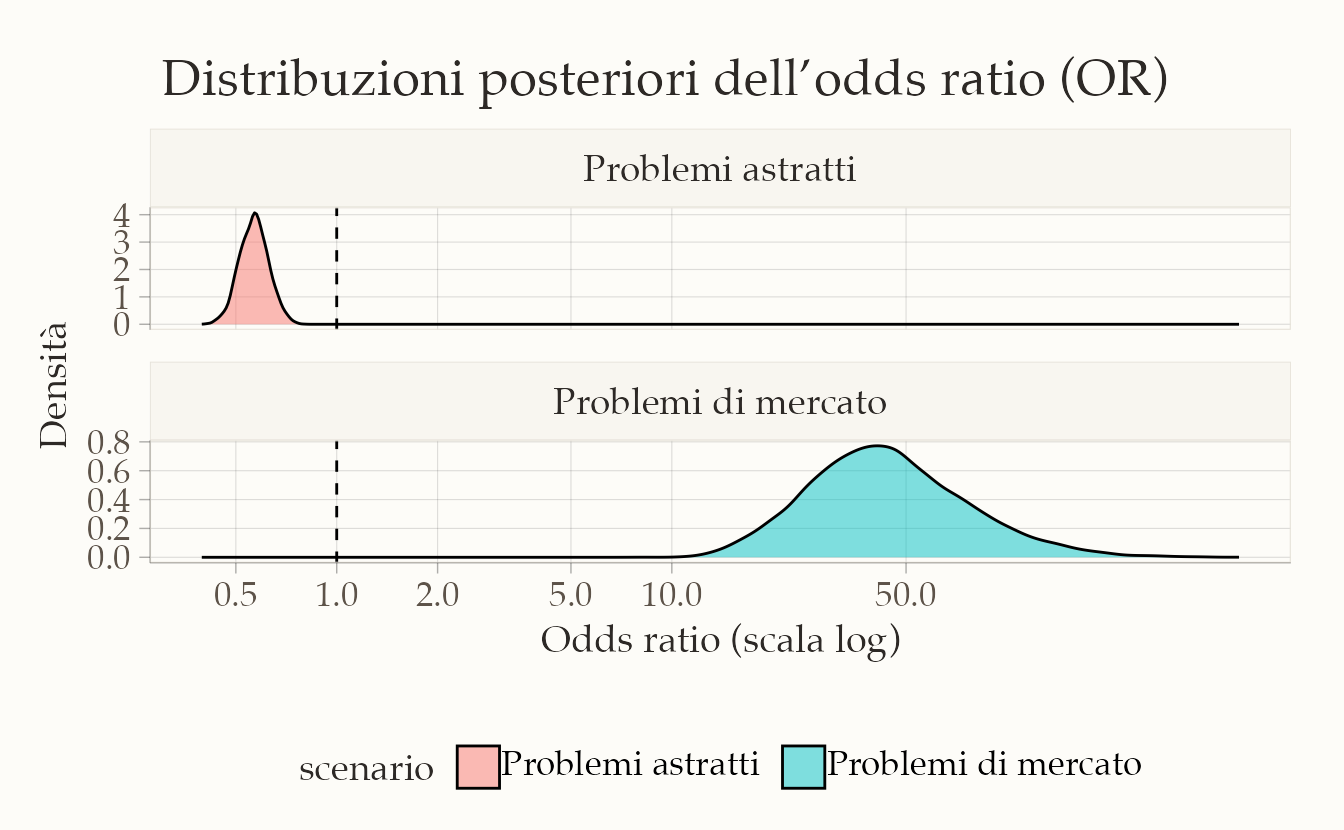
Queste figure completano l’analisi, mostrando visivamente come lo stesso modello possa descrivere due situazioni opposte. La regressione logistica, in chiave bayesiana, fornisce un linguaggio comune per esprimere risultati che nei dati appaiono così divergenti: vantaggio per i bambini scolarizzati nei compiti astratti, e vantaggio per i bambini lavoratori nei compiti concreti di mercato.
72.8 Proporzioni posteriori di successo per gruppo
Per completare il quadro conviene mostrare direttamente le probabilità di successo stimate per ciascun gruppo, nei due scenari. L’idea è di partire dai draw posteriori già calcolati e di riassumerli con mediana e intervalli credibili. Il grafico risultante rende evidente, a colpo d’occhio, sia la distanza fra i gruppi sia l’ampiezza dell’incertezza.
# Raccogliamo i draw di p per ciascuno scenario e gruppo
post_props <- bind_rows(
post %>%
transmute(
scenario = "Problemi astratti",
`non-working` = p_ref,
`working` = p_work
),
post_m %>%
transmute(
scenario = "Problemi di mercato",
`non-working` = p_ref,
`working` = p_work
)
) |>
pivot_longer(cols = c(`non-working`, `working`),
names_to = "gruppo", values_to = "p")
# Riassunto con mediana e intervalli credibili
summ_props <- post_props |>
group_by(scenario, gruppo) |>
median_qi(p, .width = c(.95, .89)) |>
ungroup()
# Grafico punto + intervallo credibile
ggplot(summ_props, aes(x = gruppo, y = p, ymin = .lower, ymax = .upper)) +
geom_pointrange(position = position_dodge(width = 0.4)) +
facet_wrap(~ scenario, ncol = 1) +
scale_y_continuous(labels = scales::percent_format(accuracy = 1)) +
labs(
title = "Proporzioni posteriori di successo per gruppo",
x = NULL,
y = "Probabilità di successo (posterior)"
) 
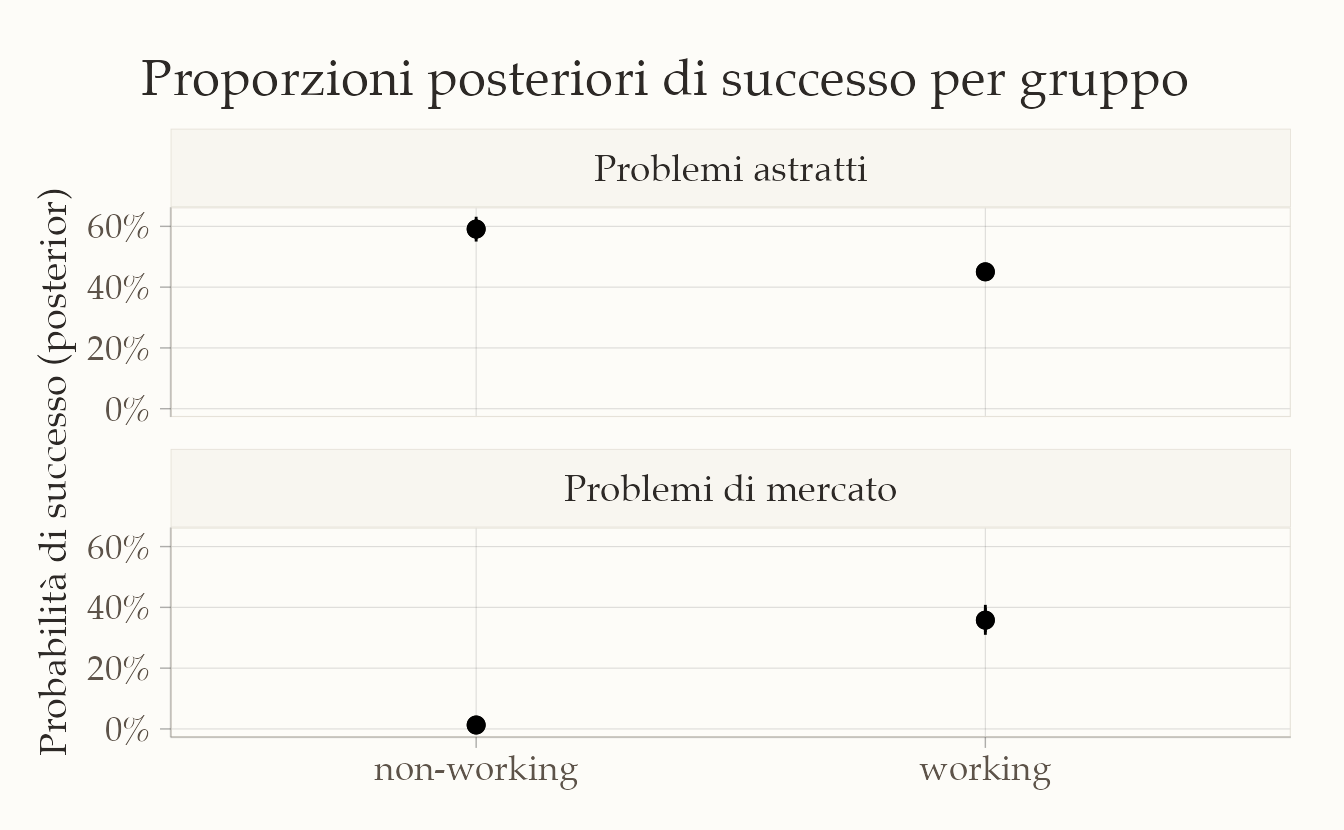
Il pannello sui problemi astratti mostra una probabilità di successo più alta per i bambini scolarizzati rispetto ai lavoratori, con intervalli credibili che riflettono l’incertezza ma mantengono un chiaro distacco fra i gruppi. Il pannello sui problemi di mercato, al contrario, evidenzia un’inversione marcata: i lavoratori presentano una probabilità sensibilmente maggiore, mentre gli scolarizzati rimangono vicini allo zero. La lettura combinata di questi due pannelli rafforza l’interpretazione proposta nei paragrafi precedenti e rende visiva la coerenza fra scale diverse, perché le conclusioni tratte da RD, OR e RR trovano una corrispondenza immediata nelle probabilità stimate.
72.9 Il modello scritto in Stan
Per completezza, possiamo mostrare come la stessa analisi sia realizzabile direttamente in Stan, senza passare da brms. Questo esempio ha uno scopo puramente didattico: nel capitolo “Regressione logistica con Stan” troveremo la discussione più dettagliata della sintassi e delle scelte di modellizzazione. Qui ci interessa soprattutto vedere come la struttura logistica con variabile dummy possa essere implementata in modo molto semplice.
Il modello prevede due gruppi. Per ciascun gruppo conosciamo il numero di successi e il numero totale di prove. Introduciamo inoltre un predittore dummy che vale 0 per il gruppo di riferimento (non-working) e 1 per il gruppo di confronto (working). Il modello utilizza una parametrizzazione logit con due coefficienti: l’intercetta \(\alpha\), che descrive i log-odds del gruppo di riferimento, e il coefficiente \(\gamma\), che rappresenta la differenza di log-odds fra i gruppi. A partire da questi due parametri possiamo ricavare tutte le quantità di interesse già discusse, cioè le probabilità di successo nei due gruppi, la differenza di rischio, l’odds ratio e il risk ratio.
stan_code <- '
data {
int<lower=1> G; // numero di gruppi (=2)
array[G] int<lower=0> y; // successi osservati per ciascun gruppo
array[G] int<lower=0> n; // prove totali per ciascun gruppo
array[G] int<lower=0,upper=1> D; // dummy: 0 = non-working, 1 = working
}
parameters {
real alpha; // intercetta (log-odds gruppo di riferimento)
real gamma; // coefficiente della dummy (log-odds ratio)
}
model {
// prior deboli sulla scala logit
alpha ~ normal(0, 2.5);
gamma ~ normal(0, 2.5);
// verosimiglianza binomiale per ciascun gruppo
for (g in 1:G) {
real eta = alpha + gamma * D[g];
y[g] ~ binomial(n[g], inv_logit(eta));
}
}
generated quantities {
real p_ref = inv_logit(alpha); // probabilità nel gruppo di riferimento
real p_work = inv_logit(alpha + gamma); // probabilità nel gruppo working
real RD = p_work - p_ref; // differenza di probabilità
real OR = exp(gamma); // odds ratio
real RR = p_work / p_ref; // risk ratio
}
'I dati da fornire a Stan sono molto semplici: i conteggi di successi e prove nei due gruppi, più la variabile dummy che distingue i gruppi.
Compiliamo quindi il modello e avviamo il campionamento MCMC.
mod <- cmdstan_model(write_stan_file(stan_code))
fitS <- mod$sample(data = dat_stan, seed = 1234,
chains = 4, parallel_chains = 4)Infine, estraiamo le quantità derivate di maggiore interesse, esattamente le stesse già calcolate nel caso di brms.
fitS$summary(variables = c("p_ref","p_work","RD","OR","RR"))
#> # A tibble: 5 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 p_ref 0.59 0.59 0.02 0.02 0.55 0.62 1.00 929.93 853.06
#> 2 p_work 0.45 0.45 0.01 0.01 0.43 0.47 1.00 3200.94 2588.52
#> 3 RD -0.14 -0.14 0.02 0.02 -0.18 -0.10 1.01 877.41 873.29
#> 4 OR 0.57 0.57 0.06 0.06 0.48 0.68 1.01 874.90 869.35
#> 5 RR 0.76 0.76 0.04 0.03 0.71 0.83 1.01 929.62 1006.13I risultati ottenuti coincidono con quelli ricavati tramite brms. Questo conferma che la parametrizzazione logit con dummy è del tutto equivalente all’impostazione con predittore categoriale, e che da essa possiamo derivare in modo trasparente tutte le grandezze interpretative: probabilità nei gruppi, differenza di rischio, odds ratio e risk ratio. In questo modo il modello Stan, pur scritto in forma minimale, ci permette di vedere con chiarezza la logica interna dell’analisi e rafforza la comprensione concettuale della regressione logistica come strumento per il confronto fra proporzioni.
72.10 Posterior predictive check
Un vantaggio di Stan è che possiamo generare, nello stesso modello, dei dati replicati secondo la distribuzione predittiva posteriore. Questo ci consente di confrontare i dati osservati con quelli che il modello si aspetta, valutando così la bontà dell’adattamento.
Basta aggiungere, nella sezione generated quantities, delle variabili che rappresentino i successi simulati a posteriori per ciascun gruppo. Queste repliche, combinate con le quantità già calcolate (\(p_{ref}\), \(p_{work}\), \(RD\), \(OR\), \(RR\)), ci permettono di eseguire controlli predittivi direttamente in R dopo l’esecuzione del modello.
stan_code_ppc <- '
data {
int<lower=1> G; // numero gruppi (=2)
array[G] int<lower=0> y; // successi osservati
array[G] int<lower=0> n; // prove totali
array[G] int<lower=0,upper=1> D; // dummy: 0 = non-working, 1 = working
}
parameters {
real alpha; // intercetta (log-odds gruppo di riferimento)
real gamma; // coefficiente dummy (log-odds ratio)
}
model {
// prior deboli
alpha ~ normal(0, 2.5);
gamma ~ normal(0, 2.5);
for (g in 1:G) {
real eta = alpha + gamma * D[g];
y[g] ~ binomial(n[g], inv_logit(eta));
}
}
generated quantities {
real p_ref = inv_logit(alpha);
real p_work = inv_logit(alpha + gamma);
real RD = p_work - p_ref;
real OR = exp(gamma);
real RR = p_work / p_ref;
// dati replicati per i due gruppi
array[G] int y_rep;
for (g in 1:G) {
real eta = alpha + gamma * D[g];
y_rep[g] = binomial_rng(n[g], inv_logit(eta));
}
}
'Prepariamo i dati nello stesso modo di prima:
Compiliamo e lanciamo il modello:
mod_ppc <- cmdstan_model(write_stan_file(stan_code_ppc))
fit_ppc <- mod_ppc$sample(data = dat_stan, seed = 1234,
chains = 4, parallel_chains = 4)Ora possiamo esaminare le repliche generate a posteriori. Ad esempio, visualizziamo le distribuzioni predittive delle proporzioni replicate e confrontiamole con quelle osservate.
# Estraiamo le repliche
y_rep <- fit_ppc$draws("y_rep") |> as_draws_matrix()
y_rep_df <- as_tibble(y_rep) |>
mutate(draw = row_number()) |>
pivot_longer(-draw, names_to = "var", values_to = "count_rep") |>
mutate(group = ifelse(var == "y_rep[1]", "non-working", "working"),
tot = ifelse(group == "non-working", n_non, n_work),
observed = ifelse(group == "non-working", x_non, x_work),
prop_rep = count_rep / tot,
prop_obs = observed / tot)
ggplot(y_rep_df, aes(x = prop_rep)) +
geom_density(alpha = 0.5, fill = okabe_ito["sky"]) +
geom_vline(aes(xintercept = prop_obs), linetype = "dashed") +
facet_wrap(~ group, scales = "free") +
scale_x_continuous(labels = scales::percent_format(accuracy = 1)) +
labs(
title = "Posterior predictive check (Stan)",
subtitle = "Linea tratteggiata = proporzione osservata;\ncurva = distribuzione delle proporzioni replicate",
x = "Proporzione di successi (repliche posteriori)",
y = "Densità"
) 
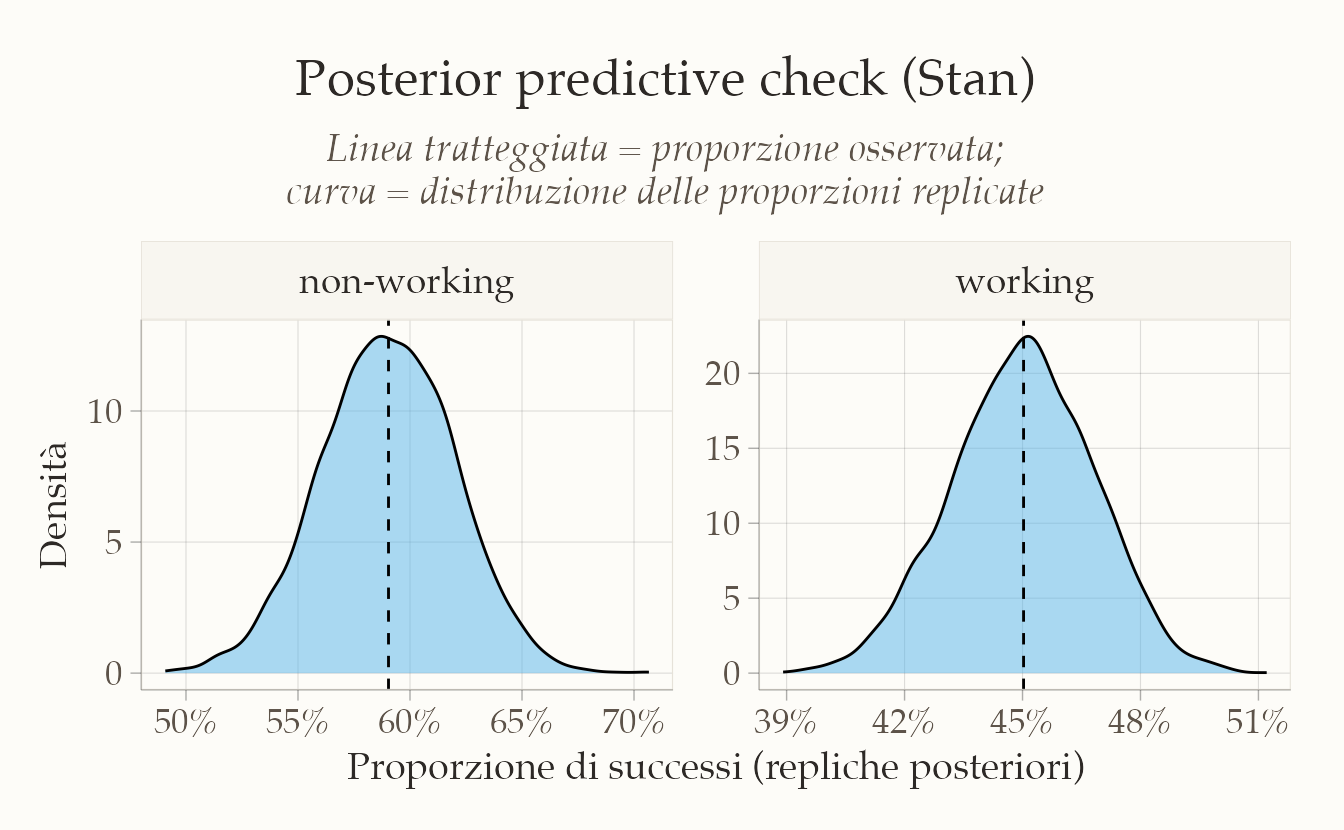
Il grafico mostra che le proporzioni osservate nei due gruppi ricadono all’interno delle distribuzioni predittive generate dal modello. Questo è un segnale positivo: il modello è capace di riprodurre i dati reali con buona coerenza. Naturalmente, controlli più sofisticati possono includere altre statistiche riassuntive o l’uso di funzioni dedicate, ma questo esempio illustra bene il principio fondamentale: Stan non si limita a stimare parametri, ma permette anche di simulare nuovi dati per verificare in modo diretto l’adeguatezza del modello.
Riflessioni conclusive
Il confronto tra due proporzioni rappresenta uno degli esempi più semplici, ma anche più istruttivi, di regressione logistica. La struttura con una sola variabile dummy mostra in modo trasparente come il coefficiente stimato corrisponda al log-odds ratio, da cui si possono ricavare direttamente tutte le quantità che interessano: le probabilità di successo nei due gruppi, la loro differenza, l’odds ratio e il risk ratio. L’approccio bayesiano aggiunge a questo schema la possibilità di quantificare l’incertezza attraverso le distribuzioni posteriori, permettendo di rispondere a domande probabilistiche che restano fuori portata in un’impostazione puramente frequentista.
In questo capitolo abbiamo visto come un modello molto compatto possa unificare prospettive apparentemente diverse. La regressione logistica con dummy riproduce infatti le analisi viste in precedenza sull’odds ratio, ma al tempo stesso si inserisce in un quadro più ampio che comprende predittori multipli, continui o categoriali, e le loro interazioni. Il passaggio da questo caso elementare a modelli più complessi è quindi naturale: basta aggiungere predittori o trasformare la codifica, e la logica del modello rimane invariata.
Per questo motivo il capitolo trova la sua giusta collocazione subito dopo quello dedicato alla regressione logistica con Stan. Partendo dal caso più semplice, lo studente ha modo di comprendere a fondo la logica del modello e di vedere come, passo dopo passo, essa si estenda senza difficoltà a situazioni più ricche e realistiche. Il confronto tra due proporzioni non è dunque solo un esempio introduttivo, ma costituisce anche la base concettuale su cui costruire le analisi che affronteremo nei capitoli successivi.
Bibliografia
Banerjee, A. V., Bhattacharjee, S., Chattopadhyay, R., Duflo, E., Ganimian, A. J., Rajah, K., & Spelke, E. S. (2025). Children’s arithmetic skills do not transfer between applied and academic mathematics. Nature, 1–9.