here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(brms, posterior, cmdstanr, tidybayes, loo, patchwork)64 Errore di specificazione e bias da variabile omessa
“The coefficients may be useful for descriptive purposes, but not for causal inference or even prediction.”
— David A. Freedman, From Association to Causation via Regression
Introduzione
Uno degli aspetti più delicati dei modelli di regressione è il rischio di errore di specificazione (Ramsey, 1969). Questo si verifica quando il modello che stimiamo non corrisponde al “vero” modello che ha generato i dati. In particolare, parleremo del caso in cui omettiamo una variabile esplicativa che:
- è correlata con almeno uno dei regressori inclusi nel modello, e
- ha un effetto diretto sulla variabile dipendente \(Y\).
Quando entrambe queste condizioni si verificano, la stima dei coefficienti parziali di regressione risulta sistematicamente distorta.
Panoramica del capitolo
- Bias da variabile omessa: escludere una variabile rilevante altera sistematicamente i coefficienti.
- Condizioni del bias.
- Implicazioni: i coefficienti OLS non sono interpretabili in chiave causale; la regressione è fenomenologica.
- Prospettiva: privilegiare modelli meccanicistici (es., Rescorla–Wagner, DDM, dinamici EMA).
64.1 Errore di specificazione e bias da variabile omessa
64.1.1 Idea chiave
Se il vero modello è
\[ Y=\beta_0+\beta_1X_1+\beta_2X_2+\varepsilon,\qquad \mathbb{E}[\varepsilon\mid X_1,X_2]=0, \] ma stimiamo erroneamente il modello che omette \(X_2\),
\[ Y=\alpha_0+\alpha_1X_1+u, \] allora il coefficiente su \(X_1\) risulta distorto quando:
- \(X_2\) ha effetto diretto su \(Y\) (\(\beta_2\neq 0\));
- \(X_2\) è correlata con \(X_1\) (\(\mathrm{Corr}(X_1,X_2)\neq 0\)).
64.1.2 Dimostrazione (via standardizzazione)
64.1.2.1 Passo 1 — Standardizza le variabili
Definiamo medie \(\mu_1,\mu_2,\mu_Y\) e deviazioni standard \(\sigma_1,\sigma_2,\sigma_Y\). Poniamo
\[ Z_1=\frac{X_1-\mu_1}{\sigma_1},\qquad Z_2=\frac{X_2-\mu_2}{\sigma_2},\qquad Z_Y=\frac{Y-\mu_Y}{\sigma_Y}. \]
Per costruzione:
- \(\mathrm{Var}(Z_1)=\mathrm{Var}(Z_2)=1\),
- \(\mathrm{Cov}(Z_1,Z_2)=\rho_{12}=\mathrm{Corr}(X_1,X_2)\).
Il modello vero standardizzato è
\[ Z_Y=\gamma_1 Z_1+\gamma_2 Z_2+\varepsilon_z,\qquad \mathbb{E}[\varepsilon_z\mid Z_1,Z_2]=0, \] con beta standardizzati
\[ \gamma_1=\beta_1\,\frac{\sigma_1}{\sigma_Y},\qquad \gamma_2=\beta_2\,\frac{\sigma_2}{\sigma_Y}. \]
64.1.2.2 Passo 2 — Stima (erronea) che omette \(Z_2\)
Stimiamo la regressione univariata
\[ Z_Y=\delta_1 Z_1 + \text{errore}. \]
Per OLS,
\[ \hat\delta_1=\frac{\mathrm{Cov}(Z_1,Z_Y)}{\mathrm{Var}(Z_1)}=\mathrm{Cov}(Z_1,Z_Y), \] dato che \(\mathrm{Var}(Z_1)=1\).
Usiamo il modello vero standardizzato:
\[ \begin{align} \mathrm{Cov}(Z_1,Z_Y) &=\mathrm{Cov}\big(Z_1,\gamma_1Z_1+\gamma_2Z_2+\varepsilon_z\big)\notag\\ &=\gamma_1\underbrace{\mathrm{Var}(Z_1)}_{=1} +\gamma_2\,\mathrm{Cov}(Z_1,Z_2) +\underbrace{\mathrm{Cov}(Z_1,\varepsilon_z)}_{=0}. \end{align} \]
Quindi
\[ \boxed{\;\hat\delta_1=\gamma_1+\gamma_2\,\rho_{12}\;}. \]
Lettura immediata: il coefficiente stimato univariato mescola l’effetto diretto standardizzato di \(X_1\) (\(\gamma_1\)) con un termine spurio \(\gamma_2\rho_{12}\) dovuto all’omissione di \(X_2\).
64.1.3 Ritraduzione ai coefficienti non standardizzati
Tra i coefficienti vale
\[ \hat\delta_1=\frac{\sigma_1}{\sigma_Y}\,\hat\alpha_1,\qquad \gamma_1=\beta_1\,\frac{\sigma_1}{\sigma_Y},\qquad \gamma_2=\beta_2\,\frac{\sigma_2}{\sigma_Y}. \]
Dalla formula standardizzata
\[ \hat\delta_1=\gamma_1+\gamma_2\rho_{12} \] segue
\[ \frac{\sigma_1}{\sigma_Y}\,\hat\alpha_1 =\beta_1\frac{\sigma_1}{\sigma_Y} +\beta_2\frac{\sigma_2}{\sigma_Y}\rho_{12}. \]
Moltiplicando per \(\sigma_Y/\sigma_1\) e ricordando che \(\rho_{12}=\dfrac{\mathrm{Cov}(X_1,X_2)}{\sigma_1\sigma_2}\), ottieniamo la forma non standardizzata:
\[ \boxed{\;\hat\alpha_1=\beta_1+\beta_2\,\frac{\mathrm{Cov}(X_1,X_2)}{\mathrm{Var}(X_1)}\;}. \]
Bias (in media):
\[ \boxed{\;\mathbb{E}[\hat\alpha_1]-\beta_1 =\beta_2\,\frac{\mathrm{Cov}(X_1,X_2)}{\mathrm{Var}(X_1)}\;} \quad\Longleftrightarrow\quad \boxed{\;\mathbb{E}[\hat\delta_1]-\gamma_1=\gamma_2\rho_{12}\;}. \]
64.1.4 Interpretazione didattica
- Condizioni per il bias: serve sia \(\beta_2\neq 0\) (l’omessa \(X_2\) conta davvero su \(Y\)) sia \(\rho_{12}\neq 0\) (l’omessa \(X_2\) è correlata con \(X_1\)). Se una condizione manca, il bias svanisce.
-
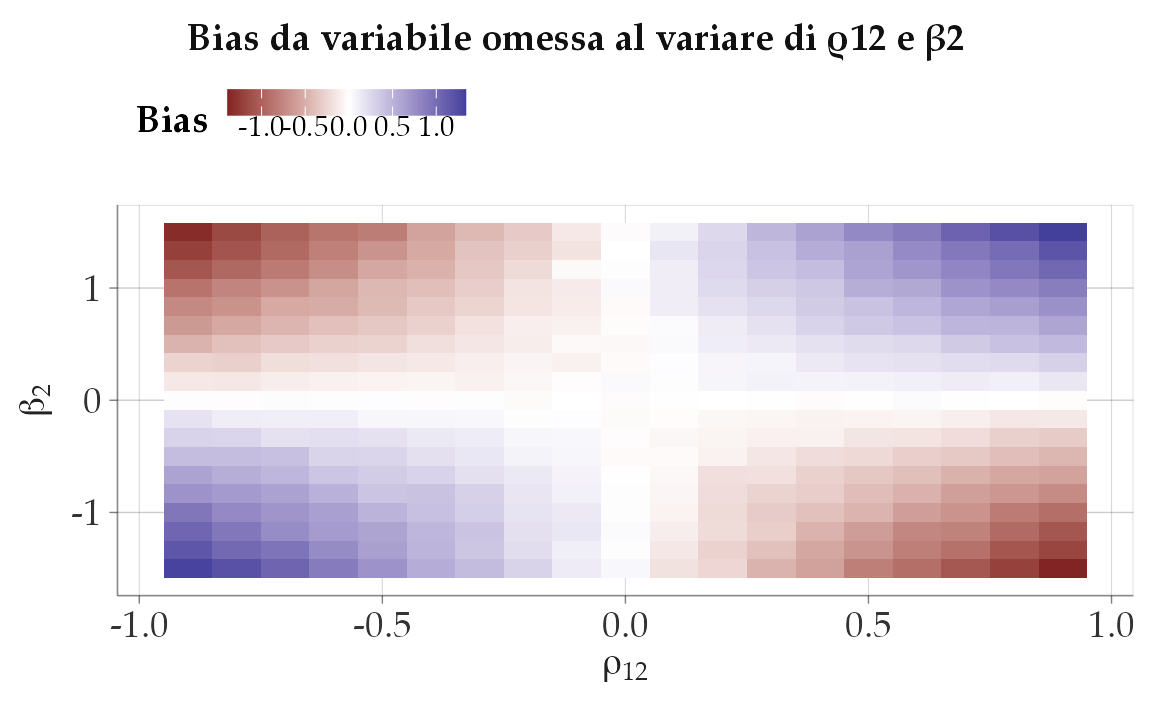
Segno del bias (scala standardizzata): \(\mathrm{Bias}(\hat\delta_1)=\gamma_2\rho_{12}\).
- \(\gamma_2>0\) e \(\rho_{12}>0\) ⇒ sovrastima;
- \(\gamma_2>0\) e \(\rho_{12}<0\) ⇒ sottostima.
64.1.5 Perché conta in psicologia
La regressione multipla è un modello fenomenologico: fotografa associazioni tra variabili, non i meccanismi che le generano. In contesti psicologici, l’omissione di variabili rilevanti è spesso inevitabile: non conosciamo o non misuriamo tutti i determinanti di \(Y\). Ne segue che i coefficienti parziali possono essere sistematicamente distorti e, dunque, fuorvianti.
64.1.6 Oltre la regressione: modelli formali dei processi
Per queste ragioni, i modelli di regressione multipla dovrebbero avere un ruolo limitato in psicologia. Molto più promettente è l’uso di modelli formali che cercano di rappresentare i meccanismi psicologici sottostanti. Esempi discussi in questa dispensa sono:
- il modello di apprendimento di Rescorla–Wagner, che spiega come gli individui aggiornano le loro aspettative sulla base del feedback;
- il Drift Diffusion Model (DDM), che descrive i processi decisionali come un accumulo di evidenza nel tempo;
- i modelli dinamici per dati EMA, che mostrano come l’umore e altre variabili psicologiche cambiano nel tempo.
Questi modelli non si limitano a descrivere correlazioni, ma cercano di catturare i processi causali che generano i dati osservati.
Mappa del bias: variazione di \(\rho_{12}\) e \(\beta_2\)
Esaminiamo come segno e magnitudo del bias cambino al variare della correlazione tra regressori (\(\rho_{12}\)) e dell’effetto dell’omessa (\(\beta_2\)). La heatmap visualizza \(\hat\alpha_1-\beta_1\).
set.seed(1)
n <- 3000; beta1 <- 1; sig <- 1
rho_seq <- seq(-.9,.9,length=19); b2_seq <- seq(-1.5,1.5,length=19)
grid <- expand.grid(rho=rho_seq, b2=b2_seq)
sim_once <- function(rho, beta2){
X1 <- rnorm(n)
X2 <- rho*X1 + sqrt(1-rho^2)*rnorm(n) # Corr(X1,X2)=rho
Y <- beta1*X1 + beta2*X2 + rnorm(n,0,sig)
coef(lm(Y ~ X1))[2] - beta1 # ritorna uno scalare, senza nome
}
grid$bias <- mapply(sim_once, grid$rho, grid$b2) # <-- niente t(), niente [, "bias"]
ggplot(grid, aes(x=rho, y=b2, fill=bias)) +
geom_tile() + scale_fill_gradient2() +
labs(x=expression(rho[12]), y=expression(beta[2]), fill="Bias",
title="Bias da variabile omessa al variare di ρ12 e β2")
Commento e interpretazione. L’asse orizzontale riporta la correlazione tra i regressori \(\rho_{12}=\mathrm{Corr}(X_1,X_2)\); l’asse verticale l’effetto dell’omessa \(X_2\) su \(Y\) (\(\beta_2\)). Il riempimento (“Bias”) è \(\hat\alpha_1-\beta_1\), cioè di quanto il coefficiente sul regressore incluso \(X_1\) sovrastima (valori > 0) o sottostima (valori < 0) il suo valore vero.
-
Segno del bias. Il bias è (in media) \(\beta_2\,\rho_{12}\). Quadranti:
- \(\beta_2>0,\ \rho_{12}>0\) → positivo (sovrastima);
- \(\beta_2>0,\ \rho_{12}<0\) → negativo (sottostima);
- \(\beta_2<0,\ \rho_{12}>0\) → negativo;
- \(\beta_2<0,\ \rho_{12}<0\) → positivo.
Le bande di colore cambiano segno attraversando le linee \(\rho_{12}=0\) o \(\beta_2=0\), dove il bias si annulla (zona chiara).
Magnitudo. Aumenta con \(|\beta_2|\) e \(|\rho_{12}|\): gli angoli (|ρ|≈0.9, |β₂|≈1.5) mostrano i bias maggiori. La diagonale basso-sinistra → alto-destra evidenzia bias positivo; l’altra diagonale bias negativo.
Simmetria e teoria. La mappa è sostanzialmente simmetrica perché il bias teorico è \(\beta_2\rho_{12}\). Le piccole irregolarità dipendono dal rumore Monte Carlo della simulazione (con \(n\) finito).
Lettura pratica. Se anche solo una tra correlazione tra regressori (\(\rho_{12}\)) o effetto dell’omessa (\(\beta_2\)) è prossima a zero, il bias è trascurabile (aree chiare lungo gli assi). Quando entrambi sono lontani da zero, l’OLS nel modello omesso è fuorviante.
Riflessioni conclusive
L’errore di specificazione, e in particolare il bias da variabile omessa, ci ricorda che la regressione multipla non può essere considerata uno strumento neutro e affidabile per spiegare i fenomeni psicologici. Il suo valore è limitato a descrivere associazioni, ma il rischio di distorsione è sempre presente. Per costruire conoscenza solida, la psicologia deve andare oltre i modelli fenomenologici e puntare a modelli meccanicistici e computazionali, capaci di rappresentare i processi che danno origine ai dati (McElreath, 2020).
Bibliografia
McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2nd Edition). CRC Press.
Ramsey, J. B. (1969). Tests for specification errors in classical linear least-squares regression analysis. Journal of the Royal Statistical Society Series B: Statistical Methodology, 31(2), 350–371.