44  Il rapporto di verosimiglianze

In questo capitolo, imparerai a:

• comprendere il concetto di rapporto di verosimiglianza;
• interpretare l’associato valore-p.

Prerequisiti

• Leggere il capitolo Estimation (Schervish & DeGroot, 2014).
• Leggere il capitolo Bayes’ rule (Johnson et al., 2022).

Preparazione del Notebook

here::here("code", "_common.R") |> 
  source()

44.1 Introduzione

Quando conduciamo un’analisi statistica, spesso ci troviamo di fronte alla necessità di confrontare due modelli che cercano di spiegare gli stessi dati. Immaginiamo, ad esempio, di voler capire qual è la media di una certa variabile (come il punteggio a un test, il tempo di reazione, ecc.). Potremmo avere due ipotesi alternative sull’effettivo valore della media:

• secondo un primo modello, la media è \(\mu_1\) (ad esempio, l’ipotesi “nulla”, che rappresenta uno stato di riferimento o di assenza di effetto),
• secondo un secondo modello, la media è \(\mu_2\) (ad esempio, l’ipotesi “alternativa”, che rappresenta un cambiamento o un effetto).

Per decidere quale modello è più compatibile con i dati osservati, possiamo usare la verosimiglianza (likelihood). La verosimiglianza misura quanto bene un certo valore del parametro spiega i dati osservati. Più la verosimiglianza è alta, più i dati sono “coerenti” con quel valore.

44.1.1 Il confronto: il rapporto di verosimiglianze

Per confrontare i due modelli, calcoliamo la verosimiglianza dei dati in ciascun caso, e ne facciamo il rapporto:

\[ \lambda = \frac{L(\mu_2 \mid \text{dati})}{L(\mu_1 \mid \text{dati})} \tag{44.1}\]

dove:

• \(L(\mu_2 \mid \text{dati})\) è la verosimiglianza del modello alternativo (cioè, quanto sono compatibili i dati con \(\mu_2\)),
• \(L(\mu_1 \mid \text{dati})\) è la verosimiglianza del modello nullo (cioè, quanto sono compatibili i dati con \(\mu_1\)).

Questa quantità si chiama rapporto di verosimiglianze (likelihood ratio, LR), e rappresenta uno strumento per quantificare quanto i dati favoriscono un modello rispetto all’altro.

44.1.2 Come si interpreta \(\lambda\)?

• Se \(\lambda > 1\), significa che i dati supportano più il modello alternativo: i dati sono più probabili sotto \(\mu_2\) che sotto \(\mu_1\).
• Se \(\lambda < 1\), significa che i dati supportano più il modello nullo: i dati sono più probabili sotto \(\mu_1\) che sotto \(\mu_2\).
• Se \(\lambda \approx 1\), allora i dati non permettono di distinguere chiaramente tra i due modelli.

💡 Il rapporto di verosimiglianze ci dice quale modello rende i dati osservati più “plausibili”.

44.2 Un Esempio Semplice

Immagina di aver lanciato una moneta 10 volte e di aver ottenuto 7 teste. Ti chiedi ora quale tra questi due modelli spiega meglio i dati:

• Modello 1 (nullo): la moneta è equa, quindi la probabilità di testa è \(\mu_1 = 0.5\);
• Modello 2 (alternativo): la moneta è truccata a favore delle teste, e la probabilità di testa è \(\mu_2 = 0.7\).

44.2.1 Calcolo delle verosimiglianze

Useremo la distribuzione binomiale, che descrive il numero di successi (in questo caso, teste) in un numero fisso di prove (10 lanci), dato un certo valore di probabilità.

La verosimiglianza è semplicemente la probabilità di ottenere 7 teste su 10 lanci, sotto ciascun modello:

• sotto il modello nullo (\(\mu_1 = 0.5\)):

  \[ L(0.5 \mid \text{7 teste}) = \binom{10}{7} (0.5)^7 (1 - 0.5)^3 = 120 \cdot (0.5)^{10} \approx 0.117 \]

• sotto il modello alternativo (\(\mu_2 = 0.7\)):

  \[ L(0.7 \mid \text{7 teste}) = \binom{10}{7} (0.7)^7 (0.3)^3 \approx 120 \cdot 0.0824 \cdot 0.027 = 0.267 \]

44.2.2 Calcolo del rapporto di verosimiglianze

Ora possiamo calcolare il rapporto:

\[ \lambda = \frac{L(0.7 \mid \text{7 teste})}{L(0.5 \mid \text{7 teste})} \approx \frac{0.267}{0.117} \approx 2.28 \]

👉 Questo significa che i dati sono circa 2.3 volte più compatibili con l’ipotesi che la moneta sia truccata (con \(\mu = 0.7\)) rispetto a quella che sia equa (\(\mu = 0.5\)).

44.2.3 Visualizzare le funzioni di verosimiglianza

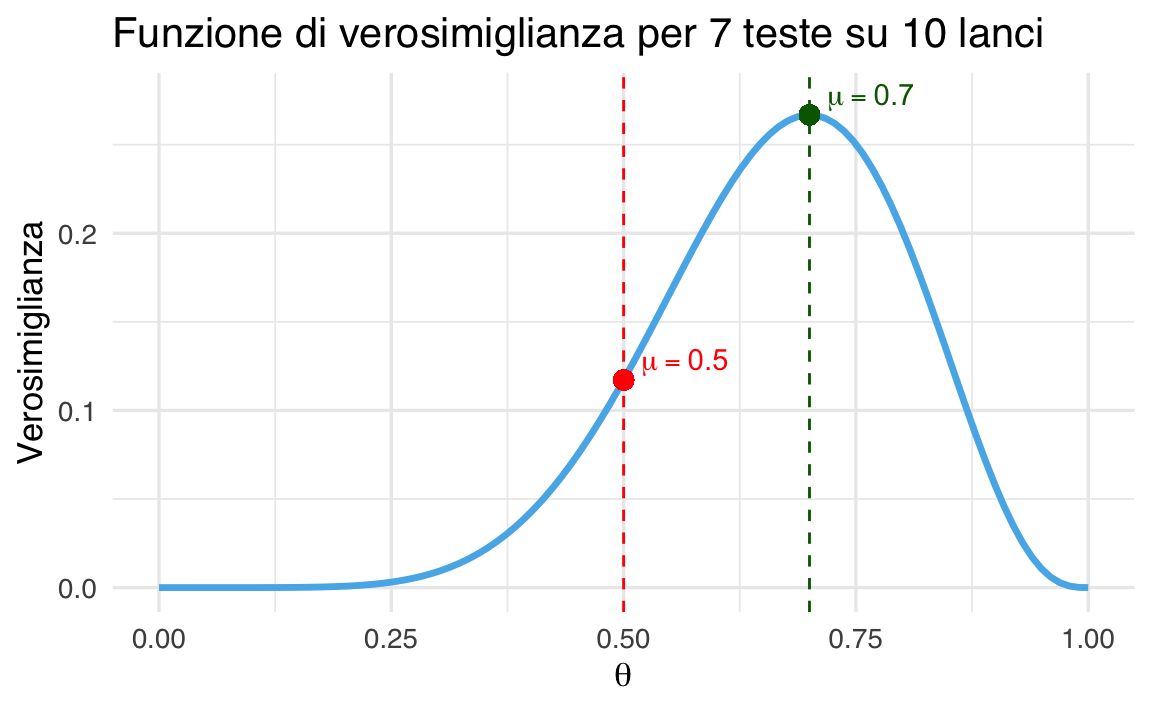
Possiamo visualizzare graficamente come cambia la verosimiglianza al variare della probabilità di testa (\(\theta\)), mantenendo fisso il numero di lanci e il numero di teste osservate.

44.2.3.1 Codice R

# Parametri osservati
n <- 10        # numero totale di lanci
x <- 7         # numero di teste osservate

# Sequenza di probabilità (theta)
theta <- seq(0, 1, length.out = 100)

# Verosimiglianza per ogni theta
likelihood <- dbinom(x, size = n, prob = theta)

# Crea dataframe per ggplot
df <- data.frame(theta = theta, likelihood = likelihood)

# Verosimiglianza nei due modelli
L_0.5 <- dbinom(x, size = n, prob = 0.5)
L_0.7 <- dbinom(x, size = n, prob = 0.7)
LR <- L_0.7 / L_0.5

# Crea grafico
ggplot(df, aes(x = theta, y = likelihood)) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  geom_vline(xintercept = 0.5, linetype = "dashed", color = "red") +
  geom_vline(xintercept = 0.7, linetype = "dashed", color = "darkgreen") +
  geom_point(aes(x = 0.5, y = L_0.5), color = "red", size = 3) +
  geom_point(aes(x = 0.7, y = L_0.7), color = "darkgreen", size = 3) +
  labs(
    title = "Funzione di verosimiglianza per 7 teste su 10 lanci",
    x = expression(theta),
    y = "Verosimiglianza"
  ) +
  annotate(
    "text", x = 0.5, y = L_0.5 + 0.01, 
    label = "mu == 0.5", 
    parse = TRUE, hjust = -0.2, color = "red"
  ) +
  annotate(
    "text", x = 0.7, y = L_0.7 + 0.01, 
    label = "mu == 0.7", parse = TRUE, hjust = -0.2, color = "darkgreen")

# Stampa dei risultati numerici
cat("L(mu = 0.5) =", round(L_0.5, 3), "\n")
#> L(mu = 0.5) = 0.117
cat("L(mu = 0.7) =", round(L_0.7, 3), "\n")
#> L(mu = 0.7) = 0.267
cat("Likelihood Ratio =", round(LR, 2), "\n")
#> Likelihood Ratio = 2.28

Il grafico mostra come cambia la verosimiglianza al variare di \(\theta\), e indica visivamente i valori assunti nei due modelli specifici. Si vede chiaramente che \(\theta = 0.7\) è più compatibile con l’osservazione di 7 teste.

In sintesi, il rapporto di verosimiglianze è uno strumento per confrontare due ipotesi. Non richiede che una delle due sia vera, ma solo di confrontare quanto bene ciascuna spiega i dati osservati. In questo esempio, i dati favoriscono l’ipotesi che la moneta sia truccata, ma non in modo schiacciante. Il valore di \(\lambda = 2.28\) indica un’evidenza moderata a favore del modello alternativo.

44.3 Rapporti di Verosimiglianza Aggiustati e Criterio di Akaike

Spesso il rapporto di verosimiglianza “grezzo” (\(\lambda\)) deve essere aggiustato per tenere conto della differenza nel numero di parametri tra i modelli confrontati. Infatti, quando confrontiamo due modelli, quello con più parametri tende quasi sempre a descrivere meglio i dati osservati, ma ciò può essere dovuto semplicemente alla sua maggiore complessità. Questo fenomeno è noto come sovradattamento (overfitting).

Per correggere questa tendenza, si usa un rapporto di verosimiglianza aggiustato (Adjusted Likelihood Ratio, indicato con \(\lambda_{\text{adj}}\). Questo tipo di aggiustamento penalizza i modelli più complessi, rendendo il confronto tra modelli più equo e affidabile.

44.3.1 Relazione con il Criterio di Akaike (AIC)

Una modalità comune per effettuare questa correzione è tramite il Criterio di Akaike (AIC). L’AIC è definito come:

\[ \text{AIC} = 2k - 2\log(\lambda), \tag{44.2}\]

in cui:

• \(k\) è il numero dei parametri del modello.
• \(\lambda\) è il rapporto di verosimiglianza grezzo.

Da questa equazione possiamo ricavare una formula per calcolare il rapporto di verosimiglianza aggiustato utilizzando l’AIC:

\[ \lambda_{\text{adj}} = \lambda \times e^{(k_1 - k_2)}, \]

dove:

• \(k_1\) è il numero di parametri del modello più semplice,
• \(k_2\) è il numero di parametri del modello più complesso,
• \(e^{(k_1 - k_2)}\) è il fattore correttivo che penalizza il modello più complesso.

In breve, più parametri ha un modello, maggiore sarà la penalizzazione applicata.

44.3.2 Rapporto tra Likelihood Ratio e AIC

Il rapporto di verosimiglianza aggiustato tramite l’AIC consente di confrontare in modo equo modelli con un numero differente di parametri. Senza questa correzione, rischieremmo di scegliere sempre modelli più complessi, indipendentemente dalla loro reale capacità esplicativa, con il rischio di sovrastimare la qualità della loro spiegazione.

Utilizzare il rapporto di verosimiglianza aggiustato, quindi, permette di scegliere il modello migliore considerando sia la capacità di adattarsi ai dati, sia la semplicità del modello stesso.

44.4 Illustrazione

Immaginiamo un semplice esperimento psicologico sulla memoria visiva. Vogliamo capire se mostrare immagini emotivamente intense aiuta le persone a ricordare meglio, rispetto a immagini neutre.

Abbiamo due gruppi di partecipanti:

• il gruppo neutro vede 30 immagini neutre e ne ricorda correttamente 14;
• il gruppo emozionale vede 30 immagini emotivamente intense e ne ricorda 22.

44.4.1 Obiettivo

Vogliamo confrontare due modelli alternativi:

• modello nullo (H₀): la probabilità di ricordare un’immagine è uguale nei due gruppi;
• modello alternativo (H₁): la probabilità di ricordare è diversa nei due gruppi.

44.4.2 Dati osservati

successi_neutro <- 14
successi_emozione <- 22
prove <- 30

44.4.3 1. Calcolo della Verosimiglianza

Ipotesi nulla: probabilità comune.

Se la probabilità è la stessa in entrambi i gruppi, possiamo stimarla combinando i successi totali:

p_null <- (successi_neutro + successi_emozione) / (2 * prove)

Log-verosimiglianza sotto H₀.

Sotto l’ipotesi nulla, i dati di entrambi i gruppi devono essere spiegati da una sola probabilità:

ll_null <- dbinom(successi_neutro, prove, p_null, log = TRUE) + 
           dbinom(successi_emozione, prove, p_null, log = TRUE)

Ipotesi alternativa: probabilità diversa per ogni gruppo.

Stimiamo separatamente la probabilità di ricordare in ciascun gruppo:

p_neutro <- successi_neutro / prove
p_emozione <- successi_emozione / prove

Log-verosimiglianza sotto H₁.

Ogni gruppo ha la propria verosimiglianza:

ll_alt <- dbinom(successi_neutro, prove, p_neutro, log = TRUE) + 
          dbinom(successi_emozione, prove, p_emozione, log = TRUE)

44.4.4 2. Confronto tra Modelli

Rapporto di verosimiglianza (non penalizzato).

Calcoliamo il rapporto tra le due verosimiglianze:

lr <- exp(ll_alt - ll_null)

Questo ci dice quanto meglio il modello alternativo spiega i dati rispetto al modello nullo.

44.4.5 3. Penalizzazione per la Complessità

I modelli più complessi tendono a spiegare meglio i dati, ma rischiano di adattarsi troppo. Per questo, usiamo un criterio che penalizza la complessità: l’AIC (Akaike Information Criterion).

Numero di parametri:

k_null <- 1  # un'unica probabilità per entrambi i gruppi
k_alt <- 2   # probabilità distinte per ciascun gruppo

Calcolo dell’AIC per ciascun modello:

AIC_null <- 2 * k_null - 2 * ll_null
AIC_alt <- 2 * k_alt - 2 * ll_alt

Rapporto di verosimiglianza aggiustato.

Usiamo l’AIC per calcolare una versione penalizzata del rapporto di verosimiglianze:

lr_adj <- exp((AIC_null - AIC_alt) / 2)

Risultati:

cat("Rapporto di verosimiglianza grezzo:", round(lr, 2), "\n")
#> Rapporto di verosimiglianza grezzo: 9.54
cat("Rapporto di verosimiglianza aggiustato (λ_adj):", round(lr_adj, 2), "\n")
#> Rapporto di verosimiglianza aggiustato (λ_adj): 3.51

Interpretazione:

• se λ_adj > 1, i dati sono più compatibili con il modello alternativo (due probabilità distinte);
• se λ_adj ≈ 1, non c’è abbastanza evidenza per preferire un modello all’altro.

44.4.6 4. Test del Rapporto di Verosimiglianza

Possiamo testare formalmente se la differenza tra i modelli è rilevante o potrebbe essere dovuta al caso.

La statistica test è:

\[ -2 \cdot (\log L_{H_0} - \log L_{H_1}) \]

Questa statistica segue (approssimativamente) una distribuzione chi-quadrato con un numero di gradi di libertà pari alla differenza nel numero di parametri tra i modelli:

LR_test <- -2 * (ll_null - ll_alt)
df <- k_alt - k_null
p_value <- 1 - pchisq(LR_test, df)

cat("Statistica test (-2 log LR):", round(LR_test, 2), "\n")
#> Statistica test (-2 log LR): 4.51
cat("Gradi di libertà:", df, "\n")
#> Gradi di libertà: 1
cat("Valore p del test:", round(p_value, 4), "\n")
#> Valore p del test: 0.0337

In sintesi,

• se p < 0.05, possiamo concludere che il modello alternativo è da preferire: i dati sono difficilmente compatibili con l’ipotesi di probabilità uguali nei due gruppi;
• se p > 0.05, non abbiamo evidenza sufficiente per preferire il modello alternativo.

Nel nostro esempio:

• la statistica test è ≈ 4.48;
• il valore-p è ≈ 0.0337.

👉 Poiché il valore-p è inferiore a 0.05, possiamo concludere che il gruppo emozionale ha una probabilità di ricordare credibilmente diversa da quella del gruppo neutro.

44.5 Riflessioni Conclusive

In conclusione, usando il rapporto di verosimiglianza aggiustato e l’AIC possiamo confrontare modelli statistici in maniera equilibrata, tenendo conto sia dell’adattamento ai dati che della semplicità del modello.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.4
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] thematic_0.1.6   MetBrewer_0.2.0  ggokabeito_0.1.0 see_0.11.0      
#>  [5] gridExtra_2.3    patchwork_1.3.0  bayesplot_1.11.1 psych_2.5.3     
#>  [9] scales_1.3.0     markdown_2.0     knitr_1.50       lubridate_1.9.4 
#> [13] forcats_1.0.0    stringr_1.5.1    dplyr_1.1.4      purrr_1.0.4     
#> [17] readr_2.1.5      tidyr_1.3.1      tibble_3.2.1     ggplot2_3.5.1   
#> [21] tidyverse_2.0.0  rio_1.2.3        here_1.0.1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] generics_0.1.3    stringi_1.8.4     lattice_0.22-6    hms_1.1.3        
#>  [5] digest_0.6.37     magrittr_2.0.3    evaluate_1.0.3    grid_4.4.2       
#>  [9] timechange_0.3.0  fastmap_1.2.0     rprojroot_2.0.4   jsonlite_1.9.1   
#> [13] mnormt_2.1.1      cli_3.6.4         rlang_1.1.5       munsell_0.5.1    
#> [17] withr_3.0.2       tools_4.4.2       parallel_4.4.2    tzdb_0.5.0       
#> [21] colorspace_2.1-1  pacman_0.5.1      vctrs_0.6.5       R6_2.6.1         
#> [25] lifecycle_1.0.4   htmlwidgets_1.6.4 pkgconfig_2.0.3   pillar_1.10.1    
#> [29] gtable_0.3.6      glue_1.8.0        xfun_0.51         tidyselect_1.2.1 
#> [33] rstudioapi_0.17.1 farver_2.1.2      htmltools_0.5.8.1 nlme_3.1-167     
#> [37] labeling_0.4.3    rmarkdown_2.29    compiler_4.4.2

Bibliografia

Johnson, A. A., Ott, M., & Dogucu, M. (2022). Bayes Rules! An Introduction to Bayesian Modeling with R. CRC Press.

Schervish, M. J., & DeGroot, M. H. (2014). Probability and statistics (Vol. 563). Pearson Education London, UK: