43  La verosimiglianza gaussiana

In questo capitolo, imparerai a:
  • comprendere il concetto di verosimiglianza nel contesto del modello gaussiano.
Prerequisiti
Preparazione del Notebook 
here::here("code", "_common.R") |> 
  source()

Introduzione

La distribuzione gaussiana (o distribuzione normale) è una delle distribuzioni più utilizzate in statistica perché descrive molti fenomeni naturali e psicologici. In questo capitolo esploreremo come si calcola la verosimiglianza, ovvero la plausibilità dei parametri, nel caso della distribuzione normale.

43.1 Modello Gaussiano e Verosimiglianza

43.1.1 Caso di una Singola Osservazione

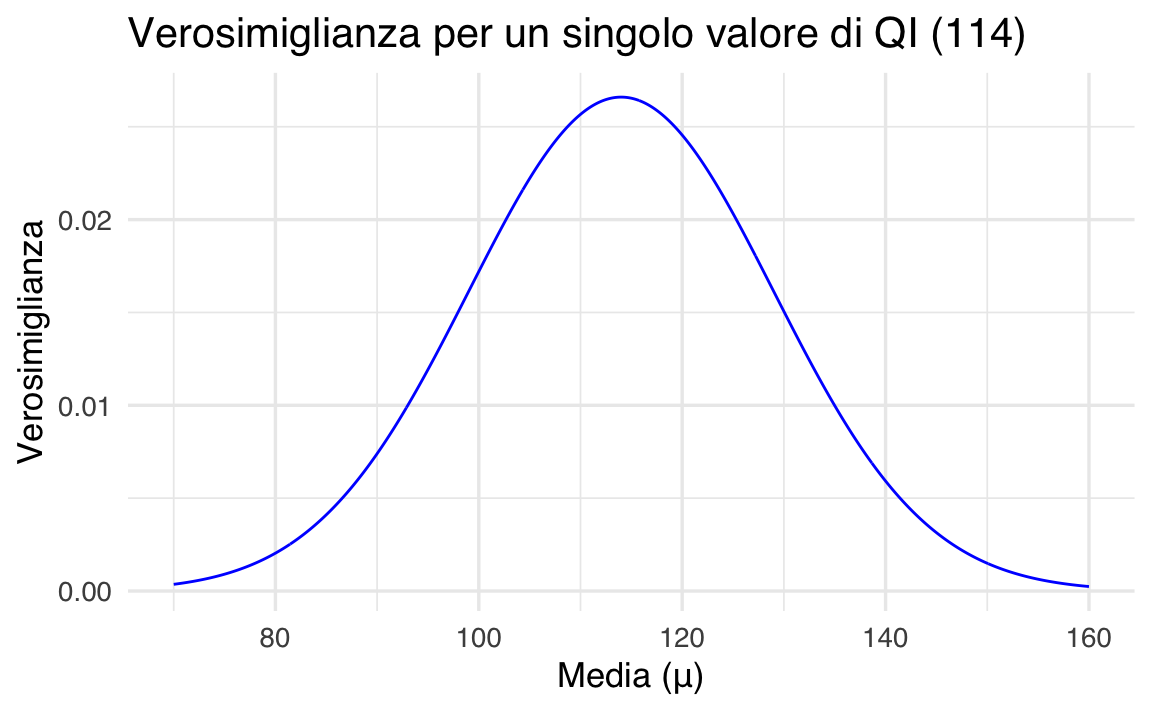
Immaginiamo di misurare il Quoziente Intellettivo (QI) di una persona e ottenere un valore specifico, ad esempio 114. Assumiamo che il QI segua una distribuzione normale con media \(\mu\) sconosciuta e deviazione standard \(\sigma\) nota (ad esempio \(\sigma = 15\)).

La funzione di densità di probabilità per una distribuzione normale è:

\[ f(y \mid \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(y-\mu)^2}{2\sigma^2}\right) , \]

dove:

  • \(y\) è il valore osservato,
  • \(\mu\) è la media (il parametro che vogliamo stimare),
  • \(\sigma\) è la deviazione standard (conosciuta).

La verosimiglianza misura quanto diversi valori di \(\mu\) sono plausibili, dato il valore osservato (114).

Esempio pratico in R:

# Dati iniziali
y_obs <- 114
sigma <- 15
mu_values <- seq(70, 160, length.out = 1000)

# Calcolo della verosimiglianza
likelihood <- dnorm(y_obs, mean = mu_values, sd = sigma)

# Grafico della verosimiglianza
ggplot(data.frame(mu = mu_values, likelihood = likelihood), aes(x = mu, y = likelihood)) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  labs(
    title = "Verosimiglianza per un singolo valore di QI (114)",
    x = "Media (μ)",
    y = "Verosimiglianza"
  )

Qual è il valore migliore per \(\mu\)?

Il valore migliore di \(\mu\) sarà quello che rende massima la verosimiglianza. In questo semplice caso, è esattamente il valore osservato (114):

mu_ottimale <- mu_values[which.max(likelihood)]
cat("Il valore ottimale di μ è:", mu_ottimale)
#> Il valore ottimale di μ è: 114

43.1.2 Log-Verosimiglianza

Spesso, per semplicità di calcolo, si usa la log-verosimiglianza, che trasforma i prodotti in somme, rendendo i calcoli più semplici e stabili:

\[ \log L(\mu \mid y, \sigma) = -\frac{1}{2}\log(2\pi) - \log(\sigma) - \frac{(y-\mu)^2}{2\sigma^2}. \]

Calcolo pratico con R:

# Funzione di log-verosimiglianza negativa usando dnorm()
negative_log_likelihood <- function(mu, y, sigma) {
  # Ritorniamo il valore negativo della log-verosimiglianza
  -dnorm(y, mean = mu, sd = sigma, log = TRUE)
}

result <- optim(
  par = 100, # Valore iniziale
  fn = negative_log_likelihood,
  y = y_obs,
  sigma = sigma,
  method = "L-BFGS-B",
  lower = 70,
  upper = 160
)

mu_max_loglik <- result$par
cat("Il valore ottimale di μ dalla log-verosimiglianza è:", mu_max_loglik)
#> Il valore ottimale di μ dalla log-verosimiglianza è: 114

In questo caso, otteniamo nuovamente \(\mu = 114\).

43.2 Campione di Osservazioni Indipendenti

Supponiamo di aver raccolto i punteggi alla scala BDI-II per 30 persone. Ciascun punteggio è un’osservazione indipendente da una distribuzione normale con media incognita \(\mu\) e deviazione standard nota \(\sigma = 6.5\).

# Dati osservati (punteggi BDI-II)
y <- c(
  26, 35, 30, 25, 44, 30, 33, 43, 22, 43, 24, 19, 39, 31, 25, 
  28, 35, 30, 26, 31, 41, 36, 26, 35, 33, 28, 27, 34, 27, 22
)

sigma <- 6.5

43.2.1 Calcolo della Log-Verosimiglianza

Definiamo una funzione che calcola la log-verosimiglianza totale:

log_likelihood <- function(mu, y, sigma) {
  sum(dnorm(y, mean = mu, sd = sigma, log = TRUE))
}

Esploriamo ora un intervallo di valori plausibili per \(\mu\) e calcoliamo la log-verosimiglianza per ciascun valore:

# Intervallo di valori possibili per μ
mu_range <- seq(mean(y) - 2 * sigma, mean(y) + 2 * sigma, length.out = 1000)

# Inizializza vettore dei risultati
log_lik_values <- numeric(length(mu_range))

# Ciclo esplicito per chiarezza didattica
for (i in seq_along(mu_range)) {
  mu_val <- mu_range[i]
  log_lik_values[i] <- log_likelihood(mu_val, y, sigma)
}

43.2.2 Visualizzazione della Log-Verosimiglianza

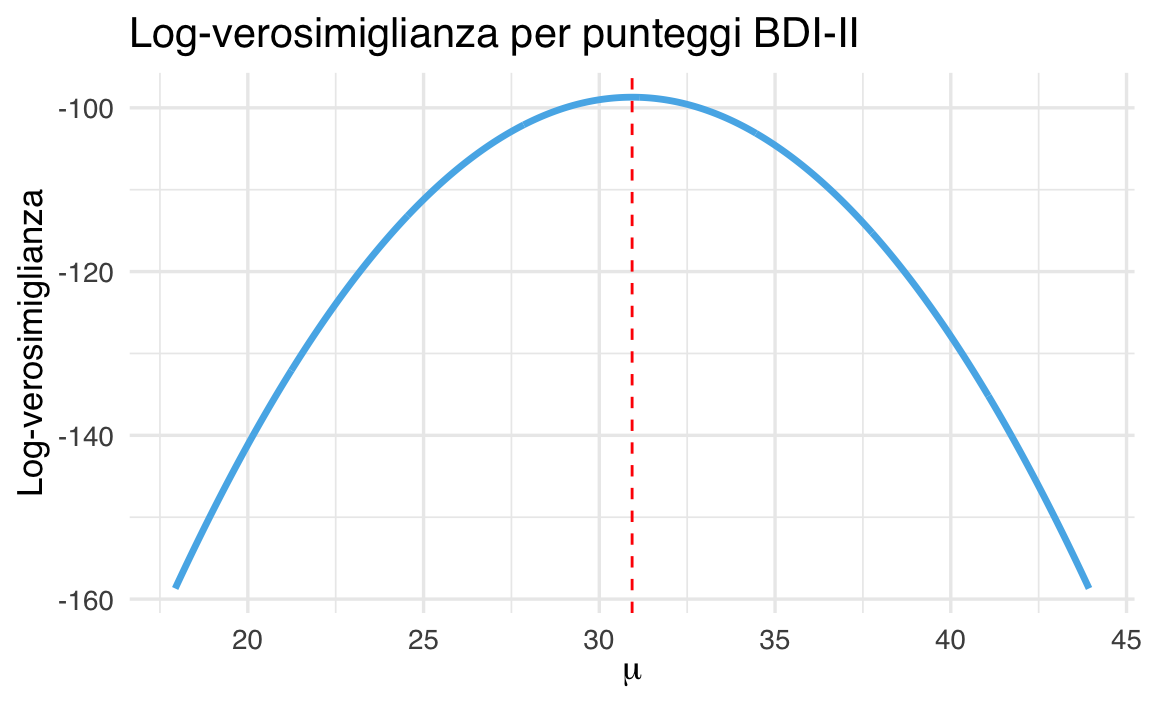
ggplot(
  data.frame(mu = mu_range, log_likelihood = log_lik_values),
  aes(x = mu, y = log_likelihood)
) +
  geom_line(color = okabe_ito_palette[2], linewidth = 1.2) +
  geom_vline(xintercept = mean(y), linetype = "dashed", color = "red") +
  labs(
    title = "Log-verosimiglianza per punteggi BDI-II",
    x = expression(mu),
    y = "Log-verosimiglianza"
  )

La linea tratteggiata rossa indica la media campionaria, che — come ci aspettiamo — è anche il valore che massimizza la log-verosimiglianza.

43.2.3 Ottimizzazione Numerica

Se volessimo calcolare il valore ottimale di \(\mu\) in modo automatico:

# Funzione negativa da minimizzare
negative_log_likelihood <- function(mu, y, sigma) {
  -sum(dnorm(y, mean = mu, sd = sigma, log = TRUE))
}

# Ottimizzazione con limiti
result <- optim(
  par = mean(y),                   # Valore iniziale
  fn = negative_log_likelihood,   # Funzione da minimizzare
  y = y,
  sigma = sigma,
  method = "L-BFGS-B",
  lower = min(mu_range),
  upper = max(mu_range)
)

mu_optimal <- result$par
cat("Il valore ottimale di μ è:", mu_optimal)
#> Il valore ottimale di μ è: 30.93
  • Abbiamo utilizzato dnorm(..., log = TRUE) per calcolare in modo semplice e numericamente stabile la log-verosimiglianza.
  • Il valore di \(\mu\) che massimizza la log-verosimiglianza corrisponde alla media campionaria.
  • Questo è un caso in cui la stima di massima verosimiglianza ha una forma chiusa, ma l’approccio numerico resta utile e generalizzabile.

43.3 Riflessioni Conclusive

  • Nel caso di una distribuzione normale con \(\sigma\) nota, la miglior stima di \(\mu\) (stima di massima verosimiglianza) è sempre la media delle osservazioni.
  • Visualizzare la funzione di verosimiglianza aiuta a capire la plausibilità relativa dei diversi valori di \(\mu\).
  • La log-verosimiglianza semplifica e rende più stabili i calcoli numerici.

Esercizi

Supponi di aver misurato il livello di ansia (ad esempio usando una scala standardizzata) in un campione di 15 persone con i seguenti punteggi:

ansia <- c(23, 27, 30, 29, 25, 28, 26, 24, 31, 29, 27, 26, 28, 30, 25)

Assumendo che la deviazione standard sia nota e pari a 3.5, svolgi le seguenti attività in R:

  1. Calcola la funzione di verosimiglianza gaussiana per diversi valori di \(\mu\) nell’intervallo da 20 a 35.
  2. Trova numericamente il valore di \(\mu\) che rende massima la verosimiglianza (stima di massima verosimiglianza, MLE).
  3. Disegna un grafico della funzione di verosimiglianza per visualizzare il risultato.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.5.0 (2025-04-11)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.5
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] thematic_0.1.6   MetBrewer_0.2.0  ggokabeito_0.1.0 see_0.11.0      
#>  [5] gridExtra_2.3    patchwork_1.3.0  bayesplot_1.12.0 psych_2.5.3     
#>  [9] scales_1.4.0     markdown_2.0     knitr_1.50       lubridate_1.9.4 
#> [13] forcats_1.0.0    stringr_1.5.1    dplyr_1.1.4      purrr_1.0.4     
#> [17] readr_2.1.5      tidyr_1.3.1      tibble_3.2.1     ggplot2_3.5.2   
#> [21] tidyverse_2.0.0  rio_1.2.3        here_1.0.1      
#> 
#> loaded via a namespace (and not attached):
#>  [1] generics_0.1.4     stringi_1.8.7      lattice_0.22-7    
#>  [4] hms_1.1.3          digest_0.6.37      magrittr_2.0.3    
#>  [7] evaluate_1.0.3     grid_4.5.0         timechange_0.3.0  
#> [10] RColorBrewer_1.1-3 fastmap_1.2.0      rprojroot_2.0.4   
#> [13] jsonlite_2.0.0     mnormt_2.1.1       cli_3.6.5         
#> [16] rlang_1.1.6        withr_3.0.2        tools_4.5.0       
#> [19] parallel_4.5.0     tzdb_0.5.0         pacman_0.5.1      
#> [22] vctrs_0.6.5        R6_2.6.1           lifecycle_1.0.4   
#> [25] htmlwidgets_1.6.4  pkgconfig_2.0.3    pillar_1.10.2     
#> [28] gtable_0.3.6       glue_1.8.0         xfun_0.52         
#> [31] tidyselect_1.2.1   rstudioapi_0.17.1  farver_2.1.2      
#> [34] htmltools_0.5.8.1  nlme_3.1-168       labeling_0.4.3    
#> [37] rmarkdown_2.29     compiler_4.5.0

Bibliografia

Johnson, A. A., Ott, M., & Dogucu, M. (2022). Bayes Rules! An Introduction to Bayesian Modeling with R. CRC Press.
Schervish, M. J., & DeGroot, M. H. (2014). Probability and statistics (Vol. 563). Pearson Education London, UK: