32  Errore di misurazione e attenuazione: una soluzione bayesiana

Introduzione

La ricerca psicologica si confronta costantemente con una sfida epistemologica e metodologica fondamentale: i costrutti d’interesse – quali l’ansia, l’intelligenza o la motivazione – sono entità latenti, non direttamente osservabili. La loro rilevazione avviene necessariamente attraverso approssimazioni operative, quali questionari, test psicometrici e scale di valutazione, che incorporano inevitabilmente una componente di errore di misura.

Trascurare la bassa affidabilità psicometrica di tali strumenti non costituisce un mero dettaglio tecnico, bensì un problema metodologico sostanziale, in grado di alterare in maniera sistematica la validità delle inferenze scientifiche. Un esempio paradigmatico è fornito dal fenomeno dell’attenuazione della stima: quando una variabile predittiva continua, affetta da errore di misura, viene trattata in un’analisi di regressione come se fosse misurata in modo perfetto, il coefficiente di regressione stimato risulta sistematicamente distorto verso lo zero. Questa distorsione statistica, nota come attenuazione del coefficiente di regressione, sottostima artificialmente l’entità della relazione tra il costrutto latente e l’esito di interesse, compromettendo l’accuratezza delle conclusioni.

Il presente capitolo illustra l’utilità di un approccio bayesiano come metodo operativo per contrastare tale problematica. Modellizzando esplicitamente il processo di misura, possiamo correggere queste distorsioni e recuperare stime più veritiere della relazione tra i costrutti latenti di interesse. In pratica, questo ci permette di riportare l’analisi statistica sul piano del tratto latente che ci interessa davvero, propagando in modo coerente l’incertezza legata alla sua misurazione.

Per fissare le idee, si consideri un caso semplice: una regressione lineare in cui un esito \(y\) è regredito su un predittore latente \(x\). Nei dati osservativi, tuttavia, non si misura \(x\) ma una sua versione contaminata da errore, \(x^*\). L’utilizzo di \(x^*\) al posto di \(x\) produce una stima attenuata del coefficiente di regressione.

La soluzione bayesiana consiste nel separare esplicitamente il modello strutturale dal modello di misura. Si specifica un modello tale per cui:

  1. il modello strutturale regredisce \(y\) sul costrutto latente \(x\),
  2. il modello di misura definisce come il punteggio osservato \(x^*\) sia generato a partire da \(x\) (ad esempio, \(x^* \sim \mathcal{N}(x, \sigma^2_{errore})\)).

In questo framework, l’errore di misura viene modellato e isolato nella componente di misura, prevenendo l’attenuazione della stima della relazione strutturale tra \(x\) e \(y\). Nel presente capitolo, questo approccio sarà dimostrato tramite simulazioni e implementato in Stan.

Nella seconda parte del capitolo, estenderemo il quadro concettuale precedentemente delineato al contesto dell’analisi della correlazione tra due costrutti psicologici latenti. La Teoria Classica dei Test (CTT) fornisce una soluzione formale a questo problema mediante la procedura nota come correzione per disattenuazione. Questo metodo permette di stimare il coefficiente di correlazione “vero” tra i costrutti latenti, partendo dal coefficiente di correlazione osservato tra le misurazioni empiriche e correggendolo in funzione dell’affidabilità degli strumenti di misura utilizzati. Formalmente, la correzione si esprime come il rapporto tra la correlazione osservata e la radice quadrata del prodotto delle attendibilità delle due scale. Questa procedura, tuttavia, è valida solo sotto forti assunzioni, tra cui l’indipendenza degli errori di misura (ad esempio, l’assenza di bias da metodo condiviso) e la conoscenza esatta dell’attendibilità (condizione difficilmente verificabile nella pratica, dato che l’alfa di Cronbach o l’omega di McDonald sono essi stessi delle stime campionarie).

Quando queste assunzioni non sono soddisfatte – ad esempio, in presenza di un effetto di metodo o di una fonte di varianza condivisa che induce correlazione tra gli errori – la formula classica tende a sovracorreggere, producendo stime della correlazione vera distorte e instabili (Carroll et al., 2006). L’approccio bayesiano supera questi limiti specificando un modello di misurazione congiunto in cui entrambi i costrutti sono trattati come variabili latenti. Questo modello permette di esplicitare la struttura di covarianza degli errori (ammettendo, se necessario, correlazioni residue) e di incorporare eventuali fattori di metodo latenti.

In questo framework, la correlazione di tratto viene stimata direttamente, evitando i bias della CTT e propagando l’incertezza sulle attendibilità in modo appropriato. È importante sottolineare che, se le assunzioni della CTT sono verificate, il modello bayesiano converge verso la stima classica; in caso contrario, esso fornisce un’alternativa più robusta e generalizzabile.

In sintesi, il capitolo svilupperà una progressione concettuale e metodologica articolata in tre fasi. In primo luogo, mediante dati simulati, verrà illustrato il fenomeno dell’attenuazione nei modelli di regressione e verrà dimostrato come un modello bayesiano che incorpori il predittore latente consenta di recuperare il parametro strutturale corretto. In seguito, estenderemo l’analisi al contesto della correlazione, mettendo in luce i limiti della correzione per disattenuazione nella CTT e i vantaggi di una modellazione congiunta con variabili latenti. Infine, presenteremo modelli bayesiani implementati in Stan in cui la distinzione tra tratto latente e la componente metodologica è resa esplicita, anche per costrutti multidimensionali misurati da più indicatori. L’adeguatezza dei modelli sarà valutata mediante strumenti diagnostici quali i posterior predictive checks.

L’obiettivo finale è mostrare come la modellazione della misura – ovvero la specificazione esplicita di un modello di misurazione – costituisca un autentico cambio di prospettiva epistemologica. Questo approccio non è un esercizio tecnico formale, ma una pratica che migliora l’interpretazione sostanziale e l’affidabilità inferenziale, in quanto consente di dichiarare il processo di generazione dei dati e di distinguere, in modo probabilistico, la varianza attribuibile al costrutto da quella dovuta all’errore o al metodo di misurazione.

here::here("code", "_common.R") |> source()

if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(
  tidyverse, cmdstanr, posterior, bayesplot, bayestestR, brms, ggdist, broom, 
  glue, tibble
)
conflicts_prefer(stats::sd)

32.1 Perché l’errore di misurazione conta

Nella ricerca psicologica, i predittori sono spesso costruiti a partire da strumenti di misura imperfetti, come questionari, test o scale psicometriche. Per esempio, quando in un’analisi di regressione si utilizza il punteggio osservato \(x^*\) come se fosse la vera variabile latente \(x\), si introduce un errore sistematico: la stima della pendenza risulta attenuata, cioè spinta verso lo zero. La standardizzazione dei punteggi non risolve il problema: nella regressione semplice, la pendenza standardizzata coincide con la correlazione osservata \(r_{y,x^*}\) che, a sua volta, è attenuata rispetto alla correlazione vera.

Per comprendere formalmente l’origine dell’attenuazione, consideriamo il modello di misura classico con errore additivo:

\[ y = \beta x + \varepsilon, \] dove \(\varepsilon\) è un termine di errore con \(\mathbb{E}[\varepsilon] = 0\), \(\operatorname{Var}(\varepsilon) = \sigma_\varepsilon^2\), e \(\operatorname{Cov}(x, \varepsilon) = 0\).

Tuttavia, non osserviamo \(x\) direttamente, ma una sua misura rumorosa:

\[ x^* = x + \delta, \] dove \(\delta\) è l’errore di misurazione con \(\mathbb{E}[\delta] = 0\), \(\operatorname{Var}(\delta) = \sigma_\delta^2\), e assumiamo \(\operatorname{Cov}(x, \delta) = 0\) e \(\operatorname{Cov}(\varepsilon, \delta) = 0\).

Lo stimatore ingenuo di \(\beta\) si ottiene regredendo \(y\) su \(x^*\): \[ \hat{\beta}_{\text{naive}} = \frac{\operatorname{Cov}(x^*, y)}{\operatorname{Var}(x^*)}. \]

Calcoliamo ora l’aspettativa di \(\hat{\beta}_{\text{naive}}\).

  • Passaggio 1: Calcolo di \(\operatorname{Cov}(x^*, y)\). \[ \begin{aligned} \operatorname{Cov}(x^*, y) &= \operatorname{Cov}(x + \delta, \beta x + \varepsilon) \\ &= \beta \operatorname{Cov}(x + \delta, x) + \operatorname{Cov}(x + \delta, \varepsilon). \end{aligned} \]

    Per le assunzioni:

    • \(\operatorname{Cov}(x, \varepsilon) = 0\) e \(\operatorname{Cov}(\delta, \varepsilon) = 0\) ⇒ \(\operatorname{Cov}(x + \delta, \varepsilon) = 0\),
    • \(\operatorname{Cov}(\delta, x) = 0\) ⇒ \(\operatorname{Cov}(x + \delta, x) = \operatorname{Var}(x)\).

    Quindi: \[ \operatorname{Cov}(x^*, y) = \beta \operatorname{Var}(x). \]

  • Passaggio 2: Calcolo di \(\operatorname{Var}(x^*)\). \[ \begin{aligned} \operatorname{Var}(x^*) &= \operatorname{Var}(x + \delta) \\ &= \operatorname{Var}(x) + \operatorname{Var}(\delta) + 2 \operatorname{Cov}(x, \delta) \\ &= \operatorname{Var}(x) + \operatorname{Var}(\delta) \quad (\text{poiché } \operatorname{Cov}(x, \delta) = 0). \end{aligned} \]

  • Passaggio 3: Aspettativa dello stimatore ingenuo. \[ \mathbb{E}[\hat{\beta}_{\text{naive}}] = \frac{\operatorname{Cov}(x^*, y)}{\operatorname{Var}(x^*)} = \frac{\beta \operatorname{Var}(x)}{\operatorname{Var}(x) + \operatorname{Var}(\delta)}. \]

    Introducendo le notazioni \(\sigma_x^2 = \operatorname{Var}(x)\) e \(\sigma_\delta^2 = \operatorname{Var}(\delta)\), otteniamo:

    \[ \mathbb{E}[\hat{\beta}_{\text{naive}}] = \beta \cdot \frac{\sigma_x^2}{\sigma_x^2 + \sigma_\delta^2}. \]

  • Passaggio 4: Definizione del fattore di affidabilità \(\lambda\). Definiamo il rapporto di affidabilità: \[ \lambda = \frac{\sigma_x^2}{\sigma_x^2 + \sigma_\delta^2}. \] Allora: \[ \mathbb{E}[\hat{\beta}_{\text{naive}}] = \beta \cdot \lambda. \]

    Osservazione: Poiché \(0 < \lambda < 1\) (a meno che \(\sigma_\delta^2 = 0\)), lo stimatore ingenuo è distorto verso lo zero (attenuation bias). La distorsione verso lo zero implica che il valore assoluto dell’effetto stimato è inferiore al vero parametro \(\beta\).

    • Casi particolari:
      • Se \(\sigma_\delta^2 = 0\) (assenza di errore di misura), allora \(\lambda = 1\) e lo stimatore è corretto.
      • Se \(\sigma_\delta^2 \gg \sigma_x^2\), allora \(\lambda \approx 0\) e lo stimatore tende a zero.

Conseguenza operativa.
Se un predittore è affetto da un errore di misura non trascurabile, una regressione che lo tratta come una variabile osservata sottostima sistematicamente l’effetto del costrutto latente. L’unico approccio metodologicamente solido consiste nel modellare esplicitamente il processo di misurazione, eventualmente avvalendosi di informazioni ausiliarie (come le stime di affidabilità) per identificare la componente di errore.

32.2 Il modello bayesiano dell’errore di misurazione

Il modello bayesiano dell’errore di misurazione specifica esplicitamente due componenti distinte: il modello strutturale e il modello di misurazione:

\[ \begin{aligned} x_i &\sim \mathcal{N}(\mu_x, \sigma_x^2) && \text{(Prior della variabile latente)} \\ y_i \mid x_i &\sim \mathcal{N}(\alpha + \beta x_i, \sigma_y^2) && \text{(Modello strutturale)} \\ x_i^* \mid x_i &\sim \mathcal{N}(x_i, \sigma_{\text{meas}}^2) && \text{(Modello di misura)} \end{aligned} \] In questa specificazione, assumiamo che la varianza dell’errore di misura \(\sigma_{\text{meas}}^2\) sia nota (ad esempio, ricavata da stime di affidabilità precedenti1). Questa assunzione semplifica il problema di identificazione del modello e permette di illustrare chiaramente come la corretta specificazione del processo di misurazione prevenga l’attenuazione della stima del parametro strutturale \(\beta\).

32.3 Piano dell’esperimento didattico

Nelle sezioni successive, verranno simulati dati con parametri noti, introducendo deliberatamente un errore di misura nel predittore. Confronteremo due approcci analitici:

  1. Un’analisi ingenua che utilizza il predittore misurato con errore \(x^*\) (sia in scala originale che standardizzata), dimostrando il fenomeno dell’attenuazione delle stime.
  2. Un’analisi bayesiana che modella esplicitamente \(x\) come variabile latente, con \(x^*\) come suo indicatore rumoroso, mostrando il corretto recupero del parametro strutturale vero.

32.3.1 Simulazione dei dati “veri” e delle osservazioni con errore di misura

Definiamo parametri con valori semplici e interpretabili per illustrare chiaramente il fenomeno:

set.seed(20250912)  # Per riproducibilità

N <- 300            # Dimensione campionaria
a_true <- 1.0       # Intercetta vera
b_true <- 2.0       # Coefficiente di regressione vero
sigma_true <- 1.0   # Deviazione standard dell'errore nell'outcome
mu_x_true <- 0.0    # Media della variabile latente x
sigma_x_true <- 1.5 # Deviazione standard della variabile latente x  
sigma_xstar <- 1.0  # Deviazione standard dell'errore di misura (nota a priori)

# Generazione del predittore latente e dell'outcome
x_true <- rnorm(N, mean = mu_x_true, sd = sigma_x_true)
y <- a_true + b_true * x_true + rnorm(N, 0, sigma_true)

# Generazione del predittore osservato con errore di misura
x_star <- x_true + rnorm(N, 0, sigma_xstar)

# Creazione del dataframe dei dati
dat <- tibble(x_true, x_star, y)
head(dat)
#> # A tibble: 6 × 3
#>   x_true x_star      y
#>    <dbl>  <dbl>  <dbl>
#> 1  1.20   0.771  2.94 
#> 2 -3.03  -2.60  -4.62 
#> 3  2.56   1.83   5.93 
#> 4 -0.913 -1.55   0.626
#> 5  2.29   2.63   5.63 
#> 6  0.914 -0.168  5.05

Calcolo del fattore di attenuazione teorico:

lambda_theory <- sigma_x_true^2 / (sigma_x_true^2 + sigma_xstar^2)
lambda_theory
#> [1] 0.692

32.3.2 Ispezione visiva della relazione osservata

ggplot(dat, aes(x = x_star, y = y)) +
  geom_point(alpha = 0.6, shape = 16) +
  geom_smooth(method = "lm", formula = y ~ x, se = FALSE, color = "#0072B2") +
  labs(x = "x* (predittore osservato, affetto da errore di misura)", 
       y = "y (outcome)")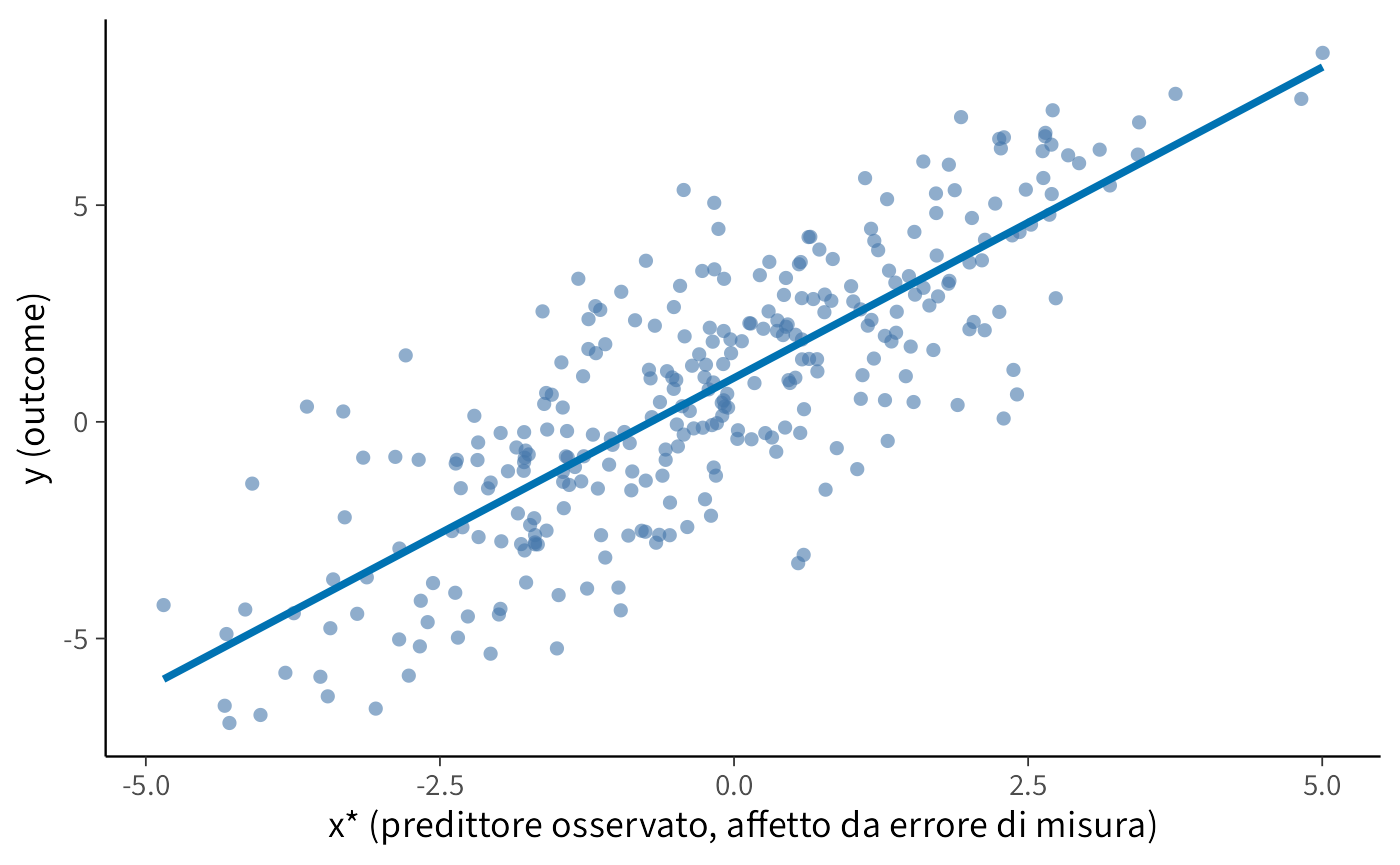

Relazione osservata tra y e x* (misura con errore del costrutto latente). La retta di regressione evidenzia l’attenuazione del coefficiente stimato.

32.4 Analisi ingenua (ignorando l’errore di misura)

32.4.1 Regressione sulla scala originale

# Regressione lineare che ignora l'errore di misura
fit_naive_raw <- lm(y ~ x_star, data = dat)
naive_raw_tab <- broom::tidy(fit_naive_raw, conf.int = TRUE)
naive_raw_tab
#> # A tibble: 2 × 7
#>   term        estimate std.error statistic  p.value conf.low conf.high
#>   <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
#> 1 (Intercept)     1.01    0.107       9.44 1.13e-18    0.802      1.23
#> 2 x_star          1.43    0.0597     24.0  1.04e-71    1.32       1.55

Verifica teorica. Ci si aspetta che la stima ingenua del coefficiente sia approssimativamente uguale al prodotto tra il parametro vero e il fattore di attenuazione: \(\hat \beta_{\text{ingenua}} \approx \beta_{\text{vero}} \times \lambda\).

b_naive <- coef(fit_naive_raw)[["x_star"]]
tibble(
  beta_vero = b_true,
  lambda_teorico = lambda_theory,
  beta_vero_per_lambda = b_true * lambda_theory,
  beta_naive_osservato = unname(b_naive)
)
#> # A tibble: 1 × 4
#>   beta_vero lambda_teorico beta_vero_per_lambda beta_naive_osservato
#>       <dbl>          <dbl>                <dbl>                <dbl>
#> 1         2          0.692                 1.38                 1.43

32.4.2 Regressione su variabili standardizzate

# Standardizzazione delle variabili e regressione
dat_std <- dat %>%
  mutate(
    y_z = as.numeric(scale(y)),
    x_star_z = as.numeric(scale(x_star))
  )

fit_naive_std <- lm(y_z ~ x_star_z, data = dat_std)
broom::tidy(fit_naive_std, conf.int = TRUE)
#> # A tibble: 2 × 7
#>   term         estimate std.error statistic   p.value conf.low conf.high
#>   <chr>           <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
#> 1 (Intercept) -7.47e-17    0.0337 -2.21e-15 1.000e+ 0  -0.0664    0.0664
#> 2 x_star_z     8.12e- 1    0.0338  2.40e+ 1 1.04 e-71   0.746     0.879

Interpretazione. La standardizzazione non elimina l’attenuazione: il coefficiente di regressione standardizzato corrisponde al coefficiente di correlazione \(r_{y,x^*}\), che rimane attenuato rispetto alla correlazione tra i costrutti latenti.

cor(dat$x_true, dat$y)
#> [1] 0.945

32.5 Modello bayesiano con correzione per errore di misurazione (Stan)

Nel contesto del modello bayesiano per l’errore di misurazione, vengono modellate esplicitamente sia la componente strutturale, che definisce la relazione tra il predittore latente \(x\) e la variabile di outcome \(y\), sia il processo di misurazione, che caratterizza la relazione tra il predittore latente \(x\) e il valore osservato \(x^*\). Si assume nota la deviazione standard dell’errore di misurazione \(\sigma_{\delta}\). Il modello utilizza prior debolmente informativi robusti.

32.5.1 Implementazione in Stan

stancode <- "
data {
  int<lower=1> N;              // Dimensione campionaria
  vector[N] y;                 // Outcome
  vector[N] x_star;            // Predittore osservato con errore
  real<lower=0> sigma_x_star;  // SD dell'errore di misura (nota)
}
parameters {
  real a;                      // Intercetta
  real b;                      // Coefficiente di regressione
  real mu_x;                   // Media del predittore latente
  real<lower=0> sigma;         // SD dell'errore nell'outcome
  real<lower=0> sigma_x;       // SD del predittore latente (eterogeneità tra x_n)
  vector[N] x;                 // Predittore latente (parametrizzazione centered)
}
model {
  // Priors debolmente informativi e robusti
  a ~ normal(0, 5);
  b ~ student_t(3, 0, 5);          // code pesanti per b
  mu_x ~ normal(0, 5);
  sigma ~ student_t(3, 0, 2.5);    // half-Student-t implicita (vincolo <lower=0>)
  sigma_x ~ student_t(3, 0, 2.5);  // half-Student-t implicita

  // Prior gerarchica (centered) sul predittore latente
  x ~ normal(mu_x, sigma_x);

  // Modello strutturale: y | x
  y ~ normal(a + b * x, sigma);

  // Modello di misura: x_star | x
  x_star ~ normal(x, sigma_x_star);
}
generated quantities {
  vector[N] y_rep;               // posterior predictive checks
  for (n in 1:N)
    y_rep[n] = normal_rng(a + b * x[n], sigma);
}
"

32.5.2 Preparazione dati e campionamento della posterior

mod_reg <- cmdstan_model(
  write_stan_file(stancode),
  compile = TRUE
)
stan_data <- list(
  N = N,
  y = y,
  x_star = x_star,
  sigma_x_star = sigma_xstar
)
fit <- mod_reg$sample(
  data = stan_data,
  seed = 20250917,
  chains = 4, 
  parallel_chains = 4,
  iter_warmup = 1000, 
  iter_sampling = 1000,
  adapt_delta = 0.95,  
  max_treedepth = 12,
  refresh = 0
)

32.5.3 Sintesi delle distribuzioni posteriori e confronto con valori veri

draws <- as_draws_df(fit$draws(c("a", "b", "mu_x", "sigma", "sigma_x")))

sum_tab <- summarise_draws(
  draws,
  mean, median, sd, 
  ~quantile(.x, probs = c(0.025, 0.25, 0.75, 0.975)),
  rhat = rhat,
  ess_bulk = ess_bulk,
  ess_tail = ess_tail
) %>%
  mutate(
    true_value = c(a_true, b_true, mu_x_true, sigma_true, sigma_x_true),
    bias = mean - true_value,
    relative_bias = bias / true_value
  )

sum_tab
#> # A tibble: 5 × 14
#>   variable   mean median    sd `2.5%`  `25%`  `75%` `97.5%`  rhat ess_bulk
#>   <chr>     <dbl>  <dbl> <dbl>  <dbl>  <dbl>  <dbl>   <dbl> <dbl>    <dbl>
#> 1 a         1.160  1.157 0.132  0.911  1.070  1.244   1.426 1.003  418.829
#> 2 b         2.076  2.072 0.113  1.876  2.003  2.144   2.300 1.013   92.900
#> 3 mu_x     -0.233 -0.231 0.103 -0.443 -0.302 -0.163  -0.035 1.002  955.300
#> 4 sigma     0.663  0.668 0.242  0.167  0.498  0.829   1.117 1.078   39.596
#> 5 sigma_x   1.491  1.489 0.092  1.318  1.430  1.551   1.677 1.007  307.346
#>   ess_tail true_value   bias relative_bias
#>      <dbl>      <dbl>  <dbl>         <dbl>
#> 1  800.395      1.000  0.160         0.160
#> 2  162.506      2.000  0.076         0.038
#> 3 1676.210      0.000 -0.233      -Inf    
#> 4   15.891      1.000 -0.337        -0.337
#> 5  495.917      1.500 -0.009        -0.006
mcmc_dens(fit$draws("b")) +
  geom_vline(xintercept = b_true, linetype = 2, color = "red") +
  geom_vline(xintercept = b_true * lambda_theory, linetype = 3, color = "blue") +
  labs(x = expression(beta), y = "Densità a posteriori") +
  annotate("text", x = b_true, y = 0.5, label = "Valore vero", 
           color = "red", hjust = -0.1) +
  annotate("text", x = b_true * lambda_theory, y = 0.5, 
           label = "Stima attenuata attesa", color = "blue", hjust = -0.1)

Distribuzione a posteriori del coefficiente b rispetto al valore vero (linea tratteggiata) e alla stima attenuata attesa (linea punteggiata)

32.5.4 Confronto quantitativo tra approccio ingenuo e bayesiano

naive_est <- broom::tidy(fit_naive_raw, conf.int = TRUE) %>%
  filter(term == "x_star") %>%
  transmute(
    model = "Ingenuo (OLS)",
    estimate = estimate,
    conf.low = conf.low,
    conf.high = conf.high
  )

bayesian_est <- sum_tab %>%
  filter(variable == "b") %>%
  transmute(
    model = "Bayesiano (corretto)",
    estimate = mean,
    conf.low = `2.5%`,
    conf.high = `97.5%`
  )

comparison_table <- bind_rows(naive_est, bayesian_est) %>%
  mutate(
    true_value = b_true,
    attenuation_factor = lambda_theory
  )

comparison_table
#> # A tibble: 2 × 6
#>   model                estimate conf.low conf.high true_value attenuation_factor
#>   <chr>                   <dbl>    <dbl>     <dbl>      <dbl>              <dbl>
#> 1 Ingenuo (OLS)            1.43     1.32      1.55          2              0.692
#> 2 Bayesiano (corretto)     2.08     1.88      2.30          2              0.692

In conclusione, l’analisi dimostra che la stima ingenua risulta attenuata verso \(b \times \lambda\), mentre il modello bayesiano, incorporando esplicitamente la struttura di misurazione, recupera efficacemente il parametro strutturale vero (\(b_{\text{true}}\)). I parametri del modello bayesiano (\(a\), \(b\), \(\sigma_x\)) mostrano una sostanziale coerenza con i valori di simulazione, considerando l’incertezza campionaria. L’uso di prior robuste garantisce stime affidabili.

32.6 Oltre Spearman: quando la disattenuazione sovrastima

Nella sezione precedente abbiamo visto che l’errore di misurazione in un predittore \(x\) comporta un’attenuazione della stima del suo coefficiente di regressione. Un fenomeno del tutto analogo si presenta quando si vuole stimare la correlazione tra due costrutti latenti, come ansia e depressione, che vengono osservati indirettamente tramite indicatori, come i punteggi dei questionari.

Nel quadro della Teoria Classica dei Test, i punteggi osservati si rappresentano come somma di un “punteggio vero” e di un errore di misurazione (Lord & Novick, 2008):

\[ X^* = X + \varepsilon_x,\qquad Y^* = Y + \varepsilon_y, \] dove \(X^*\) e \(Y^*\) sono i valori osservati, \(X\) e \(Y\) i tratti latenti di interesse, ed \(\varepsilon_x,\varepsilon_y\) gli errori. Se gli errori hanno media zero e sono indipendenti sia dai rispettivi tratti sia tra loro, la correlazione osservata \(r_{X^*Y^*}\) risulta attenuata rispetto alla correlazione “vera” \(\rho_{XY}\) tra i costrutti. La correzione proposta da Spearman (1904) è:

\[ \rho_{XY} \;=\; \frac{r_{X^*Y^*}}{\sqrt{r_{xx}\, r_{yy}}}\,, \] dove \(r_{xx}\) e \(r_{yy}\) sono le affidabilità delle due misure (rapporto tra varianza vera e varianza osservata). In pratica, tali coefficienti si stimano con procedure come test–retest, forme parallele e indici di coerenza interna (ad es., alfa di Cronbach, o meglio ancora \(\omega\)).

Questa correzione è utile, ma poggia su ipotesi forti (indipendenza e assenza di errori correlati).

32.6.1 Il problema: quando gli errori non sono indipendenti

La correzione di Spearman funziona solo se gli errori sono indipendenti dal tratto e tra loro. Quando questa ipotesi è violata, la disattenuazione può sovrastimare—talvolta in modo marcato—la correlazione tra i costrutti.

Una violazione tipica è data dalla varianza di metodo condivisa: stessa fonte informativa, stessa modalità di somministrazione, stesso contesto, stesse convenzioni di risposta Podsakoff et al. (2024). In tali casi è utile esplicitare un componente sistematico di metodo \(M\) comune alle due misure:

\[ X^* = X + M + \varepsilon_x,\qquad Y^* = Y + M + \varepsilon_y, \] dove \(X\) e \(Y\) sono i costrutti latenti di interesse, \(M\) cattura la porzione di varianza dovuta al metodo (ad es., desiderabilità sociale, stile acquiescente, contesto), ed \(\varepsilon_x,\varepsilon_y\) sono gli errori residui.

In questo schema,

\[ \operatorname{Cov}(X^*,Y^*) = \operatorname{Cov}(X,Y) + \operatorname{Var}(M) + \operatorname{Cov}(\varepsilon_x,\varepsilon_y), \] e \[ \operatorname{Var}(X^*)=\operatorname{Var}(X)+\operatorname{Var}(M)+\operatorname{Var}(\varepsilon_x), \]

\[ \operatorname{Var}(Y^*)=\operatorname{Var}(Y)+\operatorname{Var}(M)+\operatorname{Var}(\varepsilon_y). \]

Ora, se definiamo le affidabilità rispetto ai costrutti \(r_{xx}=\operatorname{Var}(X)/\operatorname{Var}(X^*)\) e \(r_{yy}=\operatorname{Var}(Y)/\operatorname{Var}(Y^*)\), la correzione di Spearman applicata a \(r_{X^*Y^*}\) si semplifica nel modo seguente:

\[ \frac{r_{X^*Y^*}}{\sqrt{r_{xx}r_{yy}}} \;=\; \frac{\operatorname{Cov}(X^*,Y^*)}{\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}} \;=\; \rho_{XY}\;+\;\frac{\operatorname{Var}(M)+\operatorname{Cov}(\varepsilon_x,\varepsilon_y)}{\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}}. \]

Questa identità mostra che, non appena esiste una componente di metodo condivisa \(\operatorname{Var}(M)>0\) (o residui correlati), la “correzione” non recupera la correlazione vera \(\rho_{XY}\), ma la gonfia aggiungendo un termine di bias positivo. In altre parole, anche se l’affidabilità è perfettamente definita rispetto ai costrutti, la disattenuazione di Spearman sovrastima \(\rho_{XY}\) quando gli errori non sono indipendenti. Nei casi estremi, il valore “corretto” può persino superare 1 in valore assoluto, rendendo esplicita la violazione delle ipotesi.

Nella pratica, la situazione è spesso peggiore: molte stime di affidabilità (test–retest, forme parallele, indici di coerenza interna come \(\alpha\) o \(\omega\)) assorbono parte della varianza di metodo trattandola come varianza “vera” stabile. Ciò rende \(r_{xx}\) e \(r_{yy}\) artificialmente elevati, lasciando il numeratore, già aumentato dalla varianza di metodo, pressoché invariato e la disattenuazione finisce per amplificare ulteriormente la sovrastima.

Di seguito mostriamo passo per passo perché la correzione di Spearman può sovrastimare la correlazione tra costrutti quando esiste una componente di metodo condivisa (o residui correlati).

Impostazione del modello (con metodo):

\[ X^* = X + M + \varepsilon_x,\qquad Y^* = Y + M + \varepsilon_y , \] dove

  • \(X,Y\): costrutti latenti di interesse,
  • \(M\): componente di metodo comune (es. desiderabilità sociale, stile acquiescente, stesso contesto/istruzioni),
  • \(\varepsilon_x,\varepsilon_y\): errori residui specifici di ciascuna misura.

Assunzioni per la dimostrazione:

  1. \(\mathbb E[X]=\mathbb E[Y]=\mathbb E[M]=\mathbb E[\varepsilon_x]=\mathbb E[\varepsilon_y]=0\) (possiamo sempre centrare).
  2. \(M\) è incorrelato con \(X\) e \(Y\): \(\operatorname{Cov}(X,M)=\operatorname{Cov}(Y,M)=0\).
  3. Gli errori sono incorrelati con i costrutti e con \(M\): \(\operatorname{Cov}(X,\varepsilon_y)=\operatorname{Cov}(Y,\varepsilon_x)=0\), \(\operatorname{Cov}(\varepsilon_x,M)=\operatorname{Cov}(\varepsilon_y,M)=0\).
  4. Gli errori possono essere tra loro correlati: \(\operatorname{Cov}(\varepsilon_x,\varepsilon_y)\) arbitraria (spesso \(\ge 0\) in presenza di fonte/metodo comuni).

Le assunzioni 2–3 rendono chiaro dove compare il bias: tutto ciò che non è “vero tratto” condiviso finisce nel termine \(M\) o nella correlazione dei residui.

32.6.1.1 1) Calcoliamo \(\operatorname{Cov}(X^*,Y^*)\) espandendo ogni termine

Per bilinearità della covarianza:

\[ \begin{aligned} \operatorname{Cov}(X^*,Y^*) &= \operatorname{Cov}(X+M+\varepsilon_x,\;Y+M+\varepsilon_y)\\ &= \underbrace{\operatorname{Cov}(X,Y)}_{\text{correlazione vera}} + \underbrace{\operatorname{Cov}(X,M)}_{=0} + \underbrace{\operatorname{Cov}(X,\varepsilon_y)}_{=0}\\ &\quad + \underbrace{\operatorname{Cov}(M,Y)}_{=0} + \underbrace{\operatorname{Cov}(M,M)}_{=\operatorname{Var}(M)} + \underbrace{\operatorname{Cov}(M,\varepsilon_y)}_{=0}\\ &\quad + \underbrace{\operatorname{Cov}(\varepsilon_x,Y)}_{=0} + \underbrace{\operatorname{Cov}(\varepsilon_x,M)}_{=0} + \operatorname{Cov}(\varepsilon_x,\varepsilon_y)\\[2mm] &= \operatorname{Cov}(X,Y) \;+\; \operatorname{Var}(M) \;+\; \operatorname{Cov}(\varepsilon_x,\varepsilon_y). \end{aligned} \]

32.6.1.2 2) Calcoliamo \(\operatorname{Var}(X^*)\) e \(\operatorname{Var}(Y^*)\)

Ancora per proprietà della varianza/covarianza:

\[ \begin{aligned} \operatorname{Var}(X^*) &= \operatorname{Var}(X+M+\varepsilon_x)\\ &= \operatorname{Var}(X)+\operatorname{Var}(M)+\operatorname{Var}(\varepsilon_x) \\ &\quad + 2\,\underbrace{\operatorname{Cov}(X,M)}_{=0} + 2\,\underbrace{\operatorname{Cov}(X,\varepsilon_x)}_{=0} + 2\,\underbrace{\operatorname{Cov}(M,\varepsilon_x)}_{=0}\\[1mm] &= \operatorname{Var}(X)+\operatorname{Var}(M)+\operatorname{Var}(\varepsilon_x). \end{aligned} \]

In modo del tutto analogo,

\[ \operatorname{Var}(Y^*)=\operatorname{Var}(Y)+\operatorname{Var}(M)+\operatorname{Var}(\varepsilon_y). \]

32.6.1.3 3) Correlazione osservata tra \(X^*,Y^*\)

Per definizione:

\[ \begin{align} r_{X^*Y^*} &= \frac{\operatorname{Cov}(X^*,Y^*)}{\sqrt{\operatorname{Var}(X^*)\,\operatorname{Var}(Y^*)}}\notag\\ &= \frac{\operatorname{Cov}(X,Y)+\operatorname{Var}(M)+\operatorname{Cov}(\varepsilon_x,\varepsilon_y)} {\sqrt{\big(\operatorname{Var}(X)+\operatorname{Var}(M)+\operatorname{Var}(\varepsilon_x)\big)\, \big(\operatorname{Var}(Y)+\operatorname{Var}(M)+\operatorname{Var}(\varepsilon_y)\big)}}. \end{align} \]

32.6.1.4 4) Richiamo: affidabilità rispetto ai costrutti

Definiamo (coerentemente con la TCT riferita ai costrutti)

\[ r_{xx} \equiv \frac{\operatorname{Var}(X)}{\operatorname{Var}(X^*)},\qquad r_{yy} \equiv \frac{\operatorname{Var}(Y)}{\operatorname{Var}(Y^*)}. \] cioè la quota di varianza osservata che appartiene al tratto (non a \(M\) o al residuo).

Da qui segue:

\[ \sqrt{r_{xx}\,r_{yy}}\;\sqrt{\operatorname{Var}(X^*)\,\operatorname{Var}(Y^*)} = \sqrt{\operatorname{Var}(X)\,\operatorname{Var}(Y)}. \]

32.6.1.5 5) Correzione di Spearman e semplificazione esatta

La disattenuazione di Spearman applicata a \(r_{X^*Y^*}\) è

\[ \frac{r_{X^*Y^*}}{\sqrt{r_{xx}\,r_{yy}}} = \frac{\operatorname{Cov}(X^*,Y^*)}{\sqrt{\operatorname{Var}(X)\,\operatorname{Var}(Y)}}. \] Sostituendo il risultato del punto 1:

\[ \frac{r_{X^*Y^*}}{\sqrt{r_{xx}r_{yy}}} = \frac{\operatorname{Cov}(X,Y)}{\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}} \;+\; \frac{\operatorname{Var}(M)+\operatorname{Cov}(\varepsilon_x,\varepsilon_y)} {\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}}. \] Riconoscendo \(\rho_{XY}\equiv \dfrac{\operatorname{Cov}(X,Y)}{\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}}\), otteniamo l’identità chiave:

\[ \boxed{\; \frac{r_{X^*Y^*}}{\sqrt{r_{xx}r_{yy}}} \;=\; \rho_{XY}\;+\; \underbrace{\frac{\operatorname{Var}(M)+\operatorname{Cov}(\varepsilon_x,\varepsilon_y)} {\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}}}_{\text{termine di bias}} \;} \]

32.6.1.6 6) Interpretazione del termine di bias

  • Se esiste metodo condiviso (\(\operatorname{Var}(M)>0\)) e/o residui sono positivamente correlati (\(\operatorname{Cov}(\varepsilon_x,\varepsilon_y)>0\)), allora il termine di bias è positivo → la “correzione” sovrastima \(\rho_{XY}\).
  • In casi estremi, la somma può superare 1 in valore assoluto (campanello d’allarme: ipotesi violate).
  • Se \(\operatorname{Cov}(\varepsilon_x,\varepsilon_y)<0\) (raro ma possibile), quel pezzo può controbilanciare parzialmente \(\operatorname{Var}(M)\), ma la presenza di \(M\) resta di norma inflattiva.

32.6.1.7 7) (Facoltativo ma istruttivo) Se \(M\) non è incorrelato con \(X\) o \(Y\)

Senza l’assunzione 2, al punto 1 restano anche \(\operatorname{Cov}(X,M)\) e \(\operatorname{Cov}(Y,M)\). Allora

\[ \frac{r_{X^*Y^*}}{\sqrt{r_{xx}r_{yy}}} = \rho_{XY} + \frac{\operatorname{Cov}(X,M)+\operatorname{Cov}(Y,M)+\operatorname{Var}(M)+\operatorname{Cov}(\varepsilon_x,\varepsilon_y)} {\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}}, \] cioè il bias include ulteriori addendi dovuti all’associazione tra metodo e tratti (tipico se, ad es., il metodo favorisce sistematicamente punteggi elevati in entrambi i costrutti).

32.6.1.8 8) Nota pratica sulle stime di affidabilità usate in applicazione

La dimostrazione sopra usa \(r_{xx}=\operatorname{Var}(X)/\operatorname{Var}(X^*)\), cioè affidabilità rispetto al costrutto. In pratica, però, indici come \(\alpha\) o \(\omega\) spesso trattano parte di \(M\) come “varianza vera stabile” (specialmente se \(M\) agisce su tutti gli item): di fatto assorbono metodo nel “vero punteggio”. Così:

  • il numeratore \(\operatorname{Cov}(X^*,Y^*)\) è già aumentato da \(M\);
  • le affidabilità stimate risultano artificialmente alte, quindi la correzione di Spearman (che divide per \(\sqrt{r_{xx}r_{yy}}\)) non rimuove il contributo di metodo; nella metrica corretta rimane (al più attenuato) il termine di bias, e la correlazione “corretta” continua a sovrastimare \(\rho_{XY}\).
ImportanteMessaggio operativo

Quando si sospetta la presenza di varianza di metodo condivisa (o residui correlati), la strategia corretta non è la disattenuazione di Spearman, ma un modello di misurazione congiunto (SEM bayesiana o classica; Raykov & Marcoulides (2011)) che separa: (i) fattori di tratto, (ii) fattori/metodi condivisi, (iii) residui (eventualmente correlati). Solo così la correlazione tra i tratti \(\rho_{XY}\) viene stimata senza il bias indotto dal metodo.

32.6.2 La soluzione adottata: modello bayesiano tratto–metodo (Stan)

In questo capitolo adottiamo un modello bayesiano tratto–metodo con fattore di metodo comune. L’idea generativa è:

\[ \begin{aligned} X_1 &= T_x + M + e_{x1},\qquad &X_2 &= T_x + M + e_{x2},\\ Y_1 &= T_y + M + e_{y1},\qquad &Y_2 &= T_y + M + e_{y2}, \end{aligned} \] dove \(T_x\) e \(T_y\) sono i tratti di interesse, \(M\) è la fonte di metodo condivisa, e \(e_{\cdot}\) sono errori specifici d’indicatore. La correlazione latente che vogliamo stimare è \(\rho = \mathrm{Cor}(T_x,T_y)\).

Nel codice Stan:

  • \((T_x, T_y)\) sono modellati per ogni osservazione con una normale bivariata standard e correlazione \(\rho\) (blocco model, matrice Sigma), in modo che la scala dei tratti sia ancorata (varianze unità) e \(\rho\) sia identificato.
  • \(M\) è un fattore di metodo comune con prior \(M \sim \mathcal N(0,\sigma_M)\); la sua varianza \(\sigma_M^2\) è stimata dai dati.
  • Le saturazioni di tratto e metodo sugli indicatori sono fissate a 1 (una scelta didattica che semplifica l’identificazione della scala).
  • Le deviazioni standard specifiche (\(\sigma_{x1},\sigma_{x2},\sigma_{y1},\sigma_{y2}\)) sono stimate con prior robuste (Student-t).

Questa specifica separa esplicitamente la covarianza osservata in: componente di tratto, componente di metodo e errori specifici, consentendo una stima diretta e coerente dell’oggetto d’interesse \(\rho\) senza ricorrere a correzioni post-hoc come proposto da Spearman.

NotaIdentificazione (coerente con lo Stan code)
  • Scala dei tratti: \(\operatorname{Var}(T_x)=\operatorname{Var}(T_y)=1\) tramite la distribuzione normale bivariata standard (carichi di tratto fissati a 1).
  • Scala del metodo: stimiamo \(\sigma_M\) (carichi di metodo fissati a 1).
  • La scelta “carichi = 1, varianze libere” rende l’interpretazione delle varianze più chiara e mantiene semplice il codice. Alternative (non trattate qui) sono possibili, ad esempio fissare \(\sigma_M=1\) e stimare i carichi di metodo.

32.6.2.1 Cosa leggiamo dai risultati

  • \(\rho\): la correlazione latente tra i tratti, depurata dalla varianza di metodo.
  • \(\sigma_M\): quanta varianza di metodo condivisa è necessaria per spiegare la covarianza tra indicatori oltre ai tratti.
  • Posterior predictive check (r_comp_rep): verifica che il modello rigeneri la correlazione tra compositi osservata; se l’osservato cade nel ventaglio predittivo, la scomposizione tratto–metodo è coerente con i dati.

Messaggio chiave. In presenza di possibili effetti di metodo (condizione usuale nelle misure psicologiche), una stima bayesiana con struttura tratto–metodo esplicita consente di evitare sia l’attenuazione sia la sovracorrezione tipica delle formule di disattenuazione, fornendo direttamente la distribuzione a posteriori di \(\rho\) con propagazione completa dell’incertezza.

ConsiglioQuando usare cosa
  • Correzione di Spearman: utile solo quando gli errori sono davvero indipendenti e non vi è varianza di metodo condivisa.
  • Modello tratto-metodo: necessario quando si sospettano effetti di metodo (che è la regola più che l’eccezione nella pratica psicometrica).

32.6.3 Disegno didattico della simulazione

Per illustrare empiricamente i limiti dell’approccio classico e i vantaggi della modellazione bayesiana, utilizzeremo la seguente simulazione.

32.6.3.1 Scenario simulato

  • Modello strutturale vero: due tratti latenti \(T_x\) e \(T_y\) correlati con coefficiente \(\rho_{\text{vero}} = 0.60\).
  • Fonte di distorsione metodologica: un fattore di metodo comune \(M\) che influisce su tutti gli indicatori osservati
  • Modello di misura: per ogni costrutto latente sono disponibili due indicatori:
    • gli indicatori \(X_1, X_2\) del costrutto \(T_x\): \(X_i = \lambda_{X_i} T_x + \lambda_{M_i} M + e_{X_i}\).
    • gli indicatori \(Y_1, Y_2\) del costrutto \(T_y\): \(Y_i = \lambda_{Y_i} T_y + \lambda_{M_i} M + e_{Y_i}\).

Qui poniamo \(\lambda_{X_i}=\lambda_{Y_i}=\lambda_{M_i}=1\) per identificazione, in coerenza con il codice Stan.

32.6.3.1.1 Confronto metodologico

Approccio Tradizionale (CTT + Spearman) Nell’approccio tradizionale, basato sulla Teoria Classica dei Test (CTT) e sulla correzione di Spearman, il calcolo procede attraverso una serie di passaggi sequenziali. Inizialmente, si calcolano i punteggi compositi per ciascun costrutto, definiti come la media semplice degli item corrispondenti: \(\bar{X} = (X_1 + X_2)/2\) per il primo costrutto e \(\bar{Y} = (Y_1 + Y_2)/2\) per il secondo. In seguito, si stima la correlazione osservata direttamente tra questi punteggi compositi, indicata come \(r_{\text{obs}} = \operatorname{Cor}(\bar{X}, \bar{Y})\). Le affidabilità di ciascuna delle due scale vengono stimate ricorrendo al coefficiente \(\alpha\) di Cronbach, denominate rispettivamente \(\alpha_X\) e \(\alpha_Y\). Infine, per correggere l’effetto di attenuazione causato dall’errore di misura, la stima della correlazione viene rettificata applicando la formula di Spearman: \(r_{\text{corretta}} = r_{\text{obs}} / \sqrt{\alpha_X \cdot \alpha_Y}\).

Approccio Bayesiano L’approccio bayesiano adotta una strategia fondamentalmente differente, modellando l’intera struttura di misurazione e le relazioni latenti in un unico quadro analitico coerente. Questo metodo utilizza un modello di equazioni strutturali che incorpora esplicitamente sia i tratti latenti di interesse (\(T_x\) e \(T_y\)) sia un eventuale fattore di metodo comune (\(M\)), qualora si ritenga che sia presente. Tutti i parametri del modello, inclusi i coefficienti di regressione e le varianze, vengono stimati assegnando loro prior debolmente informativi, i quali, pur regolarizzando la stima, esercitano un’influenza minima sui risultati quando sono disponibili dati sufficienti. Il risultato principale è una stima diretta della correlazione latente \(\rho\) tra i costrutti \(T_x\) e \(T_y\), ottenuta dal campione posteriore del parametro. Questo approccio consente di quantificare l’incertezza in modo completo, tramite gli intervalli di credibilità, e di correggere le distorsioni metodologiche all’interno del modello stesso, senza dover ricorrere a correzioni post hoc.

32.6.3.2 Risultato atteso

L’approccio di Spearman produrrà una sovrastima della correlazione vera (\(\rho > 0.60\)), interpretando erroneamente la varianza di metodo come varianza del tratto. Il modello bayesiano, modellando esplicitamente la fonte di distorsione, recupererà il parametro vero (\(\rho \approx 0.60\)).

32.6.4 Simulazione: metodo comune ⇒ Spearman sovracorregge

set.seed(20250912)

N  <- 1200                  # dimensione campione
rho_true <- 0.60            # correlazione VERA tra i tratti
sigma_M_true <- 0.90        # deviazione standard del metodo comune

# Generiamo i tratti latenti (standardizzati: varianza = 1)
Tx <- rnorm(N, 0, 1)
Ty <- rho_true * Tx + sqrt(1 - rho_true^2) * rnorm(N, 0, 1)

# Generiamo il fattore di METODO comune
M  <- rnorm(N, 0, sigma_M_true)

# Deviazioni standard degli errori specifici per ciascun indicatore
sx1 <- 0.60; sx2 <- 0.60    # errori per gli indicatori di X
sy1 <- 0.50; sy2 <- 0.50    # errori per gli indicatori di Y

# Generiamo gli indicatori osservati
# Ogni indicatore = tratto + metodo + errore specifico
# (coefficienti di saturazione = 1 per semplicità)
X1 <- Tx + M + rnorm(N, 0, sx1)
X2 <- Tx + M + rnorm(N, 0, sx2)
Y1 <- Ty + M + rnorm(N, 0, sy1)
Y2 <- Ty + M + rnorm(N, 0, sy2)

# Creiamo i compositi (medie degli indicatori)
Xbar <- (X1 + X2)/2
Ybar <- (Y1 + Y2)/2
r_obs <- cor(Xbar, Ybar)

# Calcoliamo l'alfa di Cronbach per scale a 2 item
# Formula: alpha = 2*r12/(1+r12)
alpha_two <- function(u, v) { 
  r12 <- cor(u, v)
  2 * r12 / (1 + r12)
}
alpha_x <- alpha_two(X1, X2)
alpha_y <- alpha_two(Y1, Y2)

# Applichiamo la correzione di Spearman
r_spearman <- r_obs / sqrt(alpha_x * alpha_y)

# Mostriamo i risultati
tibble(
  r_obs = round(r_obs, 3),
  alpha_x = round(alpha_x, 3),
  alpha_y = round(alpha_y, 3),
  r_spearman = round(r_spearman, 3),
  rho_true = rho_true
)
#> # A tibble: 1 × 5
#>   r_obs alpha_x alpha_y r_spearman rho_true
#>   <dbl>   <dbl>   <dbl>      <dbl>    <dbl>
#> 1   0.7   0.908   0.932      0.761      0.6

Interpretazione dei risultati:

  • r_obs: correlazione osservata tra i compositi (già gonfiata dal metodo comune);
  • alpha_x, alpha_y: affidabilità delle scale (anche queste gonfiate dal metodo comune);
  • r_spearman: correlazione “corretta” con il metodo di Spearman;
  • rho_true: vera correlazione tra i tratti (0.60).

Come previsto, in presenza di metodo comune, la correzione di Spearman produce una stima che supera la vera correlazione di 0.60.

32.6.5 Modello bayesiano: separazione di tratto e metodo

Il nostro modello bayesiano separa esplicitamente tratto e metodo. Fissiamo la varianza dei tratti a 1 per identificazione e stimiamo:

  • la correlazione latente \(\rho\) tra i tratti;
  • la varianza del metodo comune \(\sigma_M^2\);
  • le varianze degli errori specifici per ciascun indicatore.
stancode <- "
data {
  int<lower=1> N;           // numero di osservazioni
  vector[N] X1;             // primo indicatore del costrutto X
  vector[N] X2;             // secondo indicatore del costrutto X  
  vector[N] Y1;             // primo indicatore del costrutto Y
  vector[N] Y2;             // secondo indicatore del costrutto Y
}
parameters {
  // === STRUTTURA LATENTE ===
  real<lower=-1, upper=1> rho;   // correlazione tra Tx e Ty
  vector[N] Tx;                  // tratto X (standardizzato: Var=1)
  vector[N] Ty;                  // tratto Y (standardizzato: Var=1)  
  vector[N] M;                   // fattore di metodo comune

  // === PARAMETRI DI SCALA ===
  real<lower=0> sigma_M;         // deviazione standard del metodo
  real<lower=0> sigma_x1;        // deviazione standard errore X1
  real<lower=0> sigma_x2;        // deviazione standard errore X2
  real<lower=0> sigma_y1;        // deviazione standard errore Y1
  real<lower=0> sigma_y2;        // deviazione standard errore Y2
}
model {
  // === PRIOR PER LA STRUTTURA LATENTE ===
  // Distribuzioni congiunte per (Tx, Ty) con correlazione rho
  {
    vector[2] mu = [0, 0]';      // medie = 0 (standardizzati)
    matrix[2,2] Sigma;           // matrice di covarianza
    Sigma[1,1] = 1;      Sigma[1,2] = rho;    // Var(Tx)=1, Cov(Tx,Ty)=rho
    Sigma[2,1] = rho;    Sigma[2,2] = 1;      // Cov(Ty,Tx)=rho, Var(Ty)=1
    
    // Per ogni osservazione, (Tx[n], Ty[n]) segue una normale bivariata
    for (n in 1:N) {
      vector[2] t;
      t[1] = Tx[n];
      t[2] = Ty[n];
      t ~ multi_normal(mu, Sigma);
    }
  }

  // Fattore di metodo comune: normale con media 0 e varianza sigma_M^2
  M ~ normal(0, sigma_M);

  // === PRIOR DEBOLMENTE INFORMATIVE ===
  rho      ~ normal(0, 0.5);        // correlazione centrata su 0
  sigma_M  ~ student_t(3, 0, 2.5);  // prior robusta per la scala del metodo
  sigma_x1 ~ student_t(3, 0, 2.5);  // prior robuste per gli errori specifici
  sigma_x2 ~ student_t(3, 0, 2.5);
  sigma_y1 ~ student_t(3, 0, 2.5);
  sigma_y2 ~ student_t(3, 0, 2.5);

  // === EQUAZIONI DI MISURAZIONE ===
  // Ogni indicatore = tratto + metodo + errore specifico
  X1 ~ normal(Tx + M, sigma_x1);   // X1 dipende da Tx, M, e errore
  X2 ~ normal(Tx + M, sigma_x2);   // X2 dipende da Tx, M, e errore  
  Y1 ~ normal(Ty + M, sigma_y1);   // Y1 dipende da Ty, M, e errore
  Y2 ~ normal(Ty + M, sigma_y2);   // Y2 dipende da Ty, M, e errore
}
generated quantities {
  // === CONTROLLO PREDITTIVO POSTERIORE ===
  // Generiamo dati replicati per verificare la bontà del modello
  vector[N] X1_rep;
  vector[N] X2_rep;
  vector[N] Y1_rep;
  vector[N] Y2_rep;
  real r_comp_rep;               // correlazione tra compositi replicati

  // Per ogni osservazione, generiamo repliche degli indicatori
  for (n in 1:N) {
    X1_rep[n] = normal_rng(Tx[n] + M[n], sigma_x1);
    X2_rep[n] = normal_rng(Tx[n] + M[n], sigma_x2);
    Y1_rep[n] = normal_rng(Ty[n] + M[n], sigma_y1);
    Y2_rep[n] = normal_rng(Ty[n] + M[n], sigma_y2);
  }

  // Calcoliamo la correlazione tra compositi replicati
  {
    vector[N] Xbar_rep = 0.5 * (X1_rep + X2_rep);  // composto X replicato
    vector[N] Ybar_rep = 0.5 * (Y1_rep + Y2_rep);  // composto Y replicato
    real mx = mean(Xbar_rep);
    real my = mean(Ybar_rep);
    real sxx = 0;    // somma scarti quadrati X
    real syy = 0;    // somma scarti quadrati Y  
    real sxy = 0;    // somma prodotti scarti X*Y
    
    for (n in 1:N) {
      real dx = Xbar_rep[n] - mx;
      real dy = Ybar_rep[n] - my;
      sxx += dx * dx;
      syy += dy * dy;
      sxy += dx * dy;
    }
    r_comp_rep = sxy / sqrt(sxx * syy);  // formula della correlazione
  }
}
"

32.6.5.1 Struttura del modello Stan

Il codice Stan sopra implementa il modello tratto-metodo. Vediamo le parti principali:

1. Struttura latente (blocco model):

  • Tratti correlati: i tratti Tx e Ty seguono una distribuzione normale bivariata con correlazione rho e varianze unitarie.
  • Metodo comune: il fattore M segue una normale con media 0 e deviazione standard sigma_M.

2. Equazioni di misurazione:

  • ogni indicatore osservato è la somma di: tratto + metodo + errore specifico.
  • ad esempio: X1 ~ normal(Tx + M, sigma_x1).

3. Controllo predittivo (blocco generated quantities):

  • genera dati replicati dal modello stimato.
  • calcola la correlazione tra compositi replicati per confronto con i dati osservati.
mod_tm <- cmdstan_model(
  write_stan_file(stancode),
  compile = TRUE
)
fit_tm <- mod_tm$sample(
  data = list(N = N, X1 = X1, X2 = X2, Y1 = Y1, Y2 = Y2),
  seed = 20250917, 
  chains = 4, 
  parallel_chains = 4,
  iter_warmup = 1000, 
  iter_sampling = 1000,
  adapt_delta = 0.95, 
  max_treedepth = 12, 
  refresh = 0
)

32.6.5.2 Risultati: correlazione \(\rho\) senza distorsione

# Estraiamo i risultati posteriori per i parametri di interesse
post <- posterior::as_draws_df(
  fit_tm$draws(
    c("rho","sigma_M","sigma_x1","sigma_x2","sigma_y1","sigma_y2","r_comp_rep")
  )
)

# Riassunti statistici dei parametri stimati
summ_all <- posterior::summarise_draws(
  post,
  mean, sd,
  ~stats::quantile(.x, probs = c(0.025, 0.5, 0.975)),
  rhat = posterior::rhat,
  ess_bulk = posterior::ess_bulk,
  ess_tail = posterior::ess_tail
)

# Focalizziamo sulla correlazione rho
summ_rho <- dplyr::filter(summ_all, variable == "rho")
summ_rho
#> # A tibble: 1 × 9
#>   variable  mean    sd `2.5%` `50%` `97.5%`  rhat ess_bulk ess_tail
#>   <chr>    <dbl> <dbl>  <dbl> <dbl>   <dbl> <dbl>    <dbl>    <dbl>
#> 1 rho      0.579 0.024  0.529 0.580   0.625 1.003 4166.258 2801.174

Come possiamo vedere, il modello bayesiano recupera correttamente la correlazione vera di 0.60, mentre la correzione di Spearman l’aveva sovrastimata.

32.6.6 Controllo predittivo posteriore sulla correlazione tra compositi

Un aspetto fondamentale della modellazione bayesiana è verificare che il modello stimato sia coerente con i dati osservati. Lo facciamo attraverso un Posterior Predictive Check (PPC).

32.6.6.1 Cosa verifichiamo

Vogliamo controllare se il nostro modello tratto-metodo è capace di rigenerare la correlazione osservata tra i compositi \(\bar{X}=(X_1+X_2)/2\) e \(\bar{Y}=(Y_1+Y_2)/2\). Se il fattore di metodo e le varianze d’errore stimati dal modello spiegano davvero la correlazione che vediamo nei compositi, allora:

\[ T(y) = r_{\text{obs,comp}} = \operatorname{Cor}(\bar{X}, \bar{Y}) \] deve risultare plausibile sotto la distribuzione predittiva del modello.

32.6.6.2 Procedura del PPC

\[ T(y)=r_{\text{obs,comp}}=\operatorname{Cor}(\bar{X},\bar{Y}), \]

\[ T(y^{\mathrm{rep}})=r_{\text{rep,comp}}=\operatorname{Cor}(\bar{X}^{\mathrm{rep}},\bar{Y}^{\mathrm{rep}}). \]

  1. Per ogni campione posteriore dei parametri \(\theta^{(s)}\):
    • si genera o repliche predittive degli indicatori;
    • si calcola la correlazione tra i compositi replicati: \(r_{\text{rep,comp}}^{(s)}\).
  2. Si confronta \(r_{\text{obs,comp}}\) con la distribuzione \(\{\,r_{\text{rep,comp}}^{(s)}\,\}\).
# Correlazione osservata tra compositi
Xbar <- (X1 + X2)/2
Ybar <- (Y1 + Y2)/2
r_obs_comp <- cor(Xbar, Ybar)

# Estraiamo le correlazioni replicate dal modello
r_ppc <- posterior::as_draws_df(fit_tm$draws("r_comp_rep"))$r_comp_rep

# Riassunti numerici del controllo predittivo
ppc_summary <- tibble(
  r_obs_comp      = r_obs_comp,                            # correlazione osservata
  mean_pred       = mean(r_ppc),                          # media delle repliche
  q025_pred       = quantile(r_ppc, 0.025),              # 2.5° percentile
  q975_pred       = quantile(r_ppc, 0.975),              # 97.5° percentile  
  perc_pred       = mean(r_ppc <= r_obs_comp),           # percentile dell'osservato
  p_upper_1sided  = mean(r_ppc >= r_obs_comp),           # p-value a una coda
  p_two_sided     = 2 * pmin(perc_pred, 1 - perc_pred)   # p-value a due code
)
ppc_summary
#> # A tibble: 1 × 7
#>   r_obs_comp mean_pred q025_pred q975_pred perc_pred p_upper_1sided p_two_sided
#>        <dbl>     <dbl>     <dbl>     <dbl>     <dbl>          <dbl>       <dbl>
#> 1      0.700     0.699     0.677     0.720     0.527          0.473       0.946

32.6.6.3 Grafico del controllo predittivo

ggplot(tibble(r_ppc), aes(x = r_ppc)) +
  geom_histogram(bins = 40, linewidth = 0.2, alpha = 0.7) +
  geom_vline(xintercept = r_obs_comp, linetype = 2, color = "red", linewidth = 1) +
  annotate(
    "rect",
    xmin = quantile(r_ppc, .025), xmax = quantile(r_ppc, .975),
    ymin = 0, ymax = Inf, alpha = .15, fill = "blue"
  ) +
  labs(
    x = "Correlazione tra compositi (repliche predittive posteriori)",
    y = "Frequenza",
    title = "Controllo Predittivo Posteriore",
    subtitle = paste0(
      "r osservato = ", round(r_obs_comp, 3), 
      # " | Media predittiva = ", round(mean(r_ppc), 3),
      " | 95% CrI = [", round(quantile(r_ppc,.025),3), ", ",
                          round(quantile(r_ppc,.975),3), "]"
    ),
    caption = "Linea rossa tratteggiata: correlazione osservata tra compositi\nArea blu: intervallo di credibilità al 95% delle predizioni"
  )

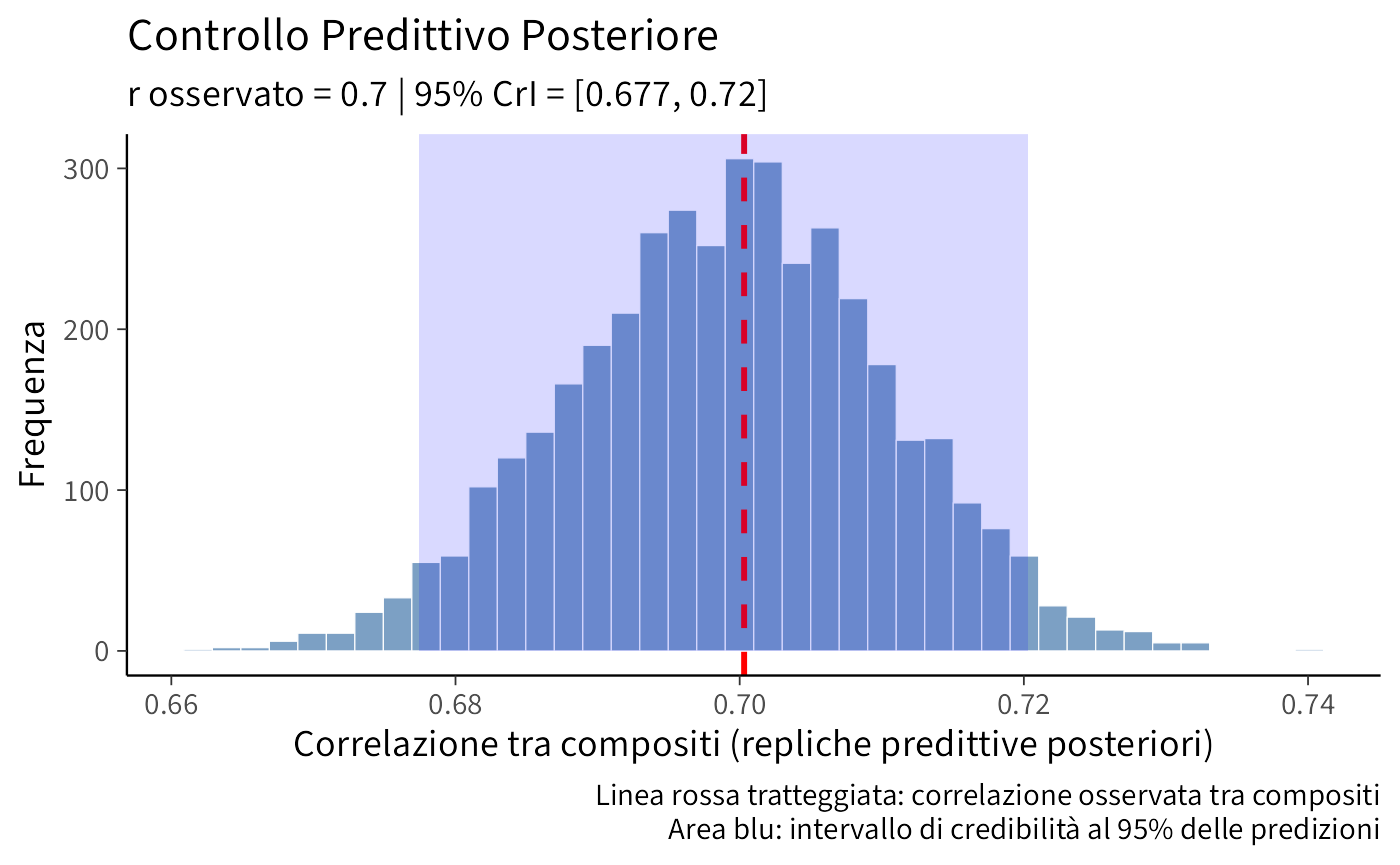
32.6.6.4 Interpretazione del PPC

Il Posterior Predictive Check (PPC) è uno strumento diagnostico per valutare la coerenza del modello proposto con i dati osservati. La sua interpretazione si basa sulla posizione del valore osservato, in questo caso la correlazione \(r_{\text{obs,comp}}\), all’interno della distribuzione predittiva a posteriori generata dal modello. Se il valore osservato cade all’interno dell’intervallo predittivo, rappresentato graficamente dall’area blu della distribuzione nella figura precedente, ciò indica che il modello è in grado di riprodurre adeguatamente la correlazione effettivamente misurata nei dati, confermandone la coerenza. Al contrario, un valore osservato che si collochi drasticamente a destra della distribuzione segnalerebbe una sottostima sistematica da parte del modello, che non riuscirebbe a generare una correlazione sufficientemente elevata. Al contrario, un valore osservato situato estremamente a sinistra della distribuzione indicherebbe una sovrastima, suggerendo che il modello tende a generare una correlazione eccessiva. Nel caso specifico qui analizzato, il valore osservato cade in modo convincente all’interno dell’intervallo predittivo, confermando che la struttura del modello tratto-metodo cattura in modo soddisfacente la struttura sottostante dei dati.

32.6.7 Conclusioni e implicazioni pratiche

32.6.7.1 Perché la correzione di Spearman fallisce

La correzione classica di Spearman, sebbene importante dal punto di vista storico, presenta limitazioni cruciali in contesti applicati. Il suo fallimento è dovuto a tre presupposti spesso violati nella pratica della ricerca. In primo luogo, la formula presuppone l’indipendenza degli errori di misurazione tra le diverse scale. Tuttavia, nella realtà sperimentale, le misurazioni psicologiche condividono spesso fonti di varianza metodologica, come il contesto di somministrazione, la formulazione degli item o le caratteristiche del rispondente, che creano correlazioni spurie tra gli errori. In secondo luogo, il trattamento dell’affidabilità come una quantità nota è un’idealizzazione problematica: l’alfa di Cronbach, comunemente utilizzato come stima dell’affidabilità, cattura infatti sia la varianza vera che quella di metodo, incorporando quindi nelle stime proprio la componente che la correzione vorrebbe eliminare. Infine, l’approccio tradizionale è cieco rispetto alla natura della covarianza osservata e non è in grado di distinguere la correlazione autentica tra tratti latenti dalla correlazione artificiale generata da fattori metodologici comuni. Questa cecità concettuale conduce sistematicamente a sovracorrezioni, producendo stime della correlazione vera che possono risultare artificialmente elevate.

32.6.7.2 I vantaggi del modello bayesiano tratto-metodo

Il modello bayesiano tratto-metodo supera queste criticità attraverso un approccio di modellazione più sofisticato e realistico. Esso separa esplicitamente le componenti di tratto e metodo mediante l’utilizzo di molteplici indicatori per ciascun costrutto, consentendo di scomporre la varianza osservata nelle sue fonti latenti. Questa architettura consente di stimare direttamente la correlazione \(\rho\) tra i tratti senza dover assumere parametri noti, ma riconoscendo l’incertezza insita in tutti i parametri del modello. Un vantaggio cruciale risiede nella corretta propagazione dell’incertezza attraverso l’inferenza bayesiana: invece di produrre stime puntuali, il modello quantifica l’incertezza completa riguardante tutti i parametri, generando distribuzioni posteriori che riflettono la nostra conoscenza plausibile sui valori dei parametri alla luce dei dati osservati. Inoltre, il modello bayesiano consente di implementare controlli di qualità rigorosi attraverso i posterior predictive checks, che permettono di valutare la capacità del modello di riprodurre i pattern essenziali dei dati osservati, fornendo un riscontro empirico sull’adeguatezza del modello stesso. Questa integrazione di modellazione esplicita e verifica empirica rappresenta un avanzamento metodologico sostanziale nella stima delle relazioni tra i costrutti latenti.

L’utilizzo del coefficiente di correlazione di Spearman-Brown risulta appropriato esclusivamente in presenza di errori di misurazione tra scale che possano considerarsi genuinamente indipendenti, qualora le stime di affidabilità degli strumenti impiegati siano note, robuste e validate da evidenze empiriche estese, e quando l’obiettivo dell’analisi sia di tipo descrittivo.

Al contrario, il ricorso al modello tratto-metodo, noto anche come modello di correlazione disattenuata per la varianza di metodo, è fortemente raccomandato nello scenario più comune in cui si sospetti la presenza di una sostanziale varianza attribuibile al metodo di misurazione. La sua applicazione presuppone la disponibilità di almeno due indicatori per ciascun costrutto latente ed è particolarmente indicata quando la finalità della ricerca include l’inferenza statistica sui parametri del modello.

Indipendentemente dalla scelta metodologica, è importante condurre una serie di controlli analitici. Questi includono, in ambito bayesiano, la verifica della convergenza degli algoritmi di stima, con valori di \(\hat{R}\) inferiori a 1.01 e Effective Sample Sizes (ESS) adeguati, l’esecuzione di controlli predittivi posteriori (Posterior Predictive Checks - PPC), un’analisi di sensibilità rispetto alla scelta delle distribuzioni a priori, e un confronto sistematico con i risultati ottenuti tramite approcci tradizionali per metterne in luce eventuali divergenze.

In sede di rendicontazione dei risultati, è necessario riportare in modo completo e trasparente la distribuzione posteriore del coefficiente di correlazione \(\rho\), sintetizzata attraverso la sua media (o mediana) e i relativi intervalli di credibilità, le stime dei parametri di varianza (sia per il metodo che per l’errore), gli esiti dei controlli predittivi posteriori e, ove utile ai fini interpretativi, un confronto illustrativo con le stime prodotte dalla correlazione di Spearman.

Il messaggio chiave è che in presenza di potenziali effetti di metodo – che rappresentano la norma piuttosto che l’eccezione nella pratica psicometrica – è essenziale modellare esplicitamente la struttura di misurazione per ottenere stime accurate e non distorte delle relazioni tra costrutti teorici.

Riflessioni conclusive

Quando una variabile esplicativa è soggetta a errore di misurazione, trattarla come se fosse priva di rumore porta sistematicamente a un fenomeno di attenuazione: i coefficienti di regressione tendono verso lo zero e le loro versioni standardizzate, ovvero le correlazioni osservate, appaiono indebolite. In questo contesto, la standardizzazione non corregge la distorsione, ma tende piuttosto a nasconderla.

L’approccio bayesiano affronta il problema alla radice, articolando in modo esplicito un livello strutturale, in cui si definiscono le relazioni tra i costrutti latenti, e un livello di misura, in cui si specifica come gli indicatori osservati riflettono tali costrutti. Questa separazione concettuale produce tre vantaggi fondamentali:

  1. Nella regressione, modellare l’errore di misura nei predittori evita l’attenuazione, recuperando la relazione strutturale sottostante e propagando in modo coerente l’incertezza metrica fino ai parametri di interesse sostanziale;
  2. Nella stima della correlazione tra costrutti, la correzione classica (Spearman) è affidabile solo in condizioni restrittive: errori di misura indipendenti e affidabilità note e pertinenti. In presenza di varianza di metodo condivisa o di stime di affidabilità imperfette, tale correzione tende a sovrastimare la correlazione vera;
  3. L’impiego di più indicatori per costrutto e l’incorporazione di un fattore di metodo (o di correlazioni tra unicità) permette al modello latente di distinguere la covarianza attribuibile al tratto da quella spuria, impedendo che quest’ultima contamini la stima della relazione teorica.

Questo passaggio, dalla semplice correzione “algebrica” alla modellazione generativa esplicita del processo di misura, rappresenta un cambiamento epistemologico profondo e non un mero affinamento tecnico. Dichiarare il meccanismo attraverso cui i dati sono generati rende l’inferenza coerente con la natura intrinsecamente rumorosa dei dati psicologici, fornisce distribuzioni posteriori per le pendenze, le correlazioni latenti e le componenti di varianza e consente verifiche predittive (PPC) sullo stesso tipo di statistiche (ad esempio la correlazione tra i compositi) utilizzate nelle analisi tradizionali. Quando è necessario confrontare specifiche alternative, la valutazione predittiva out-of-sample (ad esempio tramite LOO-CV/ELPD) integra i PPC, privilegiando i modelli con maggiore capacità di generalizzazione.

Le implicazioni operative sono chiare. Se le ipotesi forti della teoria classica dei test sono plausibili e l’obiettivo è puramente descrittivo, la correzione di Spearman può costituire un’approssimazione accettabile. Tuttavia, quando la ricerca richiede stime accurate e massima trasparenza – scenario comune in presenza di un metodo comune, di un’affidabilità incerta, di pochi indicatori o predittori misurati con errore – la scelta metodologicamente più solida ricade sul modello di misura bayesiano. Questo approccio restituisce parametri meno distorti, intervalli di credibilità che riflettono l’incertezza in modo genuino e una netta separazione tra varianza di tratto e varianza di misura. Inoltre, la stessa architettura modellistica si estende facilmente a contesti più complessi: errori eteroschedastici, strutture di misura non note (identificate mediante repliche, standard di riferimento o prior informative), indicatori multipli (ponte naturale verso la modellazione SEM), link non Gaussiani e dati mancanti trattati come parametri latenti.

AttenzioneIdentificazione: aspetti cruciali

Con sole due misure per costrutto e parametri d’errore non vincolati, il rischio di confusione tra varianza di tratto e varianza di metodo è elevato. L’identificazione del modello si consolida attraverso:

  1. l’uso di indicatori multipli per ciascun costrutto,
  2. repliche misurazioni o standard di riferimento che informino direttamente l’errore,
  3. prior informative su varianze e caricamenti fattoriali,
  4. verifiche predittive posteriori (PPC) focalizzate su statistiche osservabili cruciali (come la correlazione tra compositi) e, ove necessario, il confronto predittivo tra modelli alternativi.

In sintesi, il capitolo sottolinea una duplice lezione: modellare il processo di misura è tanto necessario quanto modellare le relazioni sostantive di interesse; in psicologia, dove il metodo è parte costitutiva del dato, distinguere chiaramente tra tratto e metodo si conferma la strada maestra per un’inferenza robusta, trasparente e interpretabile.

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] glue_1.8.0            broom_1.0.10          bayestestR_0.17.0    
#>  [4] cmdstanr_0.9.0        lubridate_1.9.4       forcats_1.0.0        
#>  [7] stringr_1.5.2         purrr_1.1.0           readr_2.1.5          
#> [10] tidyverse_2.0.0       pillar_1.11.1         tinytable_0.13.0     
#> [13] patchwork_1.3.2       ggdist_3.3.3          tidybayes_3.0.7      
#> [16] bayesplot_1.14.0      ggplot2_4.0.0         reliabilitydiag_0.2.1
#> [19] priorsense_1.1.1      posterior_1.6.1       loo_2.8.0            
#> [22] rstan_2.32.7          StanHeaders_2.32.10   brms_2.23.0          
#> [25] Rcpp_1.1.0            sessioninfo_1.2.3     conflicted_1.2.0     
#> [28] janitor_2.2.1         matrixStats_1.5.0     modelr_0.1.11        
#> [31] tibble_3.3.0          dplyr_1.1.4           tidyr_1.3.1          
#> [34] rio_1.2.3             here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] gridExtra_2.3         inline_0.3.21         sandwich_3.1-1       
#>  [4] rlang_1.1.6           magrittr_2.0.4        multcomp_1.4-28      
#>  [7] snakecase_0.11.1      compiler_4.5.1        mgcv_1.9-3           
#> [10] reshape2_1.4.4        systemfonts_1.2.3     vctrs_0.6.5          
#> [13] pkgconfig_2.0.3       arrayhelpers_1.1-0    fastmap_1.2.0        
#> [16] backports_1.5.0       labeling_0.4.3        utf8_1.2.6           
#> [19] rmarkdown_2.29        tzdb_0.5.0            ps_1.9.1             
#> [22] ragg_1.5.0            xfun_0.53             cachem_1.1.0         
#> [25] jsonlite_2.0.0        parallel_4.5.1        R6_2.6.1             
#> [28] stringi_1.8.7         RColorBrewer_1.1-3    estimability_1.5.1   
#> [31] knitr_1.50            zoo_1.8-14            pacman_0.5.1         
#> [34] Matrix_1.7-4          splines_4.5.1         timechange_0.3.0     
#> [37] tidyselect_1.2.1      abind_1.4-8           yaml_2.3.10          
#> [40] codetools_0.2-20      processx_3.8.6        curl_7.0.0           
#> [43] pkgbuild_1.4.8        plyr_1.8.9            lattice_0.22-7       
#> [46] withr_3.0.2           bridgesampling_1.1-2  S7_0.2.0             
#> [49] coda_0.19-4.1         evaluate_1.0.5        survival_3.8-3       
#> [52] RcppParallel_5.1.11-1 tensorA_0.36.2.1      checkmate_2.3.3      
#> [55] stats4_4.5.1          insight_1.4.2         distributional_0.5.0 
#> [58] generics_0.1.4        rprojroot_2.1.1       hms_1.1.3            
#> [61] rstantools_2.5.0      scales_1.4.0          xtable_1.8-4         
#> [64] emmeans_1.11.2-8      tools_4.5.1           data.table_1.17.8    
#> [67] mvtnorm_1.3-3         grid_4.5.1            QuickJSR_1.8.0       
#> [70] colorspace_2.1-1      nlme_3.1-168          cli_3.6.5            
#> [73] textshaping_1.0.3     svUnit_1.0.8          Brobdingnag_1.2-9    
#> [76] V8_7.0.0              gtable_0.3.6          digest_0.6.37        
#> [79] TH.data_1.1-4         htmlwidgets_1.6.4     farver_2.1.2         
#> [82] memoise_2.0.1         htmltools_0.5.8.1     lifecycle_1.0.4      
#> [85] MASS_7.3-65

Bibliografia

Carroll, R. J., Ruppert, D., Stefanski, L. A., & Crainiceanu, C. M. (2006). Measurement error in nonlinear models: a modern perspective. Chapman; Hall/CRC.
Lord, F. M., & Novick, M. R. (2008). Statistical theories of mental test scores. IAP.
Podsakoff, P. M., MacKenzie, S. B., Lee, J.-Y., & Podsakoff, N. P. (2003). Common method biases in behavioral research: a critical review of the literature and recommended remedies. Journal of Applied Psychology, 88(5), 879–903.
Podsakoff, P. M., Podsakoff, N. P., Williams, L. J., Huang, C., & Yang, J. (2024). Common method bias: It’s bad, it’s complex, it’s widespread, and it’s not easy to fix. Annual Review of Organizational Psychology and Organizational Behavior, 11(1), 17–61.
Raykov, T., & Marcoulides, G. A. (2011). Introduction to psychometric theory. Routledge.
Spearman, C. (1904). The Proof and Measurement of Association between Two Things. The American Journal of Psychology, 15(1), 72–101.

  1. Nei termini della Teoria Classica dei Test, l’errore standard di misurazione può essere scritto come \(\sigma_{\text{meas}}=\sigma_{x^*}\sqrt{1-r}\) oppure \(\sigma_{\text{meas}}=\sigma_x \sqrt{(1-r)/r}\), dove \(r\) è l’affidabilità.↩︎