3  La quantificazione dell’incertezza

Introduzione

Nel capitolo precedente abbiamo visto perché l’incertezza non è un problema da eliminare, ma una componente essenziale della ricerca psicologica. Abbiamo anche discusso come l’approccio bayesiano, a differenza di quello frequentista, permetta di trattare questa incertezza in modo più coerente e trasparente.

In questo capitolo facciamo un passo avanti: ci chiediamo come l’incertezza possa essere rappresentata e quantificata in pratica. Lo strumento fondamentale per farlo è la distribuzione di probabilità. Una distribuzione non restituisce un numero unico, ma un intero ventaglio di valori possibili, ciascuno associato a un grado di plausibilità. È questo che ci permette di descrivere in modo formale quanto siamo incerti riguardo a un parametro o a un’ipotesi.

Vedremo quindi come funziona l’aggiornamento bayesiano: partiremo da ciò che sappiamo prima dei dati (prior), incorporeremo l’evidenza empirica (verosimiglianza) e otterremo una nuova rappresentazione delle nostre credenze (posterior). Questo processo è dinamico e mai concluso: ogni nuovo dato modifica la distribuzione, permettendoci di accumulare conoscenza in modo coerente.

Il nostro obiettivo in questo capitolo è duplice:

1. introdurre i concetti di distribuzione e aggiornamento bayesiano in forma semplice e intuitiva;
   
2. mostrarne il funzionamento con un esempio classico e intuitivo (il globo terrestre), arricchito da riflessioni su cosa questo significhi per la ricerca psicologica.

In questo modo, passeremo dal piano concettuale a quello operativo, ponendo le basi per i capitoli successivi, dove useremo questi strumenti in contesti più complessi.

NotaIntuizione

Il pensiero bayesiano non elimina il dubbio, ma ci permette di trattarlo in modo sistematico: i dati non sostituiscono le nostre ipotesi, ma le trasformano.

Panoramica del capitolo

• Come quantificare e rappresentare matematicamente l’incertezza attraverso le distribuzioni di densità.
• Il processo di integrazione delle nuove evidenze con le conoscenze preesistenti.
• Come i parametri sconosciuti determinano i dati osservati attraverso processi probabilistici.

ConsiglioPrerequisiti

• Leggere Bayesian statistics for clinical research di Goligher et al. (2024).
• Leggere Dicing with the unknown di Tony O’Hagan, per una descrizione chiara della distinzione tra incertezza aleatoria e incertezza epistemica.
• Leggere il capitolo Estimation (Schervish & DeGroot, 2014).

AttenzionePreparazione del Notebook

here::here("code", "_common.R") |> 
  source()

3.1 Distribuzioni di probabilità

Per rappresentare l’incertezza in modo quantitativo ci serve uno strumento che mostri non solo un valore “tipico”, ma anche tutti i valori alternativi che consideriamo possibili. Questo strumento è la distribuzione di probabilità.

Una distribuzione ci dice due cose fondamentali:

1. quali valori sono possibili per un certo fenomeno;
2. quanto ciascun valore è plausibile alla luce delle nostre conoscenze.

3.1.1 Un esempio psicologico

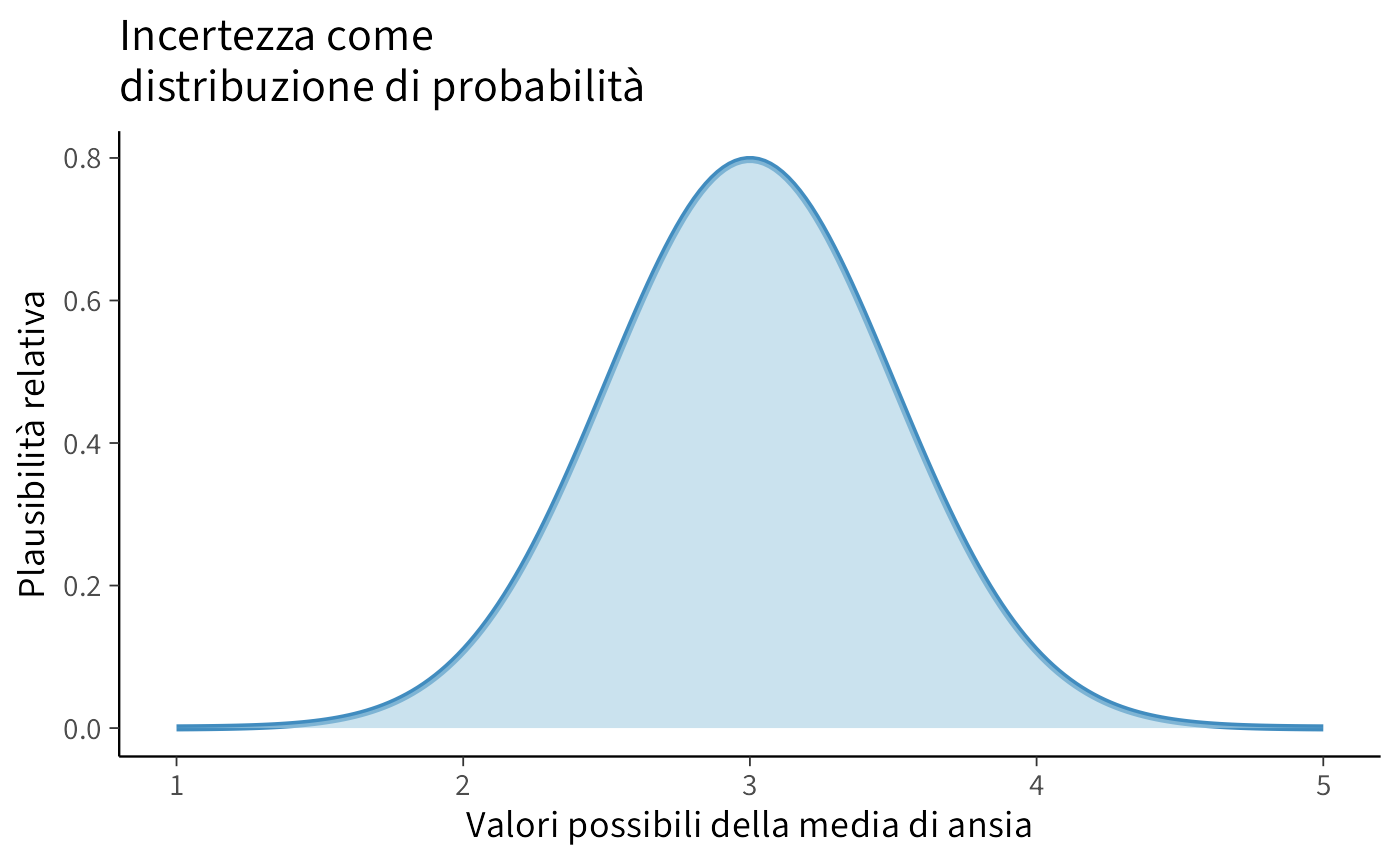
Supponiamo di misurare il livello di ansia in un gruppo di studenti prima di un esame. I punteggi non saranno tutti uguali: alcuni studenti avranno valori bassi, altri molto alti, la maggior parte sarà in una zona intermedia. Invece di limitarsi a dire “il livello medio è 20”, una distribuzione ci permette di descrivere l’intero profilo di variabilità: quali valori sono più frequenti, quali sono rari e quali estremi sono comunque possibili.

In psicologia, quasi tutti i fenomeni che studiamo — dall’autostima alle prestazioni cognitive — possono essere rappresentati meglio con una distribuzione piuttosto che con un singolo numero.

E già qui si intravede la logica bayesiana: se, ad esempio, stiamo stimando l’efficacia di una terapia cognitivo-comportamentale, non ci basta sapere che l’effetto medio stimato è 0.3. Ci interessa sapere quali altri valori dell’effetto rimangono plausibili e con quale grado di fiducia.

3.1.2 Distribuzioni discrete e continue

Esistono due grandi famiglie di distribuzioni:

• Discrete, quando i valori possibili sono separati e contabili.
  • Esempio classico: il lancio di una moneta (testa o croce) o di un dado (sei possibili esiti).
    
  • In psicologia: il numero di risposte corrette in un test a scelta multipla.
• Continue, quando i valori possibili formano un intervallo continuo.
  • Esempio classico: l’altezza di una persona o il tempo di reazione in millisecondi.
    
  • In psicologia: il livello di ansia misurato con una scala continua, la durata dell’attenzione in un compito sperimentale.

3.1.3 Perché le distribuzioni sono fondamentali

La potenza delle distribuzioni sta nel fatto che non riducono la realtà a un singolo numero, ma ci mostrano tutta la gamma di possibilità insieme al grado di plausibilità di ciascuna. In questo modo, l’incertezza diventa parte integrante della descrizione del fenomeno.

Nei prossimi paragrafi vedremo come le distribuzioni non siano solo uno strumento descrittivo, ma diventino il cuore dell’aggiornamento bayesiano: collegano ciò che sappiamo prima dei dati (prior), le nuove osservazioni (verosimiglianza) e le credenze aggiornate (posterior).

NotaMessaggio chiave

Rappresentare l’incertezza come distribuzione di probabilità significa passare da una visione rigida (“il valore è uno solo”) a una prospettiva più realistica e informativa (“alcuni valori sono più plausibili di altri”).

Figura 3.1: Rappresentare l’incertezza sulla media dell’ansia come distribuzione di probabilità.

3.2 L’aggiornamento bayesiano

Il cuore dell’approccio bayesiano è il teorema di Bayes, che descrive come aggiornare in modo coerente le nostre convinzioni alla luce dei dati. L’idea è semplice: partiamo da ciò che sappiamo prima dei dati (prior), osserviamo nuove evidenze (verosimiglianza) e otteniamo credenze aggiornate (posterior).

Formalmente:

\[ P(\text{ipotesi | dati}) \;=\; \frac{P(\text{dati | ipotesi}) \; P(\text{ipotesi})}{P(\text{dati})}, \]

• Posterior, \(P(\text{ipotesi | dati})\): la probabilità aggiornata dell’ipotesi, dopo aver visto i dati.
  
• Likelihood (verosimiglianza), \(P(\text{dati | ipotesi})\): quanto i dati sono compatibili con l’ipotesi.
  
• Prior, \(P(\text{ipotesi})\): le nostre convinzioni prima di osservare i dati.
  
• Evidenza, \(P(\text{dati})\): una costante di normalizzazione che assicura che le probabilità sommino a 1.

3.2.1 Perché l’aggiornamento è dinamico

Una delle intuizioni più potenti dell’approccio bayesiano è che l’aggiornamento delle nostre conoscenze non è mai definitivo: ogni nuovo dato contribuisce a ridefinire la distribuzione delle nostre credenze. La conoscenza scientifica non si “chiude” mai una volta per tutte, ma rimane sempre aperta a revisioni.

3.2.1.1 Messaggio chiave

L’aggiornamento bayesiano è cumulativo e dinamico: non produce verdetti, ma posterior sempre più informative man mano che i dati aumentano.

3.3 L’esempio del globo terrestre

Per capire in modo concreto come funziona l’aggiornamento bayesiano, consideriamo l’esempio del globo terrestre discusso da Richard McElreath nel suo Statistical Rethinking (McElreath, 2020). Immaginiamo di avere un globo coperto da due colori: blu per il mare, marrone per la terra. Senza guardare, lo giriamo e puntiamo un dito su una posizione casuale. Vogliamo stimare la proporzione di superficie terrestre che è blu (cioè la proporzione del globo ricoperta dall’acqua).

3.3.1 L’accumulo dell’evidenza

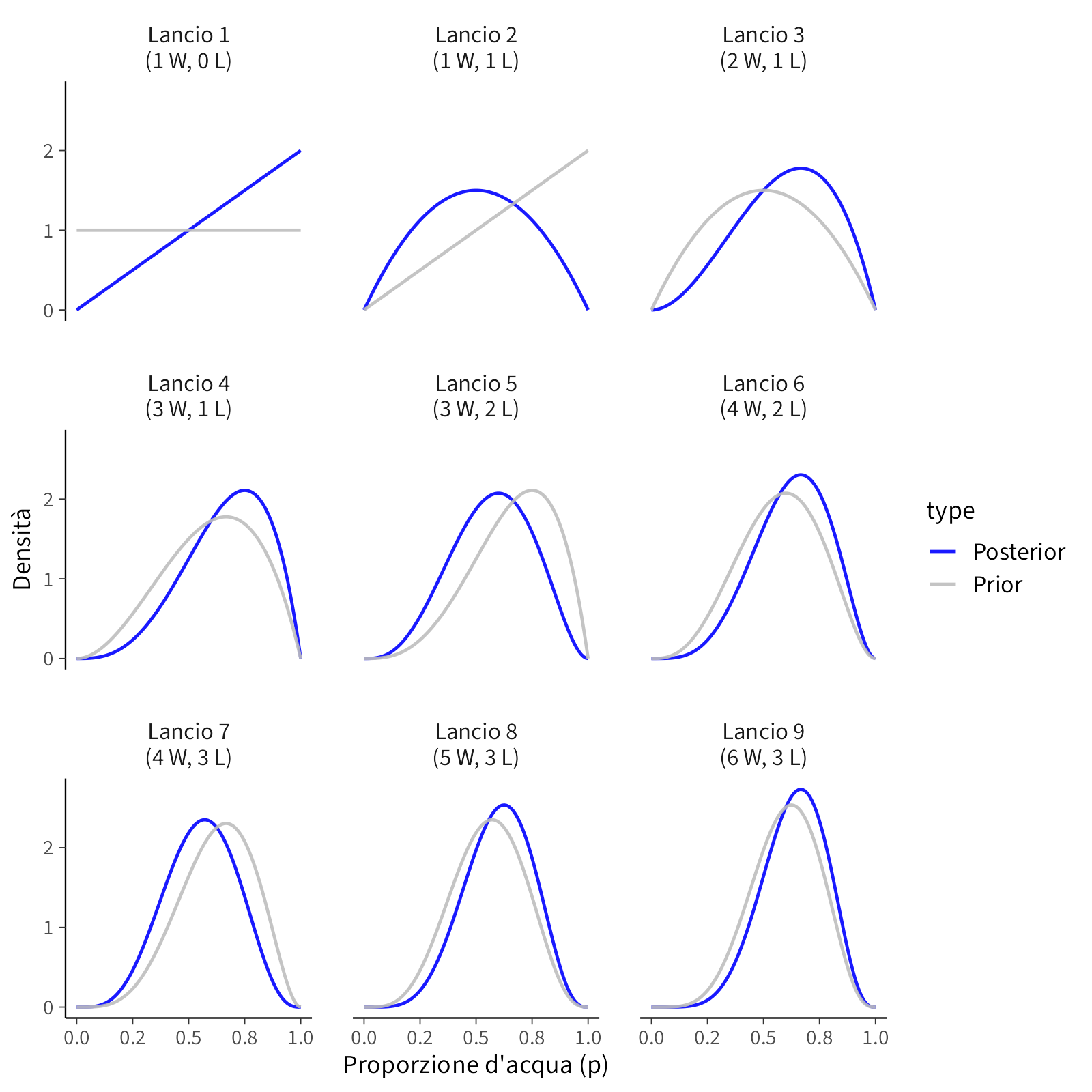
Consideriamo la sequenza: W, L, W, W, L, W, L, W, W, dove W indica acqua (water) e L terra (land). Dopo ogni nuova osservazione, la distribuzione delle plausibilità sui valori di \(p\) — la proporzione di oceano sulla superficie del globo — viene aggiornata.

• Prima della prima osservazione. Non abbiamo alcuna informazione. Tutti i valori di \(p\), da 0 a 1, sono considerati ugualmente plausibili. La distribuzione iniziale (prior) è piatta: ogni ipotesi ha lo stesso peso. È come dire: qualsiasi proporzione di oceano è per ora concepibile.

• Dopo la prima osservazione (W). Puntiamo il dito e tocchiamo acqua. A questo punto sappiamo che \(p = 0\) è impossibile: il globo non può essere interamente terra, perché abbiamo osservato almeno una goccia d’acqua. La plausibilità dei valori alti di \(p\) (vicini a 1) cresce. La linea continua nel primo pannello mostra questa nuova distribuzione (posterior), mentre la linea tratteggiata rappresenta la distribuzione precedente (prior). In altre parole: le ipotesi che prevedono “tutto terra” sono escluse, quelle che prevedono “quasi tutto oceano” diventano più plausibili.

• Dopo la seconda osservazione (L). Tocchiamo terra. Ora sappiamo che anche \(p = 1\) è impossibile: non può trattarsi di un globo interamente coperto d’acqua. La plausibilità si concentra quindi su valori intermedi, perché ora abbiamo evidenza sia di oceano che di terra. Nel grafico, la linea continua riflette questa nuova credenza aggiornata. Rispetto alla prima osservazione, la distribuzione si è riallineata: non privilegia più solo i valori alti di \(p\), ma si sposta verso ipotesi che tengano conto di entrambe le evidenze.

• Dopo la terza osservazione (W). Tocchiamo di nuovo acqua. Questo spinge la curva nuovamente verso destra, in direzione di valori più alti di \(p\). Notiamo un aspetto importante: non stiamo semplicemente “contando” acqua e terra, ma traducendo queste osservazioni in un profilo di plausibilità che tiene insieme tutte le informazioni disponibili. Ogni osservazione contribuisce, ma nessuna singola osservazione domina: il modello “pesa” coerentemente l’insieme dei dati raccolti fino a quel momento.

• Proseguendo con le osservazioni. Ogni nuovo dato modifica le plausibilità: un’osservazione di acqua spinge la curva verso destra (valori alti di \(p\)), un’osservazione di terra la spinge verso sinistra (valori bassi). Con l’accumularsi delle evidenze, la curva diventa più alta e più stretta: meno valori di \(p\) rimangono compatibili con i dati, e la nostra conoscenza si affina. Ciò che prima era “ampiamente possibile” diventa ora “altamente improbabile”.

NotaIteratività

Ogni posterior diventa il prior del passo successivo. L’apprendimento bayesiano è un processo iterativo, non un verdetto finale.

3.3.2 Il significato

Ogni nuova osservazione raffina la credenza: la posterior si restringe progressivamente (senza mai annullare del tutto l’incertezza). La distribuzione evolve non solo in posizione (quali valori di \(p\) sono più plausibili), ma anche in forma (quanto stretta o larga è l’incertezza intorno a quei valori).

• Con pochi dati, la distribuzione è larga e riflette molta incertezza.
• Con più osservazioni, la distribuzione diventa più stretta: la conoscenza si affina.
• La velocità del restringimento dipende dai dati: sequenze molto coerenti riducono rapidamente l’incertezza, mentre sequenze contrastanti la riducono più lentamente.

In altre parole: l’incertezza non viene eliminata, ma organizzata e ridotta progressivamente grazie all’accumulo dell’evidenza.

Figura 3.2: Aggiornamento bayesiano della distribuzione di plausibilità della proporzione di oceano (\(p\)) sul globo terrestre. In ciascun pannello, la linea grigia rappresenta la distribuzione a priori prima di osservare il dato, mentre la linea blu rappresenta la distribuzione a posteriori dopo l’osservazione. Ogni nuovo lancio (W = acqua, L = terra) modifica la distribuzione: alcune ipotesi diventano impossibili (es. p=0 dopo il primo W), altre perdono plausibilità, altre ancora la guadagnano. La curva si restringe progressivamente: la nostra incertezza si riduce, senza mai scomparire del tutto.

3.3.3 Come leggere il grafico (e perché ci deve interessare in psicologia)

In ogni pannello, la linea tratteggiata rappresenta ciò che ritenevamo plausibile prima del nuovo dato (prior), mentre la linea continua rappresenta la distribuzione aggiornata (posterior). Il punto non è “indovinare un numero”, ma ridistribuire la plausibilità sui valori coerenti con i dati. Due aspetti chiave:

1. Direzione: un “W” sposta massa di plausibilità verso valori più alti, un “L” verso valori più bassi.
2. Forma (ampiezza): con l’aumentare dei dati, la curva si stringe, ovvero diminuisce il numero di valori compatibili e l’incertezza si riduce.

La stessa logica viene utilizzata in psicologia quando si passa da ipotesi teoriche generali a stime più circoscritte, man mano che si accumulano studi, repliche e dati di migliore qualità.

3.3.3.1 Dalla sfera terrestre ai problemi psicologici (tre mappe mentali)

• Prevalenza/parametri di popolazione. Stimare la prevalenza di un comportamento a rischio tra gli studenti è analogo a stimare \(p\) sul globo: ogni nuova rilevazione (studente che presenta/non presenta il comportamento) aggiorna la distribuzione della prevalenza effettiva. Con pochi questionari, la distribuzione è larga; con campioni più grandi o campioni stratificati, invece, si stringe.

• Effetto di un intervento. Valutare l’effetto medio di un training DBT sulle scale di disregolazione emotiva funziona allo stesso modo: il prior può incorporare l’evidenza pregressa (ad esempio, una meta-analisi), la verosimiglianza deriva dal modello di misura (affidabilità, errori, missing), e la posterior concentra plausibilità intorno agli effetti compatibili con i dati dello studio. Ogni nuova coorte/studio aggiorna ulteriormente la stima.

• Modelli meccanicistici (es. apprendimento). Nei compiti di reinforcement learning, il parametro di interesse (es. tasso di apprendimento \(\alpha\)) si aggiorna man mano che si osservano scelte e feedback. Sequenze coerenti (feedback consistenti) “spingono” la plausibilità verso regioni più strette, mentre sequenze rumorose mantengono la distribuzione più larga. Si tratta della stessa dinamica vista con \(p\), solo applicata a un parametro psicologico.

Buone pratiche di lettura (e modellazione)

• Il prior è un modello esplicito. In psicologia spesso disponiamo di una letteratura pregressa: utilizzare queste conoscenze come prior rende trasparenti le ipotesi di partenza e chiarisce che non partiamo mai “da zero”.¹
• La verosimiglianza descrive il modo in cui i dati vengono prodotti. Qui entrano in gioco l’affidabilità degli strumenti, gli errori di misura e la struttura dei dati (soggetti, sessioni, item). Ignorare questi aspetti significa distorcere l’inferenza.
• L’ordine dei dati non conta. Che i dati vengano analizzati uno per volta o tutti insieme, il risultato finale è lo stesso: ciò riflette la coerenza del metodo bayesiano e il concetto di scambiabilità.²
• Conta la forma della distribuzione, non solo il picco. Una curva molto stretta e centrata è più informativa di una curva larga, anche se entrambe hanno lo stesso massimo. Guardare soltanto al valore più alto rischia di far perdere l’informazione sull’incertezza residua.³
• L’informazione è cumulativa. Ogni nuova analisi non cancella quanto già sapevamo, ma lo aggiorna. In questo senso la ricerca psicologica procede come un processo di apprendimento collettivo: ogni studio diventa la base su cui costruire il successivo.

In sintesi, leggere i pannelli dell’esempio del globo significa allenarsi a leggere qualsiasi grafico bayesiano in psicologia. Il punto cruciale non è individuare “il numero giusto”, ma comprendere “come si ridistribuisce la plausibilità quando le evidenze cambiano, date le nostre assunzioni sulla misurazione e il modello”.

NotaPosterior diverse a confronto

Lo stesso insieme di dati può produrre distribuzioni differenti a seconda del prior. Questo non è un difetto, ma un punto di forza: rende esplicite le assunzioni e permette di discutere la loro influenza con analisi di sensibilità.

NotaApprofondimento: il modello Beta-Binomiale

Nel testo precedente abbiamo visto che ogni nuova osservazione del globo terrestre aggiorna le nostre credenze sulla proporzione di oceano presente sul pianeta. Lo stesso processo può essere descritto in modo molto elegante attraverso il modello Beta-Binomiale.

Struttura del modello.

• La nostra incertezza iniziale sulla proporzione \(p\) di oceano è descritta da una distribuzione Beta con parametri \((a,b)\).
  
• Le osservazioni (successi/insuccessi: acqua o terra) seguono una Binomiale con parametro \(p\).
  
• Grazie alla proprietà di coniugazione, anche la distribuzione a posteriori resta una Beta, con parametri aggiornati in modo semplice.

La regola generale è:

\[ p \mid \text{dati} \;\sim\; \text{Beta}(a + W, \; b + L), \] dove:

• \(a\) e \(b\) sono i parametri della prior (nell’esempio \(a=b=1\), cioè una prior uniforme),
  
• \(W\) è il numero di osservazioni acqua (Water),
  
• \(L\) è il numero di osservazioni terra (Land).

In altre parole, \(a\) e \(b\) possono essere visti come successi e insuccessi immaginari che portiamo nel modello come conoscenza iniziale.

Aggiornamento passo per passo.

Ecco come la distribuzione si evolve con la sequenza osservata (W, L, W, W, L, W, L, W, W):

• Dopo 1 osservazione (W): \(\text{Beta}(2,1)\) → la curva si sposta verso valori alti di \(p\).
  
• Dopo 2 osservazioni (W,L): \(\text{Beta}(2,2)\) → si riequilibra, rendendo plausibili valori intermedi.
  
• Dopo 5 osservazioni (3W,2L): \(\text{Beta}(4,3)\) → la distribuzione si concentra intorno a \(p \approx 0.57\).
  
• Dopo 9 osservazioni (6W,3L): \(\text{Beta}(7,4)\) → la distribuzione diventa più stretta, con incertezza ridotta.

Sintesi.

Il modello Beta-Binomiale ci mostra come il Bayes renda l’apprendimento cumulativo e coerente:

• ogni nuovo dato aggiorna la distribuzione,
  
• l’incertezza si riduce progressivamente,
  
• la stima si concentra intorno ai valori più compatibili con l’evidenza.

Questo semplice esempio è il prototipo di tanti altri modelli bayesiani: anche in contesti psicologici complessi, l’idea di base rimane la stessa.

Riflessioni conclusive

In questo capitolo abbiamo compiuto il primo ingresso operativo nel pensiero bayesiano. Abbiamo visto come l’incertezza possa essere rappresentata da distribuzioni di probabilità e come il teorema di Bayes colleghi in modo coerente convinzioni iniziali, dati osservati e convinzioni aggiornate. L’esempio del globo terrestre ha reso tangibile questa dinamica: ogni osservazione sposta o restringe la distribuzione su \(p\), mostrando che l’apprendimento è progressivo e cumulativo.

Per la ricerca psicologica, ciò significa tre cose fondamentali:

1. i dati non producono certezze, ma affinano gradualmente le ipotesi;
2. ogni studio è un contributo a un processo cumulativo;
3. l’incertezza diventa una risorsa esplicita, non un problema da nascondere.

Come ogni osservazione restringe le ipotesi plausibili sulla proporzione di oceano sulla superficie terrestre, così in psicologia ogni nuovo dato restringe l’incertezza sulle nostre teorie e modelli, senza però azzerarla.

Da qui discendono alcune conseguenze pratiche. Il lavoro dell’analista non si esaurisce nel “trovare un numero”, ma consiste nel modellare con cura il problema, rendere esplicite le assunzioni e valutarne l’impatto. Scelta dei prior, oneri computazionali, interpretazione dei risultati e qualità del modello sono aspetti che accompagnano inevitabilmente l’applicazione concreta dei metodi bayesiani.

Il messaggio centrale è chiaro: l’approccio bayesiano non elimina l’incertezza, ma invece la organizza. Invece di nasconderla dietro esiti dicotomici, la rende visibile e misurabile, permettendo di comunicare quali valori dei parametri siano plausibili e con quale grado di fiducia.

Nei capitoli successivi tradurremo queste idee in pratica, costruendo modelli bayesiani via via più ricchi e applicandoli a contesti psicologici reali. L’obiettivo non è cercare una “certezza definitiva”, ma sviluppare l’abitudine a ragionare in termini di plausibilità e apprendimento continuo dai dati.

NotaInformazioni sull’ambiente di sviluppo

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] pillar_1.11.1         tinytable_0.13.0      patchwork_1.3.2      
#>  [4] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.14.0     
#>  [7] ggplot2_4.0.0         reliabilitydiag_0.2.1 priorsense_1.1.1     
#> [10] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [13] StanHeaders_2.32.10   brms_2.23.0           Rcpp_1.1.0           
#> [16] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [19] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [22] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [25] here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] svUnit_1.0.8          tidyselect_1.2.1      farver_2.1.2         
#>  [4] S7_0.2.0              fastmap_1.2.0         TH.data_1.1-4        
#>  [7] tensorA_0.36.2.1      digest_0.6.37         timechange_0.3.0     
#> [10] estimability_1.5.1    lifecycle_1.0.4       survival_3.8-3       
#> [13] magrittr_2.0.4        compiler_4.5.1        rlang_1.1.6          
#> [16] tools_4.5.1           yaml_2.3.10           knitr_1.50           
#> [19] labeling_0.4.3        bridgesampling_1.1-2  htmlwidgets_1.6.4    
#> [22] curl_7.0.0            pkgbuild_1.4.8        RColorBrewer_1.1-3   
#> [25] abind_1.4-8           multcomp_1.4-28       withr_3.0.2          
#> [28] purrr_1.1.0           grid_4.5.1            stats4_4.5.1         
#> [31] colorspace_2.1-2      xtable_1.8-4          inline_0.3.21        
#> [34] emmeans_1.11.2-8      scales_1.4.0          MASS_7.3-65          
#> [37] cli_3.6.5             mvtnorm_1.3-3         rmarkdown_2.29       
#> [40] ragg_1.5.0            generics_0.1.4        RcppParallel_5.1.11-1
#> [43] cachem_1.1.0          stringr_1.5.2         splines_4.5.1        
#> [46] parallel_4.5.1        vctrs_0.6.5           V8_7.0.0             
#> [49] Matrix_1.7-4          sandwich_3.1-1        jsonlite_2.0.0       
#> [52] arrayhelpers_1.1-0    systemfonts_1.2.3     glue_1.8.0           
#> [55] codetools_0.2-20      distributional_0.5.0  lubridate_1.9.4      
#> [58] stringi_1.8.7         gtable_0.3.6          QuickJSR_1.8.1       
#> [61] htmltools_0.5.8.1     Brobdingnag_1.2-9     R6_2.6.1             
#> [64] textshaping_1.0.3     rprojroot_2.1.1       evaluate_1.0.5       
#> [67] lattice_0.22-7        backports_1.5.0       memoise_2.0.1        
#> [70] broom_1.0.10          snakecase_0.11.1      rstantools_2.5.0     
#> [73] gridExtra_2.3         coda_0.19-4.1         nlme_3.1-168         
#> [76] checkmate_2.3.3       xfun_0.53             zoo_1.8-14           
#> [79] pkgconfig_2.0.3

Bibliografia

Goligher, E. C., Heath, A., & Harhay, M. O. (2024). Bayesian statistics for clinical research. The Lancet, 404(10457), 1067–1076. https://doi.org/10.1016/S0140-6736(24)00055-9

McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan (2nd Edition). CRC Press.

Schervish, M. J., & DeGroot, M. H. (2014). Probability and statistics (Vol. 563). Pearson Education London, UK:

---

1. Il tema delle analisi di sensibilità verrà trattato in seguito, quando discuteremo come valutare l’influenza del prior sui risultati.

2. L’assunzione di scambiabilità implica che la distribuzione dei dati sia invariante rispetto all’ordine in cui vengono osservati.

3. Più avanti introdurremo strumenti come gli intervalli credibili e la distribuzione predittiva a posteriori, che aiutano a interpretare la forma della distribuzione.