Test t di Student per campioni indipendenti#
In questo capitolo, esamineremo il test \(t\) di Student per campioni indipendenti, uno dei test statistici frequentisti più ampiamente utilizzati nella pratica.
Preparazione del Notebook#
import numpy as np
import pandas as pd
import scipy.stats as stats
from scipy.stats import gaussian_kde
import matplotlib.pyplot as plt
from scipy.stats import t
from scipy.stats import ttest_ind
import arviz as az
import seaborn as sns
import itertools
import pingouin as pg
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
sns.set_theme(palette="colorblind")
Applicazioni del Test t di Student#
Il test t di Student per due campioni indipendenti è un metodo statistico utilizzato per determinare se le medie di due campioni indipendenti sono significativamente diverse. Questo test si applica quando i due campioni sono estratti da popolazioni diverse e non vi è alcuna correlazione tra le osservazioni di un campione e quelle dell’altro.
Per condurre il test t di Student per due campioni indipendenti, calcoliamo la differenza tra le medie dei due campioni e le stime delle varianze campionarie delle rispettive popolazioni. L’ipotesi nulla del test è che le medie dei due campioni siano uguali, mentre l’ipotesi alternativa a due code è che le medie dei due campioni siano diverse. La statistica del test t viene calcolata come il rapporto tra la differenza delle medie campionarie e la deviazione standard media campionaria.
Successivamente, confrontiamo la statistica t con la distribuzione t di Student con \(n_1 + n_2 - 2\) gradi di libertà, dove \(n_1\) e \(n_2\) sono le dimensioni dei due campioni. Calcoliamo quindi il valore-p dalla distribuzione t per determinare la significatività del test.
Esistono due approcci per stimare la varianza. Se assumiamo che le due popolazioni abbiano la stessa varianza (omoschedasticità), utilizziamo una stima pooled della varianza. Questo metodo è considerato efficiente quando l’omoschedasticità è verificata. Invece, se supponiamo che le due popolazioni abbiano varianze diverse, utilizziamo due stime separate delle varianze per i due campioni, chiamato test di Welch. Questo approccio è più robusto quando le varianze dei due gruppi sono significativamente diverse.
Le principali assunzioni del test t di Student per due campioni indipendenti sono l’indipendenza dei due campioni e la normalità della distribuzione delle popolazioni da cui sono stati estratti i campioni.
Di seguito è riportato il calcolo della stima della deviazione standard pooled, utilizzata per standardizzare la differenza tra le medie dei due campioni quando l’assunzione di omoschedasticità è verificata:
dove \(s_p\) è la deviazione standard pooled, \(n_0\) e \(n_1\) sono le dimensioni dei due campioni, \(s^2_0\) e \(s^2_1\) sono le varianze campionarie dei due gruppi.
La statistica del test t è quindi calcolata come:
dove \(\bar{x}_0\) e \(\bar{x}_1\) sono le medie campionarie dei due gruppi.
Esaminiamo un esempio concreto. Supponiamo di disporre di nove misure del peso per un gruppo di donne e di nove misure di peso per un gruppo di uomini. Ci chiediamo se, nella popolazione, la media del peso dei due gruppi sia diversa.
Creiamo due array con i dati e li inseriamo in un DataFrame.
women_weight = np.array([38.9, 61.2, 73.3, 21.8, 63.4, 64.6, 48.4, 48.8, 48.5])
men_weight = np.array([67.8, 60, 63.4, 76, 89.4, 73.3, 67.3, 61.3, 62.4])
weight = np.concatenate((women_weight, men_weight))
print(weight)
[38.9 61.2 73.3 21.8 63.4 64.6 48.4 48.8 48.5 67.8 60. 63.4 76. 89.4
73.3 67.3 61.3 62.4]
Creaiamo una variabile che specifica l’appartenenza al gruppo.
is_female = np.repeat([1, 0], 9)
is_female
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
df = pd.DataFrame({"is_female": is_female, "weight": weight})
df
| is_female | weight | |
|---|---|---|
| 0 | 1 | 38.9 |
| 1 | 1 | 61.2 |
| 2 | 1 | 73.3 |
| 3 | 1 | 21.8 |
| 4 | 1 | 63.4 |
| 5 | 1 | 64.6 |
| 6 | 1 | 48.4 |
| 7 | 1 | 48.8 |
| 8 | 1 | 48.5 |
| 9 | 0 | 67.8 |
| 10 | 0 | 60.0 |
| 11 | 0 | 63.4 |
| 12 | 0 | 76.0 |
| 13 | 0 | 89.4 |
| 14 | 0 | 73.3 |
| 15 | 0 | 67.3 |
| 16 | 0 | 61.3 |
| 17 | 0 | 62.4 |
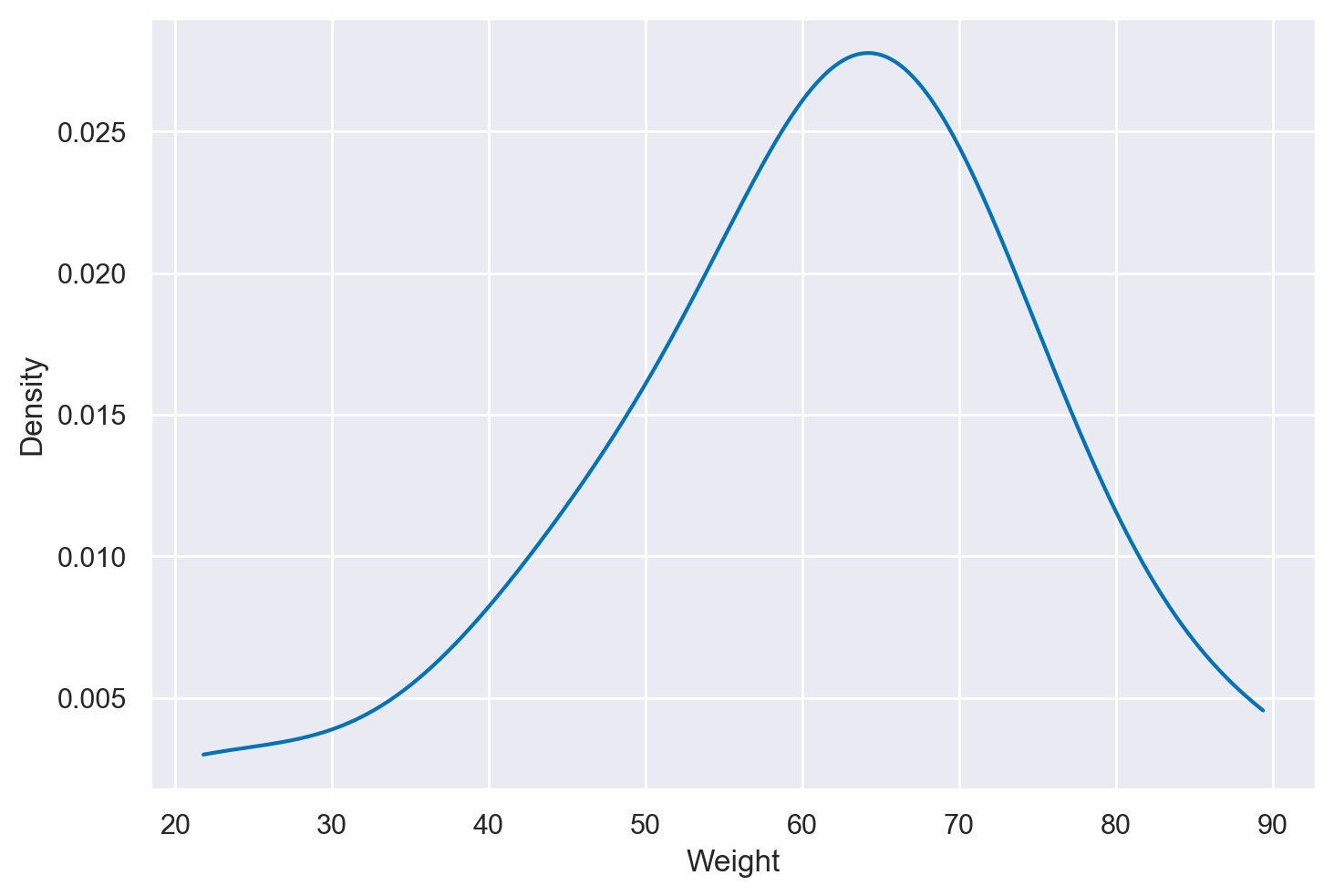
Qui sotto è riportato un KDE plot per i dati di tutto il campione.
density = gaussian_kde(df["weight"])
x_vals = np.linspace(min(df["weight"]), max(df["weight"]), 1000)
density = density.evaluate(x_vals)
plt.plot(x_vals, density)
plt.xlabel('Weight')
_ = plt.ylabel('Density')
/Users/corrado/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/outdated/utils.py:14: OutdatedPackageWarning: The package pingouin is out of date. Your version is 0.5.3, the latest is 0.5.4.
Set the environment variable OUTDATED_IGNORE=1 to disable these warnings.
return warn(
Dal DataFrame estraiamo due array contenenti i valori dei pesi dei due gruppi.
weight_f = df.loc[df["is_female"] == 1, "weight"]
weight_m = df.loc[df["is_female"] == 0, "weight"]
Calcoliamo la deviazione standard pooled.
s_pool_num = np.sum(
[
(len(weight_f) - 1) * np.std(weight_f, ddof=1) ** 2,
(len(weight_m) - 1) * np.std(weight_m, ddof=1) ** 2,
]
)
s_pool_denom = len(weight_f) + len(weight_m) - 2
s_pool = np.sqrt(np.divide(s_pool_num, s_pool_denom))
s_pool
12.86771368796942
Calcoliamo la statistica test.
t_num = np.mean(weight_f) - np.mean(weight_m)
t_denom = s_pool * np.sqrt(1 / len(weight_f) + 1 / len(weight_m))
T = np.divide(t_num, t_denom)
T
-2.7842353699254567
I gradi di libertà sono:
len(weight_f) + len(weight_m) - 2
16
Il valore-p è uguale a
stats.t.cdf(T, df=16) * 2
0.013265602643801042
Rifacciamo ora i calcoli usando la funzione ttest del pacchatto pingouin. L’argomento paired = False specifica che i due campioni sono indipendenti; l’argomento correction=False specifica che non verrà usata la correzione di Welch per varianze separate.
res = pg.ttest(weight_m, weight_f, paired=False, correction=False)
print(res)
T dof alternative p-val CI95% cohen-d BF10 \
T-test 2.784235 16 two-sided 0.013266 [4.03, 29.75] 1.312501 4.251
power
T-test 0.743519
Il risultato conferma quanto trovato in precedenza attraverso i calcoli effettuati. Il valore-\(p\) indica che possiamo rifiutare l’ipotesi nulla di uguaglianza delle medie delle due popolazioni. Quindi, possiamo concludere con un livello di confidenza del 95% che la media del peso dei maschi nella popolazione è superiore alla media del peso delle femmine nella popolazione.
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Fri Jan 26 2024
Python implementation: CPython
Python version : 3.11.7
IPython version : 8.19.0
arviz : 0.17.0
pandas : 2.1.4
seaborn : 0.13.0
scipy : 1.11.4
pingouin : 0.5.3
matplotlib: 3.8.2
numpy : 1.26.2
Watermark: 2.4.3

