Entropia#
In questo capitolo, esploreremo il concetto di entropia, sottolineando il suo ruolo fondamentale nel processo di quantificazione dell’incertezza all’interno delle distribuzioni di probabilità. Inoltre, affronteremo il tema cruciale di come l’entropia possa essere utilizzata per valutare la “distanza” tra un modello teorico e i dati osservati. A tale scopo, introdurremo la divergenza di Kullback-Leibler (KL), una misura che non solo misura le discrepanze tra due distribuzioni probabilistiche, ma offre anche una prospettiva approfondita sulla valutazione della concordanza tra teoria e realtà empirica.
Preparazione del Notebook#
import numpy as np
import pandas as pd
import scipy as sp
import scipy.stats as stats
import statsmodels.api as sm
from statsmodels.graphics import tsaplots
import matplotlib.pyplot as plt
import seaborn as sns
import arviz as az
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=Warning)
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
Generalizzabilità dei modelli e fondamenti del metodo scientifico#
Nella scienza, la generalizzabilità dei modelli rappresenta un aspetto fondamentale, essendo uno dei pilastri del metodo scientifico. La capacità di un modello di estendersi oltre il contesto specifico in cui è stato testato ne determina il valore scientifico. In questo contesto, la replicabilità emerge come un prerequisito essenziale, ma non sufficiente, poiché un modello può essere replicabile eppure non generalizzabile.
Per valutare la robustezza di un modello, è importante porsi tre domande fondamentali [JOD22]: Quali sono le implicazioni delle nostre inferenze? Le assunzioni del modello sono valide? E quanto accuratamente può fare previsioni? Quest’ultima domanda è cruciale per la generalizzabilità, evidenziando l’importanza di modelli che possano fare previsioni accurate su nuovi dati.
Creare modelli che evitino le insidie del sovra-adattamento e del sotto-adattamento è una sfida significativa [McE20]. Il sovra-adattamento si verifica quando un modello è troppo specifico, mentre il sotto-adattamento accade quando è troppo generico. L’approccio bayesiano offre una soluzione elegante a questo problema, concentrando l’attenzione sulla capacità predittiva del modello.
La selezione dei modelli deve bilanciare la semplicità con la precisione. Principi come il rasoio di Ockham suggeriscono di favorire la semplicità, ma senza compromettere la capacità del modello di descrivere accuratamente i dati. I test di ipotesi, sebbene critici per la loro enfasi sui valori-p, rimangono strumenti comuni, ma devono essere impiegati con cautela.
Un aspetto cruciale nella selezione del modello è la misurazione obiettiva della sua aderenza al “vero” processo generativo dei dati. In questo contesto, la divergenza di Kullback-Leibler si rivela come uno strumento efficace, misurando la “vicinanza” di un modello alla distribuzione sottostante dei dati. Tuttavia, per comprendere a fondo la divergenza di Kullback-Leibler, è fondamentale introdurre il concetto di entropia, che rappresenta l’incertezza o la sorpresa associata all’osservazione di un evento. L’entropia, così come la divergenza di Kullback-Leibler, fornisce una misura quantitativa per valutare quanto bene un modello approssima la distribuzione dei dati, sia in termini di famiglia di distribuzioni che di specifici parametri che le caratterizzano.
Entropia: Una Misura dell’Incertezza#
Nel campo dell’informatica e della teoria delle probabilità, il concetto di entropia, sviluppato da Claude Shannon durante il suo lavoro presso i Bell Labs, gioca un ruolo cruciale nel misurare l’incertezza o la “sorpresa” associata all’osservazione di un evento. Nella creazione di una metrica per misurare questa incertezza, Shannon propose tre requisiti intuitivi: continuità, aumento con la lunghezza del messaggio e additività. Questi criteri sono univocamente soddisfatti dalla cosiddetta entropia dell’informazione.
L’entropia dell’informazione di Shannon quantifica il contenuto informativo in un messaggio o, inversamente, l’estensione della riduzione dell’incertezza iniziale dopo aver ricevuto il messaggio. Ad esempio, consideriamo l’evento di scoprire che un evento con probabilità \( p \) si è verificato. La “sorpresa” di questa scoperta è quantificata da \( -\log_2(p) \), espressa in bit. Eventi rari, con bassa probabilità, generano un alto livello di sorpresa, mentre eventi certi (probabilità 1) non generano alcuna sorpresa. Il logaritmo in base 2 è utilizzato perché in informatica un bit rappresenta l’unità fondamentale di informazione, equivalente a una scelta binaria tra due esiti equiprobabili.
Nell’esempio di due eventi indipendenti \( A \) e \( B \), la sorpresa totale nell’osservare entrambi gli eventi \( A \cap B \) è la somma delle sorprese individuali, grazie alla proprietà additiva dei logaritmi.
Se consideriamo \( X \) come una variabile casuale discreta con possibili valori distinti \( a_1, a_2, \ldots, a_n \) e probabilità associate \( p_1, p_2, \ldots, p_n \) (la cui somma è 1), l’entropia di \( X \) si definisce come la media ponderata della sorpresa per ogni possibile esito di \( X \):
dove la somma si estende a tutti gli esiti di \( X \). Da notare che l’entropia dipende unicamente dalle probabilità \(p_j\) e non dai valori specifici \(a_j\). Questa misura rappresenta la quantità media di informazione o sorpresa attesa dall’osservazione di \( X \).
Per variabili continue, il concetto di entropia si generalizza come:
dove l’integrazione copre tutti i possibili esiti di \( X \).
L’entropia raggiunge il suo massimo in condizioni di completa incertezza, ovvero quando tutti gli esiti di \( X \) sono equiprobabili, indicando la massima variabilità o imprevedibilità nei dati. Al contrario, l’entropia si riduce al minimo (vale zero) quando l’esito è completamente prevedibile, come nel caso di un evento con certezza assoluta. Questo concetto è fondamentale nella teoria dell’informazione, fornendo un quadro quantitativo per valutare e gestire l’incertezza nei dati.
Divergenza di Kullback-Leibler: Un Strumento per Confrontare le Distribuzioni#
Dopo aver discusso il concetto di entropia di Shannon, che misura l’incertezza o la sorpresa associata all’osservazione di un evento, possiamo esplorare la Divergenza di Kullback-Leibler (KL), derivata da Kullback e Leibler nel 1951. Questa misura, che si rivela essere l’opposto negativo dell’entropia dell’informazione di Shannon, è fondamentale per quantificare le differenze tra due distribuzioni di probabilità.
La divergenza KL tra due distribuzioni, \(P\) e \(Q\), relative alla stessa variabile aleatoria \(X\), viene calcolata in modi differenti a seconda che le distribuzioni siano discrete o continue. Per le distribuzioni discrete, la divergenza KL si esprime come:
Mentre per le distribuzioni continue, si ha:
Questa misura, essendo sempre non negativa, rappresenta la quantità di informazione “persa” quando si utilizza la distribuzione \(Q\) per approssimare la distribuzione \(P\).
La Divergenza KL può essere interpretata anche in termini di entropia. Si può esprimere come la differenza tra l’entropia incrociata \(H(P, Q)\) e l’entropia \(H(P)\) di \(P\). L’entropia di \(P\) è definita come:
e l’entropia incrociata tra \(P\) e \(Q\) è:
In questo quadro, l’entropia \(H(P)\) misura l’incertezza intrinseca nella distribuzione \(P\). L’entropia incrociata \(H(P, Q)\), invece, quantifica l’incertezza risultante dall’uso di \(Q\) per approssimare \(P\). Di conseguenza, la divergenza KL rivela la differenza tra la sorpresa media che sperimentiamo utilizzando le probabilità reali \(p\), ma basandoci su \(q\) (ad esempio, quando \(p\) è sconosciuta e \(q\) rappresenta la nostra stima) e la sorpresa media quando operiamo con le probabilità \(p\). In pratica, la Divergenza KL fornisce una misura quantitativa dell’errore o della discrepanza introdotta nell’approssimare una distribuzione di probabilità con un’altra.
Nella pratica, la divergenza KL è spesso impiegata come criterio per la selezione di modelli. L’obiettivo è trovare un modello \(Q\) che minimizzi \(D_{KL}(P \parallel Q)\), o equivalentemente, minimizzi la differenza \(H(P, Q) - H(P)\).
È importante sottolineare che la divergenza KL è non negativa e assume valore zero se e solo se \(P\) e \(Q\) sono identiche. Inoltre, la divergenza KL non è simmetrica, cioè \(D_{KL}(P \parallel Q) \neq D_{KL}(Q \parallel P)\).
In conclusione, la divergenza di Kullback-Leibler offre un metodo quantitativo per valutare quanto una distribuzione \(Q\) sia un’efficace approssimazione di un’altra distribuzione \(P\), considerando le incertezze intrinseche a entrambe le distribuzioni.
Applicazione nella Selezione di Modelli#
Uno degli obiettivi chiave nella selezione di modelli statistici è identificare il modello \(Q\) che minimizza la divergenza di Kullback-Leibler (KL) rispetto alla distribuzione “vera” \(P\) dei dati. Tuttavia, nella realtà pratica, la distribuzione \(P\) è spesso sconosciuta e non direttamente osservabile. Pertanto, si ricorre a criteri approssimativi come il Criterio di Informazione di Akaike (AIC) o il Criterio di Informazione Bayesiano (BIC). Questi criteri forniscono stime surrogate per la minimizzazione della divergenza KL, permettendo una valutazione indiretta dell’adeguatezza del modello.
Esempi concreti per l’Entropia#
Per comprendere meglio il concetto di entropia, esaminiamo alcuni esempi pratici.
L’Entropia di un Singolo Evento#
Prendiamo in considerazione il lancio di una moneta equilibrata. In questo caso, la probabilità di ottenere testa (così come croce) è di 0.5. La quantità di informazione, o sorpresa, risultante dall’ottenimento di “testa” in un tale esperimento è calcolata mediante la formula dell’entropia:
-np.log2(0.5)
1.0
Calcolando il logaritmo in base 2 di 0.5, otteniamo un valore di 1 bit. Questo significa che, in termini di entropia, ogni risultato del lancio di una moneta (sia testa che croce) contribuisce con un bit di informazione. Questo riflette l’incertezza massima in un processo con due esiti equiprobabili: ogni lancio di una moneta equilibrata è completamente imprevedibile e, di conseguenza, fornisce la massima quantità di informazione possibile.
In questo contesto, dove tutti gli esiti sono equiprobabili, l’entropia raggiunge il suo valore massimo, indicando un’incertezza totale sul risultato prima del lancio. La sorpresa, o informazione acquisita, osservando il risultato è quindi massima.
Al contrario, se consideriamo un evento con una probabilità di 1 (per esempio, una moneta truccata che produce sempre “Testa”), l’entropia è \( H(p = 1) = 0 \). Questo implica che l’osservazione dell’esito “Testa” non fornisce alcuna informazione aggiuntiva, in quanto l’evento è prevedibile con certezza.
Se si effettuano \( n \) lanci di una moneta equilibrata, ogni lancio contribuisce con 1 bit all’informazione totale. Pertanto, una sequenza di \( n \) lanci richiede \( n \) bit di informazione per essere descritta completamente.
Consideriamo ora una moneta sbilanciata, dove la probabilità di ottenere “Testa” è solo del 10% (0.1). In questo caso, l’evento “Testa” diventa più raro e, quindi, sorprendente quando si verifica. L’entropia per l’evento “Testa” in questa situazione è calcolata come:
Calcolando questo logaritmo, otteniamo un valore superiore a 3 bit.
-np.log2(0.1)
3.321928094887362
Questo significa che l’informazione necessaria per rappresentare adeguatamente l’evento “Testa” in una moneta sbilanciata è maggiore rispetto a una moneta equilibrata. La maggiore rarità dell’evento aumenta la sorpresa e, di conseguenza, l’informazione associata alla sua osservazione.
Consideriamo ora il caso di un dado a sei facce e concentriamoci sull’evento “uscita del numero 6”. La probabilità di questo evento è di 1/6, inferiore rispetto alla probabilità di 1/2 di ottenere “testa” con un lancio di moneta. Conseguentemente, ci aspettiamo che l’evento “uscita del numero 6” generi una sorpresa maggiore rispetto all’evento “testa” in un lancio di moneta.
Per quantificare l’informazione associata all’evento “uscita del numero 6”, possiamo utilizzare la formula dell’informazione di Shannon:
-np.log2(1/6)
2.584962500721156
Questo calcolo mostra che l’informazione associata all’uscita del numero 6 è di circa 2.58 bit, significativamente superiore all’informazione di 1 bit per l’evento “testa”. In pratica, ciò significa che l’evento legato al dado è più “sorprendente” e porta con sé più informazione rispetto all’evento del lancio di moneta.
Informazione di Shannon e Entropia: Differenze e Relazioni#
L’informazione di Shannon e l’entropia sono due concetti strettamente correlati ma con alcune distinzioni chiave. La principale differenza tra i due concetti è che l’informazione di Shannon si concentra su un singolo evento, mentre l’entropia considera la distribuzione di probabilità complessiva di una variabile aleatoria.
L’informazione di Shannon \( I(x) \) è definita come la quantità di informazione contenuta in un singolo evento \( x \), in base alla sua probabilità \( p(x) \). La formula è:
L’informazione è tanto maggiore quanto più bassa è la probabilità dell’evento (ovvero, gli eventi rari sono più “sorprendenti”) e diminuisce all’aumentare della probabilità dell’evento.
D’altro canto, l’entropia \( H(X) \) rappresenta l’incertezza media associata a una variabile aleatoria \( X \), considerando la sua distribuzione di probabilità \( p(x) \). Viene calcolata come l’aspettazione matematica dell’informazione di Shannon per tutti i possibili esiti \( x \) di \( X \):
In questo modo, l’entropia rappresenta la media ponderata delle informazioni di Shannon per ogni possibile esito di \( X \). Si tratta, in altre parole, di una misura della sorpresa media o dell’informazione attesa osservando la variabile aleatoria \( X \) nel lungo termine.
In sintesi, mentre l’informazione di Shannon ci dice quanto saremmo sorpresi dall’osservare un singolo esito, l’entropia fornisce un’indicazione aggregata della nostra sorpresa media, tenendo conto di tutti gli esiti possibili.
La figura successiva mostra la relazione tra probabilità e informazione, per valori di probabilità nell’intervallo tra 0 e 1.
# Create a sequence of 1000 equally spaced points from 0 to 1
p = np.linspace(0, 1, 1000)
# Avoid log(0) by replacing 0 with a small value
p[p == 0] = 1e-10
# Compute the negative log base 2 of p
h = -np.log2(p)
df = pd.DataFrame({'Probabilità': p, 'Informazione': h})
plt.plot('Probabilità', 'Informazione', data=df)
plt.xlabel('Probabilità')
plt.ylabel('Informazione');
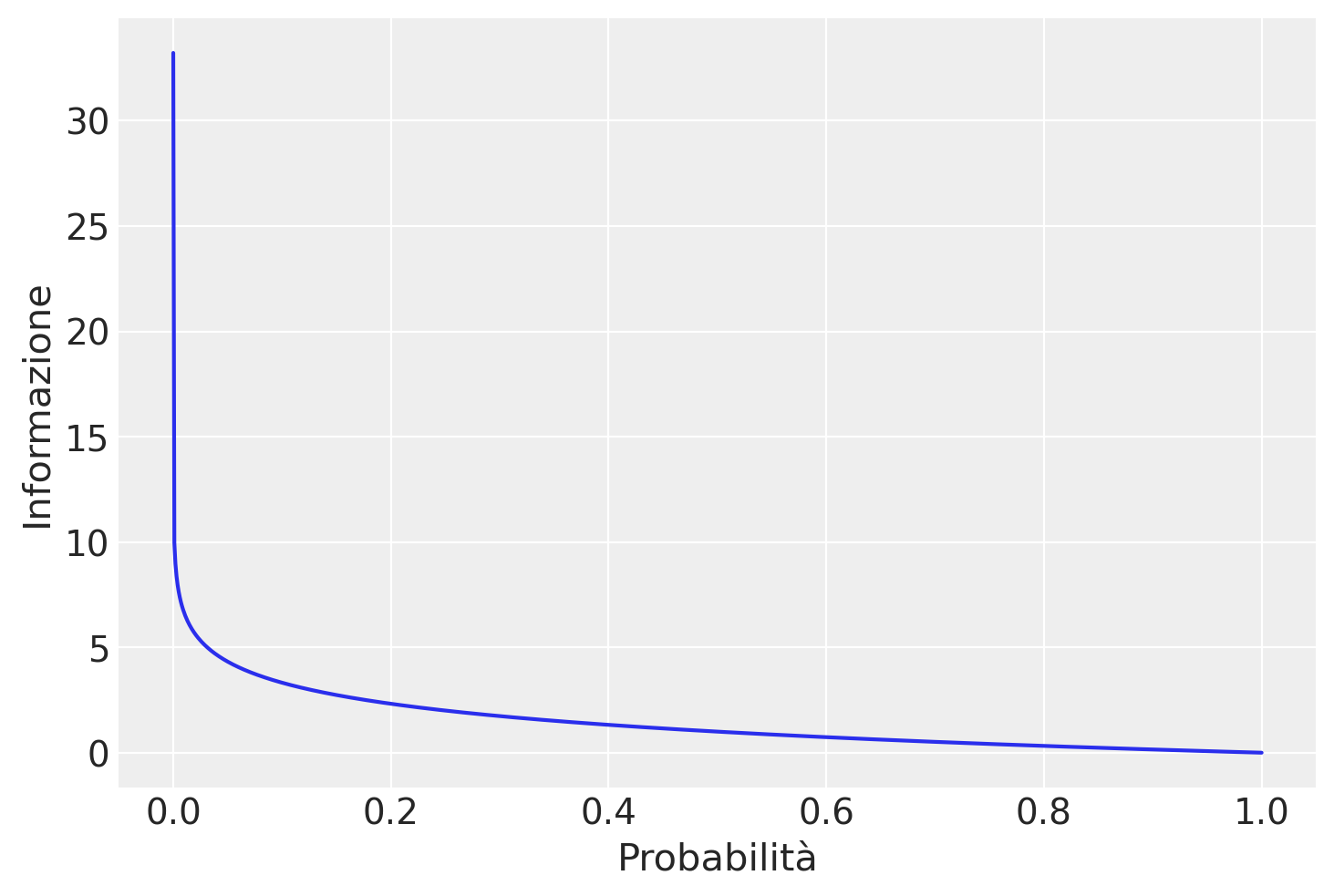
La figura mostra che questa relazione non è lineare, è infatti leggermente sublineare. Questo ha senso dato che abbiamo usato una funzione logaritmica.
Entropia e Varianza di una Distribuzione#
È comune pensare che l’entropia e la varianza di una distribuzione siano collegate in modo tale che, all’aumentare della varianza, aumenti anche l’entropia. Tuttavia, la relazione tra queste due misure non è così diretta e può variare a seconda delle caratteristiche specifiche delle distribuzioni.
Consideriamo, per esempio, il caso di distribuzioni normali con diversi valori di varianza. In Python, possiamo calcolare l’entropia di queste distribuzioni come segue:
# Intervallo di valori discreti
x = np.arange(-10, 10, 0.1)
def calculate_entropy(variance):
# Distribuzione normale con media 0 e varianza specifica
probabilities = stats.norm.pdf(x, 0, np.sqrt(variance))
# Normalizzazione delle probabilità in modo che sommino a 1
probabilities /= probabilities.sum()
# Calcolo dell'entropia
entropy = -np.sum(probabilities * np.log2(probabilities))
return entropy
# Varianze da esplorare
variances = [1, 2, 4, 8]
# Calcolo e tracciamento dell'entropia per diverse varianze
entropies = [calculate_entropy(variance) for variance in variances]
plt.plot(variances, entropies, marker='o')
plt.title('Entropia vs varianza')
plt.xlabel('Varianza')
plt.ylabel('Entropia');
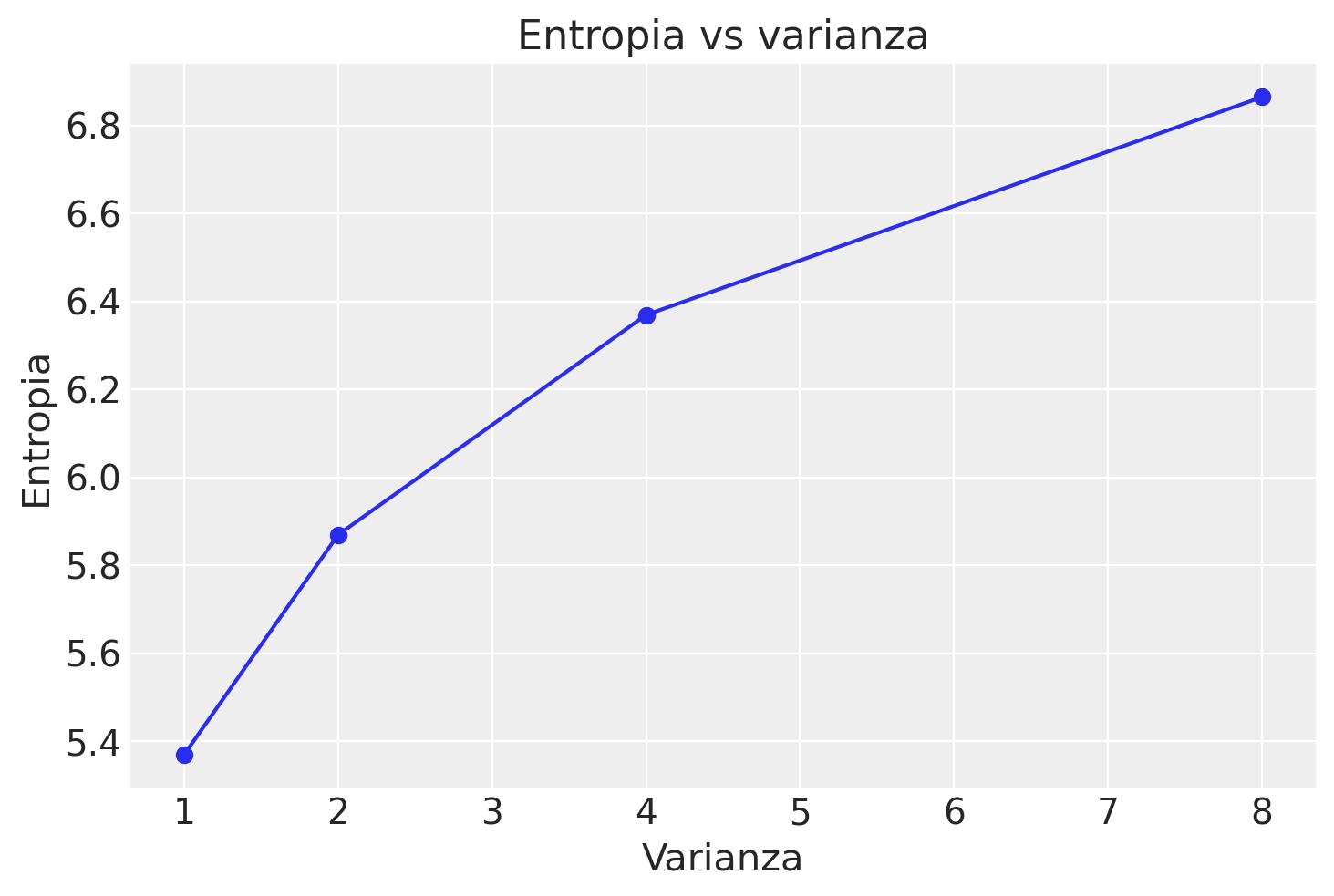
Questo script mostra che, per la distribuzione normale, l’entropia tende ad aumentare con l’aumento della varianza. Tuttavia, consideriamo ora due distribuzioni con la stessa varianza ma probabilità differenti:
def calculate_entropy(probabilities):
return -np.sum(probabilities * np.log2(probabilities))
# Distribuzioni con la stessa varianza ma diverse probabilità
probabilities1 = np.array([0.5, 0.25, 0.25])
probabilities2 = np.array([0.3333, 0.3333, 0.3334])
# Calcolo dell'entropia per entrambe le distribuzioni
entropy1 = calculate_entropy(probabilities1)
entropy2 = calculate_entropy(probabilities2)
print(f"Entropia della distribuzione 1: {entropy1}")
print(f"Entropia della distribuzione 2: {entropy2}")
Entropia della distribuzione 1: 1.5
Entropia della distribuzione 2: 1.5849624862946867
Questo esempio dimostra che due distribuzioni con la stessa varianza possono avere entropie differenti, a seconda della configurazione delle loro probabilità.
In sintesi:
Varianza: Misura la dispersione dei dati intorno alla loro media. Quantifica quanto i valori si discostano dalla media, ma non considera la probabilità di ciascun valore.
Entropia: Valuta l’incertezza nella distribuzione di probabilità. Considera la probabilità di ogni possibile esito, quantificando l’incertezza media nell’osservazione di un esito casuale.
Pertanto, distribuzioni con la stessa varianza possono avere entropie differenti e viceversa. Questo dipende da come sono distribuite le probabilità all’interno della distribuzione. La varianza e l’entropia sono, quindi, indicatori complementari dell’incertezza in una distribuzione di dati, ma esplorano questa incertezza da prospettive diverse.
Esercizio sulla Divergenza di Kullback-Leibler in un Contesto di Esame#
Immaginatevi in un contesto di esame a scelta multipla, dove, invece di selezionare una sola risposta per domanda, dovete assegnare una probabilità di correttezza a ciascuna delle opzioni. Il vostro punteggio per ogni domanda sarà calcolato usando il logaritmo della probabilità assegnata all’opzione corretta. Se la risposta giusta è \(A_i\), il vostro punteggio per quella domanda sarà \(\log(p_i)\), dove \(p_i\) è la probabilità che avete attribuito a \(A_i\).
In questo sistema di punteggio, il massimo che potete ottenere per una singola domanda è 0 (assegnando una probabilità del 100% alla risposta corretta), mentre il punteggio minimo è \(-\infty\) se assegnate una probabilità di zero alla risposta corretta. Il vostro obiettivo finale è massimizzare il punteggio atteso per l’intero esame.
Dato che non conoscete a priori la risposta corretta a ogni domanda, diventa cruciale utilizzare le vostre “migliori stime personali” delle probabilità. Supponiamo che queste stime siano rappresentate dal vettore \(p = [p_1, p_2, \ldots, p_n]\).
Il punteggio atteso, basato su queste stime personali, è dato da:
Considerando l’idea di utilizzare un set alternativo di probabilità \(q = [q_1, q_2, \ldots, q_n]\), il punteggio atteso cambierebbe a:
La divergenza di Kullback-Leibler (KL) tra i due set di probabilità \(p\) e \(q\) è calcolata come:
Questa divergenza KL, sempre non negativa, misura la differenza tra le stime \(p\) e \(q\). Si annulla solo se \(p = q\), indicando che il punteggio atteso è massimizzato quando si utilizzano le stime personali più accurate, \(p\).
In questo scenario, quindi, l’approccio ottimale è utilizzare stime basate sulle informazioni a disposizione. Qualsiasi manipolazione delle stime senza giustificazione basata su nuove informazioni riduce il punteggio atteso. Le vostre migliori stime personali rappresentano la comprensione più accurata che avete del problema. Deviare da queste stime senza validi motivi equivale a compromettere le vostre possibilità di successo.
Inoltre, nel sistema di punteggio basato sul logaritmo delle probabilità, non esiste alcun vantaggio nel tentare di “ingannare” il sistema; ogni tentativo di manipolazione si traduce in una penalizzazione del punteggio atteso. Questo allinea perfettamente con i principi della teoria delle decisioni bayesiane, che premia la trasparenza e l’accuratezza nelle stime probabilistiche.
Nella seguente simulazione abbiamo due gruppi di studenti che rispondono a un esame a scelta multipla di sei domande, ognuna con cinque alternative di risposta. Per il gruppo di studenti “onesti”, abbiamo impostato che nel 75% dei casi assegnano la probabilità più alta alla risposta corretta. Per il gruppo di studenti che “imbrogliano”, abbiamo assunto che riescano a indovinare la risposta corretta nel 60% dei casi, ma assegnano le probabilità in modo distorto.
# Numero di studenti per gruppo
num_studenti = 100
num_domande = 6
num_alternative = 5
# Funzione per calcolare il punteggio atteso usando la metrica del logaritmo delle probabilità
def calcola_punteggio(probabilita):
return np.sum(probabilita * np.log(probabilita), axis=2)
# Creazione di risposte per il gruppo di studenti onesti (75% di risposte corrette)
p_onesti = np.full((num_studenti, num_domande, num_alternative), 1 / num_alternative)
for studente in range(num_studenti):
for domanda in range(num_domande):
if (
np.random.rand() < 0.75
): # 75% di possibilità di scegliere la risposta corretta
risposta_corretta = np.random.randint(num_alternative)
p_onesti[
studente, domanda, :
] = 0.1 # probabilità di base per le risposte sbagliate
p_onesti[
studente, domanda, risposta_corretta
] = 0.6 # probabilità più alta per la risposta corretta
# Altrimenti lascia le probabilità uguali (caso in cui la risposta è sbagliata)
# Creazione di risposte per il gruppo di studenti che "imbrogliano" (60% di risposte corrette)
p_imbrogli = np.random.rand(num_studenti, num_domande, num_alternative)
for studente in range(num_studenti):
for domanda in range(num_domande):
if (
np.random.rand() < 0.60
): # 60% di possibilità di scegliere la risposta corretta
risposta_corretta = np.random.randint(num_alternative)
p_imbrogli[
studente, domanda, risposta_corretta
] += 5 # aumentare la probabilità per la risposta corretta
# Distribuzione distorta di probabilità
p_imbrogli[studente, domanda, :] /= p_imbrogli[studente, domanda, :].sum()
# Calcolo del punteggio atteso per i due gruppi di soggetti
punteggio_onesti = calcola_punteggio(p_onesti)
punteggio_imbrogli = calcola_punteggio(p_imbrogli)
# Calcolo della differenza media dei punteggi tra i due gruppi
differenza_media_onesti_imbrogli = np.mean(punteggio_onesti - punteggio_imbrogli)
differenza_media_onesti_imbrogli
-0.1927373906510967
La differenza media dei punteggi attesi tra i due gruppi, calcolata usando la metrica del logaritmo delle probabilità, è di circa -0.2. Questo risultato suggerisce che, in media, i soggetti che “imbrogliano” (assegnando le probabilità in modo distorto) hanno ottenuto punteggi attesi inferiori rispetto a quelli che hanno assegnato le probabilità in modo più accurato e onesto.
Questo dimostra che, nel contesto di questo esame a scelta multipla, un approccio accurato e onesto nella stima delle probabilità porta a un punteggio atteso più alto, mentre la manipolazione delle stime probabilistiche senza basi informative solide porta a una penalizzazione nel punteggio atteso.
Calcoliamo ora la divergenza di Kullback-Leibler (KL).
# Calcolo della divergenza di Kullback-Leibler tra i due gruppi di studenti
def calcola_divergenza_kl(p, q):
return np.sum(p * np.log(p / q), axis=2)
# Calcolo della divergenza KL per ogni studente e ogni domanda
divergenza_kl = calcola_divergenza_kl(p_onesti, p_imbrogli)
# Calcolo della media della divergenza KL tra tutti gli studenti
media_divergenza_kl = np.mean(divergenza_kl)
media_divergenza_kl
0.9103723991901927
La divergenza di KL media calcolata tra i due gruppi di studenti è di circa 0.9.
Nel contesto dell’esercizio, la divergenza KL misura la differenza, su scala logaritmica, tra due approcci di stima delle probabilità rispetto a una distribuzione di probabilità “vera” (che idealmente assegna una probabilità di 1 alla risposta corretta e 0 a tutte le altre).
La divergenza KL di circa 0.9 indica quanto la stima media fornita dal gruppo che “imbroglia” sia più distante dalla distribuzione vera rispetto alla stima media fornita dal gruppo “onesto”. In altre parole, un valore di divergenza KL di circa 0.9 indica che le stime dei rispondenti che “imbrogliano” sono in media più lontane dalla distribuzione vera rispetto a quelle dei rispondenti “onesti”.
Riflessioni Conclusive e Prospettive Future#
In questo capitolo, abbiamo esaminato il concetto di entropia, evidenziando il suo ruolo fondamentale nel quantificare l’incertezza all’interno delle distribuzioni di probabilità. Abbiamo anche affrontato la questione di come l’entropia possa essere impiegata per valutare la “distanza” tra un modello teorico e i dati reali. A tale scopo, abbiamo introdotto la divergenza di Kullback-Leibler (KL), una misura che non solo quantifica le discrepanze tra due distribuzioni probabilistiche, ma agisce anche come collegamento tra teoria e pratica, tra il modello ideale e il mondo empirico.
Nel capitolo successivo, approfondiremo ulteriormente il tema della divergenza KL. Esploreremo come questo strumento possa essere utilizzato per confrontare modelli teorici con dati empirici e ci concentreremo su come possa fornirci una comprensione più dettagliata dell’adattamento di un modello alla realtà che intende rappresentare. Questa esplorazione ci permetterà di valutare più accuratamente la validità e la generalizzabilità dei modelli scientifici nel loro tentativo di catturare e interpretare la complessità dei dati reali.
%run ../wm.py
Watermark:
----------
Last updated: 2024-01-26T19:00:26.050409+01:00
Python implementation: CPython
Python version : 3.11.7
IPython version : 8.19.0
Compiler : Clang 16.0.6
OS : Darwin
Release : 23.3.0
Machine : x86_64
Processor : i386
CPU cores : 8
Architecture: 64bit

