La misurazione in psicologia#
Measurement, measurement, measurement. It’s central to statistics. It’s central to how we learn about the world. (A. Gelman)
In questo capitolo verranno introdotte alcune nozioni di base relative ai temi della misurazione quantitativa delle caratteristiche psicologiche. In particolare, verrà presentata la teoria delle scale di misura di Stevens [Ste46]. Prima di procedere con il presente capitolo, è indispensabile leggere l’appendice Numeri binari, interi, razionali, irrazionali e reali.
Obiettivi di apprendimento
Dopo la lettura di questo capitolo, si prevede che gli studenti saranno in grado di:
conoscere le proprietà delle scale di misura di Stevens;
sapere quali operazioni aritmetiche possono essere applicate a ciscun livello di scala e perchè;
conoscere la differenza tra variabili continue e discrete;
capire la differenza tra accuratezza e attendibilità;
conoscere i diversi tipi di validità;
conoscere i diversi tipi di affidabilità.
Scaling psicologico#
Il problema dello scaling psicologico riguarda la trasformazione dei dati osservati in misure o punteggi che rappresentino accuratamente le caratteristiche o le qualità psicologiche misurate. In altre parole, quando conduciamo ricerche in psicologia, spesso vogliamo assegnare numeri ai comportamenti o alle risposte degli individui in modo da poterli confrontare e analizzare in modo più oggettivo. Tuttavia, questa trasformazione può essere un processo complesso e soggetto a diverse considerazioni.
Uno dei tipi di scaling più noti è il “Scaling di Guttman”, che viene utilizzato per rappresentare le relazioni ordinate tra gli elementi di una scala. Ad esempio, supponiamo di avere un questionario con domande relative alla gravità di sintomi di ansia, suddivise in modo crescente di intensità. I partecipanti rispondono con “sì” o “no” a ciascuna domanda. Utilizzando lo scaling di Guttman, si assegna un punteggio “1” a una risposta “sì” solo se il partecipante ha risposto “sì” anche a tutte le domande meno gravi precedenti. In questo modo, otteniamo una scala ordinata di gravità dei sintomi di ansia.
D’altra parte, lo “Scaling Thurstoniano” è utilizzato per misurare le preferenze o i giudizi soggettivi di un individuo su un insieme di oggetti o opzioni. Ad esempio, supponiamo di voler valutare la preferenza di una persona per diversi tipi di cibi, come pizza, sushi e hamburger. Con lo scaling Thurstoniano, il partecipante viene chiesto di confrontare due oggetti alla volta e di esprimere una preferenza o un giudizio, ad esempio dicendo quale degli oggetti preferisce o giudica più delizioso. Queste risposte vengono quindi utilizzate per assegnare punteggi alle opzioni sulla base della loro preferenza media.
Un altro metodo comune di scaling psicologico è l’utilizzo dei questionari Lickert. In questi questionari, vengono presentate affermazioni o domande ai partecipanti e loro devono esprimere il grado di accordo o disagio con ciascuna affermazione su una scala a più livelli, ad esempio da “fortemente in disaccordo” a “fortemente d’accordo”. Questi punteggi vengono poi sommati per ottenere un punteggio complessivo che rappresenta la posizione dell’individuo rispetto all’oggetto di studio.
Per valutare le proprietà delle scale psicologiche, esistono vari metodi. Ad esempio, possiamo analizzare l’affidabilità delle misure utilizzando il coefficiente alpha di Cronbach o il coefficiente Omega di McDonals, che misurano la coerenza interna delle risposte ai vari item del questionario. Possiamo anche esaminare la validità delle scale confrontando i risultati ottenuti con misure simili o utilizzando analisi statistiche per verificare se la scala cattura accuratamente il costrutto che si intende misurare. La validità di costrutto è un aspetto cruciale, in quanto riguarda la capacità della scala di misurare effettivamente il concetto o la caratteristica psicologica che si intende esaminare.
In conclusione, il problema dello scaling psicologico è una questione fondamentale nella ricerca psicologica, in quanto influisce sulla qualità e sull’accuratezza delle misure che utilizziamo per comprendere il comportamento e le caratteristiche umane. È necessario utilizzare metodologie appropriate e valutare attentamente le proprietà delle scale psicologiche per garantire risultati validi e affidabili.
Le scale di misurazione#
Lo scaling psicologico è il processo di assegnare numeri ai dati osservati per rappresentare le proprietà psicologiche. È strettamente collegato alla teoria della misurazione, che studia come definire, valutare e confrontare grandezze fisiche e psicologiche. L’obiettivo della teoria della misurazione è costruire una “scala di misurazione” (nominale, ordinale, ad intervalli o a rapporto) con numeri ordinati che rappresentano fedelmente le caratteristiche empiriche studiate.
Il famoso psicologo Stevens [Ste46] ha proposto una teoria delle scale di misurazione in cui si sostiene che le variabili psicologiche rappresentano con diversi gradi di precisione le relazioni qualitative dei fenomeni psicologici. Secondo questa teoria, esistono quattro tipi di scale di misurazione: nominali, ordinali, a intervalli e di rapporti. Ognuna di queste scale consente di effettuare operazioni aritmetiche diverse, poiché ciascuna di esse è in grado di “catturare” solo alcune delle proprietà dei fenomeni psicologici che si intende misurare.

Scala nominale#
ILa scala nominale è il livello di misurazione più semplice e corrisponde ad una tassonomia o classificazione delle categorie che utilizziamo per descrivere i fenomeni psicologici. I simboli o numeri che costituiscono questa scala rappresentano i nomi delle categorie e non hanno alcun valore numerico intrinseco. Con la scala nominale possiamo solo distinguere se una caratteristica psicologica è uguale o diversa da un’altra.
I dati raccolti con la scala nominale sono suddivisi in categorie qualitative e mutuamente esclusive, in cui ogni dato appartiene ad una sola categoria. In questa scala, esiste solo la relazione di equivalenza tra le misure delle unità di studio: gli elementi del campione appartenenti a classi diverse sono differenti, mentre tutti quelli della stessa classe sono tra loro equivalenti.
L’unica operazione algebrica consentita dalla scala nominale è quella di contare le unità di studio che appartengono ad ogni categoria e il numero totale di categorie. Di conseguenza, la descrizione dei dati avviene tramite le frequenze assolute e le frequenze relative.
Dalla scala nominale è possibile costruire altre scale nominali equivalenti alla prima, trasformando i valori della scala di partenza in modo tale da cambiare i nomi delle categorie, ma lasciando inalterata la suddivisione delle unità di studio nelle medesime classi di equivalenza. In altre parole, cambiando i nomi delle categorie di una variabile misurata su scala nominale, si ottiene una nuova variabile esattamente equivalente alla prima.
Scala ordinale#
La scala ordinale mantiene la caratteristica della scala nominale di classificare ogni unità di misura all’interno di una singola categoria, ma introduce la relazione di ordinamento tra le categorie. In quanto basata su una relazione di ordine, una scala ordinale descrive solo il rango di ordine tra le categorie e non fornisce informazioni sulla distanza tra di esse. Non ci dice, ad esempio, se la distanza tra le categorie \(a\) e \(b\) è uguale, maggiore o minore della distanza tra le categorie \(b\) e \(c\).
Un esempio classico di scala ordinale è quello della scala Mohs per la determinazione della durezza dei minerali. Per stabilire la durezza dei minerali si usa il criterio empirico della scalfittura. Vengono stabiliti livelli di durezza crescente da 1 a 10 con riferimento a dieci minerali: talco, gesso, calcite, fluorite, apatite, ortoclasio, quarzo, topazio, corindone e diamante. Un minerale appartenente ad uno di questi livelli se scalfisce quello di livello inferiore ed è scalfito da quello di livello superiore.
Scala ad intervalli#
La scala ad intervalli di misurazione include le proprietà della scala nominale e della scala ordinale e permette di misurare le distanze tra le coppie di unità statistiche in termini di un intervallo costante, chiamato “unità di misura”, a cui viene attribuito il valore “1”. L’origine della scala, ovvero il punto zero, è scelta arbitrariamente e non indica l’assenza della proprietà che si sta misurando. Ciò significa che la scala ad intervalli consente anche valori negativi e lo zero non viene attribuito all’unità statistica in cui la proprietà risulta assente.
La scala ad intervalli equivalenti consente l’esecuzione di operazioni algebriche basate sulla differenza tra i numeri associati ai diversi punti della scala, operazioni algebriche non possibili con le scale di misura nominale o ordinale. Tuttavia, il limite della scala ad intervalli è che non consente di calcolare il rapporto tra coppie di misure. È possibile affermare la differenza tra \(a\) e \(b\) come la metà della differenza tra \(c\) e \(d\) o che le due differenze sono uguali, ma non è possibile affermare che \(a\) abbia una proprietà misurata in quantità doppia rispetto a \(b\). In altre parole, non è possibile stabilire rapporti diretti tra le misure ottenute. Solo le differenze tra le modalità permettono tutte le operazioni aritmetiche, come la somma, l’elevazione a potenza o la divisione, che sono alla base della statistica inferenziale.
Nelle scale ad intervalli equivalenti, l’unità di misura è arbitraria e può essere cambiata attraverso una dilatazione, ovvero la moltiplicazione di tutti i valori della scala per una costante positiva. Inoltre, la traslazione, ovvero l’aggiunta di una costante a tutti i valori della scala, è ammessa poiché non altera le differenze tra i valori della scala. La scala rimane invariata rispetto a traslazioni e dilatazioni e dunque le uniche trasformazioni ammissibili sono le trasformazioni lineari:
Infatti, l’uguaglianza dei rapporti fra gli intervalli rimane invariata a seguito di una trasformazione lineare.
Esempio di scala ad intervalli è la temperatura misurata in gradi Celsius o Fahrenheit, ma non Kelvin. Come per la scala nominale, è possibile stabilire se due modalità sono uguali o diverse: 30\(^\circ\)C \(\neq\) 20\(^\circ\)C. Come per la scala ordinale è possibile mettere due modalità in una relazione d’ordine: 30\(^\circ\)C \(>\) 20\(^\circ\)C. In aggiunta ai casi precedenti, però, è possibile definire una unità di misura per cui è possibile dire che tra 30\(^\circ\)C e 20\(^\circ\)C c’è una differenza di 30\(^\circ\) - 20\(^\circ\) = 10\(^\circ\)C. I valori di temperatura, oltre a poter essere ordinati secondo l’intensità del fenomeno, godono della proprietà che le differenze tra loro sono direttamente confrontabili e quantificabili.
Il limite della scala ad intervalli è quello di non consentire il calcolo del rapporto tra coppie di misure. Ad esempio, una temperatura di 80\(^\circ\)C non è il doppio di una di 40\(^\circ\)C. Se infatti esprimiamo le stesse temperature nei termini della scala Fahrenheit, allora i due valori non saranno in rapporto di 1 a 2 tra loro. Infatti, 20\(^\circ\)C = 68\(^\circ\)F e 40\(^\circ\)C = 104\(^\circ\)F. Questo significa che la relazione “il doppio di” che avevamo individuato in precedenza si applicava ai numeri della scala centigrada, ma non alla proprietà misurata (cioè la temperatura). La decisione di che scala usare (Centigrada vs. Fahrenheit) è arbitraria. Ma questa arbitrarietà non deve influenzare le inferenze che traiamo dai dati. Queste inferenze, infatti, devono dirci qualcosa a proposito della realtà empirica e non possono in nessun modo essere condizionate dalle nostre scelte arbitrarie che ci portano a scegliere la scala Centigrada piuttosto che quella Fahrenheit.
Consideriamo ora l’aspetto invariante di una trasformazione lineare, ovvero l’uguaglianza dei rapporti fra intervalli. Prendiamo in esame, ad esempio, tre temperature: \(20^\circ C = 68^\circ F\), \(15^\circ C = 59^\circ F\), \(10^\circ C = 50 ^\circ F\).
È facile rendersi conto del fatto che i rapporti fra intervalli restano costanti indipendentemente dall’unità di misura che è stata scelta:
Scala di rapporti#
Nella scala a rapporti equivalenti, lo zero non è arbitrario e rappresenta l’elemento che ha intensità nulla rispetto alla proprietà misurata. Per costruire questa scala, si associa il numero 0 all’elemento con intensità nulla e si sceglie un’unità di misura \(u\). Ad ogni elemento si assegna un numero \(a\) definito come \(a=d/u\), dove \(d\) rappresenta la distanza dall’origine. In questo modo, i numeri assegnati riflettono le differenze e i rapporti tra le intensità della proprietà misurata.
In questa scala, è possibile effettuare operazioni aritmetiche non solo sulle differenze tra i valori della scala, ma anche sui valori stessi della scala. L’unica scelta arbitraria è l’unità di misura, ma lo zero deve sempre rappresentare l’intensità nulla della proprietà considerata.
Le trasformazioni ammissibili in questa scala sono chiamate trasformazioni di similarità e sono del tipo \(y' = by\), dove \(b>0\). In questa scala, i rapporti tra i valori rimangono invariati dopo le trasformazioni. In altre parole, se rapportiamo due valori originali e due valori trasformati, il rapporto rimane lo stesso: \(\frac{y_i}{y_j} = \frac{y'_i}{y'_j}\).
Gerarchia dei livelli delle scale di misurazione#
Secondo Stevens [Ste46], esiste una gerarchia dei livelli delle scale di misurazione, denominati “livelli di scala”. Questi livelli sono organizzati in modo gerarchico, in cui la scala nominale rappresenta il livello più basso della misurazione, mentre la scala a rapporti equivalenti rappresenta il livello più alto.
La scala nominale è il livello più elementare, in cui le categorie o le etichette vengono assegnate agli oggetti o agli individui senza alcuna valutazione di grandezza o ordine.
Al livello successivo si trova la scala ordinale, in cui le categorie sono ordinate in base a una qualche qualità o caratteristica. Qui, è possibile stabilire un ordine di preferenza o gerarchia tra le categorie, ma non è possibile quantificare la differenza tra di esse in modo preciso.
La scala intervallo rappresenta un livello successivo, in cui le categorie sono ordinate e la differenza tra di esse è quantificabile in modo preciso. In questa scala, è possibile effettuare operazioni matematiche come l’addizione e la sottrazione tra i valori, ma non è possibile stabilire un vero e proprio punto zero significativo.
Infine, la scala a rapporti equivalenti rappresenta il livello più alto. In questa scala, le categorie sono ordinate, la differenza tra di esse è quantificabile in modo preciso e esiste un punto zero assoluto che rappresenta l’assenza totale della grandezza misurata. Questo livello di scala permette di effettuare tutte le operazioni matematiche, compresa la moltiplicazione e la divisione.
Passando da un livello di misurazione ad uno più alto aumenta il numero di operazioni aritmetiche che possono essere compiute sui valori della scala, come indicato nella figura seguente.
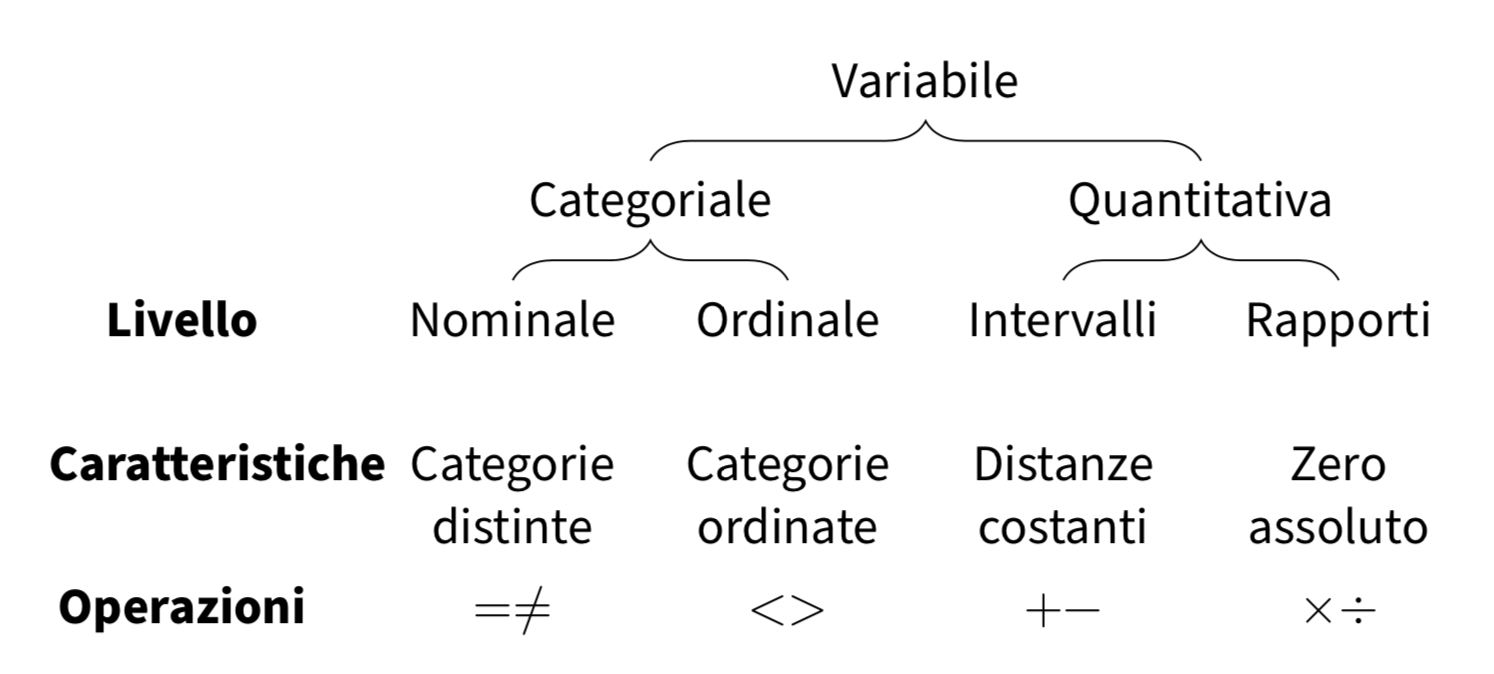
Per ciò che riguarda le trasformazioni ammissibili, più il livello di scala è basso, più le funzioni sono generali (sono minori cioè i vincoli per passare da una rappresentazione numerica ad un’altra equivalente). Salendo la gerarchia, la natura delle funzioni di trasformazione si fa più restrittiva.
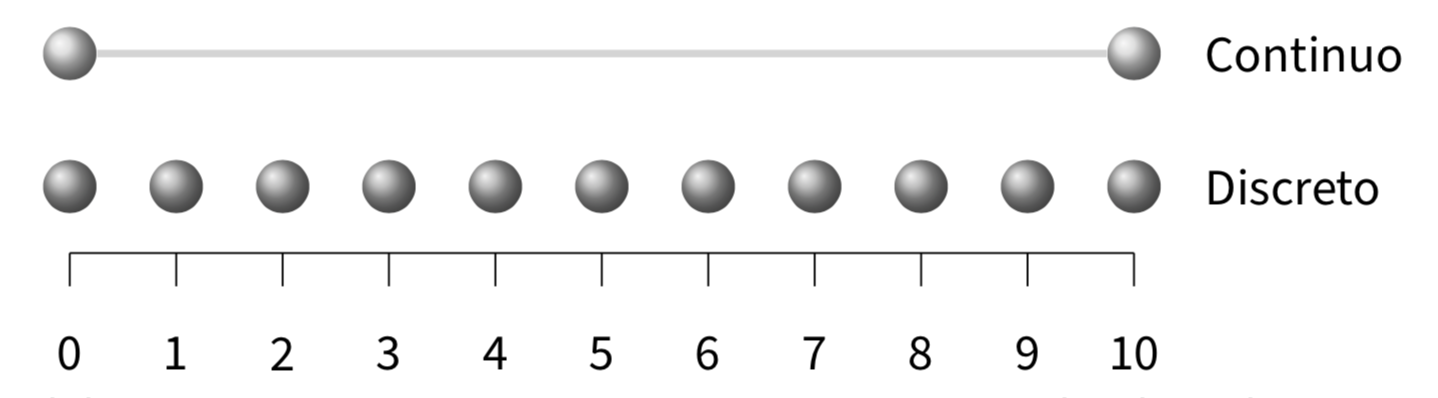
Variabili discrete o continue#
Le variabili possono essere classificate come variabili a livello di intervalli o di rapporti e possono essere sia discrete che continue.
Le variabili discrete assumono valori specifici ma non possono assumere valori intermedi. Una volta che l’elenco dei valori accettabili è stato definito, non vi sono casi che si trovano tra questi valori. In genere, le variabili discrete assumono valori interi, come il numero di eventi, il numero di persone o il numero di oggetti.
D’altra parte, le variabili continue possono assumere qualsiasi valore all’interno di un intervallo specificato. Teoricamente, ciò significa che è possibile utilizzare frazioni e decimali per ottenere qualsiasi grado di precisione.
Comprendere gli errori nella misurazione#
Nel campo della misurazione psicologica, è fondamentale padroneggiare il concetto degli errori che possono insorgere durante la valutazione di diversi fenomeni psicologici. Gli errori di misurazione indicano la discrepanza tra il valore reale di una variabile e il valore ottenuto dalla misurazione, e possono essere di due tipi: errori casuali e errori sistematici.
Tipologie di errori#
Errori casuali: Si manifestano come fluttuazioni aleatorie che influenzano la misurazione, portando ad un valore che può essere superiore o inferiore al valore effettivo. Derivano da variabili incontrollabili che incidono sulla misurazione.
Errori sistematici: Questi errori hanno un effetto costante sulla misurazione, dovuto a problematiche relative al metodo di misurazione o a strumenti non calibrati adeguatamente. Possono essere di tipo additivo o proporzionale.
Precisione e Accuratezza#
La trattazione degli errori di misurazione introduce in modo naturale i concetti di precisione e accuratezza, entrambi cruciali nell’ambito dell’assessment psicometrico:
Precisione: Indica la coerenza tra misurazioni ripetute di un fenomeno; una misura è definita precisa se le varie misurazioni sono vicine tra loro.
Accuratezza: Si riferisce alla vicinanza del valore misurato al valore reale del fenomeno in questione.
Utilizzando l’analogia del tiro al bersaglio, si può avere una serie di colpi vicini tra loro ma lontani dal centro (precisione senza accuratezza) oppure colpi distribuiti in modo sparso ma in media vicini al centro (accuratezza senza precisione).
La comprensione di errori, precisione e accuratezza pone le basi per affrontare il complesso campo dell’assessment psicometrico.
Assessment psicometrico#
Alcune misure sono migliori di altre#
In psicologia, si mira a misurare costrutti teorici non direttamente osservabili attraverso indicatori specifici quali comportamenti, risposte o altre manifestazioni associate ai costrutti. Queste misure, tuttavia, possono essere affette da imperfezioni e errori vari, derivanti sia da problematiche intrinseche del test sia da influenze esterne. Qui entra in gioco l’assessment psicometrico, un campo di studio focalizzato sullo sviluppo di metodi e strumenti per una misurazione accurata, affidabile e valida dei costrutti psicologici.
Validità#
La validità di uno strumento di misurazione si suddivide in diverse sottocategorie, tra cui la validità di costrutto, di contenuto, di criterio e di facciata, ognuna focalizzata su differenti aspetti della relazione tra il test e il costrutto che intende misurare.
La validità di costrutto riguarda il grado in cui un test misura effettivamente il costrutto che si intende misurare. Questa validità può essere suddivisa in validità convergente e validità divergente. La validità convergente si riferisce alla concordanza tra lo strumento di misurazione e altri strumenti che misurano lo stesso costrutto. La validità divergente, invece, valuta la capacità dello strumento di discriminare tra costrutti diversi. Senza una valida misura di costrutto, le altre forme di validità non hanno valore.
La validità di contenuto si riferisce alla corrispondenza tra il contenuto degli item di un test e il dominio dell’attributo psicologico che il test intende misurare. È importante che gli item del test siano pertinenti e rappresentativi dell’attributo che si desidera misurare.
La validità di criterio valuta il grado di concordanza tra i risultati ottenuti tramite lo strumento di misurazione e i risultati ottenuti da altri strumenti che misurano lo stesso costrutto o da un criterio esterno. La validità concorrente si riferisce alla misurazione simultanea del costrutto e del criterio, permettendo un confronto diretto tra di essi. La validità predittiva, invece, coinvolge la misurazione del costrutto in un momento precedente e la misurazione del criterio in un momento successivo, consentendo di valutare la capacità dello strumento di predire un evento futuro.
Infine, la validità di facciata si riferisce al grado in cui il test appare valido agli individui a cui è destinato. Questo tipo di validità è particolarmente importante in contesti particolari, come la selezione del personale, dove è importante che i candidati ritengano che il test misuri gli aspetti rilevanti per l’occupazione in questione. In generale, la validità di facciata ha un’utilità limitata, tranne in casi specifici.
Affidabilità#
L’affidabilità concerne la consistenza e stabilità delle misurazioni effettuate tramite uno strumento psicometrico. Un test affidabile fornirà risultati coerenti in circostanze simili, garantendo la riproducibilità dei risultati. Si identificano diversi tipi di affidabilità.
Affidabilità Test-Retest: Questa forma di affidabilità verifica la consistenza delle misurazioni nel tempo. Se un individuo viene testato in due momenti diversi, i risultati dovrebbero essere simili, assumendo che non ci siano stati cambiamenti significativi nel costrutto misurato.
Affidabilità Inter-rater: In questo caso, l’affidabilità è determinata dalla concordanza tra le valutazioni di diversi esaminatori. Ad esempio, se più psicologi dovessero valutare un individuo utilizzando lo stesso strumento, le loro valutazioni dovrebbero essere simili.
Affidabilità Intra-rater: Questa misura dell’affidabilità si riferisce alla consistenza delle valutazioni dello stesso esaminatore in momenti diversi.
Affidabilità Interna: Si riferisce alla coerenza delle risposte all’interno dello stesso test. Ad esempio, se un test misura un costrutto come l’ansia, gli item che misurano l’ansia dovrebbero correlare positivamente l’uno con l’altro. Un modo comune per valutare l’affidabilità interna è utilizzare il coefficiente \(\omega\) di McDonald.
Commenti e considerazioni finali#
In conclusione, la teoria della misurazione è fondamentale nella ricerca empirica per valutare l’attendibilità e la validità delle misurazioni effettuate. La distinzione tra le scale di misurazione di Stevens fornisce un quadro chiaro delle diverse caratteristiche delle variabili psicologiche. È cruciale valutare l’errore nella misurazione, che può essere casuale o sistematico, al fine di garantire la precisione e l’accuratezza delle misure. La comprensione dei concetti di errore, precisione e accuratezza aiuta a interpretare correttamente i dati e a trarre conclusioni valide. Infine, l’assessment psicometrico si occupa di valutare la qualità delle misurazioni psicologiche, considerando l’affidabilità e la validità, per garantire misure accurate dei costrutti teorici.

