Distribuzioni coniugate (2)#
In questo capitolo, esploreremo il modello normale-normale. Una caratteristica distintiva di questo modello risiede nella proprietà di auto-coniugazione della distribuzione gaussiana rispetto a una funzione di verosimiglianza anch’essa gaussiana. In altre parole, se la funzione di verosimiglianza segue una distribuzione gaussiana, scegliere una distribuzione a priori gaussiana per la media garantirà che anche la distribuzione a posteriori, a sua volta, rimanga gaussiana.
Preparazione del Notebook#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
import arviz as az
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 12345
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
sns.set_theme(palette="colorblind")
Derivazione Analitica della Distribuzione a Posteriori in un Contesto Normale con Varianza Nota#
Consideriamo un insieme di dati \( y = [Y_1, \ldots, Y_n] \), costituito da \( n \) osservazioni indipendenti e identicamente distribuite (iid) da una distribuzione normale \( \mathcal{N}(\mu, \sigma) \), dove \( \sigma \) è un valore noto. Il nostro obiettivo è inferire il parametro \( \mu \), adottando un approccio bayesiano con una distribuzione a priori normale per \( \mu \). Questo approccio è noto come modello “normale-normale coniugato”.
La funzione di verosimiglianza \( p(y \mid \mu, \sigma) \) di un campione iid è rappresentata dalla distribuzione normale. La densità a priori \( p(\mu) \) per \( \mu \) è definita come una distribuzione normale con media \( \mu_0 \) e varianza \( \sigma_0^2 \).
L’obiettivo è derivare la distribuzione a posteriori \( p(\mu \mid y) \). La densità congiunta delle osservazioni \( Y_1, \ldots, Y_n \) è espressa come:
La densità a priori per \( \mu \) si scrive:
Utilizzando queste distribuzioni, la distribuzione a posteriori di \( \mu \) è anch’essa una distribuzione normale:
dove la media a posteriori \( \mu_p \) e la varianza a posteriori \( \sigma_p^2 \) sono calcolate come:
Considerazioni Finali#
La media a posteriori \( \mu_p \) rappresenta una combinazione ponderata tra la media a priori \( \mu_0 \) e la media campionaria \( \bar{y} \). Il peso di \( \bar{y} \) aumenta con il numero di osservazioni \( n \) e diminuisce all’aumentare dell’incertezza a priori \( \sigma_0^2 \).
La varianza a posteriori \( \sigma_p^2 \) è inferiore all’incertezza a priori \( \sigma_0^2 \) e diminuisce con l’aumento del numero di osservazioni \( n \).
Questi risultati evidenziano come la conoscenza a priori e i dati osservati interagiscono in un contesto bayesiano. La media a posteriori bilancia la media a priori con la media campionaria, e i loro pesi relativi dipendono dalla dimensione del campione e dall’incertezza della conoscenza a priori. Questa analisi è fondamentale per comprendere il comportamento delle stime bayesiane, soprattutto quando confrontate con le stime di massima verosimiglianza.
Un esempio concreto#
Per esaminare un esempio pratico, consideriamo i 30 valori BDI-II dei soggetti clinici esaminati da [ZBR19].
y = np.array(
[
26.0,
35.0,
30,
25,
44,
30,
33,
43,
22,
43,
24,
19,
39,
31,
25,
28,
35,
30,
26,
31,
41,
36,
26,
35,
33,
28,
27,
34,
27,
22,
]
)
y_bar = np.mean(y)
print(y_bar)
30.933333333333334
In questo esempio, ipotizziamo che la varianza \(\sigma^2\) della popolazione sia identica alla varianza del campione:
sigma = np.std(y)
sigma
6.495810615739622
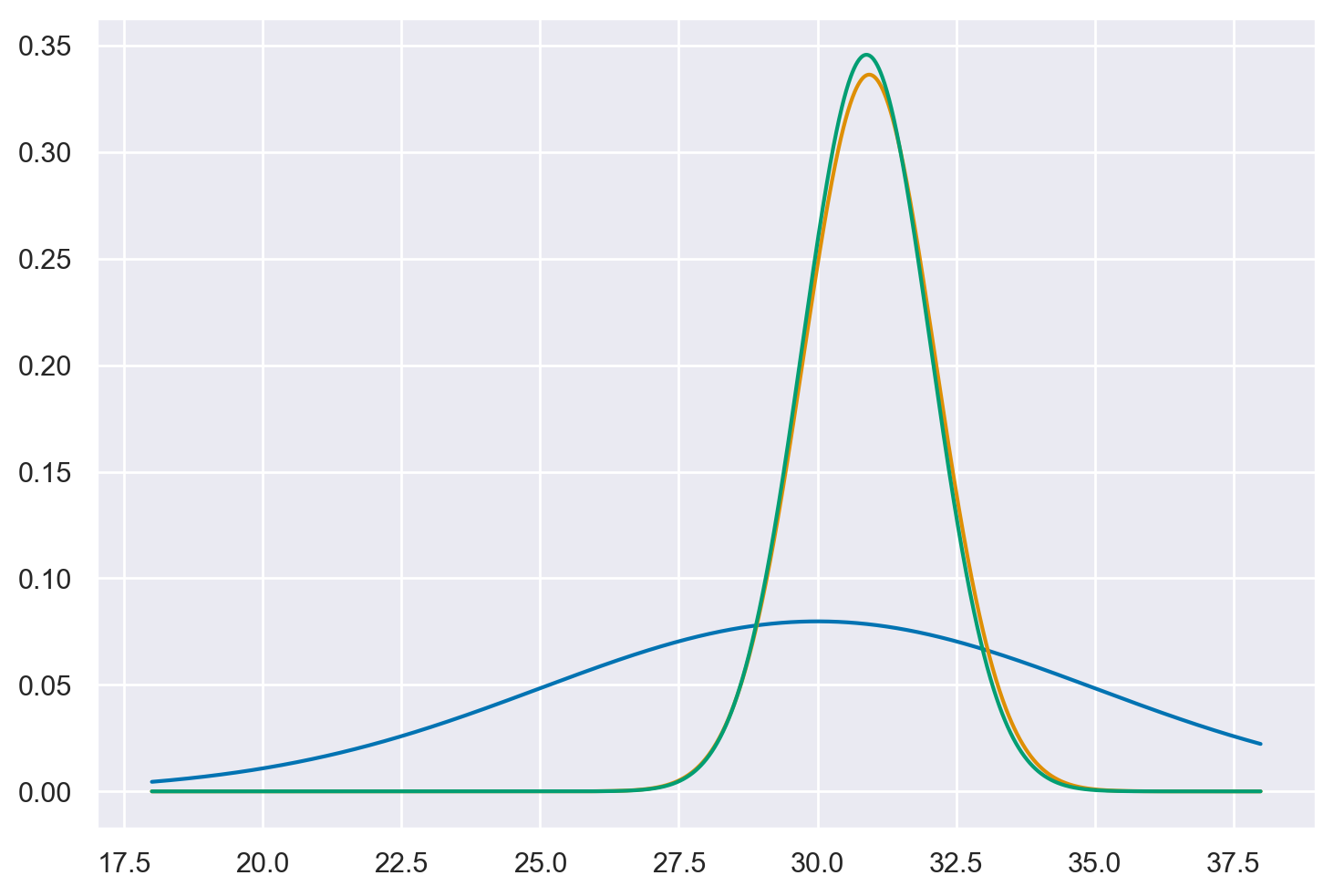
Per fare un esempio, imponiamo su \(\mu\) una distribuzione a priori \(\mathcal{N}(30, 5)\). In tali circostanze, la distribuzione a posteriori del parametro \(\mu\) può essere determinata per via analitica e corrisponde ad una Normale di media definita dall’eq. (59) e varianza definita dall’eq. (60). La figura seguente mostra un grafico della distribuzione a priori, della verosimiglianza e della distribuzione a posteriori di \(\mu\).
Iniziamo con la verosimiglianza.
def gaussian(y, m, s):
l = np.prod(stats.norm.pdf(y, loc=m, scale=s))
return l
x_axis = np.arange(18, 38, 0.01)
s = np.std(y)
like = [gaussian(y, val, s) for val in x_axis]
l = like / np.sum(like) * 100
Usando l’eq. (59), definiamo una funzione che ritorna la media della distribuzione a posteriori di \(\mu\).
def mu_post(sigma_0, mu_0, sigma, ybar, n):
return (1 / sigma_0**2 * mu_0 + n / sigma**2 * ybar) / (
1 / sigma_0**2 + n / sigma**2
)
Troviamo la media a posteriori.
mu_0 = 30 # media della distribuzione a priori per mu
sigma_0 = 5 # sd della distribuzione a priori per mu
sigma = np.std(y) # sd del campione (assunta essere sigma)
ybar = np.mean(y) # media del campione
n = len(y)
mu_post(sigma_0, mu_0, sigma, ybar, n)
30.883620206009738
Definiamo una funzione che ritorna la deviazione standard della distribuzione a posteriori di \(\mu\).
def sigma_post(sigma_0, sigma, n):
return np.sqrt(1 / (1 / sigma_0**2 + n / sigma**2))
Troviamo la deviazione standard a posteriori.
sigma = np.std(y) # sd del campione (assunta essere sigma)
n = len(y)
sigma_post(sigma_0, sigma, n)
1.1539504429303373
Possiamo ora disegnare la distribuzione a posteriori per la media della popolazione, insieme alla distribuzione a priori e alla verosimiglianza.
plt.plot(x_axis, stats.norm.pdf(x_axis, mu_0, sigma_0))
plt.plot(x_axis, l)
_ = plt.plot(
x_axis,
stats.norm.pdf(
x_axis, mu_post(sigma_0, mu_0, sigma, ybar, n), sigma_post(sigma_0, sigma, n)
),
)
Commenti e considerazioni finali#
Nel capitolo presente, abbiamo esaminato il concetto di aggiornamento bayesiano attraverso il prisma del modello normale-normale. Questo modello si distingue per la sua eleganza, in quanto se scegliamo una distribuzione normale come prior per il parametro di interesse, otteniamo una distribuzione a posteriori anch’essa di tipo normale.
Il processo ha inizio con l’assegnazione di una distribuzione a priori al parametro \( \mu \), la quale è caratterizzata da una media \( \mu_0 \) e una varianza \( \sigma_0^2 \). Dopo aver osservato nuovi dati, assumendo che essi seguano una distribuzione normale con una media campionaria \( \bar{y} \) e una varianza nota \( \sigma^2 \), abbiamo applicato il teorema normale-normale per calcolare la distribuzione a posteriori.
La media a posteriori, indicata come \( \mu_{\text{post}} \), emerge come una combinazione ponderata tra la media a priori \( \mu_0 \) e la media campionaria \( \bar{y} \). La ponderazione di queste medie è influenzata dalle varianze \( \sigma_0^2 \) e \( \sigma^2 \) della distribuzione a priori e dei dati osservati, rispettivamente. In modo analogo, la varianza a posteriori \( \sigma_{\text{post}}^2 \) è calcolata attraverso una formula che tiene conto di entrambe queste varianze.
In breve, questo capitolo ha messo in luce come l’impiego del modello normale-normale in un contesto bayesiano semplifichi notevolmente il calcolo delle distribuzioni a posteriori. Ciò è principalmente dovuto alla scelta di una distribuzione a priori di tipo normale, che preserva la “coniugatezza” e, di conseguenza, semplifica l’analisi.
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Fri Jan 26 2024
Python implementation: CPython
Python version : 3.11.7
IPython version : 8.19.0
numpy : 1.26.2
pandas : 2.1.4
arviz : 0.17.0
scipy : 1.11.4
seaborn : 0.13.0
matplotlib: 3.8.2
Watermark: 2.4.3

