Inferenza bayesiana su una media#
L’obiettivo principale di questo capitolo è esaminare un contesto che abbiamo già preso in considerazione in precedenza: ci troviamo di fronte a un campione di dati misurati su una scala a intervalli o rapporti e desideriamo effettuare inferenze sulla media della popolazione da cui il campione è stato estratto. Tuttavia, anziché procedere con una derivazione analitica della distribuzione a posteriori della media della popolazione, in questo caso utilizzeremo i metodi MCMC attraverso PyMC.
Preparazione del Notebook#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
import arviz as az
import pymc as pm
import pymc.sampling_jax
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=Warning)
/Users/corrado/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
Il modello Normale#
I priori coniugati Normali di una Normale non richiedono l’approssimazione numerica ottenuta mediante metodi MCMC. Tuttavia, per fare un esercizio e per verificare che i risultati ottenuti con MCMC corrispondano a quelli trovati per via analitica, ripetiamo l’esercizio descritto nel capitolo Distribuzioni coniugate (2) usando prima l’algoritmo di Metropolis e poi PyMC.
Un esempio concreto#
Useremo gli stessi dati usati in precedenza, ovvero il campione di 30 valori BDI-II ottenuti dai soggetti clinici esaminati da [ZBR19].
y = np.array(
[
26.0,
35.0,
30,
25,
44,
30,
33,
43,
22,
43,
24,
19,
39,
31,
25,
28,
35,
30,
26,
31,
41,
36,
26,
35,
33,
28,
27,
34,
27,
22,
]
)
df = pd.DataFrame()
df["y"] = y
La media del campione è:
np.mean(y)
30.933333333333334
Metropolis#
Scriviamo il codice per implementare l’algoritmo di Metropolis per questo problema.
def metropolis(logp, qdraw, stepsize, nsamp, xinit):
samples = np.empty(nsamp)
x_prev = xinit
accepted = 0
for i in range(nsamp):
x_star = qdraw(x_prev, stepsize)
logp_star = logp(x_star)
logp_prev = logp(x_prev)
logpdfratio = logp_star - logp_prev
u = np.random.uniform()
if np.log(u) <= logpdfratio:
samples[i] = x_star
x_prev = x_star
accepted += 1
else: # we always get a sample
samples[i] = x_prev
return samples, accepted
def prop(x, step):
return np.random.normal(x, step)
# Prior mean
mu_prior = 30
# prior std
std_prior = 5
logprior = lambda mu: stats.norm.logpdf(mu, loc=mu_prior, scale=std_prior)
loglike = lambda mu: np.sum(stats.norm.logpdf(y, loc=mu, scale=np.std(y)))
logpost = lambda mu: loglike(mu) + logprior(mu)
Per calcolare la distribuzione a priori logaritmica, utilizziamo la funzione stats.norm.logpdf, impostando gli iper-parametri a mu_prior = 30 e std_prior = 5.
La funzione di verosimiglianza è definita dal prodotto delle densità di probabilità (pdf) associate a ciascuna osservazione y. Tuttavia, poiché lavoriamo nel dominio logaritmico, la verosimiglianza logaritmica, indicata come loglike, viene calcolata sommando i logaritmi delle singole densità di probabilità, utilizzando la funzione np.sum.
La distribuzione a posteriori non normalizzata emerge come prodotto della distribuzione a priori e della funzione di verosimiglianza. In termini logaritmici, questo prodotto si trasforma in una somma dei corrispondenti valori logaritmici.
Per quanto riguarda la funzione prop, essa genera un nuovo valore x_star seguendo una distribuzione gaussiana centrata sul valore attuale della catena. La deviazione standard di questa gaussiana è definita da un valore empirico stepsize, scelto per ottenere un tasso di accettazione appropriato.
Calcoliamo la quantità logpdfratio = logp_star - logp_prev, che, nel contesto logaritmico, diventa una semplice differenza tra i logaritmi.
Infine, utilizziamo una variabile accepted, inizialmente impostata a zero, che viene incrementata durante il ciclo iterativo per calcolare il tasso di accettazione finale.
Eseguiamo il campionamento MCMC con la funzione metropolis.
x0 = np.random.uniform()
nsamps = 100000
samps, acc = metropolis(logpost, prop, 3, nsamps, x0)
Calcoliamo il tasso di accettazione.
acc / nsamps
0.41772
Esaminiamo l’autocorrelazione.
az.plot_autocorr(samps[40000::], max_lag=15)
plt.show()
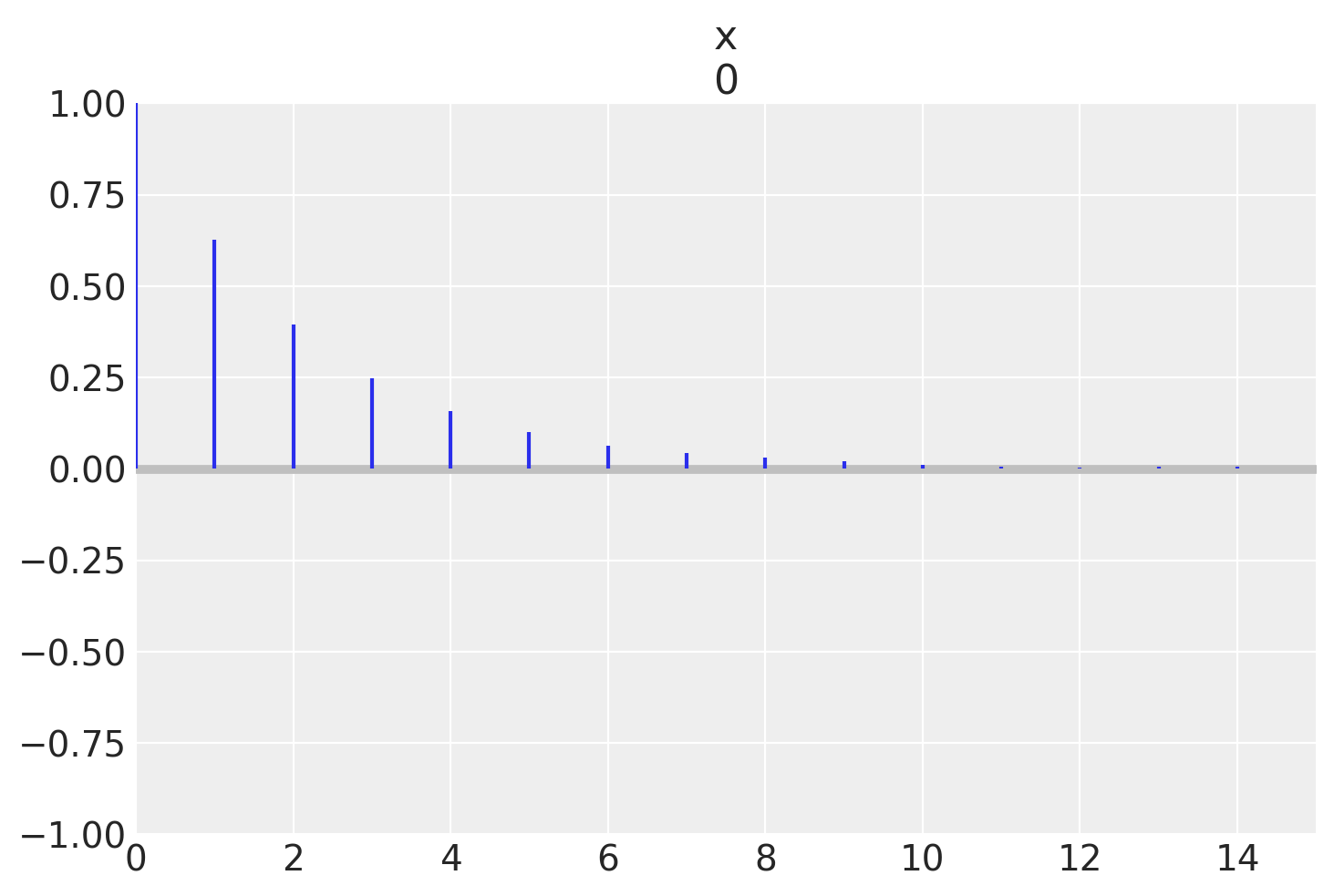
Se applichiamo un “thinning” con un intervallo di 5, l’autocorrelazione si riduce quasi a zero.
az.plot_autocorr(samps[40000::5], max_lag=15)
plt.show()
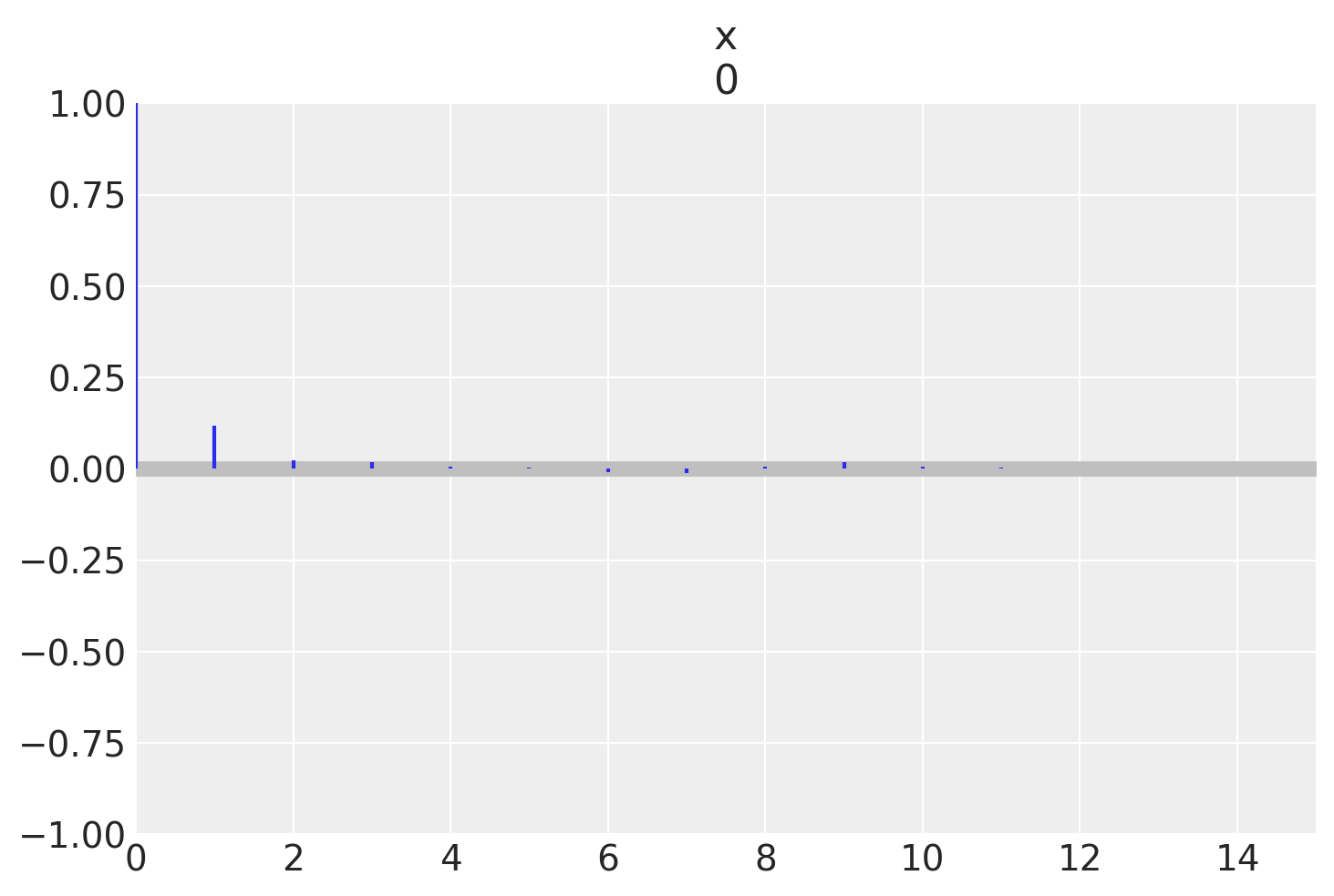
Esaminiamo la stima della distribuzione a posteriori dopo un burn-in di 40000 passi.
az.plot_posterior(samps[40000::5], hdi_prob=0.94)
plt.show()
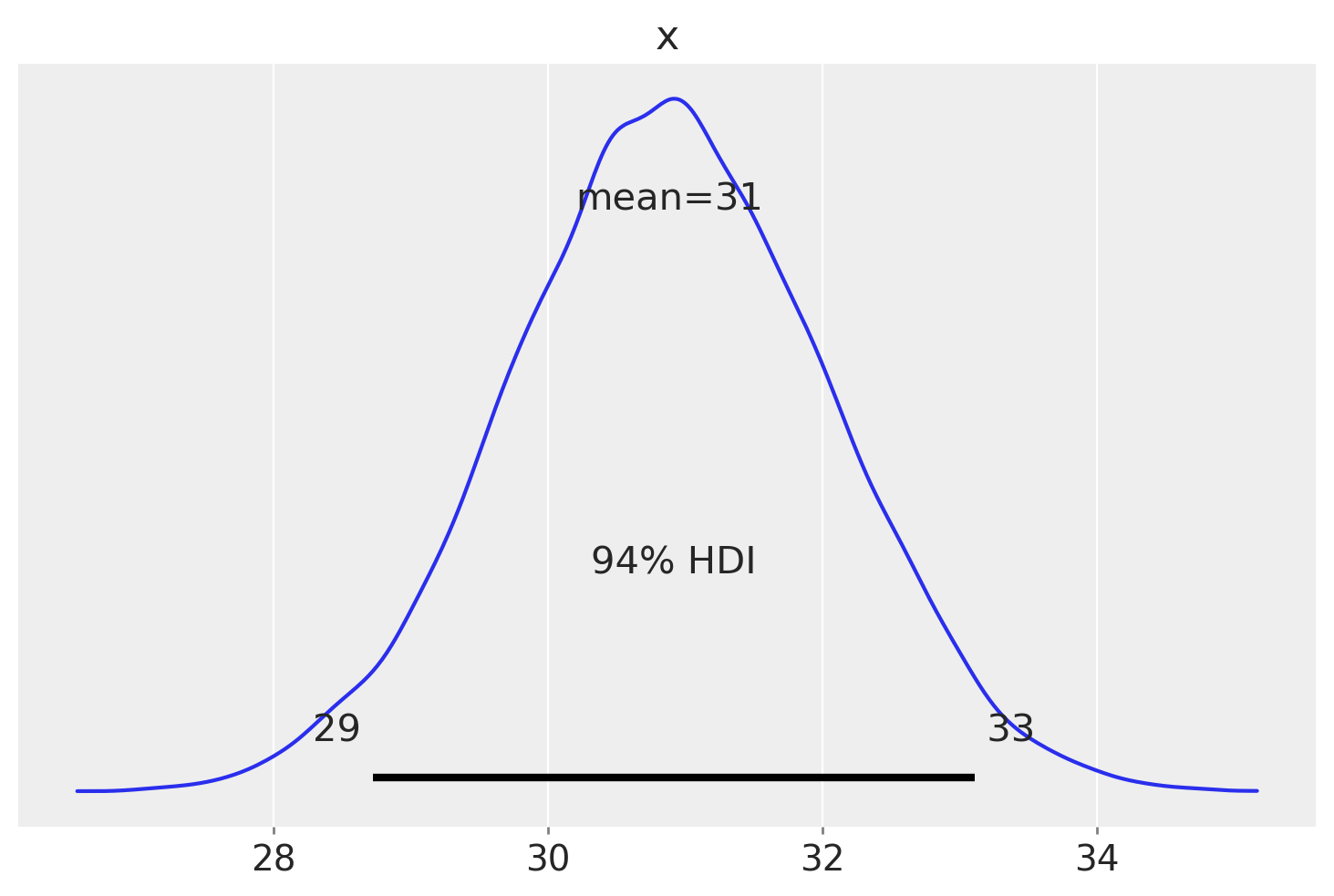
Calcoliamo l’intervallo a densità posteriore più alta del 94% per il parametro \(\mu\).
az.hdi(samps[40000::5], hdi_prob=0.94)
array([28.72657267, 33.11022257])
Campionamento con PyMC#
Utilizziamo ora PyMC per trovare la distribuzione a poteriori di \(\mu\).
Versione 1 (\(\sigma\) nota)#
Supponiamo che la varianza \(\sigma^2\) della popolazione sia nota e identica alla varianza del campione:
sigma = np.std(df["y"])
sigma
6.495810615739622
Come illustrato nel capitolo Distribuzioni coniugate (2), impostiamo una distribuzione a priori \(\mathcal{N}(30, 5)\) per il parametro \(\mu\), considerando \(\sigma\) come valore noto. Pertanto, il modello si definisce nel seguente modo:
Con questa specifica del modello, la variabile casuale \(Y\) segue una distribuzione normale con parametri \(\mu\) e \(\sigma\). Mentre il valore di \(\sigma\) è dato come noto e pari a 6.495810615739622, il parametro \(\mu\) rimane sconosciuto e rappresenta l’oggetto dell’inferenza. Sul parametro \(\mu\) imponiamo una distribuzione a priori normale con media 30 e deviazione standard 5.
Ripetiamo ora i calcoli precedenti usando PyMC. Di seguito è riportata la rappresentazione del modello in codice PyMC:
with pm.Model() as model:
data = pm.ConstantData("data", df["y"])
mu = pm.Normal("mu", mu=30, sigma=5)
pm.Normal("y", mu=mu, sigma=np.std(df["y"]), observed=data)
Eseguiamo il campionamento MCMC.
with model:
idata = pm.sampling_jax.sample_numpyro_nuts()
Show code cell output
Compiling...
Compilation time = 0:00:04.473011
Sampling...
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
Running chain 1: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 3: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 0: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 2: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 0: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1866.78it/s]
Running chain 1: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1869.23it/s]
Running chain 2: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1871.75it/s]
Running chain 3: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1873.91it/s]
Sampling time = 0:00:01.290441
Transforming variables...
Transformation time = 0:00:00.060946
Esaminiamo la traccia (cioè il vettore dei campioni del parametro \(\mu\) prodotti dalla procedura di campionamento MCMC) mediante un trace plot .
az.plot_trace(idata, combined=True, kind="rank_bars")
plt.show()

Esaminiamo l’autocorrelazione.
az.plot_autocorr(idata, combined=True, max_lag=15)
plt.show()
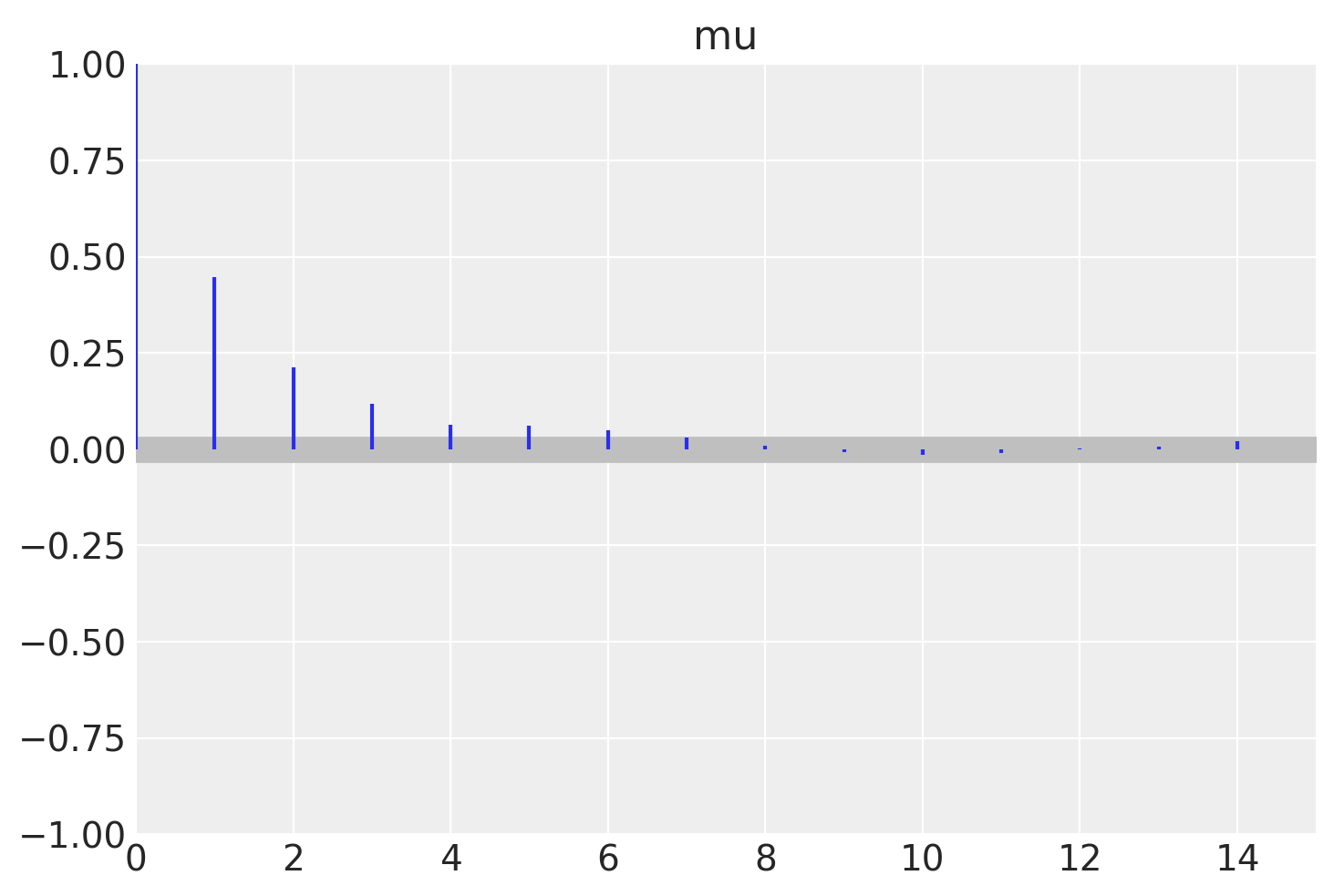
Una sintesi della distribuzione a posteriori dei parametri si ottiene nel modo seguente.
az.summary(idata, round_to=2)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| mu | 30.94 | 1.19 | 28.71 | 33.09 | 0.03 | 0.02 | 1352.74 | 1747.68 | 1.0 |
Si noti che la stima ottenuta per la media della popolazione corrisponde al valore teorico atteso fornito nel capitolo Distribuzioni coniugate (2), ovvero \(\mu_p\) = 30.88. Il valore teorico di \(\sigma_p\) è 1.15 e anch’esso è molto simile al valore ottenuto da PyMC.
Calcoliamo l’intervallo di credibilità a più alta densità a posteriori (HPD) al 94%.
az.hdi(idata, hdi_prob=0.94)
<xarray.Dataset>
Dimensions: (hdi: 2)
Coordinates:
* hdi (hdi) <U6 'lower' 'higher'
Data variables:
mu (hdi) float64 28.71 33.09Le stime così trovate sono molto simili ai quantili di ordine 0.03 e 0.97 della distribuzione a posteriori di \(\mu\) ottenuta per via analitica e a quelle ottenute con l’algoritmo di Metropolis che abbiamo implementato in precedenza.
stats.norm.ppf([0.03, 0.97], loc=30.8836, scale=1.1539)
array([28.71335226, 33.05384774])
Versione 2 (\(\sigma\) incognita)#
È facile estendere il caso precedente alla situazione in cui il parametro \(\sigma\) è incognito. Se non conosciamo \(\sigma\), è necessario imporre su tale parametro una distribuzione a priori. Supponiamo di ipotizzare per \(\sigma\) una distribuzione a priori \(\text{HalfNormal}(10)\).
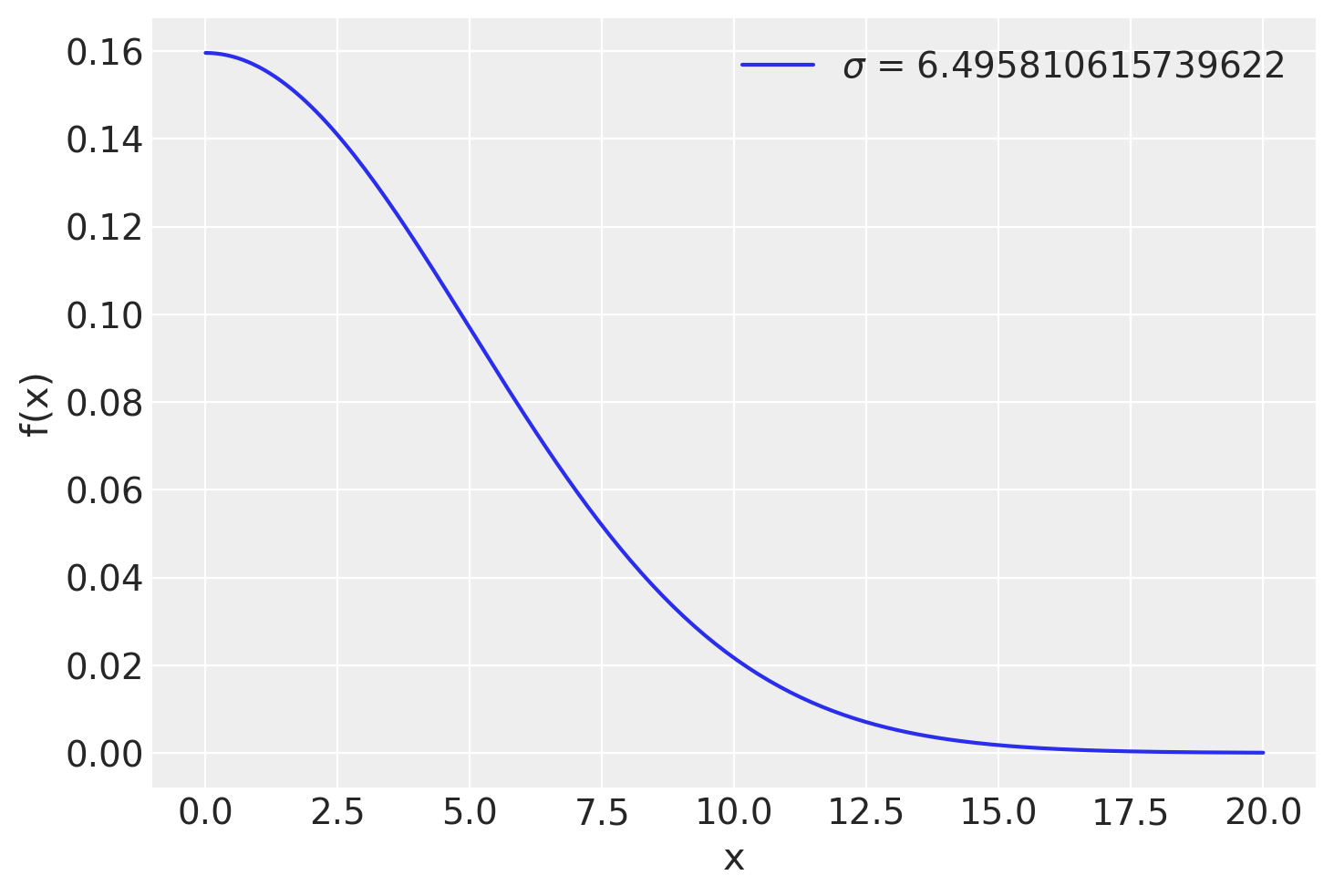
Mediante una HalfNormal(10) descriviamo il grado di credibilità soggettiva che attribuiamo ai possibili valori (> 0) del parametro \(\sigma\). Ai valori prossimi allo 0 attribuiamo la credibilità maggiore; la credibilità dei valori \(\sigma > 0\) diminuisce progressivamente quando ci si allontana dallo 0, come indicato dalla curva della figura seguente. Riteniamo poco credibili i valori \(\sigma\) maggiori di 15, anche se non escludiamo completamente che \(\sigma\) possa assumere un valore in questo intervallo.
La \(\text{HalfNormal}(10)\) è raffigurata nella figura seguente.
x = np.linspace(0, 20, 200)
pdf = stats.halfnorm.pdf(x, scale=5)
plt.plot(x, pdf, label=r'$\sigma$ = {}'.format(sigma))
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(loc=1)
plt.show()
In questo secondo scenario, più realistico, la struttura del modello è la seguente:
Questa formulazione è simile a quella esaminata precedentemente. Tuttavia, abbiamo espresso l’incertezza associata a \(\sigma\) (che è incognito) attraverso una distribuzione a priori \(\text{HalfNormal}\) con deviazione standard 10.
Di seguito è riportata la rappresentazione del modello in codice PyMC:
with pm.Model() as model2:
data = pm.ConstantData("data", df["y"])
mu = pm.Normal("mu", mu=30, sigma=5)
sigma = pm.HalfNormal("sigma", sigma=10)
pm.Normal("y", mu=mu, sigma=sigma, observed=data)
Eseguiamo il campionamento.
with model2:
idata2 = pm.sampling_jax.sample_numpyro_nuts()
Show code cell output
Compiling...
Compilation time = 0:00:00.660052
Sampling...
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
Running chain 1: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 0: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 2: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 3: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 0: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1726.34it/s]
Running chain 1: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1727.74it/s]
Running chain 2: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1729.64it/s]
Running chain 3: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1731.36it/s]
Sampling time = 0:00:01.224292
Transforming variables...
Transformation time = 0:00:00.034863
Esaminiamo la traccia con un trace plot .
az.plot_trace(idata2, combined=True, kind="rank_bars", figsize=(10, 4))
plt.tight_layout()
plt.show()
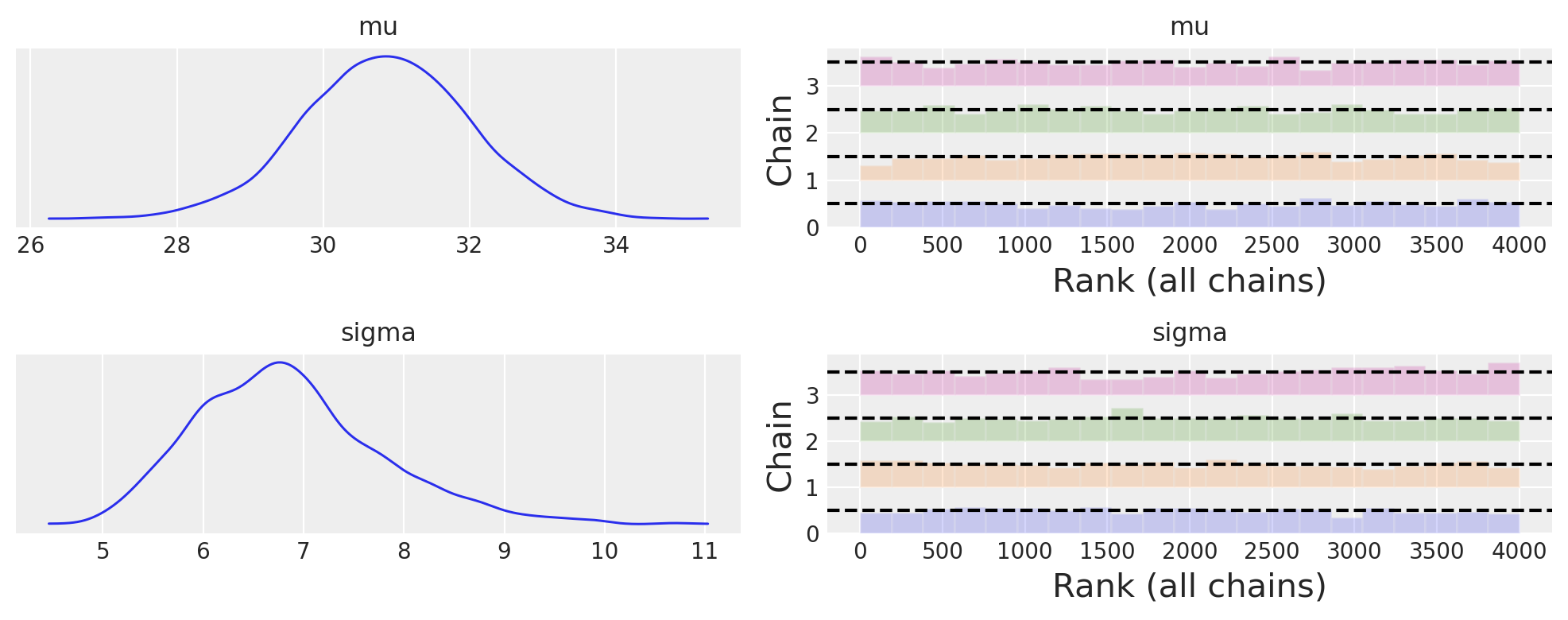
Una sintesi della distribuzione a posteriori dei parametri si ottiene nel modo seguente.
az.summary(idata2, round_to=2)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| mu | 30.86 | 1.17 | 28.62 | 33.02 | 0.02 | 0.02 | 3051.42 | 2250.89 | 1.0 |
| sigma | 6.87 | 0.97 | 5.22 | 8.72 | 0.02 | 0.01 | 2766.97 | 2357.76 | 1.0 |
Troviamo l’intervallo di credibilità a più alta densità a posteriori (HPD) al 94%.
az.hdi(idata2, hdi_prob=0.94)
<xarray.Dataset>
Dimensions: (hdi: 2)
Coordinates:
* hdi (hdi) <U6 'lower' 'higher'
Data variables:
mu (hdi) float64 28.62 33.02
sigma (hdi) float64 5.215 8.719I risultati sono molto simili a quelli ottenuti in precedenza.
Commenti e considerazioni finali#
In questo capitolo abbiamo visto come calcolare l’intervallo di credibilità per la media di una v.c. Normale usando l’algoritmo di Metropolis e PyMC. I risultati che abbiamo trovato in entrambi i casi corrispondono molto da vicino a quelli che abbiamo ottenuto per via analitica nel capitolo Distribuzioni coniugate (2).
%run ../wm.py
Watermark:
----------
Last updated: 2024-01-26T18:59:31.880467+01:00
Python implementation: CPython
Python version : 3.11.7
IPython version : 8.19.0
Compiler : Clang 16.0.6
OS : Darwin
Release : 23.3.0
Machine : x86_64
Processor : i386
CPU cores : 8
Architecture: 64bit

