Modello gerarchico gaussiano#
In questo capitolo, proseguiremo la discussione sul modello gerarchico bayesiano utilizzando PyMC, concentrandoci questa volta sul caso in cui i dati seguono una distribuzione gaussiana.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pymc as pm
import pymc.sampling_jax
import bambi as bmb
import scipy.stats as stats
from scipy.stats import gaussian_kde
from sklearn.preprocessing import scale
import arviz as az
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=Warning)
/Users/corrado/opt/anaconda3/envs/pymc9_env/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
Preparazione del notebook#
Per discutere il modello gerarchico gaussiano, utilizzeremo nuovamente i dati relativi ai pinguini Palmer.
penguins = pd.read_csv("../data/penguins.csv")
# Subset to the columns needed
missing_data = penguins.isnull()[
["bill_length_mm", "flipper_length_mm", "sex", "body_mass_g"]
].any(axis=1)
# Drop rows with any missing data
penguins = penguins.loc[~missing_data]
penguins.shape
(333, 8)
Modellizzazione bayesiana#
Il modello che abbiamo usato nel capitolo Gruppi multipli non è un modello gerarchico, poiché \( \mu \) e \( \sigma \) sono stimati in modo indipendente per ciascuna delle tre specie. In un modello gerarchico, è necessario un livello “superiore” di parametri che influenzano i parametri \( \mu \) e \( \sigma \) per ciascuna specie, permettendo la condivisione delle informazioni tra le diverse specie. In altre parole, in un modello gerarchico, i parametri \( \mu \) e \( \sigma \) per ciascuna specie vengono a loro volta modellati come estrazioni da una distribuzione “superiore”, il che permette un certo grado di pooling delle informazioni tra le diverse specie.
coords = {"species": ["Adelie", "Gentoo", "Chinstrap"]}
with pm.Model(coords=coords) as hierarchical_model:
# Constant data for species indices
species_idx = pm.ConstantData(
"species_idx",
penguins["species"].replace({"Adelie": 0, "Gentoo": 1, "Chinstrap": 2}).values,
)
# Hyperpriors
mu_mean = pm.Normal("mu_mean", 4200, 1000)
mu_sd = pm.HalfNormal("mu_sd", 500)
sigma_mean = pm.HalfNormal("sigma_mean", 500)
sigma_sd = pm.HalfNormal("sigma_sd", 100)
# Normal priors for mu and sigma for each species
mu = pm.Normal("mu", mu_mean, mu_sd, dims="species")
sigma = pm.HalfNormal("sigma", sigma=sigma_mean, dims="species")
# Likelihood
y = pm.Normal(
"y",
mu=mu[species_idx],
sigma=sigma[species_idx],
observed=penguins["body_mass_g"],
)
In questo modello gerarchico, mu_mean e mu_sd fungono da iperparametri per la distribuzione a priori di \( \mu \), mentre sigma_mean e sigma_sd servono come iperparametri per la distribuzione a priori di \( \sigma \). Gli iperparametri facilitano il “pooling parziale” delle informazioni tra le diverse categorie di specie, permettendo una condivisione strutturale delle informazioni nel modello. Questo pooling parziale consente di effettuare inferenze più robuste, specialmente quando la dimensione del campione per una determinata categoria è limitata.
In questo codice, coords è un dizionario che definisce una coordinata chiamata “species” con tre valori: “Adelie”, “Gentoo” e “Chinstrap”. Questa coordinata viene poi utilizzata per definire le dimensioni (dims) delle variabili casuali mu e sigma nel modello, permettendo di avere una variabile casuale separata per ciascuna specie di pinguino.
Definizione di
coords:coords = {"species": ["Adelie", "Gentoo", "Chinstrap"]}
Creazione del modello con
coords:with pm.Model(coords=coords) as hierarchical_model: ...
Utilizzo di
dims='species':mu = pm.Normal("mu", mu_mean, mu_sd, dims="species") sigma = pm.HalfNormal("sigma", sigma=sigma_mean, dims="species")
Qui,
dims='species'indica chemuesigmasono array di variabili casuali, una per ciascuna specie di pinguino. Le dimensioni di queste variabili casuali corrisponderanno ai valori forniti incoords.Utilizzo di
species_idx:species_idx = pm.ConstantData( "species_idx", penguins["species"].replace({"Adelie": 0, "Gentoo": 1, "Chinstrap": 2}).values, ) ... y = pm.Normal( "y", mu=mu[species_idx], sigma=sigma[species_idx], observed=penguins["body_mass_g"], )
Qui,
species_idxè una mappatura degli indici delle specie di pinguino ai corrispondenti indici numerici (0 per “Adelie”, 1 per “Gentoo”, 2 per “Chinstrap”). Questi indici vengono poi utilizzati per selezionare i valori corrispondenti dimuesigmaper ogni osservazione nel modello di probabilità. In particolare,mu[species_idx]esigma[species_idx]permettono di utilizzare il valore dimuesigmacorrispondente per ciascuna specie di pinguino quando si specifica la likelihoody.
Visualizziamo la struttura del modello.
pm.model_to_graphviz(hierarchical_model)
Eseguiamo il controllo predittivo a priori.
with hierarchical_model:
idata_pooling_prior_pred = pm.sample_prior_predictive(random_seed=rng)
Sampling: [mu, mu_mean, mu_sd, sigma, sigma_mean, sigma_sd, y]
likelihood_samples = idata_pooling_prior_pred.prior_predictive.y
flattened_array = np.ravel(likelihood_samples.values)
plt.hist(flattened_array, bins=60, density=True)
plt.xlabel('Weight (body_mass_g)')
plt.ylabel('Density')
plt.title('Prior Predictive Check')
plt.show()
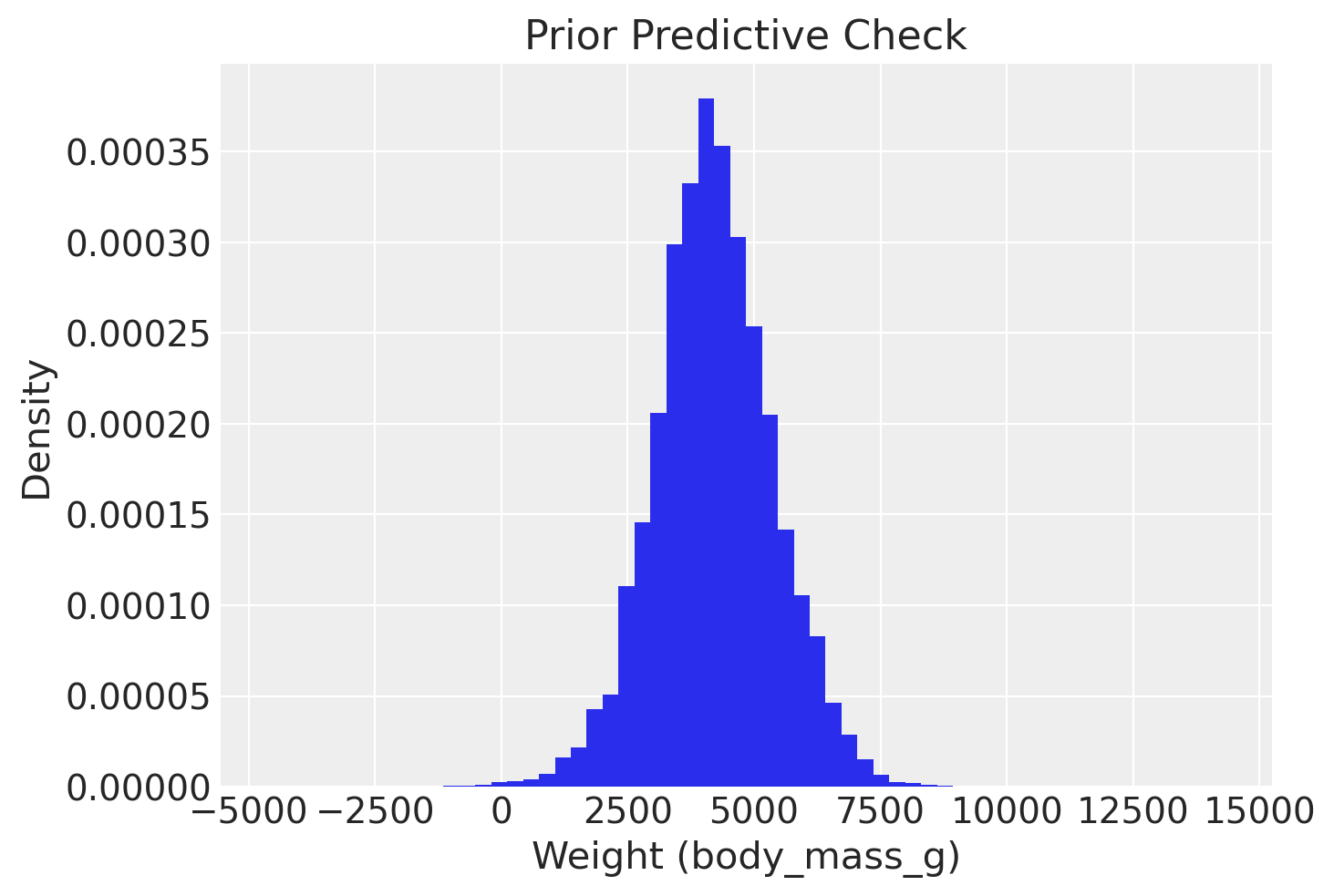
Eseguiamo il campionamento.
with hierarchical_model:
idata = pm.sampling_jax.sample_numpyro_nuts(idata_kwargs={"log_likelihood": True})
Show code cell output
Compiling...
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1699560276.643464 1 tfrt_cpu_pjrt_client.cc:349] TfrtCpuClient created.
Compilation time = 0:00:01.107612
Sampling...
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
0%| | 0/2000 [00:00<?, ?it/s]
Compiling.. : 0%| | 0/2000 [00:00<?, ?it/s]
Running chain 1: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 0: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 2: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 3: 0%| | 0/2000 [00:01<?, ?it/s]
Running chain 1: 5%|███▍ | 100/2000 [00:02<00:05, 343.05it/s]
Running chain 0: 5%|███▍ | 100/2000 [00:02<00:05, 320.10it/s]
Running chain 2: 5%|███▍ | 100/2000 [00:02<00:06, 299.74it/s]
Running chain 3: 5%|███▍ | 100/2000 [00:02<00:06, 297.02it/s]
Running chain 0: 90%|███████████████████████████████████████████████████████████▍ | 1800/2000 [00:02<00:00, 5539.17it/s]
Running chain 2: 100%|██████████████████████████████████████████████████████████████████| 2000/2000 [00:02<00:00, 5843.71it/s]
Running chain 3: 85%|████████████████████████████████████████████████████████ | 1700/2000 [00:02<00:00, 4912.37it/s]
Running chain 0: 100%|███████████████████████████████████████████████████████████████████| 2000/2000 [00:02<00:00, 844.23it/s]
Running chain 1: 100%|███████████████████████████████████████████████████████████████████| 2000/2000 [00:02<00:00, 844.72it/s]
Running chain 2: 100%|███████████████████████████████████████████████████████████████████| 2000/2000 [00:02<00:00, 845.21it/s]
Running chain 3: 100%|███████████████████████████████████████████████████████████████████| 2000/2000 [00:02<00:00, 845.63it/s]
Sampling time = 0:00:02.608735
Transforming variables...
Transformation time = 0:00:00.096423
Computing Log Likelihood...
Log Likelihood time = 0:00:00.140860
Esaminiamo le distribuzioni a posteriori dei parametri del modello.
az.plot_trace(idata, combined=True, kind="rank_bars")
plt.tight_layout()
plt.show()
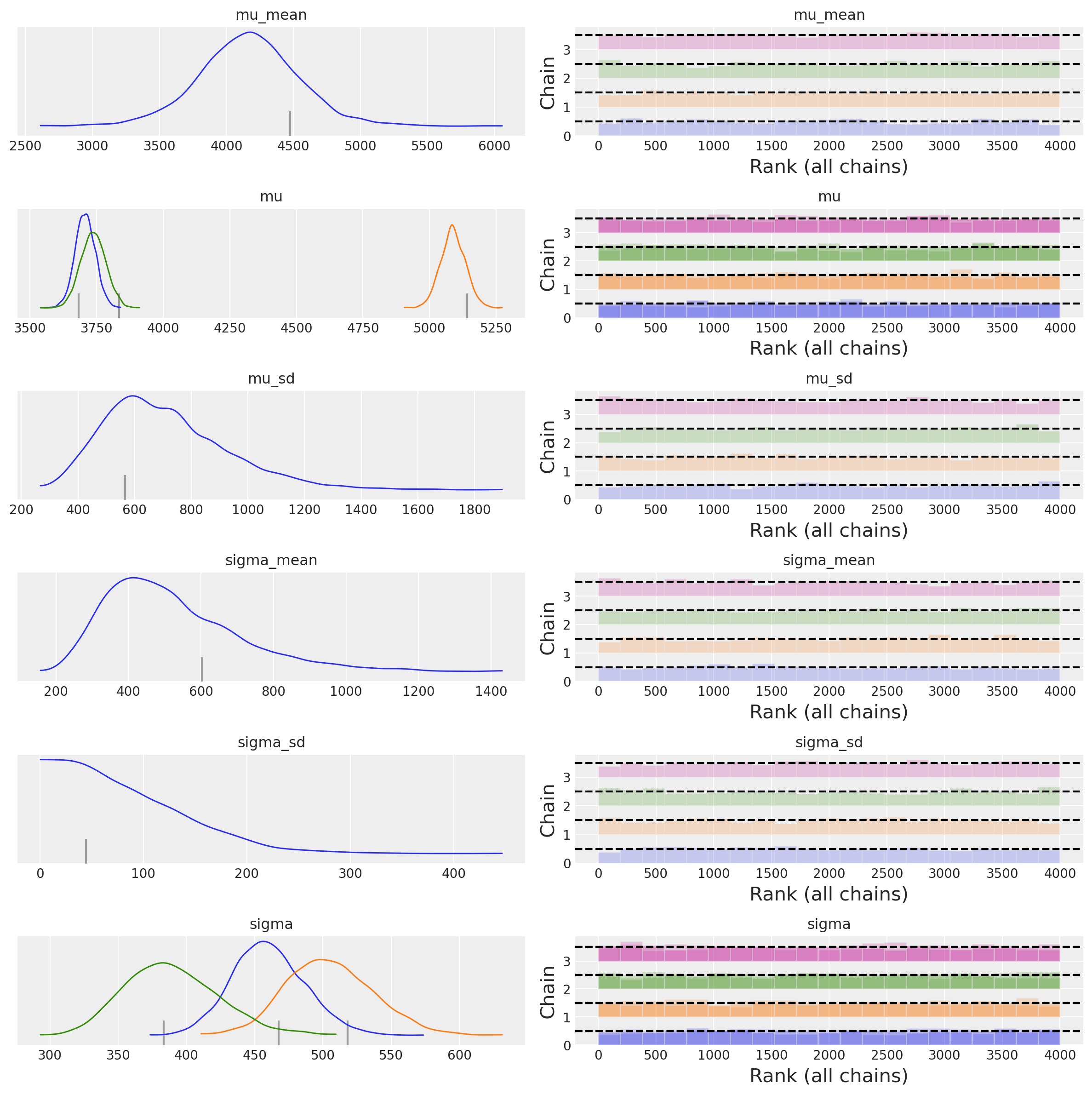
Creiamo un sommario numerico.
az.summary(idata)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| mu_mean | 4164.215 | 377.307 | 3401.162 | 4835.179 | 6.848 | 4.875 | 3148.0 | 2394.0 | 1.0 |
| mu[Adelie] | 3707.225 | 37.918 | 3632.657 | 3776.245 | 0.552 | 0.391 | 4717.0 | 2745.0 | 1.0 |
| mu[Gentoo] | 5088.068 | 46.954 | 4998.154 | 5173.480 | 0.694 | 0.491 | 4585.0 | 2857.0 | 1.0 |
| mu[Chinstrap] | 3737.218 | 46.886 | 3649.121 | 3825.680 | 0.772 | 0.547 | 3705.0 | 2963.0 | 1.0 |
| mu_sd | 708.058 | 217.546 | 361.983 | 1131.928 | 3.720 | 2.729 | 3712.0 | 2981.0 | 1.0 |
| sigma_mean | 521.303 | 186.282 | 239.950 | 878.082 | 3.240 | 2.462 | 4086.0 | 2692.0 | 1.0 |
| sigma_sd | 79.666 | 59.780 | 0.043 | 184.647 | 0.900 | 0.636 | 2882.0 | 1553.0 | 1.0 |
| sigma[Adelie] | 460.251 | 26.690 | 409.645 | 510.295 | 0.403 | 0.286 | 4423.0 | 2659.0 | 1.0 |
| sigma[Gentoo] | 505.070 | 32.247 | 449.419 | 568.143 | 0.487 | 0.348 | 4477.0 | 2936.0 | 1.0 |
| sigma[Chinstrap] | 389.097 | 34.207 | 327.894 | 452.967 | 0.528 | 0.382 | 4451.0 | 2634.0 | 1.0 |
Nel confronto tra le stime della media del peso per le tre specie di pinguini ottenute dal modello gerarchico e quelle derivanti dal modello indipendente, osserviamo un effetto di “shrinkage”. In particolare, le stime delle medie specifiche per ogni specie nel modello gerarchico tendono a convergere leggermente verso la media globale del peso, pari a 4191.570 g. Questo è in contrasto con le stime ottenute dal modello che considera le tre specie come indipendenti:
\( \mu_{\text{Adelie}} = 3707.643 \)
\( \mu_{\text{Gentoo}} = 5091.668 \)
\( \mu_{\text{Chinstrap}} = 3733.534 \)
Questo fenomeno di shrinkage è una caratteristica distintiva dei modelli gerarchici e indica una maggiore robustezza delle stime, specialmente quando la dimensione del campione per una o più categorie è relativamente piccola.
var_names=["mu_mean", "mu"]
az.plot_forest(idata, var_names=var_names, combined=True)
obs_mean=hierarchical_model["y"].eval().mean()
plt.axvline(x = obs_mean, color = 'black', alpha=0.1)
plt.show()
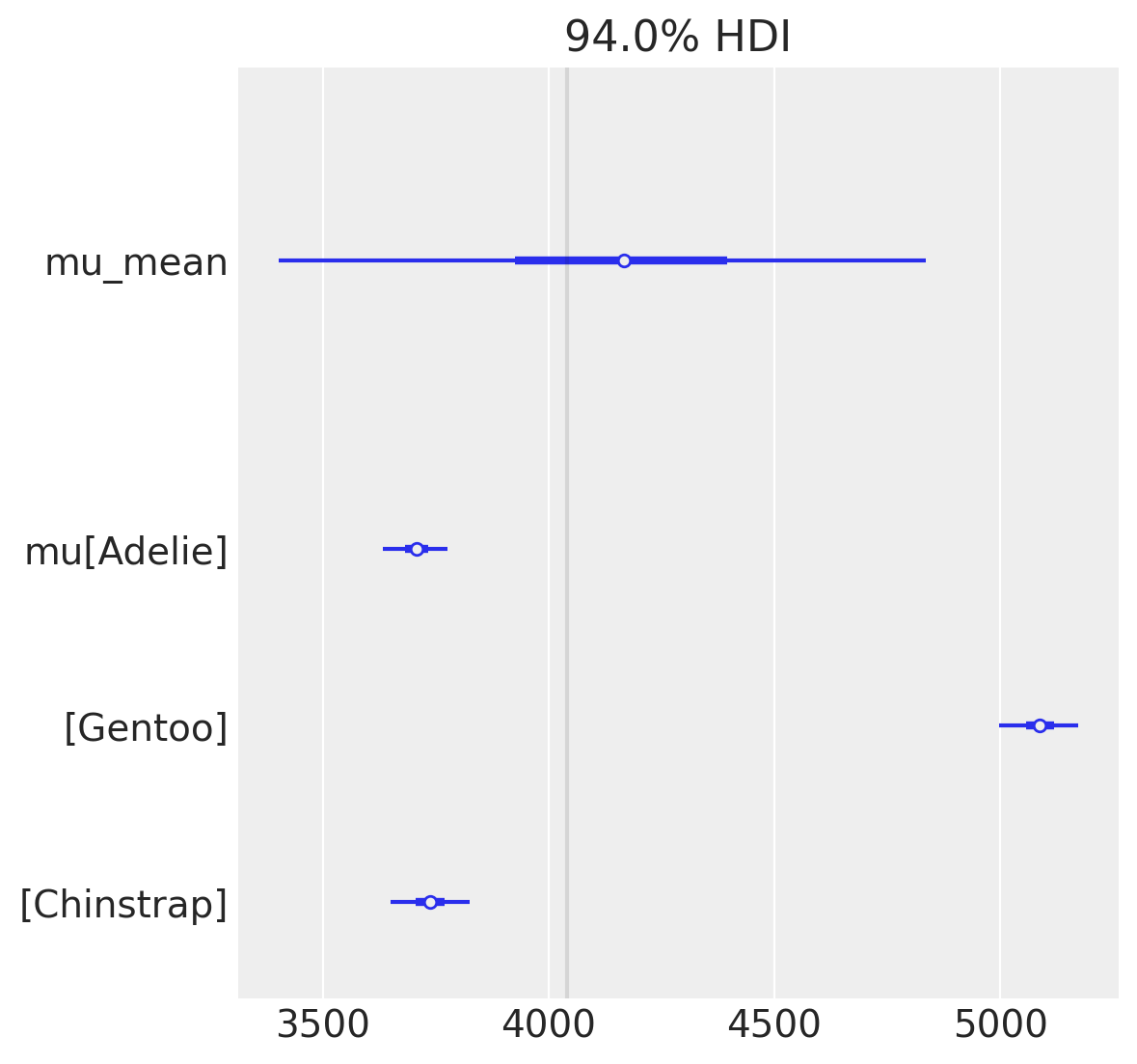
Valutiamo il modello mediante un controllo predittivo a posteriori (Posterior Predictive Check, PPC). Questa tecnica prevede la generazione di dati simulati dal modello, utilizzando i parametri estratti dalle distribuzioni a posteriori, per poi confrontare queste simulazioni con i dati osservati. Questo processo permette di verificare quanto accuratamente il modello riesca a riprodurre le caratteristiche dei dati e, di conseguenza, la sua adeguatezza.
with hierarchical_model:
post_pred = pm.sample_posterior_predictive(idata)
Sampling: [y]
az.plot_ppc(post_pred, num_pp_samples=50)
plt.show()
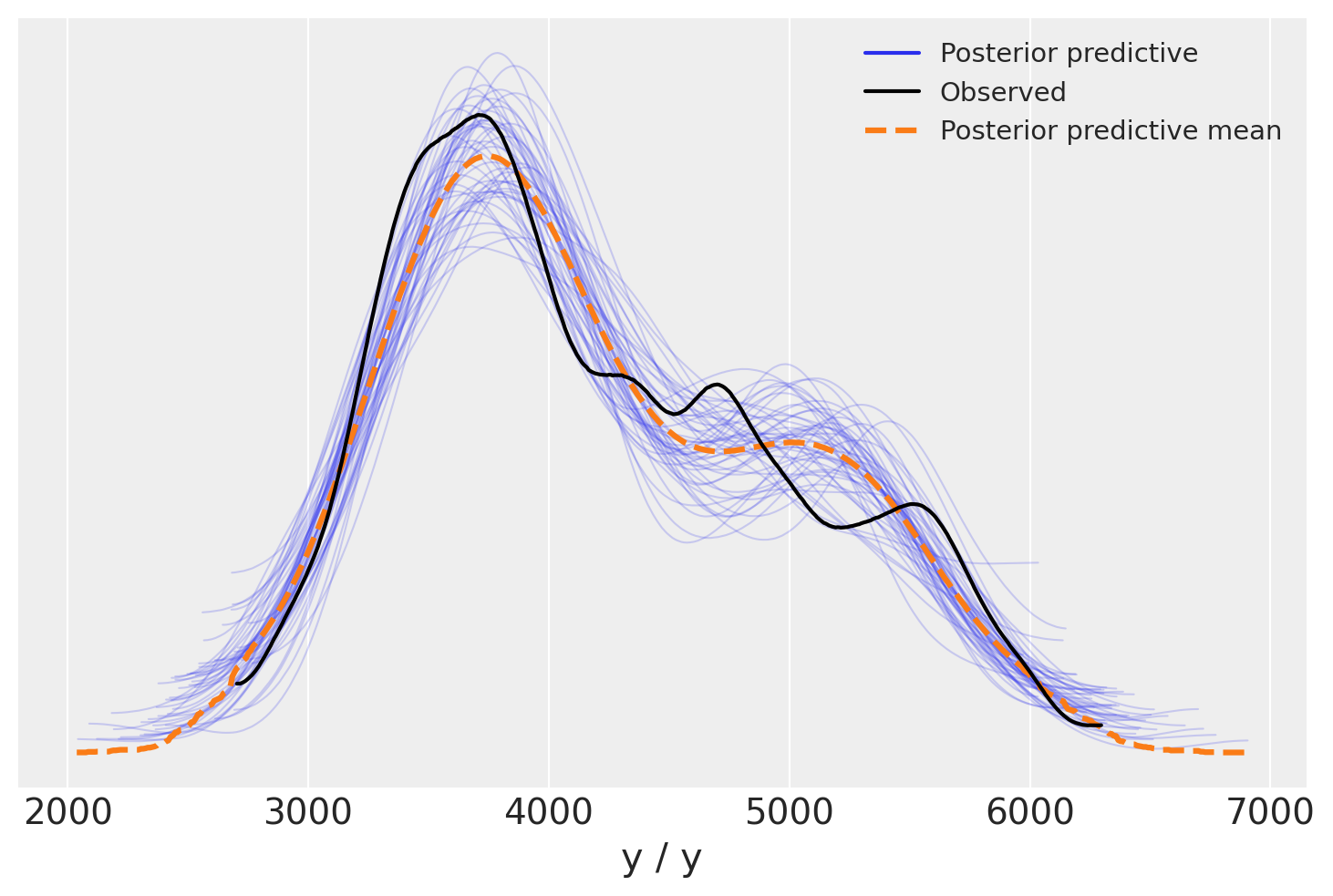
L’adattamento del modello ai dati è molto buono.
Calcoliamo ora la Expected Log Predictive Density (ELPD) e la diagnostica Pareto \(k\).
m_loo = az.loo(idata)
m_loo
Computed from 4000 posterior samples and 333 observations log-likelihood matrix.
Estimate SE
elpd_loo -2516.14 11.71
p_loo 5.49 -
------
Pareto k diagnostic values:
Count Pct.
(-Inf, 0.5] (good) 333 100.0%
(0.5, 0.7] (ok) 0 0.0%
(0.7, 1] (bad) 0 0.0%
(1, Inf) (very bad) 0 0.0%
La metrica diagnostica Pareto \(k\) non indica la presenza di valori anomali o outlier nel set di dati.
Watermark#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor
Last updated: Thu Nov 09 2023
Python implementation: CPython
Python version : 3.11.6
IPython version : 8.16.1
pytensor: 2.13.1
scipy : 1.11.3
pandas : 2.1.1
numpy : 1.25.2
arviz : 0.16.1
seaborn : 0.13.0
bambi : 0.12.0
pymc : 5.9.1
matplotlib: 3.8.0
Watermark: 2.4.3

