Incertezza inferenziale e variabilità dei risultati#
Nel presente capitolo, ci addentreremo nell’analisi degli errori standard della media. Sebbene l’errore standard sia un concetto tipico della statistica frequentista, e questo corso ponga l’accento sulla statistica bayesiana, è importante esplorare questo tema, in quanto il suo utilizzo nella ricerca è estremamente diffuso. In particolare, ci focalizzeremo su un articolo di Zhang et al. [ZHM+23], che stabilisce un collegamento tra l’incertezza inferenziale, espressa dall’errore standard, e la deviazione standard, che simboleggia la variabilità dei risultati all’interno di uno studio. Comprendere il legame tra questi due concetti è fondamentale. Infatti, Zhang et al. [ZHM+23] sottolineano che l’approccio dominante nella visualizzazione scientifica, il quale include esclusivamente l’incertezza inferenziale (vale a dire la rappresentazione grafica della media con l’aggiunta delle barre d’errore corrispondenti agli errori standard), può portare a interpretazioni fuorvianti dei dati. Questo può condurre a una sovrastima sistematica degli effetti del trattamento, un fenomeno che può verificarsi persino tra gli esperti più qualificati del settore. Attraverso questo approfondimento, miriamo a fornire una visione chiara di come l’errore standard e la deviazione standard interagiscano, e di come la loro corretta interpretazione possa evitare possibili equivoci nell’analisi e nella comunicazione dei risultati della ricerca.
Preparazione del Notebook#
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.image as mpimg
import seaborn as sns
import statistics as st
import scipy.stats as stats
import math
import itertools
import arviz as az
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
La rappresentazione dell’incertezza inferenziale#
Zhang et al. [ZHM+23] iniziano la loro analisi esplorando la relazione tra incertezza inferenziale e variabilità dei risultati nel contesto della ricerca empirica. Nell’ambito della ricerca empirica, l’obiettivo è fare inferenze sulla popolazione intera utilizzando un campione ristretto di dati. Questo può riguardare, ad esempio, il confronto tra il benessere psicologico di un gruppo sottoposto a trattamento sperimentale e un gruppo di controllo, o la valutazione dell’efficacia di un intervento psicologico tra individui con differenti caratteristiche personologiche. In tali casi, trarre conclusioni valide può essere complicato, specialmente quando si ha a che fare con campioni piccoli e risultati altamente variabili all’interno di ciascun campione.
La risposta comune a questi problemi è concentrarsi su misure aggregate, come le medie dei gruppi, invece che sui singoli risultati, e fornire una misura dell’incertezza inferenziale relativa alla precisione della stima della media. L’incertezza inferenziale è spesso espressa attraverso errori standard (SE), intervalli di confidenza, intervalli di credibilità Bayesiani, o metodologie analoghe.
La quantificazione dell’incertezza inferenziale è fondamentale, in quanto fornisce un intervallo plausibile di valori per la quantità di interesse e previene interpretazioni erronee dovute alla variazione casuale nei campioni. Ciò assicura che le conclusioni siano rappresentative delle tendenze reali nella popolazione e non siano semplici artefatti dei campioni specifici.
Tuttavia, Zhang et al. [ZHM+23] evidenziano una problematica che può sorgere quando la ricerca si focalizza unicamente sui risultati aggregati e sull’incertezza inferenziale, ovvero il fatto che viene trascurata la variabilità dei risultati individuali. Questa variabilità, spesso quantificata attraverso la deviazione standard (SD) o la varianza, è cruciale per valutare le dimensioni dell’effetto e la prevedibilità dei risultati futuri.
Benché esistano associazioni tra incertezza inferenziale e variabilità dei risultati, questi sono concetti distinti e facilmente confondibili. L’incertezza inferenziale si riferisce alla fiducia nelle stime di parametri specifici, come la media, mentre la variabilità dei risultati riguarda le differenze nei risultati individuali all’interno di un gruppo.
La confusione tra questi due aspetti e/o l’eccessiva enfasi sull’incertezza inferenziale può generare interpretazioni sbagliate riguardo all’ampiezza e alla rilevanza dei risultati della ricerca. Ciò può verificarsi anche tra gli specialisti che si occupano di creare e interpretare questi dati, sottolineando l’importanza di una comunicazione chiara e di una maggiore consapevolezza nella presentazione delle analisi statistiche.
Illusione di prevedibilità#
Per comprendere le differenze tra incertezza inferenziale e variabilità dei risultati, e cogliere come focalizzarsi sulla prima possa portare a conclusioni errate sulla seconda, Zhang et al. [ZHM+23], citando un esempio basato su un celebre studio di Anderson and Dill [AD00]. Questo studio riguarda l’effetto dei videogiochi violenti sul comportamento aggressivo dei giocatori e include una serie di esperimenti in cui i partecipanti sono stati esposti a videogiochi con diversi livelli di contenuti violenti. In seguito, sono stati misurati vari aspetti dell’aggressività attraverso questionari e osservazioni comportamentali. Gli autori hanno scoperto che c’era una correlazione significativa tra il gioco di videogiochi violenti e un aumento dell’aggressività nei partecipanti. Hanno concluso che i videogiochi violenti possono aumentare i comportamenti aggressivi e hanno suggerito che tale effetto potrebbe essere dovuto all’immersione in un contesto violento e all’apprendimento di nuovi schemi comportamentali attraverso il gioco. Questo studio è diventato un punto di riferimento nelle discussioni sulla regolamentazione dei contenuti dei videogiochi e sull’impatto potenziale che i media possono avere sul comportamento.
Ispirandosi ai risultati riportati da Anderson and Dill [AD00], Zhang et al. [ZHM+23] hanno costruito la figura seguente.
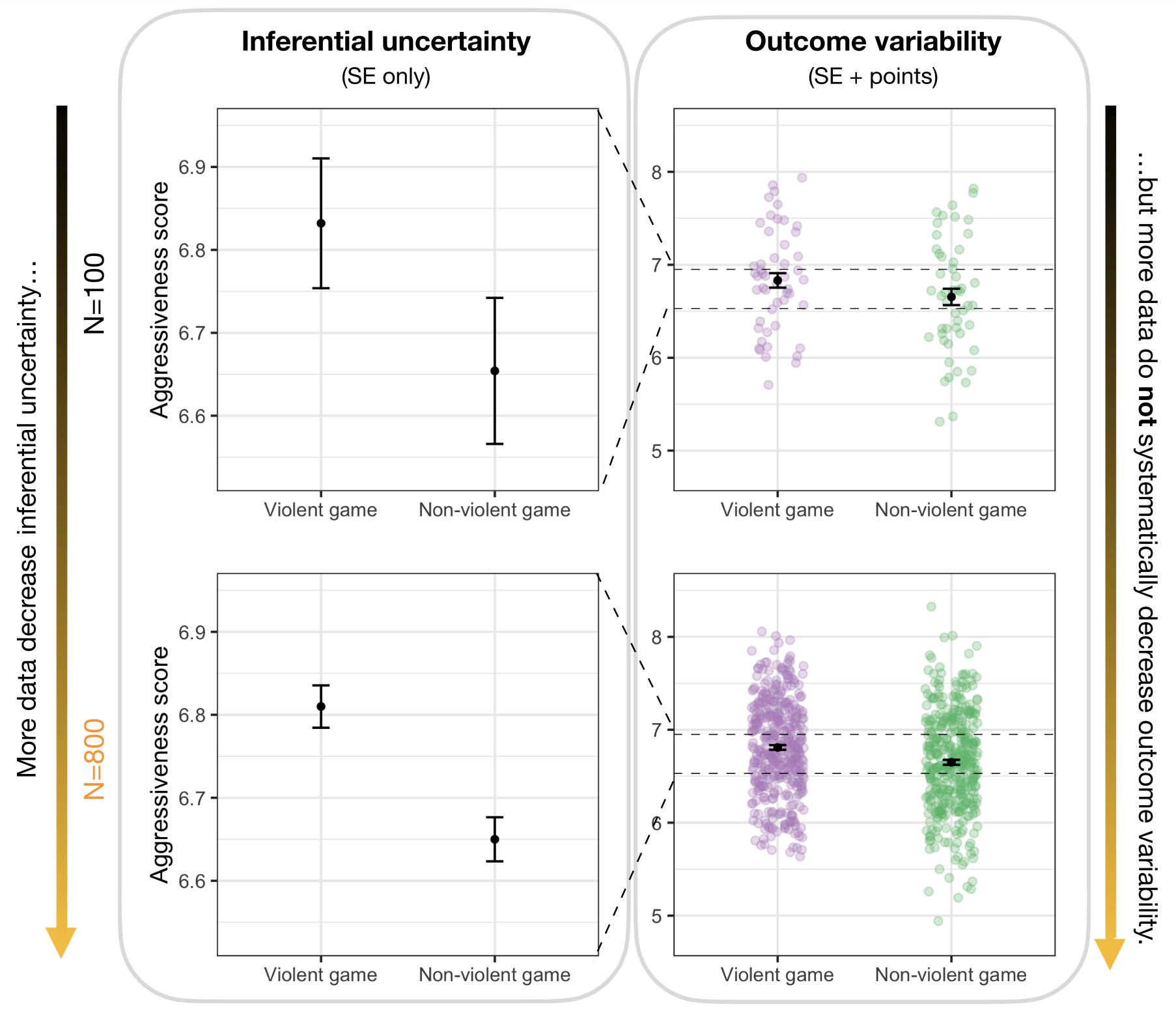
Fig. 3 Incertezza inferenziale vs. variabilità dei risultati. (Sinistra) Medie stimate e una barra di errore che rappresenta un errore standard (SE) sopra e uno sotto la media, per due condizioni in un esperimento. L’errore standard è una misura dell’incertezza nella nostra inferenza della media. (Destra) Risultati individuali mostrati in aggiunta agli stessi errori standard sulla Sinistra. Con solo 100 partecipanti per condizione (Sopra), abbiamo stime meno sicure della media rispetto a quando abbiamo 800 partecipanti per condizione (Sotto). Tuttavia, più dati non riducono sistematicamente la variabilità nei risultati stessi. La figura è tratta da Zhang et al. [ZHM+23].#
I grafici a sinistra mostrano i punteggi medi di aggressività per i due gruppi (videogioco violento e non violento), con le barre di errore che simbolizzano l’incertezza inferenziale. Questo formato agevola l‘“inferenza visiva”, permettendo una deduzione immediata dell’intervallo possibile per i valori medi.
I grafici a destra includono le stesse informazioni dei grafici a sinistra, ma aggiungono dei punti colorati che rappresentano i risultati individuali. Questo formato, proposto originariamente da Gardner e Altman, evidenzia non solo l’incertezza inferenziale ma anche la variabilità dei risultati e la dimensione dell’effetto.
Sebbene a prima vista i grafici forniti a sinistra e a destra nella figura possano sembrare equivalenti, essi enfatizzano aspetti differenti. I grafici a sinistra possono portare a un‘“illusione di prevedibilità”, dove la variabilità dei risultati viene sottovalutata e l’effetto dei videogiochi violenti sul comportamento aggressivo viene visto come più forte e determinante di quanto effettivamente sia.
I grafici a destra, invece, mettendo in luce i risultati individuali, forniscono una visione più equilibrata. Fanno capire che la relazione tra videogiochi violenti e comportamento aggressivo non è deterministica e sottolineano l’importanza di considerare la variabilità all’interno di ciascun gruppo.
Questa distinzione diventa ancora più evidente con l’aumentare della dimensione del campione. L’aumento delle dimensioni del campione non riduce necessariamente la variabilità dei risultati, e questa è una sfumatura che può essere persa se si enfatizza solo l’incertezza inferenziale.
In sintesi, la scelta del formato grafico può avere un impatto importante sulle conclusioni tratte dal lettore. Sebbene i grafici focalizzati sull’incertezza inferenziale siano spesso considerati una “migliore pratica”, Zhang et al. [ZHM+23] sottolineano che essi possono indurre in errore, specialmente se non vengono chiaramente distinti da altri concetti come la variabilità dei risultati.
In pratica, l’ambiguità nella terminologia statistica utilizzata e nelle descrizioni delle rappresentazioni grafiche può ulteriormente confondere il lettore. È invece essenziale fornire una comunicazione chiara e trasparente nella presentazione dei risultati statistici. La scelta del formato appropriato non è dunque una mera questione di stile, ma riveste un aspetto di sostanza fondamentale, mirato a garantire una comprensione accurata e onesta dei risultati della ricerca empirica.
I risultati degli esperimenti di Zhang et al. [ZHM+23], i quali hanno chiesto a gruppi di esperti di interpretare dei grafici come quelli illustrati sopraa, mettono in luce una problematica seria nella comunicazione scientifica, evidenziando come l’enfasi pervasiva sull’incertezza inferenziale nelle visualizzazioni dei dati possa ingannare persino gli esperti in merito alla dimensione e all’importanza dei risultati della ricerca. Questa situazione può portare a una percezione distorta degli effetti, facendoli apparire più significativi di quanto non siano realmente. Tale ‘illusione di prevedibilità’ sembra originarsi dalla confusione tra i concetti di incertezza inferenziale, che si riferisce all’intervallo entro cui è probabile che si trovi il valore vero di un parametro, e la variabilità dei risultati, che descrive quanto i dati individuali possano differire tra loro.
Proprio per risolvere questo problema, Zhang et al. [ZHM+23] propongono una soluzione semplice e diretta: visualizzare contemporaneamente sia l’incertezza inferenziale che la variabilità dei risultati, rappresentando i dati individuali accanto alle stime statistiche – come nei grafici forniti nella colonna di sinistra della figura precedente. Questo approccio permette ai lettori di distinguere più chiaramente tra queste due nozioni, contribuendo così a una comprensione più precisa e onesta della grandezza e della rilevanza dell’effetto studiato, senza rischiare di sovrastimarne l’importanza.
Example 10
Consideriamo ora i dati utilizzti da Zhang et al. [ZHM+23]. Poniamoci il problema di ottenere i valori numerici che rappresentano l’incertezza inferenziale e la variabilità dei risultati.
Iniziamo importando i dati.
df = pd.read_csv("../data/video_games.csv")
df.head()
| outcome | condition | |
|---|---|---|
| 0 | 7.145137 | Violent game |
| 1 | 7.484930 | Violent game |
| 2 | 7.297470 | Violent game |
| 3 | 7.760477 | Violent game |
| 4 | 6.497964 | Violent game |
Il dataset completo usato da Zhang et al. [ZHM+23] contiene 800 osservazioni.
df.shape
(800, 2)
Per il dataset completo calcoliamo la media della variabile di esito nei due gruppi, insieme alle deviazioni standard e agli errori standard della media.
summary = df.groupby('condition')['outcome'].agg(
mean='mean',
standard_deviation='std',
standard_error=lambda x: x.std() / len(x) ** 0.5
)
print(summary)
mean standard_deviation standard_error
condition
Non-violent game 6.65 0.53 0.0265
Violent game 6.81 0.51 0.0255
Consideriamo ora un sottoinsieme di questi dati, ovvero selezioniamo in maniera casuale 100 righe dal DataFrame precedente.
# Assuming df has at least 100 rows
df_100 = df.sample(n=100)
Svolgiamo gli stessi calcoli per questo sottoinsieme di dati.
summary_100 = df_100.groupby('condition')['outcome'].agg(
mean='mean',
standard_deviation='std',
standard_error=lambda x: x.std() / len(x) ** 0.5
)
print(summary_100)
mean standard_deviation standard_error
condition
Non-violent game 6.688967 0.531433 0.073696
Violent game 6.833342 0.592238 0.085482
Si noti che, nelle analisi condotte su due campioni di dimensioni differenti, \(n\) = 800 e \(n\) = 100, si manifestano delle lievi differenze nei valori delle medie e delle deviazioni standard. Queste discrepanze sono attese e si possono attribuire alla variabilità naturale dei campioni. Nonostante ciò, possiamo dire che le medie e deviazioni standard sono sostanzialmente simili nei due campioni di grandezze diverse.
Un discorso diverso invece riguarda invece l’errore standard della media: esso è, per definizione, più piccolo quando la numerosità campionaria è più grande. In altre parole, l’incertezza inferenziale sul vero valore della media della popolazione \(\mu\) diminuisce all’aumentare della grandezza del campione.
Questo fenomeno, tuttavia, non ha alcun collegamento con l’effetto che i video-game, violenti o meno, possono avere sull’aggressività del comportamento successivo. La correlazione tra il tipo di video-game giocato e il successivo comportamento aggressivo risulta essere molto debole, indipendentemente dalla grandezza del campione analizzato.
Per una valutazione più dettagliata della relazione tra tipo di videogioco e agressività successiva, possiamo calcolare l’indice \(d\) di Cohen, una misura standardizzata che quantifica la differenza tra le medie dei due gruppi. Iniziamo con il campione di dimensioni maggiori.
def cohen_d(mean1, mean2, sd1, sd2, n1, n2):
pooled_sd = math.sqrt(((n1 - 1) * sd1**2 + (n2 - 1) * sd2**2) / (n1 + n2 - 2))
return (mean2 - mean1) / pooled_sd
mean1 = 6.663322
mean2 = 6.861076
sd1 = 0.566330
sd2 = 0.519873
n1 = n2 = 100
result = cohen_d(mean1, mean2, sd1, sd2, n1, n2)
print("Cohen's d:", result)
Cohen's d: 0.3637871999925845
Calcoliamo ora il \(d\) di Cohen nel caso di \(n\) = 100.
mean1 = 6.65
mean2 = 6.81
sd1 = 0.53
sd2 = 0.51
n1 = n2 = 800
result = cohen_d(mean1, mean2, sd1, sd2, n1, n2)
print("Cohen's d:", result)
Cohen's d: 0.3076354277014899
In entrambi i casi, possiamo dire che la dimensione dell’effetto è piccola, secondo la metrica dell’indice \(d\) di Cohen, che definisce un effetto come “debole” quando il valore è compreso tra 0.2 e 0.4.
Questo significa che, all’aumentare delle dimensioni del campione, l’incertezza inferenziale nella stima della differenza tra le medie dei due gruppi diminuisce, e ciò può portare a rilevare una differenza statistica tra le medie dei due gruppi. Tuttavia, ciò non implica che un aumento della dimensione del campione renda l’effetto del trattamento più marcato. La grandezza dell’effetto del trattamento è indipendente dalla dimensione del campione; essa dipende invece dalla differenza tra le medie dei due gruppi e dalla variabilità delle osservazioni all’interno di ciascun gruppo. In altre parole, la misura dell’effetto è determinata dalle caratteristiche intrinseche del fenomeno studiato e non è influenzata dall’ampiezza dei campioni utilizzati nell’analisi.
Commenti e considerazioni conclusive#
Zhang et al. [ZHM+23] concludono il loro articolo riflettendo sul modo in cui la ricerca scientifica viene condotta e i suoi risultati vengono comunicati. Essi evidenziano che, in molti campi scientifici, l’attenzione si è concentrata per lungo tempo sull’inferenza (ossia, sull’ottenimento di stime non distorte degli effetti sperimentali) piuttosto che sulla previsione (come, ad esempio, la proiezione dei possibili risultati futuri). Questa enfasi potrebbe derivare, in parte, dalla complessità intrinseca della previsione, specialmente quando confrontata con l’inferenza. Infatti, stimare un effetto medio su una popolazione, come avviene nell’inferenza statistica standard, è indubbiamente più semplice che prevedere i risultati individuali, tenendo conto di tutti i fattori che potrebbero influenzare un fenomeno specifico. Tuttavia, questa enfasi sull’inferenza può generare confusione nella comunicazione dei risultati dello studio, dando l’impressione che i risultati della ricerca possano prevedere gli esiti individuali, quando in realtà hanno soltanto stabilito un effetto medio. Di conseguenza, anche gli esperti possono finire con l’equiparare le rappresentazioni visive che esprimono l’incertezza inferenziale con quelle che trasmettono informazioni sulla previsione dei dati individuali.
Per Zhang et al. [ZHM+23], la soluzione a questo problema sta nella comunicazione chiara e integrata sia dell’incertezza inferenziale che della variabilità dei risultati. Invece di favorire l’inferenza rispetto alla previsione (o viceversa), gli autori propongono un approccio olistico che consideri entrambi gli aspetti dell’indagine scientifica, presentandoli in modo parallelo e comprensibile. Ciò consentirebbe ai lettori di trarre inferenze più accurate ed appropriate dai dati presentati. Questa prospettiva integrata potrebbe rappresentare un passo importante verso una comprensione e una comunicazione della ricerca più trasparenti e precise, contribuendo a colmare il divario tra ciò che gli studi effettivamente dimostrano e ciò che viene percepito da chi li legge.
%load_ext watermark
%watermark -n -u -v -iv
Last updated: Thu Nov 09 2023
Python implementation: CPython
Python version : 3.11.6
IPython version : 8.16.1
seaborn : 0.13.0
matplotlib: 3.8.0
arviz : 0.16.1
pandas : 2.1.1
numpy : 1.25.2
scipy : 1.11.3

