✏️ Esercizi#

Per questi esercizi, useremo i dati tratti da O’Connell, et al. (2021). Reduced social distancing during the COVID-19 pandemic is associated with antisocial behaviors in an online United States sample. PLoS ONE.

import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
import statsmodels.api as sm

import pymc as pm
import bambi as bmb
import arviz as az

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

%config InlineBackend.figure_format = 'retina'
%load_ext watermark

RANDOM_SEED = 123
rng = np.random.default_rng(RANDOM_SEED)

plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/main/nma.mplstyle")

Questo studio ha valutato se i comportamenti di distanziamento sociale (all’inizio della pandemia di COVID-19) fossero associati a comportamenti antisociali auto-riferiti. Per misurare un indice del comportamento di distanziamento sociale, ai partecipanti è stata presentata un’immagine di una sagoma di adulto circondata da un bordo rettangolare. È stato chiesto loro di cliccare su un punto nell’immagine che rappresentasse a che distanza solitamente si trovavano dalle altre persone.

Qui è presente una heatmap che mostra a che distanza i partecipanti hanno riportato di stare dalle altre persone nell’ultima settimana, con un colore marrone scuro che indica una maggiore densità di risposte. La coordinata della risposta media, indicata con un +, rappresenta una distanza di circa 98 pollici (2.5 metri).

Figura 1

Leggiamo i dati riportati dagli autori.

df = pd.read_csv("../data/stab.csv")

VSCode tronca l’output stampato sullo schermo. Per elencare tutte le colonne uso la funzione to_string che però si applica solo ai DataFrame.

cols = df.columns

mydf = pd.DataFrame()
mydf["cols"] = cols
print(mydf["cols"].to_string()) 

0                                 subID
1                          mturk_randID
2                     suspect_itaysisso
3                               Country
4                                Region
5                                   ISP
6                                loc_US
7                             loc_state
8                           loc_zipcode
9                            loc_County
10                   loc_2010population
11                       loc_Land_Sq_Mi
12                  loc_Density_Sq_Mile
13         loc_Covid_Cases_april_1_2020
14                                attn1
15                                attn2
16                                attn3
17                            StartDate
18                              EndDate
19                             Duration
20                           worry_self
21                          likely_self
22                          health_self
23                      likely_lovedone
24                      health_lovedone
25                       worry_american
26                      likely_american
27                      health_american
28                        highrisk_self
29                    highrisk_lovedone
30            highrisk_self_or_livewith
31                       financial_self
32                   financial_american
33                   wash_perday_actual
34                    wash_perday_ideal
35                     socialdistancing
36              socialdistancing_for_me
37           socialdistancing_for_close
38       socialdistancing_for_americans
39          socialdistancing_experience
40            times_left_house_pastweek
41     distance_from_others_feet_lastwe
42                    ppe_freq_lastweek
43     times_left_house_for_vunerable_p
44          think_about_pandemic_perday
45           months_expect_gov_measures
46                   household_n_people
47                             symptoms
48                        symptoms_text
49                    silhouette_dist_X
50                    silhouette_dist_Y
51               silhouette_dist_region
52                               STAB_1
53                               STAB_2
54                               STAB_3
55                               STAB_4
56                               STAB_5
57                               STAB_6
58                               STAB_7
59                               STAB_8
60                               STAB_9
61                              STAB_10
62                              STAB_11
63                              STAB_12
64                              STAB_13
65                              STAB_14
66                              STAB_15
67                              STAB_16
68                              STAB_17
69                              STAB_18
70                              STAB_19
71                              STAB_20
72                              STAB_21
73                              STAB_22
74                              STAB_23
75                              STAB_24
76                              STAB_25
77                              STAB_26
78                              STAB_27
79                              STAB_28
80                              STAB_29
81                              STAB_30
82                              STAB_31
83                              STAB_32
84                                  sex
85                               sex_1f
86                                  age
87                                 race
88                             hispanic
89                            education
90                  occupational_status
91             occupational_status_text
92          lefthouse_for_work_lastweek
93                 coded_lefthouse_work
94                     household_income
95                         num_children
96              relatives_close_under65
97               relatives_close_over65
98                 current_mentalhealth
99            current_mentalhealth_text
100                   past_mentalhealth
101              past_mentalhealth_text
102                neurologicaldisorder
103           neurologicaldisorder_text
104                      drugs_lastweek
105                 drugs_lastweek_text
106                       STAB_physical
107                         STAB_social
108                   STAB_rulebreaking
109                          STAB_total
110                      ppe_freq_coded
111              household_income_coded
112                    income_over60000
113                    ppe_freq_coded_2
114                        age_centered
115                     education_coded
116                       education_4yr
117                 STAB_total_centered
118                    STAB_total_min32
119             silhouette_dist_X_min81
120            silhouette_dist_X_inches
121                 violated_distancing
122           STAB_rulebreak_rmECONOMIC
123               STAB_total_rmECONOMIC
124      STAB_total_rmECONOMIC_centered
125     household_income_coded_centered

Esercizio 1#

a Trovare il numero di righe e di colonne del DataFrame.

df.shape

(131, 126)

(a) Selezionare le colonne “silhouette_dist_X_min81”, rinominandola come “distance”, “STAB_total”, rinominandola come “stab”, e “times_left_house_pastweek”, rinominandola come “times_left_house”. Calcolare il numero di elementi in ciascuno di questi vettori. (b) Utilizzando un ciclo for o una list comprehension, individuare gli indici delle righe in cui la variabile “distance” presenta un valore mancante. (c) Scrivere una funzione che accetti una lista come input e restituisca il conteggio di valori NaN presenti nella lista, fornendo commenti per ciascun passaggio del codice. Sfruttare la proprietà degli NaN secondo cui non sono uguali a se stessi.

value = np.nan
print(value)

nan

value == value

False

Testare la funzione sulle liste “distance”, “stab” e “times_left_house”. (d) Creare una lista di 10 elementi contenente 5 numeri, 2 stringhe e 3 valori NaN. Testare la funzione creata su questa lista. (e) Creare un DataFrame con le variabili “distance”, “stab” e “times_left_house”. Filtrare il DataFrame in modo da escludere dati mancanti. (f) Utilizzando Seaborn, creare un istogramma con KDE sovrapposto per le variabili “times_left_house” e “stab”. Interpretare i grafici. (g) Aggiungere al DataFrame la variabile “is_high_stab”, che assume valore 1 se “stab” è minore o uguale a 80 e 0 altrimenti. Generare due violin-plot, uno per ciascuna modalità di “is_high_stab”, per la variabile “times_left_house”. Commentare i risultati. (h) Calcolare la media, la moda, la deviazione standard e la Deviazione Assoluta dalla Media (MAD) per i due gruppi.

distance = df["silhouette_dist_X_min81"]
stab = df["STAB_total"]
times_left_house = df["times_left_house_pastweek"]

len(distance)

131

len(stab)

131

b

nan_indices = [i for i in range(len(distance)) if np.isnan(distance[i])]
print(f"Observations with NaN values: {nan_indices}")

Observations with NaN values: [17, 22, 24, 25, 39, 51, 60, 67, 71, 94]

c

def count_nans(data_list):
    """Count the number of NaNs in a list

    Args:
        data_list (list): A list that contains the observations
    
    Returns:
        int: The number of NaNs found in the list
    """
    nan_count = 0
    
    for value in data_list:
        if value != value:  
            nan_count += 1
        
    return nan_count

count_nans(distance)

10

count_nans(stab)

0

count_nans(times_left_house)

0

d

new_list = [1, np.nan, 2, 3, np.nan, 4, 5, np.nan, "qualcosa", "qualcosa d'altro"]
print(new_list)

[1, nan, 2, 3, nan, 4, 5, nan, 'qualcosa', "qualcosa d'altro"]

count_nans(new_list)

3

e

new_df = pd.DataFrame()
new_df["distance"] = distance
new_df["stab"] = stab
new_df["times_left_house"] = times_left_house
new_df["subID"] = df["subID"]

new_df.head()
distance stab times_left_house subID
0 441.0 51 3 1001
1 287.0 94 5 1002
2 313.0 95 4 1003
3 452.0 45 2 1004
4 297.0 37 0 1005 
new_df.shape

(131, 4)

df_cleaned = new_df.dropna()
df_cleaned.shape

(121, 4)

f

plt.figure(figsize=(10, 6))
sns.histplot(data=df_cleaned, x='times_left_house', bins=20, kde=True);
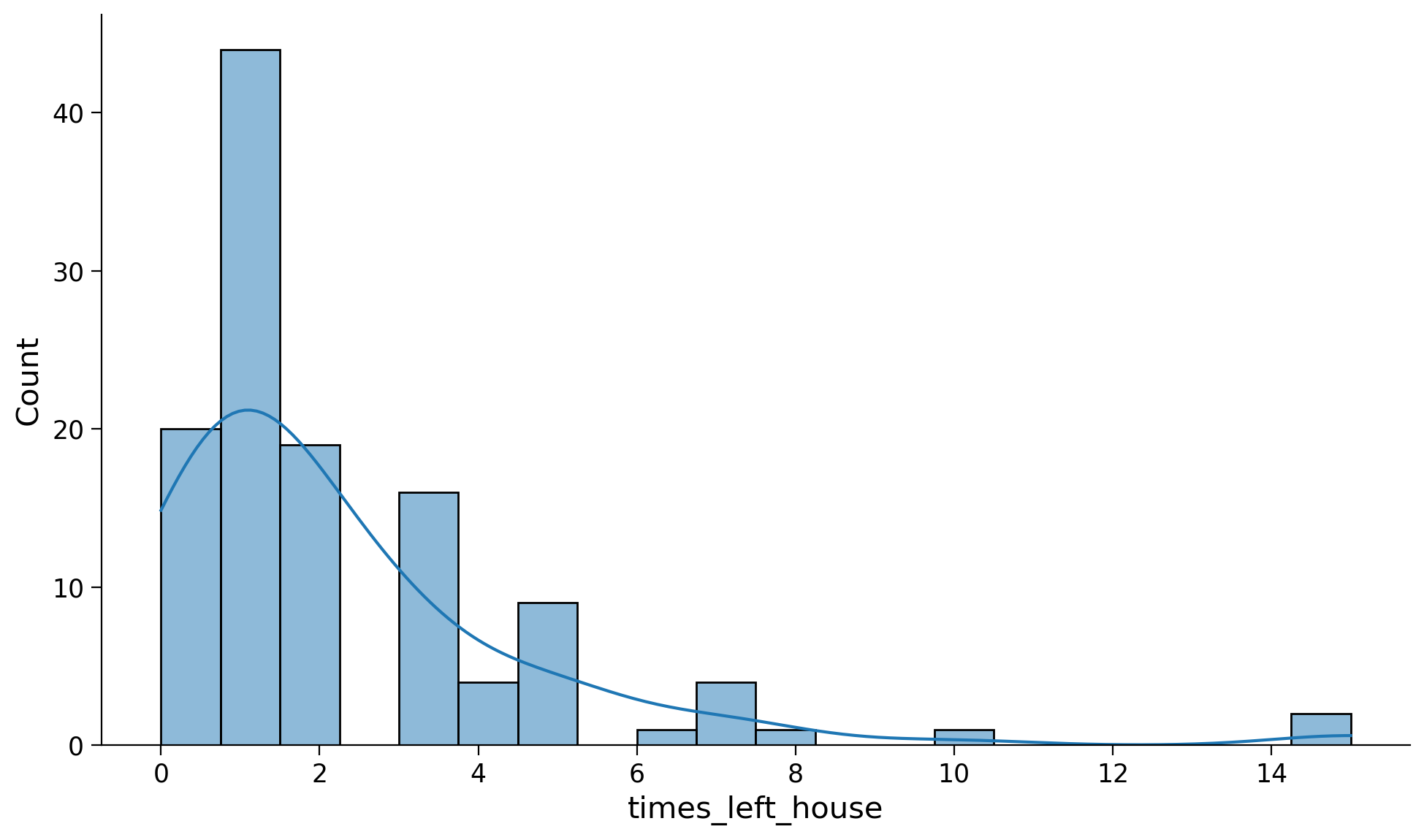
../_images/3ae51f303e702a6b56ece336c32e628c2ca5b3d7c4cb6debbe441e3690223082.png 
plt.figure(figsize=(10, 6))
sns.histplot(data=df_cleaned, x='stab', bins=20, kde=True);
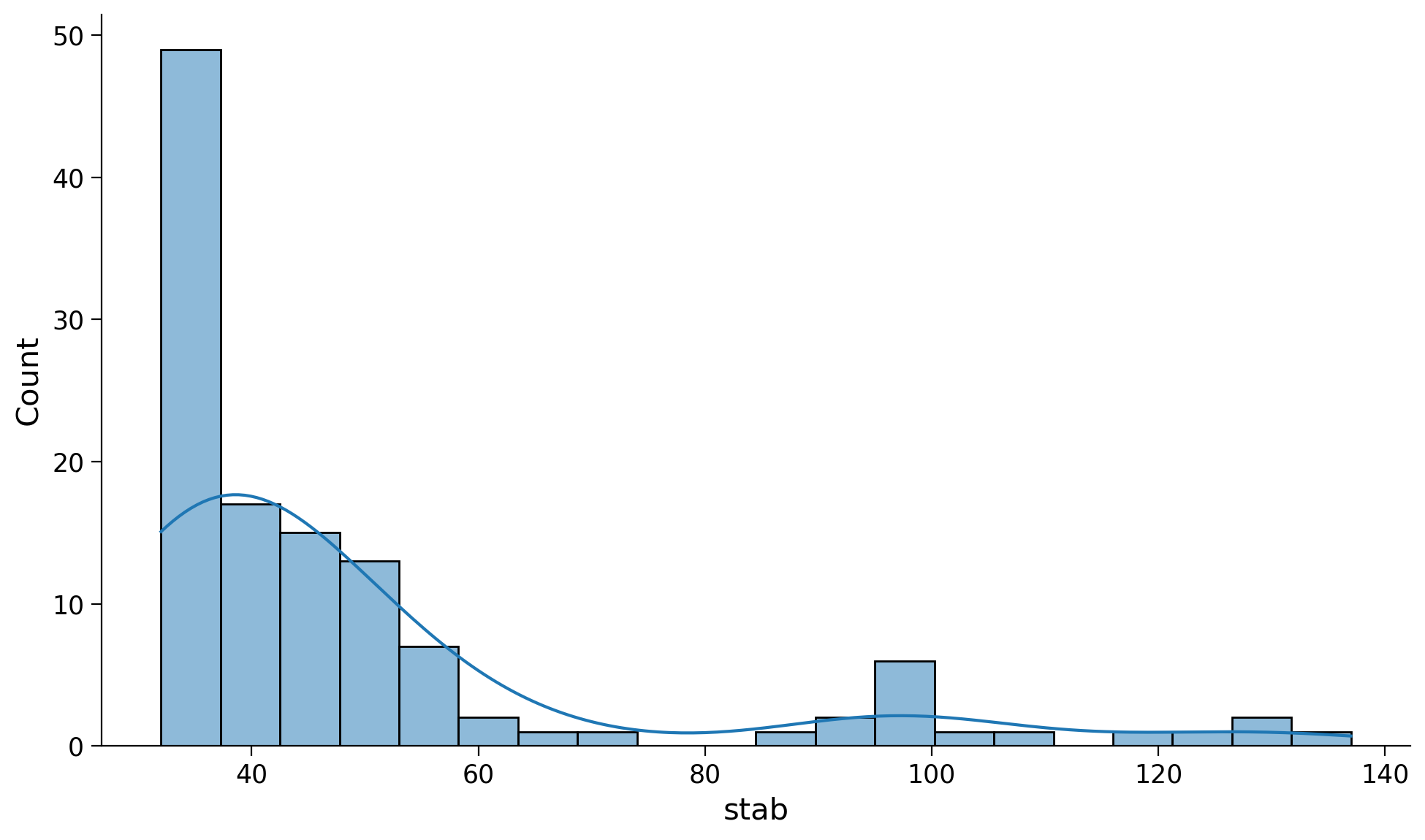
../_images/6dac766997cc60d140c831d9b7d1e5ff697e69f1cd34af079cd56376660f4279.png

g

Gli autori stanno indagando la possibile associazione tra il numero di volte in cui le persone sono uscite di casa durante la fase iniziale della pandemia di COVID-19 e la loro propensione antisociale, valutata tramite il reattivo STAB (Antisocial Behavior Score). A tal fine, i partecipanti sono stati classificati in due categorie distinte: coloro che mostrano livelli antisociali elevati (con un punteggio STAB superiore a 80) e coloro che presentano livelli antisociali bassi (con un punteggio STAB inferiore o uguale a 80).

Per analizzare questa associazione, si produca una visualizzazione grafica dei dati per i due gruppi di partecipanti. Ad esempio, potrebbe essere utile un istogramma o un violin plot che mostri la distribuzione del numero di volte in cui i partecipanti sono usciti di casa, separando i dati in base ai livelli antisociali (alti o bassi). Si interpreti.

df_cleaned["is_high_stab"] = np.where(df_cleaned["stab"] > 80, 1, 0);

/var/folders/cl/wwjrsxdd5tz7y9jr82nd5hrw0000gn/T/ipykernel_14258/262644604.py:1: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead

See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  df_cleaned["is_high_stab"] = np.where(df_cleaned["stab"] > 80, 1, 0);

plt.figure(figsize=(10, 6))
sns.violinplot(x="is_high_stab", y="times_left_house", data=df_cleaned);
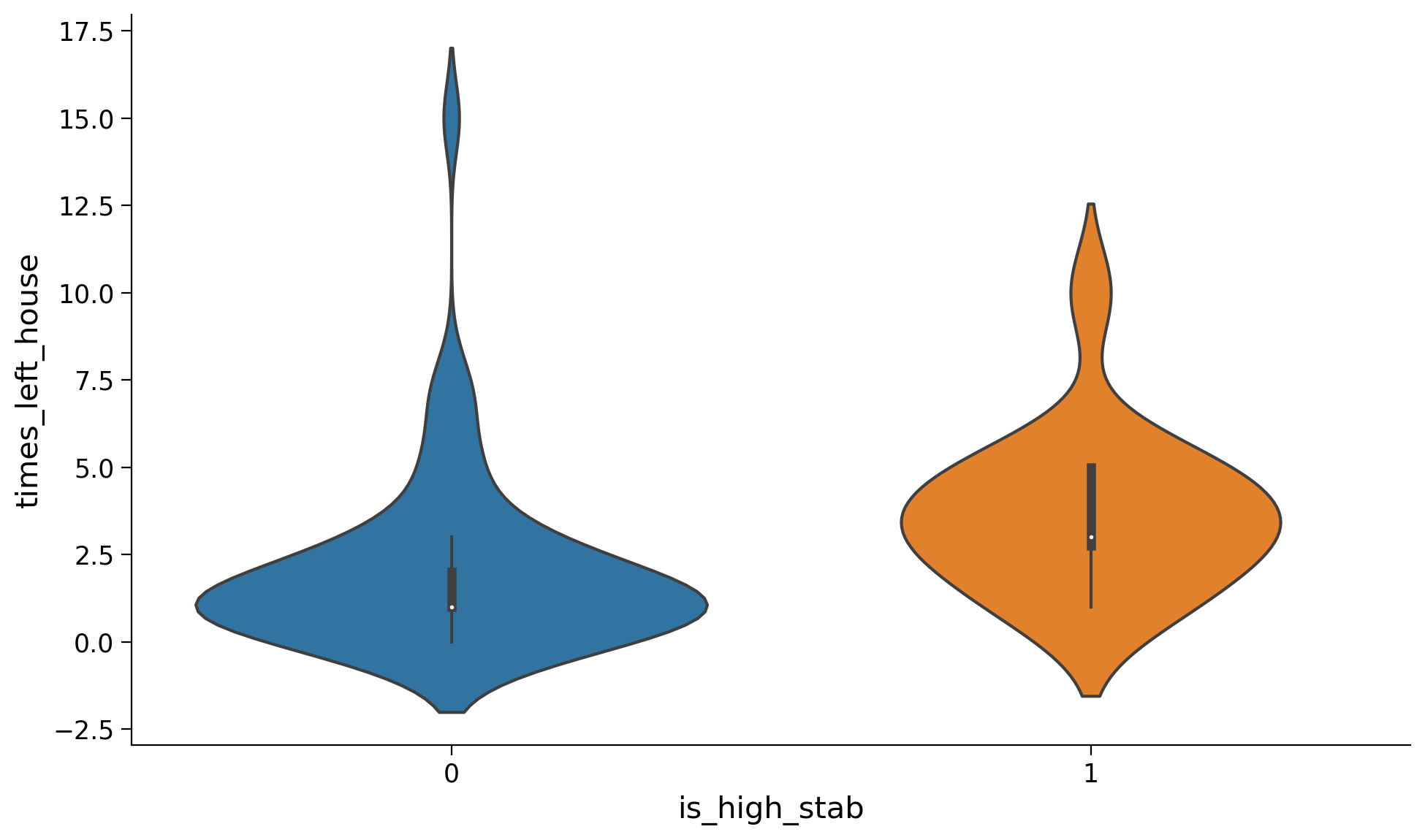
../_images/42d49a6bad668abb1db8c481fe619dbed9fb87ae230543e4603f9a0a64a8a26c.png 
y1 = df_cleaned[df_cleaned["is_high_stab"] == 1]["times_left_house"]
y0 = df_cleaned[df_cleaned["is_high_stab"] == 0]["times_left_house"]

plt.figure(figsize=(10, 6))
# Plot the histogram for y1
plt.hist(y1, alpha=0.5, label='is_high_stab = 1', density=True, bins=10)
# Plot the histogram for y0
plt.hist(y0, alpha=0.5, label='is_high_stab = 0', density=True, bins=10)

plt.title('Histogram of Times Left House by Stab Level')
plt.xlabel('Times Left House')
plt.ylabel('Frequency')
plt.legend();
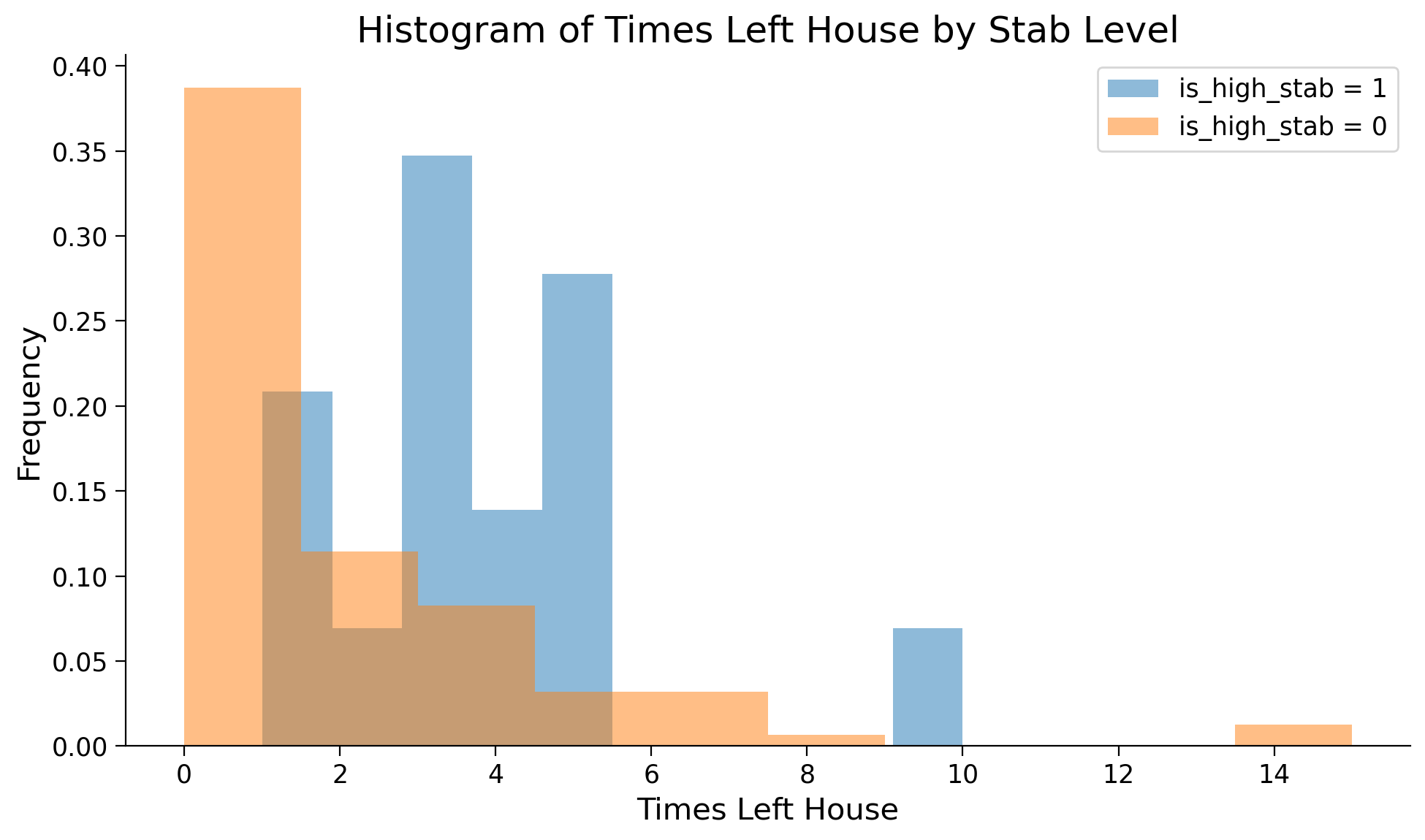
../_images/03d0ea422b2ed68f9f5ef5eb2e363333bbf74154a174438886cfc77f5ec7dbfb.png

h

Si calcolino le statistiche descrittive per i due gruppi di partecipanti e si interpreti.

grouped = df_cleaned.groupby("is_high_stab")["times_left_house"]
summary_stats = grouped.agg(median=np.median, mean=np.mean, mad=sm.robust.scale.mad, std=np.std)
print("Summary statistics per group:\n", summary_stats)

Summary statistics per group:
               median      mean       mad       std
is_high_stab                                      
0                1.0  2.047619  1.482602  2.547174
1                3.0  3.625000  2.223903  2.217356

i

Si replichino i risultati degli autori usando bambi. Si utilizzi la distribuzione negative binomial, come nell’articolo.

Una distribuzione binomiale negativa è una distribuzione di probabilità discreta che è un’estensione della distribuzione di Poisson. Mentre la distribuzione di Poisson è utile per modellare il numero di eventi che accadono in un intervallo di tempo o spazio fisso, la distribuzione binomiale negativa permette una maggiore flessibilità, in particolare quando i dati presentano una varianza maggiore rispetto alla media (fenomeno chiamato sovradispersione).

La distribuzione binomiale negativa è descritta da due parametri, \( r \) e \( p \), e può essere pensata come il numero di fallimenti necessari per raggiungere \( r \) successi in una sequenza di prove di Bernoulli indipendenti, dove ogni prova ha probabilità di successo \( p \). La funzione di massa di probabilità (PMF) per la distribuzione binomiale negativa è data da:

\[P(X = k) = \binom{k + r - 1}{k} p^r (1-p)^k\]

dove

  • \( k \) è il numero di fallimenti,

  • \( r \) è il numero fisso di successi (chiamato anche numero di successi target),

  • \( p \) è la probabilità di successo in ogni prova.

La media e la varianza della distribuzione binomiale negativa sono date rispettivamente da:

\[ \mu = \frac{r(1-p)}{p} \]
\[ \sigma^2 = \frac{r(1-p)}{p^2} \]

La distribuzione binomiale negativa è spesso utilizzata nella modellazione di dati di conteggio in cui si osserva una sovradispersione, come ad esempio il numero di incidenti in un determinato periodo, o il numero di volte che una particolare malattia si verifica in una popolazione.

Nel contesto dei modelli lineari generalizzati (GLM), la distribuzione binomiale negativa può essere usata come distribuzione di risposta con una funzione di collegamento logaritmica per modellare i dati di conteggio sovradispersi. Questo può aiutare a ottenere stime più accurate e un miglior adattamento del modello rispetto all’utilizzo di una distribuzione di Poisson, che assume uguaglianza tra media e varianza.

model = bmb.Model(
    "times_left_house ~ is_high_stab", df_cleaned, family="negativebinomial"
)

fitted = model.fit(
    draws=2000,
    idata_kwargs={"log_likelihood": True},
)

Auto-assigning NUTS sampler...

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (4 chains in 4 jobs)

NUTS: [times_left_house_alpha, Intercept, is_high_stab]

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
100.00% [12000/12000 00:02<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 14 seconds.

az.plot_trace(fitted, combined=True);
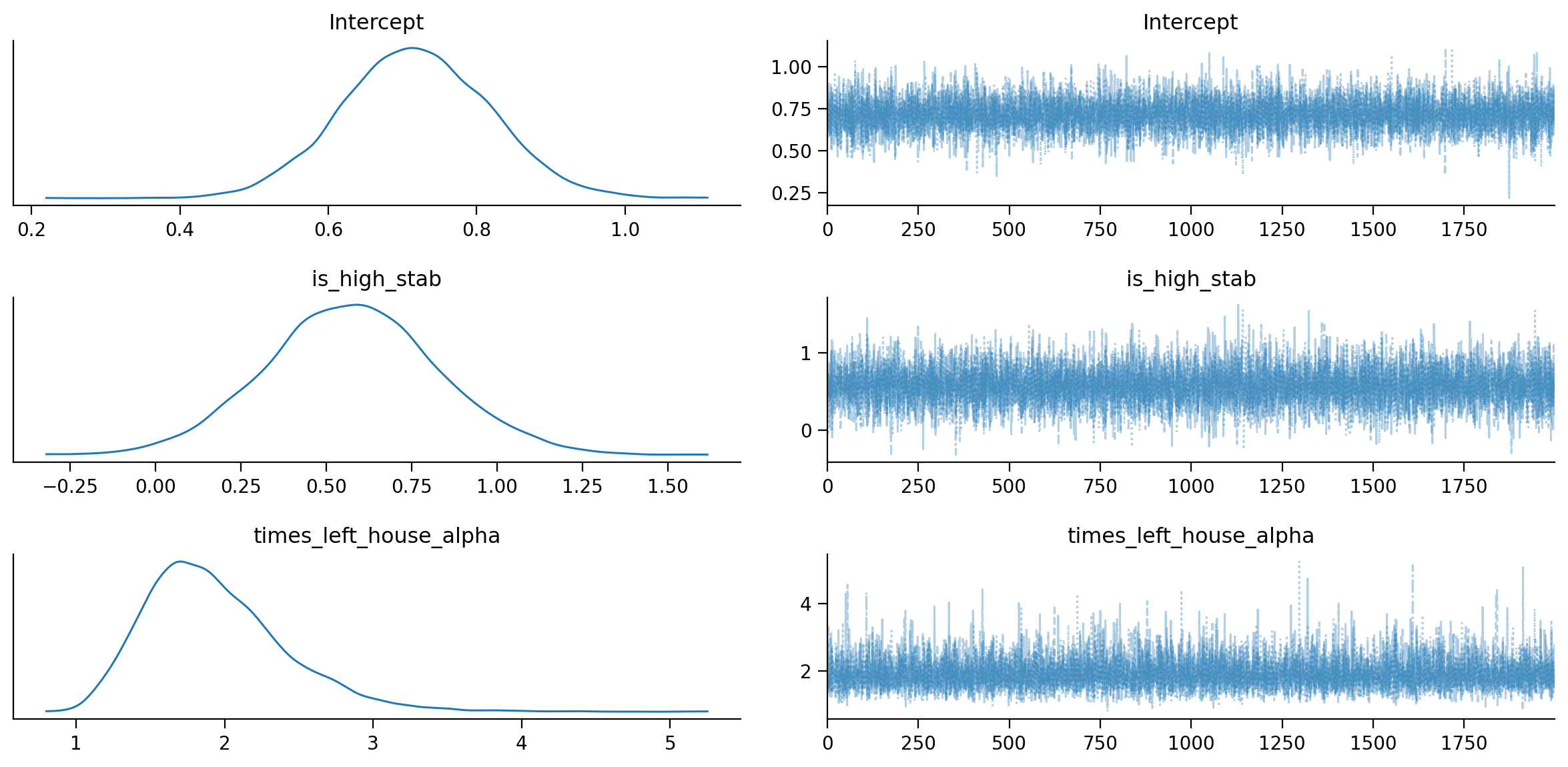
../_images/3dc7a947ca2d71f0c9fc088716592ce9b5aaf2bc4e6d7d80910561bef973a226.png 
az.summary(fitted)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
Intercept 0.717 0.100 0.526 0.899 0.001 0.001 12276.0 6063.0 1.0
is_high_stab 0.577 0.253 0.085 1.043 0.002 0.002 11015.0 6052.0 1.0
times_left_house_alpha 1.940 0.477 1.147 2.816 0.005 0.004 10896.0 6034.0 1.0

L’intercetta denota il logaritmo naturale del tasso di eventi (intensità) previsto quando tutte le variabili esplicative sono poste a zero. Per comprenderne l’effetto sulla scala naturale, è necessario eseguire l’esponenziazione del valore stimato dell’intercetta. Nel contesto attuale, questo valore corrisponde al numero stimato di occasioni in cui l’individuo ha lasciato la propria abitazione nella settimana precedente, qualora appartenga al gruppo caratterizzato da valori bassi di STAB (Antisocial Behavior Score).

np.exp(0.715)

2.0441866822585566

Nel contesto di un modello negative binomial, i coefficienti stimati per le variabili esplicative rappresentano la variazione percentuale prevista nel tasso di eventi in risposta a un aumento unitario nella variabile indipendente, mantenendo costanti le altre variabili. Questi coefficienti vengono interpretati sulla scala logaritmica. Per comprendere l’effetto delle variabili esplicative sulla scala naturale, è essenziale calcolare l’esponenziale del coefficiente stesso. Nel caso dei dati in esame, la pendenza indica la differenza nel valore medio di Y (la variabile di risposta) tra i due gruppi: in altre parole, essa rappresenta di quante volte in più (considerando il segno positivo) il gruppo con valori elevati di STAB lascia la propria abitazione nella settimana precedente rispetto al gruppo con valori bassi di STAB.

np.exp(0.715 + 0.580)

3.6509959741412716

Poiché l’intervallo di credibilità del parametro “is_high_stab” non include lo 0, possiamo affermare con un livello di confidenza soggettiva del 94% che gli individui con valori STAB alti hanno lasciato la propria abitazione un numero di volte superiore nella settimana precedente rispetto agli individui con valori STAB bassi.

Esaminiamo la distribuzione predittiva a posteriori.

posterior_predictive = model.predict(fitted, kind="pps")
fitted
arviz.InferenceData
    • <xarray.Dataset>
Dimensions:                 (chain: 4, draw: 2000, times_left_house_obs: 121)
Coordinates:
  * chain                   (chain) int64 0 1 2 3
  * draw                    (draw) int64 0 1 2 3 4 ... 1995 1996 1997 1998 1999
  * times_left_house_obs    (times_left_house_obs) int64 0 1 2 3 ... 118 119 120
Data variables:
    Intercept               (chain, draw) float64 0.7022 0.8469 ... 0.6793
    is_high_stab            (chain, draw) float64 0.7285 0.7256 ... 0.663 0.5124
    times_left_house_alpha  (chain, draw) float64 1.956 1.94 ... 1.623 2.069
    times_left_house_mean   (chain, draw, times_left_house_obs) float64 2.018...
Attributes:
    created_at:                  2023-09-17T09:22:57.092802
    arviz_version:               0.16.0
    inference_library:           pymc
    inference_library_version:   5.6.1
    sampling_time:               13.567732095718384
    tuning_steps:                1000
    modeling_interface:          bambi
    modeling_interface_version:  0.12.0

    • <xarray.Dataset>
Dimensions:               (chain: 4, draw: 2000, times_left_house_obs: 121)
Coordinates:
  * chain                 (chain) int64 0 1 2 3
  * draw                  (draw) int64 0 1 2 3 4 5 ... 1995 1996 1997 1998 1999
  * times_left_house_obs  (times_left_house_obs) int64 0 1 2 3 ... 118 119 120
Data variables:
    times_left_house      (chain, draw, times_left_house_obs) int64 1 4 ... 1 7
Attributes:
    modeling_interface:          bambi
    modeling_interface_version:  0.12.0

    • <xarray.Dataset>
Dimensions:               (chain: 4, draw: 2000, times_left_house_obs: 121)
Coordinates:
  * chain                 (chain) int64 0 1 2 3
  * draw                  (draw) int64 0 1 2 3 4 5 ... 1995 1996 1997 1998 1999
  * times_left_house_obs  (times_left_house_obs) int64 0 1 2 3 ... 118 119 120
Data variables:
    times_left_house      (chain, draw, times_left_house_obs) float64 -2.081 ...
Attributes:
    created_at:                  2023-09-17T09:22:57.433328
    arviz_version:               0.16.0
    inference_library:           pymc
    inference_library_version:   5.6.1
    modeling_interface:          bambi
    modeling_interface_version:  0.12.0

    • <xarray.Dataset>
Dimensions:                (chain: 4, draw: 2000)
Coordinates:
  * chain                  (chain) int64 0 1 2 3
  * draw                   (draw) int64 0 1 2 3 4 5 ... 1995 1996 1997 1998 1999
Data variables: (12/17)
    energy_error           (chain, draw) float64 -0.2211 0.4426 ... -0.1504
    largest_eigval         (chain, draw) float64 nan nan nan nan ... nan nan nan
    perf_counter_start     (chain, draw) float64 5.076e+03 ... 5.077e+03
    step_size_bar          (chain, draw) float64 1.076 1.076 ... 1.041 1.041
    reached_max_treedepth  (chain, draw) bool False False False ... False False
    diverging              (chain, draw) bool False False False ... False False
    ...                     ...
    energy                 (chain, draw) float64 244.1 244.8 ... 244.4 244.2
    n_steps                (chain, draw) float64 3.0 3.0 3.0 1.0 ... 1.0 3.0 3.0
    step_size              (chain, draw) float64 1.469 1.469 ... 1.097 1.097
    max_energy_error       (chain, draw) float64 -0.2211 0.4426 ... 0.12 0.3123
    index_in_trajectory    (chain, draw) int64 -1 1 -3 -1 2 2 ... -1 2 1 0 -2 -3
    perf_counter_diff      (chain, draw) float64 0.0003568 ... 0.0003296
Attributes:
    created_at:                  2023-09-17T09:22:57.104190
    arviz_version:               0.16.0
    inference_library:           pymc
    inference_library_version:   5.6.1
    sampling_time:               13.567732095718384
    tuning_steps:                1000
    modeling_interface:          bambi
    modeling_interface_version:  0.12.0

    • <xarray.Dataset>
Dimensions:               (times_left_house_obs: 121)
Coordinates:
  * times_left_house_obs  (times_left_house_obs) int64 0 1 2 3 ... 118 119 120
Data variables:
    times_left_house      (times_left_house_obs) int64 3 5 4 2 0 ... 2 2 10 0 7
Attributes:
    created_at:                  2023-09-17T09:22:57.107197
    arviz_version:               0.16.0
    inference_library:           pymc
    inference_library_version:   5.6.1
    modeling_interface:          bambi
    modeling_interface_version:  0.12.0

az.plot_ppc(fitted);
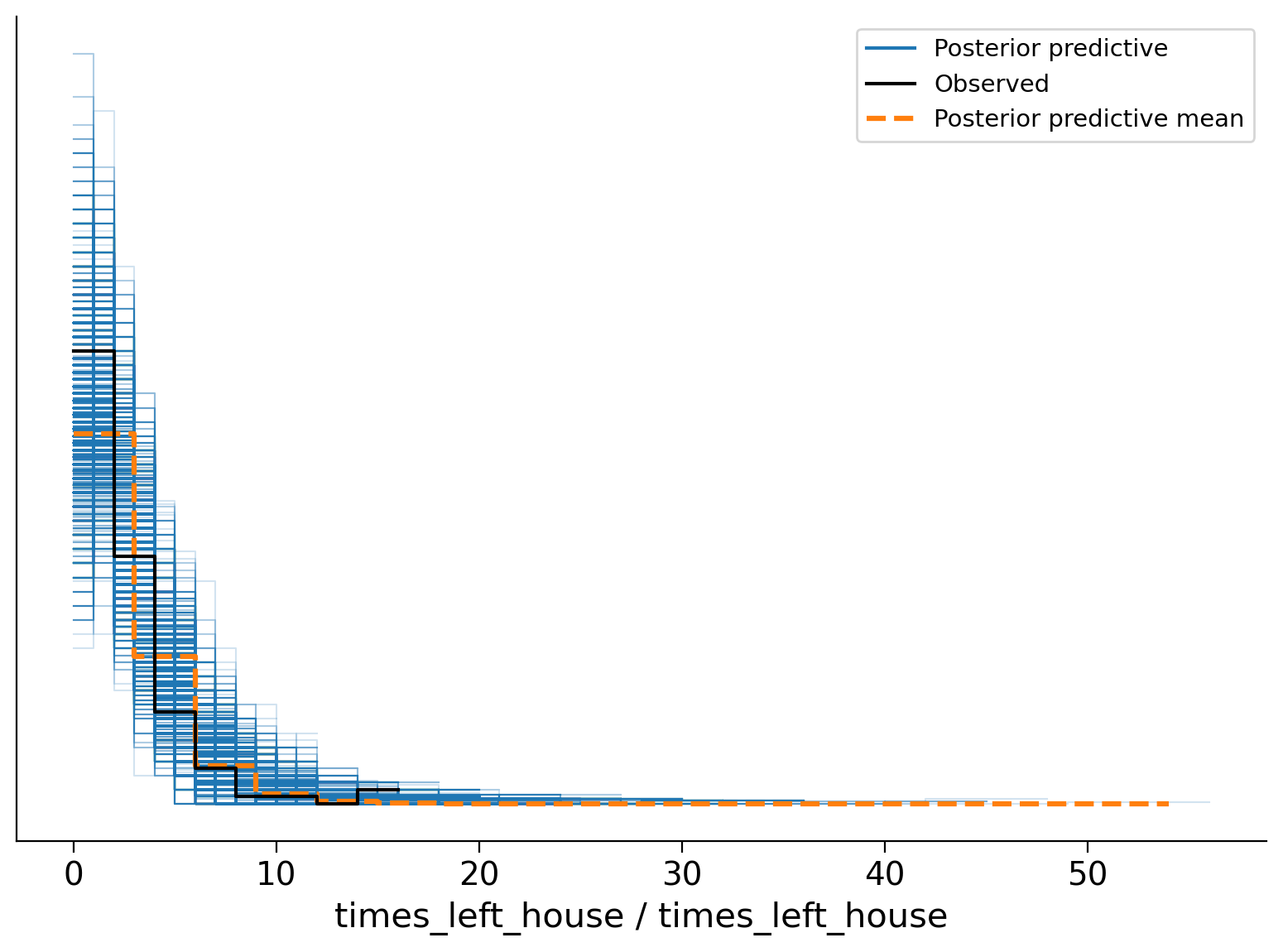
../_images/94e93ebdd015fc40b3bf590e00fff67cfdfb8e5b20b334fbf6c161806651ae3b.png

Il PP-Check indica che il modello è adeguato per i dati presenti.