Open In Colab

Drift Diffusion Model#

Nei capitoli precedenti, abbiamo affrontato l’analisi bayesiana dei dati, esplorando questioni inferenziali legate sia alle relazioni tra variabili, sia alle caratteristiche di specifiche distribuzioni. In questo capitolo, ci dedicheremo allo studio di un esempio di modellizzazione cognitiva bayesiana, approfondendo come l’approccio bayesiano possa essere impiegato per articolare in maniera formale i processi causali che sottendono i fenomeni cognitivi.

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
import arviz as az  
import pymc as pm
import pymc.sampling_jax
import hssm
from ssms.basic_simulators import simulator

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[1], line 6
      4 import seaborn as sns
      5 import arviz as az  
----> 6 import pymc as pm
      7 import pymc.sampling_jax
      8 import hssm

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/pymc/__init__.py:47
     42     augmented = f"{augmented} -fno-unwind-tables -fno-asynchronous-unwind-tables"
     44     pytensor.config.gcc__cxxflags = augmented
---> 47 __set_compiler_flags()
     49 from pymc import _version, gp, ode, sampling
     50 from pymc.backends import *

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/pymc/__init__.py:30, in __set_compiler_flags()
     28 def __set_compiler_flags():
     29     # Workarounds for PyTensor compiler problems on various platforms
---> 30     import pytensor
     32     current = pytensor.config.gcc__cxxflags
     33     augmented = f"{current} -Wno-c++11-narrowing"

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/pytensor/__init__.py:62
     59         continue
     60     raise RuntimeError("You have the pytensor directory in your Python path.")
---> 62 from pytensor.configdefaults import config
     65 # This is the api version for ops that generate C code.  External ops
     66 # might need manual changes if this number goes up.  An undefined
     67 # __api_version__ can be understood to mean api version 0.
     68 #
     69 # This number is not tied to the release version and should change
     70 # very rarely.
     71 __api_version__ = 1

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/pytensor/configdefaults.py:1419
   1417 # The functions below register config variables into the config instance above.
   1418 add_basic_configvars()
-> 1419 add_compile_configvars()
   1420 add_tensor_configvars()
   1421 add_traceback_configvars()

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/pytensor/configdefaults.py:401, in add_compile_configvars()
    399 # Test whether or not g++ is present: disable C code if it is not.
    400 try:
--> 401     rc = call_subprocess_Popen(["g++", "-v"])
    402 except OSError:
    403     rc = 1

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/pytensor/utils.py:196, in call_subprocess_Popen(command, **params)
    194     params["stderr"] = null
    195     p = subprocess_Popen(command, **params)
--> 196     returncode = p.wait()
    197 return returncode

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/subprocess.py:1264, in Popen.wait(self, timeout)
   1262     endtime = _time() + timeout
   1263 try:
-> 1264     return self._wait(timeout=timeout)
   1265 except KeyboardInterrupt:
   1266     # https://bugs.python.org/issue25942
   1267     # The first keyboard interrupt waits briefly for the child to
   1268     # exit under the common assumption that it also received the ^C
   1269     # generated SIGINT and will exit rapidly.
   1270     if timeout is not None:

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/subprocess.py:2046, in Popen._wait(self, timeout)
   2044 if self.returncode is not None:
   2045     break  # Another thread waited.
-> 2046 (pid, sts) = self._try_wait(0)
   2047 # Check the pid and loop as waitpid has been known to
   2048 # return 0 even without WNOHANG in odd situations.
   2049 # http://bugs.python.org/issue14396.
   2050 if pid == self.pid:

File ~/opt/anaconda3/envs/pymc_env/lib/python3.11/subprocess.py:2004, in Popen._try_wait(self, wait_flags)
   2002 """All callers to this function MUST hold self._waitpid_lock."""
   2003 try:
-> 2004     (pid, sts) = os.waitpid(self.pid, wait_flags)
   2005 except ChildProcessError:
   2006     # This happens if SIGCLD is set to be ignored or waiting
   2007     # for child processes has otherwise been disabled for our
   2008     # process.  This child is dead, we can't get the status.
   2009     pid = self.pid

KeyboardInterrupt: 

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-viridish")

Modellizzazione cognitiva bayesiana#

Negli anni recenti, il panorama della ricerca psicologica è stato profondamente influenzato dalla cosiddetta “rivoluzione bayesiana”. Questo movimento ha reso gli strumenti e le metodologie basate sull’inferenza bayesiana accessibili a un numero sempre maggiore di psicologi, arricchendo significativamente il campo con nuove prospettive e tecniche di analisi (S. P. Brooks, 2003; Andrews & Baguley, 2013; van de Schoot et al., 2017).

All’interno di questo contesto, i modelli lineari bayesiani hanno trovato un’ampia applicazione, diventando uno standard in molti ambiti della ricerca psicologica. L’utilizzo dell’inferenza bayesiana nella ricerca psicologica non si limita però all’analisi dei dati: essa apre infatti la porta a un ventaglio più ampio di opportunità. Un esempio è rappresentato dalla modellazione cognitiva bayesiana e dalla psichiatria computazionale, settori emergenti che impiegano principi bayesiani per formulare modelli formali dei processi cognitivi (Lee & Wagenmakers, 2013). Questi modelli, offrendo rappresentazioni formali e testabili scientificamente dei meccanismi psicologici che stanno alla base dei comportamenti osservati, contribuiscono a affinare la nostra comprensione delle complesse dinamiche cognitive che li governano (Navarro, 2021). Grazie a questo approccio, è possibile sondare in maniera più approfondita le relazioni causali e le interdipendenze presenti nei fenomeni psicologici.

Nel proseguo di questo capitolo approfondiremo un modello cognitivo bayesiano molto noto: il Drift Diffusion Model, strumento analitico di fondamentale importanza nel campo della psichiatria computazionale.

Il modello dei tempi di reazione#

Il Drift Diffusion Model (DDM) è un modello computazionale ampiamente utilizzato per analizzare i dati sui tempi di reazione e le scelte in compiti di decisione binaria. Originariamente derivato dalla teoria delle decisioni sequenziali, il DDM fornisce un quadro per comprendere come le decisioni vengano prese in situazioni di incertezza e sotto vincoli temporali. Il modello è particolarmente utile per esaminare il processo di accumulo di informazioni verso una delle due possibili scelte o “barriere decisionali”.

Parametri del Modello#

  1. Drift Rate (v): Il drift rate rappresenta la velocità con cui le informazioni vengono accumulate nel corso del tempo verso una delle due barriere decisionali. Un drift rate elevato suggerisce una raccolta rapida delle informazioni, mentre un drift rate basso indica un processo più lento. Il segno del drift rate indica la direzione della decisione. Un drift rate positivo suggerisce che le informazioni stanno accumulandosi a favore della barriera superiore (o di una delle due scelte), mentre un drift rate negativo indica l’opposto.

  2. Boundary Separation (a): Questo parametro indica la distanza tra le due barriere decisionali. Una separazione maggiore implica che è necessario accumulare più informazioni per prendere una decisione, il che di solito si traduce in tempi di reazione più lunghi ma decisioni potenzialmente più accurate. Una separazione minore, al contrario, può portare a decisioni più rapide ma potenzialmente meno accurate.

  3. Non-Decision Time (t): Questo è il tempo impiegato per processi non decisionali, come la percezione sensoriale e l’esecuzione motoria. Esso rappresenta il ritardo temporale che precede l’inizio dell’accumulo delle informazioni e segue la raggiungimento della decisione, prima dell’effettiva risposta comportamentale.

  4. A Priori Decision Bias (z): Questo parametro rappresenta il punto di partenza dell’accumulo delle informazioni. In un modello simmetrico, questo valore è tipicamente impostato a metà della separazione delle barriere (a/2), indicando l’assenza di un pregiudizio iniziale. Tuttavia, se c’è un pregiudizio a priori verso una delle due scelte, il punto di partenza sarà spostato più vicino a quella barriera.

Funzionamento del Modello#

Nel Drift Diffusion Model, si assume che un processo di decisione inizi dal punto di partenza ( z ) e che le informazioni siano accumulate nel tempo con una velocità ( v ) fino a raggiungere una delle due barriere decisionali separate da ( a ). Il tempo necessario per raggiungere una delle due barriere, sommato al tempo non decisionale ( t ), fornirà il tempo di reazione totale per quella decisione specifica.

Applicazioni e Limitazioni#

Il DDM è ampiamente utilizzato in psicologia cognitiva, neuroscienze e economia comportamentale. Esso permette di dissociare diversi processi coinvolti nella presa di decisione e offre intuizioni su come i diversi parametri possano essere influenzati da variabili come l’età, l’attenzione, e le condizioni sperimentali.

Tuttavia, il modello ha alcune limitazioni. Ad esempio, è ottimizzato per decisioni binarie e può non adattarsi bene a contesti decisionali più complessi. Inoltre, come per qualsiasi modello, la sua validità dipende dalla qualità del fit ai dati e dalla generalizzabilità a diversi contesti e popolazioni.

In sintesi, il Drift Diffusion Model offre un potente strumento per lo studio dettagliato dei processi decisionali, fornendo sia una spiegazione meccanicistica che la capacità di effettuare predizioni quantitative.

Simulazioni e stima#

Il fine della sezione seguente è illustrare il processo di stima dei parametri del Drift Diffusion Model (DDM) attraverso l’utilizzo della libreria PyMC.

Innanzitutto, procediamo con la simulazione dei dati. Immaginiamo che un individuo sottoposto a test completi 200 tentativi in un esercizio di decisione binaria. Le istruzioni che seguono servono per generare un set di dati simulati, basati sul meccanismo generativo corrispondente al DDM, utilizzando i parametri specificati di seguito.

# Specify parameters
v_true, a_true, z_true, t_true = [1.5, 0.75, 0.5, 0.15]

# Simulate data
sim_out = simulator(
    theta=[v_true, a_true, z_true, t_true],  # parameter list
    model="ddm",  # specify model (many are included in ssms)
    n_samples=200,  # number of samples for each set of parameters
)

# Turn into nice dataset
# Turn data into a pandas dataframe
dataset = pd.DataFrame(
    np.column_stack([sim_out["rts"][:, 0], sim_out["choices"][:, 0]]),
    columns=["rt", "response"],
)

dataset
rt response
0 0.471999 1.0
1 0.501999 1.0
2 0.487999 1.0
3 0.600998 1.0
4 1.715017 1.0
... ... ...
195 0.426000 1.0
196 0.730996 1.0
197 0.319000 1.0
198 0.635997 -1.0
199 0.460000 1.0

200 rows × 2 columns

I parametri del modello si possono stimare dai dati usando PyMC. Per ciascun parametro possiamo specificare la distribuzione a priori. Nel caso presente, usiamo quelle indicate di seguito.

with pm.Model() as ddm_pymc:
    v = pm.Normal("v", mu=0, sigma=4.0)
    a = pm.HalfNormal("a", sigma=2.0)
    z = pm.Uniform("z", lower= 0.0, upper= 1.0)
    t = pm.Uniform("t", lower=0.0, upper=0.6, initval=0.1)
    
    ddm = hssm.likelihoods.DDM("DDM", v=v, a=a, z=z, t=t, observed=dataset.values)

L’aspetto cruciale del modello PyMC è rappresentata dalla versomiglianza del modello DDM, hssm.likelihoods.DDM, la quale è specificata dalla funzione DDM del pacchetto hssm.

Per informazioni sull’installazione di hssm, si veda il sito dedicato.

Note

È consigliabile installare hssm in un ambiente virtuale dedicato, oppure usarlo su Colab, inquanto può interferire con i pacchetti dell’ambiente virtuale che usiamo per le altre analisi statistiche di questo corso.

Per installare hssm sul mio computer ho usato la procesura seguente.

conda create -c conda-forge -n hssm_env "pymc==5.7.2"
conda activate hssm_env

conda install numpyro
conda install blackjax
conda install -c conda-forge bambi
conda install -c conda-forge seaborn
pip install hssm
pip install aquarel

ddm_pymc
\[\begin{split} \begin{array}{rcl} \text{v} &\sim & \operatorname{Normal}(0,~4)\\\text{a} &\sim & \operatorname{HalfNormal}(0,~2)\\\text{z} &\sim & \operatorname{Uniform}(0,~1)\\\text{t} &\sim & \operatorname{Uniform}(0,~0.6)\\\text{DDM} &\sim & \operatorname{SSM}(\text{v},~\text{a},~\text{z},~\text{t}) \end{array} \end{split}\]
pm.model_to_graphviz(model=ddm_pymc)
../_images/99f0060dd4ac2065156244fbb444814f085084ae1d6b79713da607485cdd9e03.svg

Eseguiamo il campionamento.

with ddm_pymc:
    ddm_pymc_trace = pm.sampling_jax.sample_numpyro_nuts(draws=2000, tune=1000)
Hide code cell output 
Compiling...
Compilation time =  0:01:48.238677
Sampling...

Compiling.. :   0%|          | 0/3000 [00:00<?, ?it/s]







Running chain 0:   0%|          | 0/3000 [00:07<?, ?it/s]
Running chain 0:   5%|▌         | 150/3000 [00:07<00:10, 260.49it/s]


Running chain 0:  10%|█         | 300/3000 [00:08<00:09, 296.25it/s]


Running chain 0:  15%|█▌        | 450/3000 [00:08<00:09, 270.38it/s]


Running chain 0:  20%|██        | 600/3000 [00:09<00:09, 245.01it/s]


Running chain 0:  25%|██▌       | 750/3000 [00:10<00:08, 276.67it/s]


Running chain 0:  30%|███       | 900/3000 [00:10<00:06, 327.90it/s]


Running chain 0:  35%|███▌      | 1050/3000 [00:10<00:06, 306.63it/s]


Running chain 0:  40%|████      | 1200/3000 [00:11<00:06, 293.82it/s]


Running chain 0:  45%|████▌     | 1350/3000 [00:12<00:06, 256.84it/s]


Running chain 0:  50%|█████     | 1500/3000 [00:12<00:05, 264.54it/s]



Running chain 0:  55%|█████▌    | 1650/3000 [00:13<00:04, 278.59it/s]


Running chain 0:  60%|██████    | 1800/3000 [00:13<00:04, 264.39it/s]


Running chain 0:  65%|██████▌   | 1950/3000 [00:14<00:04, 252.24it/s]


Running chain 0:  70%|███████   | 2100/3000 [00:15<00:03, 241.21it/s]


Running chain 0:  75%|███████▌  | 2250/3000 [00:15<00:03, 231.17it/s]


Running chain 0:  80%|████████  | 2400/3000 [00:16<00:02, 250.74it/s]


Running chain 0:  85%|████████▌ | 2550/3000 [00:17<00:01, 238.45it/s]


Running chain 0:  90%|█████████ | 2700/3000 [00:17<00:01, 250.36it/s]


Running chain 0:  95%|█████████▌| 2850/3000 [00:18<00:00, 270.35it/s]


Running chain 0: 100%|██████████| 3000/3000 [00:18<00:00, 307.58it/s]

Running chain 0: 100%|██████████| 3000/3000 [00:18<00:00, 161.31it/s]
Running chain 1: 100%|██████████| 3000/3000 [00:18<00:00, 161.36it/s]
Running chain 2: 100%|██████████| 3000/3000 [00:18<00:00, 161.44it/s]
Running chain 3: 100%|██████████| 3000/3000 [00:18<00:00, 161.50it/s]

Sampling time =  0:00:19.822851
Transforming variables...
Transformation time =  0:00:00.087737

# simple_ddm_model = hssm.HSSM(data=dataset)
# print(simple_ddm_model)

Otteniamo in questo modo un oggetto idata come abbiamo visto in precedenza.

ddm_pymc_trace
arviz.InferenceData
    • <xarray.Dataset>
Dimensions:  (chain: 4, draw: 2000)
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 0 1 2 3 4 5 6 7 ... 1993 1994 1995 1996 1997 1998 1999
Data variables:
    v        (chain, draw) float64 1.796 1.567 1.849 1.862 ... 1.637 1.7 1.986
    a        (chain, draw) float64 0.744 0.8019 0.8339 ... 0.7798 0.897 0.9006
    z        (chain, draw) float64 0.4642 0.5004 0.4592 ... 0.5309 0.4828 0.4599
    t        (chain, draw) float64 0.1706 0.157 0.1309 ... 0.1691 0.1236 0.123
Attributes:
    created_at:     2023-09-08T06:19:25.447845
    arviz_version:  0.16.1

    • <xarray.Dataset>
Dimensions:          (chain: 4, draw: 2000)
Coordinates:
  * chain            (chain) int64 0 1 2 3
  * draw             (draw) int64 0 1 2 3 4 5 ... 1994 1995 1996 1997 1998 1999
Data variables:
    acceptance_rate  (chain, draw) float64 0.935 0.9891 0.9791 ... 0.569 1.0
    step_size        (chain, draw) float64 0.2852 0.2852 ... 0.3062 0.3062
    diverging        (chain, draw) bool False False False ... False False False
    energy           (chain, draw) float64 44.13 41.77 41.13 ... 47.72 44.18
    n_steps          (chain, draw) int64 7 7 15 15 7 7 15 ... 7 15 15 7 7 15 15
    tree_depth       (chain, draw) int64 3 3 4 4 3 3 4 3 4 ... 4 4 3 4 4 3 3 4 4
    lp               (chain, draw) float64 41.24 40.02 40.36 ... 42.74 41.98
Attributes:
    created_at:     2023-09-08T06:19:25.456297
    arviz_version:  0.16.1

    • <xarray.Dataset>
Dimensions:    (DDM_dim_0: 200, DDM_dim_1: 2)
Coordinates:
  * DDM_dim_0  (DDM_dim_0) int64 0 1 2 3 4 5 6 7 ... 193 194 195 196 197 198 199
  * DDM_dim_1  (DDM_dim_1) int64 0 1
Data variables:
    DDM        (DDM_dim_0, DDM_dim_1) float64 0.472 1.0 0.502 ... -1.0 0.46 1.0
Attributes:
    created_at:                 2023-09-08T06:19:25.458613
    arviz_version:              0.16.1
    inference_library:          numpyro
    inference_library_version:  0.12.1
    sampling_time:              19.822851

az.plot_trace(ddm_pymc_trace, combined=True, kind="rank_bars")
plt.tight_layout()
plt.show()
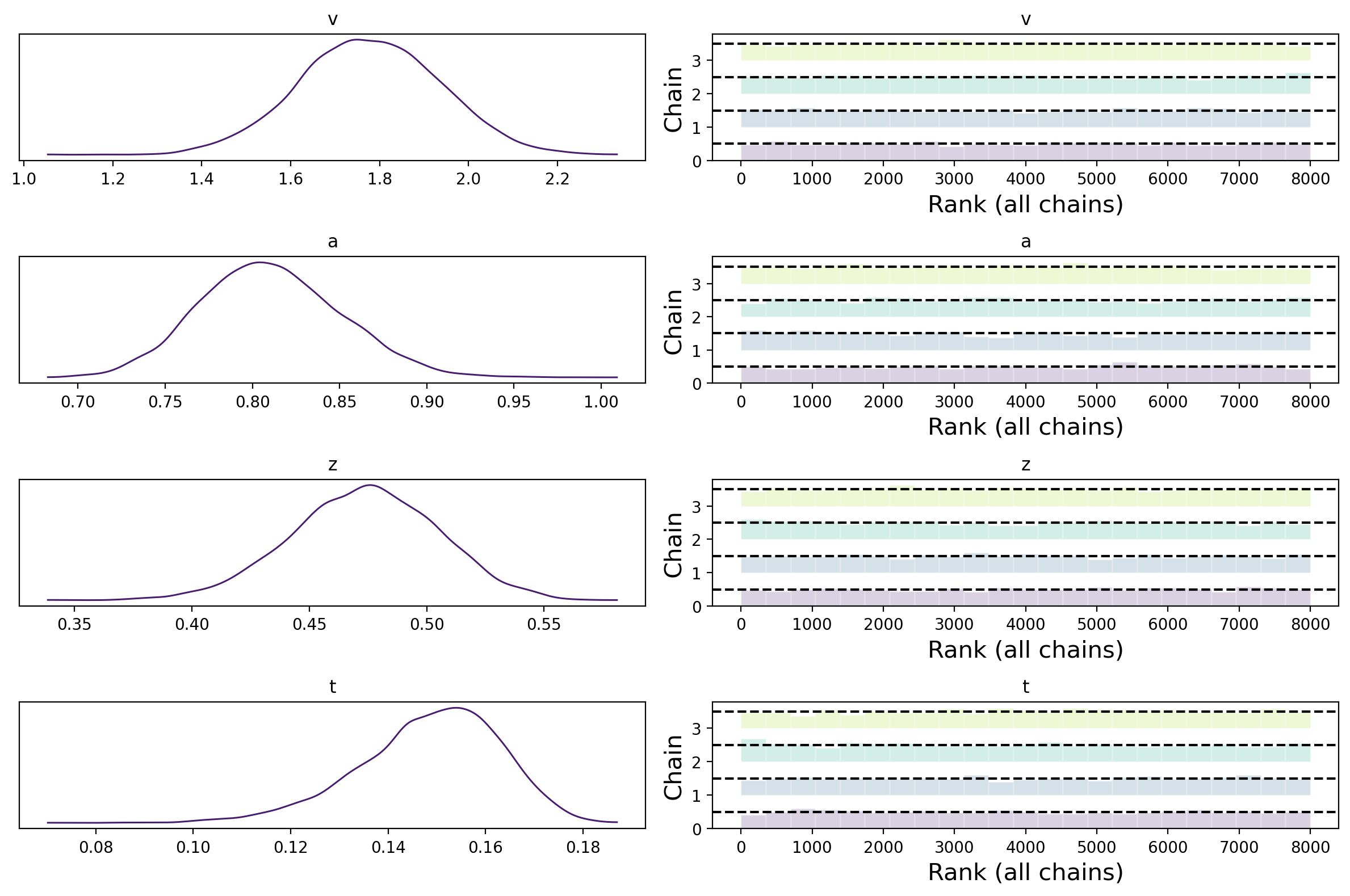
../_images/29ed1316def819ca23c482db6ebf92edd1b4b9d99f3ac747f8b0c40f810bb765.png 
az.plot_posterior(ddm_pymc_trace);
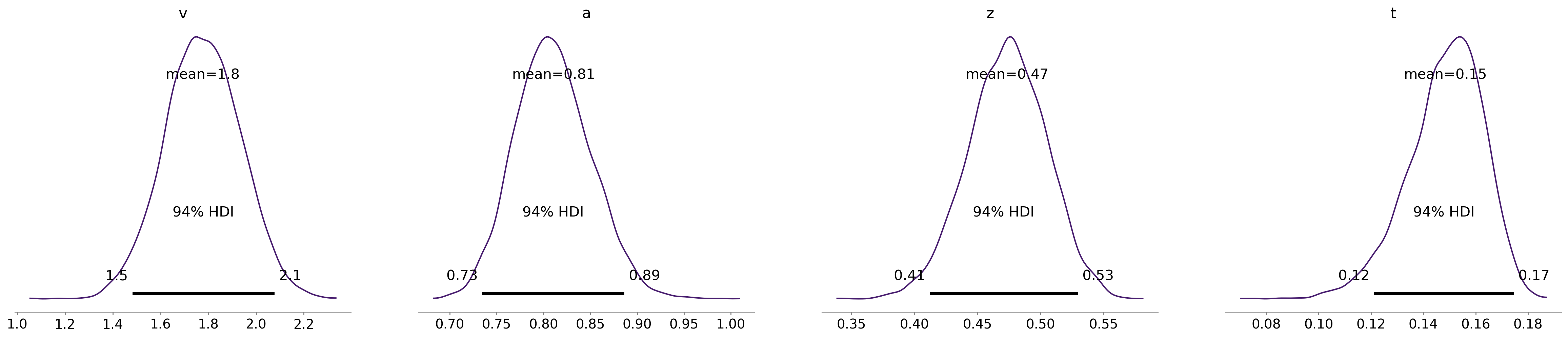
../_images/7ea807fd0c8851c87b9c71f4672d99e2bf2bba2c76aff9234125bb3d52f82584.png 
az.plot_pair(ddm_pymc_trace, kind="kde")
plt.show()
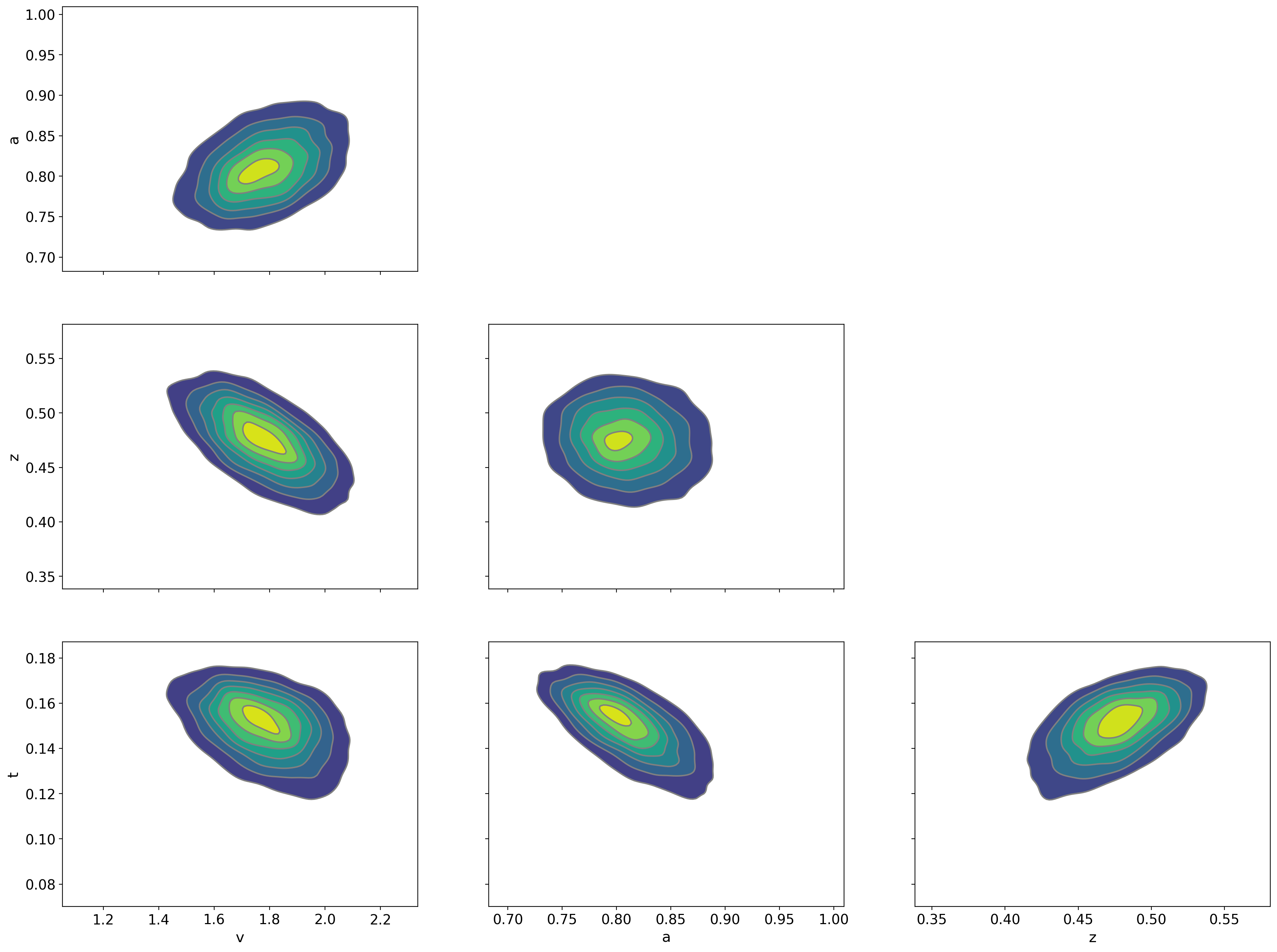
../_images/5d44bea705ffdff5ff954d47942c5b4f3dcfa8b74d0df8756bcccbcafb752fe6.png 
az.summary(ddm_pymc_trace)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
v 1.776 0.159 1.482 2.077 0.003 0.002 3589.0 4176.0 1.0
a 0.811 0.041 0.735 0.886 0.001 0.001 3210.0 3913.0 1.0
z 0.473 0.031 0.412 0.529 0.001 0.000 3024.0 3696.0 1.0
t 0.148 0.015 0.121 0.175 0.000 0.000 3078.0 3410.0 1.0

Si noti che, con solo 200 osservazioni per soggetto, è stato possibile recuperare con una buona precisione i valore dei parametri del modello DDM usati per simulare i dati.