Probabilità condizionata

L’inferenza bayesiana si basa sul principio del condizionamento come strumento centrale. Questo approccio statistico sfrutta le probabilità per esprimere i gradi di credenza o incertezza relativi a diversi risultati o ipotesi. Nella pratica bayesiana, si inizia con una probabilità nota come probabilità a priori, rappresentata dalla notazione \( P(A) \). Questa probabilità riflette la nostra credenza iniziale riguardo all’ipotesi \( A \), formulata prima di ricevere nuove evidenze o dati. Tale credenza a priori deriva da conoscenze o ipotesi già esistenti.

Il cuore dei metodi bayesiani risiede nel processo di aggiornamento di questa credenza a fronte di nuove informazioni. Al ricevimento di nuove prove, indicate con \( E \), l’analisi bayesiana adotta il condizionamento per rivedere la credenza a priori. Questo porta alla formulazione di una probabilità a posteriori, simboleggiata come \( P(A \mid E) \), che incarna la credenza aggiornata sull’ipotesi \( A \) dopo aver considerato la nuova evidenza \( E \).

La formula che governa questo aggiornamento di credenze nell’analisi bayesiana è il Il teorema di Bayes:

\[ P(A \mid E) = \frac{P(E \mid A) \times P(A)}{P(E)} \]

Questa formula include:

• \( P(A \mid E) \): la probabilità a posteriori, ovvero la probabilità dell’ipotesi \( A \) alla luce della prova \( E \).

• \( P(E \mid A) \): la verosimiglianza, cioè la probabilità di osservare la prova \( E \) assumendo che l’ipotesi \( A \) sia vera.

• \( P(A) \): la probabilità a priori, il livello iniziale di credenza nell’ipotesi \( A \).

• \( P(E) \): la probabilità di osservare la prova \( E \), considerando tutte le ipotesi possibili.

In questo capitolo, approfondiremo alcuni concetti fondamentali per comprendere meglio l’aggiornamento bayesiano:

• Probabilità Congiunta: Indica la probabilità che due eventi si verifichino insieme, anche in momenti diversi. Per esempio, potrebbe essere la probabilità di estrarre una pallina rossa seguita da una pallina verde da un’urna.

• Probabilità Marginale: È la probabilità di un singolo evento, valutata indipendentemente da altri eventi. Ad esempio, si potrebbe calcolare la probabilità di estrarre una pallina verde da un’urna.

• Probabilità Condizionata: Rappresenta la probabilità che un evento avvenga, dato che un altro evento correlato si è già verificato. Per esempio, conoscendo l’estrazione di una pallina verde, potremmo voler sapere la probabilità di estrarre una seconda pallina verde dalla stessa urna.

Inoltre, esamineremo i principali teoremi legati alla probabilità condizionata. Iniziamo con l’analisi di un famoso problema della teoria delle probabilità: il paradosso di Monty Hall.

Preparazione del Notebook

import numpy as np
import pandas as pd
import random 

Il paradosso di Monty Hall

Il paradosso di Monty Hall rappresenta un curioso esempio di come l’introduzione di nuove informazioni possa influenzare l’esito di una situazione probabilistica. Questo famoso problema trae origine dal popolare programma televisivo americano “Let’s Make a Deal” e deve la sua notorietà al conduttore Monty Hall.

Nel gioco ci sono tre porte chiuse: dietro una si nasconde un’automobile, mentre dietro le altre due ci sono delle capre. Inizialmente, il concorrente sceglie una delle tre porte senza aprirla. Successivamente, Monty Hall apre una delle due porte rimaste, rivelando una capra. A questo punto, offre al concorrente la possibilità di cambiare la sua scelta iniziale e optare per l’altra porta ancora chiusa. Il paradosso si presenta quando si scopre che cambiando la scelta in questa fase, il concorrente aumenta le sue probabilità di vincere l’automobile, passando da 1/3 a 2/3.

Per confermare questo risultato inaspettato, è possibile eseguire una simulazione in Python. In questa simulazione, consideriamo due scenari: uno in cui il concorrente mantiene la sua scelta iniziale e un altro in cui cambia la sua scelta dopo che Monty Hall ha svelato una capra. Ripetendo questa simulazione migliaia di volte, possiamo confrontare i risultati empirici e confermare come effettivamente il cambiamento di scelta aumenti le probabilità del concorrente di vincere l’automobile.

Di seguito è riportato lo script di una simulazione progettata per illustrare il paradosso di Monty Hall.

porte = [
    "capra1",
    "capra2",
    "macchina",
]  # definisco il gioco, scelgo una porta a caso per n volte
counter = 0
contatore_cambio = 0
n = 10000
porta_vincente = "macchina"
for i in range(n):
    scelta_casuale = random.choice(porte)
    porte_rimaste = [x for x in porte if x != scelta_casuale]
    porta_rivelata = random.choice([x for x in porte_rimaste if x != porta_vincente])
    porta_alternativa = [
        x for x in porte if x != scelta_casuale and x != porta_rivelata
    ]
    if "macchina" in porta_alternativa:
        contatore_cambio += 1
    if scelta_casuale == "macchina":
        counter += 1

print(counter / n)  # quante volte vinco non cambiando porta
print(contatore_cambio / n)  # quante volte vinco cambiando porta

0.331
0.669

Questo script Python è stato creato da un gruppo di studenti di Psicometria nell’AA 2023-2023. La simulazione mostra che, effettivamente, la probabilità di vincere la macchina aumenta quando il concorrente sceglie di cambiare porta.

Ecco una spiegazione del paradosso:

1. Fase Iniziale: Nel gioco, il concorrente deve scegliere una delle tre porte (A, B, C), dietro una delle quali si trova una macchina. Inizialmente, la probabilità che la macchina si trovi dietro la porta scelta è \(1/3\), dato che esistono tre possibilità ugualmente probabili e solo una contiene la macchina.

2. Aggiunta di Informazioni: Dopo la scelta iniziale, Monty Hall, che conosce il contenuto dietro ogni porta, apre una delle due porte non scelte, rivelando sempre una capra. Questo passaggio è fondamentale: non cambia la probabilità \(1/3\) che la macchina sia dietro la porta originariamente scelta dal concorrente, ma la probabilità che la macchina si trovi dietro l’altra porta non scelta aumenta ora a \(2/3\). Questo aumento di probabilità deriva dal fatto che Monty ha scelto deliberatamente una porta con una capra, basando la sua scelta sulla posizione della macchina.

Consideriamo i tre possibili scenari dopo che il concorrente ha scelto la porta A:

• La macchina è dietro la porta A: La probabilità di questo scenario è \(1/3\). Monty può aprire sia la porta B che la porta C, poiché entrambe nascondono una capra. Se il concorrente cambia la sua scelta, perderà.

• La macchina è dietro la porta B: La probabilità di questo scenario è \(1/3\). Monty aprirà la porta C, perché sa che la macchina è dietro la porta B e non può rivelarla. Se il concorrente cambia la sua scelta da A a B, vincerà.

• La macchina è dietro la porta C: La probabilità di questo scenario è \(1/3\). Monty aprirà la porta B. Se il concorrente cambia la sua scelta da A a C, vincerà.

In conclusione, cambiare la scelta originale porta alla vittoria in due dei tre scenari possibili. Pertanto, la probabilità complessiva di vincere cambiando la scelta è \(2/3\).

Questo paradosso evidenzia come, in presenza di informazioni aggiuntive, le probabilità iniziali possano essere riviste significativamente. È un classico esempio di come l’intuizione umana spesso si scontri con i principi della teoria delle probabilità, sottolineando l’importanza della revisione bayesiana delle probabilità alla luce di nuove informazioni.

Probabilità condizionata su altri eventi

La probabilità di un evento è intrinsecamente condizionata dal nostro stato di informazione. In presenza di un determinato insieme di informazioni, attribuiamo a un evento una probabilità specifica di occorrenza. Tuttavia, qualora il nostro stato informativo subisca una modifica, anche la probabilità associata all’evento verrà corrispondentemente aggiornata.

In realtà, tutte le probabilità possono essere intese come probabilità condizionate, anche quando la variabile o l’evento condizionante non è esplicitamente specificato. Ciò implica che le probabilità sono sempre contestualizzate e dipendono dal set informativo disponibile in un dato scenario.

Questo quadro concettuale ci induce a considerare le probabilità come una ‘misura di plausibilità’ che riflette la nostra conoscenza corrente del sistema o del fenomeno sotto indagine. A seguito dell’acquisizione di nuove informazioni o di cambiamenti nel contesto, la nostra misura di plausibilità, e quindi la probabilità attribuita agli eventi, può essere rivista.

Definizione

Siano \(A\) e \(B\) due eventi definiti su uno spazio campionario \(S\). Supponendo che l’evento \(B\) sia verificato, la probabilità condizionata di \(A\) dato \(B\) è data da

(10)\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)}, \quad \text{per}\, P(B) > 0, \]

dove \(P(A\cap B)\) rappresenta la probabilità congiunta dei due eventi, ovvero la probabilità che entrambi si verifichino.

È importante notare che \(P(A \mid B)\) non è definita se \(P(B) = 0\).

La probabilità condizionata può essere interpretata come una ricalibrazione dello spazio campionario da \(S\) a \(B\). Per spazi campionari discreti, la probabilità condizionata è espressa come

\[ P(A \mid B) = \frac{| A \cap B |}{| B |}. \]

Probabilità condizionata e lancio di due dadi

Consideriamo un esempio. Lanciamo due dadi equilibrati e vogliamo calcolare la probabilità che la somma dei punteggi ottenuti sia minore di 8.

Inizialmente, quando non abbiamo ulteriori informazioni, possiamo calcolare la probabilità in modo tradizionale. Ci sono 21 risultati possibili con somma minore di 8. Poiché ci sono 36 possibili combinazioni di lancio dei due dadi, la probabilità di ottenere una somma minore di 8 è 21/36, che equivale a circa 0.58.

Supponiamo ora di sapere che la somma del lancio di due dadi ha prodotto un risultato dispari. In questo caso, ci sono solo 18 possibili combinazioni di lancio dei due dadi (dato che abbiamo escluso i risultati pari). Tra essi, vi sono 12 risultati che soddisfano la condizione per cui la somma è minore di 8. Quindi, la probabilità di ottenere una somma minore di 8 cambia da circa 0.58 a 12/18, ovvero 0.67 quando consideriamo l’informazione aggiuntiva del risultato dispari.

Svolgiamo il problema in Python.

r = range(1, 7)
sample = [(i, j) for i in r for j in r]
sample

[(1, 1),
 (1, 2),
 (1, 3),
 (1, 4),
 (1, 5),
 (1, 6),
 (2, 1),
 (2, 2),
 (2, 3),
 (2, 4),
 (2, 5),
 (2, 6),
 (3, 1),
 (3, 2),
 (3, 3),
 (3, 4),
 (3, 5),
 (3, 6),
 (4, 1),
 (4, 2),
 (4, 3),
 (4, 4),
 (4, 5),
 (4, 6),
 (5, 1),
 (5, 2),
 (5, 3),
 (5, 4),
 (5, 5),
 (5, 6),
 (6, 1),
 (6, 2),
 (6, 3),
 (6, 4),
 (6, 5),
 (6, 6)]

event = [roll for roll in sample if sum(roll) < 8]
print(f"{len(event)} / {len(sample)}")

21 / 36

sample_odd = [roll for roll in sample if (sum(roll) % 2) != 0]
sample_odd

[(1, 2),
 (1, 4),
 (1, 6),
 (2, 1),
 (2, 3),
 (2, 5),
 (3, 2),
 (3, 4),
 (3, 6),
 (4, 1),
 (4, 3),
 (4, 5),
 (5, 2),
 (5, 4),
 (5, 6),
 (6, 1),
 (6, 3),
 (6, 5)]

event = [roll for roll in sample_odd if sum(roll) < 8]
print(f"{len(event)} / {len(sample_odd)}")

12 / 18

Se applichiamo l’eq. (10), abbiamo: \(P(A \cap B)\) = 12/36, \(P(B)\) = 18/36 e

\[ P(A \mid B) = \frac{12}{18}. \]

Questo esempio illustra come la probabilità di un evento possa variare in base alle informazioni aggiuntive di cui disponiamo. Nel secondo caso, avendo l’informazione che la somma è dispari, la probabilità di ottenere una somma minore di 8 aumenta notevolmente rispetto al caso iniziale in cui non avevamo questa informazione.

Mammografia e cancro al seno

In questo esempio, consideriamo uno screening per la diagnosi precoce del tumore mammario utilizzando un test con determinate caratteristiche:

• Sensibilità del test: 90%. Questo significa che il test classifica correttamente come positivo il 90% delle donne colpite dal cancro al seno.

• Specificità del test: 90%. Ciò indica che il test classifica correttamente come negativo il 90% delle donne che non hanno il cancro al seno.

• Prevalenza del cancro al seno nella popolazione sottoposta allo screening: 1% (0.01). Questo è il 1% delle donne che ha effettivamente il cancro al seno, mentre il restante 99% (0.99) non ne è affetto.

Ora cerchiamo di rispondere alle seguenti domande:

• Qual è la probabilità che una donna scelta a caso ottenga una mammografia positiva? Poiché il 1% delle donne ha il cancro al seno, la probabilità di ottenere una mammografia positiva (test positivo) è pari alla sensibilità del test, ovvero 0.90 (cioè 90%).

• Se la mammografia è positiva, qual è la probabilità che vi sia effettivamente un tumore al seno?

Per risolvere questo problema, consideriamo un campione di 1000 donne sottoposte al test di screening per il tumore al seno. Di queste 1000 donne:

• 10 donne (1% del campione) hanno effettivamente il cancro al seno. Per queste 10 donne con il cancro, il test darà un risultato positivo (vera positività) in 9 casi (90%).

• Per le restanti 990 donne (99% del campione) che non hanno il cancro al seno, il test darà un risultato positivo (falsa positività) in 99 casi (10%).

Questa situazione può essere rappresentata graficamente nel seguente modo:

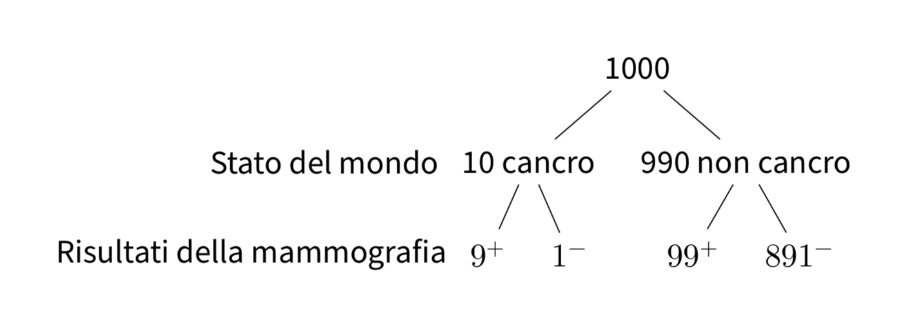
Combinando i due risultati precedenti, vediamo che il test dà un risultato positivo per 9 donne che hanno effettivamente il cancro al seno e per 99 donne che non lo hanno, per un totale di 108 risultati positivi su 1000. Pertanto, la probabilità di ottenere un risultato positivo al test è \(\frac{108}{1000}\) = 0.108.

Tuttavia, tra le 108 donne che hanno ottenuto un risultato positivo al test, solo 9 hanno effettivamente il cancro al seno. Quindi, la probabilità di avere il cancro al seno, dato un risultato positivo al test, è pari a \(\frac{9}{108}\) = 0.083, corrispondente all’8.3%.

In questo esempio, la probabilità dell’evento “ottenere un risultato positivo al test” è una probabilità non condizionata, poiché calcoliamo semplicemente la proporzione di risultati positivi nel campione totale. D’altra parte, la probabilità dell’evento “avere il cancro al seno, dato che il test ha prodotto un risultato positivo” è una probabilità condizionata, poiché calcoliamo la proporzione delle donne con il cancro al seno tra quelle che hanno ottenuto un risultato positivo al test.

Questo esempio illustra come la conoscenza di ulteriori informazioni (il risultato positivo al test) può influenzare la probabilità di un evento (avere il cancro al seno), mostrando chiaramente la differenza tra probabilità condizionate e non condizionate.

Il paradosso di Simpson

Nel campo della probabilità condizionata, uno dei fenomeni più interessanti e, nel contempo, più controintuitivi, è rappresentato dal paradosso di Simpson. Quando applicato al mondo della psicologia, il fenomeno può essere descritto come segue.

Due psicoterapeuti, Rossi e Bianchi, praticano due tipi di terapie: terapia per disturbi d’ansia e coaching per migliorare le prestazioni lavorative. Ogni terapia può avere un esito positivo o negativo. I rispettivi bilanci dei due terapeuti sono riportati nelle seguenti tabelle.

Rossi

Tipo di terapia	Successo	Fallimento
Disturbi d’ansia	70	20
Coaching lavorativo	10	0
Totale	80	20

Bianchi

Tipo di terapia	Successo	Fallimento
Disturbi d’ansia	2	8
Coaching lavorativo	81	9
Totale	83	17

Rossi ha un tasso di successo superiore a Bianchi nella terapia per i disturbi d’ansia: 70 su 90 rispetto a 2 su 10. Anche nel coaching lavorativo, Rossi ha un tasso di successo superiore: 10 su 10 rispetto a 81 su 90. Tuttavia, se aggregiamo i dati dei due tipi di terapia per confrontare i tassi di successo globali, Rossi è efficace in 80 su 100 terapie, mentre Bianchi in 83 su 100: il tasso di successo globale di Bianchi risulta superiore!

Questo fenomeno è un esempio del paradosso di Simpson, dove una tendenza osservata in diversi gruppi si inverte quando i gruppi sono combinati.

Per essere più precisi, possiamo calcolare i tassi di successo per ciascun terapeuta e per ciascun tipo di terapia, oltre al tasso di successo globale.

1. Rossi

   • Tasso di successo in terapia per disturbi d’ansia: \(\frac{70}{70+20} = \frac{70}{90} \approx 0.778\)

   • Tasso di successo in coaching lavorativo: \(\frac{10}{10+0} = \frac{10}{10} = 1\)

   • Tasso di successo globale: \(\frac{70+10}{70+20+10+0} = \frac{80}{100} = 0.8\)

2. Bianchi

   • Tasso di successo in terapia per disturbi d’ansia: \(\frac{2}{2+8} = \frac{2}{10} = 0.2\)

   • Tasso di successo in coaching lavorativo: \(\frac{81}{81+9} = \frac{81}{90} \approx 0.9\)

   • Tasso di successo globale: \(\frac{2+81}{2+8+81+9} = \frac{83}{100} = 0.83\)

Quello che sta succedendo è che Rossi, presumibilmente a causa della sua reputazione come terapeuta più esperto, sta effettuando un numero maggiore di terapie per disturbi d’ansia, che sono intrinsecamente più complesse e con una probabilità di successo variabile rispetto al coaching lavorativo. Il suo tasso di successo globale è inferiore non a causa di una minore abilità in un particolare tipo di terapia, ma perché una frazione maggiore delle sue terapie riguarda casi più complessi.

L’aggregazione dei dati tra diversi tipi di terapia presenta un quadro fuorviante delle abilità dei terapeuti perché perdiamo l’informazione su quale terapeuta tende a effettuare quale tipo di terapia. Quando sospettiamo la presenza di variabili di confondimento, come ad esempio il tipo di terapia in questo contesto, è fondamentale analizzare i dati in modo disaggregato per comprendere con precisione la dinamica in atto.

Teorema della probabilità composta

È possibile scrivere l’eq. (10) nella forma:

(11)\[ P(A \cap B) = P(B)P(A \mid B) = P(A)P(B \mid A). \]

Questo secondo modo di scrivere l’equazione (10) è chiamato teorema della probabilità composta (o regola moltiplicativa, o regola della catena). La legge della probabilità composta ci dice che la probabilità che si verifichino contemporaneamente due eventi \(A\) e \(B\) è pari alla probabilità di uno dei due eventi moltiplicata per la probabilità dell’altro evento condizionata al verificarsi del primo.

L’eq. (11) si estende al caso di \(n\) eventi \(A_1, \dots, A_n\) nella forma seguente:

(12)\[ P\left( \bigcap_{k=1}^n A_k \right) = \prod_{k=1}^n P\left( A_k \ \Biggl\lvert \ \bigcap_{j=1}^{k-1} A_j \right). \]

Per esempio, nel caso di quattro eventi abbiamo

\[\begin{split} \begin{split} P(&A_1 \cap A_2 \cap A_3 \cap A_4) = \\ & P(A_1) \cdot P(A_2 \mid A_1) \cdot P(A_3 \mid A_1 \cap A_2) \cdot P(A_4 \mid A_1 \cap A_2 \cap A_{3}).\notag \end{split} \end{split}\]

Per fare un esempio, consideriamo il problema seguente. Da un’urna contenente 6 palline bianche e 4 nere si estrae una pallina per volta, senza reintrodurla nell’urna. Indichiamo con \(B_i\) l’evento: “esce una pallina bianca alla \(i\)-esima estrazione” e con \(N_i\) l’estrazione di una pallina nera. L’evento: “escono due palline bianche nelle prime due estrazioni” è rappresentato dalla intersezione \(\{B_1 \cap B_2\}\) e, per l’eq. (11), la sua probabilità vale

\[ P(B_1 \cap B_2) = P(B_1)P(B_2 \mid B_1). \]

\(P(B_1)\) vale 6/10, perché nella prima estrazione \(\Omega\) è costituito da 10 elementi: 6 palline bianche e 4 nere. La probabilità condizionata \(P(B_2 \mid B_1)\) vale 5/9, perché nella seconda estrazione, se è verificato l’evento \(B_1\), lo spazio campionario consiste di 5 palline bianche e 4 nere. Si ricava pertanto:

\[ P(B_1 \cap B_2) = \frac{6}{10} \cdot \frac{5}{9} = \frac{1}{3}. \]

In modo analogo si ha che

\[ P(N_1 \cap N_2) = P(N_1)P(N_2 \mid N_1) = \frac{4}{10} \cdot \frac{3}{9} = \frac{4}{30}. \]

Se l’esperimento consiste nell’estrazione successiva di 3 palline, la probabilità che queste siano tutte bianche, per l’eq. (12), vale

\[\begin{split} \begin{aligned} P(B_1 \cap B_2 \cap B_3) &=P(B_1)P(B_2 \mid B_1)P(B_3 \mid B_1 \cap B_2) \notag\\ &=\frac{6}{10}\cdot\frac{5}{9} \cdot\frac{4}{8} \notag\\ &= \frac{1}{6}. \end{aligned} \end{split}\]

La probabilità dell’estrazione di tre palline nere è invece:

\[\begin{split} \begin{aligned} P(N_1 \cap N_2 \cap N_3) &= P(N_1)P(N_2 \mid N_1)P(N_3 \mid N_1 \cap N_2)\notag\\ &= \frac{4}{10} \cdot \frac{3}{9} \cdot \frac{2}{8} \notag\\ &= \frac{1}{30}.\notag \end{aligned} \end{split}\]

Il teorema della probabilità totale

Il teorema della probabilità totale (detto anche teorema delle partizioni) afferma che se abbiamo una partizione di uno spazio campionario \(\Omega\) in \(n\) eventi mutualmente esclusivi e tali che la loro unione formi \(\Omega\), allora la probabilità di un qualsiasi evento in \(\Omega\) può essere calcolata sommando la probabilità dell’evento su ciascun sottoinsieme della partizione, pesata in base alla probabilità del sottoinsieme.

In altre parole, se \(H_1, H_2, \dots, H_n\) sono eventi mutualmente esclusivi e tali che \(\bigcup_{i=1}^n H_i = \Omega\), allora per ogni evento \(E \subseteq \Omega\), la probabilità di \(E\) è data dalla formula:

(13)\[ P(E) = \sum_{i=1}^n P(E \mid H_i)P(H_i), \]

dove \(P(E \mid H_i)\) rappresenta la probabilità condizionata di \(E\) dato che si è verificato l’evento \(H_i\), e \(P(H_i)\) è la probabilità dell’evento \(H_i\).

Il teorema della probabilità totale riveste un ruolo fondamentale in quanto fornisce il denominatore nel teorema di Bayes, svolgendo la funzione di costante di normalizzazione. Questa costante di normalizzazione è di vitale importanza per assicurare che la distribuzione a posteriori sia una distribuzione di probabilità valida. Per ulteriori dettagli e approfondimenti, è possibile fare riferimento al capitolo Pensare ad una proporzione in termini soggettivi.

Nell’ambito della probabilità discreta, questo teorema viene usato quando abbiamo una partizione dello spazio campionario e vogliamo calcolare la probabilità di un evento, sfruttando le probabilità dei singoli eventi della partizione. Il caso più semplice è quello di una partizione dello spazio campione in due sottoinsiemi: \(P(E) = P(E \cap H_1) + P(E \cap H_2)\).

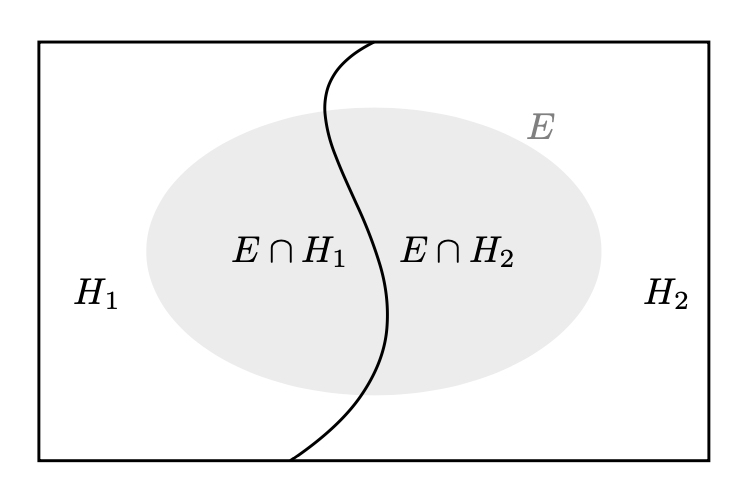
In tali circostanza abbiamo che

\[ P(E) = P(E \mid H_1) P(H_1) + P(E \mid H_2) P(H_2). \]

L’eq. (13) è utile per calcolare \(P(E)\), se \(P(E \mid H_i)\) e \(P(H_i)\) sono facili da trovare. Quale esempio, consideriamo il seguente problema. Abbiamo tre urne, ciascuna delle quali contiene 100 palline:

• Urna 1: 75 palline rosse e 25 palline blu,

• Urna 2: 60 palline rosse e 40 palline blu,

• Urna 3: 45 palline rosse e 55 palline blu.

Una pallina viene estratta a caso da un’urna anch’essa scelta a caso. Qual è la probabilità che la pallina estratta sia di colore rosso?

Sia \(R\) l’evento “la pallina estratta è rossa” e sia \(U_i\) l’evento che corrisponde alla scelta dell’\(i\)-esima urna. Sappiamo che

\[ P(R \mid U_1) = 0.75, \quad P(R \mid U_2) = 0.60, \quad P(R \mid U_3) = 0.45. \]

Gli eventi \(U_1\), \(U_2\) e \(U_3\) costituiscono una partizione dello spazio campione in quanto \(U_1\), \(U_2\) e \(U_3\) sono eventi mutualmente esclusivi ed esaustivi, ovvero \(P(U_1 \cup U_2 \cup U_3) = 1.0\). In base al teorema della probabilità totale, la probabilità di estrarre una pallina rossa è dunque

\[\begin{split} \begin{split} P(R) &= P(R \mid U_1)P(U_1) + P(R \mid U_2)P(U_2) + P(R \mid U_3)P(U_3) \\ &= 0.75 \cdot \frac{1}{3}+0.60 \cdot \frac{1}{3}+0.45 \cdot \frac{1}{3} \\ &=0.60. \end{split} \end{split}\]

Facciamo un altro esempio. Usiamo ora il teorema della probabilità totale per risolvere il paradosso di Monty Hall. Immaginiamo tre scenari, rappresentati dai tre eventi \( C_1 \), \( C_2 \), e \( C_3 \), che indicano rispettivamente che l’auto si trovi dietro la porta 1, 2 o 3.

1. Se l’auto è dietro la porta 1 e decidiamo di cambiare la nostra scelta, perderemo. In questo caso, la probabilità di vincere l’auto, data la nostra scelta iniziale di porta 1, è \( P(\text{vincere l'auto} \mid C_1) = 0 \).

2. Se, invece, l’auto è dietro la porta 2 o 3, Monty aprirà l’altra porta che nasconde una capra. Se decidiamo di cambiare la nostra scelta, vinceremo. Quindi, in questi casi, la probabilità di vincere è \( P(\text{vincere l'auto} \mid C_2) = 1 \) e \( P(\text{vincere l'auto} \mid C_3) = 1 \).

Ora, applicando il teorema della probabilità totale, la probabilità complessiva di vincere l’auto se cambiamo la porta è:

\[ P(\text{vincere l'auto}) = 0 \cdot \frac{1}{3} + 1 \cdot \frac{1}{3} + 1 \cdot \frac{1}{3} = \frac{2}{3}. \]

In pratica, cambiare la porta ci dà una probabilità del \( \frac{2}{3} \) di vincere l’auto, mentre mantenerla ci darebbe solo \( \frac{1}{3} \). Quindi, è statisticamente più vantaggioso cambiare la porta.

L’indipendendenza stocastica

L’indipendenza stocastica è un concetto fondamentale nell’applicazione della probabilità in campo statistico. Possiamo esprimere in modo intuitivo l’indipendenza tra due eventi \(A\) e \(B\) utilizzando l’equazione (10). Se \(A\) e \(B\) sono indipendenti, ciò significa che il verificarsi di uno degli eventi non influisce sulla probabilità del verificarsi dell’altro, e viceversa. In altre parole, il verificarsi di uno dei due eventi non condiziona la probabilità dell’altro evento.

Per esprimere l’indipendenza con l’equazione (10), consideriamo \(A\) e \(B\) come eventi indipendenti. Allora, abbiamo:

\[ P(A \mid B) = \frac{P(A)P(B)}{P(B)} = P(A), \]

\[ P(B \mid A) = \frac{P(A)P(B)}{P(A)} = P(B). \]

Possiamo quindi affermare che due eventi \(A\) e \(B\) sono indipendenti se soddisfano le seguenti condizioni:

\[\begin{split} \begin{split} P(A \mid B) &= P(A), \\ P(B \mid A) &= P(B). \end{split} \end{split}\]

Questo implica che la probabilità dell’evento \(A\) rimane invariata, indipendentemente dal verificarsi dell’evento \(B\), e viceversa.

Tre eventi \(A\), \(B\) e \(C\) sono indipendenti se soddisfano le seguenti condizioni:

\[\begin{split} \begin{align} P(A \cap B) &= P(A) P(B) \notag\\ P(A \cap C) &= P(A) P(C) \notag\\ P(B \cap C) &= P(B) P(C) \notag\\ P(A \cap B \cap C) &= P(A) P(B) P(C). \notag \end{align} \end{split}\]

In altre parole, l’intersezione di ciascuna coppia di eventi deve avere una probabilità uguale al prodotto delle probabilità dei singoli eventi. Se queste prime tre condizioni sono soddisfatte, allora gli eventi si dicono “indipendenti a due a due”. Tuttavia, per essere completamente indipendenti, è necessario che anche l’intersezione di tutti e tre gli eventi abbia una probabilità uguale al prodotto delle probabilità dei singoli eventi. Solo in questo caso possiamo dire che gli eventi sono completamente indipendenti.

Consideriamo il seguente problema. Nel lancio di due dadi non truccati, si considerino gli eventi: \(A\) = “esce un 1 o un 2 nel primo lancio” e \(B\) = “il punteggio totale è 8”. Gli eventi \(A\) e \(B\) sono indipendenti?

Calcoliamo \(P(A)\):

r = range(1, 7)
sample = [(i, j) for i in r for j in r]
A = [roll for roll in sample if roll[0] == 1 or roll[0] == 2]
print(A)
print(f"{len(A)} / {len(sample)}")

[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)]
12 / 36

Calcoliamo \(P(B)\):

B = [roll for roll in sample if roll[0] + roll[1] == 8]
print(B)
print(f"{len(B)} / {len(sample)}")

[(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)]
5 / 36

Calcoliamo \(P(A \cap B)\):

I = [
    roll
    for roll in sample
    if (roll[0] == 1 or roll[0] == 2) and (roll[0] + roll[1] == 8)
]
print(I)
print(f"{len(I)} / {len(sample)}")

[(2, 6)]
1 / 36

Gli eventi \(A\) e \(B\) non sono statisticamente indipendenti dato che \(P(A \cap B) \neq P(A)P(B)\):

12/36 * 5/36 == 1/36

False

Commenti e considerazioni finali

La probabilità condizionata riveste un ruolo fondamentale poiché ci permette di definire in modo preciso il concetto di indipendenza statistica. Uno degli aspetti cruciali dell’analisi statistica riguarda la valutazione dell’associazione tra due variabili. Nel capitolo attuale, ci siamo concentrati sul concetto di indipendenza, che indica l’assenza di relazione tra le variabili. Tuttavia, in futuro, esploreremo come fare inferenze sulla correlazione tra variabili, ovvero come determinare se le variabili sono associate tra loro o se esiste una relazione statistica credibile tra di esse. Questo approfondimento ci permetterà di studiare le connessioni tra variabili e comprendere meglio i fenomeni osservati nei dati.

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Sun Jan 28 2024

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.19.0

numpy : 1.26.2
pandas: 2.1.4

Watermark: 2.4.3