La predizione bayesiana

Nel presente capitolo, esamineremo il ruolo e l’importanza della distribuzione predittiva a posteriori nell’analisi di un set di dati, denotato come \({X, Y}\). In ambito statistico, è fondamentale identificare le funzioni matematiche che descrivono in modo ottimale la relazione tra questi dati. Tuttavia, l’analisi non si limita alla semplice descrizione dei dati; si estende anche alla comprensione delle cause e dei meccanismi che stanno alla base della generazione di tali dati, incarnando l’essenza dell’inferenza causale. Quest’ultima trascende la mera correlazione tra variabili, tentando di delineare come una variabile influenzi l’altra.

Un elemento centrale di questa analisi è l’idea di intervento, che può essere realizzato attraverso modifiche sperimentali o teoriche applicate ai dati. Ci si interroga, ad esempio, sull’impatto che una modifica in un punto dei dati potrebbe avere sulla distribuzione congiunta dei dati stessi. Questa indagine ci introduce al concetto di manipolazione causale, che permette di esplorare l’effetto delle variazioni di una variabile sulle altre.

Il passo successivo è la previsione. Quando si osserva un nuovo dato, sorge spontanea la domanda: “Qual è il valore atteso corrispondente?” Qui entra in gioco la previsione bayesiana. Grazie ai principi della statistica bayesiana, siamo capaci non solo di adattare una curva ai dati esistenti, ma anche di fare previsioni su dati non ancora osservati, basandoci sulle conoscenze pregresse e sull’evidenza disponibile.

Durante questo capitolo, ci concentreremo sulla previsione bayesiana. L’approccio bayesiano ci permette di quantificare l’incertezza nelle nostre previsioni, affinare la comprensione dei meccanismi sottostanti e migliorare la precisione e la pertinenza delle previsioni nella ricerca.

L’analisi bayesiana persegue diversi obiettivi, inclusa la stima della distribuzione a posteriori dei parametri, la valutazione delle ipotesi e la previsione di dati futuri. Una volta determinate le distribuzioni a posteriori, si procede alla stima delle caratteristiche dei dati futuri, portando alla creazione di una distribuzione predittiva a posteriori, uno strumento fondamentale per la verifica e la validazione del modello statistico adottato. Questa distribuzione ci consente di confrontare direttamente le previsioni del modello con i dati osservati nel campione, e se queste previsioni concordano con i dati raccolti, possiamo concludere che il modello rappresenta accuratamente i dati.

Un altro motivo per generare previsioni dall’analisi è diagnosticare problemi relativi al modello, ai dati o a entrambi. Non possiamo osservare direttamente i parametri, ma possiamo osservare le misurazioni. Chiedere cosa si aspetta il modello, dopo aver appreso dai dati, è un modo efficace per valutare ciò che il modello ha imparato e ciò che non ha imparato. Un controllo predittivo a posteriori può rivelarsi utile per individuare situazioni in cui il modello fallisce, offrendo spunti per scoprire errori nella codifica o nuove opportunità di modellazione.

Infine, la distribuzione predittiva a priori rappresenta la distribuzione dei dati osservabili prima dell’osservazione effettiva di qualsiasi dato. Essa tiene conto delle nostre conoscenze o credenze iniziali sui parametri del modello, fornendo un quadro per comprendere e anticipare fenomeni complessi in un contesto statistico.

Preparazione del Notebook

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats 
import pymc as pm
import pymc.sampling_jax
import arviz as az
import warnings

warnings.filterwarnings("ignore", category=UserWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=Warning)

/Users/corrado/opt/anaconda3/envs/pymc_env/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
sns.set_theme(palette="colorblind")

La distribuzione predittiva a posteriori

Un modo molto intuitivo per valutare la qualità complessiva di un modello è esaminare quanto bene il modello si adatti ai dati reali. Questo tipo di approccio è diffuso nelle statistiche frequentiste, spesso basato su misure di “badness-of-fit” (inadeguatezza dell’adattamento). Nel contesto delle statistiche Bayesiane, l’analisi dell’adattamento del modello ai dati si avvale del concetto di verifica predittiva a posteriori (Posterior Predictive Checking, PPC) [GS13].

L’idea fondamentale della verifica predittiva a posteriori è che dovrebbe esserci una minima, se non assente, discrepanza tra i dati generati dal modello e i dati reali. In sostanza, la verifica predittiva a posteriori rappresenta un metodo per valutare la qualità della specificazione del modello. Qualsiasi divergenza tra i dati prodotti dal modello e i dati effettivi indica una errata specificazione del modello.

Per esemplificare il concetto di “distribuzione predittiva a posteriori”, esploriamo il modello beta-binomiale. In questo contesto, il parametro \(\theta\) (che indica la probabilità di successo) segue una distribuzione a priori modellizzata attraverso una distribuzione Beta, mentre la verosimiglianza dei dati è delineata da una distribuzione Binomiale. I dati vengono rappresentati dal numero \(y\) di successi in \(n\) prove Bernoulliane indipendenti.

Esaminiamo un caso pratico precedentemente discusso, relativo alla rappresentanza di artisti della generazione X o successive al MOMA. In uno specifico campione di 100 artisti, abbiamo notato che solo 14 di essi appartengono a queste generazioni, registrando così 14 “successi” in 100 prove Bernoulliane indipendenti. Ora, immaginiamo di analizzare un nuovo campione casuale di \(m\)=20 artisti al MOMA, con l’intento di stimare quanti di essi siano della generazione X o successive. In modo più ampio, l’obiettivo è formulare previsioni riguardanti i risultati di futuri campioni potenziali composti da \(m\) osservazioni.

Introduciamo la variabile casuale \(\tilde{Y}\) che denota il numero di “successi” in un nuovo campione di \(m\) prove. In tale campione, \(\tilde{Y}\) può assumere valori come \(\tilde{y}_1\) (per esempio, 12), \(\tilde{y}_2\) (per esempio, 7), e così via. L’obiettivo è di calcolare le probabilità associate a ciascuno dei valori possibili di \(\tilde{Y}\), che variano da 0 a 20 inclusi. Questa distribuzione di probabilità discreta è definita come “distribuzione predittiva a posteriori”, \(p(\tilde{Y} = \tilde{y} \mid Y = y)\), e rappresenta la probabilità di ciascuno dei possibili valori di \(\tilde{Y}\) (0, 1, …, 19, 20) in futuri campioni di \(m\) = 20 osservazioni.

In questo capitolo, esploriamo tre strategie per ottenere tale distribuzione:

1. Approccio analitico: Risolveremo matematicamente la distribuzione.

2. Simulazione: Applicheremo tecniche di simulazione per raggiungere i risultati desiderati.

3. Campionamento MCMC: Utilizzeremo il metodo di campionamento MCMC per stimare la distribuzione predittiva a posteriori.

Sebbene i tre metodi conducano agli stessi risultati, è importante notare che l’approccio MCMC facilita l’ottenimento della soluzione, specialmente quando una soluzione analitica non è disponibile, come nei casi al di fuori delle famiglie coniugate.

Derivazione analitica

Nel contesto in esame, la variabile casuale \( \tilde{Y} \) è governata da una distribuzione che dipende dal parametro \( \theta \). Le informazioni relative a \( \theta \) sono contenute nella distribuzione a posteriori \( p(\theta | y) \). Utilizzando la regola della probabilità congiunta, la distribuzione congiunta delle variabili \( \tilde{y} \) e \( \theta \) può essere rappresentata come:

\[ p(\tilde{y}, \theta | y) = p(\tilde{y} | \theta, y) p(\theta | y). \]

La distribuzione \( p(\tilde{y}, \theta | y) \) descrive la probabilità congiunta di osservare dati futuri \( \tilde{y} \) e un valore specifico del parametro \( \theta \), dati i dati storici \( y \). Si scompone in due parti:

1. \( p(\tilde{y} | \theta, y) \): la probabilità di osservare \( \tilde{y} \) dato un valore specifico di \( \theta \) e i dati storici \( y \).

2. \( p(\theta | y) \): la distribuzione a posteriori di \( \theta \), che rappresenta una versione aggiornata della nostra conoscenza su \( \theta \) dopo aver osservato i dati \( y \).

Se assumiamo che le osservazioni passate \( y \) e le future \( \tilde{y} \) siano indipendenti, condizionate al valore di \( \theta \), la formula si semplifica in:

\[ p(\tilde{y}, \theta | y) = p(\tilde{y} | \theta) p(\theta | y). \]

Per ottenere la distribuzione predittiva a posteriori \( p(\tilde{y} | y) \), è necessario integrare la distribuzione congiunta rispetto a \( \theta \). Questo passaggio è noto come “marginalizzazione” e serve a eliminare la dipendenza da \( \theta \):

\[ p(\tilde{y} | y) = \int p(\tilde{y} | \theta) p(\theta | y) \, d\theta. \]

Nel caso del modello beta-binomiale, \( p(\tilde{y} | \theta) \) è una distribuzione binomiale con parametri \( m \) e \( \theta \), mentre \( p(\theta | y) \) è una distribuzione Beta con parametri \( \alpha + y \) e \( \beta + n - y \).

L’integrazione può essere risolta esplicitamente, data la forma funzionale delle distribuzioni Beta e Binomiale. Il risultato è una formula chiusa per \( p(\tilde{y} | y) \), che rappresenta una distribuzione beta-binomiale.

\[\begin{split} \begin{align*} p(\tilde{y} | y) &= \int_0^1 p(\tilde{y} | \theta) p(\theta | y) \, d\theta \\ &= \int_0^1 \binom{m}{\tilde{y}} \theta^{\tilde{y}} (1 - \theta)^{m - \tilde{y}} \cdot \frac{1}{B(\alpha + y, \beta + n - y)} \theta^{\alpha + y - 1} (1 - \theta)^{\beta + n - y - 1} \, d\theta \\ &= \binom{m}{\tilde{y}} \frac{B(\tilde{y} + \alpha + y, \beta + n - y + m - \tilde{y})}{B(\alpha + y, \beta + n - y)} \end{align*} \end{split}\]

In conclusione, nel contesto del modello beta-binomiale, la distribuzione predittiva a posteriori è una distribuzione beta-binomiale con parametri \( m \), \( \alpha + y \), e \( \beta + n - y \):

(64)\[ \begin{equation} f(\tilde{y} | y) = \binom{m}{\tilde{y}} \frac{B(\alpha + y + \tilde{y}, \beta + n - y + m - \tilde{y})}{B(\alpha + y, \beta + n - y)}. \end{equation} \]

È importante notare che, se il nostro modello è ben specificato, la distribuzione predittiva a posteriori e la distribuzione dei dati osservati dovrebbero somigliarsi, essendo governate dalla stessa funzione di densità di probabilità (PDF). Per assicurarsi di questa congruenza, è usuale effettuare verifiche predittive a posteriori, mettendo a confronto la distribuzione predittiva a posteriori con i dati empirici. Un approccio consolidato per tale verifica utilizza le stime di densità Kernel (KDE, dall’inglese Kernel Density Estimates). Una KDE è in pratica una stima empirica della PDF di una variabile aleatoria, basata su un campione finito di dati. Confrontando la KDE derivata dai dati osservati con quella generata dalla distribuzione predittiva a posteriori, siamo in grado di valutare l’adeguatezza del nostro modello nel rappresentare la struttura sottostante dei dati, nonché la sua idoneità per effettuare inferenze future.

Un esempio concreto

Nell’esempio riguardante gli artisti della generazione X esposti al MOMA, la funzione di verosimiglianza dei dati è modellata mediante una distribuzione binomiale, registrando 14 successi su un totale di 100 tentativi. La distribuzione a priori per il parametro di successo, indicato come \(\theta\), è descritta da una distribuzione Beta con parametri (4, 6). Di conseguenza, la distribuzione a posteriori relativa al parametro \(\theta\) sarà una distribuzione Beta con parametri (18, 92).

Ipotizziamo ora di voler determinare la distribuzione predittiva a posteriori per un nuovo campione di dati che comprende \(m\) = 20 osservazioni.

Con riferimento all’eq. (64), sappiamo che la distribuzione predittiva a posteriori assume la forma di una distribuzione beta-binomiale con i parametri \(m\), \(\alpha + y\) e \(\beta + n - y\). Qui, \(m\) denota il numero di prove nel nuovo campione, \(\alpha\) e \(\beta\) rappresentano i parametri della distribuzione a priori, mentre \(y\) e \(n\) indicano rispettivamente il numero di successi e il numero totale di prove nel campione attuale. Nell’esempio in esame, otteniamo i seguenti valori per i parametri della distribuzione beta-binomiale: \(m = 20\), \(\alpha' = 4 + 14 = 18\), \(\beta' = 6 + 100 - 14 = 92\).

Possiamo rappresentare graficamente la distribuzione predittiva a posteriori che abbiamo definito usando la funzione betabinom.pmf.

alpha = 4
beta = 6
y = 14
n = 100
alpha_prime = alpha + y
beta_prime = beta + n - y
m = 20
x = np.arange(0, 20)

plt.plot(
    x,
    stats.betabinom.pmf(x, m, alpha_prime, beta_prime),
    "C0o",
    ms=5,
    label="betabinom pmf",
)
_ = plt.vlines(
    x,
    0,
    stats.betabinom.pmf(x, m, alpha_prime, beta_prime),
    colors="C1",
    lw=2,
    alpha=0.5,
)

# Set x-ticks to be every 5 units
plt.xticks(np.arange(0, 21, 5))

plt.xlabel("x")
plt.ylabel("Probability")
_ = plt.title("Beta-Binomial PMF")

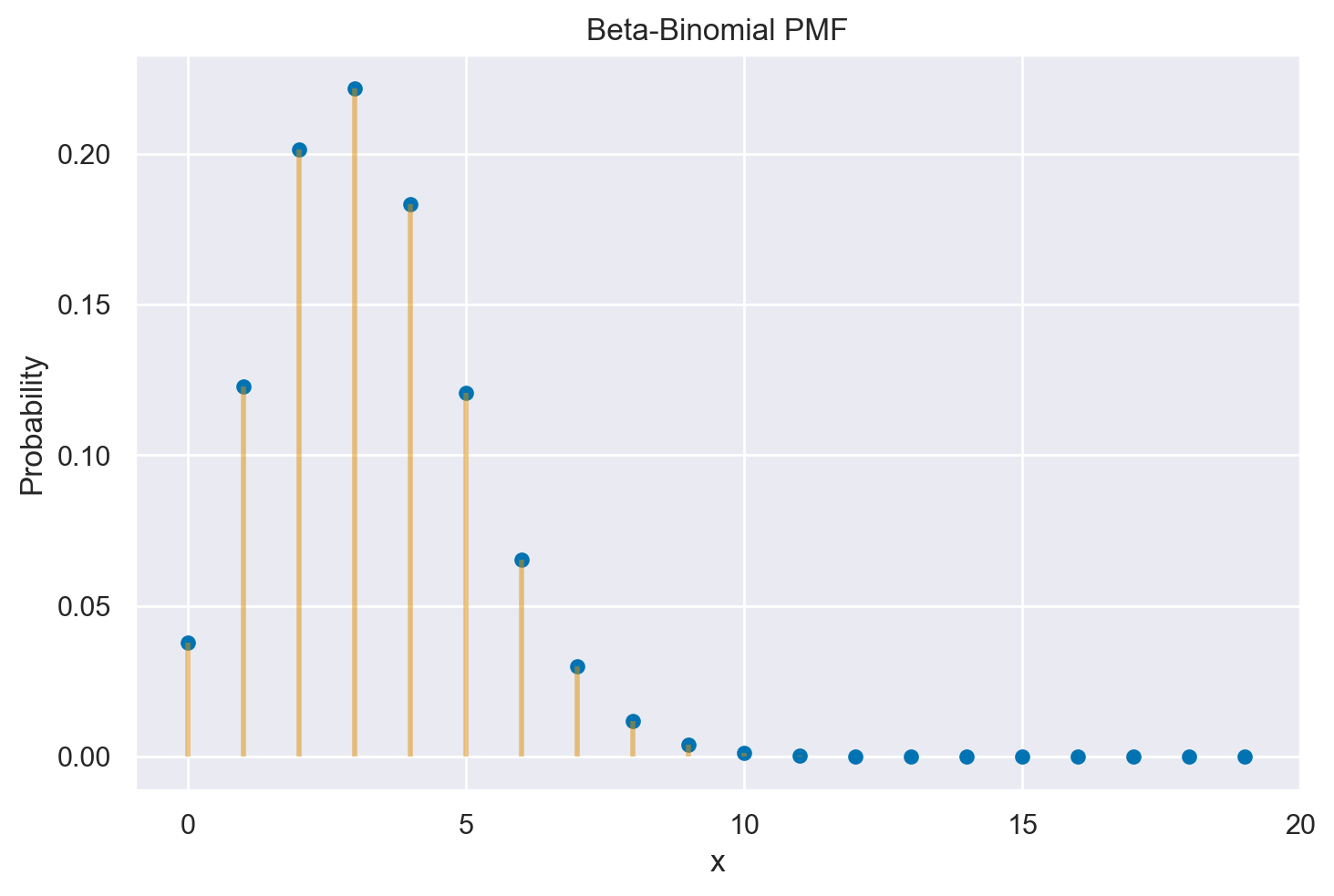
La distribuzione predittiva a posteriori, mostrata nella figura precedente, fornisce informazioni sulla probabilità di osservare \(0, 1, \dots, 20\) successi su \(m = 20\) prove in un futuro campione di \(m\) = 20 osservazioni. Queste probabilità sono valutate tenendo conto dei dati osservati nel campione corrente (14 successi su 100 prove) e delle nostre opinioni iniziali sulla plausibilità dei possibili valori di \(\theta\) (rappresentate dalla distribuzione a priori Beta(4, 6)). In altre parole, la distribuzione predittiva a posteriori ci offre una visione delle possibili frequenze di successo che potremmo osservare nei futuri campioni, basandoci sulle nostre conoscenze attuali e sull’esperienza passata.

La distribuzione predittiva a posteriori rivela che, nei potenziali campioni futuri composti da 20 osservazioni, il valore \(\tilde{y}\) con la probabilità più elevata è 3. Tuttavia, la distribuzione predittiva a posteriori ci fornisce informazioni sulla probabilità relativa di ciascuno dei possibili valori futuri di \(\tilde{y}\). Questi valori rappresentano il numero di artisti della Generazione X o successive che potrebbero trovarsi all’interno di un futuro campione di 20 osservazioni.

Una volta ottenuta la distribuzione predittiva a posteriori possiamo rispondere a ulteriori domande. Ad esempio, Qual è la probabilità a posteriori che almeno 5 degli 20 artisti siano della generazione X, ossia \(P(\tilde{Y} \geq 5 \mid Y = 14)\)?

Il risultato è dato da \(\sum_i(P(\tilde{Y} = \tilde{y}_i)\), con \(i \in 5, \dots, 20\).

1 - stats.betabinom.cdf(4, m, alpha_prime, beta_prime).sum()

0.23298739435887628

È altresì possibile calcolare il valore atteso della distribuzione predittiva a posteriori, cioè il numero previsto di artisti appartenenti alla Generazione X o successiva in un campione casuale di 20.

x = np.arange(0, 21)
px = stats.betabinom.pmf(np.arange(0, 21), m, alpha_prime, beta_prime)

ev = sum(x * px)
print(ev)

3.272727272727284

In conclusione, per il caso beta-binomiale, possiamo affermare che la previsione bayesiana di una nuova osservazione futura è rappresentata dalla distribuzione beta-binomiale con parametri \(m\), \(\alpha + y\) e \(\beta + n - y\). Qui, \(m\) rappresenta il numero di prove nel nuovo campione, \(\alpha\) e \(\beta\) sono i parametri della distribuzione a priori, e \(y\) e \(n\) sono le caratteristiche del campione attuale. In altre parole, la distribuzione beta-binomiale ci fornisce una stima delle possibili frequenze di successi che potremmo osservare in futuri campioni, tenendo conto dei dati osservati e delle nostre conoscenze iniziali sulla probabilità di successo.

Metodo basato sulla simulazione

In situazioni in cui non è possibile ottenere esattamente la distribuzione predittiva a posteriori, è comunque possibile ottenere un campione casuale di valori dalla distribuzione mediante simulazione. Nel caso in esame, supponiamo di voler generare un campione casuale di \(n\) osservazioni dalla distribuzione predittiva a posteriori. Per farlo, possiamo seguire due fasi di simulazione:

1. Estraiamo casualmente \(n\) valori del parametro \(\theta\) dalla distribuzione a posteriori \(p(\theta \mid y)\).

2. Utilizziamo i valori del parametro \(\theta\) estratti per generare \(n\) valori casuali di \(\tilde{y}\), utilizzando il modello binomiale con i parametri \(m\) e \(\theta_i\) (con \(i = 1, \dots, n\)).

In questo modo, otteniamo \(n\) realizzazioni casuali di \(n\) distribuzioni binomiali, ciascuna con i parametri specificati sopra, le quali rappresentano un campione casuale di valori della distribuzione predittiva a posteriori.

Vediamo come ottenere questo risultato in pratica. Per l’esempio che stiamo discutendo, la distribuzione a posteriori di \(\theta\) è una Beta(25, 17). Procediamo con l’estrazione casuale di 100,000 valori da questa distribuzione e esaminiamo i primi 10 valori:

nrep = 100000
theta = stats.beta.rvs(alpha_prime, beta_prime, size=nrep)
print(*theta[0:10])

0.1876466712617734 0.14123655133040988 0.09937032001331003 0.16564151313455117 0.2237071151882042 0.13647177755716866 0.16296610647400755 0.147306876911047 0.13423480535179516 0.11815022376184366

Per ciascuno dei 100,000 valori estratti per \(\theta\), generiamo casualmente un valore dalla distribuzione binomiale con parametri \(n = 20\) e probabilità \(\theta\). Esaminiamo i primi 50 valori così ottenuti.

y_tilde = [stats.binom.rvs(n=20, p=th, size=1) for th in theta]
y_tilde = np.concatenate(y_tilde)
print(*y_tilde[0:50])

2 5 2 4 4 3 4 3 3 3 6 3 5 1 1 7 3 1 5 2 5 4 3 5 3 8 10 1 6 3 5 6 4 7 3 2 2 3 5 3 1 6 1 3 4 3 7 2 3 2

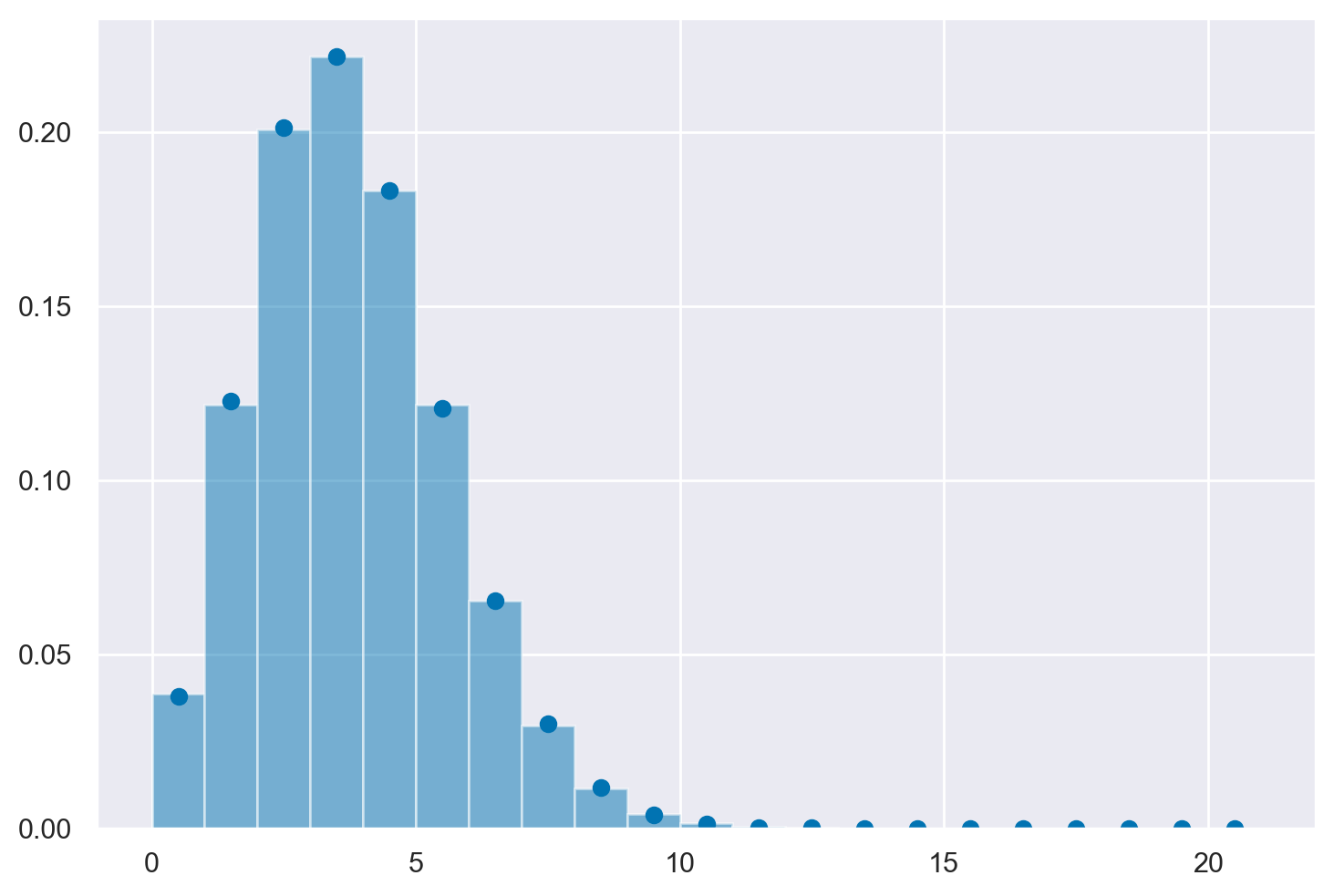
L’insieme dei valori y_tilde costituisce un campione casuale dalla distribuzione predittiva a posteriori. Nella figura seguente, è presentato un istogramma che mostra la distribuzione dei valori y_tilde. I punti corrispondenti alla distribuzione predittiva a posteriori corretta, ossia una distribuzione Beta-Binomiale con parametri \(m = 20\), \(\alpha' = 18\), e \(\beta' = 92\), sono sovrapposti sull’istogramma. Si può notare una quasi perfetta concordanza tra i valori ottenuti tramite la simulazione e quelli ricavati con la derivazione analitica.

hist, bins, _ = plt.hist(y_tilde, bins=range(0, 22), density=True, alpha=0.5)
bin_centers = (bins[:-1] + bins[1:]) / 2
px = stats.betabinom.pmf(np.arange(0, 21), m, alpha_prime, beta_prime)
plt.plot(bin_centers, px, "o", color="C0", label="Beta-Binomial");

Un intervallo di credibilità all’80% si può facilmente ottenere usando ArviZ.

az.plot_posterior(y_tilde, hdi_prob=0.8, kind="kde", bw=0.5);

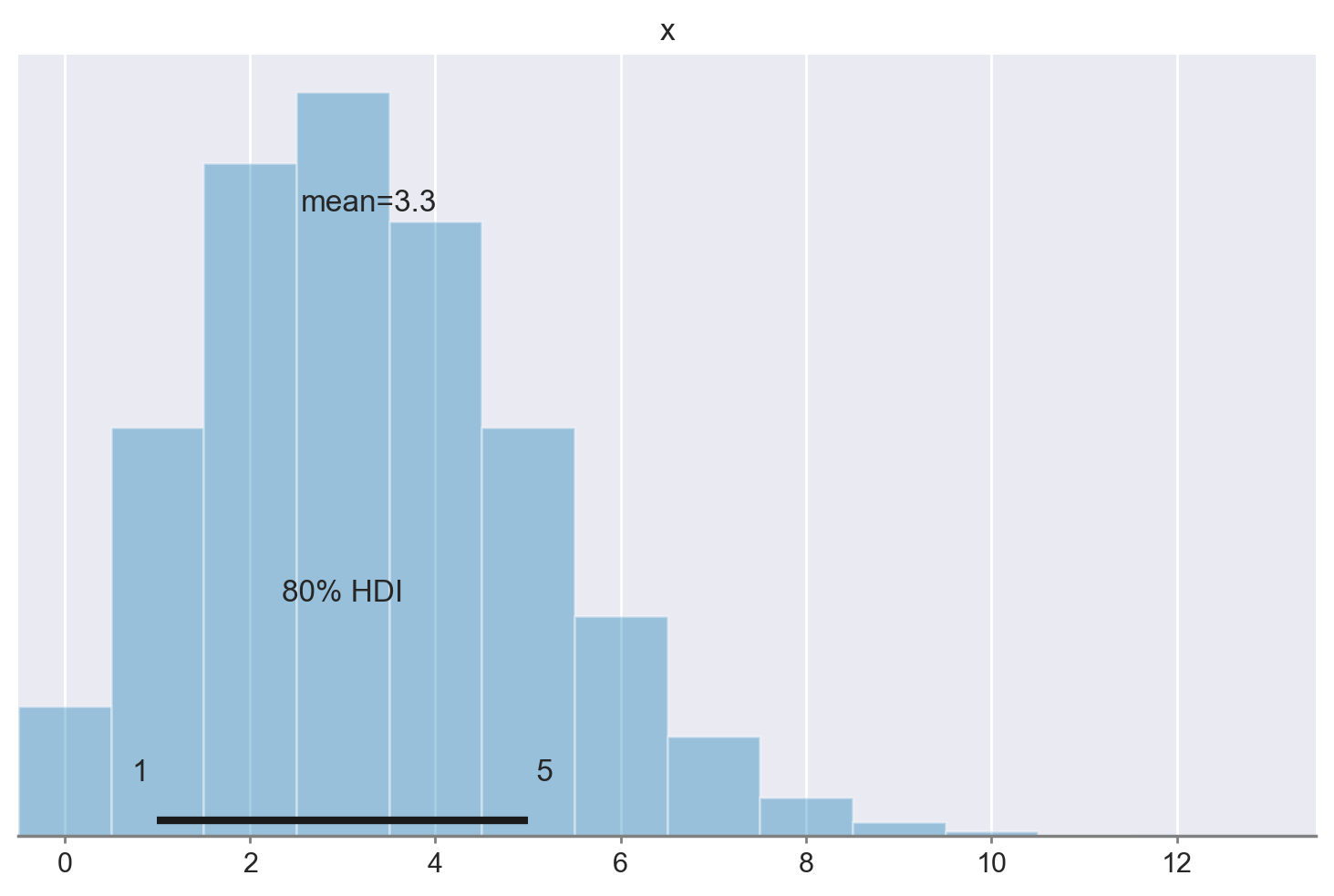
Possiamo concludere affermando che, nel caso in cui analizzassimo un nuovo campione di 20 artisti provenienti dal MOMA, ci potremmo attendere che solamente 3 di questi artisti facciano parte della generazione X o di una generazione successiva. Tuttavia, è importante sottolineare che questa stima è soggetta a un certo grado di incertezza. Considerando un livello di fiducia soggettivo dell’80%, l’intervallo di variabilità stimato va da un minimo di 1 ad un massimo di 5 artisti, che potrebbero essere rappresentativi di queste generazioni successive.

Metodo MCMC

Il metodo di simulazione discusso sopra segue la stessa logica utilizzata dai metodi MCMC per ottenere un’approssimazione della distribuzione predittiva a posteriori. Mediante i metodi MCMC, vengono stimate le possibili osservazioni future \(p(\tilde{y} \mid y)\), rappresentate come \(p(y^{rep} \mid y)\), attraverso i seguenti passaggi:

1. Campionare \(\theta_i \sim p(\theta \mid y)\): Viene selezionato casualmente un valore del parametro dalla distribuzione a posteriori.

2. Campionare \(y^{rep} \sim p(y^{rep} \mid \theta_i)\): Viene selezionata casualmente un’osservazione dalla funzione di verosimiglianza, condizionata al valore del parametro ottenuto nel passo precedente.

Ripetendo questi due passaggi un numero sufficiente di volte, l’istogramma risultante approssimerà la distribuzione predittiva a posteriori. In alcuni casi, come nel presente esempio, è possibile ottenere analiticamente la distribuzione predittiva a posteriori. In altre situazioni, invece, l’utilizzo dei metodi MCMC consente di ottenere un’approssimazione accurata della distribuzione predittiva a posteriori quando una derivazione analitica non è possibile.

Esaminiamo ora come ottenere la distribuzione predittiva a posteriori con PyMC per i dati dell’esempio. Iniziamo a creare la distribuzione a posteriori di \(\theta\).

ntrials = 100
y = 14

alpha_prior = 4
beta_prior = 6

with pm.Model() as model:
    theta = pm.Beta("theta", alpha=alpha_prior, beta=beta_prior)
    obs = pm.Binomial("obs", p=theta, n=ntrials, observed=y)

with model:
    idata = pm.sampling_jax.sample_numpyro_nuts()

Show code cell output Hide code cell output

Compiling...

Compilation time = 0:00:09.306001

Sampling...

  0%|                                                                                  | 0/2000 [00:00<?, ?it/s]

Compiling.. :   0%|                                                                    | 0/2000 [00:00<?, ?it/s]

  0%|                                                                                  | 0/2000 [00:00<?, ?it/s]

Compiling.. :   0%|                                                                    | 0/2000 [00:00<?, ?it/s]

  0%|                                                                                  | 0/2000 [00:00<?, ?it/s]

Compiling.. :   0%|                                                                    | 0/2000 [00:00<?, ?it/s]

  0%|                                                                                  | 0/2000 [00:00<?, ?it/s]

Compiling.. :   0%|                                                                    | 0/2000 [00:00<?, ?it/s]

Running chain 2:   0%|                                                                 | 0/2000 [00:01<?, ?it/s]

Running chain 0:   0%|                                                                 | 0/2000 [00:01<?, ?it/s]

Running chain 3:   0%|                                                                 | 0/2000 [00:01<?, ?it/s]

Running chain 1:   0%|                                                                 | 0/2000 [00:01<?, ?it/s]

Running chain 0: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1131.58it/s]

Running chain 1: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1132.36it/s]

Running chain 2: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1133.58it/s]

Running chain 3: 100%|████████████████████████████████████████████████████| 2000/2000 [00:01<00:00, 1134.74it/s]

Sampling time = 0:00:02.691235

Transforming variables...

Transformation time = 0:00:00.090847

az.summary(idata)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
theta	0.164	0.035	0.103	0.234	0.001	0.001	1338.0	1608.0	1.0

Il processo della simulazione descritta in precedenza può essere automatizzato usando PyMC, ma solo per un campione futuro avente la stessa ampiezza del campione presente (\(n = m\) = 100). Le istruzioni necessarie per generare la distribuzione predittiva a posteriori, \(y^{rep} \sim p(y^{rep} \mid \theta_i)\) sono fornite di seguito.

with model:
    post_pred = pm.sample_posterior_predictive(idata)

Sampling: [obs]

100.00% [4000/4000 00:00<00:00]

Esaminiamo il risultato ottenuto.

post_pred.posterior_predictive.obs

<xarray.DataArray 'obs' (chain: 4, draw: 1000)>
array([[15, 17, 23, ..., 12, 13, 13],
       [15, 12, 17, ..., 10, 17, 20],
       [15, 19, 12, ..., 14, 13, 19],
       [17,  6, 18, ...,  8, 15, 22]])
Coordinates:
  * chain    (chain) int64 0 1 2 3
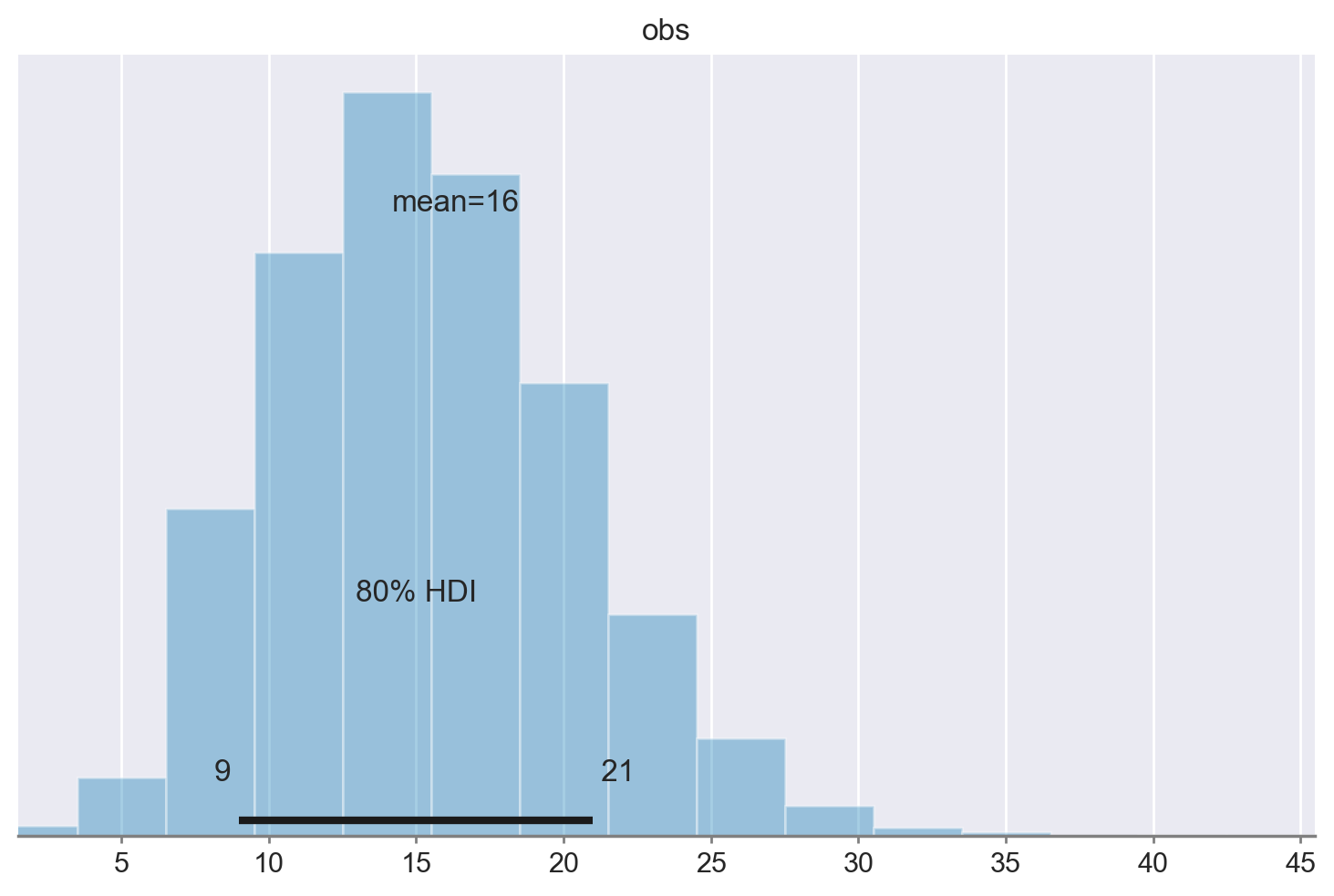
  * draw     (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999

xarray.DataArray

'obs'

• chain: 4
• draw: 1000

• 15 17 23 15 15 16 23 12 15 25 10 ... 19 11 20 11 19 17 15 18 8 15 22

  array([[15, 17, 23, ..., 12, 13, 13],
         [15, 12, 17, ..., 10, 17, 20],
         [15, 19, 12, ..., 14, 13, 19],
         [17,  6, 18, ...,  8, 15, 22]])

• Coordinates: (2)
  • chain
    (chain)
    int64
    0 1 2 3

    array([0, 1, 2, 3])

  • draw
    (draw)
    int64
    0 1 2 3 4 5 ... 995 996 997 998 999

    array([  0,   1,   2, ..., 997, 998, 999])

• Indexes: (2)
  • chain
    PandasIndex

    PandasIndex(Index([0, 1, 2, 3], dtype='int64', name='chain'))

  • draw
    PandasIndex

    PandasIndex(Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
           ...
           990, 991, 992, 993, 994, 995, 996, 997, 998, 999],
          dtype='int64', name='draw', length=1000))

• Attributes: (0)

Creiamo un istogramma con i dati \(y^{rep}\). L’intervallo di credibilità dell’80% è [9, 21].

az.plot_posterior(post_pred.posterior_predictive.obs, hdi_prob=0.8)
plt.show()

Se invece vogliamo una distribuzione predittiva a posteriori nel caso di \(m\) = 20 dobbiamo procedere svolgendo i calcoli “manualmente”.

Il modello predittivo a posteriori riflette due fonti di variabilità:

• la prima fonte di variabilità riguarda la varianza della distribuzione binomiale \(\tilde{Y} \mid \pi \sim \text{Binomiale}(20, \pi)\);

• la seconda fonte di variabilità riguarda l’incertezza su \(\pi\) che è espressa dalla distribuzione a posteriori di questo parametro.

Per considerare entrambe le fonti di variabilità nelle previsioni a posteriori di \(\tilde{Y}\), possiamo impiegare stats.binom.rvs per simulare un singolo risultato \(\tilde{Y}\) dalla distribuzione Binomiale(20, \(\theta\)) per ciascuno dei 4000 valori nella catena di Markov relativa a \(\theta\).

Iniziamo combinando catene e iterazioni della catena di Markov in un unico vettore.

post = az.extract(idata)
post["theta"].size

4000

Generiamo poi un valore casuale dalla distribuzione Binomiale di parametri \(n\) = 20 e \(\theta\), per ciascuno dei 4000 valori \(\theta\) della distribuzione a posteriori. Il vettore così risultante sarà un campione dalla distribuzione predittiva a posteriori, nel caso di un’ampiezza campionaria pari a 20.

y_rep = stats.binom.rvs(n=20, p=post["theta"])

Usiamo ArviZ per creare un istogramma della distribuzione di y_rep e per trovare l’intervallo di credibilità all’80%.

az.plot_posterior(y_rep, hdi_prob=0.8, kind="kde", bw=0.5)
plt.show()

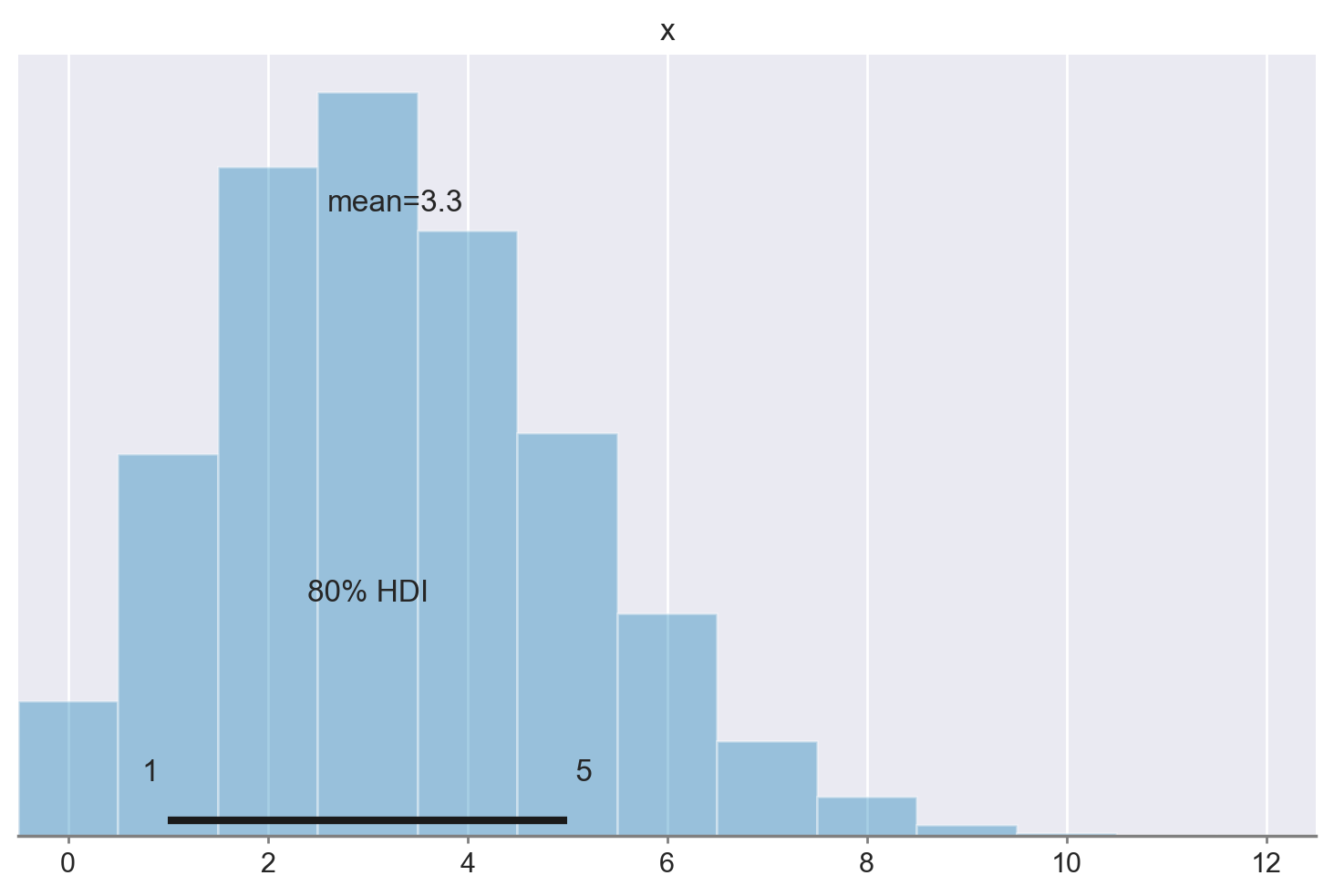
Posterior predictive checks

La distribuzione predittiva a posteriori è utilizzata per eseguire i controlli predittivi a posteriori (PPC), noti come Posterior Predictive Checks. I PPC consistono in un confronto grafico tra \(p(y^{rep} \mid y)\), ossia la distribuzione delle osservazioni future previste, e i dati osservati \(y\). Questo confronto visivo permette di valutare se il modello utilizzato è adeguato per descrivere le proprietà dei dati osservati.

Oltre al confronto grafico tra le distribuzioni \(p(y)\) e \(p(y^{rep})\), è possibile effettuare un confronto tra le distribuzioni di varie statistiche descrittive calcolate su diversi campioni \(y^{rep}\) e le corrispondenti statistiche calcolate sui dati osservati. Tipicamente, vengono considerate statistiche descrittive come la media, la varianza, la deviazione standard, il minimo o il massimo, ma è possibile confrontare qualsiasi altra statistica rilevante.

I controlli predittivi a posteriori offrono un valido strumento per un’analisi critica delle prestazioni del modello e, se necessario, per apportare eventuali modifiche o considerare modelli alternativi più adatti ai dati in esame.

Distribuzione predittiva a priori

Prima di procedere con un’analisi Bayesiana completa, è cruciale valutare l’adeguatezza della distribuzione a priori, specie alla luce di una preesistente conoscenza del dominio che può permettere di scartare distribuzioni a priori manifestamente erronee. Questa metodologia di valutazione delle distribuzioni a priori è conosciuta come verifica predittiva a priori, ed è stata introdotta inizialmente da Box [Box80] e successivamente promossa da Gelman et al. [GSB17].

Nella sezione precedente, abbiamo esaminato l’uso della distribuzione predittiva per rappresentare l’incertezza relativa alla distribuzione di futuri dati osservabili. Tale distribuzione predittiva incorpora sia la distribuzione a posteriori del parametro \(\theta\) che la scelta del modello basata sui dati precedentemente osservati. Un concetto affine, ma distinto, è la distribuzione predittiva a priori, che proietta le aspettative sulle future osservazioni del modello, prima dell’acquisizione di qualsiasi dato. Questa distribuzione è definita dalla seguente espressione matematica:

\[ p(y) = \int p(y \mid \theta) p(\theta) d\theta, \]

dove

• \(p(y \mid \theta)\) rappresenta la funzione di verosimiglianza, ovvero la dipendenza dei dati dai parametri,

• \(p(\theta)\) è la distribuzione a priori dei parametri, che manifesta le nostre credenze iniziali riguardo ai valori dei parametri.

Se i dati osservati discostano significativamente dalla distribuzione predittiva a priori, ciò può indicare una possibile inadeguatezza nel modello Bayesiano (relativa alla distribuzione a priori, al meccanismo generativo dei dati, o entrambi). In pratica, ciò suggerisce che, data la formulazione del modello Bayesiano, i dati effettivamente osservati risultano improbabili, il che potrebbe implicare un’insufficienza del modello.

La distribuzione predittiva a priori risulta utile per molteplici motivi:

• Esplorazione delle credenze iniziali: permette di investigare come le credenze iniziali sui parametri (es. la probabilità di ottenere testa nel lancio di una moneta) si traducano in aspettative concrete riguardo agli esiti osservabili.

• Confronto con dati reali: confrontando i dati effettivamente osservati con la distribuzione predittiva a priori, è possibile valutare l’adeguatezza del modello e delle credenze a priori.

• Analisi di sensibilità: la distribuzione predittiva a priori può anche illustrare quanto le conclusioni del modello siano sensibili alle diverse scelte della distribuzione a priori.

La distribuzione predittiva a priori può essere ottenuta mediante metodi MCMC, replicando il procedimento utilizzato per la distribuzione predittiva a posteriori, ma in assenza di dati osservati.

Nell’esempio con i dati di Zetsche et al. [ZBR19], se avessimo scelto una distribuzione Beta(2, 10) come a priori, l’analisi predittiva a priori avrebbe potuto rivelare che questa scelta non era adeguata per i dati considerati. Questo esempio dimostra come la distribuzione predittiva a priori possa servire come potente strumento diagnostico nell’analisi bayesiana, aiutando a guidare e rifinire le scelte del modello.

Ritorniamo all’esempio con i dati degli artisti della generazione X al MOMA. Per questi dati abbiamo scelto una distribuzione a priori Beta(4, 6) per il parametro di successo \(\theta\).

print(alpha_prior, beta_prior)

4 6

Eseguiamo l’analisi predittiva a priori con sample_prior_predictive.

with model:
    idata_prior_pred = pm.sample_prior_predictive()

Sampling: [obs, theta]

Esaminiamo l’oggetto idata_prior_pred che abbiamo creato.

idata_prior_pred

arviz.InferenceData

• prior

  <xarray.Dataset>
  Dimensions:  (chain: 1, draw: 500)
  Coordinates:
    * chain    (chain) int64 0
    * draw     (draw) int64 0 1 2 3 4 5 6 7 8 ... 492 493 494 495 496 497 498 499
  Data variables:
      theta    (chain, draw) float64 0.5313 0.3526 0.4764 ... 0.2465 0.2935 0.4641
  Attributes:
      created_at:                 2024-01-27T08:08:28.182962
      arviz_version:              0.17.0
      inference_library:          pymc
      inference_library_version:  5.10.3

  xarray.Dataset

  • Dimensions:
    • chain: 1
    • draw: 500
  • Coordinates: (2)
    • chain
      (chain)
      int64
      0

      array([0])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 495 496 497 498 499

      array([  0,   1,   2, ..., 497, 498, 499])

  • Data variables: (1)
    • theta
      (chain, draw)
      float64
      0.5313 0.3526 ... 0.2935 0.4641

      array([[0.53127412, 0.35260081, 0.47638805, 0.17068326, 0.59757417,
              0.56705043, 0.59297074, 0.38145054, 0.54718922, 0.54465506,
              0.69290532, 0.16431122, 0.4739868 , 0.35401033, 0.48532005,
              0.35654345, 0.40502931, 0.42808317, 0.48717621, 0.16141782,
              0.29175876, 0.29234339, 0.45311889, 0.41322389, 0.41609037,
              0.55869784, 0.22781216, 0.47795971, 0.19219103, 0.37755127,
              0.24867943, 0.47729808, 0.72507423, 0.4680475 , 0.46616834,
              0.30140181, 0.67257135, 0.52082742, 0.32785457, 0.23172023,
              0.50562117, 0.39482751, 0.29064826, 0.20928049, 0.34494292,
              0.65903602, 0.42572407, 0.53769553, 0.54972433, 0.34710068,
              0.66888978, 0.34434294, 0.73594381, 0.21858811, 0.24663917,
              0.32421861, 0.42684289, 0.33517249, 0.5441403 , 0.68988346,
              0.29285121, 0.34557377, 0.26671279, 0.58599245, 0.28063249,
              0.42287865, 0.39514071, 0.38494125, 0.63603547, 0.5670066 ,
              0.46007836, 0.29079   , 0.26956203, 0.20782303, 0.44108054,
              0.36258429, 0.179861  , 0.23234068, 0.28801843, 0.4438211 ,
              0.4980554 , 0.63339405, 0.4160265 , 0.62238403, 0.71388925,
              0.39037293, 0.28374932, 0.17852792, 0.07564811, 0.4981073 ,
              0.56846574, 0.2706045 , 0.52725349, 0.38099294, 0.71642716,
              0.64951454, 0.53402435, 0.51728915, 0.41147532, 0.6491175 ,
      ...
              0.39021661, 0.33518958, 0.39468678, 0.47289638, 0.41151983,
              0.34320612, 0.60865435, 0.70056855, 0.58597965, 0.38879403,
              0.53268055, 0.21917889, 0.59746582, 0.68031377, 0.35466476,
              0.45220711, 0.26053712, 0.43968884, 0.39688883, 0.19992108,
              0.38878459, 0.3948322 , 0.27178658, 0.388753  , 0.51900522,
              0.35102626, 0.22062471, 0.54826182, 0.56318989, 0.26315645,
              0.27574553, 0.21954627, 0.44493522, 0.5423316 , 0.19112091,
              0.24108464, 0.51280184, 0.56729644, 0.24159421, 0.46369806,
              0.35168374, 0.49490494, 0.26304765, 0.44558884, 0.42863381,
              0.51053722, 0.20296954, 0.09843283, 0.26752525, 0.54149457,
              0.66723889, 0.63090689, 0.23362576, 0.66158144, 0.3872874 ,
              0.58981087, 0.42649151, 0.48371787, 0.27737675, 0.28942677,
              0.4695578 , 0.37275297, 0.26626224, 0.64786235, 0.37593597,
              0.34573991, 0.25383893, 0.35161213, 0.47478195, 0.69176082,
              0.49360048, 0.31203656, 0.44219962, 0.39958156, 0.61351055,
              0.67773495, 0.15267445, 0.55835355, 0.14422606, 0.29253468,
              0.32997152, 0.68385826, 0.23587348, 0.17381906, 0.30209643,
              0.36798009, 0.38238972, 0.75509989, 0.1568741 , 0.63699618,
              0.49730773, 0.37671646, 0.3896713 , 0.34665718, 0.52064659,
              0.14011576, 0.56564361, 0.24650274, 0.29346195, 0.4640624 ]])

  • Indexes: (2)
    • chain
      PandasIndex

      PandasIndex(Index([0], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
             ...
             490, 491, 492, 493, 494, 495, 496, 497, 498, 499],
            dtype='int64', name='draw', length=500))

  • Attributes: (4)

    created_at :

    2024-01-27T08:08:28.182962

    arviz_version :

    0.17.0

    inference_library :

    pymc

    inference_library_version :

    5.10.3

  
  
• prior_predictive

  <xarray.Dataset>
  Dimensions:  (chain: 1, draw: 500)
  Coordinates:
    * chain    (chain) int64 0
    * draw     (draw) int64 0 1 2 3 4 5 6 7 8 ... 492 493 494 495 496 497 498 499
  Data variables:
      obs      (chain, draw) int64 51 34 45 20 55 54 55 ... 30 48 15 60 26 32 49
  Attributes:
      created_at:                 2024-01-27T08:08:28.184819
      arviz_version:              0.17.0
      inference_library:          pymc
      inference_library_version:  5.10.3

  xarray.Dataset

  • Dimensions:
    • chain: 1
    • draw: 500
  • Coordinates: (2)
    • chain
      (chain)
      int64
      0

      array([0])

    • draw
      (draw)
      int64
      0 1 2 3 4 5 ... 495 496 497 498 499

      array([  0,   1,   2, ..., 497, 498, 499])

  • Data variables: (1)
    • obs
      (chain, draw)
      int64
      51 34 45 20 55 ... 15 60 26 32 49

      array([[51, 34, 45, 20, 55, 54, 55, 36, 55, 53, 63, 13, 59, 41, 53, 36,
              44, 48, 53, 16, 36, 28, 49, 42, 32, 56, 19, 45, 17, 42, 23, 49,
              71, 46, 48, 34, 62, 54, 33, 19, 47, 43, 28, 26, 30, 72, 44, 57,
              51, 30, 62, 36, 71, 23, 33, 31, 37, 33, 58, 69, 30, 43, 28, 54,
              24, 34, 44, 42, 58, 49, 47, 29, 29, 17, 50, 33, 18, 25, 29, 37,
              47, 70, 38, 70, 70, 36, 26, 22, 12, 48, 54, 24, 57, 34, 71, 64,
              59, 56, 39, 68, 50, 37, 39, 46, 44, 40, 47, 52, 62, 24, 48, 27,
              53, 47, 52, 47, 52, 33, 26, 53, 60, 41, 55, 55, 60, 55, 23, 65,
              41, 56, 17, 39, 43, 30, 35, 44,  7, 17, 45, 21, 38, 62, 61, 22,
              70, 33, 41, 17, 31, 18, 56, 12, 21, 42, 33, 48, 38, 48, 57, 73,
              45, 45, 22, 47, 60, 54, 59, 26, 30, 38, 33, 30,  8, 48, 65, 33,
              48, 51, 34, 44, 21, 24, 38, 39, 34, 53, 22, 38, 11, 41, 56, 54,
              54, 35, 39,  9, 29, 28, 31, 47, 62, 41, 54, 62, 37, 59, 66, 18,
              32, 28, 38, 33, 65, 62, 44, 30, 43, 13, 40, 23, 44, 38, 52, 48,
              32, 53, 16, 33, 30, 36, 67, 71, 34, 29, 39, 23, 35, 52, 37, 28,
              35, 55, 29, 71, 35, 43, 41, 57, 29, 21, 50, 46, 18, 57, 27, 37,
              43, 27, 32, 34, 23, 65, 70, 31, 34, 33, 48, 85, 60, 30, 28, 22,
              27, 41, 22, 42, 63,  7, 19, 43, 41, 51, 62, 41, 41, 32, 35, 52,
              16, 69, 50, 38, 19, 45, 63, 43, 67, 69, 32, 31, 21, 51, 51, 33,
              71, 32, 28, 38, 48, 41, 36, 53, 52, 59, 68, 12, 41, 19, 36, 15,
              62, 33, 40, 57, 53, 39, 64, 14, 57, 36, 26, 27, 57, 36, 28, 13,
              50, 38, 56, 51, 28, 26, 37, 23, 41, 14, 59, 54, 26, 15, 27, 32,
              40, 35, 39, 19, 45, 31, 11, 11, 39, 53, 62, 27, 46, 56, 18, 54,
              58, 15, 39, 42, 69, 55, 45, 41, 36, 27, 52, 52, 41, 63, 15,  4,
              70, 29, 24, 64, 47, 43, 16, 32, 26, 22, 41, 31, 69, 46, 76, 33,
              42, 25, 35, 47, 34, 26, 57, 68, 56, 46, 54, 19, 56, 67, 34, 37,
              17, 48, 34, 17, 45, 49, 39, 40, 52, 37, 19, 51, 56, 23, 26, 25,
              43, 60, 21, 13, 47, 51, 27, 51, 32, 46, 29, 49, 48, 47, 19, 11,
              30, 52, 75, 61, 22, 64, 41, 60, 42, 44, 29, 30, 50, 48, 23, 69,
              33, 37, 28, 30, 47, 69, 50, 33, 45, 36, 57, 68, 17, 51, 12, 24,
              37, 76, 25, 23, 30, 31, 41, 78, 12, 68, 55, 36, 38, 30, 48, 15,
              60, 26, 32, 49]])

  • Indexes: (2)
    • chain
      PandasIndex

      PandasIndex(Index([0], dtype='int64', name='chain'))

    • draw
      PandasIndex

      PandasIndex(Index([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,
             ...
             490, 491, 492, 493, 494, 495, 496, 497, 498, 499],
            dtype='int64', name='draw', length=500))

  • Attributes: (4)

    created_at :

    2024-01-27T08:08:28.184819

    arviz_version :

    0.17.0

    inference_library :

    pymc

    inference_library_version :

    5.10.3

  
  
• observed_data

  <xarray.Dataset>
  Dimensions:    (obs_dim_0: 1)
  Coordinates:
    * obs_dim_0  (obs_dim_0) int64 0
  Data variables:
      obs        (obs_dim_0) int64 14
  Attributes:
      created_at:                 2024-01-27T08:08:28.186059
      arviz_version:              0.17.0
      inference_library:          pymc
      inference_library_version:  5.10.3

  xarray.Dataset

  • Dimensions:
    • obs_dim_0: 1
  • Coordinates: (1)
    • obs_dim_0
      (obs_dim_0)
      int64
      0

      array([0])

  • Data variables: (1)
    • obs
      (obs_dim_0)
      int64
      14

      array([14])

  • Indexes: (1)
    • obs_dim_0
      PandasIndex

      PandasIndex(Index([0], dtype='int64', name='obs_dim_0'))

  • Attributes: (4)

    created_at :

    2024-01-27T08:08:28.186059

    arviz_version :

    0.17.0

    inference_library :

    pymc

    inference_library_version :

    5.10.3

  
  

I dati (sulla scala delle osservazioni \(y\)) sono contenuti in idata.prior_predictive.obs. Possiamo usare arviz per generare un istogramma della distribuzione predittiva a priori usando la funzione plot_posterior:

az.plot_posterior(idata_prior_pred.prior_predictive.obs)
plt.show()

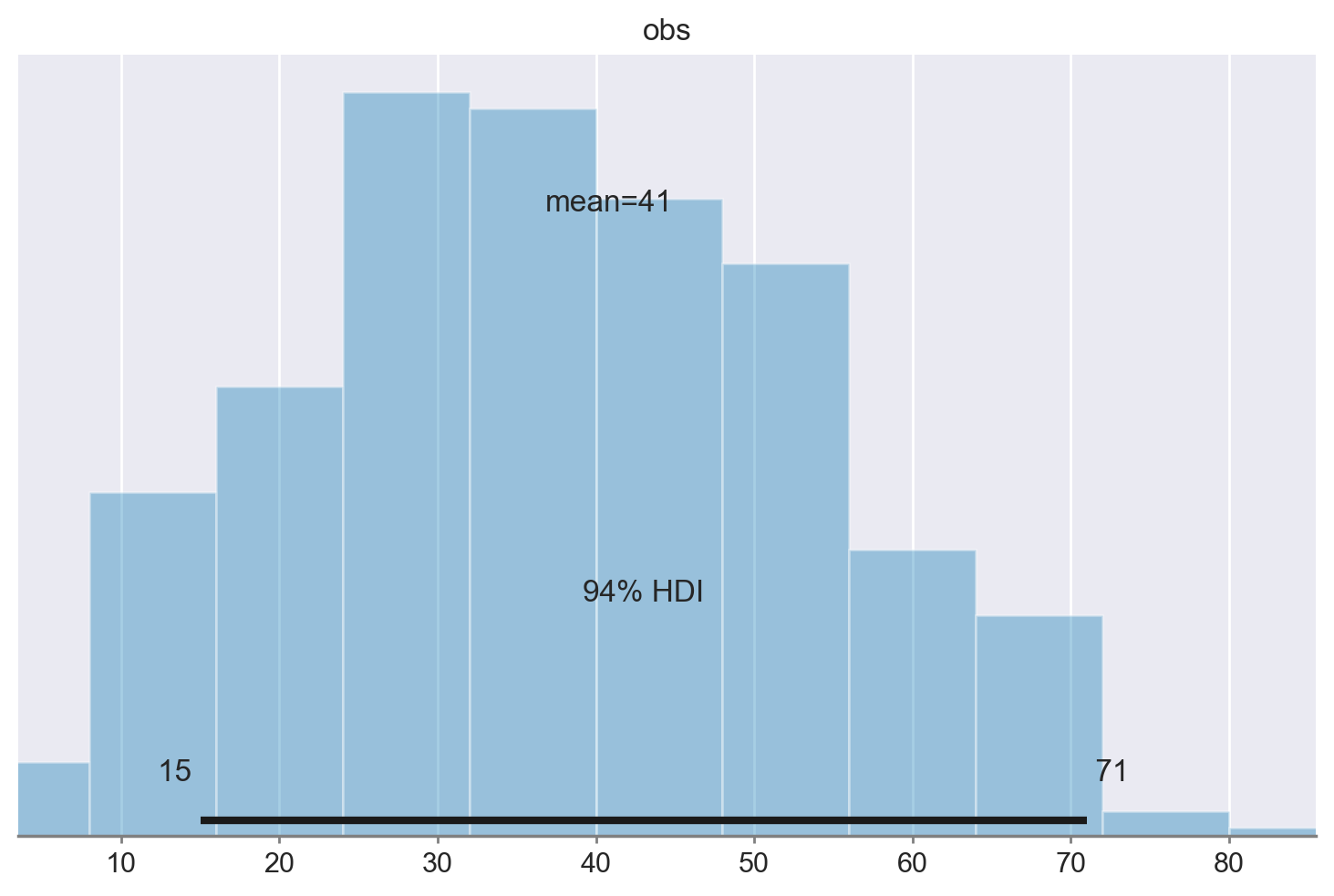
La regione dell’intervallo di credibilità ad alta densità (HDI) al 94% è [9, 67]. Nel nostro campione, abbiamo osservato un valore di \(y\) = 14. Poiché questo risultato rientra nell’intervallo di credibilità della distribuzione predittiva a priori, possiamo dedurre che la scelta di una distribuzione Beta(4, 6) come distribuzione a priori sembra essere adeguata per i dati in questione.

Esempio con Stan

Per sviluppare un’intuizione relativa alla distribuzione predittiva a priori, consideriamo il seguente codice Stan, il quale mira a stimare i parametri di una distribuzione gaussiana. Nonostante non sia necessario avere una conoscenza approfondita della sintassi Stan, è possibile comprendere l’essenza del processo. Nel codice, viene specificata solo la dimensione del campione, n, senza fornire i dati effettivi. Vengono definiti i prior per i parametri \(\mu\) e \(\sigma\). Nel blocco generated quantities, viene generata la distribuzione predittiva a priori.

Il codice illustra che, per il numero n dell’ampiezza campionaria specificata, si estrae un valore casuale da una distribuzione gaussiana, la cui media e deviazione standard sono a loro volta estratte casualmente dalle distribuzioni a priori specificate per \(\mu\) e \(\sigma\). Questo processo produce n valori, e viene ripetuto 1000 o più volte, a seconda del numero di iterazioni specificate in Stan, per ottenere una rappresentazione della distribuzione predittiva a priori.

mod <-"
    data {
        int n;  // Dimensione del campione
    }

    parameters {
        real<lower=0> mu;  // Media
        real<lower=0> sigma;  // Deviazione standard
    }

    model {
        // Distribuzioni a priori
        mu ~ normal(400,1);  // Prior per la media
        sigma ~ normal(100,5);  // Prior per la deviazione standard
    }

    generated quantities {
        vector[n] prior_rep;  // Vettore per contenere la distribuzione predittiva a priori
        // Generazione della distribuzione predittiva a priori
        for(i in 1:n) {
            prior_rep[i] = normal_rng(mu,sigma);  // Estrazione di un valore casuale dalla distribuzione gaussiana
        } 
    }
"

In questo modo, il codice Stan fornisce un mezzo per esplorare e comprendere come i prior sui parametri della distribuzione gaussiana influenzano la distribuzione predittiva a priori, anche senza un insieme di dati osservati.

%load_ext watermark
%watermark -n -u -v -iv -w 

Last updated: Sat Jan 27 2024

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.19.0

numpy     : 1.26.2
pandas    : 2.1.4
seaborn   : 0.13.0
scipy     : 1.11.4
pymc      : 5.10.3
matplotlib: 3.8.2
arviz     : 0.17.0

Watermark: 2.4.3