Modellazione bayesiana

Modellazione bayesiana#

L’obiettivo di questo Capitolo è di introdurre il quadro concettuale dela modellizzazione bayesiana.

Esplorazione dei Fondamenti dei Metodi Bayesiani in Psicologia#

Introduzione ai Principi Bayesiani#

Nel campo della psicologia, l’adozione dei metodi bayesiani ha guadagnato crescente attenzione e utilizzo. La formalizzazione dell’uso delle probabilità, un elemento centrale dell’approccio bayesiano, permette di rappresentare numericamente insiemi di convinzioni razionali e di aggiornare queste convinzioni in base a nuove informazioni attraverso la regola di Bayes. Questo processo, noto come inferenza bayesiana, è particolarmente rilevante in psicologia dove le incertezze e le informazioni parziali sono la norma.

Crescita dei Metodi Bayesiani nella Psicologia#

Il paradigma bayesiano in psicologia ha visto un notevole aumento di interesse grazie alla disponibilità di risorse educative e pubblicazioni che facilitano l’integrazione dei modelli bayesiani nell’analisi dei dati psicologici. Autori come Brooks [Bro03], Van De Schoot et al. [VDSWR+17], Kruschke [Kru14], McElreath [McE20], Johnson et al. [JOD22]), hanno contribuito a questa evoluzione, fornendo agli psicologi una solida base per applicare approcci bayesiani ai dati psicologici.

Il Ciclo Continuo dell’Apprendimento Bayesiano#

Il framework bayesiano costituisce un modello matematico che cattura il processo di apprendimento continuo. Fondato sul teorema di Bayes, questo ciclo iterativo consente l’aggiornamento sequenziale delle informazioni, in cui la distribuzione a posteriori di un ciclo diventa la distribuzione a priori del ciclo successivo. Questa dinamica di aggiornamento costante delle credenze gioca un ruolo cruciale nell’ambito della ricerca e della creatività, come sottolineato [WDS18].

Dalla Generazione dei Dati alla Modellizzazione Bayesiana#

Nel contesto dell’inferenza bayesiana, uno degli aspetti centrali riguarda l’analisi dei processi generativi dei dati, noti come “Data-Generating Processes” (DGP), che sono responsabili della produzione dei dati osservati. L’identificazione di questi meccanismi sottostanti, anche se non direttamente osservabili, riveste un’importanza fondamentale per la comprensione e la rappresentazione delle ipotesi sulla realtà attraverso l’utilizzo di modelli statistici.

Riallocazione della Credibilità e Aggiornamento Sequenziale#

La dinamica dell’aggiornamento delle informazioni nel contesto bayesiano è stata esemplificata attraverso l’uso dell’esempio di Sherlock Holmes. Come dimostrato nel libro Kruschke [Kru14], questo processo si basa sull’idea che acquisire nuove prove in un’indagine può portare all’esclusione di una causa tra molte possibili, con conseguente redistribuzione delle probabilità tra le cause rimanenti.

Per comprendere meglio questo concetto, consideriamo un’indagine su un crimine con quattro possibili colpevoli, identificati come A, B, C e D. Inizialmente, tutte e quattro le opzioni hanno probabilità simili di essere il colpevole. Tuttavia, man mano che Sherlock Holmes raccoglie nuove prove e informazioni, potrebbe essere in grado di escludere uno dei sospettati, diciamo il colpevole A, sulla base di queste nuove prove. Quando ciò avviene, la probabilità associata a A viene annullata e riallocata tra i rimanenti sospettati, ossia B, C e D. Di conseguenza, la probabilità di ciascuno di loro come colpevole diventa più elevata e, inizialmente, tutti hanno probabilità uguali. Questo processo rappresenta l’essenza dell’aggiornamento bayesiano delle credenze.

Tuttavia, è importante notare che in psicologia e in molti altri contesti, raramente un’ipotesi o una causa viene completamente esclusa. Piuttosto, la sua credibilità viene ridimensionata o modificata in base alle nuove evidenze, aumentando la plausibilità delle alternative. Questo principio è espressamente sintetizzato nella famosa citazione di Dennis Lindley: “Il posterior di oggi diventa il prior di domani”. In altre parole, ciò che impariamo oggi influenzerà le nostre credenze future e il processo di aggiornamento continuo delle nostre conoscenze.

Questa dinamica di riallocazione della credibilità e aggiornamento sequenziale è fondamentale nel contesto dell’applicazione dei metodi bayesiani, inclusi quelli utilizzati nella psicologia, per valutare e rivedere costantemente le nostre ipotesi in base alle nuove evidenze a disposizione.

La Modellizzazione Statistica: Collegamento tra Teoria e Dati#

La modellizzazione statistica bayesiana svolge un ruolo fondamentale nel collegare la teoria psicologica con i dati empirici. Questo approccio suddivide la complessità dei fenomeni psicologici in componenti più gestibili, rendendo più agevole la comprensione e la simulazione dei comportamenti o dei processi in esame. Tuttavia, la modellizzazione richiede una sinergia tra conoscenza settoriale e competenze statistiche. Questa sinergia è cruciale per tradurre teorie e dati empirici in modelli computazionali efficaci, che possano catturare in modo accurato e significativo i fenomeni psicologici oggetto di studio.

Elementi Fondamentali della Modellazione Statistica Bayesiana#

I concetti chiave essenziali per comprendere la modellazione statistica bayesiana sono i seguenti:

Variabili Casuali: Queste rappresentano componenti essenziali in qualsiasi modello statistico bayesiano, fungendo da rappresentazioni quantitative di elementi sconosciuti o incerti. Le variabili casuali sono utilizzate per modellare e stabilire relazioni tra diverse grandezze all’interno del modello. Ciò consente di esprimere in termini probabilistici sia le osservazioni (dati) sia i parametri del modello.
Distribuzioni Statistiche: Nel contesto bayesiano, le distribuzioni statistiche sono fondamentali per strutturare e quantificare l’incertezza. In particolare:
- Distribuzioni Priori: Queste sono centrali nella modellazione bayesiana. Le distribuzioni priori esprimono le conoscenze o le convinzioni iniziali relative alle variabili incognite prima dell’analisi dei dati. Queste distribuzioni sono poi aggiornate in base alle informazioni ottenute dai dati.
- Distribuzioni Posteriori: Sono il risultato dell’aggiornamento delle credenze priori alla luce dei dati osservati. Rappresentano la sintesi delle informazioni originali (priori) e quelle nuove (dati), offrendo una visione aggiornata delle stime del modello.
Aggiornamento Bayesiano: Questo processo rappresenta il cuore dell’inferenza bayesiana. Utilizzando il teorema di Bayes, le distribuzioni priori vengono aggiornate in base ai dati osservati. L’aggiornamento bayesiano consente di combinare le informazioni preesistenti con nuove evidenze, per affinare le stime dei parametri del modello e ridurre l’incertezza associata. Questo processo iterativo si adatta continuamente all’arrivo di nuove informazioni, permettendo una comprensione sempre più precisa dei fenomeni studiati.

Questi elementi, insieme, formano il quadro metodologico della modellazione statistica bayesiana, consentendo di interpretare dati complessi e incerti in modo flessibile e informato.

Il Processo di Sviluppo di un Modello Bayesiano#

La costruzione di un modello bayesiano si articola in tre fasi principali:

Progettazione del Modello: In questa fase iniziale, il modello viene progettato sulla base delle conoscenze preliminari e delle ipotesi relative al meccanismo generativo dei dati.
Esecuzione dell’Inferenza Bayesiana: In questo stadio, si applica il teorema di Bayes per rivedere e aggiornare le credenze priori alla luce dei dati osservati, portando alla formulazione di una distribuzione a posteriori.
Analisi e Confronto dei Modelli: In questa fase finale, si valuta l’adeguatezza del modello, esaminando la sua coerenza e affidabilità attraverso diversi criteri. Se necessario, si confronta il modello con altre alternative per determinare quale sia il più appropriato.

Nei successivi capitoli, approfondiremo ciascuna di queste fasi, delineando il processo standard adottato nel flusso di lavoro bayesiano [BC23].

Riesame del Teorema di Bayes#

Prima di discutere il flusso di lavoro bayesiano, esaminiamo nuovamente il teorema di Bayes. Il teorema di Bayes rappresenta un pilastro fondamentale della statistica bayesiana, fornendo il meccanismo attraverso il quale le credenze iniziali (priori) vengono aggiornate alla luce di nuovi dati. Per approfondire la comprensione di questo teorema, è essenziale esaminarne la formulazione sia in termini di probabilità discrete che di distribuzioni di densità di probabilità. La formula chiave del teorema di Bayes è la seguente:

\[ p(\theta \mid \text{data}) = \frac{p(\text{data} \mid \theta)p(\theta)}{p(\text{data})} \propto p(\text{data} \mid \theta)p(\theta), \]

dove:

\(\theta\) rappresenta un insieme di parametri (ad esempio, coefficienti di regressione).
\(p(\theta \mid \text{data})\) è la distribuzione posteriore dei parametri, ottenuta aggiornando la distribuzione a priori \(p(\theta)\) con i dati osservati, espressi nella funzione di verosimiglianza \(p(\text{data} \mid \theta)\).
\(p(\text{data})\), la probabilità marginale dei dati, funge da costante di normalizzazione per assicurare che la distribuzione posteriore sommi a 1.

Nella statistica Bayesiana, le convinzioni aggiornate (posteriori) sui parametri sono utilizzate per l’inferenza. Per esempio, la distribuzione posteriore può essere riassunta per calcolare la probabilità che un parametro rientri in un determinato intervallo.

La specificità dell’inferenza bayesiana è legata all’utilizzo delle distribuzioni a priori, indicate con \(p(\theta)\). Di solito, i ricercatori basano queste distribuzioni a priori su risultati precedenti, meta-analisi e/o l’expertise di esperti, oppure, in modo ancora più comune, utilizzano distribuzioni non informative note come “distribuzioni di regolarizzazione”. Un aspetto cruciale, che come vedremo rappresenta un notevole vantaggio, è che l’effetto delle distribuzioni a priori è più significativo quando il campione di dati è di dimensioni ridotte. In questa situazione, l’impiego di una distribuzione a priori “di regolarizzazione” ha un impatto conservativo sull’inferenza statistica, contribuendo a mitigare le fluttuazioni dovute alla limitata dimensione del campione.

Passando al contesto della modellazione, consideriamo una variabile casuale \( Y \), che assume un valore realizzato \( y \). Ad esempio, il punteggio di uno studente in un esame di Psicometria può essere modellato come \( Y \), con un insieme di possibili valori. Una volta ottenuto il voto, \( Y \) si realizza come \( y \). Per modellare come i dati effettivi \( y \) sono stati ottenuti, dobbiamo specificare un modello di probabilità, noto come processo generatore di dati (DGP).

Denotiamo con \( \theta \) un parametro che caratterizza il modello di probabilità di interesse, che può essere uno scalare (come la media o la varianza di una distribuzione) o un vettore (ad esempio, un insieme di coefficienti di regressione). Nell’inferenza statistica, l’obiettivo è stimare questi parametri sconosciuti dai dati. La principale differenza tra l’inferenza frequentista e quella bayesiana è nella concezione di \( \theta \): nella prima, \( \theta \) è fisso ma sconosciuto; nella seconda, è considerato una variabile casuale con una distribuzione di probabilità a priori.

Nell’inferenza bayesiana, calcoliamo la probabilità congiunta di parametri e dati come funzione della distribuzione condizionale dei dati dati i parametri e della distribuzione a priori dei parametri. La distribuzione posteriore di \( \theta \) dato \( y \) si ottiene moltiplicando la distribuzione dei dati \( p(y \mid \theta) \) per la distribuzione a priori \( p(\theta) \), normalizzata per \( p(y) \). In modelli complessi con molti parametri, la distribuzione posteriore è difficile da valutare, richiedendo metodi computazionali avanzati.

Possiamo esprimere la distribuzione congiunta dei parametri e dei dati come:

(55)#\[ \begin{equation} p(\theta, y) = p(y \mid \theta)p(\theta). \end{equation} \]

Utilizzando il teorema di Bayes dell’eq. (16) otteniamo:

(56)#\[ \begin{equation} p(\theta \mid y) = \frac{p(\theta, y)}{p(y)} = \frac{p(y \mid \theta)p(\theta)}{p(y)}. \end{equation} \]

In questa formulazione, \( p(y \mid \theta) \) è la funzione di verosimiglianza, e l’equazione sopra rappresenta l’essenza dell’inferenza statistica bayesiana, differenziandola dalla statistica frequentista.

Per variabili discrete,

\[ p(y) = \sum_\theta p(y \mid \theta)p(\theta) \]

e per variabili continue,

\[ p(y) = \int p(y \mid \theta)p(\theta)d\theta. \]

La validità dell’approccio bayesiano è sostenuta dai lavori di Cox e Savage, che hanno dimostrato che, se \(p(\theta)\) e \(p(y \mid \theta)\) rappresentano convinzioni razionali, la regola di Bayes è il metodo ottimale per aggiornarle alla luce di nuove informazioni.

L’aggiornamento bayesiano#

Per offrire una illustrazione quantitativa del procedimento di aggiornamento bayesiano, prendiamo in considerazione un esempio pratico: la localizzazione di un aeromobile disperso in mare. In questo capitolo, ci concentriamo esclusivamente sulla comprensione della struttura logica del problema e sulla sua formalizzazione tramite l’impiego di distribuzioni di probabilità. In questa fase, tralasciamo i dettagli implementativi e mettiamo invece l’accento sul significato delle diverse fasi e degli obiettivi del processo di aggiornamento bayesiano. Successivamente, esamineremo le metodologie per conseguire tali obiettivi, approfondendo gli aspetti di natura computazionale.

L’illustrazione coinvolge un ipotetico scenario in cui un aereo è disperso nell’Oceano Pacifico. Ci troviamo in un contesto in cui la latitudine è determinata, ma la longitudine rimane ignota (disponiamo unicamente dell’indicazione della direzione del viaggio, senza conoscere la distanza percorsa). L’obiettivo principale è rifinire la stima della posizione approssimata (\(\theta\)) dell’aereo. Per raggiungere questo fine, gli operatori di soccorso raccolgono dati dai frammenti dei detriti che sono stati individuati.

Iniziamo il processo con una stima iniziale, definita come distribuzione a priori. Questa distribuzione di probabilità rappresenta il nostro grado di conoscenza sulla posizione dell’aereo prima di ricevere ulteriori dati o informazioni.

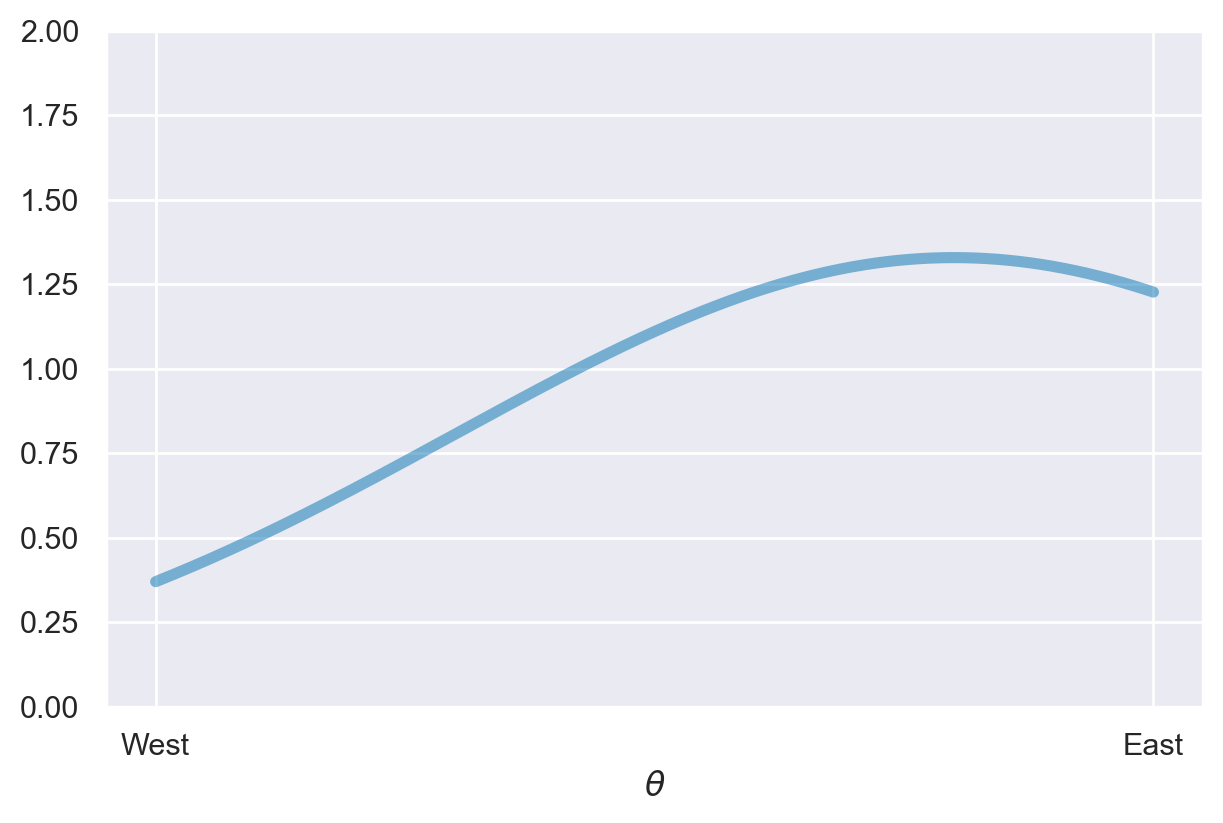
../_images/b3620897460c69323bf84f5430653566ca0e98f3398681e4ba45ac0605a9e970.png

Nel contesto bayesiano, una distribuzione di probabilità assume il compito di rappresentare l’incertezza o le convinzioni che nutriamo riguardo ai molteplici valori possibili che un parametro può assumere. Nel caso attuale, il parametro \(\theta\) indica la longitudine associata alla posizione dell’aereo disperso nell’oceano Pacifico. La posizione esatta dell’aereo rimane sconosciuta. Tuttavia, formuliamo delle ipotesi iniziali sulle possibili localizzazioni. Per ogni valore possibile di \(\theta\), la distribuzione di probabilità attribuisce un livello di fiducia che rispecchia quanto riteniamo probabile che quel valore specifico rappresenti il vero valore del parametro. I valori di \(\theta\) associati a ordinate più elevate nella funzione indicano un grado superiore di fiducia, in quanto riteniamo che tali valori siano più propensi a rappresentare il vero valore del parametro. In contrasto, i valori di \(\theta\) associati a ordinate più basse denotano convinzioni più deboli.

Sull’asse \(x\) del grafico sopra riportato sono indicati i valori di \(\theta\), cioè i diversi possibili valori della longitudine dell’aereo. Le estremità dell’asse delle ascisse sono etichettate come “West” (Ovest) e “East” (Est), per indicare che \(\theta\) spazia da ovest a est. Lungo l’asse delle ordinate (\(y\)), sono tracciati i valori delle densità di probabilità associati a ciascun valore di \(\theta\).

Nel nostro caso specifico, la distribuzione a priori è centrata intorno a \(\theta = 0.8\), suggerendo una previsione iniziale che l’aereo sia più verosimilmente situato ad est. Tuttavia, permangono incertezze considerevoli riguardo alla posizione esatta. Possiamo affermare, comunque, che inizialmente riteniamo che sia due volte più probabile che l’aereo si trovi ad est rispetto a ovest.

La scelta della distribuzione a priori rispecchia le convinzioni del ricercatore riguardo al problema in questione. Di conseguenza, diversi ricercatori potrebbero formulare diverse distribuzioni a priori per lo stesso problema, e tale diversità è accettabile, a patto che tali distribuzioni siano ragionevolmente giustificate. Nel prosieguo, scopriremo che nelle analisi Bayesiane, anche con campioni di dimensioni moderate, le varie distribuzioni a priori generano solitamente differenze trascurabili.

Ora, supponiamo di aver raccolto dei detriti nelle posizioni mostrate nel grafico seguente.

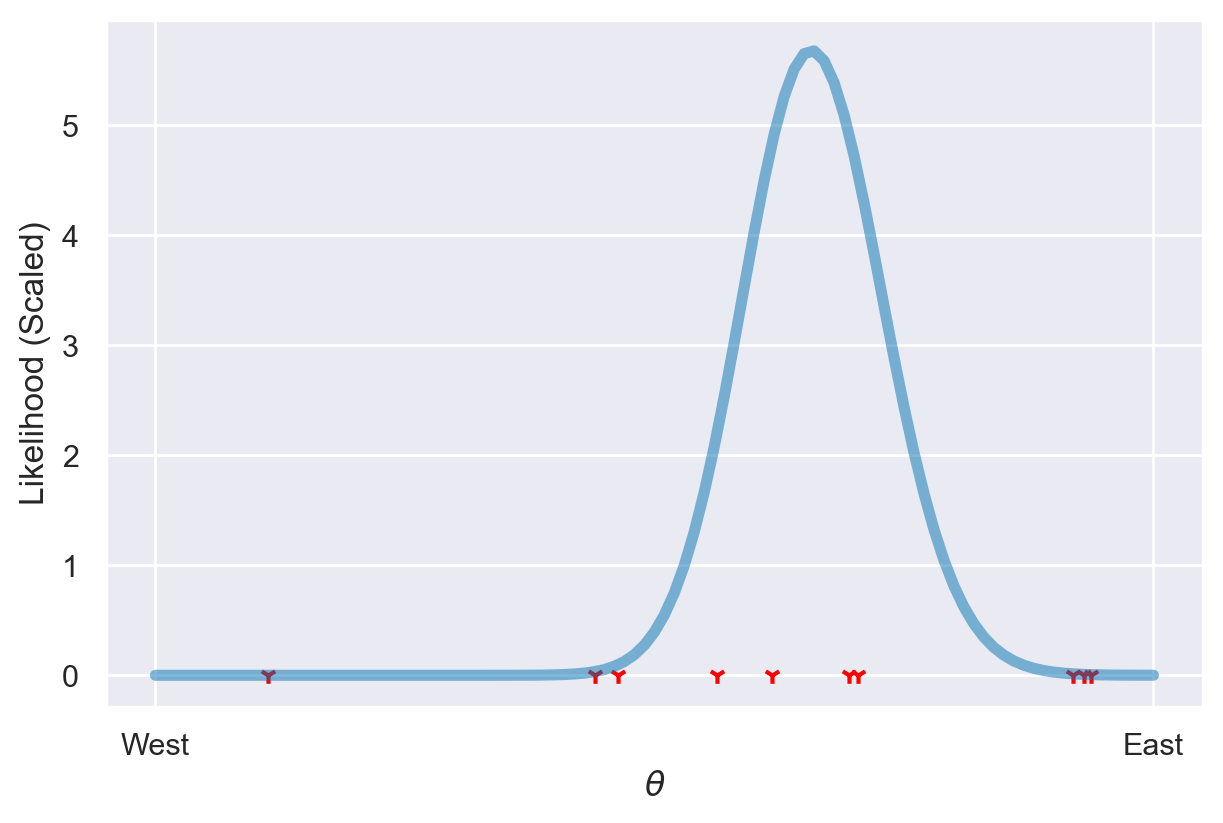
../_images/2bcc9e8ce034017c501ba1fc9b2ff1ce373b37635647ba1bb1cfede2a597deef.png

Dal Teorema di Bayes, è possibile derivare la distribuzione a posteriori attraverso il seguente procedimento:

\[ \text{Probabilità a posteriori} \propto \text{Probabilità a priori} \times \text{Verosimiglianza}. \]

In altre parole, è sufficiente moltiplicare le probabilità a priori e la verosimiglianza al fine di ottenere la probabilità posteriore per ciascuna posizione. È importante garantire che l’area sotto la curva sia normalizzata a 1. Questo processo è conosciuto come aggiornamento bayesiano.

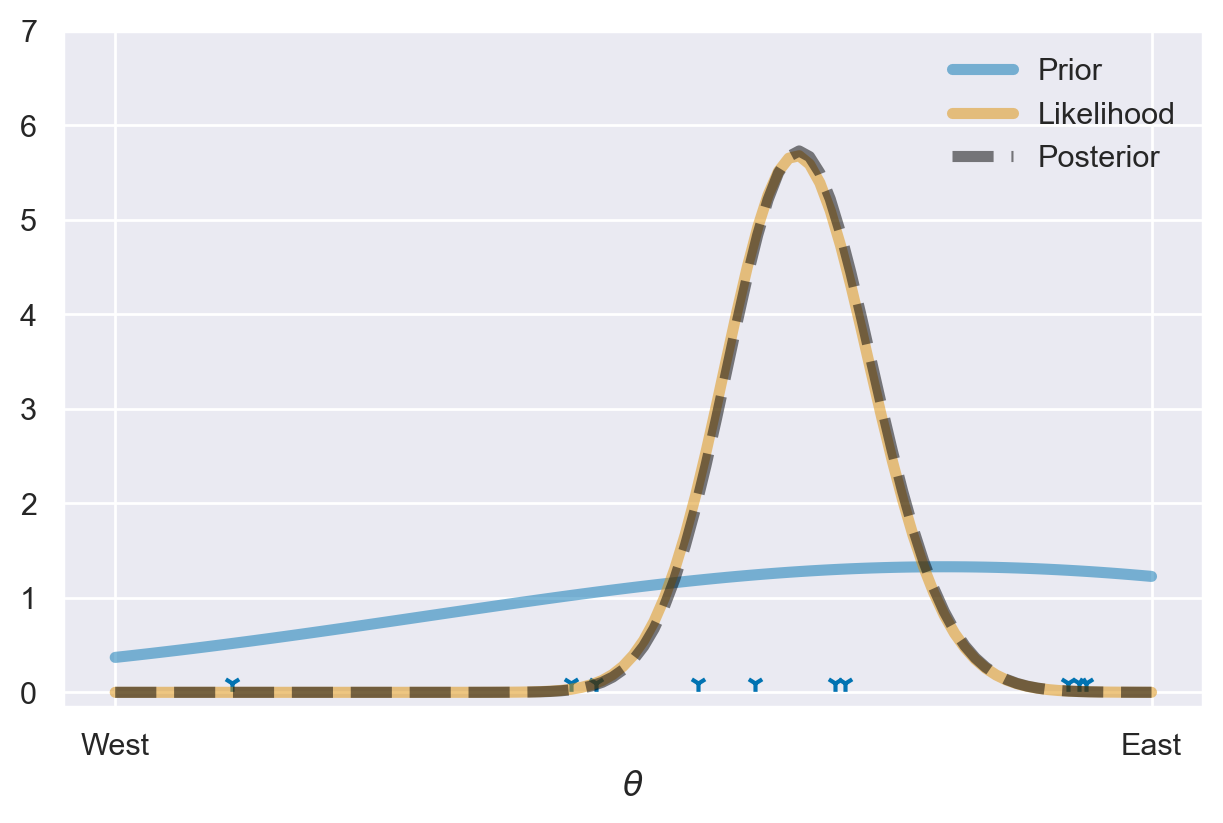
../_images/27eae14bfbff4f4c642d9ea99e7bcb30d9de739ca4e88c595a30ff2a7eab642c.png

In questa situazione, è evidente che una distribuzione a priori come quella descritta in precedenza, che definiremo “debolmente informativa”, ha un impatto trascurabile e la distribuzione a posteriori risulta quasi indistinguibile dalla verosimiglianza (che è stata normalizzata).

Ora, esamineremo come si comporta una distribuzione a priori maggiormente informativa.

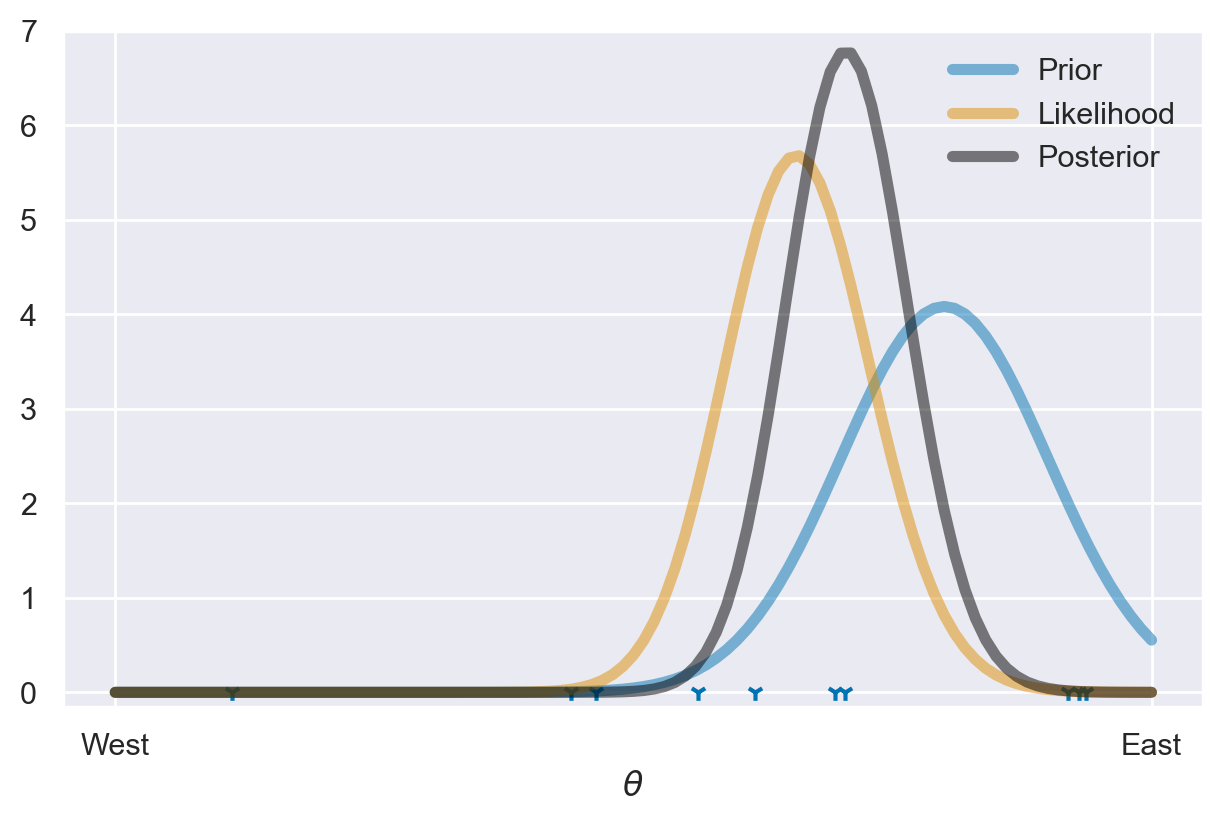
../_images/f12b7b97cfc730bc11e71db919feeec4b46ce5173b8ca4a1551df7174025ef6d.png

Il grafico illustra le tre distribuzioni coinvolte nell’aggiornamento bayesiano.

La curva tratteggiata rossa rappresenta la distribuzione a priori di \(\theta\). Questa curva riflette le nostre credenze iniziali o le aspettative riguardo ai possibili valori di \(\theta\) prima di effettuare qualsiasi osservazione. Nel nostro esempio, la distribuzione a priori è una distribuzione normale con una media di 0.8 e una deviazione standard di 0.1. Questo implica che, prima di raccogliere dati, prevediamo che il valore di \(\theta\) sia prossimo a 0.8, con una limitata variazione intorno a questa media.
La curva continua blu rappresenta la verosimiglianza dei dati osservati dato un valore specifico di \(\theta\). In altre parole, essa descrive quanto i dati osservati supportano ogni possibile valore di \(\theta\). La forma della curva indica quale valore di \(\theta\) risulta più plausibile in base a ciò che è stato osservato. Maggiore è l’altezza della curva in un determinato punto, maggiore è il supporto fornito dai dati a quel valore di \(\theta\).
La curva tratteggiata nera rappresenta la distribuzione a posteriori di \(\theta\). Questa curva rappresenta la nostra stima aggiornata di \(\theta\) dopo aver incorporato i dati osservati e le credenze iniziali attraverso il calcolo bayesiano. La distribuzione a posteriori combina la distribuzione a priori con la verosimiglianza dei dati, fornendo una stima più precisa e informativa di \(\theta\). In sostanza, essa riflette la nostra comprensione aggiornata del valore di \(\theta\) più probabile, tenendo conto sia delle informazioni iniziali che dei dati osservati.
- Il valore di \(\theta\) più probabile nella distribuzione a posteriori corrisponde al punto in cui la curva raggiunge l’apice, ovvero il valore di \(\theta\) in cui la densità è massima. Questo punto rappresenta la stima del parametro \(\theta\) che appare più plausibile alla luce dei dati osservati e delle credenze iniziali.
- Inoltre, la distribuzione a posteriori fornisce indicazioni sulla nostra incertezza riguardo al valore di \(\theta\). Se la distribuzione a posteriori è concentrata attorno a un valore specifico di \(\theta\) e presenta un picco netto, ciò suggerisce che siamo più sicuri nella stima di \(\theta\) e l’incertezza è ridotta. In altre parole, i dati osservati sono informativi e hanno ridotto l’incertezza sul valore di \(\theta\). Invece, se la distribuzione a posteriori è ampia e ha una forma meno definita, implica maggiore incertezza nella stima di \(\theta\). Questo può accadere quando i dati osservati sono scarsi o poco informativi, oppure se la distribuzione a priori era ampia, consentendo una vasta gamma di valori di \(\theta\). In sintesi, la forma della distribuzione a posteriori riflette quanto i dati raccolti ci abbiano aiutato a restringere le possibili valutazioni di \(\theta\).

Costruzione del Modello dell’Aggiornamento Bayesiano#

Per spiegare il concetto di aggiornamento bayesiano, McElreath [McE20] propone il seguente esempio. Supponiamo di avere un mappamondo e di volere stimare qual è la proporzione coperta d’acqua del globo. Per stimare questa proporzione eseguiamo il seguente esperimento casuale: lanciamo in aria il mappamondo e poi lo afferriamo quando cade. Registriamo se la superficie sotto il nostro indice destro è terra o acqua. Ripetiamo questa procedura un certo numero di volte e calcoliamo la proporzione di volte in cui abbiamo osservato “acqua”. In ogni lancio, ogni valore della proporzione sconosciuta \(p\) può essere più o meno plausibile, date le evidenze fornite dai lanci precedenti.

Un modello bayesiano inizia assegnando un insieme di plausibilità iniziali a ciascuno dei possibili valori \(p\), dette plausibilità priori. Poi, queste plausibilità vengono aggiornate alla luce dei dati raccolti, producendo le plausibilità posteriori. Questo processo di aggiornamento è una forma di apprendimento, conosciuto come aggiornamento bayesiano.

Nell’esempio di McElreath [McE20], supponiamo che il nostro modello bayesiano assegni inizialmente la stessa plausibilità a ogni possibile valore di \(p\) (proporzione di acqua). Ora, osserviamo il primo grafico in alto a sinistra nella figura generata dallo script. La linea tratteggiata orizzontale rappresenta la plausibilità iniziale di ciascun possibile valore di \(p\). Dopo aver visto il primo lancio, che risulta in “W” (acqua), il modello aggiorna le plausibilità alla linea continua. La plausibilità che \(p\) = 0 scende a zero, indicando che è “impossibile” non avere acqua, dato che abbiamo osservato almeno una traccia di acqua sul globo. Allo stesso modo, la plausibilità che \(p\) > 0.5 aumenta, poiché non c’è ancora evidenza di terra sul globo, quindi le plausibilità iniziali vengono modificate per essere coerenti con questa osservazione. Tuttavia, le differenze nelle plausibilità non sono ancora molto grandi, poiché le evidenze raccolte finora sono limitate. In questo modo, la quantità di evidenza vista finora si riflette nelle plausibilità di ciascun valore di \(p\): la plausibilità che \(p\) sia 0 è zero e la plausibilità che \(p\) sia 1 è massima. Quindi, la distribuzione a posteriori di \(p\) è rappresentata dalla linea continua che collega questi due estremi.

Nei grafici successivi, vengono introdotti ulteriori campioni dal globo, uno alla volta. Ogni curva tratteggiata rappresenta la curva continua dal grafico precedente, spostandosi da sinistra a destra e dall’alto in basso. La seconda osservazione è “terra” (L). La distribuzione a priori è la linea tratteggiata del secondo pannello e la distribuzione a postriori è la linea curva. Otteniamo questa curva perché assegniamo una verosimiglianza 0 agli eventi \(p\) = 0 (abbiamo osservato “acqua”) e \(p\) = 1 (abbiamo osservato “terra”). In due lanci abbiamo osservato una volta “terra” e una volta “acqua”. Dunque la plausibilità che \(p\) = 0.5 è massima. Da cui la curva che abbiamo disegnato.

Il terzo lancio del mappamondo produce nuovamente “acqua”. Quindi a questo punto il valore più plausibile di \(p\) è 0.75. modifichiamo dunque la distribuzione a priori (linea tratteggiata nel terzo pannello) in modo da rappresentare le nostre nuove conoscenze, come indicato dalla linea continua.

Ogni volta che viene osservato un “W”, il picco della curva di plausibilità si sposta a destra, verso valori maggiori di \(p\). Ogni volta che viene osservato un “L” (terra), si sposta nella direzione opposta. L’altezza massima della curva aumenta con ogni campione, significando che la plausibilità complessiva (1) viene ridistribuita ad un numero minore di valori di \(p\) i quali accumulano una maggiore plausibilità man mano che aumenta la quantità di evidenza. Con l’aggiunta di ogni nuova osservazione, la curva viene aggiornata in modo coerente con tutte le osservazioni precedenti.

È importante notare che ogni set aggiornato di plausibilità diventa la plausibilità iniziale per l’osservazione successiva. Ogni conclusione è il punto di partenza per l’inferenza futura. Questo processo di aggiornamento funziona anche al contrario: conoscendo l’ultimo set di plausibilità e l’ultima osservazione, è possibile matematicamente dedurre la curva di plausibilità precedente. I dati potrebbero essere presentati al modello in qualsiasi ordine, o anche tutti insieme. Nella maggior parte dei casi, i dati verranno considerati tutti insieme per comodità, ma è importante capire che ciò rappresenta solo l’abbreviazione di un processo di apprendimento iterato.

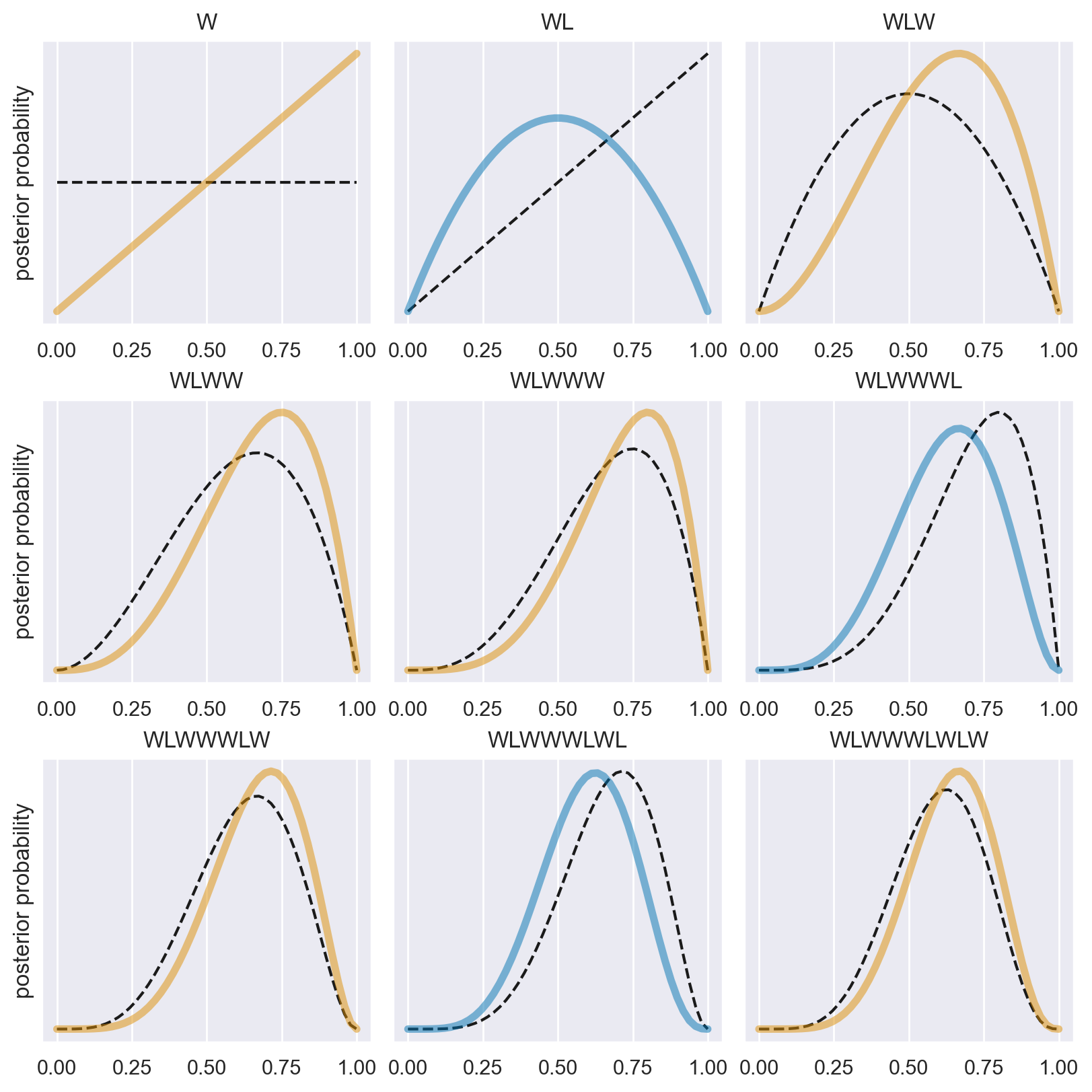
../_images/432c255dce230c77a62841c4ab93aa280409404e8d9cafaccea3a3755bacb6a7.png

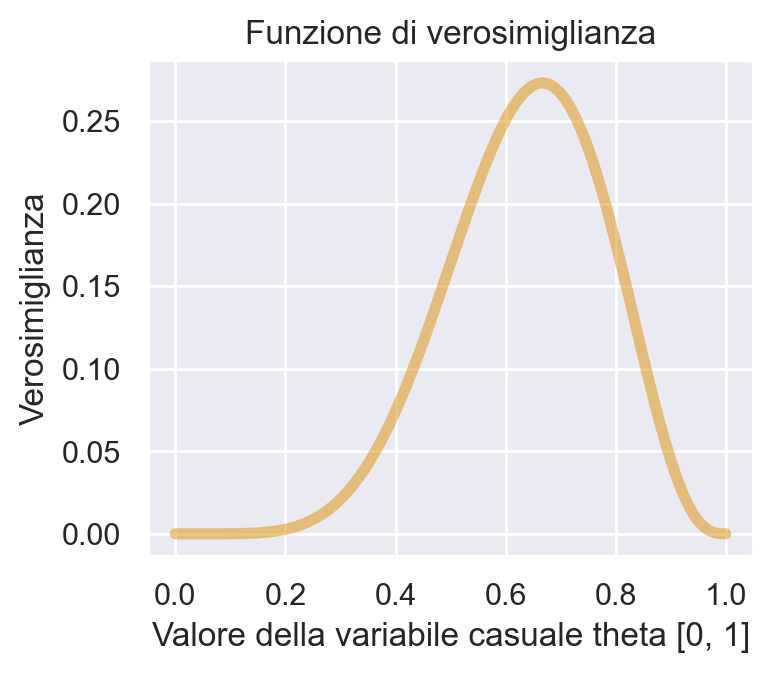
Il lettore attento si sarà chiesto se la curva continua dell’ultimo pannello non sia in realtà identica alla funzione di verosimiglianza binomiale con 6 successi in 9 prove – si veda il capitolo La verosimiglianza. In effetti è proprio così.

y = 6
n = 9
theta = np.linspace(0.0, 1.0, num=100)

like = stats.binom.pmf(y, n, theta)

plt.figure(figsize=(3.75, 3.25))
plt.plot(theta, like, "-", color = "C1", linewidth=4, alpha=.5)
plt.title("Funzione di verosimiglianza")
plt.xlabel("Valore della variabile casuale theta [0, 1]")
_ = plt.ylabel("Verosimiglianza")

../_images/7683ded27e333baa56bc767a96bb0dc8e8ae47765fe5c07f12ed89b951fdcbf8.png

Linguaggi di programmazione probabilistici#

I precedenti esempi illustrano il problema al quale la modellazione bayesiana mira a rispondere, cioè la stima delle distribuzioni di probabilità posteriori, e la soluzione proposta per affrontarlo mediante l’aggiornamento bayesiano. Fino a questo punto, abbiamo introdotto il concetto dell’aggiornamento bayesiano senza ancora approfondire il problema di come può essere calcolato, ovvero senza descrivere i dettagli computazionali. Questo sarà l’obiettivo dei capitoli successivi.

È fondamentale notare che l’attuale statistica bayesiana si avvale ampiamente di un linguaggio di programmazione probabilistico, noto come “Probabilistic Programming Language” (PPL), implementato su computer per eseguire l’aggiornamento bayesiano. Questo approccio ha rivoluzionato il modo in cui vengono condotte le analisi statistiche bayesiane. L’adozione di tali metodi computazionali ha semplificato la formulazione di modelli statistici complessi, abbassando il livello di competenze matematiche e computazionali richieste, rendendo il processo di modellazione bayesiana più accessibile. Inoltre, questi strumenti hanno aperto nuove opportunità per affrontare problemi di analisi dei dati che, in passato, sarebbero stati notevolmente complessi da trattare. La capacità di definire modelli probabilistici in un linguaggio di programmazione probabilistico consente agli analisti di esprimere le loro ipotesi in modo più chiaro e flessibile, agevolando così l’esplorazione delle distribuzioni posteriori e l’analisi di fenomeni complessi attraverso la statistica bayesiana.

Notazione#

Per chiarire la notazione, nel seguito utilizzeremo \(y\) per rappresentare i dati osservati e \(\theta\) per indicare i parametri sconosciuti di un modello statistico. Entrambi, \(y\) e \(\theta\), saranno trattati come variabili casuali. Utilizzeremo invece \(x\) per denotare le quantità note, come ad esempio i predittori di un modello lineare.

Al fine di rappresentare in modo più conciso i modelli probabilistici, adotteremo una notazione specifica. Ad esempio, anziché scrivere la distribuzione di probabilità di \(\theta\) come \(p(\theta) = Beta(1, 1)\), scriveremo semplicemente \(\theta \sim Beta(1, 1)\). Il simbolo “\(\sim\)” viene comunemente letto come “segue la distribuzione di”. Possiamo anche interpretarlo nel senso che \(\theta\) è un campione casuale estratto dalla distribuzione Beta(1, 1). Analogamente, la verosimiglianza di un modello binomiale sarà espressa come \(y \sim \text{Bin}(n, \theta)\), dove “\(\sim\)” indica che \(y\) segue una distribuzione binomiale con parametri \(n\) e \(\theta\). Questa notazione semplifica la rappresentazione dei modelli probabilistici, rendendo più chiara la relazione tra i dati, i parametri e le distribuzioni di probabilità coinvolte nelle analisi statistiche.

La Distribuzione a Priori#

La distribuzione a priori è un elemento chiave nell’approccio bayesiano, in quanto rappresenta le nostre conoscenze pregresse o le nostre assunzioni sui parametri del modello prima di osservare i dati. Questo concetto è fondamentale poiché consente di combinare le informazioni pregresse con i dati osservati per ottenere una stima più accurata dei parametri. Le distribuzioni a priori possono variare in base al grado di certezza che attribuiamo ai valori dei parametri.

Distribuzioni a Priori Non Informative#

Le distribuzioni a priori non informative rappresentano una mancanza completa di conoscenza pregressa e assegnano la stessa credibilità a tutti i valori dei parametri. Un esempio comune di distribuzione a priori non informativa è la distribuzione uniforme, che si basa sul “Principio della Ragione Insufficiente” formulato per la prima volta da Laplace (1774/1951). Questo principio sostiene che in assenza di evidenze rilevanti pregresse, tutte le possibili configurazioni dei parametri dovrebbero essere considerate equiprobabili.

Distribuzioni a Priori Debolmente Informative#

Le distribuzioni a priori debolmente informative consentendo di integrare una quantità limitata di informazioni pregresse nei modelli statistici. Queste distribuzioni sono progettate per riflettere le nostre assunzioni su quali possono essere i valori “ragionevoli” dei parametri del modello, tenendo conto delle incertezze presenti nell’analisi. L’uso di informazioni a priori debolmente informative può contribuire a migliorare la stabilità dell’analisi senza influenzare in modo significativo le conclusioni derivate da essa.

Le distribuzioni a priori debolmente informative hanno la caratteristica di non “spostare” in modo significativo la distribuzione a posteriori in una direzione specifica. In altre parole, sono centrate su valori “neutri” dei parametri. Ad esempio, quando si trattano parametri che possono assumere valori positivi o negativi, la distribuzione a priori debolmente informativa potrebbe essere centrata sullo zero. Nel caso di parametri che rappresentano proporzioni, essa potrebbe essere centrata su 0.5.

Tuttavia, ciò che rende queste distribuzioni debolmente informative è la specifica definizione di un intervallo “plausibile” di valori dei parametri. Questo intervallo indica quali valori dei parametri sono considerati plausibili e quali sono invece considerati implausibili. Ad esempio, una distribuzione a priori debolmente informativa potrebbe suggerire che valori estremamente grandi o estremamente bassi dei parametri sono poco plausibili, concentrandosi su un intervallo più stretto di valori considerati ragionevoli.

In sintesi, le distribuzioni a priori debolmente informative sono utilizzate per incorporare informazioni pregresse limitate nei modelli bayesiani, contribuendo a stabilizzare le stime dei parametri senza influenzare in modo significativo le conclusioni derivate dai dati. Queste distribuzioni definiscono un intervallo plausibile di valori dei parametri, aiutando a guidare l’analisi verso soluzioni più verosimili senza imporre vincoli eccessivi sui risultati.

Distribuzioni a Priori Informativa#

Le conoscenze pregresse, acquisite attraverso ricerche precedenti, pareri esperti o una combinazione di entrambi, possono essere meticolosamente integrate nel processo di analisi mediante l’incorporazione nelle distribuzioni a priori. Queste distribuzioni sono comunemente conosciute come distribuzioni a priori informative. Esse rappresentano un mezzo per codificare in modo sistematico informazioni concrete e rilevanti che possono avere un notevole impatto sull’analisi statistica, fornendo una solida base di conoscenza su cui fondare l’inferenza bayesiana.

Le distribuzioni a priori informative possono derivare da una vasta gamma di fonti, comprese ricerche pregresse, pareri di esperti nel campo e altre fonti affidabili. Questo approccio offre un metodo strutturato per integrare in modo coerente le conoscenze pregresse nel processo di analisi statistica. L’incorporazione di queste informazioni aggiuntive contribuisce notevolmente a migliorare la robustezza e l’accuratezza delle conclusioni derivate dai dati, fornendo una solida base empirica su cui basare le stime dei parametri del modello e le decisioni basate sull’analisi bayesiana.

Nell’ambito della ricerca psicologica, l’utilizzo di distribuzioni a priori informative è attualmente poco diffuso, tuttavia emergono segnali che all’interno della comunità statistica sta crescendo l’interesse per questa pratica, considerandola come un avanzamento promettente nel campo della data science.

La Verosimiglianza Marginale#

La formula completa della distribuzione a posteriori può essere espressa nel seguente modo:

(57)#\[ p(\theta \mid y) = \frac{p(y \mid \theta) p(\theta)}{\int_{\Theta}p(y \mid \theta) p(\theta) \,d\theta} \quad \text{per} \quad \theta \in \Theta, \]

dove \(\Theta\) rappresenta l’insieme dei possibili valori del parametro \(\theta\).

Per calcolare \(p(\theta \mid y)\), è necessario normalizzare il prodotto tra la distribuzione a priori e la verosimiglianza tramite una costante di normalizzazione. Questa costante, conosciuta come verosimiglianza marginale, è introdotta per garantire che l’area sotto la curva di \(p(\theta \mid y)\) sia unitaria. Tuttavia, l’integrale presente al denominatore della formula (57) spesso risulta complesso da risolvere analiticamente. Di conseguenza, l’inferenza bayesiana procede generalmente mediante l’uso di metodi di approssimazione numerica.

Metodi di Stima della Distribuzione a Posteriori#

Esistono due principali strategie per calcolare la distribuzione a posteriori:

Metodo Esatto: Questo approccio è applicabile quando la distribuzione a priori e la funzione di verosimiglianza appartengono alla stessa classe di distribuzioni, conosciute come distribuzioni a priori coniugate. In questi casi, la distribuzione a posteriori può essere calcolata analiticamente, senza la necessità di approssimazioni. Questo metodo è elegante e computazionalmente efficiente, ma ha una portata limitata poiché le distribuzioni a priori coniugate esistono solo per alcune specifiche combinazioni di distribuzioni a priori e verosimiglianze.
Metodo Approssimato: Quando il metodo esatto non può essere utilizzato, ad esempio quando le distribuzioni a priori e le verosimiglianze non sono coniugate, è possibile fare affidamento sul metodo approssimato. Questo implica l’utilizzo di algoritmi computazionalmente intensivi, come le Catene di Markov Monte Carlo (MCMC), per stimare la distribuzione a posteriori. Sebbene questo approccio sia più flessibile e possa essere applicato a una vasta gamma di scenari, richiede un maggiore dispendio di risorse computazionali e può risultare più lento rispetto al metodo esatto.

Il flusso di lavoro bayesiano#

Il concetto di “flusso di lavoro bayesiano” rappresenta un processo iterativo e flessibile che integra l’aggiornamento bayesiano nella ricerca scientifica. Metaforicamente descritto come “girare la manovella bayesiana,” questo approccio offre un metodo dinamico per affrontare le sfide nell’analisi dei dati.

Il flusso di lavoro bayesiano è composto da diverse fasi cruciali.

Studio di Simulazione: Questa fase prevede la generazione di dati sintetici che riproducono il contesto di ricerca. Questo aiuta a valutare la robustezza del disegno sperimentale e ad assicurare che il modello sia adeguato.
Raccolta e Identificazione dei Dati: Qui si acquisiscono e analizzano i dati reali, assicurandosi che siano appropriati per le analisi successive.
Selezione del Modello Statistico: In questa fase si formula un modello statistico che rappresenta le teorie e le ipotesi alla base della ricerca, basandosi su una solida comprensione del fenomeno e su principi statistici.
Definizione delle Distribuzioni a Priori: Si stabiliscono le distribuzioni a priori dei parametri del modello, basandosi su conoscenze pregresse e un ragionamento teorico robusto.
Calcolo delle Distribuzioni a Posteriori: Utilizzando metodi analitici o tecniche di campionamento come le Catene di Markov Monte Carlo (MCMC), si derivano le distribuzioni a posteriori dei parametri.
Risoluzione dei Problemi e Diagnostica: In questa fase si eseguono controlli per assicurare la convergenza del modello e la validità delle inferenze, utilizzando metriche e diagnosi specializzate.
Controlli di Coerenza: Oltre alla diagnostica tecnica, si valuta la coerenza e la plausibilità del modello rispetto ai dati e al contesto teorico, incluso un esame predittivo a posteriori.
Interpretazione e Comunicazione dei Risultati: Infine, i risultati vengono interpretati nel contesto della teoria sottostante e comunicati in modo chiaro, integrandoli nell’ambito più ampio della comprensione del fenomeno in studio.

Questo processo iterativo mira a costruire modelli statistici solidi e a ottenere inferenze valide, fornendo una base solida per la ricerca scientifica in vari campi, tra cui la psicologia. Una rappresentazione visiva di questo flusso di lavoro bayesiano è illustrata nella figura tratta dall’articolo di Baribault and Collins [BC23].

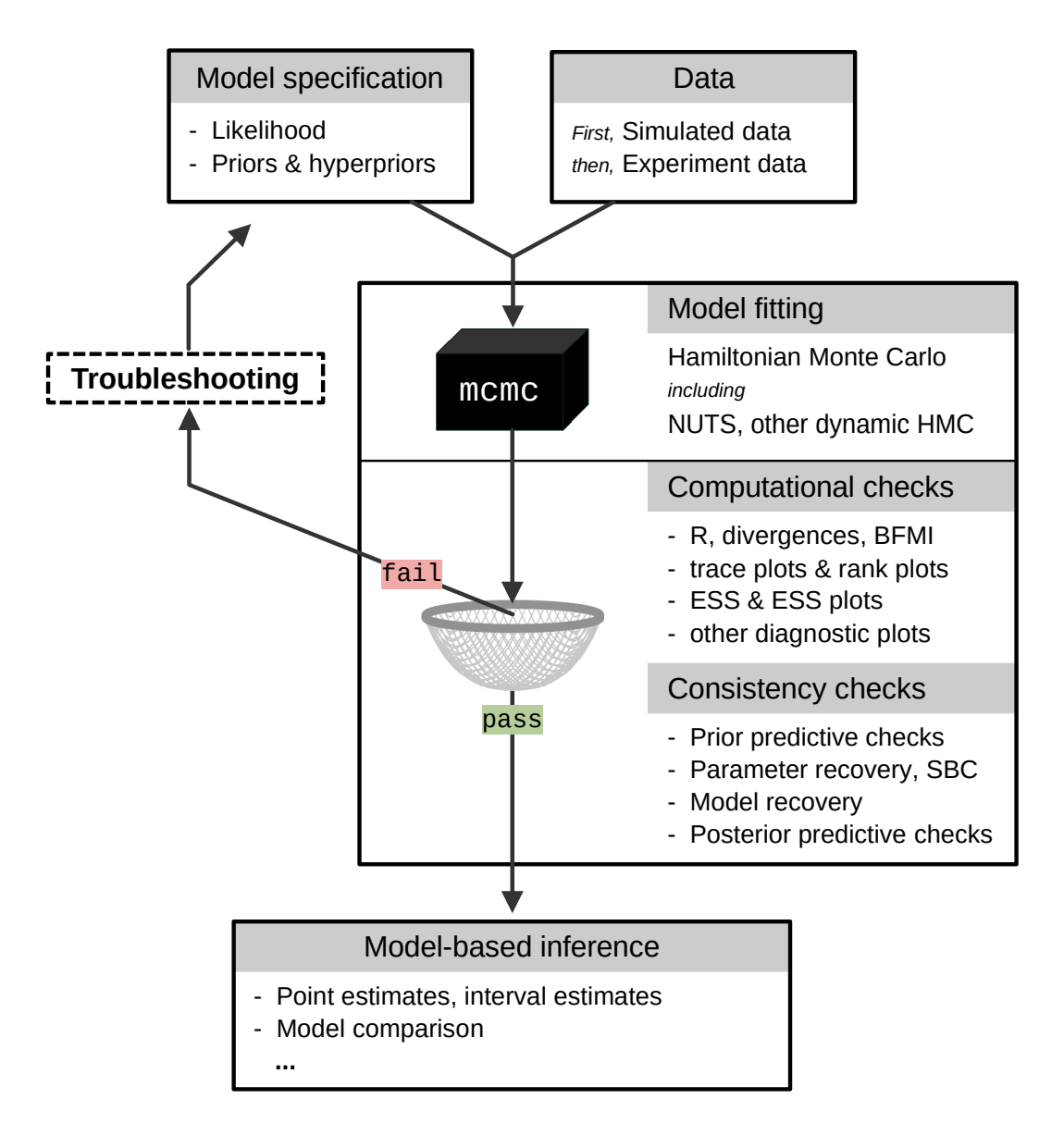
../_images/bayesian_workflow.png — Fig. 4 Una rappresentazione abbreviata del flusso di lavoro bayesiano. L’output del modello che non supera il filtro (che rappresenta i necessari controlli computazionali e di coerenza) deve essere respinto. È necessario migliorare la specifica del modello in modo che l’output possa superare tutti i controlli. Solo allora il modello bayesiano può essere utilizzato come base per l’inferenza. (Figura tratta da Baribault and Collins [BC23]).#

Commenti e considerazioni finali#

L’approccio bayesiano offre un approccio distintivo per gestire l’incertezza associata ai parametri di interesse, differenziandosi in modo significativo dalla metodologia classica. A differenza dell’idea che i parametri siano valori fissi e sconosciuti, l’approccio bayesiano li tratta come quantità probabilistiche, assegnando loro una distribuzione a priori che rappresenta le nostre credenze e intuizioni iniziali prima dell’esperimento. Attraverso l’applicazione del teorema di Bayes, queste credenze vengono raffinate e aggiornate in base ai dati raccolti, portando alla definizione della distribuzione a posteriori. Quest’ultima rappresenta una visione aggiornata dell’incertezza, incorporando sia l’evidenza empirica che le informazioni preesistenti.

La forza dell’approccio bayesiano risiede nella sua capacità di integrare le conoscenze pregresse con le nuove osservazioni, fornendo stime dei parametri di interesse che sono non solo più accurate ma anche più significative dal punto di vista interpretativo. Questa metodologia va oltre la mera analisi statistica, guidando il processo decisionale e consentendo di affrontare l’incertezza con una comprensione profonda, unendo conoscenze teoriche ed evidenze empiriche in un quadro coerente. In definitiva, l’approccio bayesiano non è solo un metodo statistico, ma un potente strumento decisionale che promuove l’interazione dinamica tra teoria ed esperienza.

Un svantaggio dell’approccio Bayesiano è che non è sempre veloce e non scala sempre bene con dataset molto grandi. Questo significa che quando si utilizzano metodi basati sulla teoria Bayesiana per l’analisi dei dati, potrebbero verificarsi problemi di efficienza computazionale quando si affrontano insiemi di dati estremamente grandi.