Generazione di numeri casuali#
In questo insegnamento introdurremo molti concetti tramite la simulazione. Pertanto deve essere ben chiaro come sia possibile generare numeri casuali da varie distribuzioni di probabilità. In questo capitolo esamineremo NumPy dato che questo modulo offre generatori di numeri casuali per tutte le principali distribuzioni di probabilità.
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
import arviz as az
from scipy.constants import golden
import scipy.stats as stats
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
%config InlineBackend.figure_format = 'retina'
%load_ext watermark
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
sns.set_theme(palette="colorblind")
Tutto ciò che succede sul nostro computer è generato da un algoritmo. L’algoritmo che genera i numeri “casuali” su computer è necessariamente deterministico. Questo diventa chiaro quando notiamo che otteniamo sempre lo stesso insieme di numeri casuali quando usiamo lo stesso seme (punto di partenza), su qualsiasi macchina o per diverse ripetizioni sulla stessa macchina. Per generare un numero veramente casuale sui nostri computer è necessario ottenere dei dati casuali da una fonte esterna; questa fonte esterna può essere la nostra sequenza di tasti, i movimenti del mouse, i dati sulla rete, ecc. La necessità di ottenere dei numeri veramente casuali nasce solo in contesti specifici, per esempio nei contesti legati alla sicurezza (crittografia, ecc.). Per gli scopi della data science, invece, sono sufficienti i numeri pseudo-casuali generati dal computer. In Python, il principale generatore di numeri (pseudo)casuali è NumPy.
Il generatore rng può usare una serie di metodi per generare numeri casuali estratti da una varietà di distribuzioni di probabilità. Oltre agli argomenti specifici della distribuzione, ogni metodo prende un argomento size il cui valore predefinito è None. Se size è None, viene generato e restituito un singolo valore. Se size è un numero intero, viene restituito un array 1-D riempito con i valori generati.
Distribuzione uniforme#
Consideriamo la distribuzione uniforme: uniform([low, high, size]). Genero un singolo valore:
Lo genero una seconda volta:
rng.uniform(0, 1, size=1)
array([0.77395605])
Genero 20 valori:
rng.uniform(0, 1, size=20)
array([0.43887844, 0.85859792, 0.69736803, 0.09417735, 0.97562235,
0.7611397 , 0.78606431, 0.12811363, 0.45038594, 0.37079802,
0.92676499, 0.64386512, 0.82276161, 0.4434142 , 0.22723872,
0.55458479, 0.06381726, 0.82763117, 0.6316644 , 0.75808774])
Creo un istogramma.
_ = plt.hist(rng.uniform(0, 1, size=100000), bins=50, density=True)
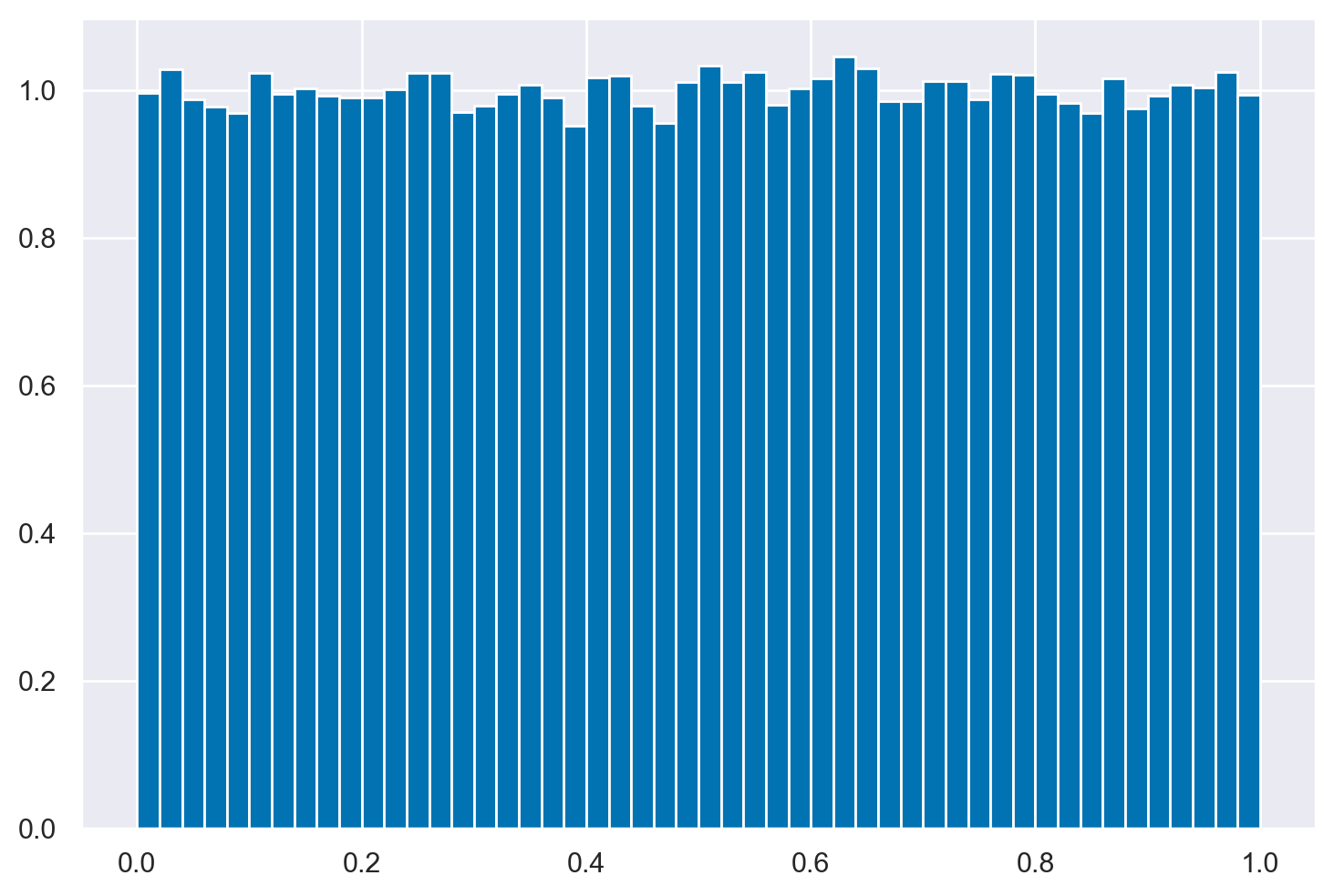
Distribuzione normale#
Estraiamo ora dei campioni casuali dalla distribuzione Gaussiana, normal([loc, scale, size]). Per esempio, generiamo 10 valori dalla distribuzione \(\mathcal{N}(\mu = 100, \sigma = 15)\):
x = rng.normal(loc=100, scale=15, size=10)
print(x)
[ 94.43605826 111.7309541 81.26336296 81.17729066 100.84159754
83.32674644 119.49706508 95.16799064 79.23341602 97.77136425]
Ora genero un grande numero (1000000) di valori casuali dalla \(\mathcal{N}(\mu = 100, \sigma = 15)\). Con questi valori creo un istogramma e a tale istogramma sovrappongo la funzione di densità \(\mathcal{N}(\mu = 100, \sigma = 15)\). In questo modo posso accertarmi che i numeri casuali che ho ottenuto si riferiscano veramente alla densità desiderata. Per trovare la densità della distribuzione normale, uso norm.pdf da scipy.stats. Si noti rng.normal() per la generazione dei numeri casuali.
n = 1000000
mu = 100
sigma = 15
# create x's
xs = np.linspace(55, 145, 100001)
y_pdf = stats.norm.pdf(xs, mu, sigma)
# create random samples
samps = rng.normal(loc=mu, scale=sigma, size=n)
# plot them
plt.plot(xs, y_pdf, color="r")
plt.hist(samps, bins=50, density=True)
plt.title("Distribuzione Normale $\mathcal{N}(\mu=100, \sigma=15)$")
plt.ylabel("$f(X)$")
plt.xlabel("Valore della variabile casuale $X$")
plt.xlim(40, 160)
(40.0, 160.0)
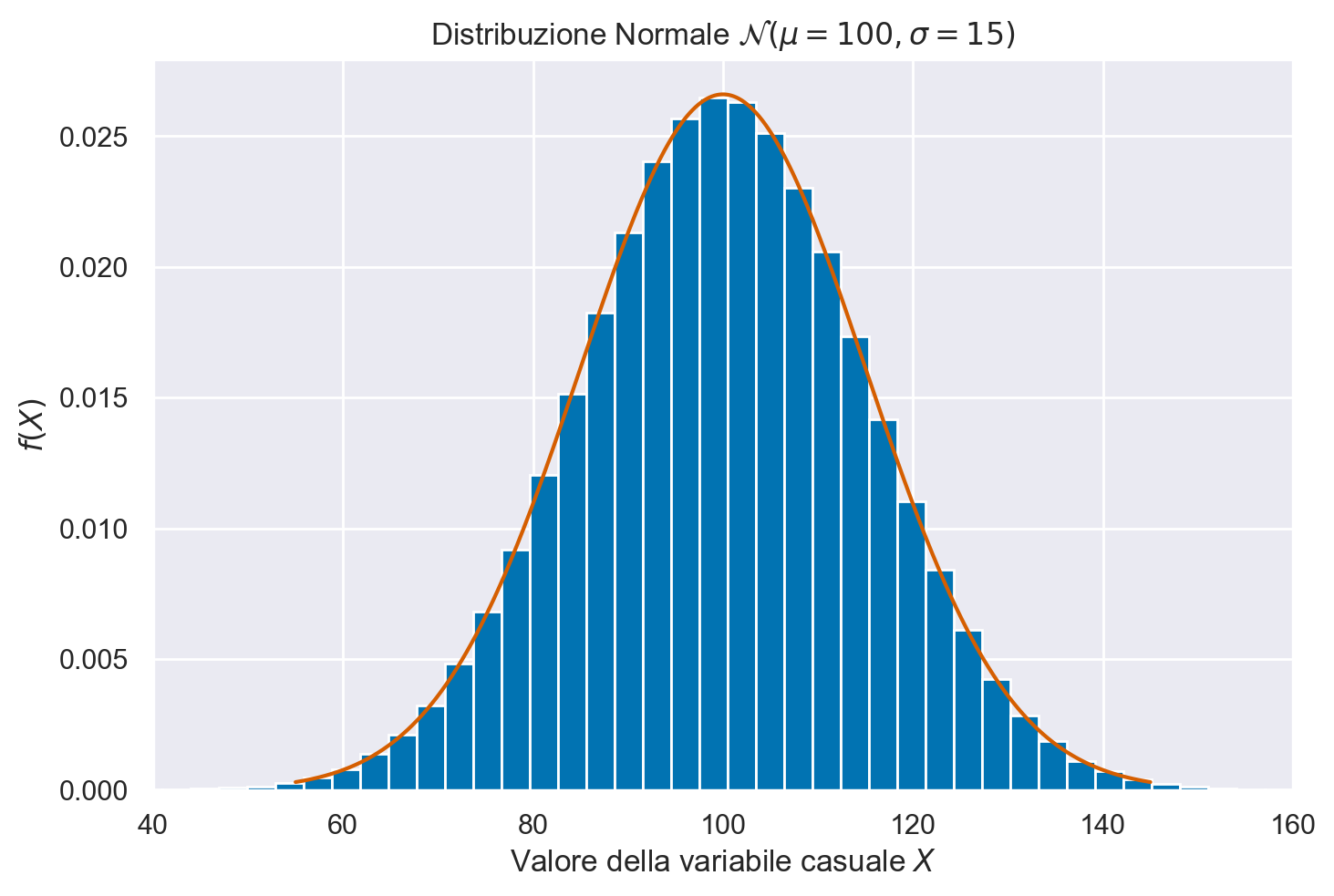
La stessa procedura può essere usata per tutte le distribuzioni implementate da NumPy. Presento alcuni esempi qui sotto.
Distribuzione Beta#
Per estrarre dei campioni casuali dalla distribuzione Beta uso il generatore rng con beta(a, b[, size]); per la densità Beta uso beta.pdf da scipy.stats.
a = 3
b = 9
# create x's
xs = np.linspace(0, 1, 100001)
y_pdf = stats.beta.pdf(xs, a, b)
# create random samples
samps = rng.beta(a=a, b=b, size=n)
# plot them
plt.plot(xs, y_pdf, color="r")
plt.hist(samps, bins=50, density=True)
plt.title("Distribuzione Beta(3,9)")
plt.ylabel("$f(X)$")
plt.xlabel("Valore della variabile casuale $X$")
Text(0.5, 0, 'Valore della variabile casuale $X$')
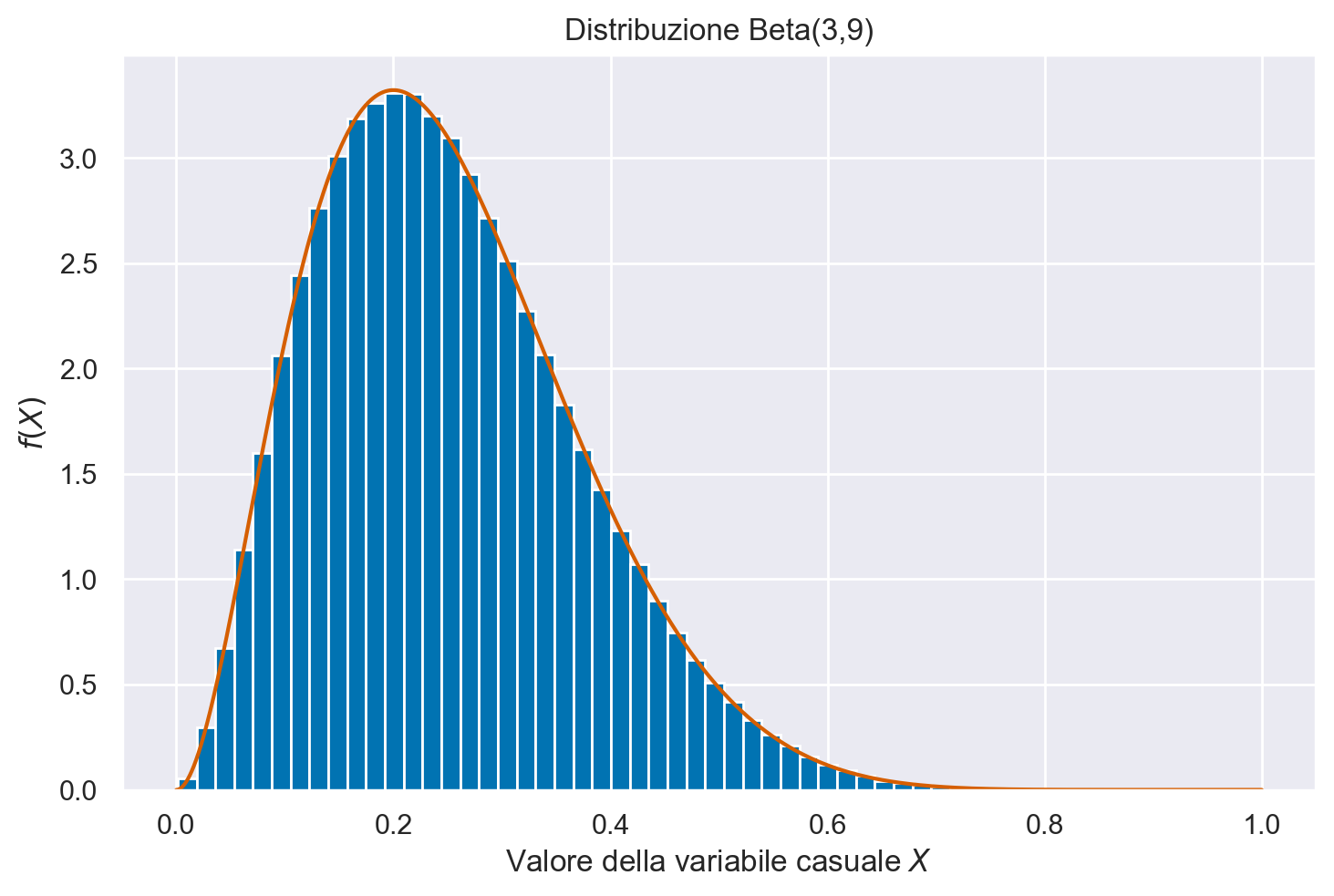
Distribuzione binomiale#
Per estrarre dei campioni casuali dalla distribuzione Binomiale uso il generatore rng con binomial(n, p[, size]); per la distribuzione di massa Binomiale uso binom.pmf da scipy.stats.
n = 10
p = 0.3
n_samples = 100001
# create r values
r_values = list(range(n + 1))
# pmf
y_pmf = [stats.binom.pmf(r, n, p) for r in r_values]
# create random samples
r_samps = rng.binomial(n=n, p=p, size=n_samples)
plt.plot(r_values, y_pmf, "x")
plt.hist(r_samps, bins=np.arange(-0.5, 11.5, 1), density=True)
plt.title("Distribuzione Binomiale($n$=10, $p$=0.3)")
plt.ylabel("$f(X)$")
plt.xlabel("Valore della variabile casuale $X$")
Text(0.5, 0, 'Valore della variabile casuale $X$')
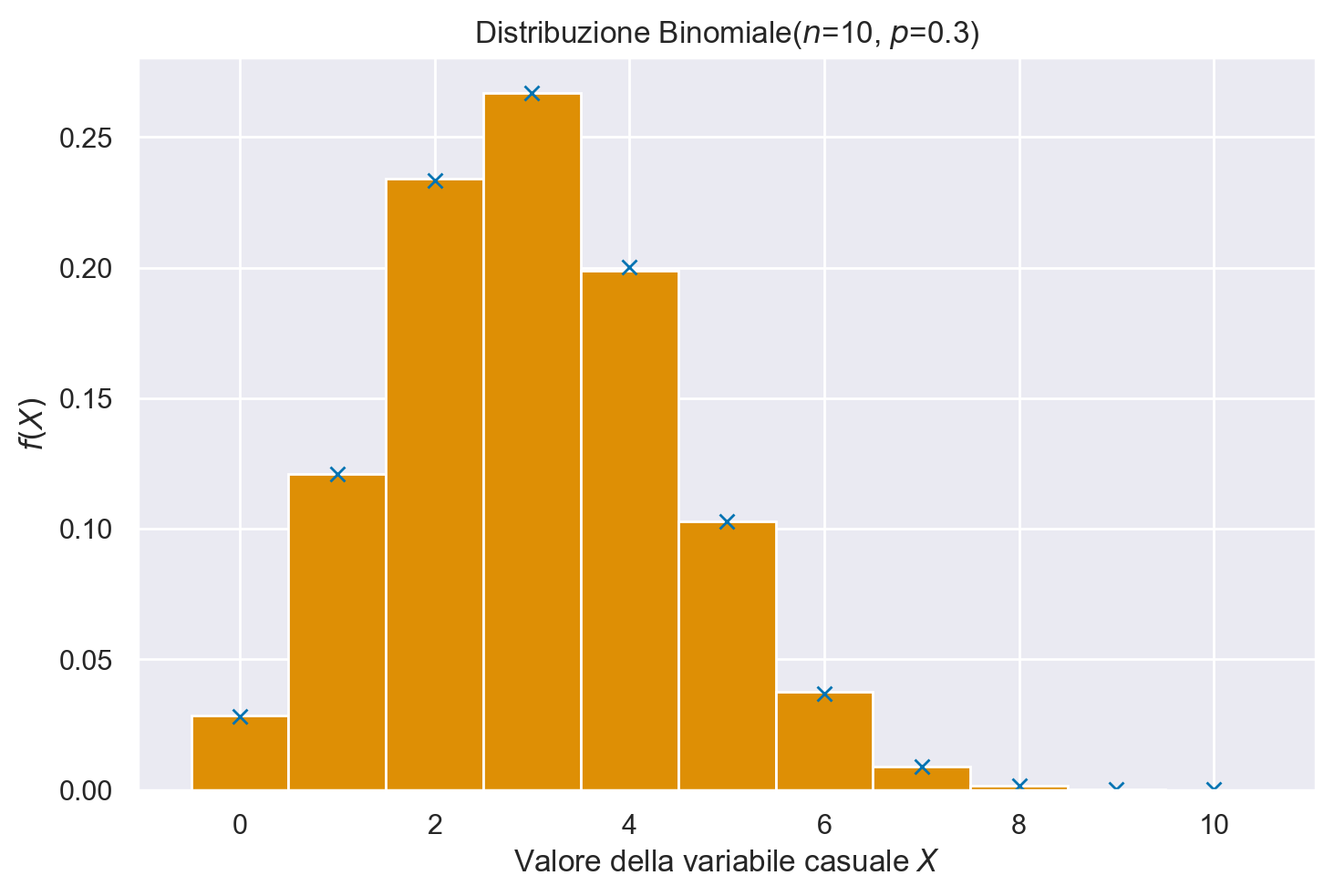
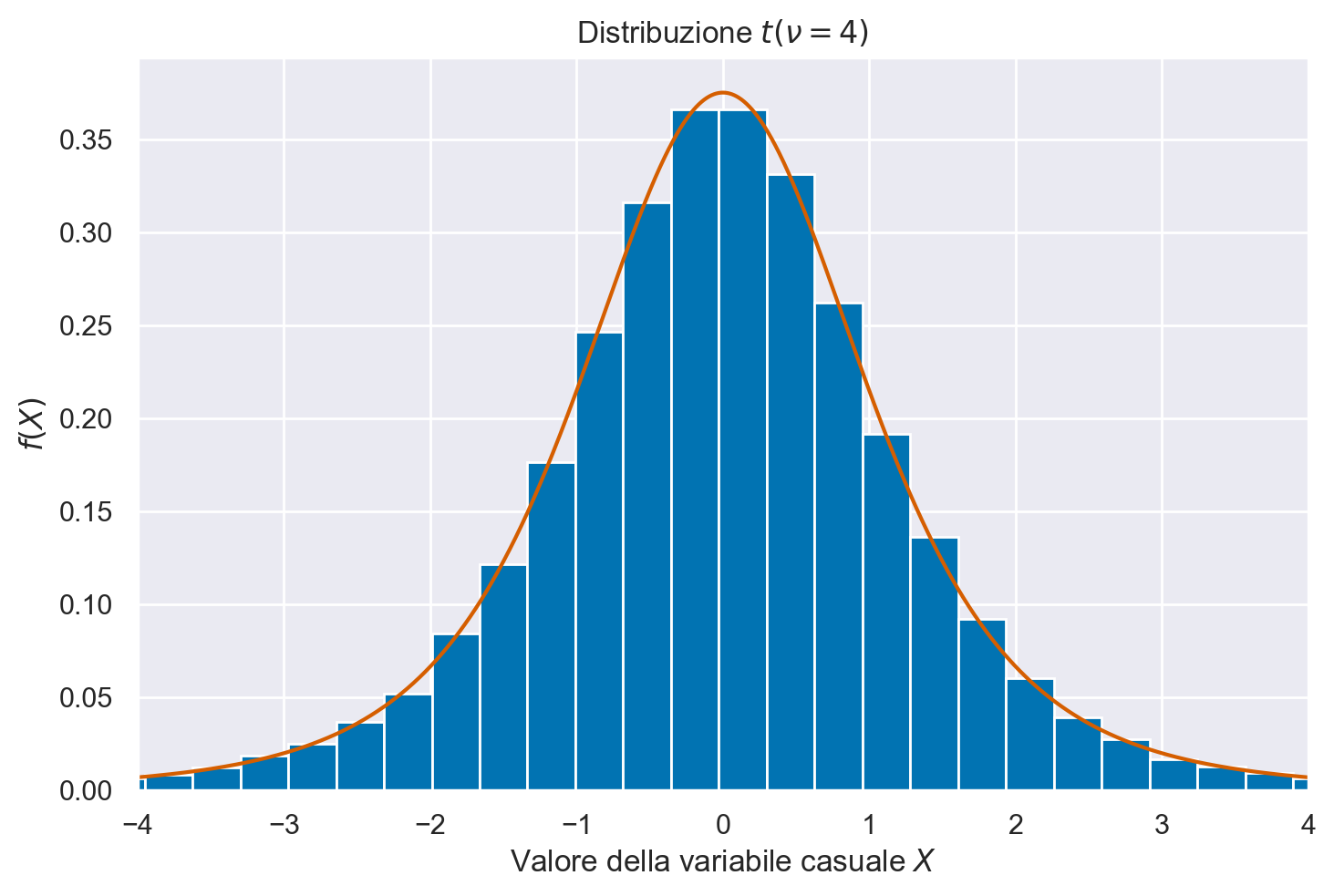
Distribuzione \(t\) di Student#
Per estrarre dei campioni casuali dalla distribuzione \(t\) di Student uso il generatore rng con standard_t(df, size=None); per la densità \(t\) di Student uso t.pdf da scipy.stats.
df = 4
size = 100001
# create x's
xs = np.linspace(-4, 4, 100001)
y_pdf = stats.t.pdf(xs, df=df)
# create random samples
samps = rng.standard_t(df=df, size=size)
# plot them
fig, ax = plt.subplots()
plt.plot(xs, y_pdf, color="r")
plt.hist(samps, bins=150, density=True)
plt.title("Distribuzione $t(\\nu=4)$")
plt.ylabel("$f(X)$")
plt.xlabel("Valore della variabile casuale $X$")
plt.xlim(-4, 4)
(-4.0, 4.0)
Distribuzione arbitraria di una variabile casuale distreta#
Con la funzione random.choices è possible specificare i valori di una variabile casuale discreta con una distribuzione di massa di probabilità arbitraria.
# Define the set of values
x_rv = [1, 2, 3, 4]
# Define the weights for each value
weights = [0.1, 0.1, 0.3, 0.5]
x_sample = rng.choice(x_rv, size=10, p=weights)
print(f"Random Sample: {x_sample}")
Random Sample: [3 1 1 4 4 4 3 4 4 1]
Nell’esempio, i pesi weights indicano che, nella distribuzione, il valore 4 è presente con una frequenza di cinque volte maggiore dei valori 1 e 2.
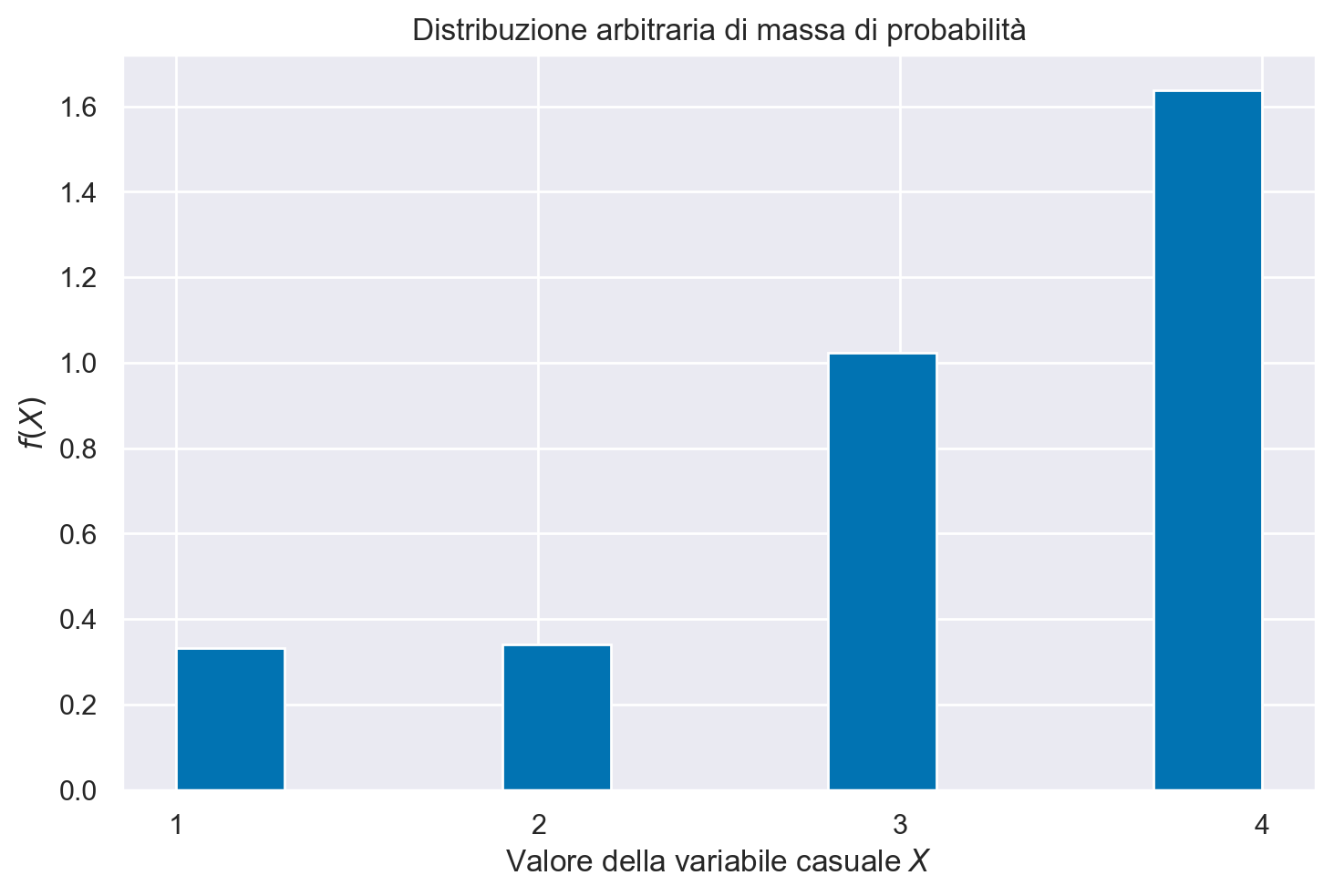
Se aggiungiamo l’argomento k possiamo definire i pesi (indirettamente, le probabilità) dei diversi valori della variabile casuale che sono stati specificati. Nell’esempio, i pesi [1, 1, 3, 6] indicano che, nella distribuzione, il valore 4 è presente con una frequenza di sei volte maggiore dei valori 1 e 2.
x = rng.choice(x_rv, size=10000, p=weights)
bins = plt.hist(x, density=True)
plt.title("Distribuzione arbitraria di massa di probabilità")
plt.ylabel("$f(X)$")
plt.xlabel("Valore della variabile casuale $X$")
plt.xticks(x_rv)
([<matplotlib.axis.XTick at 0x144390c10>,
<matplotlib.axis.XTick at 0x144a46fd0>,
<matplotlib.axis.XTick at 0x1448481d0>,
<matplotlib.axis.XTick at 0x144a9b610>],
[Text(1, 0, '1'), Text(2, 0, '2'), Text(3, 0, '3'), Text(4, 0, '4')])
Commenti e considerazioni finali#
Dalla libreria scipy.stats utilizzo
.pdfper ottenere i valori della funzione di densità di probabilità oppure.pmfper ottenere i valori della distribuzione di massa di probabilità;.ppfper ottenere i quantili della distribuzione;.cdfper ottenere la probabilità – nel caso di una variabile casuale continua, il valore della funzione di ripartizione, ovvero l’area sottesa alla curva di densità nella coda di sinistra; nel caso di una variabile casuale discreta, la somma delle probabilità della distribuzione di massa di probabilità dal valore minimo fino al valore indicato (incluso).
Dalla libreria numpy utilizzo
.randomper ottenere un campione di numeri casuali da una distribuzione.
Watermark#
%watermark -n -u -v -iv -w -p pytensor
Last updated: Sun Sep 17 2023
Python implementation: CPython
Python version : 3.11.5
IPython version : 8.15.0
pytensor: 2.12.3
numpy : 1.25.2
scipy : 1.10.1
matplotlib: 3.7.2
arviz : 0.16.0
seaborn : 0.12.2
pandas : 2.0.3
Watermark: 2.4.3

