Regressione di Poisson con Stan#
In questo tutorial, approfondiremo l’utilizzo di CmdStanPy per condurre un’analisi di regressione di Poisson. La regressione di Poisson rappresenta una forma di modello lineare generalizzato impiegato nell’analisi di regressione per modellare dati di conteggio. Essa si basa sull’assunzione che la variabile di risposta Y segua una distribuzione di Poisson, con il logaritmo del suo valore atteso modellabile attraverso una combinazione lineare di parametri sconosciuti.
L’esempio che esploreremo amplia l’analisi dei dati precedentemente trattati nel capitolo Modello di Poisson. Dopo aver investigato il calcolo della media a posteriori e dell’incertezza correlata al tasso di sparatorie fatali da parte della polizia negli Stati Uniti per ogni anno, ci interrogheremo se vi siano evidenze di una tendenza all’aumento di tale tasso nel corso del tempo.
Preparazione del Notebook#
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import arviz as az
import scipy.stats as stats
from scipy.special import expit # Funzione logistica
from cmdstanpy import cmdstan_path, CmdStanModel
# set seed to make the results fully reproducible
seed: int = sum(map(ord, "stan_poisson_regression"))
rng: np.random.Generator = np.random.default_rng(seed=seed)
az.style.use("arviz-darkgrid")
plt.rcParams["figure.dpi"] = 100
plt.rcParams["figure.facecolor"] = "white"
%config InlineBackend.figure_format = "retina"
Introduzione alla Regressione di Poisson#
La regressione di Poisson è una tecnica avanzata per modellare dati di conteggio, particolarmente efficace in situazioni dove è necessario analizzare la frequenza di occorrenza di eventi in specifici intervalli di tempo o spazio. Un esempio pratico di applicazione è la previsione del numero di comportamenti ripetitivi manifestati da un paziente con disturbo ossessivo-compulsivo (DOC), analizzando variabili come l’età del paziente o il numero di sedute di terapia cognitivo-comportamentale.
Fondamenti del Modello di Poisson#
Il modello si basa sulla distribuzione di Poisson, una distribuzione probabilistica che descrive eventi con una probabilità costante di occorrenza in un intervallo di tempo o spazio definito. La funzione di probabilità della distribuzione di Poisson è definita come:
dove \(\mu\) rappresenta il numero atteso di eventi nell’intervallo considerato e \(y\) i possibili conteggi di eventi, assumendo valori interi non negativi (0, 1, 2, …). Importante notare che in questa distribuzione, il valore atteso \(\mu\) coincide anche con la varianza.
Regressione di Poisson e sue Caratteristiche#
Nel modello di regressione di Poisson, si cerca di collegare il valore atteso di un conteggio, \(\mu_i\), a un insieme di variabili esplicative (come età, sesso, sintomi di depressione, ecc.) tramite una relazione funzionale. A differenza dei modelli lineari tradizionali, che possono produrre stime di conteggi negative e quindi non sensate, la regressione di Poisson utilizza una funzione di legame esponenziale per garantire che le stime dei conteggi siano sempre non negative. La relazione è espressa come segue:
dove \(\beta_0\) e \(\beta_1\) sono i parametri del modello che devono essere stimati. Questi parametri quantificano l’effetto delle variabili esplicative sui conteggi previsti. L’utilizzo della funzione esponenziale come legame assicura che il valore atteso \(\mu_i\) sia sempre positivo.
Procedura per Costruire il Modello di Regressione di Poisson#
Assunzione di Base: Si assume che il conteggio degli eventi per un dato livello della variabile esplicativa segua una distribuzione di Poisson, con un parametro di tasso (\(\mu_i\)) specifico per ciascuna osservazione.
Definizione del Predittore Lineare: Si definisce un predittore lineare, \(\eta_i\), come una combinazione lineare dei coefficienti del modello (\(\beta\)) e delle variabili esplicative (\(x_i\)).
Funzione di Legame: Si applica la funzione di legame esponenziale per stabilire che il tasso medio di eventi, \(\mu_i\), sia determinato dal predittore lineare, così che \(\mu_i = e^{\eta_i} = e^{\alpha + \beta x_i}\).
Questi passaggi consentono di costruire un modello che non solo predice accuratamente i conteggi, ma offre anche insight significativi sull’effetto delle variabili esplicative studiate.
Un Esempio Pratico#
Per fare un esempio, consideriamo nuovamente i dati corrispondenti alle sparatorie mortale negli Stati Uniti ad opera di agenti di polizia, a partire dal 1° gennaio 2015.
Importiamo i dati.
url = "https://raw.githubusercontent.com/washingtonpost/data-police-shootings/master/v2/fatal-police-shootings-data.csv"
fps_dat = pd.read_csv(url)
fps_dat.head()
| id | date | threat_type | flee_status | armed_with | city | county | state | latitude | longitude | location_precision | name | age | gender | race | race_source | was_mental_illness_related | body_camera | agency_ids | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 2015-01-02 | point | not | gun | Shelton | Mason | WA | 47.246826 | -123.121592 | not_available | Tim Elliot | 53.0 | male | A | not_available | True | False | 73 |
| 1 | 4 | 2015-01-02 | point | not | gun | Aloha | Washington | OR | 45.487421 | -122.891696 | not_available | Lewis Lee Lembke | 47.0 | male | W | not_available | False | False | 70 |
| 2 | 5 | 2015-01-03 | move | not | unarmed | Wichita | Sedgwick | KS | 37.694766 | -97.280554 | not_available | John Paul Quintero | 23.0 | male | H | not_available | False | False | 238 |
| 3 | 8 | 2015-01-04 | point | not | replica | San Francisco | San Francisco | CA | 37.762910 | -122.422001 | not_available | Matthew Hoffman | 32.0 | male | W | not_available | True | False | 196 |
| 4 | 9 | 2015-01-04 | point | not | other | Evans | Weld | CO | 40.383937 | -104.692261 | not_available | Michael Rodriguez | 39.0 | male | H | not_available | False | False | 473 |
# Convert date
fps_dat["date"] = pd.to_datetime(fps_dat["date"])
# Create a new column 'year' to store the year information from the 'date' column
fps_dat["year"] = fps_dat["date"].dt.year
fps_dat.columns
Index(['id', 'date', 'threat_type', 'flee_status', 'armed_with', 'city',
'county', 'state', 'latitude', 'longitude', 'location_precision',
'name', 'age', 'gender', 'race', 'race_source',
'was_mental_illness_related', 'body_camera', 'agency_ids', 'year'],
dtype='object')
# Filter out rows with year equal to 2024
fps = fps_dat[fps_dat["year"] != 2024]
# Count occurrences of each year in fps
year_counts = fps["year"].value_counts()
print(year_counts)
year
2023 1161
2022 1095
2021 1050
2020 1020
2019 996
2015 995
2018 992
2017 984
2016 959
Name: count, dtype: int64
years = year_counts.index.to_numpy()
year = years - 2019
year
array([ 4, 3, 2, 1, 0, -4, -1, -2, -3], dtype=int32)
counts = year_counts.values
counts
array([1161, 1095, 1050, 1020, 996, 995, 992, 984, 959])
Creiamo un dizionario con i dati nel formato richiesto per CmdStan.
stan_data = {
"N" : len(year),
"y" : counts,
"x" : year
}
stan_data
{'N': 9,
'y': array([1161, 1095, 1050, 1020, 996, 995, 992, 984, 959]),
'x': array([ 4, 3, 2, 1, 0, -4, -1, -2, -3], dtype=int32)}
Leggiamo il file che contiene il modello di regressione di Poisson.
stan_file = os.path.join('stan', 'poisson_regression.stan')
with open(stan_file, 'r') as f:
print(f.read())
data {
int<lower=0> N; // Numero di osservazioni
array[N] int<lower=0> y; // Dati di conteggio (frequenze)
vector[N] x; // Variabile predittore (anni, già standardizzata)
}
parameters {
real alpha; // Intercetta
real beta; // Pendenza
}
model {
// Priors debolmente informativi
alpha ~ normal(0, 10);
beta ~ normal(0, 10);
// Modello di regressione di Poisson
y ~ poisson_log(alpha + beta * x);
}
generated quantities {
array[N] int<lower=0> y_pred = poisson_log_rng(alpha + beta * x);
}
Questo modello Stan specifica una regressione di Poisson per dati di conteggio, dove l’obiettivo è modellare il numero di eventi (espressi dalla variabile y) in funzione di una variabile predittiva x (in questo caso, anni standardizzati). Il modello è strutturato in quattro blocchi principali: data, parameters, model, e generated quantities. Ecco una panoramica dettagliata di ciascuna sezione e il suo ruolo nel contesto del modello:
Blocco data#
N: Un intero che specifica il numero totale di osservazioni nel dataset. Serve a definire le dimensioni degli array e dei vettori utilizzati nel modello.
y: Un array di interi che rappresenta i dati di conteggio osservati. Ogni elemento in
ycorrisponde al numero di eventi registrati in ciascuna delleNunità di osservazione.x: Un vettore di lunghezza
Nche contiene i valori della variabile predittiva (ad esempio, anni).
Blocco parameters#
alpha: Un parametro reale che rappresenta l’intercetta del modello. In un contesto di regressione di Poisson,
alphacorrisponde al logaritmo del tasso atteso di eventi quando la variabile predittivaxè zero.beta: Un parametro reale che rappresenta la pendenza o il coefficiente della variabile predittiva
x. Questo parametro indica come il logaritmo del tasso atteso di eventi cambia in risposta a variazioni di una unità inx.
Blocco model#
I priors per alpha e beta sono definiti come distribuzioni normali con media 0 e deviazione standard 10, rappresentando priors debolmente informativi che permettono ai dati di guidare principalmente l’inferenza sui parametri.
Nella tradizionale regressione di Poisson, il parametro \(\mu_i\) (il tasso medio di eventi per l’unità osservata) è collegato alle variabili esplicative tramite una funzione esponenziale: \(\mu_i = e^{\eta_i} = e^{\beta_0 + \beta_1 x_i}\). Questa trasformazione assicura che il valore predetto di \(\mu_i\) sia sempre positivo, indipendentemente dai valori assunti dalle variabili esplicative, una necessità quando si modellano conteggi che non possono essere negativi.
La funzione poisson_log, invece di lavorare direttamente con \(\mu_i\) come nella forma esponenziale \(e^{\eta_i}\), opera sul logaritmo di \(\mu_i\). Questo significa che la funzione specifica il logaritmo del tasso medio di eventi come lineare rispetto ai predittori. In altre parole, anziché modellare \(\mu_i\) direttamente e poi trasformarlo, si modella il logaritmo di \(\mu_i\) (che è \(\log(\mu_i)\)) come funzione lineare delle variabili esplicative: \(\log(\mu_i) = \eta_i = \beta_0 + \beta_1 x_i\).
Questa specificazione ha diversi vantaggi:
Stabilità numerica: Lavorare con il logaritmo di \(\mu_i\) può ridurre i problemi di stabilità numerica che talvolta emergono quando si lavora con valori estremamente grandi o piccoli di \(\mu_i\).
Interpretazione diretta dei parametri: Poiché si modella il logaritmo di \(\mu_i\), i coefficienti (come \(\beta_1\)) possono essere interpretati in termini di variazione percentuale. Un incremento di una unità in \(x_i\) è associato a un moltiplicatore esponenziale di \(e^{\beta_1}\) sul tasso medio di eventi.
Nel codice Stan, la linea y ~ poisson_log(alpha + beta * x); specifica quindi che i dati di conteggio y seguono una distribuzione di Poisson, con il logaritmo del parametro di tasso (\(\log(\mu_i)\)) modellato come una funzione lineare di x attraverso alpha + beta * x.
Blocco generated quantities#
y_pred: Un array di interi che contiene valori predetti generati dalla distribuzione di Poisson. Per ogni osservazione,
poisson_log_rnggenera un valore di conteggio casuale basato sul tasso atteso calcolato comealpha + beta * x. Questi valori predetti possono essere utilizzati per verifiche predittive posteriori o per ottenere una distribuzione predittiva degli eventi.
Compiliamo il modello.
model = CmdStanModel(stan_file=stan_file)
print(model)
CmdStanModel: name=poisson_regression
stan_file=/Users/corradocaudek/_repositories/temp/chapter_5/stan/poisson_regression.stan
exe_file=/Users/corradocaudek/_repositories/temp/chapter_5/stan/poisson_regression
compiler_options=stanc_options={}, cpp_options={}
Eseguiamo il campionamento.
fit = model.sample(data=stan_data)
Show code cell output
09:49:32 - cmdstanpy - INFO - CmdStan start processing
09:49:32 - cmdstanpy - INFO - CmdStan done processing.
Esaminiamo un sommario della distribuzione a posteriori per i parametri.
az.summary(fit, var_names=(["alpha", "beta"]), hdi_prob=0.95)
| mean | sd | hdi_2.5% | hdi_97.5% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha | 6.934 | 0.011 | 6.912 | 6.954 | 0.0 | 0.0 | 2589.0 | 2120.0 | 1.0 |
| beta | 0.020 | 0.004 | 0.012 | 0.028 | 0.0 | 0.0 | 3875.0 | 2741.0 | 1.0 |
L’ess_bulk (Effective Sample Size per il bulk dell’estimatore) e ess_tail (Effective Sample Size per la coda dell’estimatore) sono relativamente alti per entrambi i parametri, indicando che il campionamento ha fornito una buona approssimazione della distribuzione a posteriori. Inoltre, il valore di r_hat vicino a 1.0 per entrambi i parametri suggerisce che il campionamento ha raggiunto la convergenza, indicando che i risultati sono affidabili.
Interpretazione del Parametro alpha#
Il parametro alpha è una stima del logaritmo del tasso atteso di eventi (frequenze) quando il valore della variabile esplicativa x è zero, ossia quando si trova nella sua media, che in questo contesto è stata standardizzata e centrata sull’anno 2019. Il valore medio di alpha è 6.934, indicando che il logaritmo naturale del tasso atteso di eventi quando x = 0 è circa 6.934.
L’intervallo di alta densità (HDI) del 95% per alpha va da 6.912 a 6.954, fornendo un intervallo di stime plausibili per il valore di alpha con un alto grado di certezza statistica.
Per interpretare alpha in termini di tasso atteso di eventi, usiamo exp(alpha). Questo trasforma il logaritmo del tasso di eventi nel tasso effettivo. Ad esempio, exp(6.934) dà il tasso atteso di eventi per l’anno di riferimento 2019.
np.exp(6.934)
1026.5921464104808
Interpretazione del Parametro beta#
Il parametro beta rappresenta la variazione logaritmica attesa nelle frequenze per ogni incremento unitario in x (l’anno, in questo caso). Un valore medio di beta pari a 0.020, con un HDI del 95% che va da 0.012 a 0.028, suggerisce una tendenza positiva: all’aumentare degli anni, ci si aspetta un incremento nelle frequenze degli eventi.
Utilizzando il link logaritmico del modello, l’effetto di un incremento di un anno su x si traduce in una moltiplicazione del tasso di frequenza per exp(beta). Quindi, un aumento di un anno implica che il tasso di frequenza sarà moltiplicato per exp(0.020), che è approssimativamente 1.02, indicando un aumento previsto del 2% nelle frequenze per ogni anno successivo.
np.exp([0.020, 0.012, 0.028])
array([1.02020134, 1.01207229, 1.02839568])
Calcolo dell’Aumento Effettivo in Frequenza#
Per calcolare l’aumento effettivo in frequenza per ogni anno, utilizziamo la seguente formula:
Calcolo del Fattore di Moltiplicazione:
exp(beta)è il fattore di moltiplicazione che descrive come cambia il tasso di frequenza con un incremento di un anno. Conbeta = 0.020,exp(beta)è circa 1.0202.Determinazione dell’Aumento Attuale in Frequenza:
exp(alpha)fornisce il tasso di base delle frequenze quandox = 0. Moltiplicando questo tasso di base per(\exp(\beta) - 1), otteniamo l’aumento effettivo in frequenza per ogni anno aggiuntivo. Sottraendo 1 aexp(beta), otteniamo l’incremento percentuale dovuto solamente all’aumento di un anno.
Questa metodologia fornisce un modo intuitivo e statistico per quantificare come le variabili nel tempo influenzano la frequenza degli eventi, permettendo di fare previsioni basate su modelli storici e tendenze osservate.
# Parametri del modello
alpha_mean = 6.934
beta_mean = 0.020
# Calcolo del tasso di frequenza base per l'anno centrato (exp(alpha))
tasso_base = np.exp(alpha_mean)
# Calcolo del fattore di moltiplicazione per l'aumento (exp(beta))
fattore_moltiplicazione = np.exp(beta_mean)
# Aumento atteso in frequenza per un anno
aumento_atteso = tasso_base * (fattore_moltiplicazione - 1)
aumento_atteso
20.738537018435174
Basandosi sul modello di regressione di Poisson, si stima un incremento medio di circa 20.74 nel numero di sparatorie fatali da parte della polizia negli Stati Uniti per ogni anno aggiuntivo. In altre parole, il modello prevede che, anno dopo anno, il numero di tali incidenti potrebbe crescere di circa 21 casi. Questa previsione riflette una dinamica esponenziale tra il passare degli anni e l’aumento della frequenza assoluta di sparatorie fatali, come evidenziato dai dati analizzati.
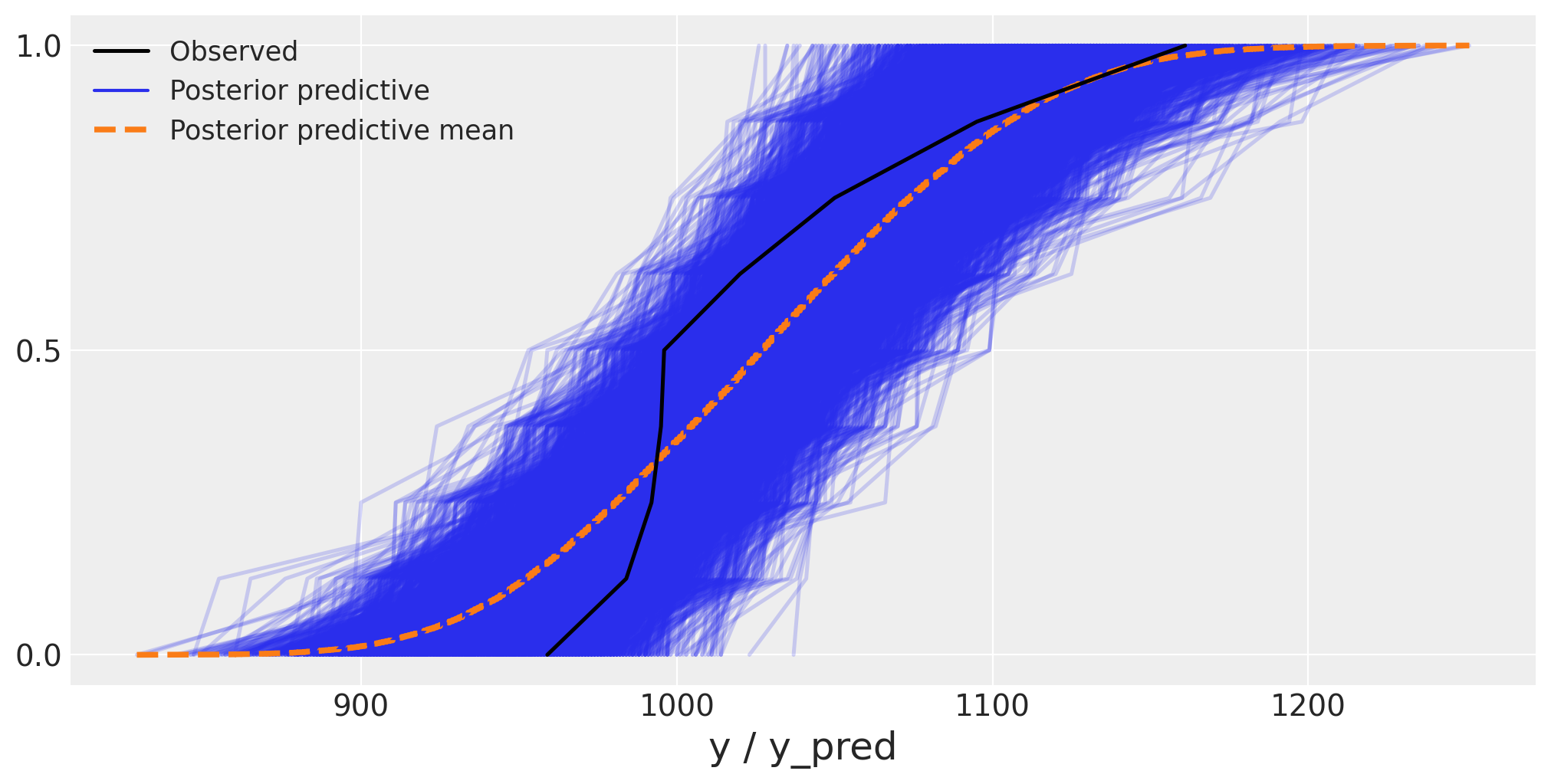
Posterior-Predictive Check#
Esaminiamo il posterior-predictive check per il modello esaminato:
y_observed = stan_data["y"]
idata = az.from_cmdstanpy(
posterior=fit,
posterior_predictive='y_pred',
observed_data={'y': y_observed}
)
Informazioni sull’Ambiente di Sviluppo#
%load_ext watermark
%watermark -n -u -v -iv -w -m -p cmdstanpy
Last updated: Sun Jun 16 2024
Python implementation: CPython
Python version : 3.12.3
IPython version : 8.25.0
cmdstanpy: 1.2.3
Compiler : Clang 16.0.6
OS : Darwin
Release : 23.4.0
Machine : arm64
Processor : arm
CPU cores : 8
Architecture: 64bit
seaborn : 0.13.2
numpy : 1.26.4
pandas : 2.2.2
matplotlib: 3.8.4
scipy : 1.13.1
arviz : 0.18.0
Watermark: 2.4.3