✏️ Esercizi#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import arviz as az
import pingouin as pg
import seaborn as sns
%config InlineBackend.figure_format = 'retina'
# set seed to make the results fully reproducible
seed: int = sum(map(ord, "quiz_t_test"))
rng: np.random.Generator = np.random.default_rng(seed=seed)
az.style.use("arviz-darkgrid")
Iniziamo descrivendo le due funzioni necessarie per trovare l’area in una coda della distribuzione t (p-value) specificando i gradi di libertà e per trovare il valore critico t specificando la probabilità.
Funzione per trovare l’area in una coda della distribuzione t (p-value):
stats.t.cdf(value, df)
Per esempio, la probabilità di osservare un valore maggiore di 2.2 in una t di Student con 10 gradi di libertà è
1 - stats.t.cdf(2.2, 10)
0.026220534224676517
La probabilità di un valore minore di -2.2 in una t di Student con 10 gradi di libertà è
stats.t.cdf(-2.2, 10)
0.02622053422467655
Funzione per trovare il valore critico t (valore t per una data probabilità):
critical_value = stats.t.ppf(1 - prob, df)
Per esempio, il valore t con 10 gradi di libertà che lascia sopra di sè una probabilità di 0.026220534224676517 è
prob = 0.026220534224676517
df = 10
stats.t.ppf(1 - prob, df)
2.1999999999825763
Il valore t con 10 gradi di libertà che lascia sotto di sè una probabilità di 0.026220534224676517 è
stats.t.ppf(prob, df)
-2.1999999999825763
Esercizio 1#
Supponiamo di voler esaminare l’efficacia di un breve intervento psicologico per ridurre i livelli di stress. Un piccolo gruppo di partecipanti ha compilato un questionario di autovalutazione per misurare il loro livello di stress su una scala da 0 a 100 (dove 100 indica il massimo stress) prima di partecipare all’intervento. Dopo l’intervento, questi stessi partecipanti compilano di nuovo il questionario. Gli scienziati vogliono sapere se ci sia stata una riduzione statisticamente significativa nei livelli di stress.
Per questo esercizio, supponiamo di avere solo i dati post-intervento di 10 partecipanti. I dati sono i seguenti. Post-intervention stress levels: [45,50,35,40,50,35,30,55,40,60].
Obiettivi dell’Esercizio:#
Calcolo dell’Intervallo di Confidenza: Calcolare l’intervallo di confidenza al 95% per la media dei livelli di stress post-intervento.
Test dell’Ipotesi Nulla:
Bidirezionale: Testare se la media è significativamente diversa da 50.
Monodirezionale Destro: Testare se la media è significativamente maggiore di 50.
Monodirezionale Sinistro: Testare se la media è significativamente inferiore di 50.
Replicazione con
pingouin: Usare la libreria Pythonpingouinper replicare i test t.
Intervallo di Confidenza#
Per calcolare manualmente l’intervallo di confidenza al 95% per una media campionaria, possiamo seguire i passaggi seguenti, applicando esplicitamente le formule.
L’intervallo di confidenza per la media di una popolazione, quando la deviazione standard della popolazione non è conosciuta e il campione è piccolo, si basa sulla distribuzione t di Student. L’intervallo di confidenza si calcola con la formula:
dove:
\( \bar{x} \) è la media del campione
\( t^* \) è il valore critico t per il livello di confidenza desiderato (95% nel nostro caso), determinato dalla distribuzione t di Student con \( n-1 \) gradi di libertà
\( s \) è la deviazione standard del campione
\( n \) è la dimensione del campione
Dati.
data = np.array([45, 50, 35, 40, 50, 35, 30, 55, 40, 60])
Calcolo della media, della deviazione standard e della numerosità campionaria.
mean = np.mean(data)
std_dev = np.std(data, ddof=1) # ddof=1 per usare lo stimatore non distorto
n = len(data)
Livello di confidenza e gradi di libertà.
confidence_level = 0.95
degrees_freedom = n - 1
Trovare il valore critico t*.
t_critical = stats.t.ppf((1 + confidence_level) / 2, degrees_freedom)
print(t_critical)
2.262157162854099
Stima dell’errore standard della media dei campioni.
standard_error = std_dev / np.sqrt(n)
print(standard_error)
3.055050463303893
Calcolo dell’intervallo di confidenza.
margin_of_error = t_critical * standard_error
confidence_interval = (mean - margin_of_error, mean + margin_of_error)
print("Media del campione:", mean)
print("Deviazione standard del campione:", std_dev)
print("Errore standard del campione:", standard_error)
print("Intervallo di confidenza al 95%:", confidence_interval)
Media del campione: 44.0
Deviazione standard del campione: 9.66091783079296
Errore standard del campione: 3.055050463303893
Intervallo di confidenza al 95%: (37.088995711556365, 50.911004288443635)
Replichiamo i risultati con pingouin.
null_hypothesis_mean = 50
results = pg.ttest(x=data, y=null_hypothesis_mean, alternative="two-sided")
print(results)
T dof alternative p-val CI95% cohen-d BF10 \
T-test -1.963961 9 two-sided 0.081126 [37.09, 50.91] 0.621059 1.229
power
T-test 0.418816
In alternativa, possiamo usare la funzione stats.t.interval come indicato qui sotto:
confidence_level = 0.95
degrees_freedom = len(data) - 1
confidence_interval = stats.t.interval(
confidence_level, degrees_freedom, mean, std_dev / np.sqrt(len(data))
)
print("Media dei livelli di stress:", mean)
print("Intervallo di confidenza al 95%:", confidence_interval)
Media dei livelli di stress: 44.0
Intervallo di confidenza al 95%: (37.088995711556365, 50.911004288443635)
Test dell’ipotesi nulla#
Per svolgere manualmente il test t di Student su un campione, utilizziamo la formula standard per il calcolo della statistica t. Successivamente, discuteremo come interpretare questa statistica per i test bidirezionali, monodirezionali destro e monodirezionale sinistro.
Formula per il Test t di Student#
La formula per calcolare la statistica t è:
dove:
\( \bar{x} \) è la media del campione.
\( \mu_0 \) è la media della popolazione sotto l’ipotesi nulla.
\( s \) è la deviazione standard del campione.
\( n \) è la dimensione del campione.
Passaggi per il Calcolo#
Calcolo della statistica t.
Confronto della statistica t calcolata con il valore critico t dalla distribuzione t di Student per il livello di significatività \( \alpha \) e \( n-1 \) gradi di libertà.
Decisione sull’ipotesi nulla in base al p-value.
Calcolo in Python#
Implementiamo il test t di Student manualmente, considerando:
\( \mu_0 = 50 \) (ipotizziamo che la media della popolazione sia 50 per i test).
Livello di significatività \( \alpha = 0.05 \).
mu_0 = 50
alpha = 0.05
mean = np.mean(data)
std_dev = np.std(data, ddof=1)
n = len(data)
standard_error = std_dev / np.sqrt(n)
Calcolo della statistica t.
t_statistic = (mean - mu_0) / standard_error
print("T-statistic:", t_statistic)
T-statistic: -1.9639610121239317
Calcolo dei p-value per i diversi tipi di test.
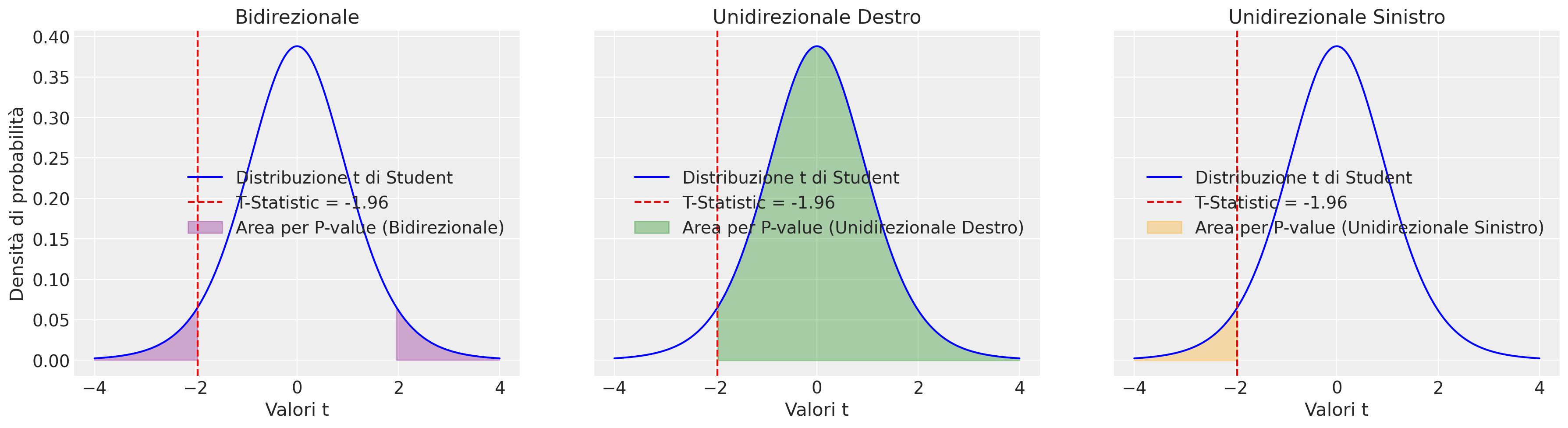
Bidirezionale.
p_value_two_tailed = stats.t.sf(np.abs(t_statistic), df=n - 1) * 2
print("P-value per il test bidirezionale:", p_value_two_tailed)
P-value per il test bidirezionale: 0.08112618884584051
Monodirezionale destro.
p_value_one_tailed_right = stats.t.sf(t_statistic, df=n - 1)
print("P-value per il test monodirezionale destro:", p_value_one_tailed_right)
P-value per il test monodirezionale destro: 0.9594369055770797
Monodirezionale sinistro.
p_value_one_tailed_left = stats.t.cdf(t_statistic, df=n - 1)
print("P-value per il test monodirezionale sinistro:", p_value_one_tailed_left)
P-value per il test monodirezionale sinistro: 0.040563094422920255
# Dati del campione
data = np.array([45, 50, 35, 40, 50, 35, 30, 55, 40, 60])
mu_0 = 50
n = len(data)
std_dev = np.std(data, ddof=1)
standard_error = std_dev / np.sqrt(n)
t_statistic = (np.mean(data) - mu_0) / standard_error
df = n - 1
# Creazione della distribuzione t
t_values = np.linspace(-4, 4, 1000)
t_distribution = stats.t.pdf(t_values, df)
# Creazione di tre subplot
fig, ax = plt.subplots(1, 3, figsize=(18, 5), sharey=True)
# Titoli per i subplot
titles = ["Bidirezionale", "Unidirezionale Destro", "Unidirezionale Sinistro"]
colors = ["purple", "green", "orange"]
# Funzione per aggiungere le aree
def plot_t_dist(ax, area, color, title):
ax.plot(t_values, t_distribution, label="Distribuzione t di Student", color="blue")
ax.axvline(
x=t_statistic,
color="red",
linestyle="--",
label=f"T-Statistic = {t_statistic:.2f}",
)
ax.fill_between(
t_values,
0,
t_distribution,
where=area(t_values),
color=color,
alpha=0.3,
label=f"Area per P-value ({title})",
)
ax.set_title(title)
ax.set_xlabel("Valori t")
ax.legend()
# Bidirezionale
plot_t_dist(ax[0], lambda t: np.abs(t) >= np.abs(t_statistic), colors[0], titles[0])
# Unidirezionale Destro
plot_t_dist(ax[1], lambda t: t >= t_statistic, colors[1], titles[1])
# Unidirezionale Sinistro
plot_t_dist(ax[2], lambda t: t <= t_statistic, colors[2], titles[2])
# Asse y comune
ax[0].set_ylabel("Densità di probabilità")
# Mostra grafico
plt.tight_layout()
plt.show()
Replichiamo ora i risultati usando pingouin.
# Dati del campione
data = np.array([45, 50, 35, 40, 50, 35, 30, 55, 40, 60])
mu_0 = 50
# Calcolo del t-test Bidirezionale
results_two_tailed = pg.ttest(x=data, y=mu_0, alternative="two-sided")
print("Risultati del Test Bidirezionale:")
print(results_two_tailed)
# Calcolo del t-test Unidirezionale Destro
results_one_tailed_right = pg.ttest(x=data, y=mu_0, alternative="greater")
print("\nRisultati del Test Unidirezionale Destro:")
print(results_one_tailed_right)
# Calcolo del t-test Unidirezionale Sinistro
results_one_tailed_left = pg.ttest(x=data, y=mu_0, alternative="less")
print("\nRisultati del Test Unidirezionale Sinistro:")
print(results_one_tailed_left)
Risultati del Test Bidirezionale:
T dof alternative p-val CI95% cohen-d BF10 \
T-test -1.963961 9 two-sided 0.081126 [37.09, 50.91] 0.621059 1.229
power
T-test 0.418816
Risultati del Test Unidirezionale Destro:
T dof alternative p-val CI95% cohen-d BF10 \
T-test -1.963961 9 greater 0.959437 [38.4, inf] 0.621059 0.407
power
T-test 0.000255
Risultati del Test Unidirezionale Sinistro:
T dof alternative p-val CI95% cohen-d BF10 \
T-test -1.963961 9 less 0.040563 [-inf, 49.6] 0.621059 2.458
power
T-test 0.567089
Interpretazione:#
Test Bidirezionale: L’ipotesi nulla viene rifiutata se il p-value è inferiore al livello di significatività \( \alpha \), indicando che la media è significativamente diversa da 50.
Test Monodirezionale Destro: L’ipotesi nulla viene rifiutata se il p-value è inferiore a \( \alpha \), indicando che la media è significativamente maggiore di 50.
Test Monodirezionale Sinistro: L’ipotesi nulla viene rifiutata se il p-value è inferiore a \( \alpha \), indicando che la media è significativamente inferiore a 50.
Questi passaggi dimostrano come eseguire manualmente il test t di Student in Python, distinguendo tra diversi tipi di test, il tutto basato su principi statistici frequentisti.
Esercizio 2#
Immagina di essere uno psicologo interessato a studiare l’effetto di due differenti tipi di terapia (A e B) sul livello di ansia dei pazienti. Hai raccolto i dati sui livelli di ansia di 10 pazienti per ciascuna terapia. I dati sono i seguenti:
Terapia A: [23, 20, 22, 21, 24, 19, 18, 20, 21, 23]
Terapia B: [27, 25, 26, 24, 28, 26, 25, 27, 26, 28]
Si richiede di:
Calcolare il test t di Student per due gruppi indipendenti assumendo che le varianze delle due popolazioni siano uguali.
Calcolare l’intervallo di confidenza del 95% per la differenza tra le due medie.
Eseguire i calcoli manualmente in Python.
Utilizzare la libreria Pingouin per confermare i risultati ottenuti.
Soluzione#
1. Calcolo del test t di Student per due gruppi indipendenti#
Iniziamo con i calcoli manuali. Dobbiamo calcolare la media, la varianza e la deviazione standard per ciascun gruppo, quindi utilizzare queste informazioni per calcolare il valore del test t.
# Dati
terapia_A = np.array([23, 20, 22, 21, 24, 19, 18, 20, 21, 23])
terapia_B = np.array([27, 25, 26, 24, 28, 26, 25, 27, 26, 28])
# Calcolo delle medie
mean_A = np.mean(terapia_A)
mean_B = np.mean(terapia_B)
# Calcolo delle varianze
var_A = np.var(terapia_A, ddof=1)
var_B = np.var(terapia_B, ddof=1)
# Calcolo della varianza combinata
n_A = len(terapia_A)
n_B = len(terapia_B)
pooled_var = ((n_A - 1) * var_A + (n_B - 1) * var_B) / (n_A + n_B - 2)
# Calcolo dell'errore standard della differenza delle medie
se = np.sqrt(pooled_var * (1 / n_A + 1 / n_B))
# Calcolo del valore t
t_stat = (mean_A - mean_B) / se
# Gradi di libertà
df = n_A + n_B - 2
# P-value
p_value = 2 * stats.t.cdf(-abs(t_stat), df)
# Intervallo di confidenza del 95%
ci = stats.t.interval(0.95, df, loc=(mean_A - mean_B), scale=se)
# Output dei risultati
print(f"Media Terapia A: {mean_A}")
print(f"Media Terapia B: {mean_B}")
print(f"Varianza Terapia A: {var_A}")
print(f"Varianza Terapia B: {var_B}")
print(f"Varianza combinata: {pooled_var}")
print(f"Errore standard: {se}")
print(f"Valore t: {t_stat}")
print(f"P-value: {p_value}")
print(f"Intervallo di confidenza al 95%: {ci}")
Media Terapia A: 21.1
Media Terapia B: 26.2
Varianza Terapia A: 3.6555555555555554
Varianza Terapia B: 1.7333333333333334
Varianza combinata: 2.6944444444444446
Errore standard: 0.7340905181848414
Valore t: -6.947372120553443
P-value: 1.7185095025904068e-06
Intervallo di confidenza al 95%: (-6.642266949186438, -3.5577330508135576)
2. Calcolo utilizzando Pingouin#
Utilizziamo la libreria Pingouin per confermare i risultati ottenuti.
# Creazione del DataFrame
data = pd.DataFrame(
{
"gruppo": ["A"] * n_A + ["B"] * n_B,
"ansia": np.concatenate([terapia_A, terapia_B]),
}
)
# Esecuzione del test t
test_t = pg.ttest(
data[data["gruppo"] == "A"]["ansia"],
data[data["gruppo"] == "B"]["ansia"],
correction=False,
)
# Output dei risultati
print(test_t)
T dof alternative p-val CI95% cohen-d \
T-test -6.947372 18 two-sided 0.000002 [-6.64, -3.56] 3.106959
BF10 power
T-test 6649.934 0.999998
I risultati ottenuti da Pingouin confermano i valori calcolati manualmente, mostrando un valore t simile, un p-value molto basso e un intervallo di confidenza che non include zero, confermando che la differenza tra le due terapie è degna di nota.
Esercizio 3#
Modello di regressione.
Predire il punteggio di stress (y) considerando un numero di ore di sonno (x) pari a 7, dopo aver fittato un modello di regressione lineare ai dati.
# Dati ipotetici
data = {
"Ore_sonno": [6, 7, 8, 5, 7, 6, 8, 7, 5, 6],
"Punteggio_stress": [70, 65, 60, 75, 64, 68, 62, 66, 74, 69],
}
df = pd.DataFrame(data)
print(df)
Ore_sonno Punteggio_stress
0 6 70
1 7 65
2 8 60
3 5 75
4 7 64
5 6 68
6 8 62
7 7 66
8 5 74
9 6 69
# Esegui la regressione lineare
reg = pg.linear_regression(df[["Ore_sonno"]], df["Punteggio_stress"])
print(reg)
names coef se T pval r2 \
0 Intercept 96.085714 2.052359 46.817209 4.789361e-11 0.961834
1 Ore_sonno -4.428571 0.311896 -14.198887 5.892825e-07 0.961834
adj_r2 CI[2.5%] CI[97.5%]
0 0.957063 91.352966 100.818462
1 0.957063 -5.147804 -3.709339
# Predici il punteggio di stress per un numero specifico di ore di sonno
ore_sonno_nuove = 7
y_pred = reg["coef"][0] + reg["coef"][1] * ore_sonno_nuove
print(f"Punteggio di stress predetto per {ore_sonno_nuove} ore di sonno: {y_pred}")
Punteggio di stress predetto per 7 ore di sonno: 65.08571428571426
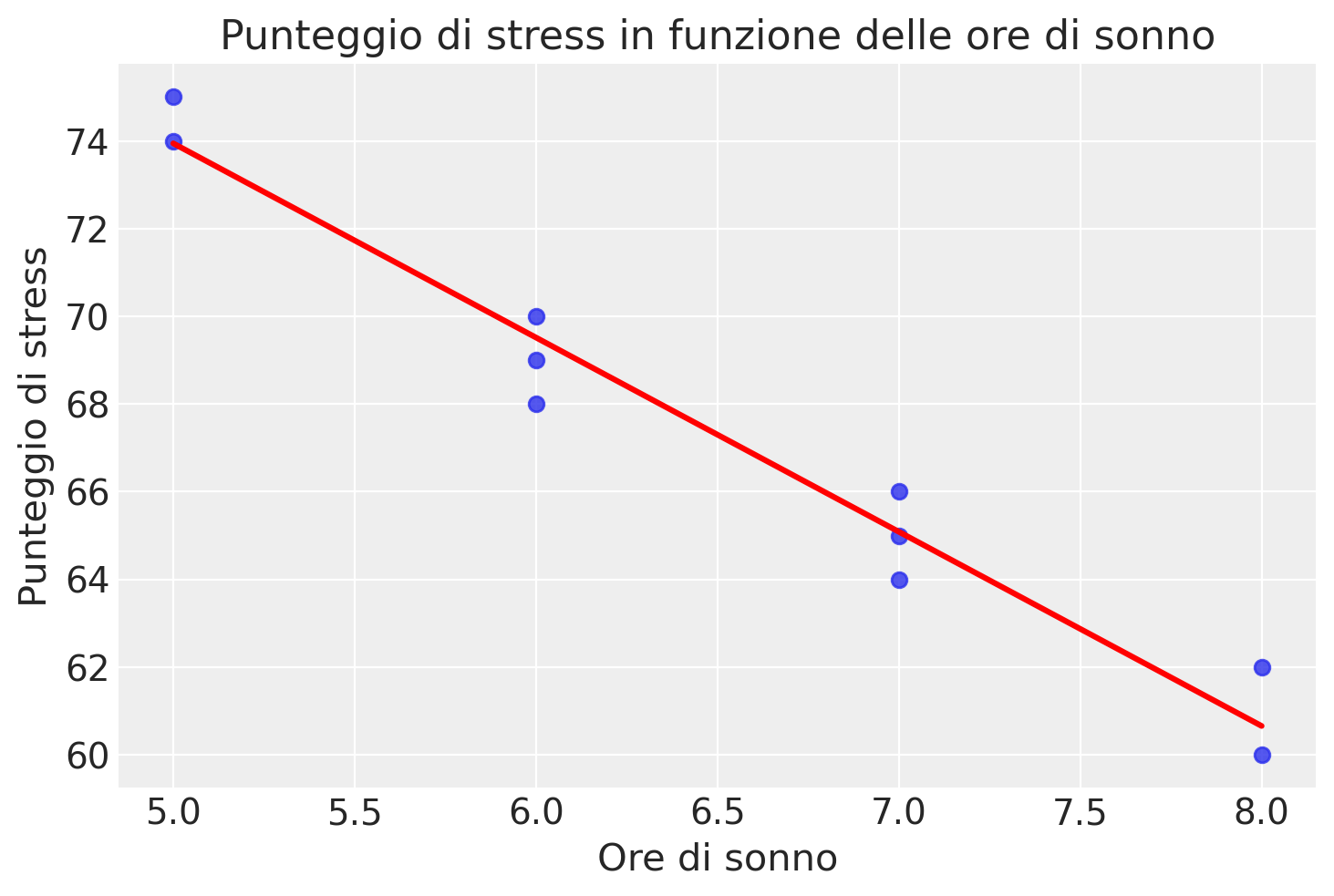
sns.regplot(
x="Ore_sonno", y="Punteggio_stress", data=df, ci=None, line_kws={"color": "red"}
)
plt.xlabel("Ore di sonno")
plt.ylabel("Punteggio di stress")
plt.title("Punteggio di stress in funzione delle ore di sonno")
plt.show()
Interpretare il coefficiente b.
Calcolare il valore predetto di stress in corrispondenza del numero medio di ore di sonno.
df["Ore_centrate"] = df["Ore_sonno"] - np.mean(df["Ore_sonno"])
reg = pg.linear_regression(df[["Ore_centrate"]], df["Punteggio_stress"])
print(reg)
names coef se T pval r2 \
0 Intercept 67.300000 0.319598 210.577063 2.894993e-16 0.961834
1 Ore_centrate -4.428571 0.311896 -14.198887 5.892825e-07 0.961834
adj_r2 CI[2.5%] CI[97.5%]
0 0.957063 66.563006 68.036994
1 0.957063 -5.147804 -3.709339
Esercizio 4#
Per i dati seguenti, trovare il valore predetto dello stress per un uomo che dorme 7 ore.
# Dati ipotetici
data = {
"Ore_sonno": [6, 7, 8, 5, 7, 6, 8, 7, 5, 6],
"Punteggio_stress": [
70,
80,
68,
85,
64,
90,
65,
66,
85,
95,
], # Stress più alto per le donne (genere=0)
"Genere": [1, 0, 1, 0, 1, 0, 0, 1, 1, 0], # 1 = uomo, 0 = donna
}
df = pd.DataFrame(data)
print(df)
Ore_sonno Punteggio_stress Genere
0 6 70 1
1 7 80 0
2 8 68 1
3 5 85 0
4 7 64 1
5 6 90 0
6 8 65 0
7 7 66 1
8 5 85 1
9 6 95 0
# Aggiungi l'interazione tra ore di sonno e genere
df["Interazione"] = df["Ore_sonno"] * df["Genere"]
# Esegui la regressione lineare
reg = pg.linear_regression(
df[["Ore_sonno", "Genere", "Interazione"]], df["Punteggio_stress"]
)
# Mostra i risultati della regressione
print(reg)
names coef se T pval r2 adj_r2 \
0 Intercept 133.461538 20.212810 6.602820 0.000580 0.745727 0.618591
1 Ore_sonno -7.884615 3.118904 -2.528008 0.044800 0.745727 0.618591
2 Genere -23.769231 29.024249 -0.818944 0.444121 0.745727 0.618591
3 Interazione 1.961538 4.410797 0.444713 0.672120 0.745727 0.618591
CI[2.5%] CI[97.5%]
0 84.002574 182.920503
1 -15.516299 -0.252931
2 -94.789011 47.250549
3 -8.831292 12.754369
# Predici il punteggio di stress per un individuo specifico
ore_sonno_nuove = 7
genere_nuovo = 1 # 1 = uomo, 0 = donna
interazione_nuova = ore_sonno_nuove * genere_nuovo
y_pred = (
reg["coef"][0]
+ reg["coef"][1] * ore_sonno_nuove
+ reg["coef"][2] * genere_nuovo
+ reg["coef"][3] * interazione_nuova
)
print(
f"Punteggio di stress predetto per {ore_sonno_nuove} ore di sonno e genere {'uomo' if genere_nuovo == 1 else 'donna'}: {y_pred}"
)
Punteggio di stress predetto per 7 ore di sonno e genere uomo: 68.23076923076923
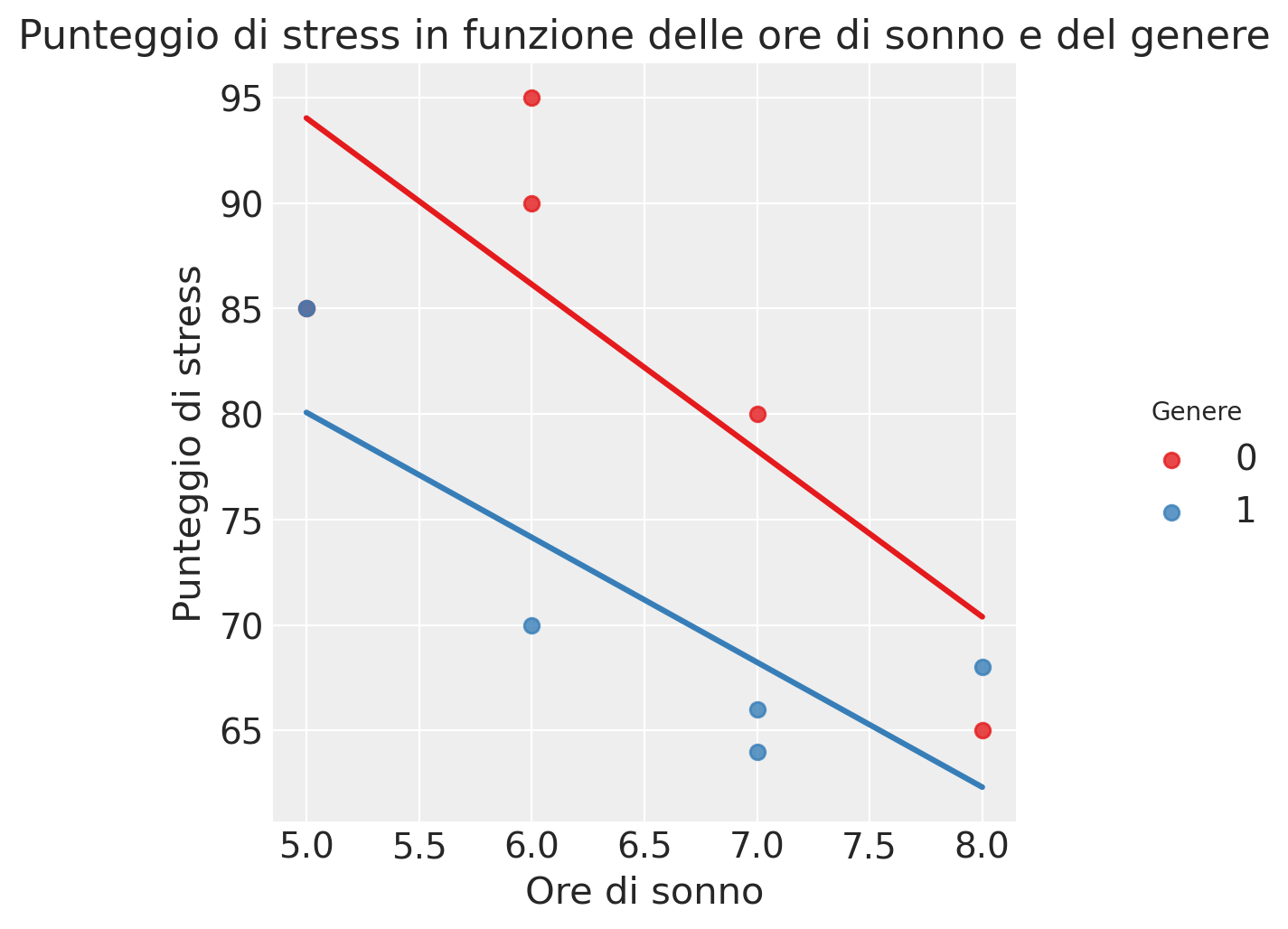
# Crea una visualizzazione della regressione separata per genere
sns.lmplot(
x="Ore_sonno", y="Punteggio_stress", hue="Genere", data=df, ci=None, palette="Set1"
)
plt.xlabel("Ore di sonno")
plt.ylabel("Punteggio di stress")
plt.title(
"Punteggio di stress in funzione delle ore di sonno e del genere"
)
plt.show()
Informazioni sull’Ambiente di Sviluppo#
%load_ext watermark
%watermark -n -u -v -iv -w -m
Last updated: Sun Jun 16 2024
Python implementation: CPython
Python version : 3.12.3
IPython version : 8.25.0
Compiler : Clang 16.0.6
OS : Darwin
Release : 23.4.0
Machine : arm64
Processor : arm
CPU cores : 8
Architecture: 64bit
matplotlib: 3.8.4
arviz : 0.18.0
numpy : 1.26.4
pingouin : 0.5.4
seaborn : 0.13.2
pandas : 2.2.2
scipy : 1.13.1
Watermark: 2.4.3