✏️ Esercizi

Preparazione del Notebook

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
import arviz as az
from scipy import stats
from scipy.integrate import trapz

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

Esempio 1

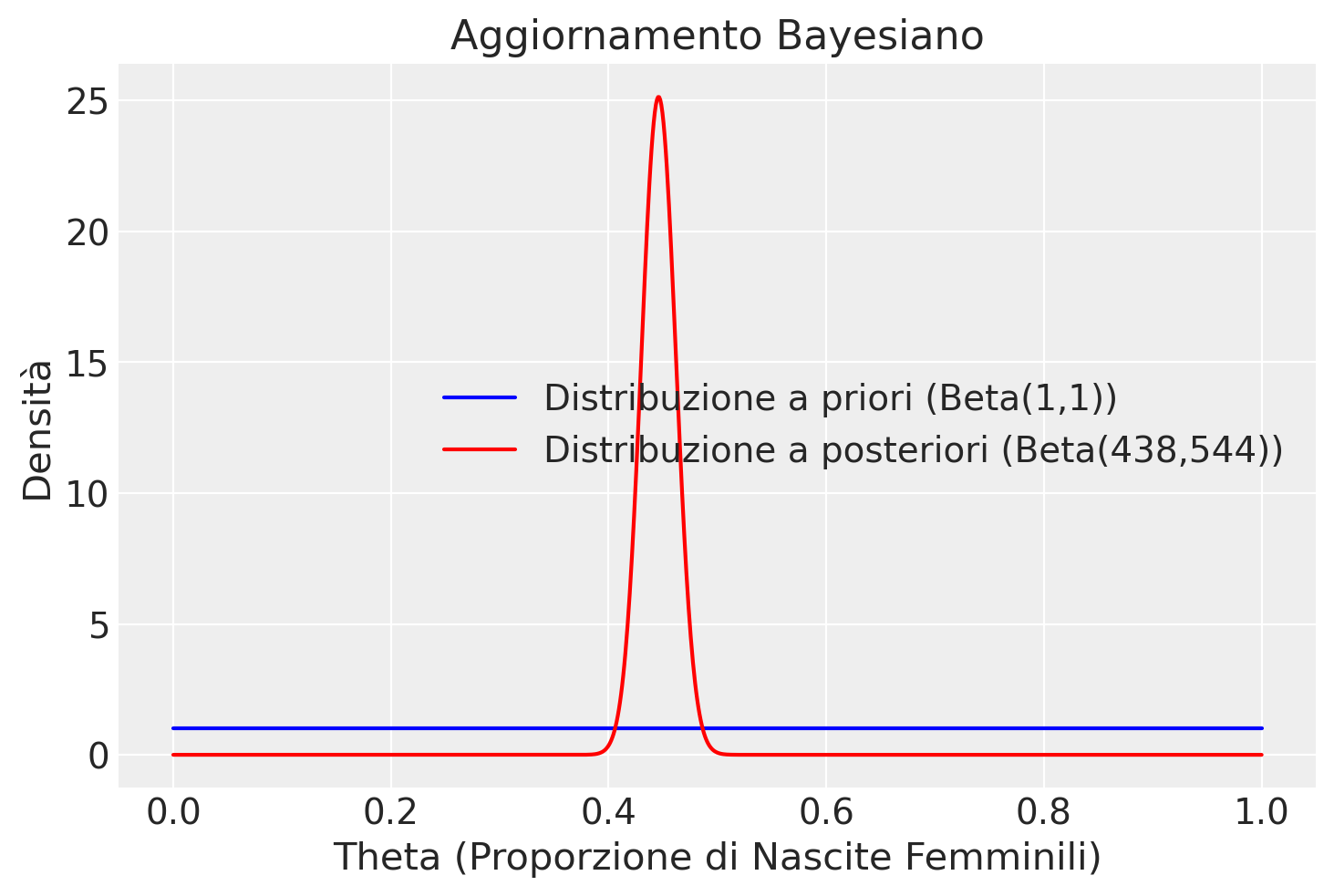
Uno studio ha esaminato un totale di 980 nascite, tra le quali 437 sono state femmine []. Per determinare la distribuzione a posteriori della proporzione di femmine, indicata con \( \theta \), si è assunta una distribuzione a priori uniforme. Questo implica l’uso di una distribuzione Beta come prior, specificatamente \( Beta(\alpha = 1, \beta = 1) \), che è equivalente a una distribuzione uniforme.

I dati specifici del problema sono: \( y = 437 \) femmine su \( n = 980 \) nascite totali. Applicando il teorema delle famiglie coniugate beta-binomiali, possiamo aggiornare i parametri della distribuzione Beta a priori con i dati osservati. La distribuzione a posteriori sarà quindi anch’essa una distribuzione Beta, ma con parametri aggiornati: \( \alpha' = \alpha + y = 1 + 437 = 438 \) e \( \beta' = \beta + n - y = 1 + 980 - 437 = 544 \). Quindi, la distribuzione a posteriori della proporzione di femmine \( \theta \) è descritta dalla distribuzione \( Beta(438, 544) \).

Show code cell source Hide code cell source

# Parameters for prior and posterior
alpha_prior, beta_prior = 1, 1
y, n = 437, 980
alpha_posterior, beta_posterior = alpha_prior + y, beta_prior + n - y

# Theta values for plotting
theta_values = np.linspace(0, 1, 1000)

# Prior Distribution (Beta(1,1) - Uniform)
prior_distribution = stats.beta(alpha_prior, beta_prior).pdf(theta_values)

# Posterior Distribution (Beta(438,544))
posterior_distribution = stats.beta(alpha_posterior, beta_posterior).pdf(theta_values)

plt.plot(
    theta_values,
    prior_distribution,
    label="Distribuzione a priori (Beta(1,1))",
    color="blue",
)
plt.plot(
    theta_values,
    posterior_distribution,
    label="Distribuzione a posteriori (Beta(438,544))",
    color="red",
)

plt.title("Aggiornamento Bayesiano")
plt.xlabel("Theta (Proporzione di Nascite Femminili)")
plt.ylabel("Densità")
plt.legend()

<matplotlib.legend.Legend at 0x145e41b20>

Esempio 2

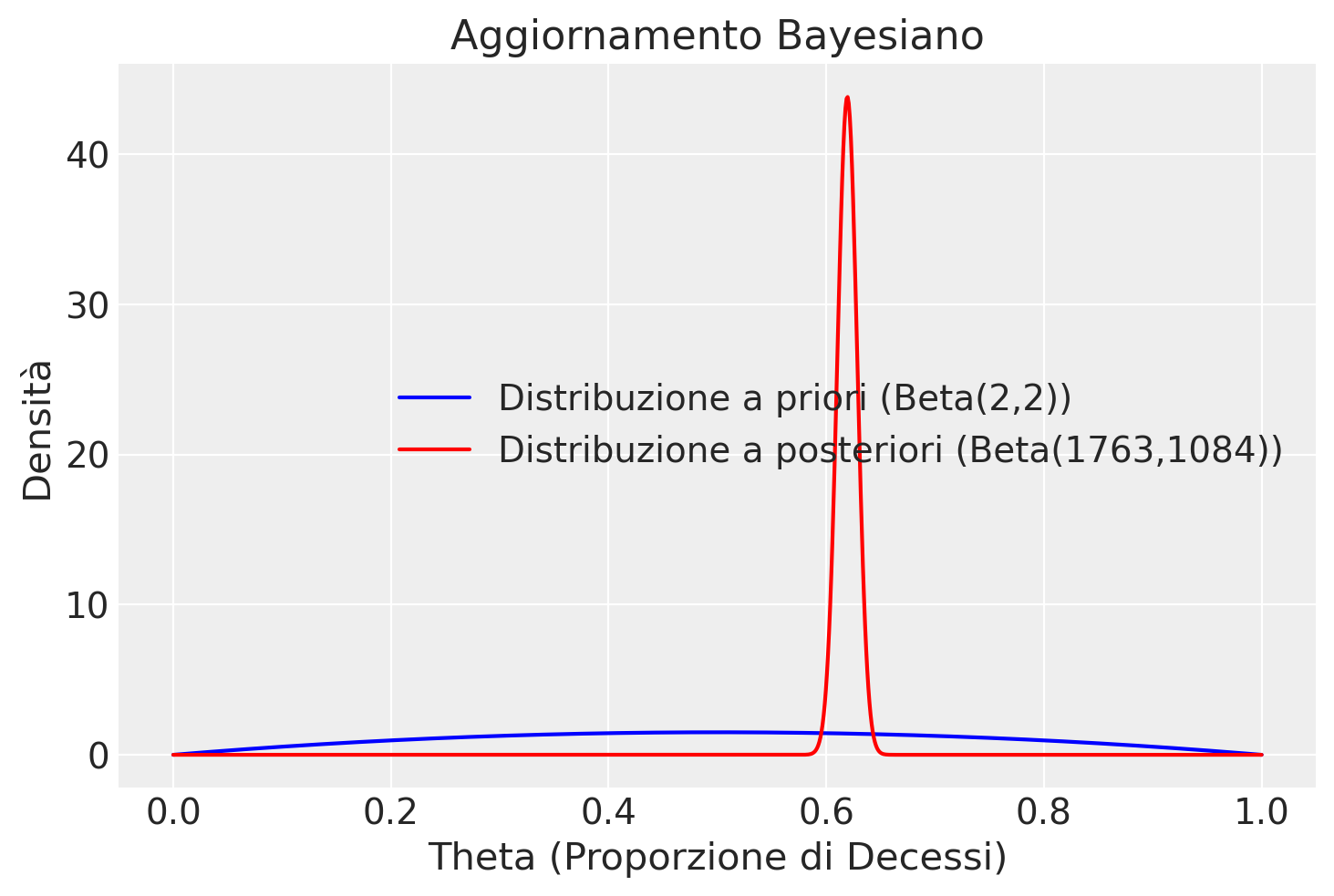
Nel nostro secondo esempio, analizzeremo i dati relativi all’AIDS forniti dall“«Australian National Centre in HIV Epidemiology and Clinical Research». Questi dati sono inclusi nel pacchetto R denominato MASS e sono raccolti nel DataFrame «Aids2». Questo dataset documenta i casi di individui diagnosticati con l’AIDS prima del 1° luglio 1991. In totale, sono stati registrati 2843 casi, di cui 1082 individui erano ancora in vita e 1761 erano deceduti fino a quella data. Il nostro obiettivo analitico è di esaminare il tasso di mortalità associato all’AIDS.

Considerando i casi come eventi indipendenti, i dati osservati (sopravvissuti \(y = 1082\)) possono essere trattati come una successione di esiti Bernoulliani. Di conseguenza, la funzione di verosimiglianza può essere modellata con una distribuzione binomiale. Adottando una distribuzione a priori Beta debolmente informativa, con parametri \( \alpha = 2 \) e \( \beta = 2 \), otteniamo che la distribuzione a posteriori sarà anch’essa una Beta, ma con parametri aggiornati, ovvero \( \alpha' = 2 + 1761 \) e \( \beta' = 2 + 2843 - 1761 \). In termini numerici, ciò corrisponde a una distribuzione Beta(1763, 1084), fornendoci un aggiornamento basato sui dati osservati e le informazioni a priori per comprendere meglio il tasso di mortalità tra i pazienti con AIDS.

Show code cell source Hide code cell source

# Parameters for prior and posterior in the AIDS example
alpha_prior, beta_prior = 2, 2
deaths, total_cases = 1761, 2843
survivors = total_cases - deaths
alpha_posterior, beta_posterior = alpha_prior + deaths, beta_prior + survivors

# Theta values for plotting
theta_values = np.linspace(0, 1, 1000)

# Prior Distribution (Beta(2,2))
prior_distribution = stats.beta(alpha_prior, beta_prior).pdf(theta_values)

# Posterior Distribution (Beta(1763,1084))
posterior_distribution = stats.beta(alpha_posterior, beta_posterior).pdf(theta_values)

plt.plot(
    theta_values,
    prior_distribution,
    label="Distribuzione a priori (Beta(2,2))",
    color="blue",
)
plt.plot(
    theta_values,
    posterior_distribution,
    label="Distribuzione a posteriori (Beta(1763,1084))",
    color="red",
)

plt.title("Aggiornamento Bayesiano")
plt.xlabel("Theta (Proporzione di Decessi)")
plt.ylabel("Densità")
plt.legend()

<matplotlib.legend.Legend at 0x145ec59d0>

La distribuzione a priori

Nell’esempio che riguarda la sopravvivenza dei pazienti con AIDS, la scelta di una distribuzione Beta come prior nel nostro modello bayesiano ci permette di quantificare le credenze iniziali riguardo a \( \theta \), la probabilità di decesso. Adottando una distribuzione a priori \( Beta(\alpha = 2, \beta = 2) \) per \( \theta \), esprimiamo una convinzione iniziale di sostanziale incertezza circa l’esito «sopravvivenza post-diagnosi di AIDS» nel 1991. Questa scelta riflette la nostra assunzione che il punto di massima verosimiglianza per \( \theta \) sia 0.5, indicando una situazione di equilibrio tra sopravvivenza e decesso. Tuttavia, questa assunzione non esclude la plausibilità di altri valori di \( \theta \), ad eccezione degli estremi, conferendo flessibilità e apertura alle nostre credenze iniziali sull’incertezza dell’evento.

Un sommario della distribuzione \(Beta(alpha=2, beta=2)\) si ottiene usando la funzione seguente:

def summarize_beta(alpha, beta):
    """Summarize a Beta Model for \eqn{\pi}

    @param alpha,beta positive shape parameters of the Beta model

    Return Pandas Series with summary
    """

    mean = alpha / (alpha + beta)
    var = alpha * beta / ((alpha + beta) ** 2 * (alpha + beta + 1))
    sd = np.sqrt(var)

    if alpha < 1 and beta < 1:
        mode = "0 and 1"
    elif alpha <= 1 and beta > 1:
        mode = 0
    elif alpha > 1 and beta < 1:
        mode = 1
    else:
        mode = (alpha - 1) / (alpha + beta - 2)
    return pd.Series({"mean": mean, "mode": mode, "var": var, "sd": sd})

<>:2: SyntaxWarning: invalid escape sequence '\e'
<>:2: SyntaxWarning: invalid escape sequence '\e'
/var/folders/s7/z86r4t9j6yx376cm120nln6w0000gn/T/ipykernel_33341/1540732752.py:2: SyntaxWarning: invalid escape sequence '\e'
  """Summarize a Beta Model for \eqn{\pi}

summarize_beta(alpha=2, beta=2)

mean    0.500000
mode    0.500000
var     0.050000
sd      0.223607
dtype: float64

Possiamo quantificare la nostra incertezza calcolando, con un grado di fiducia soggettiva del 94%, la regione nella quale, in base a tale credenza a priori, si trova il valore del parametro. Per ottenere tale intervallo di credibilità a priori, usiamo la funzione beta.ppf di scipy.stats.

li = stats.beta.ppf(0.03, 2, 2)
ls = stats.beta.ppf(0.97, 2, 2)
list([li, ls])

[0.10364483924951279, 0.8963551607504872]

Se poniamo \(\alpha=10\) e \(\beta=10\), anche questa scelta descrive una credenza a priori per la quale il valore più credibile per \(\theta\) è 0.5.

Show code cell source Hide code cell source

# Crea un array di valori di theta
theta = np.linspace(0, 1, 1000)
pdf_pre = stats.beta.pdf(theta, 10, 10)
plt.plot(theta, pdf_pre, label=r'$\alpha=10$, $\beta=10$')
plt.xlabel(r'$\theta$')
plt.ylabel('Densità di probabilità')
plt.title('Distribuzione Beta')
plt.legend()

<matplotlib.legend.Legend at 0x145ea5f40>

Tuttavia, in questo caso la nostra incertezza a priori sul valore del parametro è minore, come indicato dall’intervallo di credibilità ordine 0.94.

li = stats.beta.ppf(0.03, 10, 10)
ls = stats.beta.ppf(0.97, 10, 10)
list([li, ls])

[0.2964110284916252, 0.7035889715083747]

La scelta di una distribuzione a priori in un’analisi dati pratica dipende dalle credenze iniziali che desideriamo integrare nell’analisi. Quando non disponiamo di informazioni a priori specifiche, potremmo essere tentati di selezionare \( \alpha=1 \) e \( \beta=1 \), che equivalgono a una distribuzione a priori uniforme. Questa scelta suggerisce che tutti i possibili valori del parametro sono considerati ugualmente probabili. Tuttavia, vi sono alcune riserve sull’uso di distribuzioni a priori uniformi, tra cui questioni di instabilità numerica nella stima dei parametri. In contesti dove le informazioni a priori sono limitate o assenti, è generalmente consigliabile optare per una distribuzione a priori debolmente informativa, quale la \( Beta(2, 2) \). Questa distribuzione permette una certa flessibilità, pur fornendo un’informazione iniziale che aiuta a stabilizzare le stime dei parametri.

La distribuzione a posteriori

Una volta scelta una distribuzione a priori \(Beta(2, 2)\), i cui parametri rispecchiano le nostre credenze iniziali su \(\theta\), la distribuzione a posteriori diventa una Beta di parametri \(\alpha + y\) e \(\beta + n - y\). Per i dati dell’esempio sulla sopravvivenza dei pazienti con AIDS, otteniamo la distribuzione a posteriori \(p(\theta \mid n, y) \sim Beta(1763, 1084)\).

Essendo \(\mathbb{E}[Beta(\alpha, \beta)] = \frac{\alpha}{\alpha + \beta}\), il valore atteso a posteriori di \(\theta\) può essere calcolato come:

(46)\[ \mathbb{E}_{\text{post}} [\mathrm{Beta}(\alpha + y, \beta + n - y)] = \frac{\alpha + y}{\alpha + \beta +n}. \]

Nel caso in cui la distribuzione a priori è debolmente informativa e il campione è molto grande, la distribuzione a priori esercita un effetto trascurabile sulla distribuzione a posteriori.

Esaminiamo le caratteristiche della distribuzione a posteriori.

summarize_beta(1763, 1084)

mean    0.619248
mode    0.619332
var     0.000083
sd      0.009099
dtype: float64

li = stats.beta.ppf(0.03, 1763, 1084)
ls = stats.beta.ppf(0.97, 1763, 1084)
list([li, ls])

[0.6020654882558295, 0.6362894604661353]

Utilizzando il metodo della massima verosimiglianza, il tasso di mortalità stimato è \(\theta = 1761/2843 = 0.62\), con un errore standard (SE) di \(\sqrt{0.62(1−0.62)/n} = 0.0091\) e un intervallo di confidenza al 95% di [0.6, 0.63], che è simile all’intervallo ottenuto con l’inferenza bayesiana.

[.62 - stats.norm.ppf(0.97) * 0.0091, .62 + stats.norm.ppf(0.97) * 0.0091]

[0.6028847781658236, 0.6371152218341763]

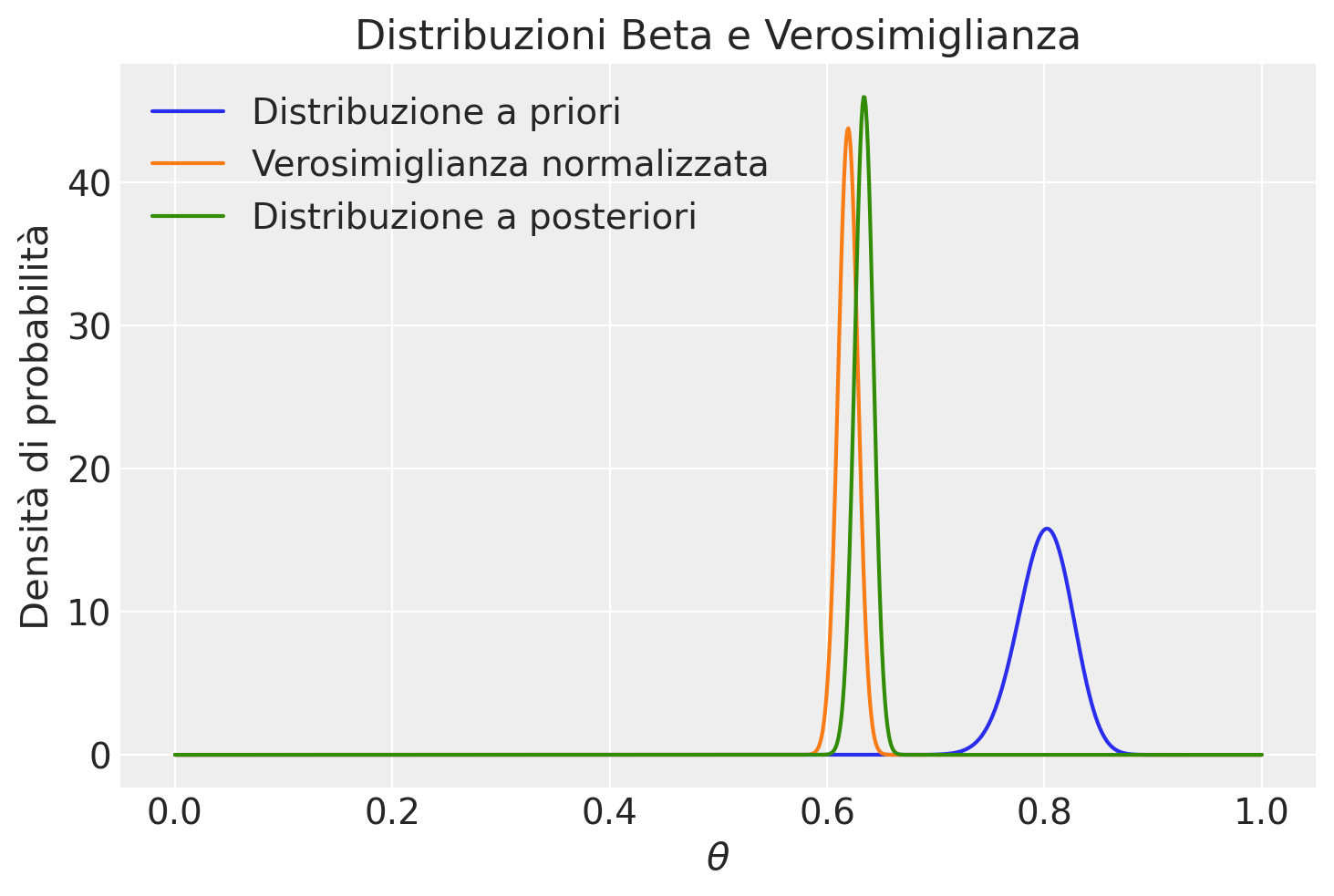
Perché una distribuzione a priori eserciti un impatto significativo sull’analisi, è importante che sia informativa e possibilmente in contrasto con i dati osservati. Ad esempio, scegliere una distribuzione a priori come Beta(200, 5) introduce una convinzione pre-esistente molto forte nel modello. Questa scelta implica una forte presunzione iniziale verso valori elevati del parametro di interesse, potenzialmente in disaccordo con i dati raccolti. Una distribuzione a priori di questo tipo può essere utilizzata per testare l’influenza delle credenze fortemente radicate rispetto ai dati effettivi, o in situazioni dove si dispone di una solida base di conoscenze a priori che si prevede possa differire significativamente dalle informazioni emergenti dai dati.

y = 1761
n = 2843

# Parametri delle distribuzioni beta
alpha_pre = 200
beta_pre = 50

alpha_post = alpha_pre + y
beta_post = beta_pre + n - y

# Calcola i valori delle distribuzioni beta
pdf_pre = stats.beta.pdf(theta, alpha_pre, beta_pre)
pdf_post = stats.beta.pdf(theta, alpha_post, beta_post)

# Calcola la log-verosimiglianza
log_likelihood = y * np.log(theta) + (n - y) * np.log(1 - theta)

# Scala la log-verosimiglianza per evitare valori molto piccoli
scaled_log_likelihood = log_likelihood - np.max(log_likelihood)

# Calcola la verosimiglianza normalizzata
normalized_likelihood = np.exp(scaled_log_likelihood)
normalized_likelihood /= np.trapz(normalized_likelihood, theta)

# Crea il grafico
plt.plot(theta, pdf_pre, label=r'Distribuzione a priori')
plt.plot(theta, normalized_likelihood, label=r'Verosimiglianza normalizzata')
plt.plot(theta, pdf_post, label=r'Distribuzione a posteriori')
plt.xlabel(r'$\theta$')
plt.ylabel('Densità di probabilità')
plt.title('Distribuzioni Beta e Verosimiglianza')
plt.legend()

/var/folders/s7/z86r4t9j6yx376cm120nln6w0000gn/T/ipykernel_33341/2248146963.py:16: RuntimeWarning: divide by zero encountered in log
  log_likelihood = y * np.log(theta) + (n - y) * np.log(1 - theta)

<matplotlib.legend.Legend at 0x147121610>

li = stats.beta.ppf(0.03, 1763, 1084)
ls = stats.beta.ppf(0.97, 1763, 1084)
list([li, ls])

[0.6020654882558295, 0.6362894604661353]

La ricerca sull’obbedienza di Milgram

Consideriamo un altro esempio relativo alla ricerca di Stanley Milgram discussa da . Nel 1963, Stanley Milgram presentò una ricerca sulla propensione delle persone a obbedire agli ordini di figure di autorità, anche quando tali ordini possono danneggiare altre persone . Nell’articolo, Milgram descrive lo studio come

consisting of ordering a naive subject to administer electric shock to a victim. A simulated shock generator is used, with 30 clearly marked voltage levels that range from IS to 450 volts. The instrument bears verbal designations that range from Slight Shock to Danger: Severe Shock. The responses of the victim, who is a trained confederate of the experimenter, are standardized. The orders to administer shocks are given to the naive subject in the context of a «learning experiment» ostensibly set up to study the effects of punishment on memory. As the experiment proceeds the naive subject is commanded to administer increasingly more intense shocks to the victim, even to the point of reaching the level marked Danger: Severe Shock.

All’insaputa del partecipante, gli shock elettrici erano falsi e l’attore stava solo fingendo di provare il dolore dello shock.

fanno inferenza sui risultati dello studio di Milgram mediante il modello Beta-Binomiale. Il parametro di interesse è la probabilità \(\theta\) che una persona obbedisca all’autorità, anche se ciò comporta il rischio di recare danno ad altri, in questo caso somministrando lo shock più severo. Gli autori ipotizzano che, prima di raccogliere dati, le credenze di Milgram riguardo a \(\theta\) possano essere rappresentate mediante una distribuzione Beta con parametri \(\alpha=1\) e \(\beta=10\).

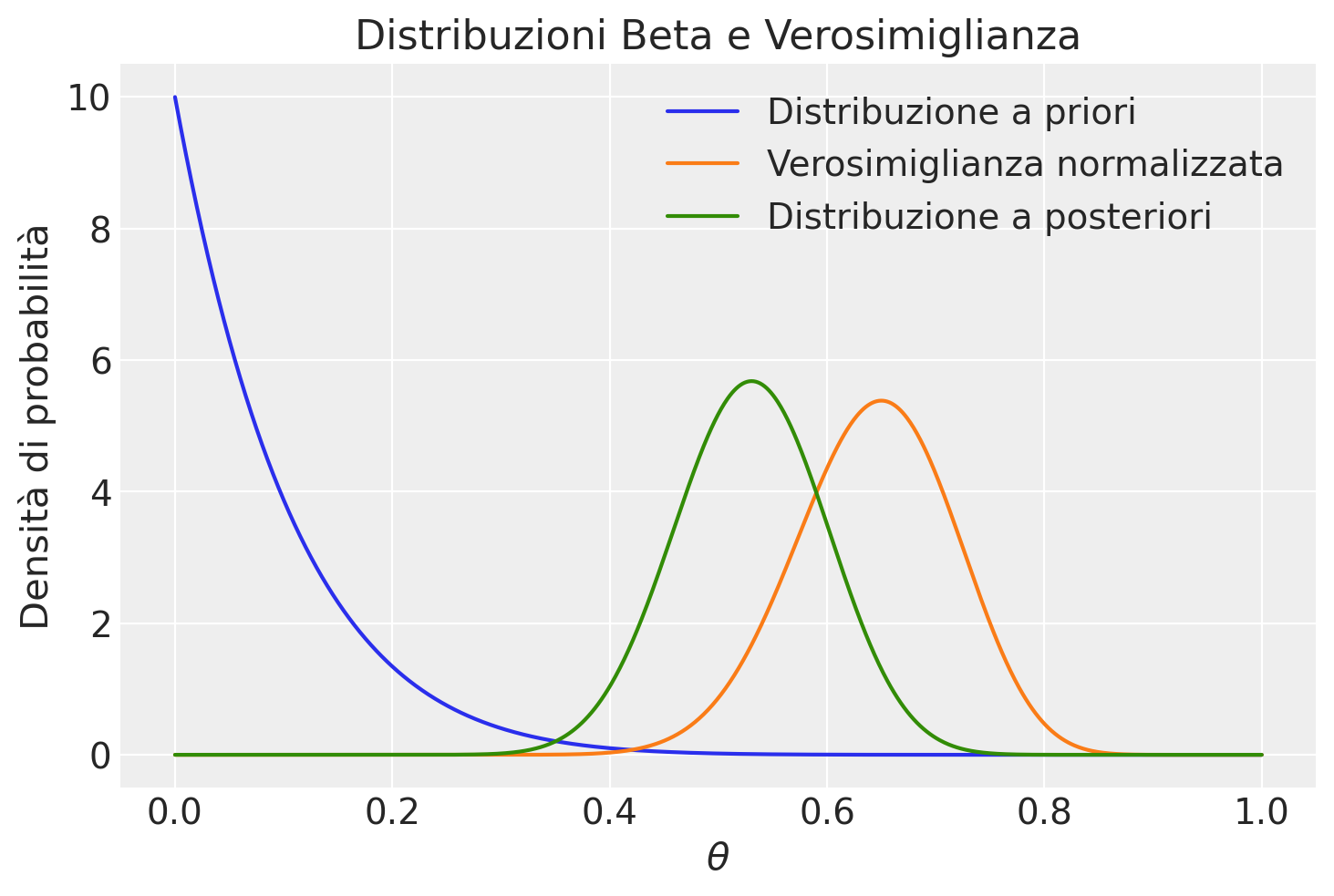
Sia \(y = 26\) il numero di soggetti, su un totale di 40 partecipanti, che hanno accettato di infliggere lo shock più severo. Poiché si assume che ciascun partecipante si comporti in modo indipendente dagli altri, la dipendenza di \(y\) da \(\theta\) può essere modellata mediante la distribuzione binomiale. Di conseguenza, si giunge al seguente modello bayesiano Beta-Binomiale:

\[\begin{split} \begin{align} y \mid \theta & \sim \text{Bin}(n = 40, \theta) \notag\\ \theta & \sim \text{Beta}(1, 10) \; . \notag \end{align} \end{split}\]

Il processo di aggiornamento bayesiano è descritto dalla figura ottenuta con la funzione plot_beta_binomial().

y = 26
n = 40

# Parametri delle distribuzioni beta
alpha_pre = 1
beta_pre = 10

alpha_post = alpha_pre + y
beta_post = beta_pre + n - y

# Calcola i valori delle distribuzioni beta
pdf_pre = stats.beta.pdf(theta, alpha_pre, beta_pre)
pdf_post = stats.beta.pdf(theta, alpha_post, beta_post)

# Calcola la log-verosimiglianza
log_likelihood = y * np.log(theta) + (n - y) * np.log(1 - theta)

# Scala la log-verosimiglianza per evitare valori molto piccoli
scaled_log_likelihood = log_likelihood - np.max(log_likelihood)

# Calcola la verosimiglianza normalizzata
normalized_likelihood = np.exp(scaled_log_likelihood)
normalized_likelihood /= np.trapz(normalized_likelihood, theta)

# Crea il grafico
plt.plot(theta, pdf_pre, label=r'Distribuzione a priori')
plt.plot(theta, normalized_likelihood, label=r'Verosimiglianza normalizzata')
plt.plot(theta, pdf_post, label=r'Distribuzione a posteriori')
plt.xlabel(r'$\theta$')
plt.ylabel('Densità di probabilità')
plt.title('Distribuzioni Beta e Verosimiglianza')
plt.legend();

/var/folders/s7/z86r4t9j6yx376cm120nln6w0000gn/T/ipykernel_33341/431063134.py:16: RuntimeWarning: divide by zero encountered in log
  log_likelihood = y * np.log(theta) + (n - y) * np.log(1 - theta)

li = stats.beta.ppf(0.03, 1 + 26, 10 + 40 - 26)
ls = stats.beta.ppf(0.97, 1 + 26, 10 + 40 - 26)
list([li, ls])

[0.3986201110959706, 0.6582462555099745]

Pertanto, possiamo giungere a una conclusione soggettiva con un livello di probabilità del 94% che una proporzione di soggetti compresa tra il 40% e il 66% seguirà le istruzioni di un’autorità, nonostante queste istruzioni comportino evidenti danni ai propri compagni.

Dieci Lanci di Una Moneta

Immaginiamo di eseguire dieci lanci di una moneta, ottenendo croce ogni volta. Mentre un statistico frequentista stimerebbe la probabilità di ottenere testa come \(0\), un approccio bayesiano offre una visione più ricca incorporando informazioni a priori e aggiornando tali credenze con i dati osservati.

Supponiamo di non avere ragioni per credere che la moneta sia truccata e quindi descriviamo le nostre credenze a priori tramite una distribuzione Beta(2,2). Questo suggerisce una moderata inclinazione verso una moneta bilanciata anziché sbilanciata, senza preferenze esplicite per testa o croce.

Dopo aver osservato 0 teste in 10 lanci, la verosimiglianza dei dati sotto il modello binomiale è \(L(p) = (1-p)^{10}\). Utilizzando la formula di Bayes, aggiorniamo la nostra distribuzione a posteriori, ottenendo una distribuzione Beta con parametri aggiornati: Beta(\(\alpha + x\), \(\beta + n - x\)), dove \(\alpha = 2\), \(\beta = 2\), \(x = 0\) (il numero di teste osservate), e \(n = 10\) (il numero totale di lanci).

Quindi, la nostra distribuzione a posteriori diventa Beta(2,12). Questa distribuzione ha una funzione di densità di probabilità data da:

\[\pi(p|x) = \frac{\Gamma(14)}{\Gamma(2)\Gamma(12)}p^{2-1}(1-p)^{12-1},\]

dove \(\Gamma\) è la funzione gamma, una generalizzazione del fattoriale.

Il valore atteso di una distribuzione Beta(\(\alpha\), \(\beta\)) è \(\frac{\alpha}{\alpha + \beta}\). Pertanto, per la nostra distribuzione a posteriori Beta(2,12), la media è:

\[E[p|x] = \frac{2}{2 + 12} = \frac{2}{14} = \frac{1}{7}.\]

Ciò implica che, incorporando le nostre conoscenze a priori attraverso una distribuzione Beta(2,2) e aggiornandole con i dati osservati (0 teste su 10 lanci), arriviamo a una probabilità a posteriori media di ottenere testa nel prossimo lancio di \(\frac{1}{7}\). Questa stima è più ottimistica rispetto alla stima di \(0\) offerta dallo statistico frequentista.

Same-sex marriage

propongono il seguente problema:

A 2017 Pew Research survey found that 10.2% of LGBT adults in the U.S. were married to a same-sex spouse.29 Now it’s the 2020s, and Bayard guesses that π, the percent of LGBT adults in the U.S. who are married to a same-sex spouse, has most likely increased to about 15% but could reasonably range from 10% to 25%. a. Identify and plot a Beta model that reflects Bayard’s prior ideas about π. b. Bayard wants to update his prior, so he randomly selects 90 US LGBT adults and 30 of them are married to a same-sex partner. What is the posterior model for π? c. Calculate the posterior mean, mode, and standard deviation of π. d. Does the posterior model more closely reflect the prior information or the data? Explain your reasoning.

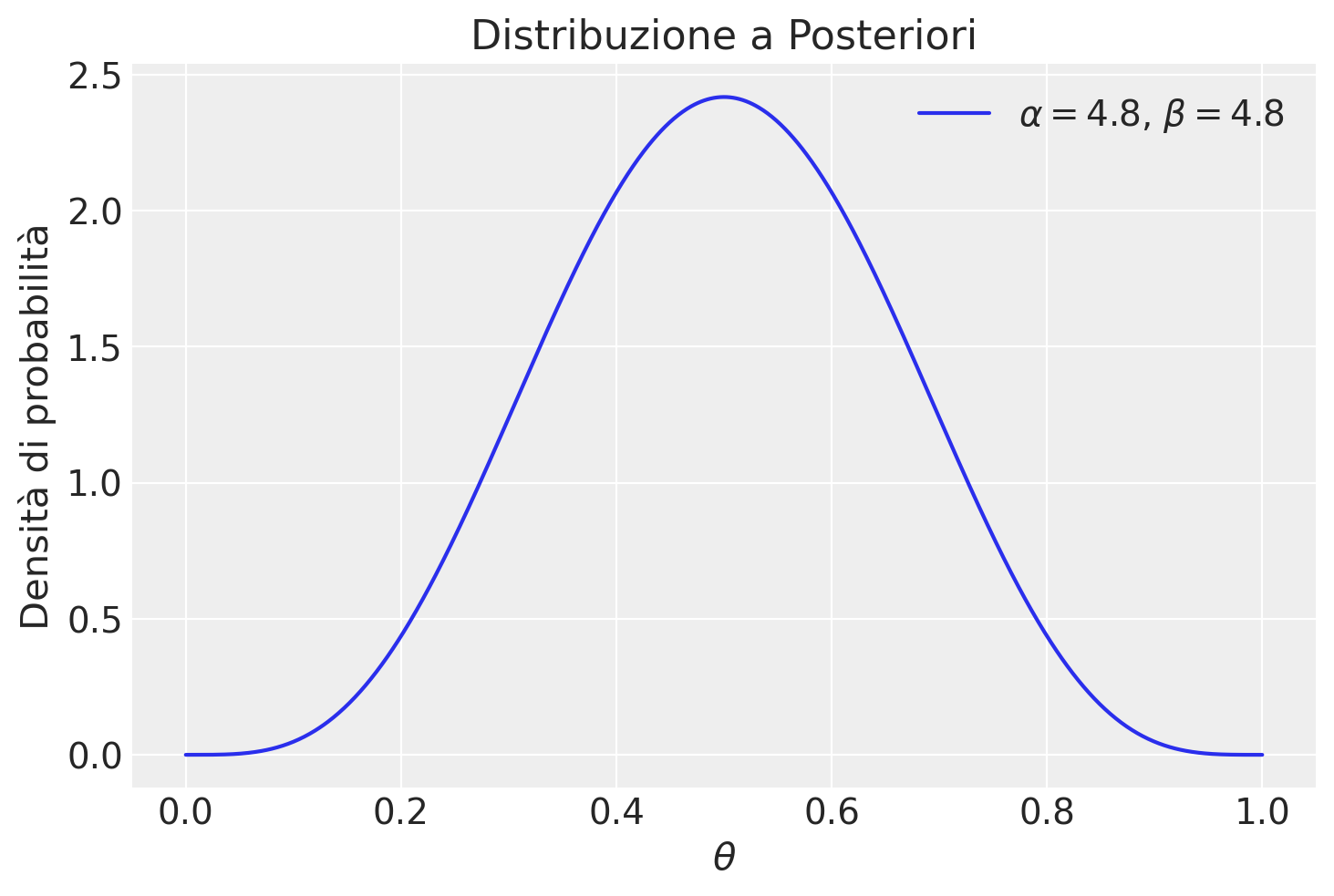
Soluzione a

# Definisci la media della distribuzione beta
mean = 0.5

# Definisci l'intervallo di credibilità (a, b)
a = 0.2
b = 0.8

# Calcola la deviazione standard della distribuzione beta
std_dev = (b - a) / (2 * stats.norm.ppf(0.975))

# Calcola i parametri della distribuzione beta
alpha = ((1 - mean) / std_dev**2 - 1 / mean) * mean**2
beta = alpha * (1 / mean - 1)

print("Parametri della distribuzione beta:")
print("Alpha:", alpha)
print("Beta:", beta)

Parametri della distribuzione beta:
Alpha: 4.8353594731862835
Beta: 4.8353594731862835

# Crea un array di valori di theta
theta = np.linspace(0, 1, 1000)
pdf_pre = stats.beta.pdf(theta, alpha, beta)
plt.plot(theta, pdf_pre, label=r'$\alpha=4.8$, $\beta=4.8$')
plt.xlabel(r'$\theta$')
plt.ylabel('Densità di probabilità')
plt.title('Distribuzione a Posteriori')
_ = plt.legend()

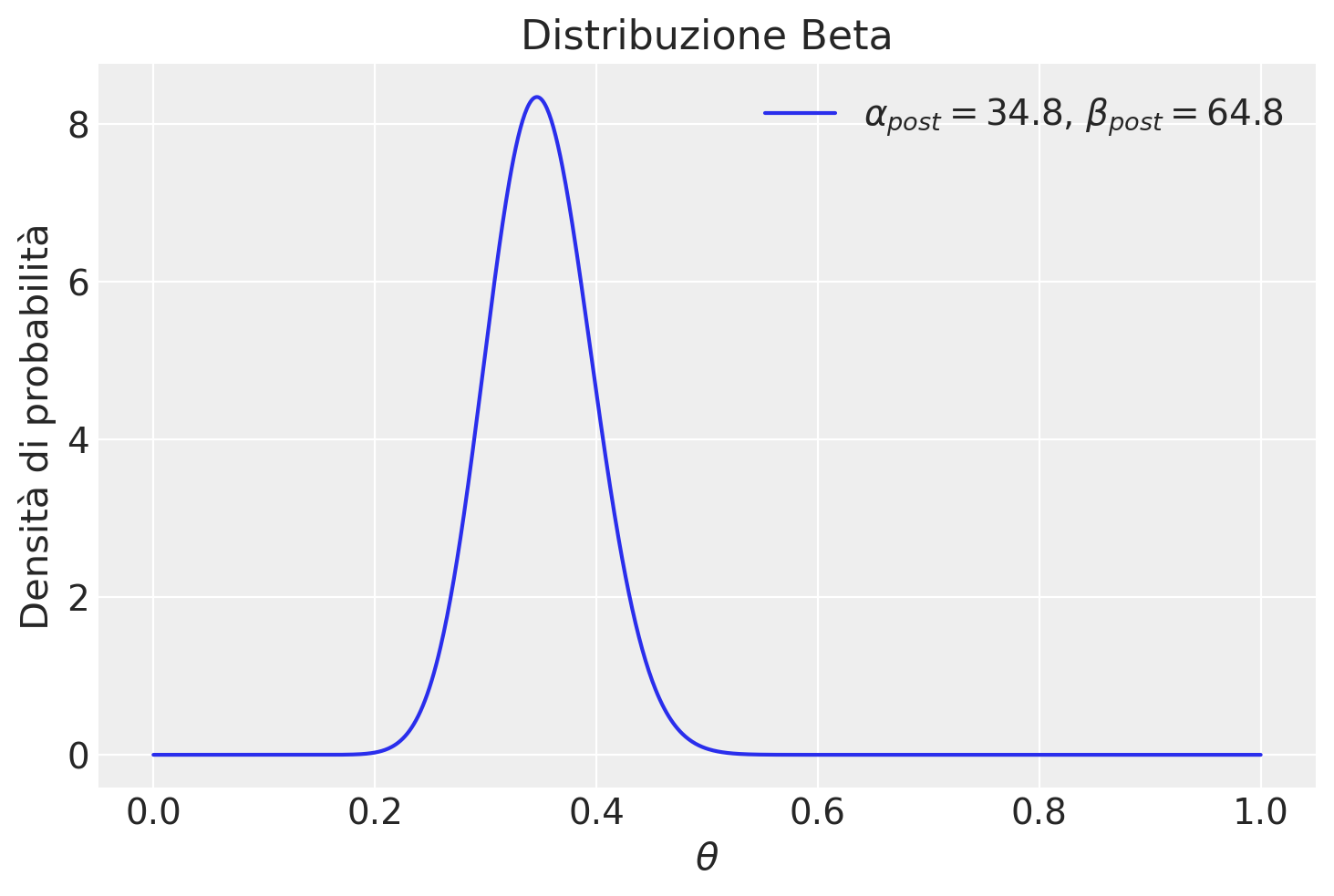
Soluzione b

Posti y = 30, n = 90 e il prior definito sopra, la distribuzione a posteriori è una \(B(\alpha', \beta')\), dove \(\alpha' = \alpha + y\) e \(\beta' = \beta + n - y\). Nel caso presente abbiamo

alpha_post = 4.8 + 30
beta_post = 4.8 + 90 - 30

pdf_post = stats.beta.pdf(theta, alpha_post, beta_post)
plt.plot(theta, pdf_post, label=r'$\alpha_{post}=34.8$, $\beta_{post}=64.8$')
plt.xlabel(r'$\theta$')
plt.ylabel('Densità di probabilità')
plt.title('Distribuzione Beta')
_ = plt.legend()

Soluzione c

media_post = alpha_post / (alpha_post + beta_post)
moda_post = (alpha_post - 1) / (alpha_post + beta_post - 2)
std = np.sqrt(
    (alpha_post * beta_post) / ((alpha_post + beta_post)**2 * (alpha_post + beta_post + 1))
)

print(media_post, moda_post, std)

0.3493975903614458 0.34631147540983603 0.04753557987430774

Informazioni sull’Ambiente di Sviluppo

%load_ext watermark
%watermark -n -u -v -iv -w -m

Last updated: Sun Jun 16 2024

Python implementation: CPython
Python version       : 3.12.3
IPython version      : 8.25.0

Compiler    : Clang 16.0.6 
OS          : Darwin
Release     : 23.4.0
Machine     : arm64
Processor   : arm
CPU cores   : 8
Architecture: 64bit

numpy     : 1.26.4
matplotlib: 3.8.4
seaborn   : 0.13.2
pandas    : 2.2.2
arviz     : 0.18.0
scipy     : 1.13.1

Watermark: 2.4.3