Probabilità condizionata

Un principio fondamentale nel campo della probabilità è il concetto di condizionamento. Il condizionamento si verifica quando, all’interno di un esperimento aleatorio, le probabilità vengono calcolate focalizzandosi esclusivamente su un sottoinsieme specifico dei risultati possibili. In pratica, questo significa che la probabilità viene determinata tenendo conto solo di quei risultati che rientrano in un certo criterio o condizione predefinita.

Preparazione del Notebook

import numpy as np
import pandas as pd
import random 

Indipendenza Stocastica

Nel contesto della probabilità condizionata, il concetto di indipendenza gioca un ruolo fondamentale. Questa caratteristica permette di semplificare notevolmente il calcolo delle probabilità in molti problemi, evidenziando come la conoscenza di un evento non fornisca alcuna informazione aggiuntiva sull’altro.

Indipendenza di Due Eventi

Due eventi \( A \) e \( B \) sono detti indipendenti se il verificarsi di uno non influenza la probabilità di verificarsi dell’altro. Formalmente, questa condizione è espressa come:

\[ \mathbb{P}(A \cap B) = \mathbb{P}(A) \mathbb{P}(B), \]

dove \( \mathbb{P}(A \cap B) \) rappresenta la probabilità che entrambi gli eventi \( A \) e \( B \) si verifichino simultaneamente.

Se questa condizione è soddisfatta, scriviamo \( A \text{ ⫫ } B \), il che significa «A è indipendente da B».

Indipendenza di un Insieme di Eventi

L’indipendenza stocastica è un concetto fondamentale nell’applicazione della probabilità in campo statistico. Un insieme di eventi \( \{ A_i : i \in I \} \) è detto indipendente se per ogni sottoinsieme finito \( J \) di \( I \), la probabilità dell’intersezione degli eventi nel sottoinsieme \( J \) è uguale al prodotto delle loro singole probabilità. Formalmente:

\[ \mathbb{P} \left( \cap_{i \in J} A_i \right) = \prod_{i \in J} \mathbb{P}(A_i). \]

Questo significa che ogni combinazione finita di eventi nell’insieme è indipendente.

L’indipendenza può essere assunta o derivata a seconda del contesto. In alcuni modelli o situazioni, assumiamo che certi eventi siano indipendenti perché questa assunzione semplifica i calcoli o riflette una conoscenza previa. In altri casi, l’indipendenza può essere derivata dai dati o da altre proprietà del modello.

Eventi Disgiunti e Indipendenza

Eventi disgiunti (o mutuamente esclusivi) sono quelli che non possono verificarsi simultaneamente, cioè \( \mathbb{P}(A \cap B) = 0 \). Se due eventi disgiunti hanno una probabilità positiva di verificarsi, allora non possono essere indipendenti. Questo perché per eventi disgiunti con \( \mathbb{P}(A) > 0 \) e \( \mathbb{P}(B) > 0 \), l’equazione di indipendenza \( \mathbb{P}(A \cap B) = \mathbb{P}(A) \mathbb{P}(B) \) non può essere soddisfatta, dato che \( \mathbb{P}(A \cap B) = 0 \) e \( \mathbb{P}(A) \mathbb{P}(B) > 0 \).

Probabilità condizionata su altri eventi

La probabilità di un evento è intrinsecamente condizionata dal nostro stato di informazione. In presenza di un determinato insieme di informazioni, attribuiamo a un evento una probabilità specifica di occorrenza. Tuttavia, qualora il nostro stato informativo subisca una modifica, anche la probabilità associata all’evento verrà corrispondentemente aggiornata.

In realtà, tutte le probabilità possono essere intese come probabilità condizionate, anche quando la variabile o l’evento condizionante non è esplicitamente specificato. Ciò implica che le probabilità sono sempre contestualizzate e dipendono dal set informativo disponibile in un dato scenario.

Questo quadro concettuale ci induce a considerare le probabilità come una “misura di plausibilità” che riflette la nostra conoscenza corrente del sistema o del fenomeno sotto indagine. A seguito dell’acquisizione di nuove informazioni o di cambiamenti nel contesto, la nostra misura di plausibilità, e quindi la probabilità attribuita agli eventi, può essere rivista.

Definizione

Siano \( A \) e \( B \) due eventi definiti su uno spazio campionario \( S \). Supponendo che l’evento \( B \) si verifichi, la probabilità condizionata di \( A \) dato \( B \) è data da

(10)\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)}, \quad \text{per}\, P(B) > 0, \]

dove \( P(A \cap B) \) rappresenta la probabilità congiunta dei due eventi, ovvero la probabilità che entrambi si verifichino.

Nell’eq. (10), \( P(A \cap B) \) è la probabilità congiunta che entrambi gli eventi si verifichino, mentre \( P(B) \) è la probabilità marginale dell’evento \( B \). Riorganizzando i termini, otteniamo la regola della moltiplicazione:

\[ P(A \cap B) = P(A \mid B)P(B) = P(B \mid A)P(A). \]

Utilizzando questa regola, possiamo derivare una forma alternativa della legge della probabilità totale:

\[ P(A) = P(A \mid B)P(B) + P(A \mid B^c)P(B^c). \]

Dove \( B^c \) rappresenta il complemento dell’evento \( B \).

È importante notare che \(P(A \mid B)\) non è definita se \(P(B) = 0\).

La probabilità condizionata può essere interpretata come una ricalibrazione dello spazio campionario da \(S\) a \(B\). Per spazi campionari discreti, la probabilità condizionata è espressa come

\[ P(A \mid B) = \frac{| A \cap B |}{| B |}. \]

Exercise 80

Lanciamo due dadi equilibrati e vogliamo calcolare la probabilità che la somma dei punteggi ottenuti sia minore di 8.

Inizialmente, quando non abbiamo ulteriori informazioni, possiamo calcolare la probabilità in modo tradizionale. Ci sono 21 risultati possibili con somma minore di 8. Poiché ci sono 36 possibili combinazioni di lancio dei due dadi, la probabilità di ottenere una somma minore di 8 è 21/36, che equivale a circa 0.58.

Supponiamo ora di sapere che la somma del lancio di due dadi ha prodotto un risultato dispari. In questo caso, ci sono solo 18 possibili combinazioni di lancio dei due dadi (dato che abbiamo escluso i risultati pari). Tra essi, vi sono 12 risultati che soddisfano la condizione per cui la somma è minore di 8. Quindi, la probabilità di ottenere una somma minore di 8 cambia da circa 0.58 a 12/18, ovvero 0.67 quando consideriamo l’informazione aggiuntiva del risultato dispari.

Svolgiamo il problema in Python.

r = range(1, 7)
sample = [(i, j) for i in r for j in r]
sample

[(1, 1),
 (1, 2),
 (1, 3),
 (1, 4),
 (1, 5),
 (1, 6),
 (2, 1),
 (2, 2),
 (2, 3),
 (2, 4),
 (2, 5),
 (2, 6),
 (3, 1),
 (3, 2),
 (3, 3),
 (3, 4),
 (3, 5),
 (3, 6),
 (4, 1),
 (4, 2),
 (4, 3),
 (4, 4),
 (4, 5),
 (4, 6),
 (5, 1),
 (5, 2),
 (5, 3),
 (5, 4),
 (5, 5),
 (5, 6),
 (6, 1),
 (6, 2),
 (6, 3),
 (6, 4),
 (6, 5),
 (6, 6)]

event = [roll for roll in sample if sum(roll) < 8]
print(f"{len(event)} / {len(sample)}")

21 / 36

sample_odd = [roll for roll in sample if (sum(roll) % 2) != 0]
sample_odd

[(1, 2),
 (1, 4),
 (1, 6),
 (2, 1),
 (2, 3),
 (2, 5),
 (3, 2),
 (3, 4),
 (3, 6),
 (4, 1),
 (4, 3),
 (4, 5),
 (5, 2),
 (5, 4),
 (5, 6),
 (6, 1),
 (6, 3),
 (6, 5)]

event = [roll for roll in sample_odd if sum(roll) < 8]
print(f"{len(event)} / {len(sample_odd)}")

12 / 18

Se applichiamo l’eq. eq-probcond, abbiamo: \(P(A \cap B)\) = 12/36, \(P(B)\) = 18/36 e

\[ P(A \mid B) = \frac{12}{18}. \]

Questo esempio illustra come la probabilità di un evento possa variare in base alle informazioni aggiuntive di cui disponiamo. Nel secondo caso, avendo l’informazione che la somma è dispari, la probabilità di ottenere una somma minore di 8 aumenta notevolmente rispetto al caso iniziale in cui non avevamo questa informazione.

Exercise 81

Consideriamo uno screening per la diagnosi precoce del tumore mammario utilizzando un test con determinate caratteristiche:

• Sensibilità del test: 90%. Questo significa che il test classifica correttamente come positivo il 90% delle donne colpite dal cancro al seno.

• Specificità del test: 90%. Ciò indica che il test classifica correttamente come negativo il 90% delle donne che non hanno il cancro al seno.

• Prevalenza del cancro al seno nella popolazione sottoposta allo screening: 1% (0.01). Questo è il 1% delle donne che ha effettivamente il cancro al seno, mentre il restante 99% (0.99) non ne è affetto.

Ora cerchiamo di rispondere alle seguenti domande:

• Qual è la probabilità che una donna scelta a caso ottenga una mammografia positiva? Poiché il 1% delle donne ha il cancro al seno, la probabilità di ottenere una mammografia positiva (test positivo) è pari alla sensibilità del test, ovvero 0.90 (cioè 90%).

• Se la mammografia è positiva, qual è la probabilità che vi sia effettivamente un tumore al seno?

Per risolvere questo problema, consideriamo un campione di 1000 donne sottoposte al test di screening per il tumore al seno. Di queste 1000 donne:

• 10 donne (1% del campione) hanno effettivamente il cancro al seno. Per queste 10 donne con il cancro, il test darà un risultato positivo (vera positività) in 9 casi (90%).

• Per le restanti 990 donne (99% del campione) che non hanno il cancro al seno, il test darà un risultato positivo (falsa positività) in 99 casi (10%).

Questa situazione può essere rappresentata graficamente nel seguente modo:

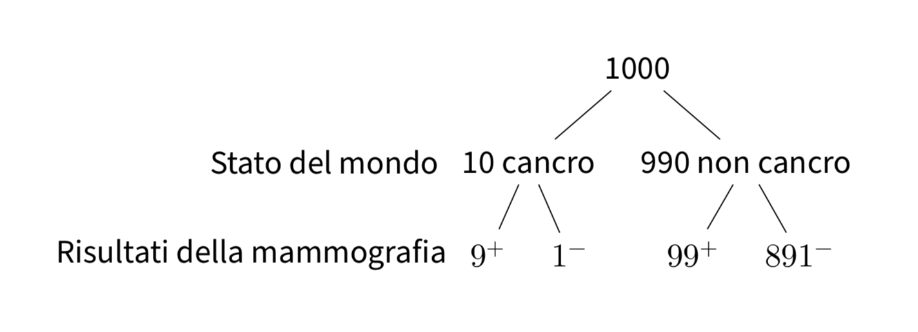
Combinando i due risultati precedenti, vediamo che il test dà un risultato positivo per 9 donne che hanno effettivamente il cancro al seno e per 99 donne che non lo hanno, per un totale di 108 risultati positivi su 1000. Pertanto, la probabilità di ottenere un risultato positivo al test è \(\frac{108}{1000}\) = 0.108.

Tuttavia, tra le 108 donne che hanno ottenuto un risultato positivo al test, solo 9 hanno effettivamente il cancro al seno. Quindi, la probabilità di avere il cancro al seno, dato un risultato positivo al test, è pari a \(\frac{9}{108}\) = 0.083, corrispondente all’8.3%.

In questo esempio, la probabilità dell’evento «ottenere un risultato positivo al test» è una probabilità non condizionata, poiché calcoliamo semplicemente la proporzione di risultati positivi nel campione totale. D’altra parte, la probabilità dell’evento «avere il cancro al seno, dato che il test ha prodotto un risultato positivo» è una probabilità condizionata, poiché calcoliamo la proporzione delle donne con il cancro al seno tra quelle che hanno ottenuto un risultato positivo al test.

Questo esempio illustra come la conoscenza di ulteriori informazioni (il risultato positivo al test) può influenzare la probabilità di un evento (avere il cancro al seno), mostrando chiaramente la differenza tra probabilità condizionate e non condizionate.

Exercise 82

Il paradosso di Monty Hall rappresenta un curioso esempio di come l’introduzione di nuove informazioni possa influenzare l’esito di una situazione probabilistica. Questo famoso problema trae origine dal popolare programma televisivo americano «Let’s Make a Deal» e deve la sua notorietà al conduttore Monty Hall.

Nel gioco ci sono tre porte chiuse: dietro una si nasconde un’automobile, mentre dietro le altre due ci sono delle capre. Inizialmente, il concorrente sceglie una delle tre porte senza aprirla. Successivamente, Monty Hall apre una delle due porte rimaste, rivelando una capra. A questo punto, offre al concorrente la possibilità di cambiare la sua scelta iniziale e optare per l’altra porta ancora chiusa. Il paradosso si presenta quando si scopre che cambiando la scelta in questa fase, il concorrente aumenta le sue probabilità di vincere l’automobile, passando da 1/3 a 2/3.

Per confermare questo risultato inaspettato, è possibile eseguire una simulazione in Python. In questa simulazione, consideriamo due scenari: uno in cui il concorrente mantiene la sua scelta iniziale e un altro in cui cambia la sua scelta dopo che Monty Hall ha svelato una capra. Ripetendo questa simulazione migliaia di volte, possiamo confrontare i risultati empirici e confermare come effettivamente il cambiamento di scelta aumenti le probabilità del concorrente di vincere l’automobile.

Di seguito è riportato lo script di una simulazione progettata per illustrare il paradosso di Monty Hall.

porte = [
    "capra1",
    "capra2",
    "macchina",
]  # definisco il gioco, scelgo una porta a caso per n volte
counter = 0
contatore_cambio = 0
n = 10000
porta_vincente = "macchina"
for i in range(n):
    scelta_casuale = random.choice(porte)
    porte_rimaste = [x for x in porte if x != scelta_casuale]
    porta_rivelata = random.choice([x for x in porte_rimaste if x != porta_vincente])
    porta_alternativa = [
        x for x in porte if x != scelta_casuale and x != porta_rivelata
    ]
    if "macchina" in porta_alternativa:
        contatore_cambio += 1
    if scelta_casuale == "macchina":
        counter += 1

print(counter / n)  # quante volte vinco non cambiando porta
print(contatore_cambio / n)  # quante volte vinco cambiando porta

0.3302
0.6698

Questo script Python è stato creato da un gruppo di studenti di Psicometria nell’AA 2023-2023. La simulazione mostra che, effettivamente, la probabilità di vincere la macchina aumenta quando il concorrente sceglie di cambiare porta.

Ecco una spiegazione del paradosso:

1. Fase Iniziale: Nel gioco, il concorrente deve scegliere una delle tre porte (A, B, C), dietro una delle quali si trova una macchina. Inizialmente, la probabilità che la macchina si trovi dietro la porta scelta è \(1/3\), dato che esistono tre possibilità ugualmente probabili e solo una contiene la macchina.

2. Aggiunta di Informazioni: Dopo la scelta iniziale, Monty Hall, che conosce il contenuto dietro ogni porta, apre una delle due porte non scelte, rivelando sempre una capra. Questo passaggio è fondamentale: non cambia la probabilità \(1/3\) che la macchina sia dietro la porta originariamente scelta dal concorrente, ma la probabilità che la macchina si trovi dietro l’altra porta non scelta aumenta ora a \(2/3\). Questo aumento di probabilità deriva dal fatto che Monty ha scelto deliberatamente una porta con una capra, basando la sua scelta sulla posizione della macchina.

Consideriamo i tre possibili scenari dopo che il concorrente ha scelto la porta A:

• La macchina è dietro la porta A: La probabilità di questo scenario è \(1/3\). Monty può aprire sia la porta B che la porta C, poiché entrambe nascondono una capra. Se il concorrente cambia la sua scelta, perderà.

• La macchina è dietro la porta B: La probabilità di questo scenario è \(1/3\). Monty aprirà la porta C, perché sa che la macchina è dietro la porta B e non può rivelarla. Se il concorrente cambia la sua scelta da A a B, vincerà.

• La macchina è dietro la porta C: La probabilità di questo scenario è \(1/3\). Monty aprirà la porta B. Se il concorrente cambia la sua scelta da A a C, vincerà.

In conclusione, cambiare la scelta originale porta alla vittoria in due dei tre scenari possibili. Pertanto, la probabilità complessiva di vincere cambiando la scelta è \(2/3\).

Questo paradosso evidenzia come, in presenza di informazioni aggiuntive, le probabilità iniziali possano essere riviste significativamente. È un classico esempio di come l’intuizione umana spesso si scontri con i principi della teoria delle probabilità, sottolineando l’importanza della revisione bayesiana delle probabilità alla luce di nuove informazioni.

Il paradosso di Simpson

Nel campo della probabilità condizionata, uno dei fenomeni più interessanti e, nel contempo, più controintuitivi, è rappresentato dal paradosso di Simpson. Il paradosso di Simpson è un fenomeno statistico in cui una tendenza che appare in diversi gruppi separati di dati scompare o si inverte quando i dati vengono combinati. Questo paradosso mette in luce l’importanza di considerare le variabili confondenti e di analizzare i dati con attenzione per evitare conclusioni errate.

Exercise 83

Due psicoterapeuti, Rossi e Bianchi, praticano due tipi di terapie: terapia per disturbi d’ansia e coaching per migliorare le prestazioni lavorative. Ogni terapia può avere un esito positivo o negativo.

I rispettivi bilanci dei due terapeuti sono riportati nelle seguenti tabelle.

Rossi

Tipo di terapia	Successo	Fallimento
Disturbi d’ansia	70	20
Coaching lavorativo	10	0
Totale	80	20

Bianchi

Tipo di terapia	Successo	Fallimento
Disturbi d’ansia	2	8
Coaching lavorativo	81	9
Totale	83	17

Rossi ha un tasso di successo superiore a Bianchi nella terapia per i disturbi d’ansia: 70 su 90 rispetto a 2 su 10. Anche nel coaching lavorativo, Rossi ha un tasso di successo superiore: 10 su 10 rispetto a 81 su 90. Tuttavia, se aggregiamo i dati dei due tipi di terapia per confrontare i tassi di successo globali, Rossi è efficace in 80 su 100 terapie, mentre Bianchi in 83 su 100: il tasso di successo globale di Bianchi risulta superiore!

Questo fenomeno è un esempio del paradosso di Simpson, dove una tendenza osservata in diversi gruppi si inverte quando i gruppi sono combinati.

Per essere più precisi, possiamo calcolare i tassi di successo per ciascun terapeuta e per ciascun tipo di terapia, oltre al tasso di successo globale.

1. Rossi

   • Tasso di successo in terapia per disturbi d’ansia: \(\frac{70}{70+20} = \frac{70}{90} \approx 0.778\)

   • Tasso di successo in coaching lavorativo: \(\frac{10}{10+0} = \frac{10}{10} = 1\)

   • Tasso di successo globale: \(\frac{70+10}{70+20+10+0} = \frac{80}{100} = 0.8\)

2. Bianchi

   • Tasso di successo in terapia per disturbi d’ansia: \(\frac{2}{2+8} = \frac{2}{10} = 0.2\)

   • Tasso di successo in coaching lavorativo: \(\frac{81}{81+9} = \frac{81}{90} \approx 0.9\)

   • Tasso di successo globale: \(\frac{2+81}{2+8+81+9} = \frac{83}{100} = 0.83\)

Quello che sta succedendo è che Rossi, presumibilmente a causa della sua reputazione come terapeuta più esperto, sta effettuando un numero maggiore di terapie per disturbi d’ansia, che sono intrinsecamente più complesse e con una probabilità di successo variabile rispetto al coaching lavorativo. Il suo tasso di successo globale è inferiore non a causa di una minore abilità in un particolare tipo di terapia, ma perché una frazione maggiore delle sue terapie riguarda casi più complessi.

L’aggregazione dei dati tra diversi tipi di terapia presenta un quadro fuorviante delle abilità dei terapeuti perché perdiamo l’informazione su quale terapeuta tende a effettuare quale tipo di terapia. Quando sospettiamo la presenza di variabili di confondimento, come ad esempio il tipo di terapia in questo contesto, è fondamentale analizzare i dati in modo disaggregato per comprendere con precisione la dinamica in atto.

Teorema della probabilità composta

È possibile scrivere l’eq. (10) nella forma:

(11)\[ P(A \cap B) = P(B)P(A \mid B) = P(A)P(B \mid A). \]

Questo secondo modo di scrivere l’equazione (10) è chiamato teorema della probabilità composta (o regola moltiplicativa, o regola della catena). La legge della probabilità composta ci dice che la probabilità che si verifichino contemporaneamente due eventi \(A\) e \(B\) è pari alla probabilità di uno dei due eventi moltiplicata per la probabilità dell’altro evento condizionata al verificarsi del primo.

L’eq. (11) si estende al caso di \(n\) eventi \(A_1, \dots, A_n\) nella forma seguente:

(12)\[ P\left( \bigcap_{k=1}^n A_k \right) = \prod_{k=1}^n P\left( A_k \ \Biggl\lvert \ \bigcap_{j=1}^{k-1} A_j \right). \]

Per esempio, nel caso di quattro eventi abbiamo

\[\begin{split} \begin{split} P(&A_1 \cap A_2 \cap A_3 \cap A_4) = \\ & P(A_1) \cdot P(A_2 \mid A_1) \cdot P(A_3 \mid A_1 \cap A_2) \cdot P(A_4 \mid A_1 \cap A_2 \cap A_{3}).\notag \end{split} \end{split}\]

Exercise 84

Per fare un esempio, consideriamo il problema seguente. Da un’urna contenente 6 palline bianche e 4 nere si estrae una pallina per volta, senza reintrodurla nell’urna. Indichiamo con \(B_i\) l’evento: «esce una pallina bianca alla \(i\)-esima estrazione» e con \(N_i\) l’estrazione di una pallina nera. L’evento: «escono due palline bianche nelle prime due estrazioni» è rappresentato dalla intersezione \(\{B_1 \cap B_2\}\) e, per l’eq. (11), la sua probabilità vale

\[ P(B_1 \cap B_2) = P(B_1)P(B_2 \mid B_1). \]

\(P(B_1)\) vale 6/10, perché nella prima estrazione \(\Omega\) è costituito da 10 elementi: 6 palline bianche e 4 nere. La probabilità condizionata \(P(B_2 \mid B_1)\) vale 5/9, perché nella seconda estrazione, se è verificato l’evento \(B_1\), lo spazio campionario consiste di 5 palline bianche e 4 nere. Si ricava pertanto:

\[ P(B_1 \cap B_2) = \frac{6}{10} \cdot \frac{5}{9} = \frac{1}{3}. \]

In modo analogo si ha che

\[ P(N_1 \cap N_2) = P(N_1)P(N_2 \mid N_1) = \frac{4}{10} \cdot \frac{3}{9} = \frac{4}{30}. \]

Se l’esperimento consiste nell’estrazione successiva di 3 palline, la probabilità che queste siano tutte bianche, per l’eq. (12), vale

\[\begin{split} \begin{aligned} P(B_1 \cap B_2 \cap B_3) &=P(B_1)P(B_2 \mid B_1)P(B_3 \mid B_1 \cap B_2) \notag\\ &=\frac{6}{10}\cdot\frac{5}{9} \cdot\frac{4}{8} \notag\\ &= \frac{1}{6}. \end{aligned} \end{split}\]

La probabilità dell’estrazione di tre palline nere è invece:

\[\begin{split} \begin{aligned} P(N_1 \cap N_2 \cap N_3) &= P(N_1)P(N_2 \mid N_1)P(N_3 \mid N_1 \cap N_2)\notag\\ &= \frac{4}{10} \cdot \frac{3}{9} \cdot \frac{2}{8} \notag\\ &= \frac{1}{30}.\notag \end{aligned} \end{split}\]

Il teorema della probabilità totale

Il teorema della probabilità totale (detto anche teorema delle partizioni) afferma che se abbiamo una partizione di uno spazio campionario \(\Omega\) in \(n\) eventi mutualmente esclusivi e tali che la loro unione formi \(\Omega\), allora la probabilità di un qualsiasi evento in \(\Omega\) può essere calcolata sommando la probabilità dell’evento su ciascun sottoinsieme della partizione, pesata in base alla probabilità del sottoinsieme.

In altre parole, se \(H_1, H_2, \dots, H_n\) sono eventi mutualmente esclusivi e tali che \(\bigcup_{i=1}^n H_i = \Omega\), allora per ogni evento \(E \subseteq \Omega\), la probabilità di \(E\) è data dalla formula:

(13)\[ P(E) = \sum_{i=1}^n P(E \mid H_i)P(H_i), \]

dove \(P(E \mid H_i)\) rappresenta la probabilità condizionata di \(E\) dato che si è verificato l’evento \(H_i\), e \(P(H_i)\) è la probabilità dell’evento \(H_i\).

Il teorema della probabilità totale riveste un ruolo fondamentale in quanto fornisce il denominatore nel teorema di Bayes, svolgendo la funzione di costante di normalizzazione. Questa costante di normalizzazione è di vitale importanza per assicurare che la distribuzione a posteriori sia una distribuzione di probabilità valida. Per ulteriori dettagli e approfondimenti, è possibile fare riferimento al capitolo Pensare ad una proporzione in termini soggettivi.

Nell’ambito della probabilità discreta, questo teorema viene usato quando abbiamo una partizione dello spazio campionario e vogliamo calcolare la probabilità di un evento, sfruttando le probabilità dei singoli eventi della partizione. Il caso più semplice è quello di una partizione dello spazio campione in due sottoinsiemi: \(P(E) = P(E \cap H_1) + P(E \cap H_2)\).

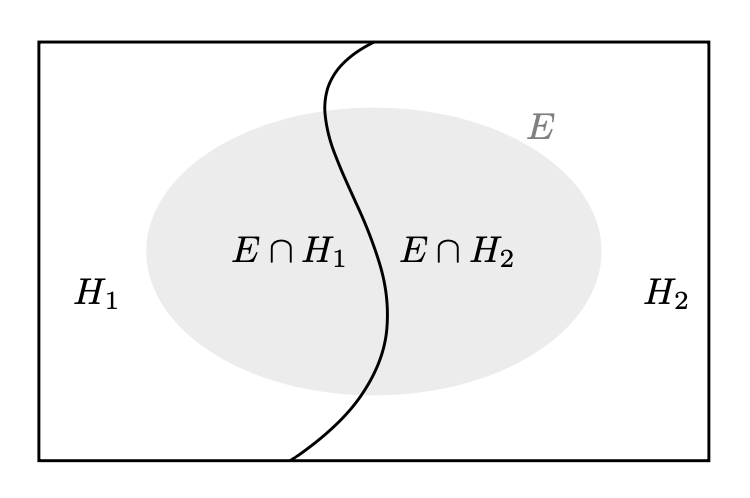
In tali circostanza abbiamo che

\[ P(E) = P(E \mid H_1) P(H_1) + P(E \mid H_2) P(H_2). \]

L’eq. (13) è utile per calcolare \(P(E)\), se \(P(E \mid H_i)\) e \(P(H_i)\) sono facili da trovare.

Exercise 85

Abbiamo tre urne, ciascuna delle quali contiene 100 palline:

• Urna 1: 75 palline rosse e 25 palline blu,

• Urna 2: 60 palline rosse e 40 palline blu,

• Urna 3: 45 palline rosse e 55 palline blu.

Una pallina viene estratta a caso da un’urna anch’essa scelta a caso. Qual è la probabilità che la pallina estratta sia di colore rosso?

Sia \(R\) l’evento «la pallina estratta è rossa» e sia \(U_i\) l’evento che corrisponde alla scelta dell”\(i\)-esima urna. Sappiamo che

\[ P(R \mid U_1) = 0.75, \quad P(R \mid U_2) = 0.60, \quad P(R \mid U_3) = 0.45. \]

Gli eventi \(U_1\), \(U_2\) e \(U_3\) costituiscono una partizione dello spazio campione in quanto \(U_1\), \(U_2\) e \(U_3\) sono eventi mutualmente esclusivi ed esaustivi, ovvero \(P(U_1 \cup U_2 \cup U_3) = 1.0\). In base al teorema della probabilità totale, la probabilità di estrarre una pallina rossa è dunque

\[\begin{split} \begin{split} P(R) &= P(R \mid U_1)P(U_1) + P(R \mid U_2)P(U_2) + P(R \mid U_3)P(U_3) \\ &= 0.75 \cdot \frac{1}{3}+0.60 \cdot \frac{1}{3}+0.45 \cdot \frac{1}{3} \\ &=0.60. \end{split} \end{split}\]

Indipendenza e probabilità condizionata

L’indipendenza tra due eventi \(A\) e \(B\) può essere espressa in modo intuitivo utilizzando la probabilità condizionata. Se \(A\) e \(B\) sono indipendenti, il verificarsi di uno degli eventi non influisce sulla probabilità del verificarsi dell’altro. In altre parole, la probabilità che \(A\) accada non cambia se sappiamo che \(B\) è avvenuto, e viceversa.

Possiamo esprimere questa idea con le seguenti equazioni:

\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)} = P(A), \]

\[ P(B \mid A) = \frac{P(A \cap B)}{P(A)} = P(B). \]

Quindi, due eventi \(A\) e \(B\) sono indipendenti se soddisfano le condizioni:

\[ P(A \mid B) = P(A), \]

\[ P(B \mid A) = P(B). \]

Questo significa che la probabilità di \(A\) rimane invariata indipendentemente dal fatto che \(B\) sia accaduto o meno, e lo stesso vale per \(B\).

Indipendenza di Tre Eventi

Tre eventi \(A\), \(B\) e \(C\) sono indipendenti se soddisfano le seguenti condizioni:

\[\begin{split} \begin{align} P(A \cap B) &= P(A) P(B), \\ P(A \cap C) &= P(A) P(C), \\ P(B \cap C) &= P(B) P(C), \\ P(A \cap B \cap C) &= P(A) P(B) P(C). \end{align} \end{split}\]

Le prime tre condizioni verificano l’indipendenza a due a due, ovvero l’indipendenza di ciascuna coppia di eventi. Tuttavia, per essere completamente indipendenti, deve essere soddisfatta anche l’ultima condizione, che riguarda l’intersezione di tutti e tre gli eventi. Solo se tutte queste condizioni sono soddisfatte possiamo dire che \(A\), \(B\) e \(C\) sono completamente indipendenti.

In sintesi, l’indipendenza tra eventi implica che la conoscenza del verificarsi di uno non fornisce alcuna informazione sulla probabilità del verificarsi degli altri.

Exercise 86

Consideriamo un esempio utilizzando un mazzo di 52 carte. Ogni seme contiene 13 carte e ci sono 4 regine in totale. Definiamo i seguenti eventi:

• Evento A: pescare una carta di picche,

• Evento B: pescare una regina.

Probabilità con un mazzo completo

In un mazzo completo, la probabilità di pescare una carta di picche (\(P(A)\)) è \( \frac{13}{52} = \frac{1}{4} \), poiché ci sono 13 picche su 52 carte totali. La probabilità di pescare una regina (\(P(B)\)) è \( \frac{4}{52} = \frac{1}{13} \), poiché ci sono 4 regine su 52 carte.

Ora consideriamo la probabilità congiunta di pescare la regina di picche (\(P(AB)\)). Poiché esiste solo una regina di picche nel mazzo, la probabilità di pescare questa specifica carta è \( \frac{1}{52} \).

Secondo la definizione di indipendenza, se gli eventi \(A\) e \(B\) sono indipendenti, allora:

\[ P(AB) = P(A)P(B) \]

Calcoliamo \(P(A)P(B)\):

\[ P(A)P(B) = \left( \frac{1}{4} \right) \left( \frac{1}{13} \right) = \frac{1}{52} \]

Poiché \(P(AB) = \frac{1}{52}\) è uguale a \(P(A)P(B)\), possiamo affermare che gli eventi \(A\) e \(B\) sono indipendenti con un mazzo completo di 52 carte.

Probabilità dopo la rimozione di una carta

Consideriamo ora un mazzo con una carta in meno, ad esempio il due di quadri, riducendo il numero totale di carte a 51. Ricalcoliamo le probabilità con questo mazzo ridotto:

La probabilità di pescare la regina di picche (\(P(AB)\)) è ora \( \frac{1}{51} \), poiché ci sono 51 carte nel mazzo.

Ricalcoliamo anche \(P(A)\) e \(P(B)\):

• \(P(A)\) diventa \( \frac{13}{51} \), poiché ci sono ancora 13 picche, ma su 51 carte.

• \(P(B)\) diventa \( \frac{4}{51} \), poiché ci sono ancora 4 regine, ma su 51 carte.

Ora calcoliamo il prodotto \(P(A)P(B)\) con queste nuove probabilità:

\[ P(A)P(B) = \left( \frac{13}{51} \right) \left( \frac{4}{51} \right) = \frac{52}{2601} \]

Confrontiamo \(P(AB)\) e \(P(A)P(B)\):

\[ \frac{1}{51} \neq \frac{52}{2601} \]

Poiché \( \frac{1}{51} \neq \frac{52}{2601} \), gli eventi \(A\) e \(B\) non sono più indipendenti dopo la rimozione del due di quadri.

Questo esempio mostra come l’indipendenza tra due eventi dipenda dal contesto. Con un mazzo completo, i due eventi sono indipendenti. Tuttavia, rimuovendo una carta dal mazzo, le probabilità cambiano e gli eventi non sono più indipendenti. Questo evidenzia l’importanza di considerare la composizione e le condizioni iniziali quando si analizzano probabilità e indipendenza. Modifiche nella composizione del mazzo possono alterare le probabilità, influenzando le relazioni di indipendenza tra eventi specifici.

In generale, l’indipendenza tra due eventi significa che la probabilità di uno non è influenzata dal verificarsi dell’altro. Questo concetto è cruciale per analisi probabilistiche e modelli statistici più complessi.

Exercise 87

Nel lancio di due dadi non truccati, si considerino gli eventi: \(A\) = «esce un 1 o un 2 nel primo lancio» e \(B\) = «il punteggio totale è 8». Gli eventi \(A\) e \(B\) sono indipendenti?

Calcoliamo \(P(A)\):

r = range(1, 7)
sample = [(i, j) for i in r for j in r]
A = [roll for roll in sample if roll[0] == 1 or roll[0] == 2]
print(A)
print(f"{len(A)} / {len(sample)}")

[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)]
12 / 36

Calcoliamo \(P(B)\):

B = [roll for roll in sample if roll[0] + roll[1] == 8]
print(B)
print(f"{len(B)} / {len(sample)}")

[(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)]
5 / 36

Calcoliamo \(P(A \cap B)\):

I = [
    roll
    for roll in sample
    if (roll[0] == 1 or roll[0] == 2) and (roll[0] + roll[1] == 8)
]
print(I)
print(f"{len(I)} / {len(sample)}")

[(2, 6)]
1 / 36

Gli eventi \(A\) e \(B\) non sono statisticamente indipendenti dato che \(P(A \cap B) \neq P(A)P(B)\):

12/36 * 5/36 == 1/36

False

Commenti e considerazioni finali

La probabilità condizionata riveste un ruolo fondamentale poiché ci permette di definire in modo preciso il concetto di indipendenza statistica. Uno degli aspetti cruciali dell’analisi statistica riguarda la valutazione dell’associazione tra due variabili. Nel capitolo attuale, ci siamo concentrati sul concetto di indipendenza, che indica l’assenza di relazione tra le variabili. Tuttavia, in futuro, esploreremo come fare inferenze sulla correlazione tra variabili, ovvero come determinare se le variabili sono associate tra loro o se esiste una relazione statistica credibile tra di esse.

Nell’ambito dell’inferenza bayesiana, il condizionamento emerge come uno strumento essenziale. L’inferenza bayesiana è un approccio statistico che sfrutta proprio il condizionamento per rivedere e aggiornare le credenze o le incertezze relative a determinate ipotesi, basandosi sull’introduzione di nuove informazioni.

Il processo inizia stabilendo una probabilità iniziale, denominata probabilità a priori (\(P(A)\)), che esprime la nostra convinzione o supposizione iniziale riguardo all’ipotesi \(A\), prima di ricevere qualsiasi dato aggiuntivo. Questa probabilità a priori si fonda su conoscenze già acquisite o su supposizioni precedentemente formulate.

Il cuore dell’inferenza bayesiana si trova nell’aggiornamento di questa credenza iniziale in risposta all’acquisizione di nuove informazioni, rappresentate dalla variabile \(E\). L’aggiornamento avviene mediante il condizionamento, culminando nella determinazione di una probabilità a posteriori (\(P(A | E)\)). Questa nuova probabilità rappresenta la nostra credenza aggiornata sull’ipotesi \(A\) dopo aver preso in esame l’evidenza \(E\) appena acquisita. In questo modo, l’inferenza bayesiana permette di affinare le nostre supposizioni e le nostre previsioni su determinati fenomeni, incorporando sistematicamente nuove prove nel nostro quadro di conoscenza.

La formula di Bayes governa questo processo di aggiornamento:

\[ P(A | E) = \frac{P(E | A) \times P(A)}{P(E)} \]

In questa formula, troviamo:

• \(P(A | E)\): la probabilità a posteriori, che è la probabilità dell’ipotesi \(A\) date le nuove prove \(E\).

• \(P(E | A)\): la verosimiglianza, ovvero la probabilità di osservare le prove \(E\) se l’ipotesi \(A\) fosse vera.

• \(P(A)\): la probabilità a priori, che indica il nostro livello di convinzione iniziale nell’ipotesi \(A\).

• \(P(E)\): la probabilità di osservare le prove \(E\), tenendo conto di tutte le ipotesi possibili.

In questo capitolo esploreremo alcuni concetti chiave per una comprensione approfondita dell’aggiornamento bayesiano:

• Probabilità Congiunta: Questa è la probabilità che due eventi avvengano insieme. Per esempio, potrebbe riferirsi alla probabilità di estrarre una pallina rossa e poi una verde da un’urna in sequenza.

• Probabilità Marginale: Si tratta della probabilità di verificarsi di un singolo evento, considerato a prescindere da altri eventi. Ad esempio, potremmo voler calcolare la probabilità di estrarre una pallina verde da un’urna, senza considerare altri eventi.

• Probabilità Condizionata: Indica la probabilità che un evento si verifichi, dato che un altro evento correlato è già accaduto. Un esempio potrebbe essere la probabilità di estrarre una seconda pallina verde, sapendo che la prima estratta era verde.

Questi concetti sono fondamentali per navigare nel processo di inferenza bayesiana e per comprendere come le probabilità si aggiornano in risposta a nuove informazioni. Inoltre, esamineremo i principali teoremi legati alla probabilità condizionata.

Informazioni sull’Ambiente di Sviluppo

%load_ext watermark
%watermark -n -u -v -iv -w -m 

Last updated: Sun Jun 16 2024

Python implementation: CPython
Python version       : 3.12.3
IPython version      : 8.25.0

Compiler    : Clang 16.0.6 
OS          : Darwin
Release     : 23.4.0
Machine     : arm64
Processor   : arm
CPU cores   : 8
Architecture: 64bit

pandas: 2.2.2
numpy : 1.26.4

Watermark: 2.4.3