La funzione lineare#
La funzione lineare#
La funzione lineare è definita come:
dove \(a\) e \(b\) sono costanti. Il grafico di questa funzione è una retta, dove il parametro \(b\) rappresenta il coefficiente angolare e il parametro \(a\) rappresenta l’intercetta con l’asse delle \(y\). In altre parole, la retta interseca l’asse \(y\) nel punto \((0,a)\) se \(b \neq 0\).
Possiamo dare un’interpretazione geometrica alle costanti \(a\) e \(b\) considerando la funzione:
Questa funzione rappresenta un caso speciale, la proporzionalità diretta tra \(x\) e \(y\). Nel caso generale della funzione lineare:
aggiungiamo una costante \(a\) a ciascun valore \(y = b x\). Nella funzione lineare, se il coefficiente \(b\) è positivo, il valore di \(y\) aumenta al crescere di \(x\); se \(b\) è negativo, il valore di \(y\) diminuisce al crescere di \(x\); se \(b=0\), la retta è orizzontale e il valore di \(y\) non varia al variare di \(x\).
Consideriamo ora il coefficiente \(b\) in modo più dettagliato. Prendiamo un punto \(x_0\) e un incremento arbitrario \(\varepsilon\), come mostrato nella figura. Le differenze \(\Delta x = (x_0 + \varepsilon) - x_0\) e \(\Delta y = f(x_0 + \varepsilon) - f(x_0)\) sono chiamate «incrementi» di \(x\) e \(y\). Il coefficiente angolare \(b\) è definito come il rapporto
indipendentemente dalla grandezza degli incrementi \(\Delta x\) e \(\Delta y\). Per dare un’interpretazione geometrica al coefficiente angolare (o pendenza) della retta, possiamo semplificare assumendo \(\Delta x = 1\). In questo caso, \(b\) è uguale a \(\Delta y\).
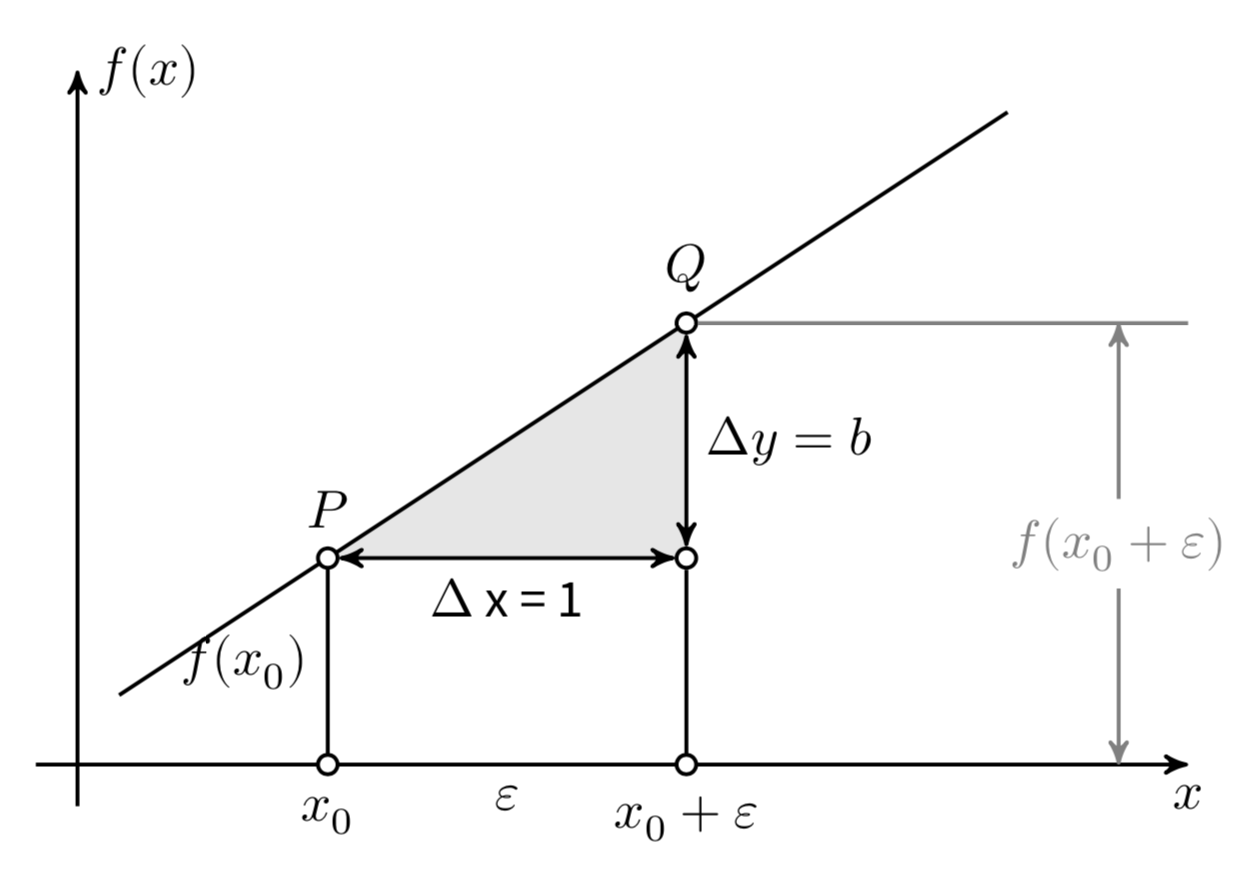
Fig. 7 La funzione lineare \(y = a + bx\).#
Possiamo dunque dire che la pendenza \(b\) di un retta è uguale all’incremento \(\Delta y\) associato ad un incremento unitario nella \(x\).

