✏️ Esercizi

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import arviz as az

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

Esercizio 1

Lanciamo 3 monete. Sia \(Y\) il numero di volte in cui si ossserva Testa. Si trovi il valore atteso di \(Y\), la sua varianza e la sua deviazione standard.

Soluzione.

Generiamo lo spazio dei risultati per 3 lanci di moneta. Il valore 0 rappresenta croce e 1 rappresenta testa.

space = np.array([[i, j, k] for i in range(2) for j in range(2) for k in range(2)])
print(space)

[[0 0 0]
 [0 0 1]
 [0 1 0]
 [0 1 1]
 [1 0 0]
 [1 0 1]
 [1 1 0]
 [1 1 1]]

Calcoliamo Y come la somma dei risultati di ogni combinazione.

Y = space.sum(axis=1)
print(Y)

[0 1 1 2 1 2 2 3]

La lista Y contiene dunque i valori della variabile casuale che abbiamo definito, in corrispondenza di ciascun evento elementare dello spazio campione.

Calcoliamo il valore atteso di Y:

\[ \mathbb{E}(Y) = \sum_{y \in Y} y P(Y = y). \]

p = 1/8  # Ogni risultato ha la stessa probabilità (1/2)^3 = 1/8
mu = (Y * p).sum()
print(mu)

1.5

La varianza si può calcolare in due modi. Usiamo la formula corrispondente alla definizione di varianza di una v.c.:

\[ \mathbb{V}(Y) = \mathbb{E}\big[(y - \mathbb{E}(Y))^2\big] \]

cioè

\[ \mathbb{V}(Y) = \sum_{y \in Y}(y - \mathbb{E}(Y))^2 P(y = Y) \]

sigma2 = ((Y - mu)**2 * p).sum()
print(sigma2)

0.75

Replichiamo il risultato usando la formula alternativa della varianza:

\[ \mathbb{V}(Y) = \mathbb{E}(Y^2) - \big[\mathbb{E}(Y)\big]^2. \]

sigma2 = (Y**2 * p).sum() - mu**2
print(sigma2)

0.75

Calcoliamo la deviazione standard di Y:

sigma = np.sqrt(sigma2)
print(sigma)

0.8660254037844386

Esercizio 2

Supponiamo di sapere che, sulla base dei dati di un campione molto grande, possiamo stabilire che nella popolazione oncologica, i punteggi di un test psicometrico atto a misurare l’astenia (ovvero, la riduzione di energia dell’individuo) seguono la distribuzione di massa di probabilità indicata qui sotto:

Valore	Probabilità
1	0.1
2	0.5
3	0.3
4	0.1

laddove la probabilità indica la frequenza con la quale ogni sintomo si manifesta. Per esempio, potremmo avere che 4 corrisponde a “molto spesso”, 3 corrisponde a “spesso”, 2 corrisponde a “alle volte” e 1 corrisponde a “raramente o mai”.

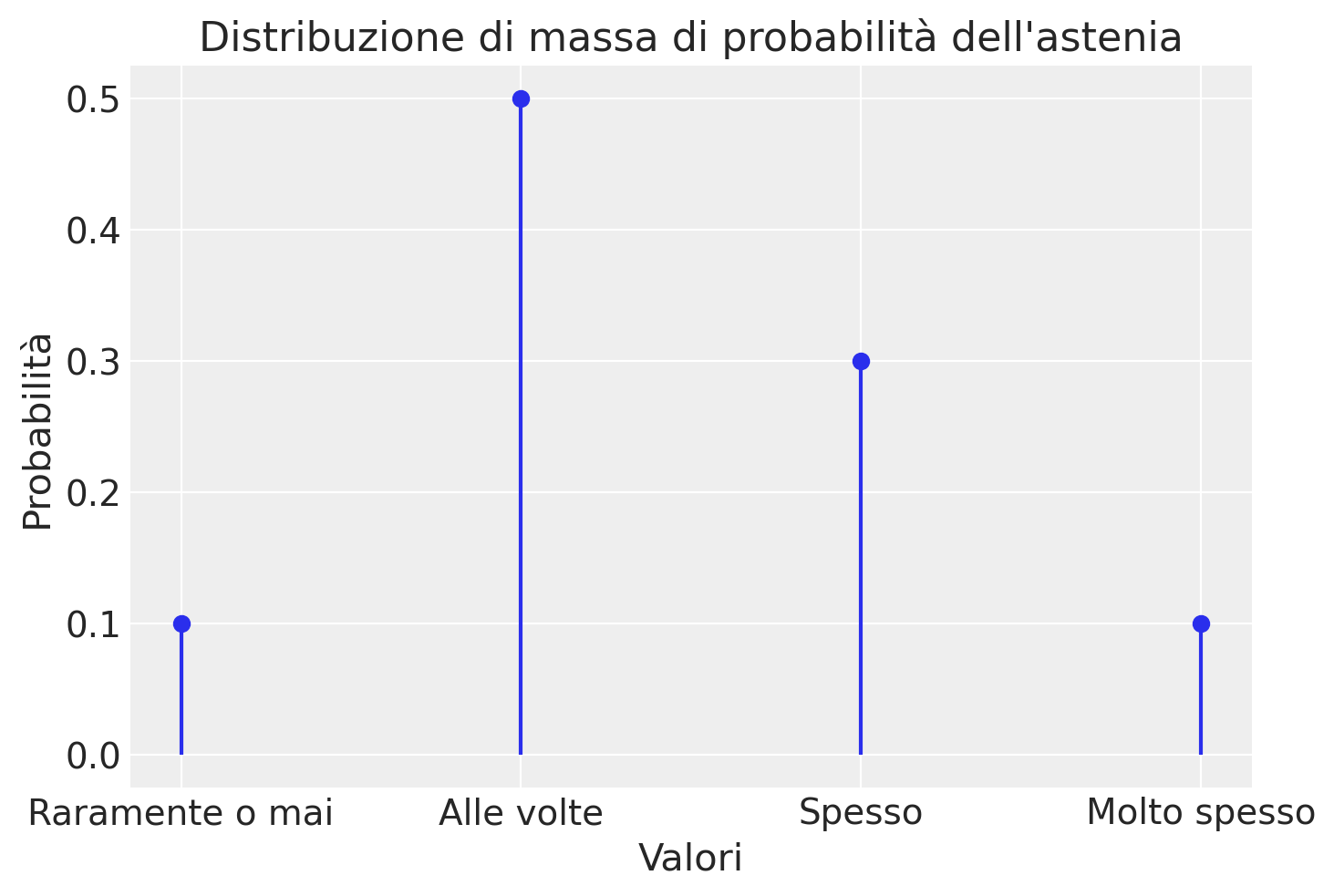
Iniziamo con la rappresentazione grafica della distribuzione di massa di probabilità.

# Definiamo i valori della distribuzione di massa di probabilità
valori = np.array([1, 2, 3, 4])
probabilita = np.array([0.1, 0.5, 0.3, 0.1])

# Creiamo lo stem plot per rappresentare la distribuzione di massa di probabilità
plt.stem(valori, probabilita, linefmt="-", markerfmt="o", basefmt=" ")

# Aggiungiamo etichette e titoli al grafico
plt.xlabel("Valori")
plt.ylabel("Probabilità")
plt.title("Distribuzione di massa di probabilità dell'astenia")
plt.xticks(valori, ["Raramente o mai", "Alle volte", "Spesso", "Molto spesso"])

# Mostrare il grafico
plt.show()

Per i punteggi di astenia di questo ipotetico test, poniamoci ora il problema di trovare il valore atteso e la varianza. In seguito, ci porreo il problema di assegnare un’interpretazione inuitiva a questi concetti.

Il valore atteso (o media) è dato da:

\[ E[X] = \sum_{i} x_i \cdot p_i. \]

La varianza è data da:

\[ Var[X] = \sum_{i} (x_i - E[X])^2 \cdot p_i. \]

Le tre istruzioni seguenti producono tutte lo stesso risultato. Le prime due usano le funzionalità di base di Python; la terza usa NumPy.

valore_atteso = sum(
    valore * probabilita for valore, probabilita in zip(valori, probabilita)
)
print(valore_atteso)

2.4

valore_atteso = sum(valori[i] * probabilita[i] for i in range(len(valori)))
print(valore_atteso)

2.4

valore_atteso = (valori * probabilita).sum()
print(valore_atteso)

2.4

Calcoliamo ora la varianza.

varianza = ((valori - valore_atteso) ** 2 * probabilita).sum()
print(varianza)

0.64

Per interare il risultato, svolgiamo una simulazione. Simuliamo la generazione di 100000 valori casuali per la variabile casuale che è stata definita.

valori_generati = np.random.choice(valori, size=100000, p=probabilita)
valori_generati.shape

(100000,)

Calcoliamo la media dei valori generati

media = np.mean(valori_generati)
print("Media dei valori generati:", media)

Media dei valori generati: 2.4022

Calcoliamo la varianza dei valori generati:

varianza = np.var(valori_generati)
print("Varianza dei valori generati:", varianza)

Varianza dei valori generati: 0.6401351600000001

Quindi l’interpretazione di valore atteso e di varianza di una v.c. è semplice: il valore atteso e la varianza di una variabile causale non sono altro che media e la varianza di un numero molto grande di realizzazioni della variabile casuale.

Watermark

%load_ext watermark
%watermark -n -u -v -iv -w -m

Last updated: Sun Jun 16 2024

Python implementation: CPython
Python version       : 3.12.3
IPython version      : 8.25.0

Compiler    : Clang 16.0.6 
OS          : Darwin
Release     : 23.4.0
Machine     : arm64
Processor   : arm
CPU cores   : 8
Architecture: 64bit

matplotlib: 3.8.4
arviz     : 0.18.0
pandas    : 2.2.2
numpy     : 1.26.4

Watermark: 2.4.3