Regressione multipla con Stan#
Preparazione del Notebook#
%run ../_config/config.py # Import the configuration settings
import logging
import cmdstanpy
import statsmodels.api as sm
cmdstanpy.utils.get_logger().setLevel(logging.ERROR)
from cmdstanpy import CmdStanModel
from scipy import stats
import pingouin as pg
Regressione multipla#
La regressione multipla rappresenta un’estensione del modello di regressione semplice, e permette di esplorare e quantificare le relazioni tra una variabile dipendente e più variabili indipendenti. Passando dal modello semplice \( y = a + bx + \text{errore} \) al modello più generale \( y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \text{errore} \), emergono nuove complessità. Queste includono le decisioni su quali predittori \( x \) includere nel modello, l’interpretazione dei coefficienti e delle loro interazioni, e la costruzione di nuovi predittori a partire dalle variabili esistenti per catturare elementi di discrezionalità e non linearità.
I coefficienti di regressione, in un contesto di regressione multipla, sono tipicamente più complicati da interpretare rispetto a quelli di un modello con un solo predittore. L’interpretazione di un dato coefficiente, infatti, è parzialmente condizionata dalle altre variabili presenti nel modello. Il coefficiente \( \beta_k \) rappresenta la differenza media o attesa nella variabile risposta \( y \), confrontando due individui che differiscono di un’unità nel predittore \( x_k \) ma sono identici per quanto riguarda gli altri predittori. Questo concetto è talvolta sintetizzato con l’espressione «confrontare due osservazionni (o persone) che differiscono per \( x_k \) a parità delle altre variabili».
Dal punto di vista dell’implementazione con Stan, l’estensione del modello per includere molteplici predittori dell’intelligenza del bambino è relativamente semplice. È necessario costruire una matrice \(X\) contenente le colonne che rappresentano i vari predittori che intendiamo analizzare. Per l’esempio specifico in questione, i predittori selezionati per l’intelligenza del bambino includono: la scolarità della madre (codificata come 0 o 1 a seconda che la madre abbia completato o meno le scuole superiori), l’intelligenza della madre e l’età della madre. Prima di procedere con l’analisi, è importante standardizzare tutte queste variabili per facilitare l’interpretazione dei risultati e migliorare la stabilità numerica del modello.
Consideriamo in dettaglio la verosimiglianza alpha + X * beta nel caso in cui \(X\) è una matrice con più di un predittore.
Prima di tutto, definiamo le variabili coinvolte:
y: è il vettore delle osservazioni, dove ogni elemento rappresenta un dato osservato.alpha: è l’intercetta del modello lineare, un singolo valore che rappresenta il punto in cui la linea del modello incrocia l’asse y quando tutte le variabili indipendenti (X) sono zero.X: è la matrice dei predittori (o variabili indipendenti), dove ogni riga corrisponde a un’osservazione e ogni colonna a una variabile indipendente.beta: è il vettore dei coefficienti, dove ogni elemento rappresenta l’effetto di una corrispondente variabile indipendente inXsulla variabile dipendentey.sigma: è la deviazione standard degli errori del modello, che misura quanto i dati reali si discostano dalla linea del modello.
L’espressione alpha + X * beta calcola i valori previsti (y predetti) per il modello lineare. Ecco come funziona, spiegato senza ricorrere all’algebra matriciale:
Moltiplicazione
X * beta: Per ogni riga inX(che rappresenta un’osservazione con le sue variabili indipendenti), moltiplichiamo ogni elemento (ogni variabile indipendente) per il corrispondente elemento inbeta(il coefficiente della variabile) e sommiamo questi prodotti. Questo ci dà un valore singolo per ogni osservazione, che rappresenta il contributo combinato di tutte le variabili indipendenti alla variabile dipendente, prima di aggiungere l’intercetta.Aggiunta di
alpha: Dopo aver calcolato il contributo combinato delle variabili indipendenti, aggiungiamo l’intercetta (alpha) a questo valore. L’intercetta rappresenta il valore diyquando tutte le variabili indipendenti sono zero. Aggiungendola, otteniamo il valore previsto finale peryper ogni osservazione.Risultato: L’espressione
alpha + X * betaproduce quindi un vettore di valori previsti di dimensione \(n \times 1\), dove \(n\) è il numero di osservazioni iny. Ogni elemento di questo vettore è il valore previsto diyper ogni osservazione, dato il modello lineare specificato.
Per fare un esempio semplice, immaginiamo di avere un modello con una sola variabile indipendente per semplificare:
Supponiamo che
alphasia 5 (l’intercetta).La matrice
Xha una sola colonna (una sola variabile indipendente) con, per esempio, tre osservazioni:[1, 2, 3].Il vettore
betaha un solo elemento, diciamo 2, che è il coefficiente della nostra variabile indipendente.
Per ogni osservazione in X, moltiplichiamo il suo valore per beta (2 in questo caso) e aggiungiamo alpha (5). Quindi, per la prima osservazione (1), otteniamo \(1 \times 2 + 5 = 7\), e così via per le altre osservazioni. Il risultato finale è un vettore di valori previsti di y.
Espandiamo ora l’esempio precedente per un caso di regressione multipla, dove abbiamo due variabili indipendenti (predittori). Questo ci permetterà di vedere come il processo di calcolo dei valori previsti si adatta quando ci sono più predittori nel modello.
alpha: l’intercetta del modello, diciamo che è 5.X: la matrice dei predittori ora ha due colonne, perché abbiamo due variabili indipendenti. Per esempio, possiamo avere tre osservazioni come segue:\[\begin{split} X = \begin{bmatrix} 1 & 3 \\ 2 & 2 \\ 3 & 1 \\ \end{bmatrix} \end{split}\]Qui, ogni riga rappresenta un’osservazione e ogni colonna rappresenta una variabile indipendente. Ad esempio, la prima riga rappresenta una osservazione dove il primo predittore ha valore 1 e il secondo predittore ha valore 3.
beta: il vettore dei coefficienti ora ha due elementi, uno per ogni variabile indipendente. Supponiamo chebeta = [2, 1], dove 2 è il coefficiente per il primo predittore e 1 è il coefficiente per il secondo predittore.sigma: la deviazione standard degli errori del modello, che per semplicità non utilizzeremo direttamente in questo esempio.
Per calcolare i valori previsti (y predetti) per ogni osservazione, seguiamo questi passi:
Moltiplicazione
X * beta:Per la prima osservazione (
[1, 3]), calcoliamo: \(1 \times 2 + 3 \times 1 = 2 + 3 = 5\).Per la seconda osservazione (
[2, 2]), calcoliamo: \(2 \times 2 + 2 \times 1 = 4 + 2 = 6\).Per la terza osservazione (
[3, 1]), calcoliamo: \(3 \times 2 + 1 \times 1 = 6 + 1 = 7\).
Questo passo ci dà il contributo combinato delle variabili indipendenti alla variabile dipendente per ogni osservazione.
Aggiunta di
alpha:Aggiungiamo l’intercetta
alpha(5) ai risultati precedenti per ottenere i valori previsti finali diy:Prima osservazione: \(5 + 5 = 10\).
Seconda osservazione: \(6 + 5 = 11\).
Terza osservazione: \(7 + 5 = 12\).
Risultato:
Otteniamo quindi un vettore di valori previsti di
ydi dimensione \(n \times 1\), dove \(n\) è il numero di osservazioni. In questo caso, il vettore dei valori previsti diysarà[10, 11, 12].
Questo esempio illustra come l’espressione alpha + X * beta in un contesto di regressione multipla produca un vettore di valori previsti. Ogni valore previsto è il risultato della somma del prodotto dei predittori per i loro rispettivi coefficienti più l’intercetta, riflettendo come il modello lineare stima y in base ai valori di più variabili indipendenti.
Un esempio pratico#
Per fare un esempio pratico, analizzeremo nuovamente i dati sull’intelligenza di un gruppo di bambini. In questo caso, cercheremo di predire l’intelligenza media dei bambini considerando tre fattori: se le madri hanno completato la scuola superiore, l’intelligenza della madre e l’età della madre.
Importiamo i dati:
kidiq = pd.read_stata("../data/kidiq.dta")
kidiq.head()
| kid_score | mom_hs | mom_iq | mom_work | mom_age | |
|---|---|---|---|---|---|
| 0 | 65 | 1.0 | 121.117529 | 4 | 27 |
| 1 | 98 | 1.0 | 89.361882 | 4 | 25 |
| 2 | 85 | 1.0 | 115.443165 | 4 | 27 |
| 3 | 83 | 1.0 | 99.449639 | 3 | 25 |
| 4 | 115 | 1.0 | 92.745710 | 4 | 27 |
Stampiamo il modello Stan di regressione multipla per questi dati. Il modello assume che i dati siano standardizzati.
stan_file = os.path.join('stan', 'linear_regression.stan')
with open(stan_file, 'r') as f:
print(f.read())
// run with 4 chains and 2k iters.
// all data should be scaled to mean 0 and std 1:
data {
int<lower=1> N; // number of observations
int<lower=1> K; // number of independent variables, including the intercept
matrix[N, K] X; // data matrix
vector[N] y; // dependent variable vector
}
parameters {
real alpha; // intercept
vector[K] beta; // coefficients for independent variables
real<lower=0> sigma; // model error
}
model {
// priors
alpha ~ student_t(3, 0, 2.5);
beta ~ student_t(3, 0, 2.5);
sigma ~ exponential(1);
// likelihood
y ~ normal(alpha + X * beta, sigma);
}
generated quantities {
vector[N] log_lik; // Log-likelihood for each observation
vector[N] y_rep; // Posterior predictions for each observation
for (n in 1:N) {
log_lik[n] = normal_lpdf(y[n] | alpha + dot_product(X[n], beta), sigma);
y_rep[n] = normal_rng(alpha + dot_product(X[n], beta), sigma);
}
}
Compiliamo il modello.
model = CmdStanModel(stan_file=stan_file)
Standaridizziamo i predittori:
x1 = stats.zscore(kidiq["mom_hs"])
x2 = stats.zscore(kidiq["mom_iq"])
x3 = stats.zscore(kidiq["mom_age"])
df = pd.DataFrame({
"one": [1] * len(x1), # Crea una lista di 1 della stessa lunghezza di x1
"x1": x1,
"x2": x2,
"x3": x3
})
df.head()
| one | x1 | x2 | x3 | |
|---|---|---|---|---|
| 0 | 1 | 0.522233 | 1.409460 | 1.562029 |
| 1 | 1 | 0.522233 | -0.710026 | 0.820727 |
| 2 | 1 | 0.522233 | 1.030732 | 1.562029 |
| 3 | 1 | 0.522233 | -0.036733 | 0.820727 |
| 4 | 1 | 0.522233 | -0.484177 | 1.562029 |
# Convert scaled DataFrame to numpy matrix
X = df.to_numpy()
# Verificare le dimensioni di X
print("Dimensioni di X:", X.shape)
Dimensioni di X: (434, 4)
Creiamo un dizionario con i dati nel formato atteso da Stan:
stan_data = {
"N": X.shape[0],
"K": X.shape[1], # Nota: questa include anche la colonna dell'intercetta
"X": X,
"y": stats.zscore(kidiq["kid_score"]) # Assumo che kid_score sia la variabile dipendente
}
Eseguiamo il campionamento MCMC:
fit2 = model.sample(
data=stan_data,
iter_warmup=1_000,
iter_sampling=2_000,
seed=123,
show_progress=False,
show_console=False
)
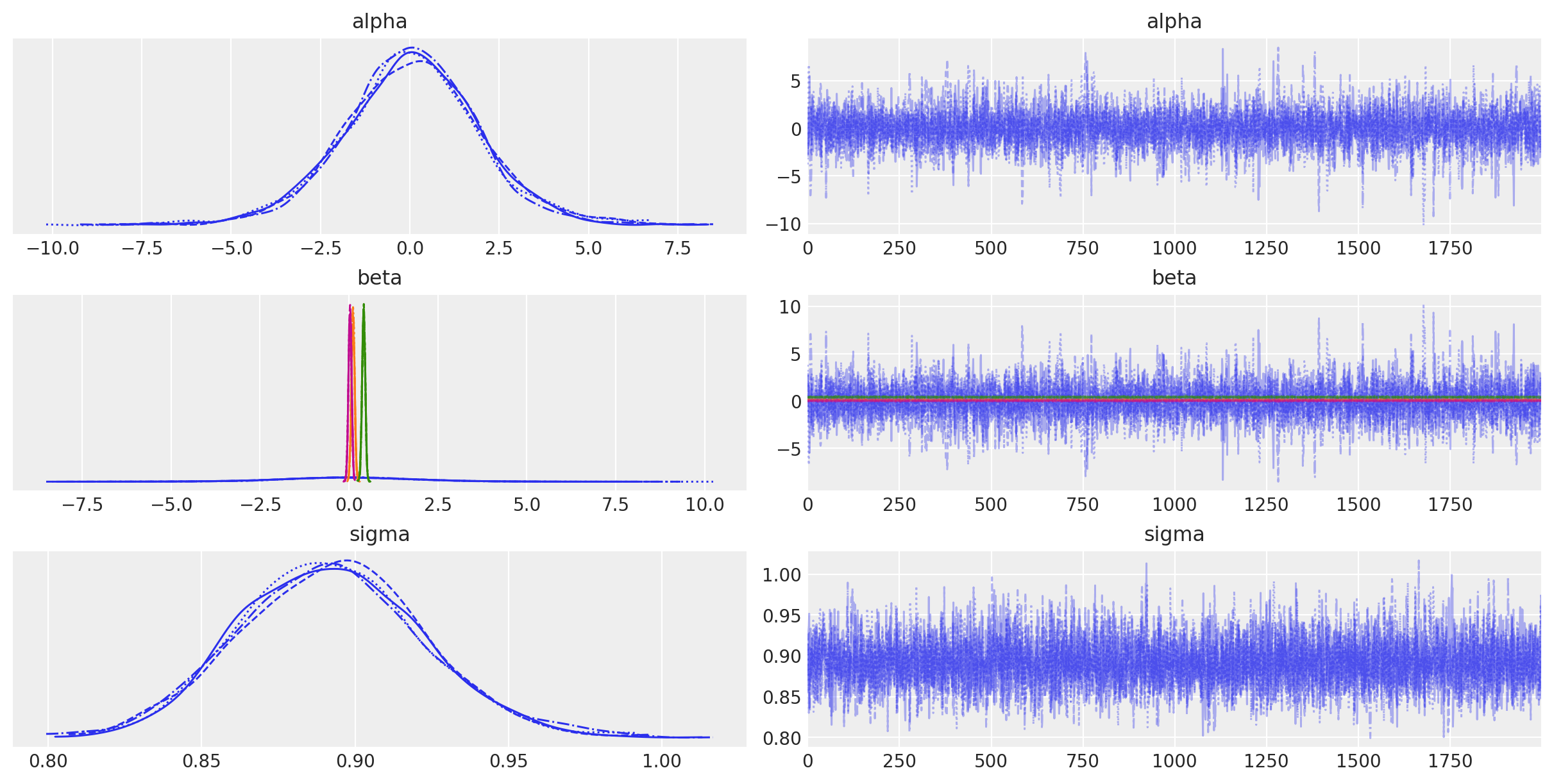
Esaminiamo le tracce dei parametri:
# Zoom in
axes = az.plot_trace(fit2, var_names=["beta"])
for ax_row in axes:
ax_row[0].set_xlim(-0.25, 0.75) # Modifica solo l'asse del grafico della densità
plt.show()
Anche nel caso della regressione multipla, i risultati ottenuti con l’approccio bayesiano sono molto simili a quelli prodotti dall’approccio basato sulla massima verosimiglianza.
Calcoliamo una sintesi delle distribuzioni a posteriori dei parametri:
az.summary(fit2, var_names=(["alpha", "beta", "sigma"]), hdi_prob=0.94)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha | 0.020 | 1.958 | -3.680 | 3.784 | 0.030 | 0.027 | 4412.0 | 2963.0 | 1.0 |
| beta[0] | -0.021 | 1.959 | -3.652 | 3.794 | 0.030 | 0.027 | 4414.0 | 3080.0 | 1.0 |
| beta[1] | 0.114 | 0.045 | 0.032 | 0.202 | 0.001 | 0.000 | 5939.0 | 5353.0 | 1.0 |
| beta[2] | 0.413 | 0.044 | 0.325 | 0.489 | 0.001 | 0.000 | 7429.0 | 5414.0 | 1.0 |
| beta[3] | 0.030 | 0.043 | -0.053 | 0.109 | 0.001 | 0.000 | 7277.0 | 5658.0 | 1.0 |
| sigma | 0.892 | 0.030 | 0.836 | 0.949 | 0.000 | 0.000 | 6955.0 | 5019.0 | 1.0 |
Replichiamo il risultato usando l’approccio di massima verosimiglianza:
lm = pg.linear_regression(X, stats.zscore(kidiq["kid_score"]))
lm.round(2)
| names | coef | se | T | pval | r2 | adj_r2 | CI[2.5%] | CI[97.5%] | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Intercept | -0.00 | 0.04 | -0.00 | 1.00 | 0.21 | 0.21 | -0.08 | 0.08 |
| 1 | x2 | 0.11 | 0.05 | 2.50 | 0.01 | 0.21 | 0.21 | 0.02 | 0.20 |
| 2 | x3 | 0.41 | 0.04 | 9.28 | 0.00 | 0.21 | 0.21 | 0.33 | 0.50 |
| 3 | x4 | 0.03 | 0.04 | 0.68 | 0.50 | 0.21 | 0.21 | -0.06 | 0.12 |
Nel contesto della regressione multivariata, l’interpretazione dei coefficienti parziali differisce da quella della regressione bivariata. Nel nostro caso, il coefficiente associato all’intelligenza della madre, indicato come \(\beta\) = 0.41, assume il seguente significato: prevediamo che l’intelligenza del bambino aumenti di 0.41 deviazioni standard in media per ogni deviazione standard aggiuntiva nell’intelligenza della madre, mantenendo costanti gli effetti del livello di istruzione e dell’età della madre. Questo implica che stiamo considerando l’impatto dell’intelligenza della madre sull’intelligenza del bambino all’interno di una popolazione di madri che sono omogenee per quanto riguarda il livello di istruzione e l’età.
Calcoliamo la distribuzione predittiva a posteriori e generiamo il PPC plot:
idata2 = az.from_cmdstanpy(
posterior=fit2,
posterior_predictive='y_rep',
observed_data={'y': stats.zscore(kidiq["kid_score"])},
)
Per fare un esercizio, riscriviamo il modello senza usare l’algebra matriciale.
stan_file = os.path.join("stan", "mreg.stan")
with open(stan_file, "r") as f:
print(f.read())
data {
int<lower=1> N; // Numero di osservazioni
int<lower=1> K; // Numero di variabili indipendenti, intercetta inclusa
vector[N] x1; // Prima variabile indipendente
vector[N] x2; // Seconda variabile indipendente
vector[N] x3; // Seconda variabile indipendente
// Aggiungi altri vettori se ci sono più variabili indipendenti
vector[N] y; // Vettore della variabile dipendente
}
parameters {
real alpha; // Intercetta
real beta1; // Coefficiente per la prima variabile indipendente
real beta2; // Coefficiente per la seconda variabile indipendente
real beta3; // Coefficiente per la terza variabile indipendente
// Definisci altri real per ulteriori coefficienti
real<lower=0> sigma; // Errore del modello
}
model {
// Prior
alpha ~ student_t(3, 0, 2.5);
beta1 ~ student_t(3, 0, 2.5);
beta2 ~ student_t(3, 0, 2.5);
beta3 ~ student_t(3, 0, 2.5);
// Definisci prior per altri coefficienti
sigma ~ exponential(1);
// Likelihood
for (n in 1:N) {
y[n] ~ normal(alpha + beta1 * x1[n] + beta2 * x2[n] + + beta3 * x3[n], sigma);
// Aggiungi termini per altri coefficienti se necessario
}
}
generated quantities {
vector[N] log_lik; // Log-likelihood per ogni osservazione
vector[N] y_rep; // Predizioni posteriori per ogni osservazione
for (n in 1:N) {
log_lik[n] = normal_lpdf(y[n] | alpha + beta1 * x1[n] + beta2 * x2[n] + + beta3 * x3[n], sigma);
// Aggiungi termini per altri coefficienti se necessario
y_rep[n] = normal_rng(alpha + beta1 * x1[n] + beta2 * x2[n] + beta3 * x3[n], sigma);
// Aggiungi termini per altri coefficienti se necessario
}
}
Compiliamo il modello.
model3 = CmdStanModel(stan_file=stan_file)
Generiamo il dizionario con i dati nel formato appropriato per Stan.
stan_data = {
"N": df.shape[0],
"K": 4, # Nota: questa include anche la colonna dell'intercetta
"x1": x1,
"x2": x2,
"x3": x3,
"y": stats.zscore(kidiq["kid_score"])
}
Eseguiamo il campionamento.
fit3 = model3.sample(
data=stan_data,
iter_warmup=1_000,
iter_sampling=2_000,
seed=123,
show_progress=False,
show_console=False
)
I risultati replicano quelli ottenuti in precedenza.
az.summary(
fit3,
var_names=(["alpha", "beta1", "beta2", "beta3", "sigma"]),
hdi_prob=0.94
)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha | -0.000 | 0.043 | -0.082 | 0.080 | 0.0 | 0.001 | 9553.0 | 5261.0 | 1.0 |
| beta1 | 0.114 | 0.045 | 0.031 | 0.201 | 0.0 | 0.000 | 9409.0 | 6308.0 | 1.0 |
| beta2 | 0.414 | 0.044 | 0.330 | 0.496 | 0.0 | 0.000 | 9556.0 | 6280.0 | 1.0 |
| beta3 | 0.029 | 0.043 | -0.050 | 0.112 | 0.0 | 0.000 | 9647.0 | 6545.0 | 1.0 |
| sigma | 0.891 | 0.031 | 0.835 | 0.949 | 0.0 | 0.000 | 9403.0 | 5961.0 | 1.0 |
Interpretazione dei coefficienti#
Una differenza chiave rispetto al modello di regressione bivariato è nell’interpretazione dei coefficienti. Nel caso bivariato, il coefficiente \(\beta_1\) viene interpretato come il cambiamento atteso in \(Y\) al variare di una unità in \(X_1\). Tuttavia, nel modello di regressione multipla, l’interpretazione di \(\beta_1\) cambia. In questo caso, \(\beta_1\) rappresenta il cambiamento atteso in \(Y\) al variare di una unità in \(X_1\), mantenendo costanti gli effetti di tutte le altre variabili \(X_2, X_3, \ldots, X_p\). In altre parole, \(\beta_1\) ci dice come varia in media \(Y\) quando \(X_1\) cambia, ma considera che altre variabili possono variare insieme a \(X_1\), e \(\beta_1\) tiene conto di queste variazioni.
Cosa significa mantenere costante l’effetto di altre variabili? Consideriamo l’esempio della correlazione tra il numero di scarpe e le abilità matematiche. Esiste una marcata correlazione positiva tra queste due variabili. Tuttavia, è evidente che i bambini, avendo in genere numeri di scarpe più piccoli rispetto agli adulti, mostrano anche, presumibilmente, minori capacità matematiche. Questo esempio illustra che, se controlliamo per l’età, ossia se consideriamo solo soggetti della stessa età, la correlazione tra il numero di scarpe e le abilità matematiche scompare. Pertanto, nell’analisi della relazione tra abilità matematiche (Y) e numero di scarpe (X), l’età (Z) agisce come variabile confondente. Controllare per Z significa esaminare la relazione tra Y e X limitandosi a individui della stessa età.
Ma ovviamente questo controllo empirico non è sempre possibile. Nel modello di regressione, esso viene «approssimato» con una procedura statistica.
Esempio. In questo esempio illustreremo la procedura statistica utilizzata per isolare l’effetto di una variabile controllando per un’altra.
# Creiamo dei dati di esempio
np.random.seed(0)
N = 100
X1 = np.random.normal(0, 1, N)
X2 = X1 + np.random.normal(0, 0.5, N)
Y = 1 + 2 * X1 + 3 * X2 + np.random.normal(0, 1, N)
# Modello completo Y ~ X1 + X2
model_full = sm.OLS(Y, sm.add_constant(np.column_stack((X1, X2))))
results_full = model_full.fit()
# Regressione di Y su X2
model_Y_on_X2 = sm.OLS(Y, sm.add_constant(X2))
residuals_Y = model_Y_on_X2.fit().resid
# Regressione di X1 su X2
model_X1_on_X2 = sm.OLS(X1, sm.add_constant(X2))
residuals_X1 = model_X1_on_X2.fit().resid
# Regressione dei residui di Y sui residui di X1
model_residuals = sm.OLS(residuals_Y, sm.add_constant(residuals_X1))
results_residuals = model_residuals.fit()
# Stampiamo i risultati
print("Coefficient from full model for X1: {:.4f}".format(results_full.params[1]))
print(
"Coefficient from regression of residuals: {:.4f}".format(
results_residuals.params[1]
)
)
Coefficient from full model for X1: 1.9782
Coefficient from regression of residuals: 1.9782
Questo esempio illustra il concetto di coefficiente parziale di regressione. Questo coefficiente quantifica l’effetto della variabile esplicativa \(X_j\) sulla variabile dipendente \(Y\), depurando l’effetto di \(X_j\) dall’influenza degli altri predittori nel modello. In sostanza, il coefficiente parziale di regressione valuta l’impiego di \(X_j\) su \(Y\) quando \(X_j\) è considerata linearmente indipendente rispetto agli altri predittori \(X\). L’effetto misurato è quindi quello della sola componente di \(X_j\) che non è spiegata linearmente dai restanti predittori \(X\) sulla parte di \(Y\) che è anch’essa indipendente dai medesimi predittori.
Per chiarire ulteriormente, questo approccio statistico si focalizza sull’analizzare l’effetto di \(X_j\) eliminando l’influenza lineare degli altri predittori \(X\). È simile a valutare la relazione tra \(Y\) e \(X_j\) in un contesto ideale dove tutti gli individui presentano livelli identici per le altre variabili \(X\). Tale metodo non eguaglia gli effetti non lineari che possono essere presenti tra le variabili, limitandosi a correggere solo per le associazioni lineari. In questo modo, il controllo statistico tenta di approssimare una condizione di omogeneità tra i soggetti rispetto alle altre variabili \(X\), consentendo di isolare e valutare più precisamente l’effetto puro di \(X_j\) su \(Y\).
Quali predittori includere nel modello?#
L’utilizzo del modello di regressione multipla ha principalmente due scopi. In primo luogo, è utilizzato per la predizione, cioè per ottenere la migliore stima possibile di \(Y\) utilizzando una combinazione lineare delle variabili \(X_1, X_2, \ldots, X_p\). In questo contesto, i coefficienti \(\beta_i\) sono considerati come pesi che permettono di effettuare questa previsione.
In secondo luogo, il modello di regressione multipla viene spesso utilizzato per descrivere le relazioni causali tra le variabili. Tuttavia, è importante sottolineare che questo modello non è stato originariamente creato per stabilire relazioni causali, ed è necessario essere cauti nell’attribuire interpretazioni causali dirette ai coefficienti \(\beta_i\). Questo perché il modello stima correttamente i coefficienti parziali di regressione solo quando tutte le variabili che influenzano \(Y\) sono incluse nel modello. Nella pratica, spesso non conosciamo tutte le variabili causalmente rilevanti, il che può portare a problemi di errore di specificazione.
I modello di regressione multipla rappresenta uno strumento potente per predire e analizzare le relazioni tra variabili. Tuttavia, è fondamentale riconoscerne le limitazioni, specialmente quando si tentano interpretazioni causali. In ambiti come la psicologia, dove è cruciale comprendere le dinamiche causali, diventa essenziale una scelta accurata delle variabili da includere nel modello per prevenire distorsioni nelle stime dei coefficienti di regressione.
Tradizionalmente, si riteneva vantaggioso includere nel modello il maggior numero possibile di variabili per ottenere un livello di «controllo» statistico più elevato. Tuttavia, come sottolineato da McElreath [McE20], questo metodo può trasformarsi in una «insalata causale». Questo termine descrive una situazione in cui la mancanza di attenzione alla struttura causale tra le variabili può portare all’inclusione di variabili di controllo inappropriate, causando distorsioni nelle stime.
In alcuni casi, l’inserimento di determinate variabili di controllo nel modello è indispensabile per evitare distorsioni, mentre in altri casi, l’inclusione di variabili non pertinenti può portare a risultati fuorvianti. Questo enfatizza l’importanza di formulare ipotesi chiare e ben ponderate sulla struttura causale che intercorre tra le variabili in esame.
L’efficacia e la validità dei risultati ottenuti tramite regressione dipendono strettamente dalla correttezza delle ipotesi causali formulate, sia esplicitamente che implicitamente, dal ricercatore. Pertanto, per superare i limiti dell’approccio dell“«insalata causale», è cruciale che la formulazione del modello di regressione rifletta attentamente tali ipotesi causali.
Una nota di cautela sui modelli di regressione#
Nel suo libro Statistical Rethinking, McElreath [McE20] introduce l’idea di modelli statistici paragonandoli ai Golem, antiche creature della mitologia, prive di volontà propria e animate solo dall’intento di chi le crea. Questi enti, pur essendo dotati di grande forza, possono diventare pericolosi se non guidati con saggezza.
McElreath [McE20] sostiene che gli scienziati, nella creazione di modelli matematici e software, diano vita a moderni equivalenti di questi Golem. Questi modelli, sebbene influenzino il mondo reale tramite le loro previsioni e le intuizioni che generano, non dovrebbero essere considerati né completamente veritieri né falsi. Essi sono piuttosto strumenti sviluppati con uno scopo specifico, capaci di operare calcoli con estrema precisione, ma privi della capacità di comprendere o interpretare il contesto più ampio in cui sono applicati.
In particolare, il modello di regressione viene esaminato come esempio di come tali strumenti possano produrre risultati concreti, ma manchino di adattabilità e giudizio autonomo, limitando la loro efficacia nel trattare questioni che richiedono un approccio più creativo e comprensivo. McElreath [McE20] enfatizza ulteriormente che nessun strumento statistico, da solo, è sufficiente per affrontare adeguatamente il complesso problema dell’inferenza causale a partire da dati empirici. Questi modelli, privi di una reale comprensione delle dinamiche di causa ed effetto, si limitano a descrivere relazioni tra variabili. Senza un’interpretazione critica e un orientamento consapevole da parte degli scienziati, questi strumenti, creati per fini ben definiti, possono rivelarsi non solo inefficaci, ma anche potenzialmente dannosi.
Informazioni sull’Ambiente di Sviluppo#
%load_ext watermark
%watermark -n -u -v -iv -w -m
Last updated: Wed Jul 17 2024
Python implementation: CPython
Python version : 3.12.4
IPython version : 8.26.0
Compiler : Clang 16.0.6
OS : Darwin
Release : 23.5.0
Machine : arm64
Processor : arm
CPU cores : 8
Architecture: 64bit
statsmodels: 0.14.2
cmdstanpy : 1.2.4
pandas : 2.2.2
logging : 0.5.1.2
pingouin : 0.5.4
arviz : 0.18.0
matplotlib : 3.9.1
scipy : 1.14.0
numpy : 1.26.4
Watermark: 2.4.3