Zucchero sintattico

I modelli lineari sono così ampiamente utilizzati che sono stati sviluppati appositamente una sintassi, dei metodi e delle librerie per la regressione. Una di queste librerie è bambi (BAyesian Model-Building Interface). bambi è un pacchetto Python progettato per adattare modelli gerarchici generalizzati lineari (di cui il modello lineare bivariato è un caso particolare), utilizzando una sintassi simile a quella presente nei pacchetti R, come lme4, nlme, rstanarm o brms. bambi si basa su PyMC, ma offre un’API di livello superiore.

In questo capitolo esploreremo come condurre un’analisi di regressione utilizzando bambi invece di cmdstan.

Preparazione del Notebook

%run ../_config/config.py # Import the configuration settings
import logging

import cmdstanpy

cmdstanpy.utils.get_logger().setLevel(logging.ERROR)
import bambi as bmb

BAyesian Model-Building Interface

Leggiamo i dati utilizzati nel capitolo precedente.

df = pd.read_csv('../data/Howell_18.csv')

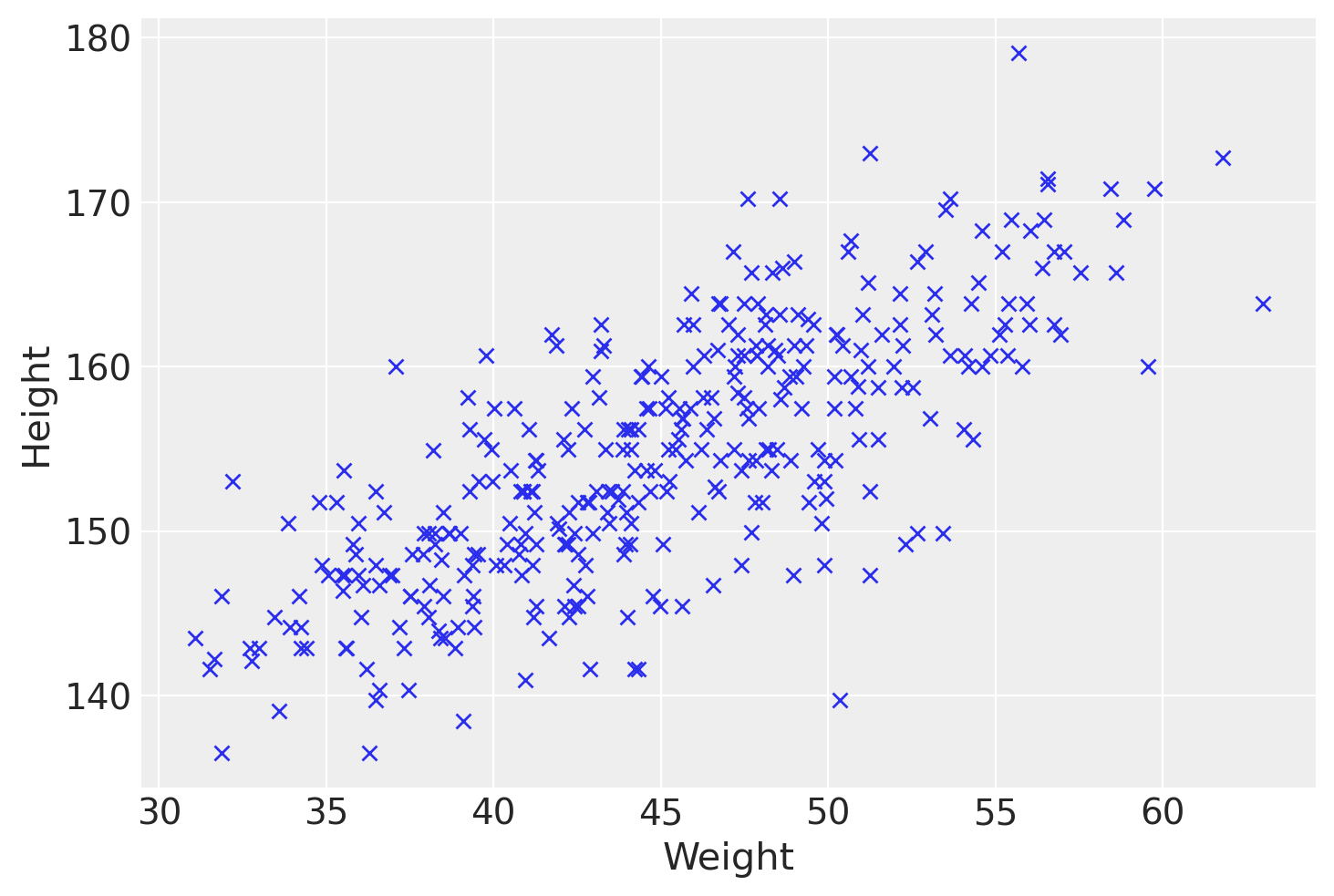
Generiamo un diagramma a dispersione:

plt.plot(df["weight"], df["height"], "x")
plt.xlabel("Weight")
plt.ylabel("Height")

Text(0, 0.5, 'Height')

Bambi si concentra sui modelli di regressione e questa restrizione porta a una sintassi più semplice, ovvero la sintassi di Wilkinson []. Inoltre, bambi implementa delle distribuzioni a priori ottimizzate, eliminando così la necessità di definirle esplicitamente. Tuttavia, se si preferisce un maggiore controllo sulle distribuzioni a priori, è possibile specificarle manualmente.

Per replicare il modello descritto nel capitolo precedente possiamo utilizzare la seguente istruzione.

df["weight_c"] = df["weight"] - np.mean(df["weight"])

model = bmb.Model("height ~ weight_c", df)

Sul lato sinistro della tilde (∼), abbiamo la variabile dipendente, e sul lato destro, le variabili indipendenti. Con questa sintassi, stiamo semplicemente specificando la media (μ nel modello lm di PyMC). Per impostazione predefinita, Bambi assume che la verosimiglianza sia gaussiana; è possibile modificarla con l’argomento family. La sintassi della formula non specifica la distribuzione delle priors, ma solo come sono associate le variabili dipendenti e indipendenti. Bambi definirà automaticamente delle priors (molto) debolmente informative per noi. Possiamo ottenere ulteriori informazioni stampando il modello Bambi.

print(model)

       Formula: height ~ weight_c
        Family: gaussian
          Link: mu = identity
  Observations: 352
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 154.5971, sigma: 19.3283)
            weight_c ~ Normal(mu: 0.0, sigma: 2.9978)
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 7.7313)

La descrizione inizia mostrando la formula utilizzata per definire il modello, y ~ x, che indica come la variabile dipendente y è predetta dalla variabile indipendente x in una relazione lineare. La seconda riga specifica che si sta utilizzando una distribuzione gaussiana (normale) come funzione di verosimiglianza per il modello, il che implica l’assunzione che i residui del modello (le differenze tra i valori osservati e i valori predetti) seguano una distribuzione normale.

La terza riga menziona la funzione di collegamento, in questo caso l’identità, che non applica alcuna trasformazione al valore atteso della variabile dipendente. Questo è caratteristico dei modelli lineari, dove il valore atteso di y è direttamente modellato come una combinazione lineare delle variabili indipendenti (E(Y) = \alpha + \beta x). È importante notare che, nei modelli lineari generalizzati, la funzione di collegamento gioca un ruolo cruciale nel collegare il valore atteso della variabile risposta alla combinazione lineare delle variabili predittive.

Segue il numero di osservazioni utilizzate per adattare il modello, indicando la dimensione del dataset su cui il modello è stato allenato.

La parte successiva dell’output dettaglia i priors utilizzati per i parametri del modello. In Bambi, i priors sono assunzioni a priori sui valori dei parametri prima di osservare i dati. Questi priors aiutano a guidare l’inferenza, soprattutto in presenza di dati limitati o per regolarizzare il modello. L’intercetta (Intercept) ha un prior normale con media (mu) 2.0759 e deviazione standard (sigma) 3.9401, indicando la posizione iniziale attesa della linea di regressione e quanto ci si aspetta che vari. Il coefficiente della variabile x ha anch’esso un prior normale, centrato in zero con una deviazione standard ampia (6.8159), riflettendo incertezza su quale possa essere il vero effetto di x su y senza presupporre una direzione specifica dell’effetto.

La sezione finale riguarda i parametri ausiliari del modello, in questo caso il parametro sigma della distribuzione gaussiana, che rappresenta la deviazione standard dei residui del modello. Questo ha un prior HalfStudentT, che è una distribuzione che ammette solo valori positivi (essendo la deviazione standard sempre positiva), con un grado di libertà (nu) 4.0 e una scala (sigma) 0.791. Questo prior è scelto per la sua flessibilità e la capacità di gestire dati con potenziali outlier.

model.build()
model.graph()

Eseguiamo il campionamento MCMC.

idata = model.fit(
    nuts_sampler="numpyro",
    idata_kwargs={"log_likelihood": True}
)

Show code cell output Hide code cell output

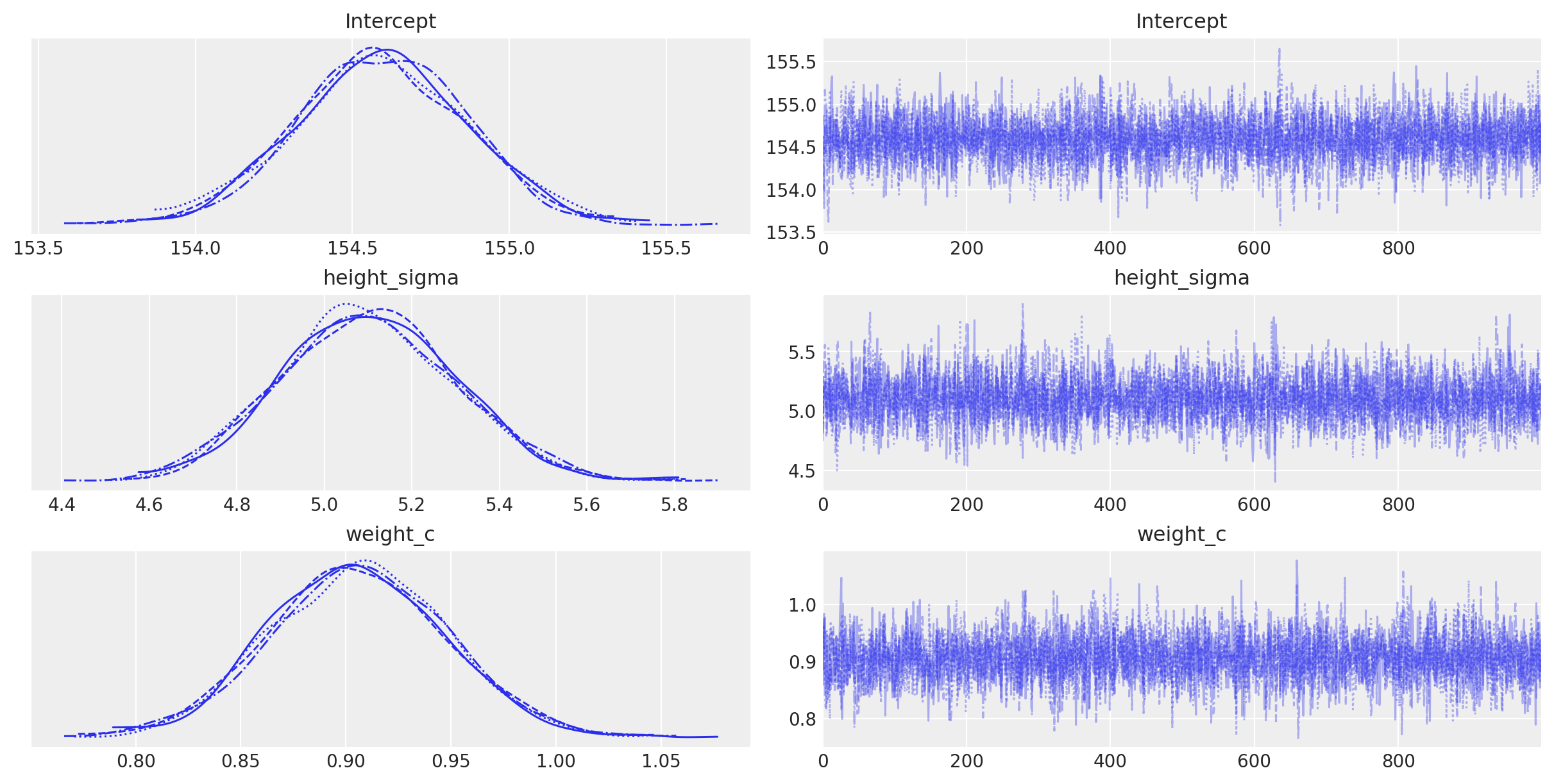
Le distribuzioni a posteriori dei parametri e i trace plot si ottengono con la seguente istruzione.

_ = az.plot_trace(idata)

Un sommario numerico delle distribuzioni a posteriori dei parametri si ottiene con az.summary.

az.summary(idata, round_to=2)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
Intercept	154.59	0.27	154.06	155.08	0.0	0.0	4702.31	2889.65	1.0
height_sigma	5.10	0.20	4.72	5.46	0.0	0.0	4241.08	2884.71	1.0
weight_c	0.91	0.04	0.83	0.99	0.0	0.0	4037.20	2604.30	1.0

I dati replicano quelli ottenuti in precedenza.

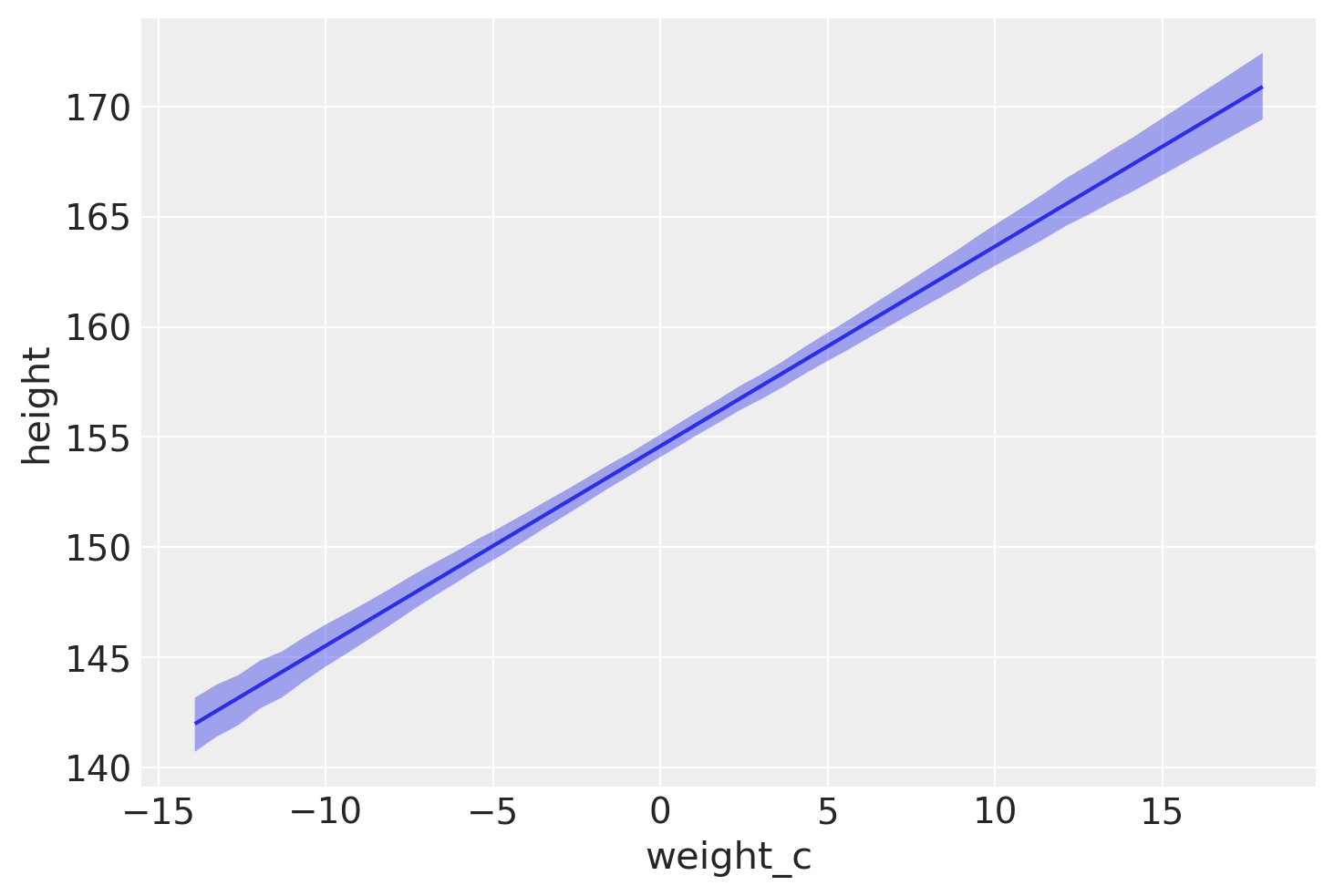
Possiamo anche generare un grafico che descrive l’incertezza a posteriori delle predizioni del modello.

La funzione plot_predictions del pacchetto Bambi serve per facilitare l’interpretazione dei modelli di regressione attraverso la visualizzazione grafica. Il metodo appartiene al sottomodulo interpret di Bambi e si concentra sulla rappresentazione delle previsioni generate dal modello.

Quando si esegue la funzione plot_predictions con i parametri specificati (model, idata, ["weight_c"]), essa produce un grafico che sintetizza le previsioni del modello in relazione a una o più variabili indipendenti. In questo caso, il parametro model indica il modello di regressione Bayesiana costruito con Bambi, idata rappresenta i dati inferenziali (ottenuti tramite il fit del modello), e ["weight_c"] specifica la variabile indipendente da considerare per il grafico.

bmb.interpret.plot_predictions(model, idata, ["weight_c"]);

Il grafico generato da questa funzione illustra due aspetti principali:

1. Media Posteriore di y: Il grafico include una linea che rappresenta la media posteriore della variabile dipendente (height) rispetto alla variabile indipendente specificata (weight_c). La media posteriore è una stima centrale delle previsioni del modello, che riflette la posizione più probabile dei valori di height data l’evidenza fornita dai dati.

2. Intervallo di Densità più Alta del 94%: Attorno alla retta della media posteriore, il grafico mostra anche un’area evidenziata che rappresenta l’intervallo di densità più alta (HDI) del 94%. Questo intervallo è un modo per quantificare l’incertezza delle previsioni del modello. L’HDI del 94% significa che, data la distribuzione posteriore delle previsioni di height, c’è il 94% di probabilità che il valore vero di height cada all’interno di questo intervallo per un dato valore di weight_c. Questo fornisce una misura visiva dell’incertezza associata alle stime del modello.

Informazioni sull’Ambiente di Sviluppo

%load_ext watermark
%watermark -n -u -v -iv -w -m 

Last updated: Sun Jun 16 2024

Python implementation: CPython
Python version       : 3.12.3
IPython version      : 8.25.0

Compiler    : Clang 16.0.6 
OS          : Darwin
Release     : 23.4.0
Machine     : arm64
Processor   : arm
CPU cores   : 8
Architecture: 64bit

logging   : 0.5.1.2
matplotlib: 3.8.4
cmdstanpy : 1.2.3
pandas    : 2.2.2
arviz     : 0.18.0
numpy     : 1.26.4
bambi     : 0.13.0

Watermark: 2.4.3