18 Analisi delle componenti principali

In questo capitolo imparerai a

eseguire la PCA usando l’algebra lineare;
eseguire la PCA usando R.

Prerequisiti

Leggere il capitolo Factor Analysis and Principal Component Analysis del testo di Petersen (2024).

Preparazione del Notebook

here::here("code", "_common.R") |> 
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(readr)

18.1 Introduzione

L’Analisi delle Componenti Principali (PCA) è una tecnica statistica utilizzata per ridurre la dimensionalità di un insieme di dati. Il suo obiettivo è quello di semplificare analisi complesse conservando quanta più informazione possibile, cioè spiegando la maggior parte della varianza presente nei dati originali.

La PCA trasforma un insieme di variabili iniziali, spesso correlate tra loro, in un nuovo insieme di variabili non correlate dette componenti principali. Queste componenti sono combinazioni lineari delle variabili originali e sono ordinate in base alla quantità di varianza che riescono a spiegare.

18.2 Perché Usare la PCA in Psicologia?

In psicologia, ci troviamo spesso a lavorare con dati ad alta dimensionalità: questionari con decine di item, batterie di test, o set di dati raccolti tramite studi longitudinali. La PCA è utile perché:

semplifica l’interpretazione dei dati, riducendo molte variabili a poche dimensioni latenti;
elimina ridondanze: se due o più variabili sono altamente correlate, la PCA può rappresentarle con un’unica componente;
favorisce la visualizzazione, soprattutto nei casi in cui si riescano a ridurre i dati a 2 o 3 componenti principali;
prepara i dati per analisi successive come regressioni o modelli strutturali, evitando collinearità tra predittori.

🧩 Esempio tipico: un questionario su tratti di personalità con 50 item può essere ridotto a 5 componenti principali che riflettono le dimensioni dei Big Five.

18.3 Cos’è la Varianza Totale?

La varianza totale rappresenta la somma della variabilità presente in ciascuna variabile del dataset.

Se abbiamo tre variabili, la varianza totale sarà:

\[ \text{Varianza Totale} = \sigma_1^2 + \sigma_2^2 + \sigma_3^2 , \]

dove \(\sigma_i^2\) è la varianza della variabile \(i\)-esima.

Nella PCA:

ogni autovalore (o eigenvalue) rappresenta la quantità di varianza spiegata da una componente principale;
la somma degli autovalori è pari alla varianza totale del dataset (dopo la standardizzazione, essa sarà uguale al numero di variabili).

18.4 Un Nuovo Sistema di Coordinate

La PCA può essere intesa come una rotazione del sistema di riferimento nello spazio delle variabili:

la prima componente principale (PC1) è la direzione lungo cui la varianza dei dati è massima;
la seconda componente (PC2) è perpendicolare alla prima (cioè ortogonale) e spiega la massima varianza residua;
le successive componenti seguono lo stesso principio.

Questo nuovo sistema è costruito in modo tale che le componenti siano non correlate tra loro (ortogonali) e spiegano, progressivamente, meno varianza.

💡 Nota importante: la PCA non elimina variabili, ma le riorganizza in modo da ridurre la complessità informativa.

18.5 Riduzione della Dimensionalità

La PCA consente di rappresentare i dati originali in un nuovo spazio, più compatto, ma informativamente ricco.

18.5.1 Cosa significa “ridurre la dimensionalità”?

Riduzione: da p variabili iniziali (es. 30 item), possiamo ottenere k componenti principali (es. 3 o 5), dove k < p;
Obiettivo: mantenere una soglia prefissata di varianza spiegata, ad esempio il 70% o l’80%.

🎯 Esempio concreto: In uno studio sui Big Five, la PCA può ridurre un set di 100 item a 5 componenti, ciascuna interpretabile come una delle dimensioni di personalità.

18.6 Interpretazione dei Risultati della PCA

La PCA produce due insiemi principali di risultati:

Punteggi delle componenti principali (scores)
Per ogni partecipante (o unità osservata), si ottiene un punteggio per ciascuna componente. Questi punteggi possono essere utilizzati come nuove variabili sintetiche.
Varianza spiegata (eigenvalues)
L’importanza di ciascuna componente è misurata dalla proporzione di varianza che essa spiega:

\[ \text{Proporzione di varianza spiegata dalla PC}_i = \frac{\lambda_i}{\sum_{j=1}^{p} \lambda_j} , \]

dove \(\lambda_i\) è l’autovalore della componente i.

🔍 Interpretazione tipica: Se la PC1 spiega il 50% della varianza e la PC2 un ulteriore 30%, possiamo dire che le prime due componenti spiegano l’80% della variabilità totale.

18.7 Geometria della PCA: Assi, Autovalori e Autovettori

La PCA si basa su concetti fondamentali dell’algebra lineare:

autovalori (eigenvalues): quantificano la varianza spiegata da ogni componente;
autovettori (eigenvectors): definiscono le direzioni lungo cui si osserva la varianza massima nei dati.

Nel piano bidimensionale:

ogni autovettore è un asse di una nuova base ortogonale;
la lunghezza dell’asse è proporzionale alla radice quadrata dell’autovalore corrispondente;
le osservazioni vengono proiettate ortogonalmente su questi assi per ottenere i punteggi delle componenti principali.

18.8 Visualizzazione: Scree Plot e Biplot

18.8.1 Scree Plot

Lo Scree Plot è un grafico che mostra gli autovalori ordinati per componente:

permette di determinare quante componenti mantenere;
un “gomito” nel grafico indica il punto oltre il quale le componenti aggiuntive spiegano poca varianza.

18.8.2 Biplot

Il biplot mostra simultaneamente:

i punteggi delle osservazioni (punti);
i contributi delle variabili originali (frecce).

🎓 Guida all’interpretazione del biplot:
- Correlazione positiva: variabili con frecce vicine tra loro (angolo piccolo tra i vettori);
- Correlazione negativa: variabili con frecce dirette in versi opposti (angolo ≈ 180°);
- Nessuna correlazione: variabili con frecce quasi perpendicolari (angolo ≈ 90°).

Ogni angolo riflette l’intensità della relazione tra le variabili analizzate.

18.9 Tutorial in R

18.9.1 Obiettivo del tutorial

Applicare la PCA passo dopo passo su un dataset simulato con due variabili correlate, comprendendo ogni fase del processo:

creazione dei dati e visualizzazione;
standardizzazione;
calcolo della PCA con algebra lineare;
interpretazione geometrica (autovalori, autovettori);
visualizzazioni: ellissi, componenti, scree plot;
proiezione dei dati nello spazio delle componenti;
verifica con prcomp();
costruzione del biplot.

18.9.2 Passo 1: Creare un dataset

Generiamo un dataset con due variabili correlate.

# Generiamo due variabili correlate
set.seed(123)
X <- data.frame(
  x1 = rnorm(100, mean = 5, sd = 2),
  x2 = rnorm(100, mean = 10, sd = 3)
)

# Aggiungiamo una correlazione lineare tra x1 e x2
X$x2 <- 0.8 * X$x1 + rnorm(100, mean = 0, sd = 1)

18.9.3 Passo 2: Standardizzare i dati

La standardizzazione è essenziale nella PCA quando le variabili hanno scale diverse. Dopo la standardizzazione, ogni variabile ha media = 0 e deviazione standard = 1.

# Standardizziamo le variabili
X_scaled <- scale(X)

Visualizziamo i dati standardizzati:

ggplot(X_scaled, aes(x = x1, y = x2)) +
  geom_point(shape = 19) +
  coord_fixed(ratio = 1) + # Imposta l'aspect ratio a 1
  labs(
    x = "x1 standardizzata",
    y = "x2 standardizzata",
    title = "Dati standardizzati (asp = 1)"
  )

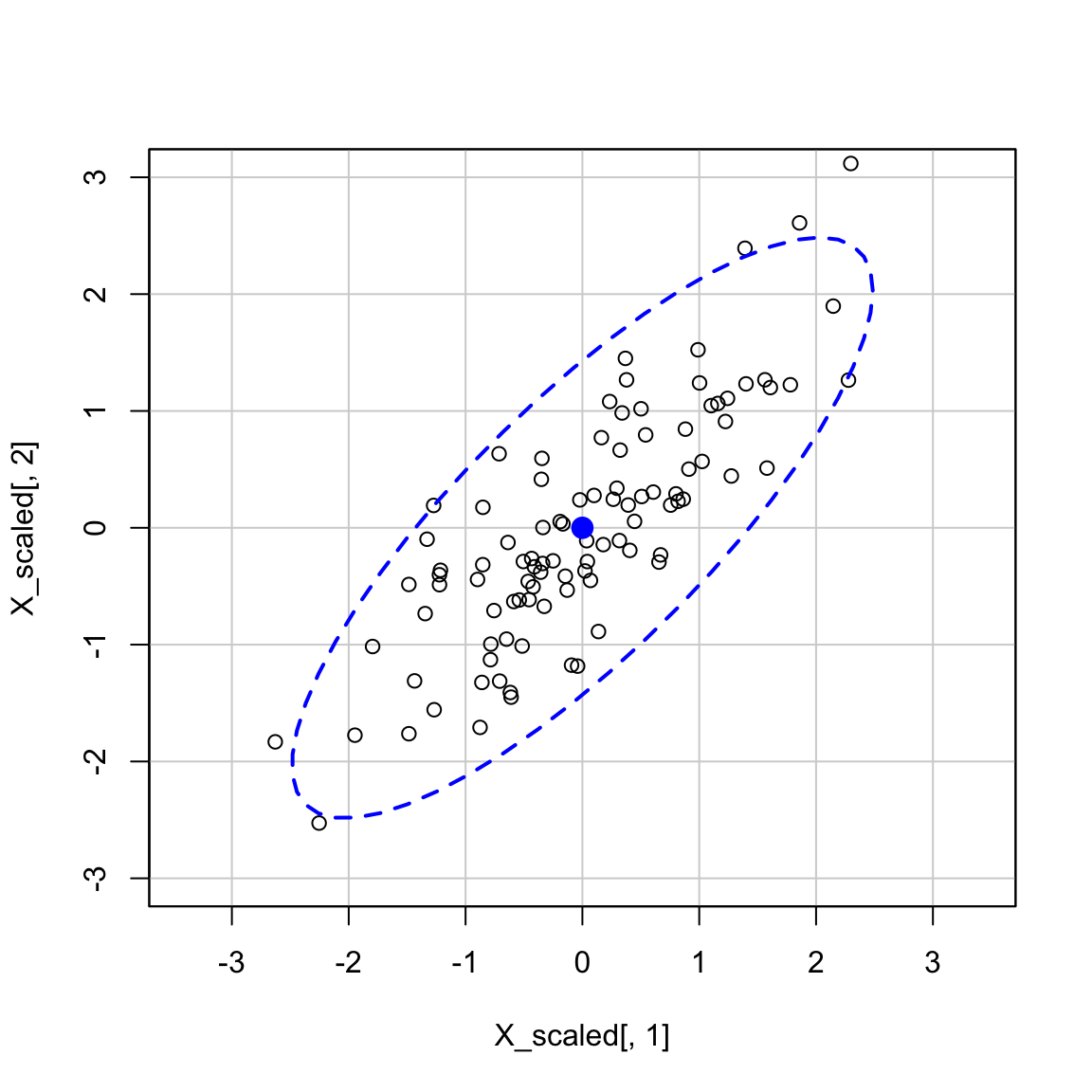
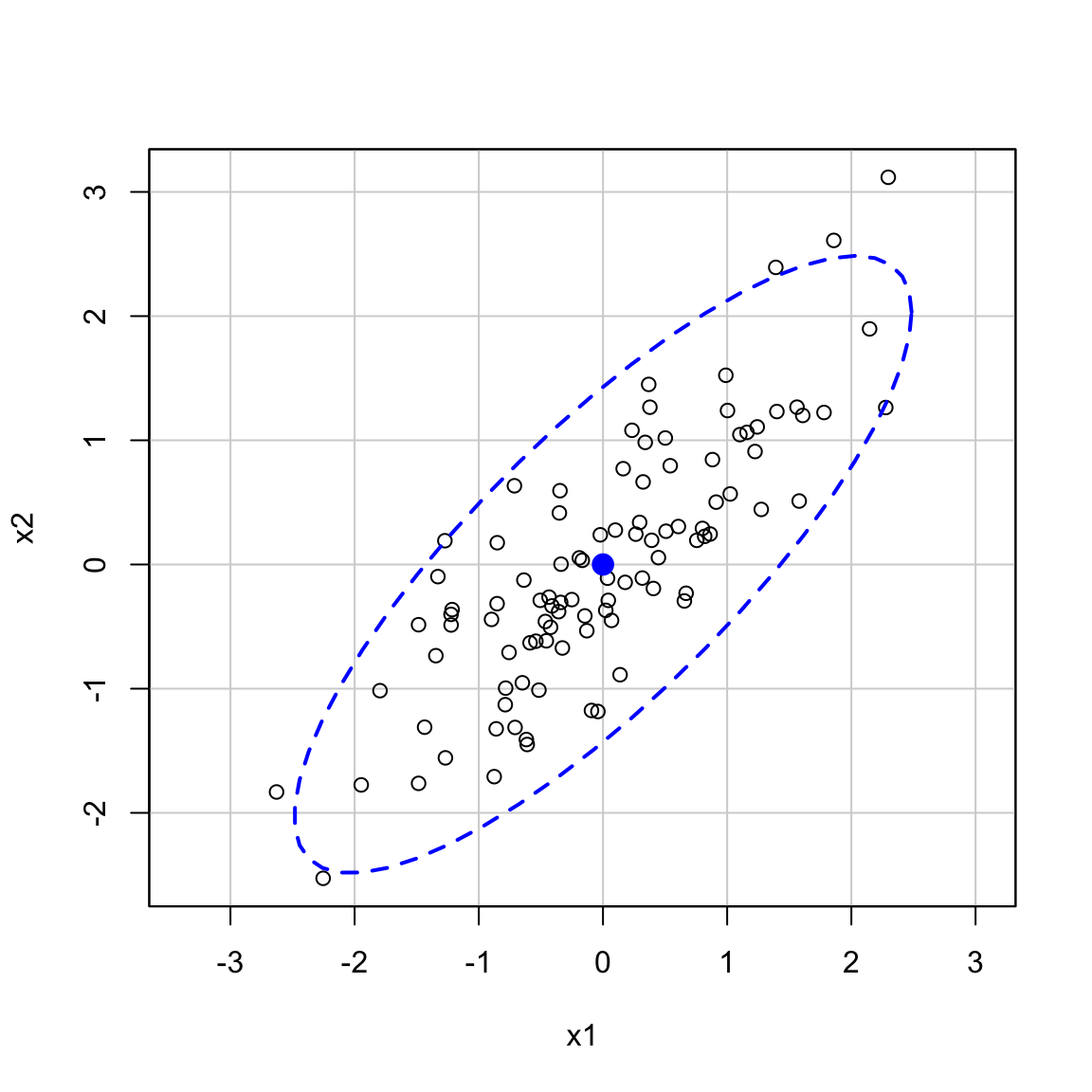
Aggiungiamo un’ellisse di confidenza per mostrare la distribuzione:

car::dataEllipse(
  X_scaled[, 1], X_scaled[, 2],
  levels = 0.95, lty = 2,
  asp = 1,
  xlab = "x1", ylab = "x2"
)

18.9.4 Passo 3: Calcolare la matrice di covarianza

cov_matrix <- cov(X_scaled)
cov_matrix
#>        x1     x2
#> x1 1.0000 0.8177
#> x2 0.8177 1.0000

18.9.5 Passo 4: Calcolare autovalori e autovettori

eigen_decomp <- eigen(cov_matrix)
eigenvalues <- eigen_decomp$values       # Varianza spiegata (autovalori)
eigenvectors <- eigen_decomp$vectors     # Direzioni principali (autovettori)

Stampiamo i risultati:

eigenvalues
#> [1] 1.8177 0.1823

eigenvectors
#>        [,1]    [,2]
#> [1,] 0.7071 -0.7071
#> [2,] 0.7071  0.7071

Verifichiamo che gli autovettori siano ortogonali (prodotto scalare = 0):

t(eigenvectors[,1]) %*% eigenvectors[,2]
#>           [,1]
#> [1,] 2.237e-17

18.9.6 Visualizzare le direzioni principali

Calcoliamo le pendenze degli autovettori:

ev1_slope <- eigenvectors[2, 1] / eigenvectors[1, 1]
ev2_slope <- eigenvectors[2, 2] / eigenvectors[1, 2]

Visualizziamo il grafico con gli autovettori sovrapposti:

data.frame(zx = X_scaled[, 1], zy = X_scaled[, 2]) |>
  ggplot(aes(x = zx, y = zy)) +
  geom_point(size = 2) +
  geom_vline(xintercept = 0, linewidth = .5) +
  geom_hline(yintercept = 0, linewidth = .5) +
  geom_abline(slope = ev1_slope, color = "red", linewidth = 1.2) +
  geom_abline(slope = ev2_slope, color = "blue", linewidth = 1.2) +
  ggtitle("Autovettori: direzioni delle componenti principali")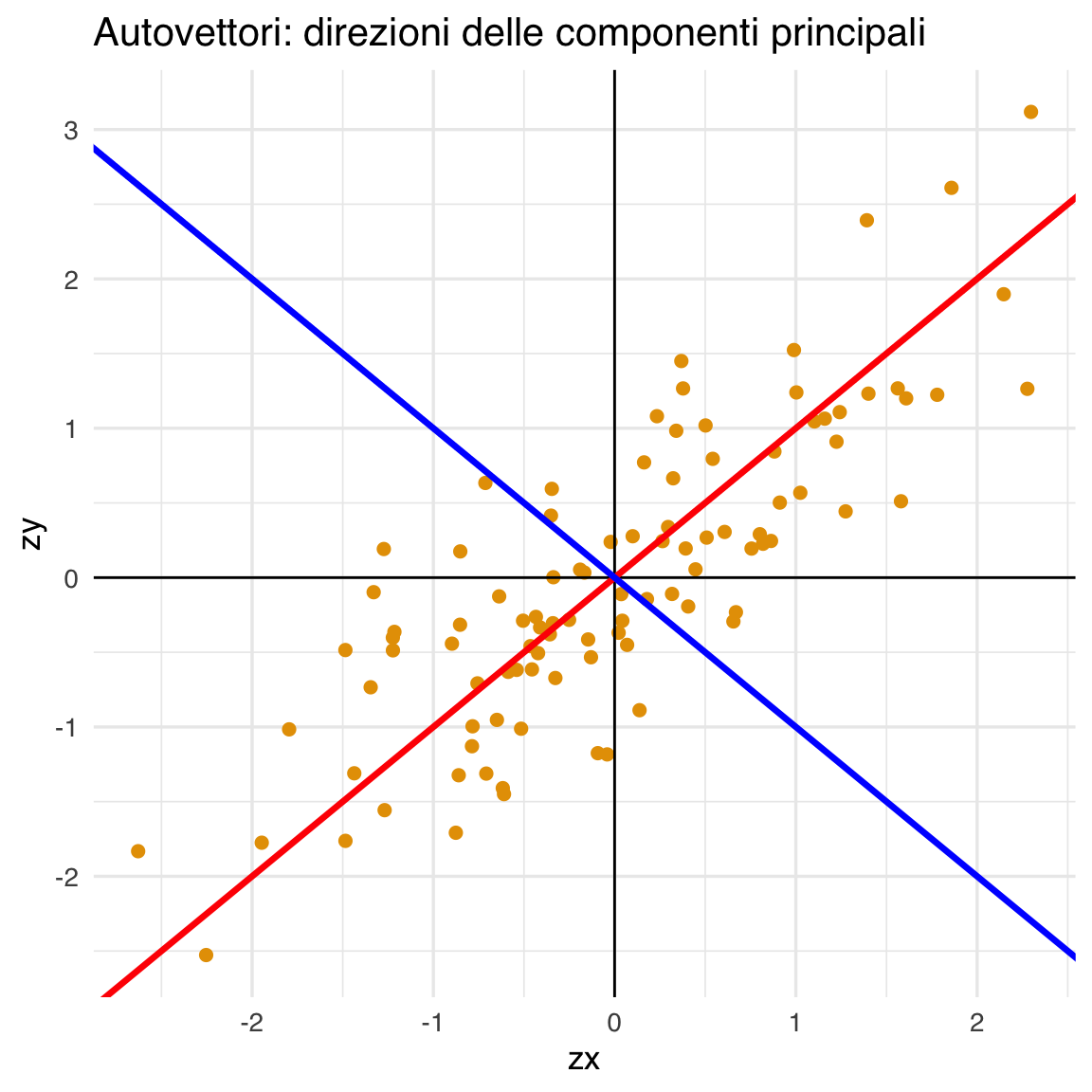

18.9.7 Scree Plot – Percentuale di varianza spiegata

# Percentuale di varianza spiegata
var_per <- tibble(
  PC = c("PC1", "PC2"),
  Percent = eigenvalues / sum(eigenvalues) * 100
)

ggplot(var_per, aes(x = PC, y = Percent)) +
  geom_col(fill = "skyblue", color = "black", width = 0.5) +
  ylab("Varianza spiegata (%)") +
  xlab("Componente Principale") +
  ggtitle("Scree Plot")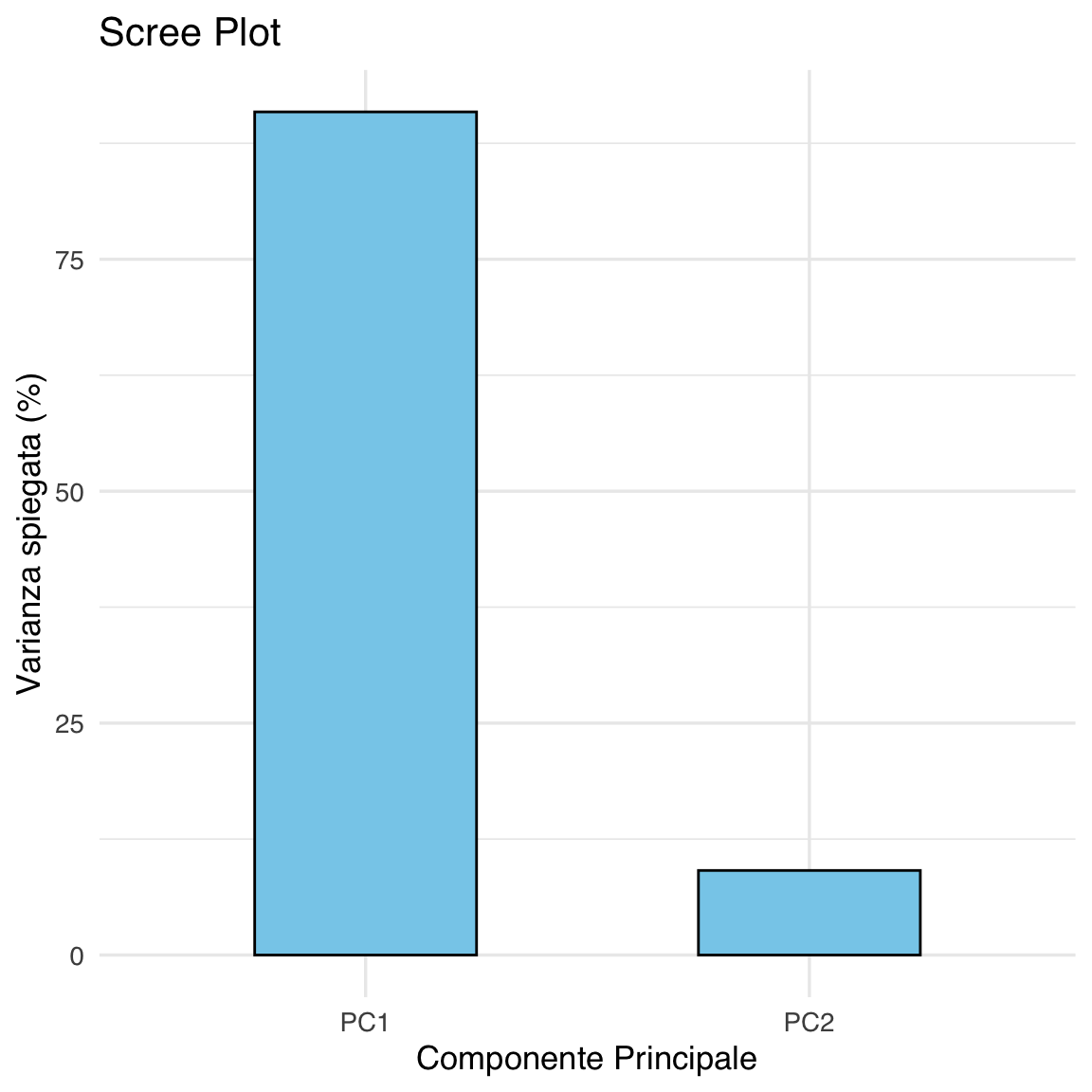

Verifica: somma degli autovalori ≈ somma delle varianze

sum(eigenvalues)
#> [1] 2
sum(apply(X_scaled, 2, var))  # Varianza totale
#> [1] 2

18.9.8 Passo 5: Visualizzazione geometrica (ellisse + assi principali)

car::dataEllipse(
  X_scaled[, 1], X_scaled[, 2],
  levels = 0.95, lty = 2,
  xlim = c(-3, 3), ylim = c(-3, 3),
  asp = 1,
  xlab = "x1", ylab = "x2"
)

# Disegniamo gli assi in base agli autovettori
k <- 2.5
arrows(0, 0,
       k * sqrt(eigenvalues[1]) * eigenvectors[1, 1],
       k * sqrt(eigenvalues[1]) * eigenvectors[2, 1],
       col = "red", lwd = 2, code = 2)

arrows(0, 0,
       k * sqrt(eigenvalues[2]) * eigenvectors[1, 2],
       k * sqrt(eigenvalues[2]) * eigenvectors[2, 2],
       col = "red", lwd = 2, code = 2)

18.9.9 Passo 6: Proiezione dei dati (calcolo dei punteggi)

pc_scores <- as.matrix(X_scaled) %*% eigenvectors
colnames(pc_scores) <- c("PC1", "PC2")

head(pc_scores)  # Mostra le prime osservazioni nel nuovo spazio
#>           PC1     PC2
#> [1,] -0.05606  0.9523
#> [2,]  0.04512  0.5418
#> [3,]  1.98607 -0.2887
#> [4,]  0.15352  0.1844
#> [5,] -0.17413 -0.2344
#> [6,]  2.12408 -0.3930

Visualizziamo le osservazioni nello spazio delle componenti:

pc_df <- as.data.frame(pc_scores)

# Grafico ggplot dei punteggi delle componenti principali
ggplot(pc_df, aes(x = PC1, y = PC2)) +
  geom_point(color = "blue", size = 2) +
  labs(
    title = "Punteggi delle Componenti Principali",
    x = "PC1",
    y = "PC2"
  ) +
  coord_fixed()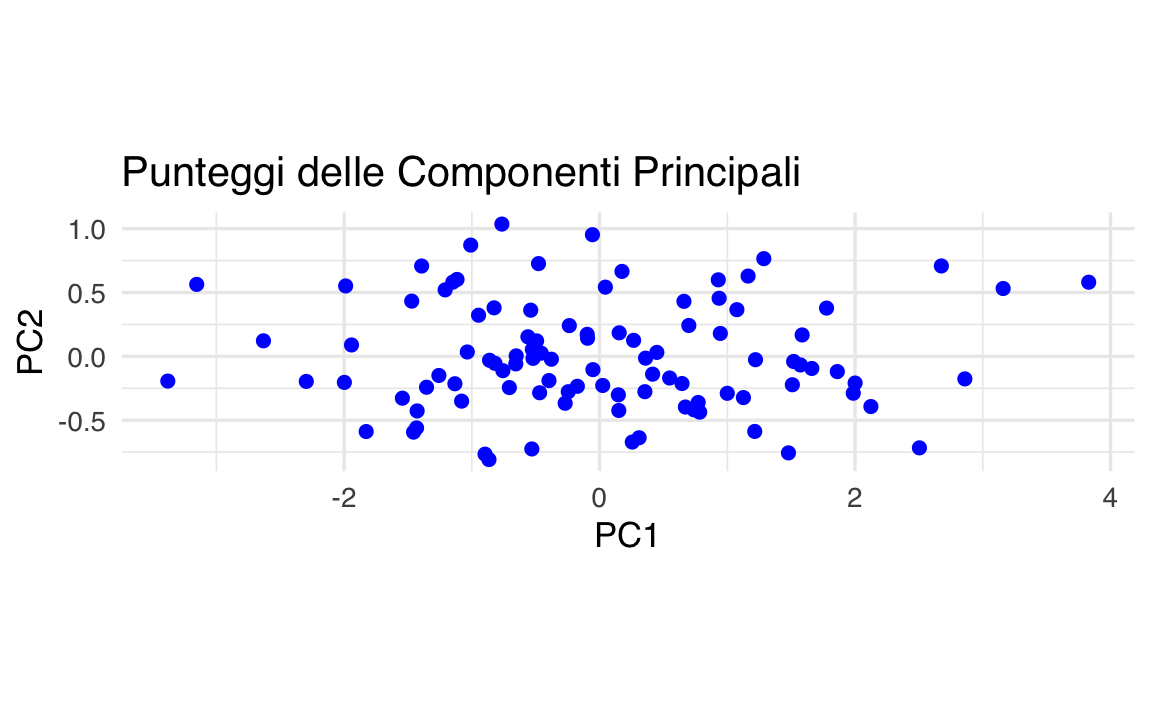

18.9.10 Passo 7: Confronto con `prcomp`

# Calcolo automatico della PCA
pca_auto <- prcomp(X, scale. = TRUE)
summary(pca_auto)
#> Importance of components:
#>                          PC1    PC2
#> Standard deviation     1.348 0.4270
#> Proportion of Variance 0.909 0.0912
#> Cumulative Proportion  0.909 1.0000

Verifica: confronta punteggi calcolati a mano con quelli di prcomp

head(pca_auto$x)  # Punteggi calcolati da prcomp
#>           PC1     PC2
#> [1,] -0.05606 -0.9523
#> [2,]  0.04512 -0.5418
#> [3,]  1.98607  0.2887
#> [4,]  0.15352 -0.1844
#> [5,] -0.17413  0.2344
#> [6,]  2.12408  0.3930

head(pc_scores)   # Punteggi calcolati a mano
#>           PC1     PC2
#> [1,] -0.05606  0.9523
#> [2,]  0.04512  0.5418
#> [3,]  1.98607 -0.2887
#> [4,]  0.15352  0.1844
#> [5,] -0.17413 -0.2344
#> [6,]  2.12408 -0.3930

18.9.11 Passo 8: Biplot

Il biplot permette di visualizzare contemporaneamente:

le osservazioni (rappresentate da numeri), proiettate nello spazio delle componenti principali;
le variabili originali (x1, x2), rappresentate come frecce rosse, che indicano come ciascuna variabile contribuisce alla definizione delle componenti.

biplot(pca_auto, scale = 0,
       main = "Biplot delle Componenti Principali",
       xlab = "PC1", ylab = "PC2")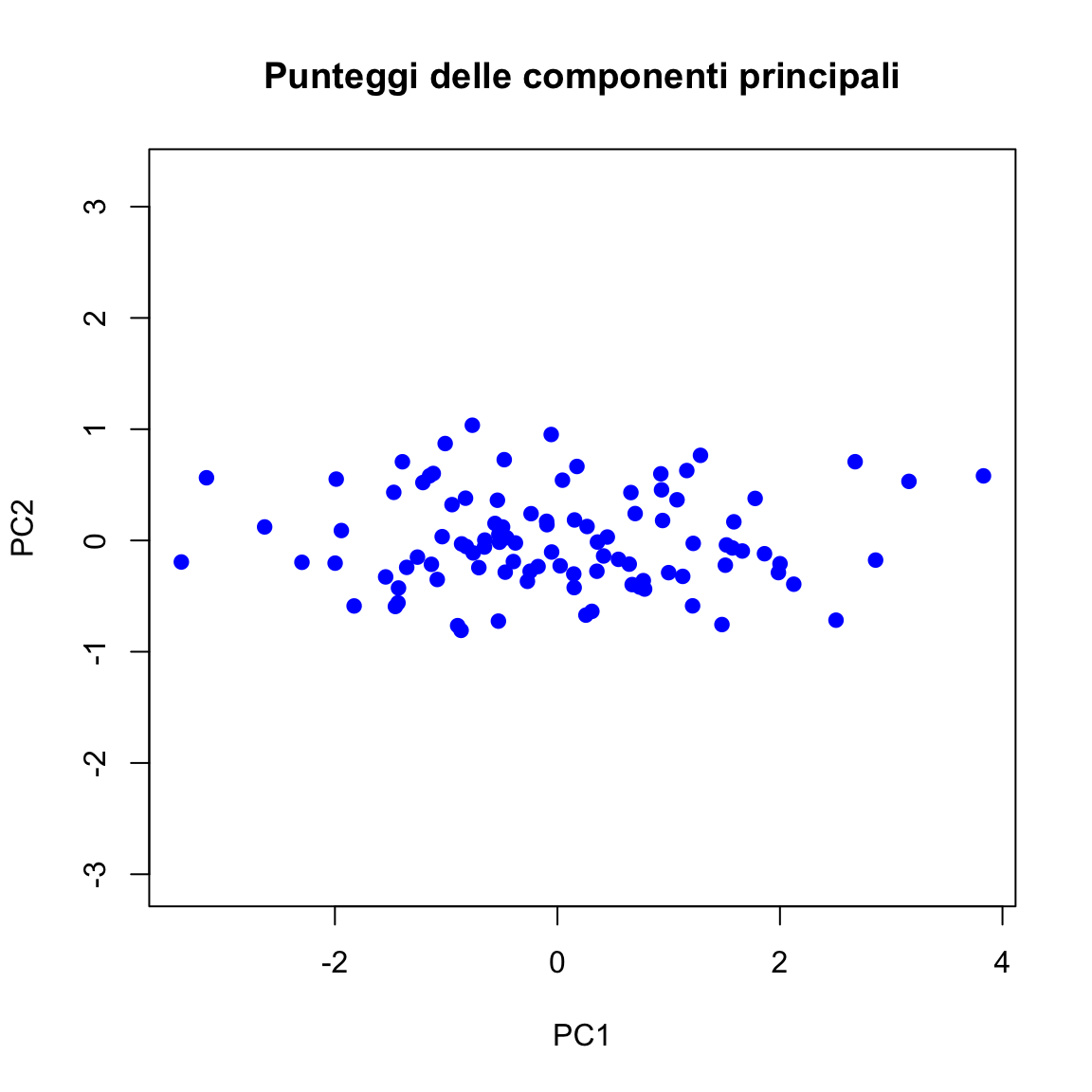

Distribuzione delle osservazioni

I numeri neri rappresentano le 100 osservazioni.
Le osservazioni si distribuiscono principalmente lungo la direzione della prima componente principale (PC1), che si estende orizzontalmente.
C’è relativamente poca variabilità lungo la seconda componente (PC2), che è verticale. Questo conferma che quasi tutta la varianza è catturata da PC1, come osservato nei passaggi precedenti (Scree Plot, autovalori).

Frecce delle variabili originali

Nel biplot vediamo due frecce:

la freccia x1 punta verso l’alto a destra;
la freccia x2 punta verso il basso a destra;
entrambe le frecce sono allineate in parte con l’asse orizzontale (PC1), ma puntano in direzioni opposte lungo PC2.

Interpretazione geometrica:

Entrambe le variabili contribuiscono positivamente a PC1, perché le componenti orizzontali delle frecce sono entrambe > 0.
La componente verticale di x1 è positiva, quella di x2 è negativa, quindi le due variabili sono positivamente correlate in generale, ma divergono leggermente lungo PC2.

Questo pattern è coerente con i coefficienti degli autovettori:

pca_auto$rotation

Es.:

           PC1      PC2
x1       0.71     0.71
x2       0.71    -0.71

Cosa significa?

La PC1 è la somma bilanciata di x1 e x2, e rappresenta la dimensione comune tra le due variabili.
La PC2 è la loro differenza: rappresenta una direzione lungo cui x1 e x2 si muovono in modo opposto. Ma in questo caso, la varianza lungo PC2 è molto piccola → questo secondo asse è poco informativo.

Lunghezza delle frecce:

le frecce hanno lunghezza simile → entrambe le variabili sono ben rappresentate dallo spazio PC1–PC2;
in un biplot, la lunghezza di una freccia indica quanto bene quella variabile è spiegata dalle componenti principali.

Conclusioni sull’interpretazione del biplot.

Il biplot mostra che la struttura dei dati può essere riassunta da una sola dimensione latente (PC1).
Le due variabili x1 e x2 sono entrambe fortemente associate a PC1, e debolmente differenziate da PC2.

18.10 Riflessioni Conclusive

Abbiamo completato un’analisi PCA manuale e automatica, verificando ogni passaggio attraverso:

algebra lineare (autovalori/autovettori);
visualizzazione geometrica (ellisse, autovettori);
scree plot;
proiezione dei dati;
biplot.

Questa struttura permette di collegare i concetti teorici alla loro implementazione pratica, fornendo agli studenti una comprensione più profonda della PCA.

18.11 ✍️ Suggerimenti per gli Studenti

Quando standardizzare? Sempre, se le variabili sono su scale diverse (es. punteggi da 0 a 10, da 1 a 100);
Quando usare la PCA? Quando l’obiettivo è descrittivo, esplorare la struttura latente o semplificare l’analisi;
Quando non usarla? Se le variabili non sono correlate: la PCA non sarà utile;
Come interpretare le componenti? Serve analizzare i coefficienti degli autovettori per capire il contributo delle variabili originali a ciascuna componente.

Informazioni sull’Ambiente di Sviluppo

sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.3.2
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] ggokabeito_0.1.0  see_0.11.0        MASS_7.3-65       viridis_0.6.5    
#>  [5] viridisLite_0.4.2 ggpubr_0.6.0      ggExtra_0.10.1    gridExtra_2.3    
#>  [9] patchwork_1.3.0   bayesplot_1.11.1  semTools_0.5-6    semPlot_1.1.6    
#> [13] lavaan_0.6-19     psych_2.4.12      scales_1.3.0      markdown_1.13    
#> [17] knitr_1.50        lubridate_1.9.4   forcats_1.0.0     stringr_1.5.1    
#> [21] dplyr_1.1.4       purrr_1.0.4       readr_2.1.5       tidyr_1.3.1      
#> [25] tibble_3.2.1      ggplot2_3.5.1     tidyverse_2.0.0   here_1.0.1       
#> 
#> loaded via a namespace (and not attached):
#>   [1] rstudioapi_0.17.1   jsonlite_1.9.1      magrittr_2.0.3     
#>   [4] TH.data_1.1-3       estimability_1.5.1  farver_2.1.2       
#>   [7] nloptr_2.2.1        rmarkdown_2.29      vctrs_0.6.5        
#>  [10] minqa_1.2.8         base64enc_0.1-3     rstatix_0.7.2      
#>  [13] htmltools_0.5.8.1   broom_1.0.7         Formula_1.2-5      
#>  [16] htmlwidgets_1.6.4   plyr_1.8.9          sandwich_3.1-1     
#>  [19] emmeans_1.10.7      zoo_1.8-13          igraph_2.1.4       
#>  [22] mime_0.13           lifecycle_1.0.4     pkgconfig_2.0.3    
#>  [25] Matrix_1.7-3        R6_2.6.1            fastmap_1.2.0      
#>  [28] rbibutils_2.3       shiny_1.10.0        digest_0.6.37      
#>  [31] OpenMx_2.21.13      fdrtool_1.2.18      colorspace_2.1-1   
#>  [34] rprojroot_2.0.4     Hmisc_5.2-3         labeling_0.4.3     
#>  [37] timechange_0.3.0    abind_1.4-8         compiler_4.4.2     
#>  [40] withr_3.0.2         glasso_1.11         htmlTable_2.4.3    
#>  [43] backports_1.5.0     carData_3.0-5       ggsignif_0.6.4     
#>  [46] corpcor_1.6.10      gtools_3.9.5        tools_4.4.2        
#>  [49] pbivnorm_0.6.0      foreign_0.8-88      zip_2.3.2          
#>  [52] httpuv_1.6.15       nnet_7.3-20         glue_1.8.0         
#>  [55] quadprog_1.5-8      nlme_3.1-167        promises_1.3.2     
#>  [58] lisrelToR_0.3       grid_4.4.2          checkmate_2.3.2    
#>  [61] cluster_2.1.8.1     reshape2_1.4.4      generics_0.1.3     
#>  [64] gtable_0.3.6        tzdb_0.5.0          data.table_1.17.0  
#>  [67] hms_1.1.3           car_3.1-3           sem_3.1-16         
#>  [70] pillar_1.10.1       rockchalk_1.8.157   later_1.4.1        
#>  [73] splines_4.4.2       lattice_0.22-6      survival_3.8-3     
#>  [76] kutils_1.73         tidyselect_1.2.1    miniUI_0.1.1.1     
#>  [79] pbapply_1.7-2       reformulas_0.4.0    stats4_4.4.2       
#>  [82] xfun_0.51           qgraph_1.9.8        arm_1.14-4         
#>  [85] stringi_1.8.4       yaml_2.3.10         pacman_0.5.1       
#>  [88] boot_1.3-31         evaluate_1.0.3      codetools_0.2-20   
#>  [91] mi_1.1              cli_3.6.4           RcppParallel_5.1.10
#>  [94] rpart_4.1.24        xtable_1.8-4        Rdpack_2.6.3       
#>  [97] munsell_0.5.1       Rcpp_1.0.14         coda_0.19-4.1      
#> [100] png_0.1-8           XML_3.99-0.18       parallel_4.4.2     
#> [103] jpeg_0.1-10         lme4_1.1-36         mvtnorm_1.3-3      
#> [106] openxlsx_4.2.8      rlang_1.1.5         multcomp_1.4-28    
#> [109] mnormt_2.1.1

18.1 Introduzione

18.2 Perché Usare la PCA in Psicologia?

18.3 Cos’è la Varianza Totale?

18.4 Un Nuovo Sistema di Coordinate

18.5 Riduzione della Dimensionalità

18.5.1 Cosa significa “ridurre la dimensionalità”?

18.6 Interpretazione dei Risultati della PCA

18.7 Geometria della PCA: Assi, Autovalori e Autovettori

18.8 Visualizzazione: Scree Plot e Biplot

18.8.1 Scree Plot

18.8.2 Biplot

18.9 Tutorial in R

18.9.1 Obiettivo del tutorial

18.9.2 Passo 1: Creare un dataset

18.9.3 Passo 2: Standardizzare i dati

18.9.4 Passo 3: Calcolare la matrice di covarianza

18.9.5 Passo 4: Calcolare autovalori e autovettori

18.9.6 Visualizzare le direzioni principali

18.9.7 Scree Plot – Percentuale di varianza spiegata

18.9.8 Passo 5: Visualizzazione geometrica (ellisse + assi principali)

18.9.9 Passo 6: Proiezione dei dati (calcolo dei punteggi)

18.9.10 Passo 7: Confronto con prcomp

18.9.11 Passo 8: Biplot

18.10 Riflessioni Conclusive

18.11 ✍️ Suggerimenti per gli Studenti

Informazioni sull’Ambiente di Sviluppo

18.9.10 Passo 7: Confronto con `prcomp`