here::here("code", "_common.R") |>
source()
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(lavaan, semPlot, corrplot, tidyr, kableExtra)23 I punteggi fattoriali
- calcolare e interpretare i punteggi fattoriali.
- Leggere il capitolo 6, Factor Analysis and Principal Component Analysis, del testo Principles of psychological assessment di Petersen (2024).
23.1 Introduzione
Uno dei passaggi più complessi e delicati nello sviluppo di un test psicometrico è rappresentato dall’interpretazione dei fattori. Mentre la verifica dell’affidabilità consente di stimare la precisione delle misure ottenute (ossia, quanto sono stabili e coerenti), essa non fornisce informazioni sul contenuto o sulla natura psicologica delle dimensioni che il test intende misurare.
L’interpretazione dei fattori è un processo eminentemente concettuale e teorico, che non è guidato da regole univoche. Non esistono criteri oggettivi e definitivi per “leggere” i fattori: molto dipende dalla competenza del ricercatore, dalla sua conoscenza del dominio teorico, e dalla sua capacità di individuare un significato comune tra le variabili che saturano su ciascun fattore. È fondamentale, tuttavia, che tale interpretazione sia ancorata ai dati e non frutto di libere associazioni o intuizioni arbitrarie.
Va inoltre ricordato che le scelte effettuate durante l’analisi fattoriale — ad esempio, il metodo di estrazione, il numero di fattori da mantenere, il tipo di rotazione (ortogonale o obliqua) — influenzano profondamente la soluzione ottenuta e, di conseguenza, anche la sua interpretazione. Questo implica che l’intero processo sia in parte soggettivo e debba essere condotto con cautela.
23.1.1 Passaggi per l’interpretazione di una matrice fattoriale ruotata
La procedura per interpretare una matrice dei carichi fattoriali dopo una rotazione può essere articolata nei seguenti passaggi:
Definizione di una soglia per i carichi fattoriali
Si stabilisce un valore soglia (ad esempio, |.40|) al di sotto del quale le saturazioni vengono considerate troppo deboli per contribuire significativamente alla definizione del fattore. Valori più alti (es. .50 o .60) o più bassi possono essere usati in base al numero di item e alla chiarezza della soluzione.Ordinamento dei carichi
Le saturazioni (in valore assoluto) vengono ordinate in senso decrescente per ciascun fattore, partendo da quelle più forti fino alla soglia stabilita.Identificazione delle variabili
A ciascun carico si associa la descrizione della variabile o dell’item corrispondente, per facilitare l’analisi del contenuto.Attribuzione di un’etichetta teorica al fattore
Considerando il contenuto degli item, il dominio teorico di riferimento e i risultati di studi precedenti, si cerca di individuare un tratto psicologico comune che li unisca. Tale tratto definisce l’etichetta interpretativa del fattore. Gli item con carichi più elevati contribuiscono maggiormente alla definizione di questo tratto.Interpretazione del segno delle saturazioni
Il segno negativo di un carico indica semplicemente una direzione opposta rispetto alle saturazioni positive. Il tratto psicologico rappresentato dal fattore può essere visto come un continuum: le variabili con segno opposto si trovano alle estremità opposte di tale continuum. È spesso utile iniziare l’interpretazione considerando le saturazioni con il segno più frequente come “positive”, per poi interpretare le altre come opposte.Fattori non interpretabili
Se non si riesce a identificare un tratto comune tra le variabili che saturano su un fattore, si può concludere che il fattore non è interpretabile. Questo può essere dovuto a errori di campionamento, rumore nella misurazione, o alla presenza di variabili che non condividono un contenuto psicologico coerente. È comune che i primi fattori estratti siano interpretabili, mentre gli ultimi — soprattutto se si sono estratti molti fattori o se la matrice delle correlazioni è debole — risultino ambigui o saturi di una sola variabile, diventando di fatto fattori “specifici”. Se molti fattori non risultano interpretabili, è preferibile rivalutare l’intera analisi fattoriale.
23.2 Esempio di interpretazione: la scala WISC-III
Il WISC-III (Wechsler Intelligence Scale for Children – III) è uno strumento standardizzato per la valutazione dell’intelligenza nei bambini e adolescenti dai 6 ai 16 anni e 11 mesi. I subtest che lo compongono sono progettati per misurare differenti abilità cognitive, contribuendo alla stima del Quoziente Intellettivo globale.
Alcuni subtest richiedono abilità verbali e di ragionamento astratto, altri valutano la memoria a breve termine, altri ancora sollecitano competenze visuo-percettive e di coordinazione motoria.
23.2.1 Matrice di correlazione tra i subtest
Consideriamo ora la matrice di correlazione tra i subtest del WISC-III (tratta dal manuale italiano):
lower <- '
1
.66 1
.57 .55 1
.70 .69 .54 1
.56 .59 .47 .64 1
.34 .34 .43 .35 .29 1
.47 .45 .39 .45 .38 .25 1
.21 .20 .27 .26 .25 .23 .18 1
.40 .39 .35 .40 .35 .20 .37 .28 1
.48 .49 .52 .46 .40 .32 .52 .27 .41 1
.41 .42 .39 .41 .34 .26 .49 .24 .37 .61 1
.35 .35 .41 .35 .34 .28 .33 .53 .36 .45 .38 1
.18 .18 .22 .17 .17 .14 .24 .15 .23 .31 .29 .24 1
'wisc_III_cov <- getCov(
lower,
names = c(
"INFO", "SIM", "ARITH", "VOC", "COMP", "DIGIT", "PICTCOM",
"CODING", "PICTARG", "BLOCK", "OBJECT", "SYMBOL", "MAZES"
)
)
wisc_III_cov
#> INFO SIM ARITH VOC COMP DIGIT PICTCOM CODING PICTARG BLOCK OBJECT
#> INFO 1.00 0.66 0.57 0.70 0.56 0.34 0.47 0.21 0.40 0.48 0.41
#> SIM 0.66 1.00 0.55 0.69 0.59 0.34 0.45 0.20 0.39 0.49 0.42
#> ARITH 0.57 0.55 1.00 0.54 0.47 0.43 0.39 0.27 0.35 0.52 0.39
#> VOC 0.70 0.69 0.54 1.00 0.64 0.35 0.45 0.26 0.40 0.46 0.41
#> COMP 0.56 0.59 0.47 0.64 1.00 0.29 0.38 0.25 0.35 0.40 0.34
#> DIGIT 0.34 0.34 0.43 0.35 0.29 1.00 0.25 0.23 0.20 0.32 0.26
#> PICTCOM 0.47 0.45 0.39 0.45 0.38 0.25 1.00 0.18 0.37 0.52 0.49
#> CODING 0.21 0.20 0.27 0.26 0.25 0.23 0.18 1.00 0.28 0.27 0.24
#> PICTARG 0.40 0.39 0.35 0.40 0.35 0.20 0.37 0.28 1.00 0.41 0.37
#> BLOCK 0.48 0.49 0.52 0.46 0.40 0.32 0.52 0.27 0.41 1.00 0.61
#> OBJECT 0.41 0.42 0.39 0.41 0.34 0.26 0.49 0.24 0.37 0.61 1.00
#> SYMBOL 0.35 0.35 0.41 0.35 0.34 0.28 0.33 0.53 0.36 0.45 0.38
#> MAZES 0.18 0.18 0.22 0.17 0.17 0.14 0.24 0.15 0.23 0.31 0.29
#> SYMBOL MAZES
#> INFO 0.35 0.18
#> SIM 0.35 0.18
#> ARITH 0.41 0.22
#> VOC 0.35 0.17
#> COMP 0.34 0.17
#> DIGIT 0.28 0.14
#> PICTCOM 0.33 0.24
#> CODING 0.53 0.15
#> PICTARG 0.36 0.23
#> BLOCK 0.45 0.31
#> OBJECT 0.38 0.29
#> SYMBOL 1.00 0.24
#> MAZES 0.24 1.0023.2.2 Analisi fattoriale
Applichiamo un’analisi delle componenti principali con rotazione Varimax (ortogonale), e scegliamo di estrarre 3 fattori:
f_pc <- psych::principal(wisc_III_cov, nfactors = 3, rotate = "varimax")
print(f_pc)
#> Principal Components Analysis
#> Call: psych::principal(r = wisc_III_cov, nfactors = 3, rotate = "varimax")
#> Standardized loadings (pattern matrix) based upon correlation matrix
#> RC1 RC3 RC2 h2 u2 com
#> INFO 0.80 0.25 0.09 0.72 0.28 1.2
#> SIM 0.81 0.25 0.08 0.72 0.28 1.2
#> ARITH 0.65 0.26 0.28 0.57 0.43 1.7
#> VOC 0.83 0.19 0.13 0.75 0.25 1.2
#> COMP 0.75 0.14 0.16 0.60 0.40 1.2
#> DIGIT 0.45 0.06 0.36 0.34 0.66 2.0
#> PICTCOM 0.43 0.61 0.02 0.56 0.44 1.8
#> CODING 0.10 0.09 0.88 0.79 0.21 1.0
#> PICTARG 0.34 0.45 0.27 0.39 0.61 2.6
#> BLOCK 0.41 0.66 0.22 0.66 0.34 1.9
#> OBJECT 0.31 0.71 0.14 0.62 0.38 1.5
#> SYMBOL 0.23 0.32 0.74 0.70 0.30 1.6
#> MAZES -0.06 0.71 0.11 0.51 0.49 1.1
#>
#> RC1 RC3 RC2
#> SS loadings 3.80 2.37 1.74
#> Proportion Var 0.29 0.18 0.13
#> Cumulative Var 0.29 0.47 0.61
#> Proportion Explained 0.48 0.30 0.22
#> Cumulative Proportion 0.48 0.78 1.00
#>
#> Mean item complexity = 1.5
#> Test of the hypothesis that 3 components are sufficient.
#>
#> The root mean square of the residuals (RMSR) is 0.07
#>
#> Fit based upon off diagonal values = 0.9723.2.3 Interpretazione dei fattori
Dai risultati:
I primi cinque subtest (“Informazioni”, “Somiglianze”, “Aritmetica”, “Vocabolario”, “Comprensione”) presentano saturazioni elevate (oltre .60) sul primo fattore. Questi item implicano la comprensione e produzione di linguaggio, e richiedono un buon livello di ragionamento verbale. È quindi coerente denominare questo fattore Comprensione Verbale.
I subtest “Cifrario” e “Ricerca di simboli” saturano sul secondo fattore. Entrambi implicano rapidità nella codifica di simboli visivi e attenzione sostenuta. Il fattore può essere chiamato Velocità di Elaborazione.
I subtest “Completamento di figure”, “Disegno con i cubi”, “Riordinamento di storie figurate” e “Labirinti” saturano sul terzo fattore. Questi subtest richiedono abilità visuo-spaziali e organizzazione percettiva. Il fattore può essere denominato Organizzazione Percettiva.
23.2.4 Calcolo delle comunalità
Nel caso di una rotazione ortogonale, la comunalità di ciascuna variabile è data dalla somma dei quadrati dei suoi carichi sui fattori. Calcoliamole:
Le comunalità rappresentano la proporzione della varianza di ciascun subtest spiegata dai fattori estratti. Valori elevati indicano che il fattore riesce a spiegare bene il comportamento della variabile. Questi risultati riproducono quelli riportati nel manuale del WISC-III, confermando la validità dell’interpretazione proposta.
23.3 Punteggi fattoriali
Finora ci siamo concentrati sulla costruzione del modello fattoriale attraverso la stima delle saturazioni fattoriali e delle comunalità. Questi passaggi rappresentano la base per comprendere la struttura latente che organizza le variabili osservate.
Tuttavia, è possibile compiere un passo ulteriore: la stima dei punteggi fattoriali (factor scores). I punteggi fattoriali rappresentano una stima dei valori dei fattori latenti per ciascun partecipante nel campione. Sono utili sia per un’interpretazione individualizzata dell’analisi fattoriale, sia per ulteriori analisi statistiche (es. regressioni, classificazioni o confronti di gruppo).
23.3.1 Metodi di stima
Esistono diversi metodi per calcolare i punteggi fattoriali. I più comuni sono:
-
Metodo di Thomson (regressione): stima i punteggi come valori previsti in un modello di regressione lineare multipla, basandosi sulla matrice delle correlazioni tra le variabili osservate e sulla matrice delle saturazioni fattoriali.
- Metodo di Bartlett: si basa su un approccio di massima verosimiglianza e produce stime meno correlate tra i fattori ma più influenzate dall’assunzione di assenza di errore.
Entrambi i metodi sono implementati nella funzione factanal() di R. Il metodo di regressione si attiva specificando scores = "regression".
23.4 Dimostrazione di Thurstone
Per illustrare in modo intuitivo il significato dei punteggi fattoriali, riprendiamo un esempio proposto da Thurstone (1947) (citato in Loehlin, 1987), poi ripreso da Jennrich (2007). L’idea è di simulare un contesto in cui i fattori latenti sono noti, così da poter valutare la bontà della stima ottenuta dai punteggi fattoriali.
Supponiamo di avere 1000 scatole le cui dimensioni reali (\(x\), \(y\), \(z\)) sono note:
Ora immaginiamo di disporre solo di misurazioni indirette e rumorose delle scatole. Queste misurazioni sono derivate da trasformazioni non lineari e prodotti tra le dimensioni, più un errore casuale:
s <- 40
y1 <- rnorm(n, mean(x), s)
y2 <- rnorm(n, mean(y), s)
y3 <- rnorm(n, mean(z), s)
y4 <- x * y + rnorm(n, 0, s)
y5 <- x * z + rnorm(n, 0, s)
y6 <- y * z + rnorm(n, 0, s)
y7 <- x^2 * y + rnorm(n, 0, s)
y8 <- x * y^2 + rnorm(n, 0, s)
y9 <- x^2 * z + rnorm(n, 0, s)
y10 <- x * z^2 + rnorm(n, 0, s)
y11 <- y^2 * z + rnorm(n, 0, s)
y12 <- y * z^2 + rnorm(n, 0, s)
y13 <- y^2 * z + rnorm(n, 0, s)
y14 <- y * z^2 + rnorm(n, 0, s)
y15 <- x / y + rnorm(n, 0, s)
y16 <- y / x + rnorm(n, 0, s)
y17 <- x / z + rnorm(n, 0, s)
y18 <- z / x + rnorm(n, 0, s)
y19 <- y / z + rnorm(n, 0, s)
y20 <- z / y + rnorm(n, 0, s)
y21 <- 2 * x + 2 * y + rnorm(n, 0, s)
y22 <- 2 * x + 2 * z + rnorm(n, 0, s)
y23 <- 2 * y + 2 * z + rnorm(n, 0, s)Mettiamo insieme tutte queste variabili in una matrice:
Y <- cbind(
y1, y2, y3, y4, y5, y6, y7, y8, y9,
y10, y11, y12, y13, y14, y15, y16,
y17, y18, y19, y20, y21, y22, y23
)23.4.1 Analisi fattoriale
Eseguiamo ora un’analisi fattoriale con tre fattori, utilizzando il metodo di regressione per la stima dei punteggi:
fa <- factanal(
Y,
factors = 3,
scores = "regression",
lower = 0.01
)Con scores = "regression" chiediamo la stima dei punteggi fattoriali secondo il metodo di Thomson. Inoltre, poiché factanal() utilizza per default una rotazione ortogonale Varimax, i punteggi stimati risultano incorrelati tra loro (fatto che possiamo verificare con la matrice delle correlazioni tra fattori):
23.4.2 Validazione dei punteggi: confronto con i fattori noti
Se la procedura ha funzionato, ci aspettiamo che:
- ciascun punteggio fattoriale sia fortemente correlato con una sola delle dimensioni originarie delle scatole (\(x\), \(y\), \(z\)),
- le altre correlazioni siano molto più deboli.
Possiamo visualizzare questi rapporti con dei diagrammi di dispersione:
# Primo fattore
p1 <- ggplot(tibble(x, fs1 = fa$scores[, 1]), aes(x, fs1)) + geom_point(alpha = 0.2)
p2 <- ggplot(tibble(y, fs1 = fa$scores[, 1]), aes(y, fs1)) + geom_point(alpha = 0.2)
p3 <- ggplot(tibble(z, fs1 = fa$scores[, 1]), aes(z, fs1)) + geom_point(alpha = 0.2)
# Secondo fattore
p4 <- ggplot(tibble(x, fs2 = fa$scores[, 2]), aes(x, fs2)) + geom_point(alpha = 0.2)
p5 <- ggplot(tibble(y, fs2 = fa$scores[, 2]), aes(y, fs2)) + geom_point(alpha = 0.2)
p6 <- ggplot(tibble(z, fs2 = fa$scores[, 2]), aes(z, fs2)) + geom_point(alpha = 0.2)
# Terzo fattore
p7 <- ggplot(tibble(x, fs3 = fa$scores[, 3]), aes(x, fs3)) + geom_point(alpha = 0.2)
p8 <- ggplot(tibble(y, fs3 = fa$scores[, 3]), aes(y, fs3)) + geom_point(alpha = 0.2)
p9 <- ggplot(tibble(z, fs3 = fa$scores[, 3]), aes(z, fs3)) + geom_point(alpha = 0.2)(p1 | p2 | p3) /
(p4 | p5 | p6) /
(p7 | p8 | p9) 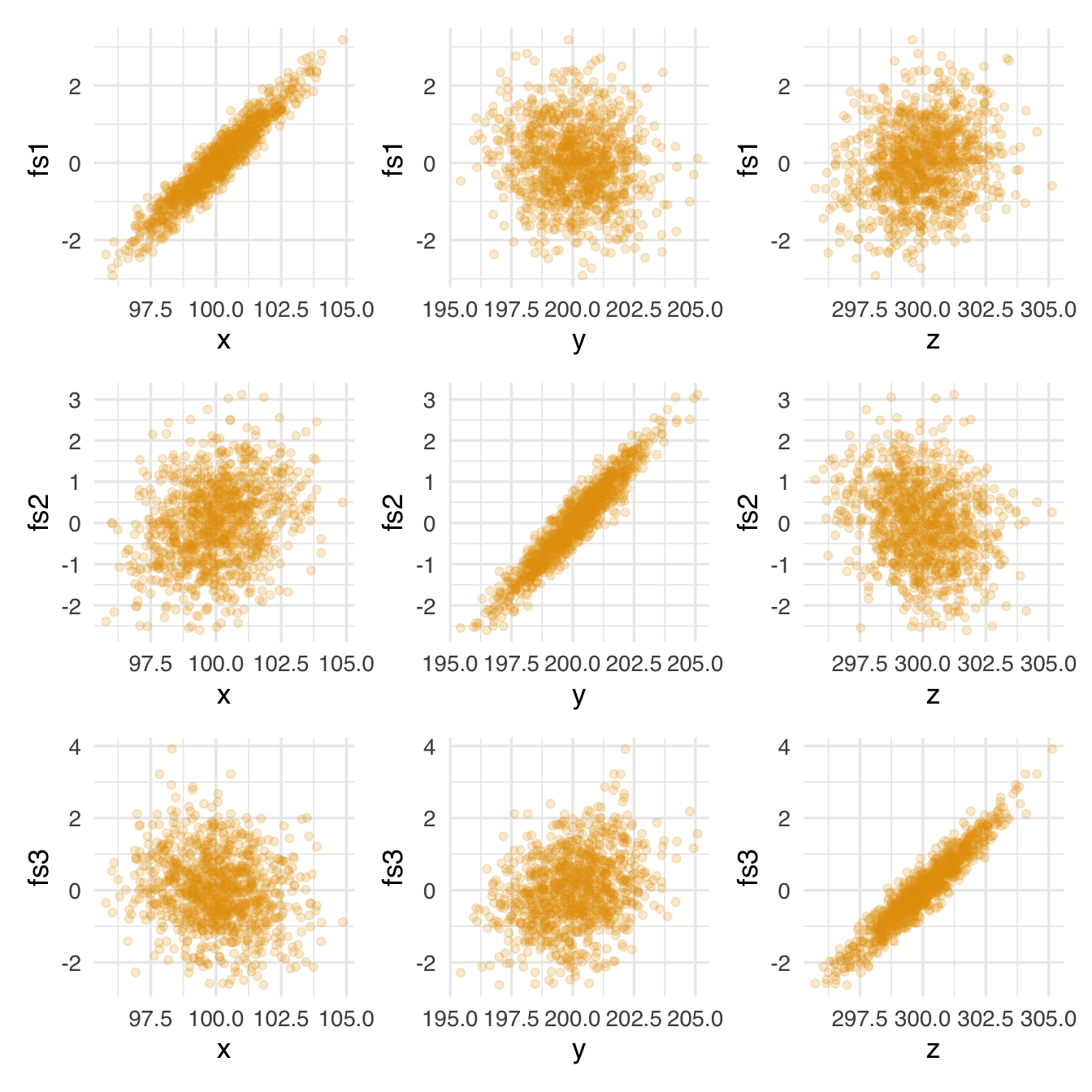
23.4.3 Interpretazione
I grafici confermano l’ipotesi: ciascun punteggio fattoriale è chiaramente associato a una sola delle dimensioni originali (\(x\), \(y\), o \(z\)), a conferma del fatto che l’analisi fattoriale è stata in grado di recuperare le dimensioni latenti a partire da misurazioni indirette e rumorose.
Questo esempio illustra molto bene:
- il significato dei punteggi fattoriali,
- la loro interpretabilità,
- e il modo in cui possono essere utilizzati per stimare valori latenti individuali.
23.5 Il Metodo della Regressione per la stima dei punteggi fattoriali
Una volta stimato un modello fattoriale (ovvero, una soluzione con un certo numero di fattori e una matrice dei pesi fattoriali \(\hat{\boldsymbol{\Lambda}}\)), è possibile stimare per ciascun individuo i punteggi fattoriali: si tratta di stime dei livelli dei fattori latenti per ogni rispondente. Il metodo della regressione, proposto da Thomson, è uno dei più diffusi per questo scopo.
23.5.1 L’idea di base
Il metodo della regressione parte da un concetto semplice ma potente: possiamo considerare ciascun fattore latente come una funzione lineare delle variabili osservate. Cioè, immaginiamo che ciascun punteggio fattoriale derivi da una regressione delle variabili osservate sul fattore. Per esempio, per il fattore \(F_j\) (il fattore \(j\)-esimo), possiamo scrivere:
\[ F_j = \beta_{1j} y_1 + \beta_{2j} y_2 + \dots + \beta_{pj} y_p + \varepsilon_j, \]
dove:
- \(y_1, y_2, \dots, y_p\) sono le variabili osservate standardizzate (cioè con media 0 e deviazione standard 1),
- \(\beta_{ij}\) sono i coefficienti di regressione da stimare,
- \(\varepsilon_j\) è l’errore di stima sul fattore \(j\).
Questa equazione indica che il fattore \(F_j\) può essere predetto a partire da una combinazione lineare delle variabili osservate.
23.5.2 Forma matriciale del modello
Per semplicità, possiamo scrivere tutto in forma matriciale. Supponiamo di avere \(p\) variabili osservate e \(m\) fattori.
- \(\mathbf{y}\) è il vettore riga delle variabili osservate standardizzate (lunghezza \(p\)),
- \(\mathbf{F}\) è il vettore riga dei fattori (lunghezza \(m\)),
- \(\mathbf{B}\) è la matrice dei coefficienti di regressione (dimensione \(p \times m\)),
- \(\boldsymbol{\varepsilon}\) è il vettore degli errori di regressione.
Il modello diventa:
\[ \mathbf{F} = \mathbf{y} \mathbf{B} + \boldsymbol{\varepsilon} \]
Il nostro obiettivo è stimare \(\mathbf{B}\), cioè i pesi che ci permettono di calcolare i punteggi fattoriali a partire dalle osservazioni.
23.5.3 Stima della matrice dei coefficienti di regressione
Per stimare \(\mathbf{B}\) si usa una formula ben nota dell’algebra della regressione lineare:
\[ \hat{\mathbf{B}} = \mathbf{R}_{yy}^{-1} \mathbf{R}_{yf} \]
dove:
- \(\mathbf{R}_{yy}\) è la matrice delle correlazioni tra le variabili osservate (dimensione \(p \times p\)),
- \(\mathbf{R}_{yf}\) è la matrice delle correlazioni tra le variabili osservate e i fattori (dimensione \(p \times m\)).
Quest’ultima matrice, \(\mathbf{R}_{yf}\), è nota anche come matrice di struttura fattoriale, e coincide con la matrice dei carichi fattoriali \(\hat{\boldsymbol{\Lambda}}\) se i fattori sono ortogonali (cioè incorrelati tra loro, come nel caso di una rotazione Varimax).
Pertanto, in presenza di fattori ortogonali:
\[ \hat{\mathbf{B}} = \mathbf{R}^{-1} \hat{\boldsymbol{\Lambda}}, \]
dove \(\mathbf{R}\) è la matrice delle correlazioni tra le variabili osservate.
23.5.4 Calcolo dei punteggi fattoriali
Una volta ottenuti i coefficienti di regressione \(\hat{\mathbf{B}}\), possiamo calcolare i punteggi fattoriali per ciascun individuo applicando la formula del modello di regressione:
\[ \hat{\mathbf{F}} = \mathbf{y} \hat{\mathbf{B}} = \mathbf{y} \mathbf{R}^{-1} \hat{\boldsymbol{\Lambda}} \]
dove:
- \(\mathbf{y}\) è la matrice delle variabili osservate standardizzate (righe = individui, colonne = variabili),
- \(\hat{\mathbf{F}}\) è la matrice dei punteggi fattoriali (righe = individui, colonne = fattori).
23.5.5 Interpretazione
- Ogni riga di \(\hat{\mathbf{F}}\) contiene i valori stimati dei fattori latenti per un individuo.
- Ciascun valore rappresenta la posizione dell’individuo su uno specifico fattore, espressa su una scala con media zero (poiché ottenuta da variabili standardizzate).
23.5.6 Vantaggi del metodo della regressione
- Semplice da calcolare: basta conoscere la matrice delle correlazioni e i carichi fattoriali.
- Punteggi stimati per tutti i soggetti: anche se il numero di soggetti è diverso dal numero di variabili.
- Utilizzabile in ulteriori analisi: ad esempio per confrontare gruppi sui fattori latenti, per costruire profili individuali o per analisi predittive.
23.5.7 Limiti
- I punteggi stimati non sono indipendenti dagli errori di misura: il metodo minimizza l’errore medio quadratico, ma non fornisce stime “pure” dei fattori.
- Se i fattori sono obliqui (cioè correlati), la formula deve essere modificata e il calcolo diventa più complesso.
Esempio 23.1 Esaminiamo ora un esempio pratico in cui calcoliamo i punteggi fattoriali del fattore Comprensione Verbale del WISC-III seguendo due strade:
- utilizzando direttamente la formula della regressione in forma matriciale: \(\hat{\mathbf{F}} = \mathbf{Y} \, \mathbf{R}^{-1} \hat{\boldsymbol{\Lambda}}\);
-
confrontando il risultato con quello ottenuto da
factanal()in R usandoscores = "regression".
Utilizzeremo solo le prime 5 variabili del test WISC-III, che saturano principalmente sul primo fattore (Comprensione Verbale): INFO, SIM, ARITH, VOC, COMP.
wisc_names <- c(
"INFO", "SIM", "ARITH", "VOC", "COMP", "DIGIT", "PICTCOM",
"CODING", "PICTARG", "BLOCK", "OBJECT", "SYMBOL", "MAZES"
)
wisc_III_cov <- getCov(lower, names = wisc_names)
# solo le prime 5 variabili (Comprensione Verbale)
R <- wisc_III_cov[1:5, 1:5]
R
#> INFO SIM ARITH VOC COMP
#> INFO 1.00 0.66 0.57 0.70 0.56
#> SIM 0.66 1.00 0.55 0.69 0.59
#> ARITH 0.57 0.55 1.00 0.54 0.47
#> VOC 0.70 0.69 0.54 1.00 0.64
#> COMP 0.56 0.59 0.47 0.64 1.00Simuliamo dati osservati standardizzati (media 0, sd 1):
set.seed(123)
n <- 100 # 100 soggetti
Y_std <- mvrnorm(n = n, mu = rep(0, 5), Sigma = R) # dati simulati coerenti con R
Y_std |> head()
#> INFO SIM ARITH VOC COMP
#> [1,] 0.4526 -0.4134 -0.5654 -0.1982 -1.70021
#> [2,] 0.1469 -0.3958 -0.6263 0.5940 -0.78535
#> [3,] 1.4065 0.7505 1.4028 1.6446 1.23083
#> [4,] 0.5866 -0.3431 0.1102 0.1921 -0.27661
#> [5,] 0.3441 -0.1589 0.7462 -0.3431 0.02788
#> [6,] 0.7813 1.3285 1.5152 2.1020 1.34216Standardizzazione ulteriore (già è standardizzato, ma è buono verificare):
Estraiamo 1 solo fattore (Comprensione Verbale):
fa <- factanal(Y_std, factors = 1, scores = "regression")La matrice dei carichi fattoriali:
Calcolo manuale: B = R⁻¹ Λ:
Calcolo manuale dei punteggi fattoriali:
Confronto con punteggi ottenuti da factanal()
cor(F_manual, F_factanal)
#> Fattore1_factanal
#> Fattore1 0.9963Il coefficiente di correlazione tra i due metodi sarà molto vicino a 1, indicando che la formula \(\hat{\mathbf{F}} = \mathbf{Y} \mathbf{R}^{-1} \hat{\boldsymbol{\Lambda}}\) è equivalente (entro errori numerici minimi) al metodo implementato da factanal() con l’opzione scores = "regression".
In sintesi,
- abbiamo visto come calcolare manualmente i punteggi fattoriali utilizzando le formule matriciali di regressione;
- abbiamo confrontato i risultati con quelli ottenuti da un pacchetto statistico (
factanal()in R); - l’equivalenza tra i due risultati conferma la validità teorica delle formule presentate nel metodo della regressione per la stima dei punteggi fattoriali.
23.6 Riflessioni Conclusive
L’analisi fattoriale non è solo una tecnica per ridurre la dimensionalità dei dati, ma un vero e proprio strumento per costruire modelli psicologici latenti a partire da manifestazioni osservabili. Se interpretata con rigore teorico e supportata da una stima accurata dei punteggi fattoriali, essa può favorire una comprensione più profonda dei costrutti psicologici e della loro struttura. Tuttavia, va ricordato che ogni decisione presa lungo il processo – dalla scelta del numero di fattori, al metodo di estrazione, alla rotazione e alla stima dei punteggi – introduce un certo grado di arbitrarietà. È proprio in questo spazio di arbitrarietà che la psicometria incontra la teoria: l’analisi fattoriale è tanto uno strumento tecnico quanto una pratica epistemica, in cui i dati non parlano da soli, ma vengono interrogati alla luce di ipotesi e modelli. Per questo motivo, lo sviluppo di test psicometrici validi richiede non solo padronanza tecnica, ma anche capacità critica e riflessività teorica.
23.7 Session Info
sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.3.2
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.0
#>
#> locale:
#> [1] C/UTF-8/C/C/C/C
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] kableExtra_1.4.0 corrplot_0.95 ggokabeito_0.1.0 see_0.11.0
#> [5] MASS_7.3-65 viridis_0.6.5 viridisLite_0.4.2 ggpubr_0.6.0
#> [9] ggExtra_0.10.1 gridExtra_2.3 patchwork_1.3.0 bayesplot_1.11.1
#> [13] semTools_0.5-6 semPlot_1.1.6 lavaan_0.6-19 psych_2.4.12
#> [17] scales_1.3.0 markdown_1.13 knitr_1.50 lubridate_1.9.4
#> [21] forcats_1.0.0 stringr_1.5.1 dplyr_1.1.4 purrr_1.0.4
#> [25] readr_2.1.5 tidyr_1.3.1 tibble_3.2.1 ggplot2_3.5.1
#> [29] tidyverse_2.0.0 here_1.0.1
#>
#> loaded via a namespace (and not attached):
#> [1] rstudioapi_0.17.1 jsonlite_1.9.1 magrittr_2.0.3
#> [4] TH.data_1.1-3 estimability_1.5.1 farver_2.1.2
#> [7] nloptr_2.2.1 rmarkdown_2.29 vctrs_0.6.5
#> [10] minqa_1.2.8 base64enc_0.1-3 rstatix_0.7.2
#> [13] htmltools_0.5.8.1 broom_1.0.7 Formula_1.2-5
#> [16] htmlwidgets_1.6.4 plyr_1.8.9 sandwich_3.1-1
#> [19] emmeans_1.10.7 zoo_1.8-13 igraph_2.1.4
#> [22] mime_0.13 lifecycle_1.0.4 pkgconfig_2.0.3
#> [25] Matrix_1.7-3 R6_2.6.1 fastmap_1.2.0
#> [28] rbibutils_2.3 shiny_1.10.0 digest_0.6.37
#> [31] OpenMx_2.21.13 fdrtool_1.2.18 colorspace_2.1-1
#> [34] rprojroot_2.0.4 Hmisc_5.2-3 labeling_0.4.3
#> [37] timechange_0.3.0 abind_1.4-8 compiler_4.4.2
#> [40] withr_3.0.2 glasso_1.11 htmlTable_2.4.3
#> [43] backports_1.5.0 carData_3.0-5 ggsignif_0.6.4
#> [46] corpcor_1.6.10 gtools_3.9.5 tools_4.4.2
#> [49] pbivnorm_0.6.0 foreign_0.8-88 zip_2.3.2
#> [52] httpuv_1.6.15 nnet_7.3-20 glue_1.8.0
#> [55] quadprog_1.5-8 nlme_3.1-167 promises_1.3.2
#> [58] lisrelToR_0.3 grid_4.4.2 checkmate_2.3.2
#> [61] cluster_2.1.8.1 reshape2_1.4.4 generics_0.1.3
#> [64] gtable_0.3.6 tzdb_0.5.0 data.table_1.17.0
#> [67] hms_1.1.3 xml2_1.3.8 car_3.1-3
#> [70] sem_3.1-16 pillar_1.10.1 rockchalk_1.8.157
#> [73] later_1.4.1 splines_4.4.2 lattice_0.22-6
#> [76] survival_3.8-3 kutils_1.73 tidyselect_1.2.1
#> [79] miniUI_0.1.1.1 pbapply_1.7-2 reformulas_0.4.0
#> [82] svglite_2.1.3 stats4_4.4.2 xfun_0.51
#> [85] qgraph_1.9.8 arm_1.14-4 stringi_1.8.4
#> [88] yaml_2.3.10 pacman_0.5.1 boot_1.3-31
#> [91] evaluate_1.0.3 codetools_0.2-20 mi_1.1
#> [94] cli_3.6.4 RcppParallel_5.1.10 rpart_4.1.24
#> [97] systemfonts_1.2.1 xtable_1.8-4 Rdpack_2.6.3
#> [100] munsell_0.5.1 Rcpp_1.0.14 coda_0.19-4.1
#> [103] png_0.1-8 XML_3.99-0.18 parallel_4.4.2
#> [106] jpeg_0.1-10 lme4_1.1-36 mvtnorm_1.3-3
#> [109] openxlsx_4.2.8 rlang_1.1.5 multcomp_1.4-28
#> [112] mnormt_2.1.1