here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(lavaan, corrr, psych)26 Valutazione della matrice di correlazione
- esaminare la matrice di correlazione tra le variabili come passo preliminare di un’analisi fattoriale.
- Leggere il capitolo Factor Analysis and Principal Component Analysis del testo di Petersen (2024).
26.1 Introduzione
Prima di eseguire un’analisi fattoriale esplorativa (EFA), è fondamentale valutare se i dati soddisfano i presupposti minimi richiesti. Il primo passo consiste nell’esaminare la matrice di correlazione tra le variabili. Se il determinante di questa matrice è pari a zero, significa che esiste collinearità perfetta tra alcune variabili: in questo caso, l’analisi fattoriale non può essere effettuata perché non sarebbe possibile distinguere contributi distinti dei fattori latenti.
Tuttavia, anche se il determinante è diverso da zero, non è detto che i dati siano adatti all’EFA. È necessario che le variabili mostrino correlazioni sufficientemente elevate tra loro, altrimenti l’analisi potrebbe produrre soluzioni instabili o difficili da interpretare. Correlazioni troppo deboli indicano che non esistono dimensioni comuni sottostanti e quindi non ha senso estrarre dei fattori.
Per valutare l’adeguatezza dei dati, possiamo:
- ispezionare visivamente la matrice di correlazione,
- calcolare il test di sfericità di Bartlett,
- calcolare l’indice di adeguatezza campionaria KMO (Kaiser-Meyer-Olkin).
Questi strumenti forniscono informazioni complementari sull’opportunità di procedere con un’analisi fattoriale.
26.2 Analisi Preliminari
Per illustrare il procedimento, utilizziamo il dataset HolzingerSwineford1939, che contiene 301 osservazioni relative a punteggi di abilità mentale su diverse prove cognitive. In questa analisi considereremo le variabili x1–x9.
Cominciamo con l’importazione del dataset e la verifica dell’integrità dei dati.
# Caricamento del dataset e visualizzazione iniziale
data(HolzingerSwineford1939)
glimpse(HolzingerSwineford1939)
#> Rows: 301
#> Columns: 15
#> $ id <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, …
#> $ sex <int> 1, 2, 2, 1, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 2,…
#> $ ageyr <int> 13, 13, 13, 13, 12, 14, 12, 12, 13, 12, 12, 12, 12, 12, 12,…
#> $ agemo <int> 1, 7, 1, 2, 2, 1, 1, 2, 0, 5, 2, 11, 7, 8, 6, 1, 11, 5, 8, …
#> $ school <fct> Pasteur, Pasteur, Pasteur, Pasteur, Pasteur, Pasteur, Paste…
#> $ grade <int> 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7,…
#> $ x1 <dbl> 3.333, 5.333, 4.500, 5.333, 4.833, 5.333, 2.833, 5.667, 4.5…
#> $ x2 <dbl> 7.75, 5.25, 5.25, 7.75, 4.75, 5.00, 6.00, 6.25, 5.75, 5.25,…
#> $ x3 <dbl> 0.375, 2.125, 1.875, 3.000, 0.875, 2.250, 1.000, 1.875, 1.5…
#> $ x4 <dbl> 2.333, 1.667, 1.000, 2.667, 2.667, 1.000, 3.333, 3.667, 2.6…
#> $ x5 <dbl> 5.75, 3.00, 1.75, 4.50, 4.00, 3.00, 6.00, 4.25, 5.75, 5.00,…
#> $ x6 <dbl> 1.2857, 1.2857, 0.4286, 2.4286, 2.5714, 0.8571, 2.8571, 1.2…
#> $ x7 <dbl> 3.391, 3.783, 3.261, 3.000, 3.696, 4.348, 4.696, 3.391, 4.5…
#> $ x8 <dbl> 5.75, 6.25, 3.90, 5.30, 6.30, 6.65, 6.20, 5.15, 4.65, 4.55,…
#> $ x9 <dbl> 6.361, 7.917, 4.417, 4.861, 5.917, 7.500, 4.861, 3.667, 7.3…
# Selezione delle variabili di interesse
hz <- HolzingerSwineford1939 |>
dplyr::select(x1:x9)
# Visualizzazione delle prime 5 righe
hz |> slice(1:5)
#> x1 x2 x3 x4 x5 x6 x7 x8 x9
#> 1 3.333 7.75 0.375 2.333 5.75 1.2857 3.391 5.75 6.361
#> 2 5.333 5.25 2.125 1.667 3.00 1.2857 3.783 6.25 7.917
#> 3 4.500 5.25 1.875 1.000 1.75 0.4286 3.261 3.90 4.417
#> 4 5.333 7.75 3.000 2.667 4.50 2.4286 3.000 5.30 4.861
#> 5 4.833 4.75 0.875 2.667 4.00 2.5714 3.696 6.30 5.91726.2.1 Valutazione dei Dati Mancanti
Prima di esaminare le correlazioni, è importante verificare l’eventuale presenza di dati mancanti, poiché anche pochi valori mancanti possono alterare significativamente la matrice di correlazione.
In questo caso, non sono presenti dati mancanti. In presenza di dati mancanti, sarà necessario adottare strategie appropriate (es. imputazione, listwise deletion, ecc.) prima di procedere.
🔍 Nota didattica: In genere, per l’analisi fattoriale è preferibile utilizzare una matrice di correlazione calcolata su dati completi, perché la presenza di dati mancanti può distorcere le relazioni tra le variabili.
26.2.2 Esplorazione delle Distribuzioni
Un controllo preliminare utile è l’esame della forma delle distribuzioni delle variabili, in particolare asimmetria (skewness) e curtosi (kurtosis), che possono indicare violazioni di normalità.
describe(hz)
#> vars n mean sd median trimmed mad min max range skew kurtosis
#> x1 1 301 4.94 1.17 5.00 4.96 1.24 0.67 8.50 7.83 -0.25 0.31
#> x2 2 301 6.09 1.18 6.00 6.02 1.11 2.25 9.25 7.00 0.47 0.33
#> x3 3 301 2.25 1.13 2.12 2.20 1.30 0.25 4.50 4.25 0.38 -0.91
#> x4 4 301 3.06 1.16 3.00 3.02 0.99 0.00 6.33 6.33 0.27 0.08
#> x5 5 301 4.34 1.29 4.50 4.40 1.48 1.00 7.00 6.00 -0.35 -0.55
#> x6 6 301 2.19 1.10 2.00 2.09 1.06 0.14 6.14 6.00 0.86 0.82
#> x7 7 301 4.19 1.09 4.09 4.16 1.10 1.30 7.43 6.13 0.25 -0.31
#> x8 8 301 5.53 1.01 5.50 5.49 0.96 3.05 10.00 6.95 0.53 1.17
#> x9 9 301 5.37 1.01 5.42 5.37 0.99 2.78 9.25 6.47 0.20 0.29
#> se
#> x1 0.07
#> x2 0.07
#> x3 0.07
#> x4 0.07
#> x5 0.07
#> x6 0.06
#> x7 0.06
#> x8 0.06
#> x9 0.06In questo caso, i valori di asimmetria e curtosi sono sufficientemente contenuti, quindi non è necessario trasformare le variabili. Tuttavia, se ci fossero valori molto estremi, una trasformazione (log, z-score, Box-Cox) potrebbe essere utile.
26.2.3 Ispezione della Matrice di Correlazione
Una matrice di correlazione è la base concettuale dell’analisi fattoriale: essa mostra quanto ogni variabile è associata con le altre. In presenza di gruppi di variabili altamente correlate tra loro e poco correlate con le altre, è plausibile che esistano fattori comuni sottostanti.
Visualizziamo la matrice utilizzando il pacchetto corrr:
cor_tb <- correlate(hz)
cor_tb |>
rearrange() |>
rplot(colors = c("red", "white", "blue"))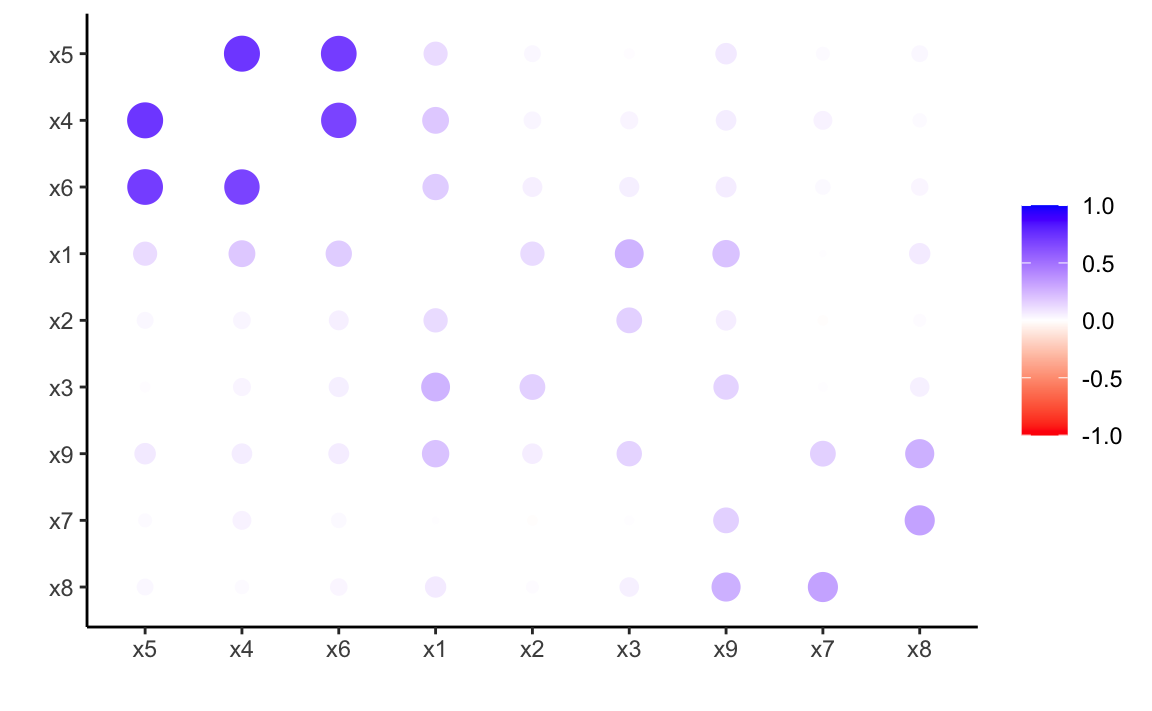
Il grafico mostra tre blocchi distinti:
- x4–x6: un primo gruppo fortemente correlato tra loro,
- x1–x3: un secondo gruppo coeso,
- x7–x9: un terzo gruppo distinto.
Questa struttura è coerente con l’idea che i punteggi derivino da tre fattori latenti diversi.
26.3 Test di Sfericità di Bartlett
Il test di sfericità di Bartlett verifica se la matrice di correlazione differisce significativamente da una matrice identità (cioè una matrice in cui tutte le variabili sono incorrelate).
Ipotesi nulla: le variabili non sono correlate tra loro.
Ipotesi alternativa: esistono correlazioni significative tra le variabili.
La formula del test è:
\[ \chi^2 = -\left[n - 1 - \frac{1}{6}(2p + 5)\right] \ln |\boldsymbol{R}|, \]
dove:
- \(n\) = numerosità campionaria,
- \(p\) = numero di variabili,
- \(|\boldsymbol{R}|\) = determinante della matrice di correlazione.
Il test restituisce una statistica \(\chi^2\) con \(p(p - 1)/2\) gradi di libertà.
Risultato: la statistica è altamente significativa → possiamo rifiutare l’ipotesi nulla. Le variabili sono sufficientemente correlate per proseguire con l’analisi fattoriale.
📌 Nota: Il test di Bartlett è molto sensibile alla numerosità campionaria: con campioni ampi, anche correlazioni deboli possono risultare statisticamente “significative”. È quindi opportuno integrare il test con altri indici, come il KMO.
26.4 Indice KMO (Kaiser-Meyer-Olkin)
L’indice KMO misura quanto le correlazioni osservate siano spiegabili da fattori latenti comuni, piuttosto che da correlazioni parziali tra le variabili (che rappresentano associazioni “spuriate”).
La formula è:
\[ \text{KMO} = \frac{\sum_i \sum_j r^2_{ij}}{\sum_i \sum_j r^2_{ij} + \sum_i \sum_j p^2_{ij}}, \]
dove \(r_{ij}\) sono le correlazioni osservate, e \(p_{ij}\) le correlazioni parziali.
Valori possibili:
- 0.90–1.00: eccellente (meravigliosa)
- 0.80–0.89: molto buona (meritevole)
- 0.70–0.79: buona (media)
- 0.60–0.69: discreta (mediocre)
- 0.50–0.59: scarsa (miserabile)
- < 0.50: inadeguata (inaccettabile)
out = KMO(cor_mat)
print(out)
#> Kaiser-Meyer-Olkin factor adequacy
#> Call: KMO(r = cor_mat)
#> Overall MSA = 0.75
#> MSA for each item =
#> x1 x2 x3 x4 x5 x6 x7 x8 x9
#> 0.81 0.78 0.73 0.76 0.74 0.81 0.59 0.68 0.79Nel nostro caso, il valore KMO è attorno a 0.70, quindi l’adeguatezza è buona, ma non eccellente. Possiamo proseguire con l’analisi, pur restando consapevoli che la qualità dei dati potrebbe essere migliorata (es. con la revisione degli item).
26.5 Riflessioni conclusive
Le analisi preliminari condotte sul dataset HolzingerSwineford1939 indicano che:
- le correlazioni tra variabili sono presenti e coerenti con una struttura a più fattori,
- il test di Bartlett conferma che la matrice di correlazione è diversa da una matrice identità,
- l’indice KMO suggerisce un’adeguatezza campionaria soddisfacente, anche se non ottimale.
Questi risultati ci consentono di procedere con l’analisi fattoriale esplorativa, ma evidenziano anche la necessità di valutazioni critiche in fase interpretativa. L’uso combinato di più strumenti diagnostici consente di fondare l’analisi su basi solide e di trarre conclusioni più affidabili riguardo alla struttura latente dei dati.
26.6 Session Info
sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.3.2
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.0
#>
#> locale:
#> [1] C/UTF-8/C/C/C/C
#>
#> time zone: Europe/Rome
#> tzcode source: internal
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] corrr_0.4.4 ggokabeito_0.1.0 see_0.11.0 MASS_7.3-65
#> [5] viridis_0.6.5 viridisLite_0.4.2 ggpubr_0.6.0 ggExtra_0.10.1
#> [9] gridExtra_2.3 patchwork_1.3.0 bayesplot_1.11.1 semTools_0.5-6
#> [13] semPlot_1.1.6 lavaan_0.6-19 psych_2.4.12 scales_1.3.0
#> [17] markdown_1.13 knitr_1.50 lubridate_1.9.4 forcats_1.0.0
#> [21] stringr_1.5.1 dplyr_1.1.4 purrr_1.0.4 readr_2.1.5
#> [25] tidyr_1.3.1 tibble_3.2.1 ggplot2_3.5.1 tidyverse_2.0.0
#> [29] here_1.0.1
#>
#> loaded via a namespace (and not attached):
#> [1] rstudioapi_0.17.1 jsonlite_1.9.1 magrittr_2.0.3
#> [4] TH.data_1.1-3 estimability_1.5.1 farver_2.1.2
#> [7] nloptr_2.2.1 rmarkdown_2.29 vctrs_0.6.5
#> [10] minqa_1.2.8 base64enc_0.1-3 rstatix_0.7.2
#> [13] htmltools_0.5.8.1 broom_1.0.7 Formula_1.2-5
#> [16] htmlwidgets_1.6.4 plyr_1.8.9 sandwich_3.1-1
#> [19] emmeans_1.10.7 zoo_1.8-13 igraph_2.1.4
#> [22] iterators_1.0.14 mime_0.13 lifecycle_1.0.4
#> [25] pkgconfig_2.0.3 Matrix_1.7-3 R6_2.6.1
#> [28] fastmap_1.2.0 rbibutils_2.3 shiny_1.10.0
#> [31] digest_0.6.37 OpenMx_2.21.13 fdrtool_1.2.18
#> [34] colorspace_2.1-1 rprojroot_2.0.4 Hmisc_5.2-3
#> [37] seriation_1.5.7 labeling_0.4.3 timechange_0.3.0
#> [40] abind_1.4-8 compiler_4.4.2 withr_3.0.2
#> [43] glasso_1.11 htmlTable_2.4.3 backports_1.5.0
#> [46] carData_3.0-5 ggsignif_0.6.4 corpcor_1.6.10
#> [49] gtools_3.9.5 tools_4.4.2 pbivnorm_0.6.0
#> [52] foreign_0.8-88 zip_2.3.2 httpuv_1.6.15
#> [55] nnet_7.3-20 glue_1.8.0 quadprog_1.5-8
#> [58] nlme_3.1-167 promises_1.3.2 lisrelToR_0.3
#> [61] grid_4.4.2 checkmate_2.3.2 cluster_2.1.8.1
#> [64] reshape2_1.4.4 generics_0.1.3 gtable_0.3.6
#> [67] tzdb_0.5.0 ca_0.71.1 data.table_1.17.0
#> [70] hms_1.1.3 car_3.1-3 sem_3.1-16
#> [73] foreach_1.5.2 pillar_1.10.1 rockchalk_1.8.157
#> [76] later_1.4.1 splines_4.4.2 lattice_0.22-6
#> [79] survival_3.8-3 kutils_1.73 tidyselect_1.2.1
#> [82] registry_0.5-1 miniUI_0.1.1.1 pbapply_1.7-2
#> [85] reformulas_0.4.0 stats4_4.4.2 xfun_0.51
#> [88] qgraph_1.9.8 arm_1.14-4 stringi_1.8.4
#> [91] yaml_2.3.10 pacman_0.5.1 boot_1.3-31
#> [94] evaluate_1.0.3 codetools_0.2-20 mi_1.1
#> [97] cli_3.6.4 RcppParallel_5.1.10 rpart_4.1.24
#> [100] xtable_1.8-4 Rdpack_2.6.3 munsell_0.5.1
#> [103] Rcpp_1.0.14 coda_0.19-4.1 png_0.1-8
#> [106] XML_3.99-0.18 parallel_4.4.2 jpeg_0.1-10
#> [109] lme4_1.1-36 mvtnorm_1.3-3 openxlsx_4.2.8
#> [112] rlang_1.1.5 TSP_1.2-4 multcomp_1.4-28
#> [115] mnormt_2.1.1