24  Attendibilità e modello fattoriale

In questo capitolo imparerai a
  • calcolare e interpretare i punteggi fattoriali.
Prerequisiti
  • Leggere il capitolo 6, Factor Analysis and Principal Component Analysis, del testo Principles of psychological assessment di Petersen (2024).
Preparazione del Notebook 
here::here("code", "_common.R") |> 
  source()

if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(lavaan, semPlot, modelsummary)

24.1 Introduzione

In questo capitolo affronteremo il tema della valutazione dell’affidabilità di uno strumento psicometrico tramite l’analisi fattoriale. Verranno introdotti tre modelli teorici che descrivono le diverse relazioni possibili tra gli indicatori osservati e un fattore latente comune: il modello congenerico, il modello tau-equivalente e il modello parallelo.

Per ciascuno di questi modelli sarà discusso un indice specifico volto a quantificare l’affidabilità intesa come coerenza interna. Gli indici presentati saranno:

  • l’indice omega di McDonald,
  • l’indice alpha di Cronbach,
  • l’indice rho, derivato dalla formula “profetica” di Spearman-Brown.

Si mostrerà come l’impiego dell’indice alpha di Cronbach sia giustificato solo in presenza di specifiche condizioni, le quali risultano però raramente soddisfatte nei dati empirici. Per tale motivo, nella pratica applicativa, è spesso preferibile fare riferimento all’indice omega di McDonald, che fornisce una stima più accurata della coerenza interna.

24.2 Teoria classica dei test e analisi fattoriale

Come illustrato da McDonald (2013), la teoria classica dei test (CTT) può essere messa in relazione diretta con il modello dell’analisi fattoriale confermativa. La figura seguente rappresenta, in termini fattoriali, il legame tra i punteggi osservati \(Y\) ottenuti da un test composto da cinque item e i corrispondenti punteggi veri.

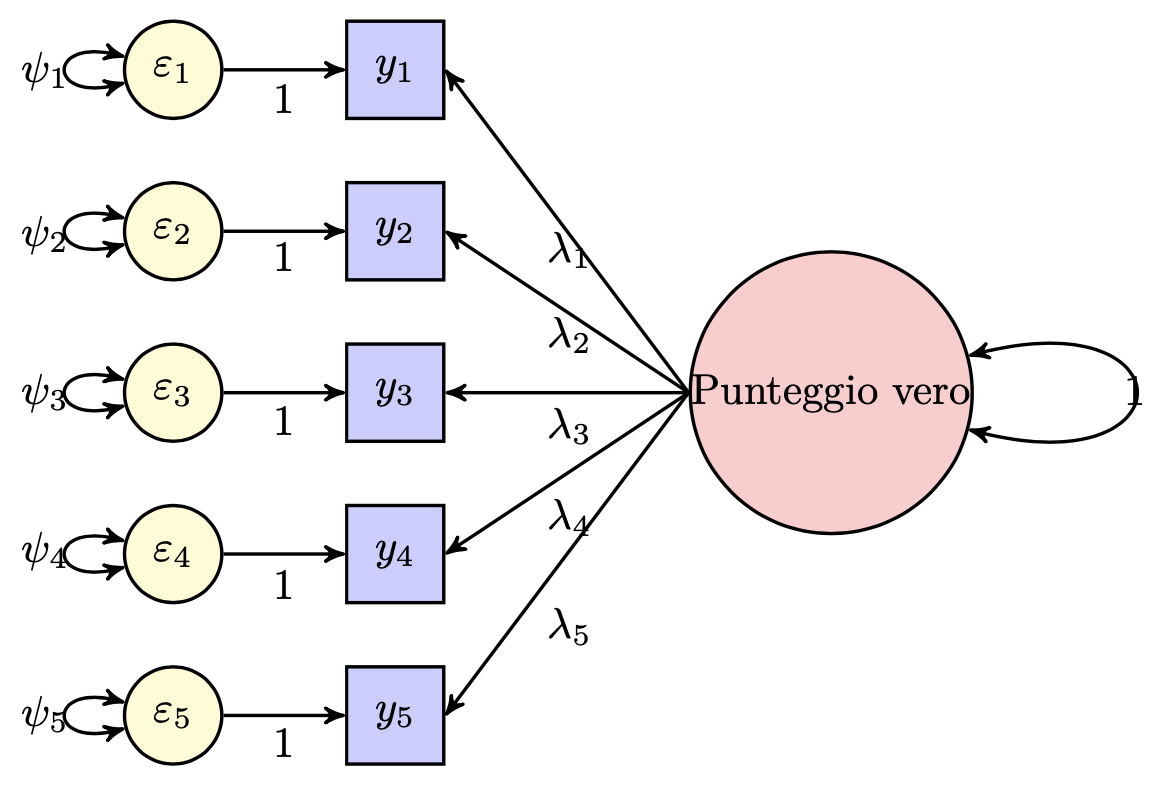
Figura 24.1: Diagramma di percorso del modello monofattoriale.

Quando si somministra un unico test, esistono diverse strategie per stimarne l’affidabilità. In questo contesto, ci concentreremo su tre approcci implementabili tramite l’analisi fattoriale:

  • il coefficiente \(\alpha\) di Cronbach,
  • il coefficiente \(\omega\) di McDonald,
  • l’indice \(\rho\) derivato dalla formula di Spearman-Brown.

Tra questi, il coefficiente \(\alpha\) di Cronbach è l’indice più diffuso per la stima dell’affidabilità come coerenza interna o omogeneità tra gli item. Tuttavia, approfondiremo come esso rappresenti una stima al ribasso dell’affidabilità del test, valida solo a patto che siano rispettate alcune ipotesi. In caso contrario, l’\(\alpha\) può risultare uno stimatore distorto.

Prima di analizzare nel dettaglio le tre metodologie, è necessario distinguere tra tre configurazioni possibili del modello unifattoriale, corrispondenti a:

  • modello con indicatori congenerici,
  • modello \(\tau\)-equivalente,
  • modello parallelo.

24.3 Modello fattoriale e teoria classica dei test

Consideriamo un insieme di \(p\) item osservati, denotati con \(X_1, X_2, \dots, X_p\) (dove \(p > 2\)). Secondo la teoria classica dei test, ciascun punteggio osservato \(X_i\) può essere scomposto in due componenti:

  • il punteggio vero \(T_i\),
  • un errore casuale \(E_i\):

\[ \begin{aligned} X_1 &= T_1 + E_1, \\ X_2 &= T_2 + E_2, \\ &\dots \\ X_p &= T_p + E_p. \end{aligned} \]

Seguendo l’approccio proposto da McDonald (2013), questa decomposizione può essere reinterpretata nel contesto dell’analisi fattoriale. La relazione tra punteggio vero ed errore viene descritta nel seguente modo:

\[ X_i = \lambda_i \xi + \delta_i, \quad \text{per } i = 1, \dots, p, \]

dove:

  • \(X_i\) è il punteggio osservato dell’item \(i\)-esimo (espresso come scarto dalla media),
  • \(\lambda_i\) è il carico fattoriale, che rappresenta il contributo del fattore comune \(\xi\) all’item \(i\),
  • \(\xi\) è il fattore latente comune (ipotizzato con media zero e varianza unitaria),
  • \(\delta_i\) è l’errore specifico (residuo) associato all’item \(i\).

Questa formulazione si basa sulle ipotesi classiche del modello monofattoriale:

  • il fattore comune \(\xi\) è incorrelato con ciascun errore \(\delta_i\),
  • gli errori \(\delta_i\) sono mutuamente incorrelati (\(\text{Cov}(\delta_i, \delta_j) = 0\) per ogni \(i \neq j\)).

Questa struttura consente di collegare direttamente i concetti della teoria classica dei test con il formalismo dell’analisi fattoriale e di derivare in modo coerente gli indici di affidabilità basati su modelli fattoriali.

24.4 Classi di modelli

Nel contesto dei modelli monofattoriali, è possibile distinguere tre principali configurazioni teoriche, ciascuna caratterizzata da un diverso insieme di assunzioni riguardanti la relazione tra gli indicatori osservati e il fattore latente comune. Queste tre configurazioni si collocano lungo un continuum che va da una maggiore flessibilità a una maggiore restrizione strutturale.

24.4.1 Modello congenerico

Il modello con indicatori congenerici rappresenta la formulazione più generale e flessibile. In questo modello:

  • ogni indicatore è influenzato dal medesimo fattore latente,
  • i carichi fattoriali (\(\lambda_i\)) possono variare da un indicatore all’altro,
  • anche le varianze degli errori (\(\delta_i\)) sono libere di differire.

In altre parole, ciascun indicatore misura lo stesso costrutto latente, ma può farlo con una diversa intensità e con un diverso grado di errore. Questo modello riflette realisticamente la maggior parte delle situazioni empiriche e costituisce il punto di partenza per valutazioni più complesse.

24.4.2 Modello tau-equivalente

Il modello \(\tau\)-equivalente è una restrizione del modello congenerico in cui si assume che:

  • tutti gli indicatori abbiano lo stesso carico fattoriale (\(\lambda_i = \lambda\) per ogni \(i\)),
  • le varianze degli errori possono comunque differire tra gli indicatori.

Questo implica che ogni indicatore contribuisce in egual misura alla misurazione del fattore latente, pur potendo avere un diverso grado di specificità residua. Il coefficiente \(\alpha\) di Cronbach si basa proprio su questo modello e fornisce una stima attendibile solo se tale assunzione è soddisfatta.

24.4.3 Modello parallelo

Il modello con indicatori paralleli rappresenta il caso più restrittivo. In esso si assume che:

  • tutti gli indicatori abbiano lo stesso carico fattoriale (\(\lambda_i = \lambda\)),
  • e che le varianze degli errori siano identiche tra gli indicatori (\(\text{Var}(\delta_i) = \sigma^2\) per ogni \(i\)).

In questa configurazione, gli indicatori sono considerati completamente equivalenti sia nella misura del fattore latente che nella quantità di errore associato. È il modello sottostante alla formula di Spearman-Brown, utilizzata, ad esempio, per prevedere l’affidabilità in funzione della lunghezza del test.

24.4.4 Confronto tra i modelli

I tre modelli possono essere letti come una gerarchia di assunzioni:

Modello Carichi fattoriali Varianze degli errori Grado di restrizione
Congenerico Liberi Libere Basso
Tau-equivalente Uguali Libere Medio
Parallelo Uguali Uguali Alto

 

All’aumentare dei vincoli imposti al modello, cresce la semplicità e la forza esplicativa teorica, ma diminuisce la flessibilità rispetto ai dati reali. È quindi essenziale scegliere il modello coerente con la struttura empirica degli item, poiché ogni indice di affidabilità presuppone uno di questi modelli:

  • Omega di McDonald è coerente con il modello congenerico,
  • Alpha di Cronbach assume il modello \(\tau\)-equivalente,
  • Rho di Spearman-Brown richiede il modello parallelo.

Nelle sezioni successive esamineremo in dettaglio ciascuno di questi indici e illustreremo come stimarli e interpretarli correttamente in funzione della struttura del modello.

24.5 Modelli monofattoriali: indicatori congenerici, τ-equivalenti e paralleli

24.5.1 Indicatori congenerici

Gli indicatori congenerici rappresentano misure di uno stesso costrutto latente, ma non è richiesto che lo riflettano con la stessa intensità né con lo stesso grado di precisione. Nel modello monofattoriale congenerico, non vengono imposti vincoli né sui carichi fattoriali né sulle varianze degli errori specifici:

\[ \lambda_1 \neq \lambda_2 \neq \dots \neq \lambda_p, \quad \psi_{11} \neq \psi_{22} \neq \dots \neq \psi_{pp}. \]

Il modello è descritto, come già visto, dall’equazione:

\[ X_i = \lambda_i \xi + \delta_i, \quad i = 1, \dots, p. \]

La matrice di varianze e covarianze riprodotta dal modello è:

\[ \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \dots & \sigma_{1p} \\ \sigma_{21} & \sigma_{22} & \dots & \sigma_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p1} & \sigma_{p2} & \dots & \sigma_{pp} \end{bmatrix}, \]

dove ogni elemento può assumere un valore diverso. Le covarianze tra gli item sono tutte positive (poiché condividono il fattore comune), ma non necessariamente uguali tra loro, e lo stesso vale per le varianze.

Questo è il modello più flessibile, adatto a situazioni empiriche in cui gli item non sono perfettamente equivalenti ma riflettono lo stesso costrutto. Il coefficiente omega di McDonald è coerente con questo modello.

24.5.2 Indicatori τ-equivalenti

Il modello con indicatori \(\tau\)-equivalenti introduce un vincolo importante: tutti gli item presentano lo stesso carico fattoriale. Tuttavia, le varianze residue possono ancora differire:

\[ \lambda_1 = \lambda_2 = \dots = \lambda_p = \lambda, \quad \psi_{11} \neq \psi_{22} \neq \dots \neq \psi_{pp}. \]

L’equazione del modello diventa quindi:

\[ X_i = \lambda \xi + \delta_i, \]

oppure, definendo \(\tau = \lambda \xi\) come componente comune scalata nell’unità dell’indicatore:

\[ X_i = \tau + \delta_i. \]

In questo modello, le covarianze tra gli item sono tutte uguali, poiché dipendono solo dalla varianza della componente comune:

\[ \sigma_{ik} = \lambda^2 = \sigma_T^2, \quad \text{per } i \neq k. \]

Invece, le varianze degli item possono differire a causa delle varianze residue:

\[ \sigma_{ii} = \lambda^2 + \psi_{ii} = \sigma_T^2 + \psi_{ii}. \]

La matrice delle varianze e covarianze risultante è dunque:

\[ \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_T^2 + \psi_{11} & \sigma_T^2 & \dots & \sigma_T^2 \\ \sigma_T^2 & \sigma_T^2 + \psi_{22} & \dots & \sigma_T^2 \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_T^2 & \sigma_T^2 & \dots & \sigma_T^2 + \psi_{pp} \end{bmatrix}. \]

Il coefficiente alpha di Cronbach assume implicitamente che gli item soddisfino questa struttura. Tuttavia, in molte applicazioni empiriche questa assunzione è violata, rendendo l’\(\alpha\) un sottostimatore distorto dell’affidabilità reale.

24.5.3 Indicatori paralleli

Il modello con indicatori paralleli rappresenta il caso più restrittivo. Oltre a imporre carichi fattoriali uguali, richiede anche che tutte le varianze residue siano identiche:

\[ \lambda_1 = \lambda_2 = \dots = \lambda_p = \lambda, \quad \psi_{11} = \psi_{22} = \dots = \psi_{pp} = \psi. \]

Di conseguenza, tutte le varianze osservate risultano uguali:

\[ \sigma_{ii} = \lambda^2 + \psi = \sigma_T^2 + \sigma^2, \quad \text{per ogni } i. \]

Anche tutte le covarianze tra item restano uguali:

\[ \sigma_{ik} = \lambda^2 = \sigma_T^2, \quad \text{per } i \neq k. \]

La matrice \(\boldsymbol{\Sigma}\) assume quindi la seguente forma simmetrica e omogenea:

\[ \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_T^2 + \sigma^2 & \sigma_T^2 & \dots & \sigma_T^2 \\ \sigma_T^2 & \sigma_T^2 + \sigma^2 & \dots & \sigma_T^2 \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_T^2 & \sigma_T^2 & \dots & \sigma_T^2 + \sigma^2 \end{bmatrix}. \]

Questo modello si colloca all’estremo del continuum di restrizione e viene assunto dalla formula di Spearman-Brown, impiegata per stimare l’effetto dell’aumento del numero di item sull’affidabilità.

24.5.4 Riepilogo concettuale

Modello Carichi fattoriali Varianze errori Varianze osservate Covarianze Indice coerente
Congenerico Diversi Diverse Diverse Diverse Omega
Tau-equivalente Uguali Diverse Diverse Uguali Alpha
Parallelo Uguali Uguali Uguali Uguali Rho

 

Comprendere queste tre configurazioni è fondamentale per scegliere l’indice di affidabilità appropriato e per valutare la validità delle assunzioni nei modelli di misura psicometrica.

24.6 Metodo dei minimi quadrati non pesati

Nel contesto del modello unifattoriale, la varianza osservata di ciascun indicatore può essere scomposta in due componenti principali:

  • la varianza spiegata dal fattore latente comune, denotata con \(\sigma^2_T\);
  • la varianza residua o specifica, indicata con \(\psi\).

Come illustrato da McDonald (2013), è possibile stimare queste due componenti direttamente a partire dalla matrice di covarianza empirica degli item. Tali stime sono poi impiegate per calcolare indici di affidabilità interna come \(\alpha\) di Cronbach e \(\omega\) di McDonald.

In precedenza, abbiamo visto che la varianza del punteggio vero può essere interpretata come la covarianza tra due forme parallele dello stesso test:

\[ \sigma_T^2 = \sigma_{XX'}. \]

Nel caso specifico del modello \(\tau\)-equivalente, la matrice teorica delle varianze e covarianze degli item assume la forma:

\[ \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_T^2 + \psi_{11} & \sigma_T^2 & \dots & \sigma_T^2 \\ \sigma_T^2 & \sigma_T^2 + \psi_{22} & \dots & \sigma_T^2 \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_T^2 & \sigma_T^2 & \dots & \sigma_T^2 + \psi_{pp} \end{bmatrix}, \]

dove tutte le covarianze fuori diagonale sono uguali a \(\sigma_T^2\), mentre le varianze diagonali variano in funzione delle specificità degli item.

24.6.1 Stima della varianza del punteggio vero

Nel modello \(\tau\)-equivalente, una stima della varianza del fattore comune, \(\hat{\sigma}_T^2\), può essere ottenuta calcolando la media delle covarianze osservate tra gli item, ovvero i valori fuori diagonale della matrice empirica \(\mathbf{S}\):

\[ \hat{\sigma}_T^2 = \frac{1}{p(p-1)} \sum_{i \neq k} s_{ik}. \tag{24.1}\]

Questa stima è nota come metodo dei minimi quadrati non pesati (unweighted least squares), in quanto si basa su una media semplice delle covarianze, senza introdurre pesi differenziati tra item.

24.6.2 Stima delle varianze specifiche

Una volta stimata la varianza comune \(\hat{\sigma}_T^2\), è possibile ottenere la stima della varianza residua specifica per ciascun item sottraendo la parte comune dalla varianza totale osservata:

\[ \hat{\psi}_{ii} = s_{ii} - \hat{\sigma}_T^2. \]

Questa operazione va effettuata per ciascun item \(i = 1, \dots, p\).

24.6.3 Caso del modello parallelo

Nel modello parallelo, si assume che anche le varianze degli errori siano uguali tra tutti gli item. In tal caso, la stima della varianza comune \(\hat{\sigma}_T^2\) rimane invariata (è ancora la media delle covarianze osservate), ma la stima della varianza specifica \(\psi\), essendo costante per tutti gli item, si ottiene come media delle differenze tra le varianze osservate e la varianza comune:

\[ \hat{\psi} = \frac{1}{p} \sum_{i=1}^{p} (s_{ii} - \hat{\sigma}_T^2). \tag{24.2}\]

24.7 Varianza del punteggio totale di un test

Consideriamo ora un test composto da \(p\) item, e definiamo il punteggio totale come:

\[ Y = \sum_{i=1}^{p} X_i. \]

Nel contesto di un modello monofattoriale congenerico, ogni item è modellato come:

\[ X_i = \lambda_i \xi + \delta_i, \]

dove:

  • \(\lambda_i\) è il carico fattoriale dell’item \(i\) sul fattore comune \(\xi\);
  • \(\delta_i\) è il residuo specifico, ossia la parte del punteggio non spiegata dal fattore.

Questa formulazione è coerente con la teoria classica dei test (\(X_i = T_i + E_i\)), dove il punteggio vero corrisponde alla componente \(\lambda_i \xi\) e l’errore di misura alla componente \(\delta_i\).

24.7.1 Decomposizione della varianza del punteggio totale

Poiché il punteggio totale \(Y\) è la somma di tutti gli item, possiamo scriverlo come:

\[ Y = \sum_{i=1}^{p} X_i = \sum_{i=1}^{p} (\lambda_i \xi + \delta_i). \]

La varianza del punteggio totale, assumendo che \(\xi\) abbia varianza unitaria e che sia incorrelato con i residui \(\delta_i\), si calcola nel seguente modo:

\[ \begin{aligned} \mathbb{V}(Y) &= \mathbb{V} \left[ \sum_i (\lambda_i \xi + \delta_i) \right] \\ &= \mathbb{V} \left[ \left( \sum_i \lambda_i \right) \xi + \sum_i \delta_i \right] \\ &= \left( \sum_i \lambda_i \right)^2 \mathbb{V}(\xi) + \sum_i \mathbb{V}(\delta_i) \\ &= \left( \sum_i \lambda_i \right)^2 + \sum_i \psi_{ii}. \end{aligned} \tag{24.3}\]

Questa equazione mostra chiaramente che la varianza del punteggio totale si scompone in:

  • una componente sistematica legata al fattore comune: \((\sum_i \lambda_i)^2\);
  • una componente casuale dovuta agli errori specifici: \(\sum_i \psi_{ii}\).

La proporzione della varianza totale attribuibile al fattore comune rappresenta, in ultima analisi, ciò che intendiamo per affidabilità del test, ed è su questa base che vengono costruiti gli indici \(\alpha\), \(\omega\) e \(\rho\).

24.8 Stima dell’attendibilità

24.8.1 Coefficiente \(\omega\)

Come visto in precedenza, la varianza del punteggio totale \(Y\) di un test costituito da \(p\) item, nel contesto di un modello monofattoriale congenerico, può essere scomposta in due componenti:

\[ \mathbb{V}(Y) = \left( \sum_{i=1}^{p} \lambda_i \right)^2 + \sum_{i=1}^{p} \psi_{ii}. \]

Sulla base di questa decomposizione, McDonald (2013) propone il coefficiente \(\omega\) come misura dell’affidabilità del test, intesa come proporzione della varianza totale spiegata dal fattore comune:

\[ \omega = \frac{\left( \sum_{i=1}^{p} \lambda_i \right)^2}{\left( \sum_{i=1}^{p} \lambda_i \right)^2 + \sum_{i=1}^{p} \psi_{ii}}. \tag{24.4}\]

Questo coefficiente è coerente con il modello congenerico e consente di stimare l’affidabilità di un test a partire da una singola somministrazione, utilizzando i parametri dell’analisi fattoriale.

In termini interpretativi, \(\omega\) indica quanto della varianza osservata nel punteggio totale è realmente riconducibile al costrutto latente che il test intende misurare.

24.8.1.1 Esempio pratico: sottoscala Openness del dataset bfi

Utilizziamo il pacchetto psych per caricare il dataset e ricodificare gli item invertiti.

data(bfi, package = "psych")
bfi$O2r <- 7 - bfi$O2
bfi$O5r <- 7 - bfi$O5

Esaminiamo la matrice di correlazione tra gli item della scala Openness.

cor(bfi[c("O1", "O2r", "O3", "O4", "O5r")], use = "pairwise.complete.obs") |>
  round(2)
#>       O1  O2r   O3   O4  O5r
#> O1  1.00 0.21 0.40 0.18 0.24
#> O2r 0.21 1.00 0.26 0.07 0.32
#> O3  0.40 0.26 1.00 0.19 0.31
#> O4  0.18 0.07 0.19 1.00 0.18
#> O5r 0.24 0.32 0.31 0.18 1.00

Eseguiamo quindi l’analisi fattoriale confermativa con il pacchetto lavaan, specificando una soluzione monofattoriale standardizzata:

mod <- "
  f =~ NA*O1 + O2r + O3 + O4 + O5r
  f ~~ 1*f
"
fit <- cfa(mod, data = bfi, std.ov = TRUE, std.lv = TRUE)

Estraiamo le saturazioni fattoriali (\(\lambda_i\)) e le varianze specifiche (\(\psi_{ii}\)):

lambda <- inspect(fit, "std")$lambda
psy <- diag(inspect(fit, "est")$theta)

Applichiamo ora la formula per calcolare \(\omega\):

sum(lambda)^2 / (sum(lambda)^2 + sum(psy))
#> [1] 0.6181

Possiamo confrontare il risultato con quello ottenuto tramite la funzione compRelSEM() del pacchetto semTools, che calcola \(\omega\) direttamente dal modello lavaan:

semTools::compRelSEM(fit, tau.eq = FALSE)
#>     f 
#> 0.618

Nel nostro esempio, otteniamo \(\omega \approx 0.62\), il che implica che circa il 62% della varianza del punteggio totale nella scala Openness è spiegato dal fattore latente comune.

24.8.2 Ipotesi del modello e possibili violazioni

La formula classica di \(\omega\) si basa su una ipotesi fondamentale della teoria classica dei test: l’assenza di covarianza tra gli errori specifici degli item, ovvero:

\[ \psi_{ik} = 0 \quad \text{per ogni } i \neq k. \]

Tuttavia, nei dati reali questa assunzione può essere violata. Se esistono covarianze significative tra gli errori specifici, la stima classica di \(\omega\) risulta sovrastimata. In questi casi, come sottolineato da Bollen (1980), è necessario utilizzare una formula corretta che tenga conto anche delle covarianze tra errori:

\[ \omega = \frac{\left( \sum_{i=1}^{p} \lambda_i \right)^2}{\left( \sum_{i=1}^{p} \lambda_i \right)^2 + \sum_{i=1}^{p} \psi_{ii} + \sum_{i \neq k} \psi_{ik}}. \]

Per valutare la presenza di covarianze spurie tra gli errori, è possibile consultare gli indici di modifica (modification indices) forniti dall’analisi fattoriale confermativa. Se le correlazioni residue tra item sono elevate, ciò può indicare la presenza di dimensioni latenti aggiuntive, suggerendo che il test non è unidimensionale.

24.8.3 Interpretazioni del coefficiente \(\omega\)

Il coefficiente \(\omega\) può essere interpretato da diversi punti di vista, tutti coerenti con la teoria classica dei test:

  • Correlazione quadrata tra punteggio totale e fattore comune:
    \(\omega\) rappresenta il quadrato della correlazione tra il punteggio totale \(Y\) e il fattore latente \(\xi\), cioè \(\rho_{Y\xi}^2\).

  • Correlazione tra forme parallele del test:
    In un contesto ipotetico in cui si somministrano due versioni equivalenti del test, \(\omega\) rappresenta la correlazione attesa tra i due punteggi totali.

  • Affidabilità nel dominio:
    \(\omega\) può essere visto come la correlazione tra il punteggio ottenuto su \(p\) item e quello che si otterrebbe da una somministrazione con un numero infinito di item tratti dallo stesso dominio latente (i.e., stesso costrutto).

In conclusione, il coefficiente \(\omega\) rappresenta oggi una alternativa più robusta e teoricamente fondata rispetto al tradizionale \(\alpha\) di Cronbach. A differenza di \(\alpha\), \(\omega\) non richiede l’assunzione di \(\tau\)-equivalenza tra gli item ed è pertanto utilizzabile in un modello congenerico, più realistico nella maggior parte delle applicazioni empiriche.

In sintesi:

  • \(\omega\) misura la quota di varianza del punteggio totale attribuibile al costrutto latente;
  • è più flessibile e accurato rispetto ad altri indici;
  • può essere stimato direttamente da un modello fattoriale confermativo, anche su una singola somministrazione del test.

24.8.4 Coefficienti \(\omega\) e \(\alpha\) nel modello \(\tau\)-equivalente

Nel contesto dei modelli monofattoriali, i coefficienti \(\omega\) e \(\alpha\) offrono due approcci distinti alla stima dell’affidabilità, differenziandosi in funzione delle assunzioni strutturali sugli item:

  • \(\omega\) è coerente con il modello congenerico, in cui i carichi fattoriali e le varianze residue possono variare tra item;
  • \(\alpha\) si basa sul modello \(\tau\)-equivalente, che assume carichi fattoriali uguali ma consente varianze residue differenti.

Nel modello \(\tau\)-equivalente, ciascun item ha la stessa carica fattoriale \(\lambda\), e la varianza totale dell’item può essere scritta come:

\[ \sigma_{ii} = \lambda^2 + \psi_{ii} = \sigma_T^2 + \sigma^2_i. \]

La varianza del punteggio totale \(Y\) (somma dei \(p\) item) sarà:

\[ \sigma_Y^2 = p^2 \lambda^2 + \sum_{i=1}^p \psi_{ii}. \]

In questo contesto, il coefficiente \(\omega\) assume la forma semplificata:

\[ \omega = \frac{p^2 \lambda^2}{\sigma_Y^2} = \frac{p^2 \sigma_T^2}{\sigma_Y^2}. \]

Applicando il metodo dei minimi quadrati non pesati, possiamo stimare \(\omega\) nel modo seguente:

\[ \hat{\omega} = \frac{p^2 \hat{\sigma}_T^2}{s_Y^2}, \]

dove \(\hat{\sigma}_T^2\) è la media delle covarianze osservate tra item:

\[ \hat{\sigma}_T^2 = \frac{1}{p(p-1)} \sum_{i \neq k} s_{ik}. \]

Sostituendo questa espressione, otteniamo:

\[ \hat{\omega} = \frac{p}{p-1} \cdot \frac{\sum_{i \neq k} s_{ik}}{s_Y^2}. \]

Oppure, espressa in funzione delle varianze:

\[ \hat{\omega} = \frac{p}{p-1} \left( 1 - \frac{\sum_{i=1}^p s_{ii}}{s_Y^2} \right). \tag{24.5}\]

Questa formula coincide con quella classica per il coefficiente \(\alpha\), che nei valori di popolazione si scrive:

\[ \alpha = \frac{p}{p - 1} \left( 1 - \frac{\sum_{i=1}^p \sigma_{ii}}{\sigma_Y^2} \right) = \frac{p}{p - 1} \cdot \frac{\sum_{i \neq k} \text{Cov}(X_i, X_k)}{\mathbb{V}(Y)}. \tag{24.6}\]

Sotto le assunzioni del modello \(\tau\)-equivalente, \(\alpha\) e \(\omega\) coincidono. Tuttavia, in presenza di carichi fattoriali disuguali (modello congenerico), \(\alpha\) tende a sottostimare \(\omega\), rendendolo un limite inferiore dell’affidabilità. Questa proprietà conservativa di \(\alpha\) è stata spesso invocata come argomento a favore del suo utilizzo, ma essa non è garantita al di fuori del modello \(\tau\)-equivalente.

24.8.4.1 Esempio pratico: \(\alpha\) per la sottoscala Openness

Calcoliamo ora il coefficiente \(\alpha\) a partire dalla matrice di covarianze empirica:

C <- cov(bfi[c("O1", "O2r", "O3", "O4", "O5r")], use = "pairwise.complete.obs")
round(C, 2)
#>       O1  O2r   O3   O4  O5r
#> O1  1.28 0.38 0.54 0.25 0.36
#> O2r 0.38 2.45 0.50 0.13 0.67
#> O3  0.54 0.50 1.49 0.29 0.50
#> O4  0.25 0.13 0.29 1.49 0.29
#> O5r 0.36 0.67 0.50 0.29 1.76

Applichiamo la formula dell’\(\alpha\) campionaria:

p <- 5
alpha <- (p / (p - 1)) * (1 - tr(C) / sum(C))
alpha
#> [1] 0.6002

24.8.5 La formula “profetica” di Spearman-Brown

La formula profetica di Spearman-Brown è utilizzata per prevedere l’affidabilità di un test costruito da item paralleli, cioè:

  • tutti gli item hanno lo stesso carico fattoriale \(\lambda\);
  • tutte le varianze residue sono uguali: \(\psi_{ii} = \psi\).

In questo caso, la varianza del punteggio totale è:

\[ \sigma_Y^2 = p^2 \lambda^2 + p \psi. \]

L’affidabilità del test è allora:

\[ \rho_p = \frac{p^2 \lambda^2}{p^2 \lambda^2 + p \psi} = \frac{p \lambda^2}{p \lambda^2 + \psi}. \]

Se definiamo l’affidabilità di un singolo item come:

\[ \rho_1 = \frac{\lambda^2}{\lambda^2 + \psi}, \]

la formula di Spearman-Brown esprime l’affidabilità del test come:

\[ \rho_p = \frac{p \rho_1}{(p - 1) \rho_1 + 1}. \tag{24.7}\]

Questa formula è particolarmente utile quando si vuole prevedere l’effetto dell’aggiunta di nuovi item su un test esistente, ed è stata storicamente uno strumento fondamentale nello sviluppo dei test psicometrici.

Nel modello parallelo, i coefficienti \(\alpha\), \(\omega\) e \(\rho_p\) coincidono, poiché tutte le assunzioni richieste per ciascuno sono soddisfatte simultaneamente.

24.8.5.1 Esempio pratico: Spearman-Brown per la sottoscala Openness

Ipotizziamo che gli item della scala Openness siano paralleli. In questo caso, possiamo calcolare l’affidabilità del test a partire dalla correlazione media tra item:

R <- cor(bfi[c("O1", "O2r", "O3", "O4", "O5r")], use = "pairwise.complete.obs")
round(R, 3)
#>        O1   O2r    O3    O4   O5r
#> O1  1.000 0.214 0.395 0.178 0.239
#> O2r 0.214 1.000 0.262 0.068 0.325
#> O3  0.395 0.262 1.000 0.195 0.311
#> O4  0.178 0.068 0.195 1.000 0.179
#> O5r 0.239 0.325 0.311 0.179 1.000

Calcoliamo la media delle correlazioni inter-item:

p <- 5
rr <- NULL
k <- 1
for (i in 1:p) {
  for (j in 1:p) {
    if (j != i) rr[k] <- R[i, j]
    k <- k + 1
  }
}
ro_1 <- mean(rr, na.rm = TRUE)
print(ro_1)
#> [1] 0.2365

Applichiamo la formula di Spearman-Brown:

(p * ro_1) / ((p - 1) * ro_1 + 1) |>
  round(3)
#> [1] 0.6078

Il risultato fornisce una stima dell’affidabilità complessiva del test sotto l’ipotesi di parallelismo degli item. Confrontare questo valore con quelli ottenuti tramite \(\omega\) e \(\alpha\) può essere utile per riflettere sulla validità delle assunzioni sottostanti al modello utilizzato.

24.8.6 Conclusioni

Modello Assunzioni principali Coefficiente coerente Formula
Congenerico \(\lambda_i\) e \(\psi_{ii}\) liberi \(\omega\) Varianza spiegata / totale
\(\tau\)-equivalente \(\lambda_i = \lambda\); \(\psi_{ii}\) liberi \(\alpha\), \(\omega\) \(\alpha\) = \(\omega\)
Parallelo \(\lambda_i = \lambda\); \(\psi_{ii} = \psi\) \(\rho\), \(\omega\), \(\alpha\) \(\omega = \alpha = \rho\)


La scelta dell’indice di affidabilità più appropriato dipende sempre dalle ipotesi del modello di misura. È quindi fondamentale:

  • comprendere la struttura del proprio strumento;
  • valutare empiricamente la bontà del modello (con CFA o EFA);
  • interpretare ciascun coefficiente alla luce delle assunzioni teoriche sottostanti.

24.9 Riflessioni Conclusive

Nel corso di questo capitolo abbiamo analizzato tre principali coefficienti di affidabilità interna – \(\alpha\), \(\omega\), e \(\rho\) – ciascuno associato a un diverso modello di misura monofattoriale:

Coefficiente Modello sottostante Ipotesi sui carichi \(\lambda\) Ipotesi sugli errori \(\psi_{ii}\) Correlazioni residue tra errori Interpretabile come…
\(\omega\) Congenerico Liberi Liberi Nessuna (idealmente zero) Varianza spiegata / totale
\(\alpha\) \(\tau\)-equivalente Uguali Liberi Nessuna Limite inferiore di \(\omega\)
\(\rho\) Parallelo Uguali Uguali Nessuna Predizione su test allungato

24.9.1 Scelte operative

  • Il coefficiente \(\alpha\) di Cronbach è il più diffuso in ambito psicometrico per la sua semplicità computazionale. Tuttavia, è valido solo quando gli item sono \(\tau\)-equivalenti, ovvero misurano lo stesso costrutto con intensità uguale ma con varianze d’errore potenzialmente differenti.

    Nella pratica, tale ipotesi è raramente soddisfatta: spesso gli item mostrano carichi diversi, oppure strutture multidimensionali latenti. In questi casi, \(\alpha\) può sottostimare l’affidabilità se gli errori sono incorrelati, oppure sovrastimarla se gli errori sono correlati.

  • Il coefficiente \(\omega\) di McDonald costituisce un’alternativa più generale e robusta, poiché richiede ipotesi meno restrittive. È compatibile con il modello congenerico, che riflette con maggiore realismo la struttura empirica di molti test. In questo senso, \(\omega\) rappresenta la scelta raccomandata per stimare l’affidabilità interna in presenza di carichi fattoriali disuguali.

  • La formula di Spearman-Brown (\(\rho\)) trova il suo uso ideale quando si assume il modello più restrittivo con item paralleli. Sebbene meno flessibile, essa è utile per stimare l’impatto della lunghezza del test sull’affidabilità, rispondendo alla domanda: “Cosa succederebbe se raddoppiassi il numero di item?”

24.9.2 Indici alternativi

Oltre a \(\alpha\) e \(\omega\), la letteratura psicometrica propone altri indici più sofisticati:

  • Il GLB (Greatest Lower Bound) di Ten Berge e Sočan (2004), che fornisce il limite inferiore teoricamente più alto dell’affidabilità. Tuttavia, è computazionalmente più complesso e sensibile alla struttura dei dati.

  • L’indice \(\beta\) di Revelle (1979), che misura la coerenza del sottoinsieme peggiore di item (worst split-half), ed è utile per rilevare problemi di dimensionalità.

Questi indici possono essere utili in situazioni in cui si sospetta che l’unidimensionalità sia violata o in cui si desidera esplorare diverse prospettive sulla coerenza interna di una scala.

24.9.3 Considerazioni finali

In sintesi:

  • Il coefficiente \(\alpha\) dovrebbe essere usato con cautela, solo quando le condizioni teoriche del modello \(\tau\)-equivalente sono empiricamente verificate.
  • Il coefficiente \(\omega\) è da preferire nella maggior parte delle applicazioni, in quanto fornisce una misura più realistica e flessibile dell’affidabilità.
  • Nessun coefficiente è “migliore” in senso assoluto: la scelta dipende sempre dalla struttura latente del test, dalla qualità dei dati e dallo scopo dell’analisi.

24.10 Session Info

sessionInfo()
#> R version 4.4.2 (2024-10-31)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Sequoia 15.3.2
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0
#> 
#> locale:
#> [1] C/UTF-8/C/C/C/C
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] modelsummary_2.3.0 ggokabeito_0.1.0   see_0.11.0        
#>  [4] MASS_7.3-65        viridis_0.6.5      viridisLite_0.4.2 
#>  [7] ggpubr_0.6.0       ggExtra_0.10.1     gridExtra_2.3     
#> [10] patchwork_1.3.0    bayesplot_1.11.1   semTools_0.5-6    
#> [13] semPlot_1.1.6      lavaan_0.6-19      psych_2.4.12      
#> [16] scales_1.3.0       markdown_1.13      knitr_1.50        
#> [19] lubridate_1.9.4    forcats_1.0.0      stringr_1.5.1     
#> [22] dplyr_1.1.4        purrr_1.0.4        readr_2.1.5       
#> [25] tidyr_1.3.1        tibble_3.2.1       ggplot2_3.5.1     
#> [28] tidyverse_2.0.0    here_1.0.1        
#> 
#> loaded via a namespace (and not attached):
#>   [1] rstudioapi_0.17.1   jsonlite_1.9.1      magrittr_2.0.3     
#>   [4] TH.data_1.1-3       estimability_1.5.1  farver_2.1.2       
#>   [7] nloptr_2.2.1        rmarkdown_2.29      vctrs_0.6.5        
#>  [10] minqa_1.2.8         base64enc_0.1-3     rstatix_0.7.2      
#>  [13] htmltools_0.5.8.1   broom_1.0.7         Formula_1.2-5      
#>  [16] htmlwidgets_1.6.4   plyr_1.8.9          sandwich_3.1-1     
#>  [19] emmeans_1.10.7      zoo_1.8-13          igraph_2.1.4       
#>  [22] mime_0.13           lifecycle_1.0.4     pkgconfig_2.0.3    
#>  [25] Matrix_1.7-3        R6_2.6.1            fastmap_1.2.0      
#>  [28] rbibutils_2.3       shiny_1.10.0        digest_0.6.37      
#>  [31] OpenMx_2.21.13      fdrtool_1.2.18      colorspace_2.1-1   
#>  [34] rprojroot_2.0.4     Hmisc_5.2-3         timechange_0.3.0   
#>  [37] abind_1.4-8         compiler_4.4.2      withr_3.0.2        
#>  [40] glasso_1.11         htmlTable_2.4.3     backports_1.5.0    
#>  [43] carData_3.0-5       ggsignif_0.6.4      corpcor_1.6.10     
#>  [46] gtools_3.9.5        tools_4.4.2         pbivnorm_0.6.0     
#>  [49] foreign_0.8-88      zip_2.3.2           httpuv_1.6.15      
#>  [52] nnet_7.3-20         glue_1.8.0          quadprog_1.5-8     
#>  [55] nlme_3.1-167        promises_1.3.2      lisrelToR_0.3      
#>  [58] grid_4.4.2          checkmate_2.3.2     cluster_2.1.8.1    
#>  [61] reshape2_1.4.4      generics_0.1.3      gtable_0.3.6       
#>  [64] tzdb_0.5.0          data.table_1.17.0   hms_1.1.3          
#>  [67] car_3.1-3           tables_0.9.31       sem_3.1-16         
#>  [70] pillar_1.10.1       rockchalk_1.8.157   later_1.4.1        
#>  [73] splines_4.4.2       lattice_0.22-6      survival_3.8-3     
#>  [76] kutils_1.73         tidyselect_1.2.1    miniUI_0.1.1.1     
#>  [79] pbapply_1.7-2       reformulas_0.4.0    stats4_4.4.2       
#>  [82] xfun_0.51           qgraph_1.9.8        arm_1.14-4         
#>  [85] stringi_1.8.4       yaml_2.3.10         pacman_0.5.1       
#>  [88] boot_1.3-31         evaluate_1.0.3      codetools_0.2-20   
#>  [91] mi_1.1              cli_3.6.4           RcppParallel_5.1.10
#>  [94] rpart_4.1.24        xtable_1.8-4        Rdpack_2.6.3       
#>  [97] munsell_0.5.1       Rcpp_1.0.14         coda_0.19-4.1      
#> [100] png_0.1-8           XML_3.99-0.18       parallel_4.4.2     
#> [103] jpeg_0.1-10         lme4_1.1-36         mvtnorm_1.3-3      
#> [106] openxlsx_4.2.8      rlang_1.1.5         multcomp_1.4-28    
#> [109] mnormt_2.1.1