27.1 Regressione bivariata

La regressione è una classe di tecniche statistiche che si pongono il problema di comprendere la relazione che intercorre tra una variabile di esito (chiamata anche criterio / risposta / variabile dipendente) e una o più predittori (chiamate anche variabili esplicative / indipendenti). Considereremo inizialmente il caso di una sola variabile esplicativa.

In maniera più specifica, possiamo dire che la regressione bivariata si pone il problema di descrivere la relazione statistica lineare che intercorre tra due variabili, \(x\) e \(y\). Per relazione “statistica” intendo dire che, in un campione di dati \(\{x, y\}\), non c’è mai una “perfetta” relazione lineare. Consideriamo le le coppie \(\{x_i, y_i\}\), con i = 1, …, N, dove N è l’ampiezza campionaria. Se rappresentiamo queste coppie di numeri un un diagramma cartesiano, otteniamo quello che si chiama un diagramma a dispersione. Nel caso di dati reali, i punti del diagramma a dispersione di \(\{x, y\}\) non si situeranno mai tutti su una retta ma, in alcuni casi, formeranno una nube di punti che può essere approssimata da una retta che passa attraverso la nube di punti. In una tale situazione, è ragionevole descrivere la relazione tra le variabili \(x\) e \(y\) mediante la retta che approssima al meglio la nube di punti nel diagramma a dispersione.

L’analisi di regressione si pone tre problemi. Il primo è quello di stabilire qual è l’inclinazione della retta che passa il più vicino possibile ai punti del diagramma a dispersione. Il secondo è quello di quantificare “la distanza media” tra i punti del diagramma a dispersione e la retta di regressione. Il terzo è quello di fare inferenza, ovvero di capire cosa ci dice la retta di regressione che abbiamo osservato nel campione a proposito della possibile relazione tra \(x\) e \(y\) nella popolazione da cui il campione è stato tratto.

27.1.1 Scioglimento del ghiaccio marino

Iniziamo con un esempio. Uno degli impatti più importanti dei cambiamenti climatici che stanno investendo il nostro Pianeta è la riduzione dell’estensione della calotta di ghiaccio marino artico. Poniamoci il problema di usare il modello di regressione per esplorare come l’estensione del ghiaccio marino artico sta cambiando nel tempo. I dati sono forniti da The National Snow and Ice Data Center e sono espressi in milioni di chilometri quadrati.

I dati sono i seguenti:

data.frame(seaice)
#>    year extent_north extent_south
#> 1  1979       12.328       11.700
#> 2  1980       12.337       11.230
#> 3  1981       12.127       11.435
#> 4  1982       12.447       11.640
#> 5  1983       12.332       11.389
#> 6  1984       11.910       11.454
#> 7  1985       11.995       11.618
#> 8  1986       12.203       11.088
#> 9  1987       12.135       11.554
#> 10 1988       11.923       12.131
#> 11 1989       11.967       11.426
#> 12 1990       11.694       11.410
#> 13 1991       11.749       11.545
#> 14 1992       12.110       11.399
#> 15 1993       11.923       11.420
#> 16 1994       12.011       11.774
#> 17 1995       11.415       11.795
#> 18 1996       11.841       11.769
#> 19 1997       11.668       11.390
#> 20 1998       11.757       11.738
#> 21 1999       11.691       11.761
#> 22 2000       11.508       11.747
#> 23 2001       11.600       11.673
#> 24 2002       11.363       11.222
#> 25 2003       11.397       11.969
#> 26 2004       11.240       11.961
#> 27 2005       10.907       11.695
#> 28 2006       10.773       11.461
#> 29 2007       10.474       11.687
#> 30 2008       10.978       12.239
#> 31 2009       10.932       12.049
#> 32 2010       10.711       12.107
#> 33 2011       10.483       11.501
#> 34 2012       10.406       12.004
#> 35 2013       10.897       12.524
#> 36 2014       10.790       12.776
#> 37 2015       10.566       12.414
#> 38 2016       10.151       11.156
#> 39 2017       10.373       10.693

Quale domanda di ricerca possiamo porci con questi dati? Propongo la seguente domanda.

Domanda di ricerca: l’estensione del ghiaccio marino artico sta diminuendo nel tempo?

Per esplorare la risposta a questa domanda, iniziamo a creare una rappresentazione grafica dei dati. Dato che abbiamo due variabi continue (il tempo, espresso in anni, e l’estensione del ghiaccio marino artico, in milioni di chilometri quadrati), questi dati possono essere rappresentati graficamente mediante un diagramma a dispersione.

Vogliamo sapere come varia l’estensione del ghiaccio marino artico in funzione del tempo e quindi rappresentiamo i dati ponendo la variabile tempo sull’asse delle ascisse e l’estensione del ghiaccio marino artico sull’asse delle ordinate.

seaice %>% 
  ggplot(aes(year, extent_north)) +
  geom_point()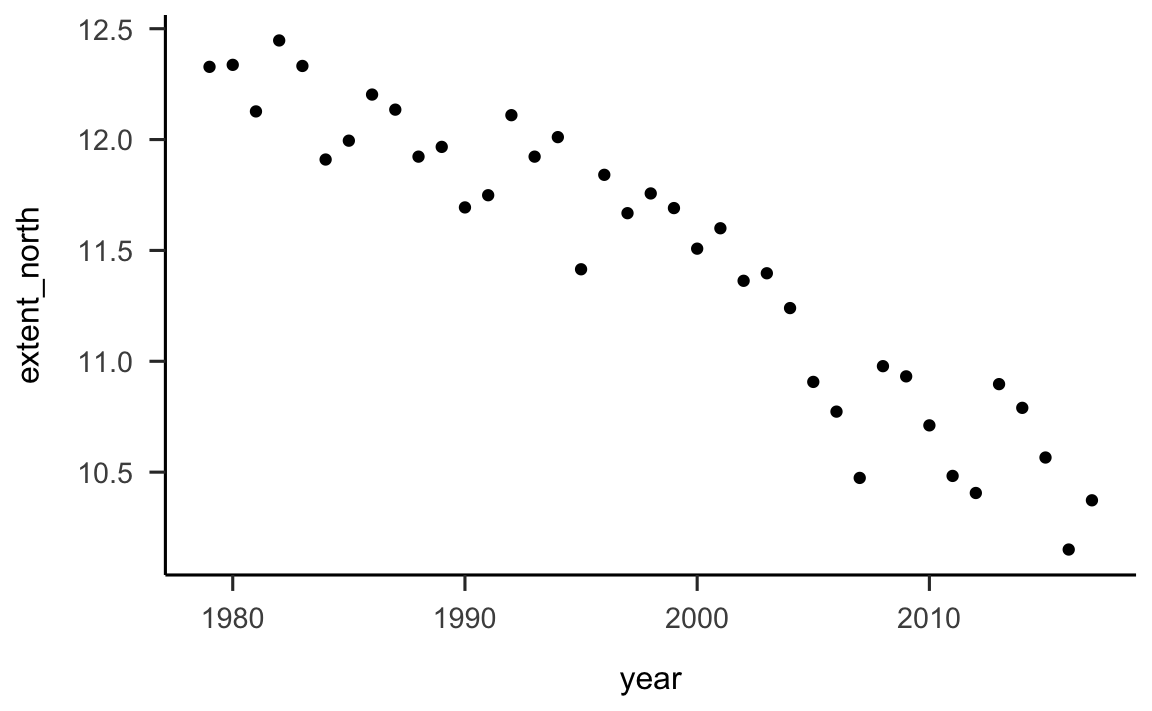

Guardando la figura vediamo che è ragionevole descrivere mediante una retta la relazione tra l’estensione del ghiaccio marino artico (chiamiamola y) e il tempo (chiamiamolo x). Aggiungiamo al diagramma di dispersione una retta, scegliendola in modo tale che si avvicini il più possibile alla nube di punti rappresentata nel grafico. Ovviamente, è possibile scegliere tra infinite rette diverse. La retta che è rappresentata qui è stata scelta in base ad un criterio particolare, detto “dei minimi quadrati.” Vedremo meglio in seguito cosa questo significa. Per ora ci accontentiamo di riconoscere che la nostra è una buona scelta, per gli scopi presenti.

seaice %>% 
  ggplot(aes(year, extent_north)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) 
#> `geom_smooth()` using formula 'y ~ x'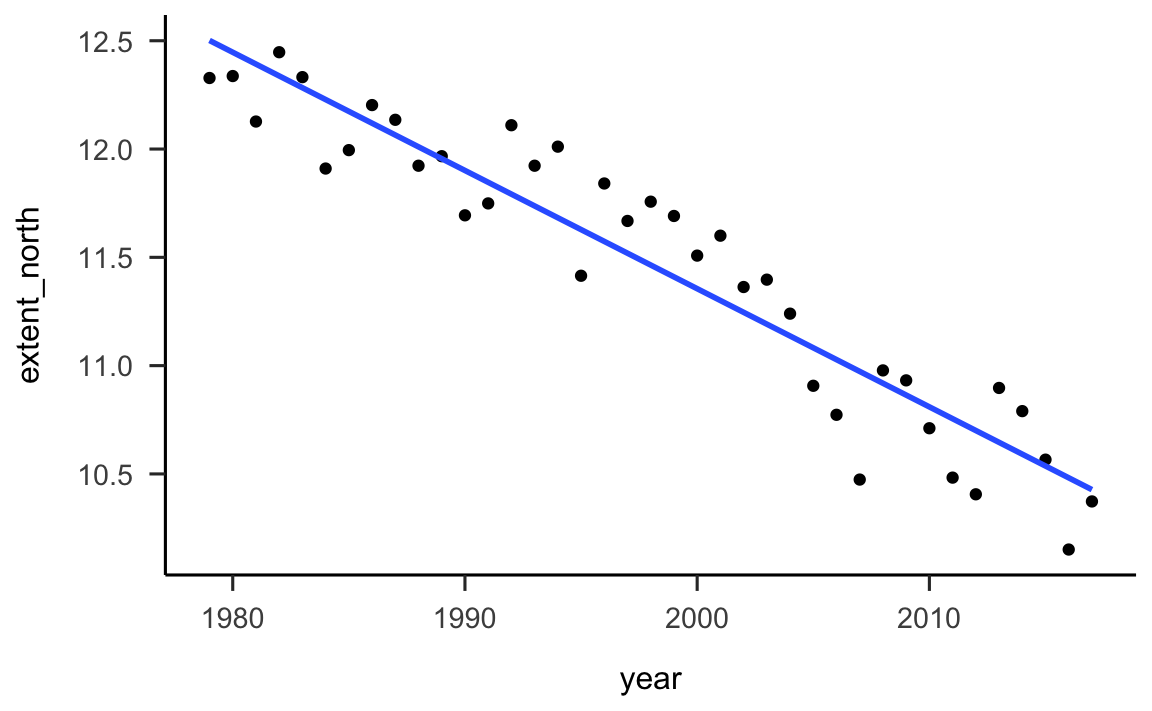

27.2 Interpretazione dei coefficienti \(a\) e \(b\)

La retta che abbiamo disegnato nella figura precedente rappresenta la risposta alla nostra domanda di ricerca: l’estensione del ghiaccio marino artico sta diminuendo nel tempo.

Anziché considerare questa risposta unicamente dal punto di vista grafico, proviamo a descrivere la retta disegnata nella figura in maniera quantitativa, con dei numeri. Per fare questo, dobbiamo innanzitutto ricordare qual è l’equazione di una retta:

\[\begin{equation} y = a + b \times x \end{equation}\]

Prima di calcolare i coefficienti \(a\) e \(b\) della retta di regressione, rimaneggiamo i nostri dati. In particolare, rinominiamo le variabili e indicizziamo gli anni da 1 a 39. Nel caso presente, vogliamo sapere se l’estensione del ghiaccio marino artico dall’inizio alla fine del periodo temporale considerato, indipendentemente dal fatto che l’anno iniziale sia il 1979 e l’anno finale il 2017. Quindi sottraiamo 1979 dalle modalità della variabile year in modo tale che il primo punto temporale corrisponda a zero.

seaice <- seaice %>% 
  mutate(
    x = year - 1979
  ) %>% 
  rename(
    y = extent_north
  )
glimpse(seaice)
#> Rows: 39
#> Columns: 4
#> $ year         <int> 1979, 1980, 1981, 1982, 1983, 1984, 1985, 1986, 1987, 1988, 1989, 1990, 1…
#> $ y            <dbl> 12.328, 12.337, 12.127, 12.447, 12.332, 11.910, 11.995, 12.203, 12.135, 1…
#> $ extent_south <dbl> 11.700, 11.230, 11.435, 11.640, 11.389, 11.454, 11.618, 11.088, 11.554, 1…
#> $ x            <dbl> 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,…

Il diagramma a dispersione avrà ora la forma seguente:

seaice %>% 
  ggplot(aes(x, y)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) 
#> `geom_smooth()` using formula 'y ~ x'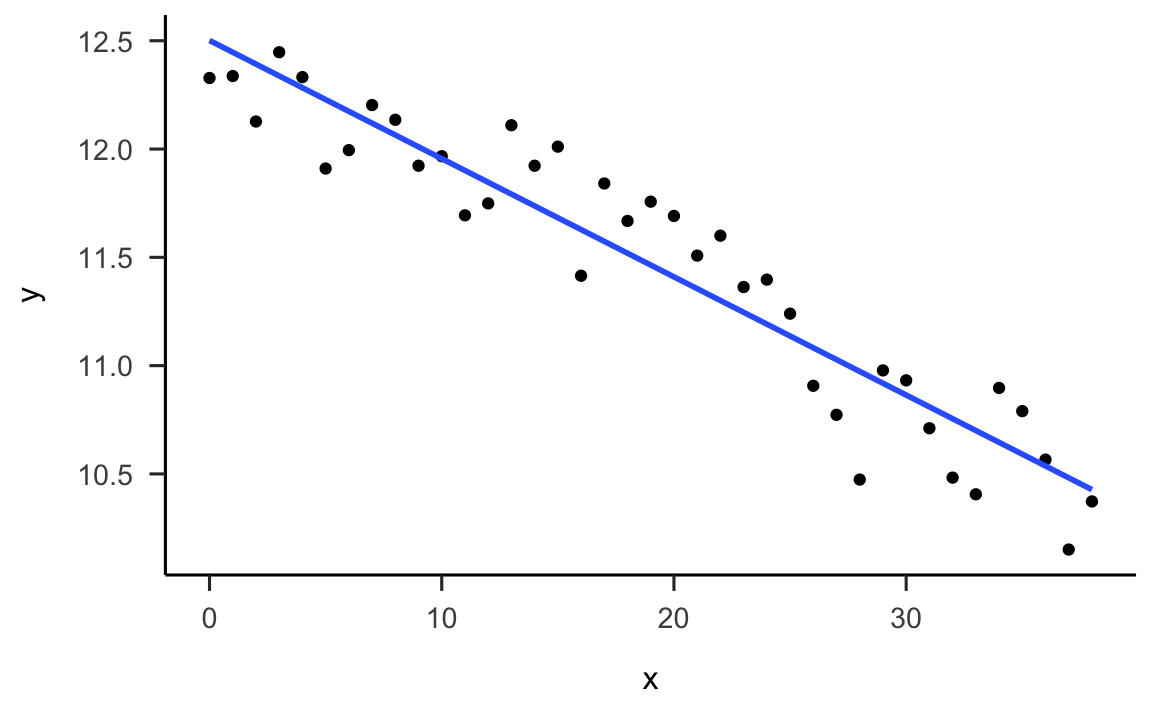

Per trovare i coefficienti \(a\) e \(b\) della retta di regressione possiamo usare, ad esempio, la funzione lm():

fm <- lm(y ~ x, data = seaice)
coef(fm)
#> (Intercept)           x 
#> 12.50131410 -0.05457389

L’output della funzione lm() ci dice che a è uguale a 12.501 e che b è uguale a -0.055. Ma che significato (geometrico) hanno questi valori?

Ai coefficienti \(a\) e \(b\) possiamo assegnare la seguente interpretazione:

• il coefficiente \(a\) rappresenta il valore della coordinata \(y\) (l’estensione del ghiaccio marino artico) della retta di regressione quando la coordinata \(x\) vale zero (nel nostro caso, l’anno 1979) – in altre parole, corrisponde al punto dove la retta di regressione interseca l’asse \(y\) del sistema di assi cartesiani;

• il coefficiente \(b\) ci dice di quanto aumenta la coordinata \(y\) della retta di regressione, quando \(x\) aumenta di un’unità.

Il valore \(a\) = 12.501 significa che, nel 1979, l’estensione del ghiaccio marino artico era pari a 12.501 milioni di chilometri quadrati, dato che la modalità x = 0 della variabile indipendente corrisponde all’anno 1979.

Il segno di \(b\) è negativo; questo significa che l’estensione del ghiaccio marino artico sta diminuendo nel corso del tempo. Il valore -0.055 ci dice che, per ogni anno che passa (nel periodo dal 1979 al 2017), l’estensione del ghiaccio marino artico diminuisce, in media, di -0.055 milioni di chilometri quadrati.

Se guardiamo la figura, infatti, vediamo che, se ci sposiamo da \(x = 10\) a \(x = 20\) (ovvero, di dieci anni), la coordinata \(y\) della retta diminuisce di 10 volte \(b\), ovvero di -0.55 milioni di chilometri quadrati. Questo è indicato nella figura qui sotto.

dplot <- data.frame(
  x1 = 10,
  x2 = 20,
  y1 = 12.50131410 + -0.05457389 * 10,
  y2 = 12.50131410 + -0.05457389 * 20
)

seaice %>%
  ggplot(aes(x, y)) +
  geom_point(color="gray") +
  geom_smooth(method = "lm", se = FALSE) +
  geom_segment(aes(x = x2, y = y1, xend = x2, yend = y2),
               arrow=arrow(), size=1.1, data = dplot) +
  geom_segment(aes(x = x1, y = y1, xend = x2, yend = y1),
               arrow=arrow(), size=1.1, data = dplot) +
  annotate("text", x = 24.0, y = 11.75, label = "10 b = -0.55") +
  annotate("text", x = 15, y = 12.15, label = "delta x = 10.0")
#> `geom_smooth()` using formula 'y ~ x'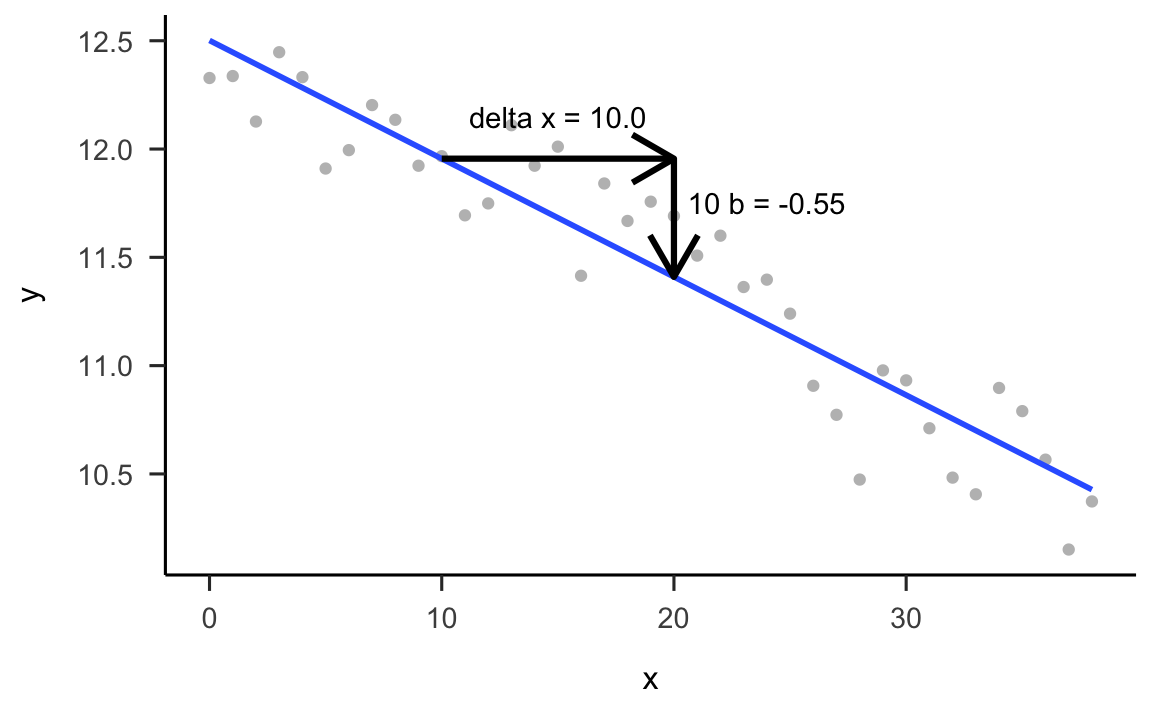

27.3 Scomposizione della \(y\)

Uno degli aspetti importanti della regressione lineare è che, in pratica, la retta di regressione scompone ciascun punteggio \(y\) in due componenti:

\[\begin{equation} y = (a + b \times x) + e \end{equation}\]

laddove \(\hat{y} = a + b \times x\) è la componente di \(y\) che è linearmente predicibile conoscendo \(x\), mentre la componente residua, \(e\), è la componente di \(y\) che non è linearmente predicibile conoscendo \(x\).

Nei nostri dati, questi significa quanto segue. Esaminiamo le prime 5 osservazioni del nostro campione:

seaice %>% 
  dplyr::select(x, y) %>% 
  top_n(5) 
#> Selecting by y
#>   x      y
#> 1 0 12.328
#> 2 1 12.337
#> 3 3 12.447
#> 4 4 12.332
#> 5 7 12.203

Aggiungo al data.frame una colonna che rappresenta i valori \(y\) predetti dal modello lineare (ovvero, \(\hat{y} = a + b \times x\): le coordinate \(y\) della retta di regressione per ciascuna delle osservazioni):

seaice$yhat <- coef(fm)[1] + coef(fm)[2] * seaice$x
seaice %>% 
  dplyr::select(x, y, yhat) %>% 
  top_n(5) 
#> Selecting by yhat
#>   x      y     yhat
#> 1 0 12.328 12.50131
#> 2 1 12.337 12.44674
#> 3 2 12.127 12.39217
#> 4 3 12.447 12.33759
#> 5 4 12.332 12.28302

Aggiungo ora al data.frame i residui del modello di regressione. I residui sono definiti come

\[\begin{equation} e = y - (a + b \times x) = y - \hat{y} \end{equation}\]

ovvero

seaice$e <- seaice$y - (coef(fm)[1] + coef(fm)[2] * seaice$x)
seaice %>% 
  dplyr::select(x, y, yhat, e) %>% 
  top_n(5) 
#> Selecting by e
#>    x      y     yhat         e
#> 1 13 12.110 11.79185 0.3181464
#> 2 15 12.011 11.68271 0.3282942
#> 3 19 11.757 11.46441 0.2925897
#> 4 20 11.691 11.40984 0.2811636
#> 5 22 11.600 11.30069 0.2993114

Ciò che volevamo dimostrare è che la somma di \(\hat{y}\) e dei residui è uguale alla \(y\). Infatti:

seaice$sum <- seaice$yhat + seaice$e
seaice %>% 
  dplyr::select(x, y, yhat, e, sum) %>% 
  top_n(5) 
#> Selecting by sum
#>   x      y     yhat           e    sum
#> 1 0 12.328 12.50131 -0.17331410 12.328
#> 2 1 12.337 12.44674 -0.10974022 12.337
#> 3 3 12.447 12.33759  0.10940756 12.447
#> 4 4 12.332 12.28302  0.04898144 12.332
#> 5 7 12.203 12.11930  0.08370310 12.203

In altre parole, il modello di regressone scompone la \(y\) in due componenti: la porzione della \(y\) che possiamo prevedere conoscendo \(x\) (ovvero, \(\hat{y} = a + b \times x\)) e la porzione della \(y\) che non possiamo prevedere sulla base di \(x\).

27.4 Inferenza sul modello di regressione

Finora siamo riusciti a descrivere la relazione statistica tra \(x\) e \(y\) in un campione di osservazioni. Siamo ben consapevoli che, in un altro campione di osservazioni, la relazione statistica tra \(x\) e \(y\) non sarà identica a quella osservata nel caso del primo campione – dato che i dati saranno diversi. La domanda cruciale dunque diventa la seguente: quanto sono simili i coefficienti dei minimi quadrati calcolati sui dati campionari ai coefficienti di un’ipotetica retta di regressione che, sempre mediante il metodo dei minimi quadrati, descriverebbe la relazione tra tutte le osservazioni \(\{x, y\}\) nella popolazione? Ciò che vogliamo è dunque una quantificazione della nostra incertezza: vogliamo sapere quanto dobbiamo fidarci delle stime campionarie come descrizioni dei valori (sconosciuti) della popolazione. Ci sono due possibilità.

• Se le stime di \(a\) e \(b\) fornite dal particolare campione che abbiamo osservato sono simili ai valori teorici della popolazione, allora i dati del campione ci forniscono informazioni utili per capire quali sono le proprietà della popolazione.

• Se invece le stime campionarie di \(a\) e \(b\) sono molto diverse dai valori teorici della popolazione, allora i dati del campione non ci aiutano a capire quali sono le proprietà della popolazione.

Il problema che abbiamo è quello di decidere in quale di queste due situazioni ci troviamo: la prima o la seconda. Questo è il problema dell’inferenza statistica sul modello di regressione.

Il problema dell’inferenza viene affrontato utilizzando gli strumenti della teoria della probabilità per costruire un intervallo di valori. Nell’approccio Bayesiano, tale intervallo di valori si chiama intervallo di credibilità. Se calcoliamo, ad esempio, l’intervallo di credibilità all’89% per il parametro \(\beta\) (inclinazione della retta di regressione nella popolazione), interpretiamo tale intervallo di valori nel modo seguente: possiamo dire che “siamo sicuri all’89% che il vero valore di \(\beta\) è contenuto nell’intervallo stimato” – laddove per “vero valore di \(\beta\)” intendiamo il valore del parametro sconosciuto della popolazione. Se calcoliamo l’intervallo di credibilità, ad un dato livello di certezza, possiamo giungere a una di tre possibili conclusioni.

• L’intervallo di credibilità non include lo 0 e il suo limite inferiore è positivo: possiamo concludere, con una certezza dell’89%, che c’è una relazione positiva tra \(x\) e \(y\) nella popolazione;
• l’intervallo di credibilità non include lo 0 e il suo limite superiore è negativo: possiamo concludere, con una certezza del’89%, che c’è una relazione negativa tra \(x\) e \(y\) nella popolazione;
• l’intervallo di credibilità include lo 0: con un un livello di certezza dell’89%, non possiamo negare la possibilità che nella popolazione la relazione tra \(x\) e \(y\) sia nulla – ovvero, non abbiamo sufficienti informazioni per sapere se è positiva o negativa.

Ritorniamo ora ai nostri dati e calcoliamo, con un metodo che discuteremo in seguito, l’intervallo di credibilità all’89%. Per ora non ci preoccupiamo della sintassi dei comandi R, né di cosa significano tali istruzioni. Ci preoccupiamo solo di ottenere le stime dei coefficienti della retta di regressione e gli intervalli di credibilità:

flist <- alist(
    y ~ dnorm(mu, sigma),
    mu <- a + b*x,
    c(a, b) ~ dnorm(0, 2), 
    sigma ~ dcauchy(0, 2)
)

fit <- quap(
  flist, 
  data = list(y=seaice$y, x=seaice$x), 
  start = list(a=0, b=0, sigma=0.1)
)

out <- round(precis(fit), 3)
out
#>         mean    sd   5.5%  94.5%
#> a     12.487 0.068 12.379 12.595
#> b     -0.054 0.003 -0.059 -0.049
#> sigma  0.215 0.024  0.176  0.254

L’intervallo di credibilità per \(b\) così ottenuto, ovvero [-0.059, -0.049], non include lo zero. Possiamo dunque concludere, con un livello di certezza dell’89%, che nella popolazione c’è una relazione negativa tra \(x\) e \(y\). In altre parole, siamo certi, con un livello di certezza dell’89%, che dal 1979 al 2017 l’estensione del ghiaccio marino artico è diminuita.

Se vogliamo, possiamo anche ottenere una stima di \(b\) che corrisponde ad un livello di certezza più alto, il che porterà ad un aumento dell’ampiezza dell’interallo di credibilità. Stimiamo dunque l’interallo di credibilità ad un livello di certezza del 99%:

out1 <- round(precis(fit, prob=0.99), 3)
out1
#>         mean    sd   0.5%  99.5%
#> a     12.487 0.068 12.313 12.661
#> b     -0.054 0.003 -0.062 -0.046
#> sigma  0.215 0.024  0.152  0.277

Anche in questo caso l’interallo di credibilità non include lo zero per cui, anche se pretendiamo un livello di certazza del 99%, confermiamo la conclusione secondo la quale dal 1979 al 2017 l’estensione del ghiaccio marino artico è diminuita.

Per quel che riguarda \(a\), con un livello di certezza dell’99% possiamo dire che il valore dell’intercetta della retta di regressione nella popolazione è incluso nell’intervallo [12.313, 12.661]. Nel caso presente, ciò ha una semplice interpretazione: significa che la nostra stima dell’esensione del ghiaccio marino artico nell’anno 1979 corrisponde a un valore compreso tra [12.313, 12.661], con un livello di certezza del 99%.

27.5 Una variabile indipendente qualitativa

Il modello statistico della regressione bivariato che abbiamo descritto sopra è molto limitato: può solo descrivere la relazione lineare tra due variabili continue. Estendiamolo ora al caso in cui, oltre ad includere un predittore continuo \(x\), il modello di regressione comprende anche una variabile che consente di suddividere le osservazioni del campione in due gruppi.

Per semplicità, simuliamo un insieme di dati che utilizzeremo nella seguente discussione.

set.seed(1234)
n <- 100
x1 <- rnorm(n, 4, 1)
y1 <- 5 + 5 * x1 + rnorm(n, 0, 2)

x2 <- rnorm(n, 4, 1)
y2 <- -3 + 2 * x2 + rnorm(n, 0, 2)

y <- c(y1, y2)
x <- c(x1, x2)
group <- rep(c("gr1", "gr2"), each = n)

d <- data.frame(x, y, group) 

d %>%
  group_by(group) %>% 
  do(head(., 5))
#> # A tibble: 10 x 3
#> # Groups:   group [2]
#>       x     y group
#>   <dbl> <dbl> <fct>
#> 1  2.79 19.8  gr1  
#> 2  4.28 25.4  gr1  
#> 3  5.08 30.6  gr1  
#> 4  1.65 12.3  gr1  
#> 5  4.43 25.5  gr1  
#> 6  4.49  4.81 gr2  
#> # … with 4 more rows

Esaminiamo il diagramma a dispersione che indica chiaramente che ci sono due gruppi distinti di osservazioni:

d %>%
  ggplot(aes(x, y)) +
  geom_point(aes(color = group))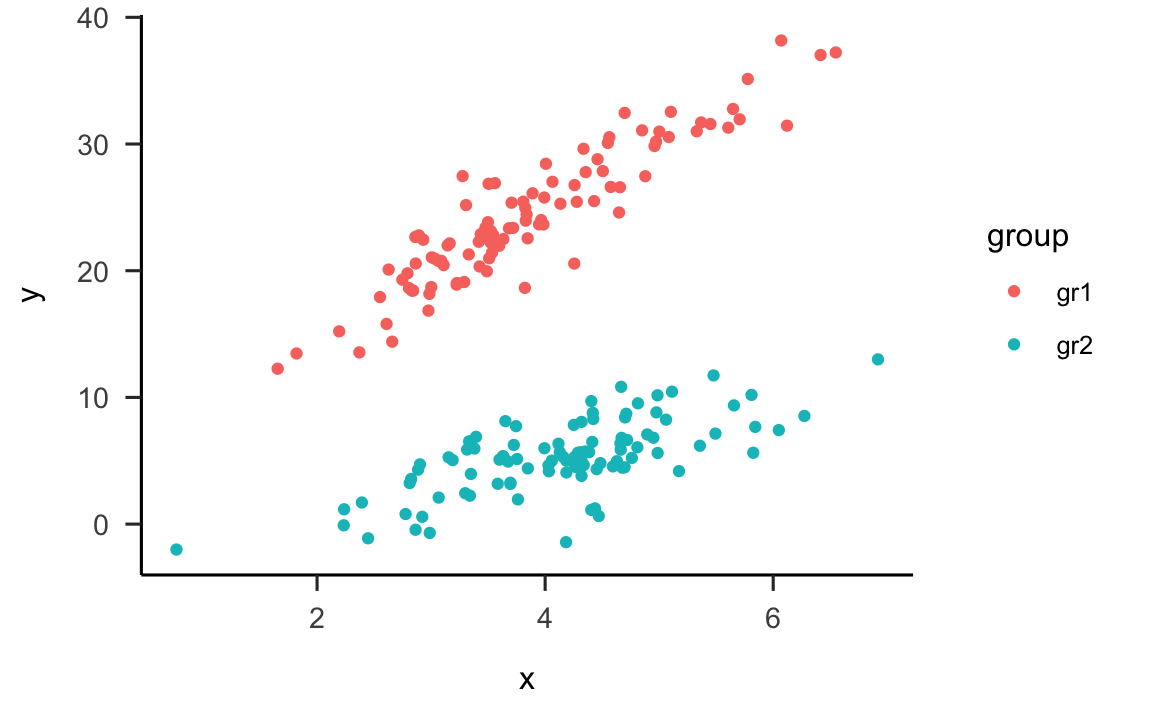

È ovvio, che nel caso presente, non è sufficiente un modello di regressione che ignora il fatto che i dati appartengono a due gruppi diversi. Infatti, se adattiamo ai dati un’unica retta di regressione, è facile rendersi conto che tale retta si situerà in una posizione molto distante dai dati.

d %>%
  ggplot(aes(x, y)) +
  geom_point(aes(color = group)) +
  geom_smooth(method = "lm", se = FALSE) 
#> `geom_smooth()` using formula 'y ~ x'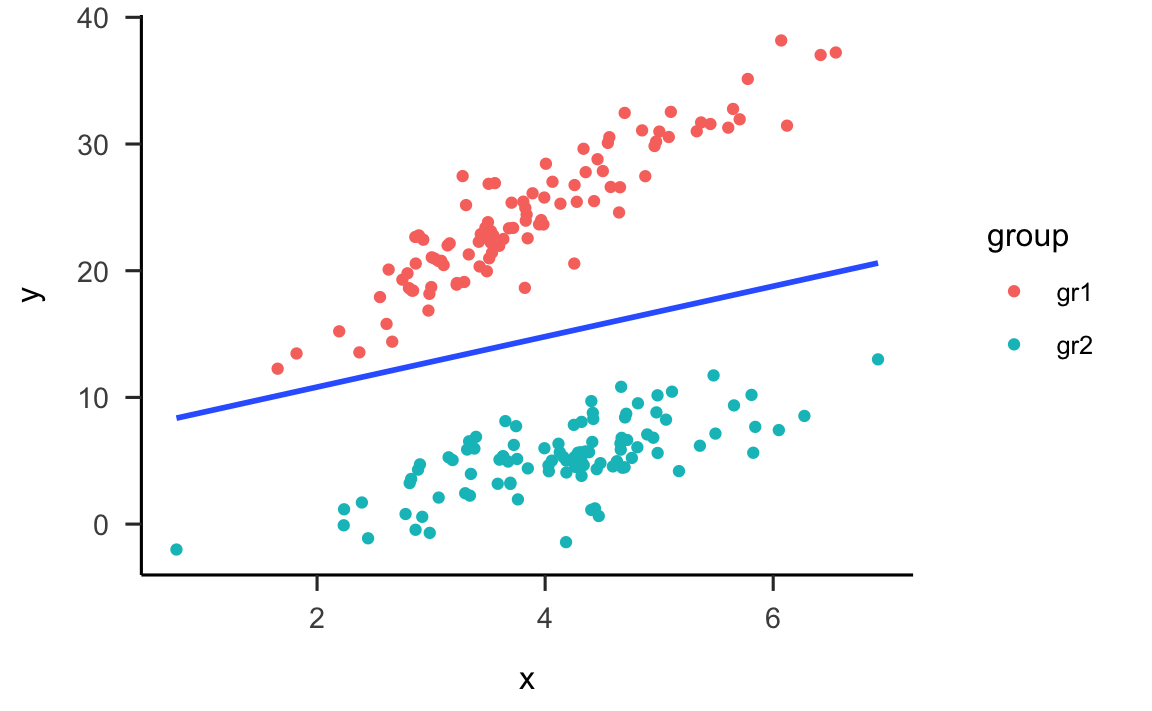

Per questi dati è ovviamente più sensato adattare una diversa retta di regressione a ciascun gruppo di osservazioni:

d %>%
  ggplot(aes(x, y, color = group)) +
  geom_point(aes(color = group)) +
  geom_smooth(method = "lm", se = FALSE)
#> `geom_smooth()` using formula 'y ~ x'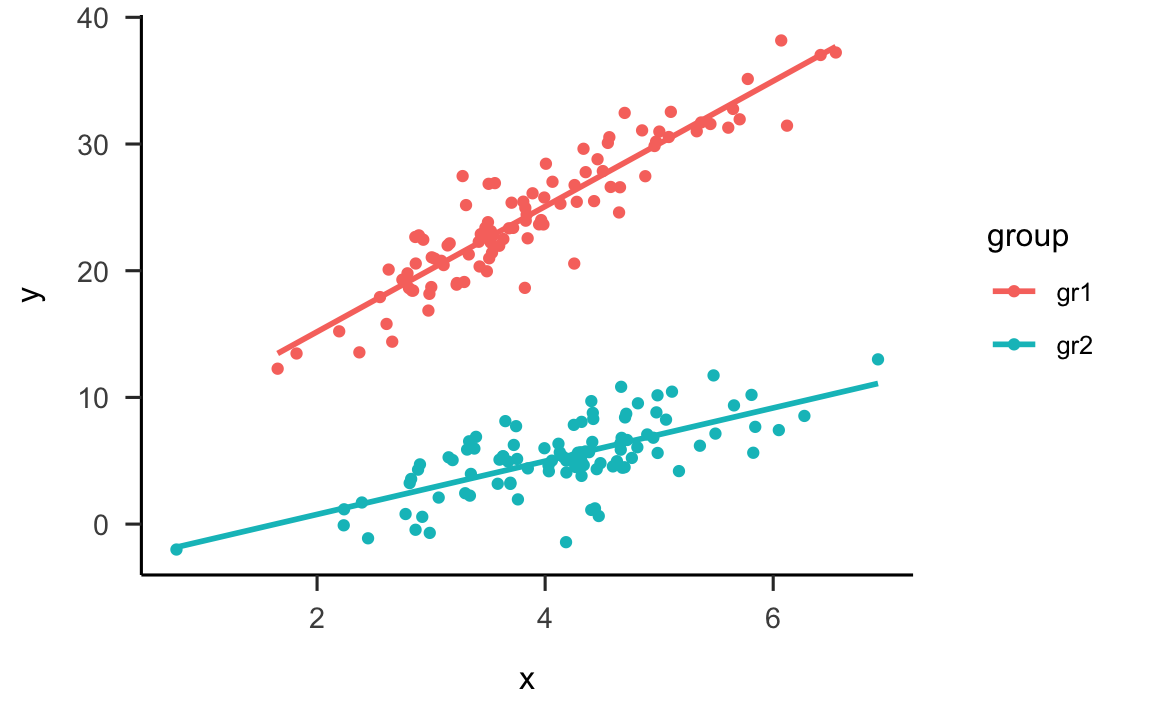

Come possiamo modificare il modello di regressione che abbiamo esaminato in precedenza in modo tale da essere in grado di stimare i coefficienti di regressione delle due rette rappresentate nella figura precedente? Questo problema si risolve nel modo seguente. Crediamo una variabile, chiamata dummy, che ha valore 0 per un gruppo, diciamo gr1, e valore 1 per l’altro gruppo:

d$gr <- ifelse(d$group == "gr1", 0, 1) 

d %>%
  group_by(gr) %>% 
  do(head(., 5)) %>% 
  as.data.frame()
#>           x         y group gr
#> 1  2.792934 19.793718   gr1  0
#> 2  4.277429 25.437709   gr1  0
#> 3  5.084441 30.554193   gr1  0
#> 4  1.654302 12.266556   gr1  0
#> 5  4.429125 25.493626   gr1  0
#> 6  4.485227  4.810540   gr2  1
#> 7  4.696769  4.486980   gr2  1
#> 8  4.185514  5.012171   gr2  1
#> 9  4.700734  8.421083   gr2  1
#> 10 4.311681  5.670615   gr2  1

Esaminiamo ora il modello di regressione che include tale variabile dummy, che chiameremo D:

\[\begin{equation} y = \alpha + \beta x + \gamma D + \varepsilon. \end{equation}\]

Quando \(D = 0\):

\[\begin{align} y &= \alpha + \beta x + \gamma D + \varepsilon,\notag\\ &= \alpha + \beta x + \gamma \times 0 + \varepsilon,\notag\\ &= \alpha + \beta x + \varepsilon.\notag \end{align}\]

Quando \(D = 1\):

\[\begin{align} y &= \alpha + \beta x + \gamma D + \varepsilon,\notag\\ &= \alpha + \beta x + \gamma \times 1 + \varepsilon,\notag\\ &= (\alpha + \gamma) + \beta x + \varepsilon.\notag \end{align}\]

Quindi, se assumiamo che le due rette di regressione siano parallele (nella discussione precedente abbiamo previsto un unico valore \(\beta\)), i coefficienti del modello avranno la seguente interpretazione:

• \(\alpha\) = intercetta della retta di regressione per il gruppo codificato con D = 0;
• \(\beta\) = pendenza della retta di regressione per il gruppo codificato con D = 0;
• \(\gamma\) = differenza tra l’intercetta della retta di regressione per il gruppo codificato con D = 1 e l’intercetta della retta di regressione per il gruppo codificato con D = 0.

d$DX <- d$gr * d$x

d %>%
  group_by(gr) %>% 
  do(head(., 5)) %>% 
  as.data.frame()
#>           x         y group gr       DX
#> 1  2.792934 19.793718   gr1  0 0.000000
#> 2  4.277429 25.437709   gr1  0 0.000000
#> 3  5.084441 30.554193   gr1  0 0.000000
#> 4  1.654302 12.266556   gr1  0 0.000000
#> 5  4.429125 25.493626   gr1  0 0.000000
#> 6  4.485227  4.810540   gr2  1 4.485227
#> 7  4.696769  4.486980   gr2  1 4.696769
#> 8  4.185514  5.012171   gr2  1 4.185514
#> 9  4.700734  8.421083   gr2  1 4.700734
#> 10 4.311681  5.670615   gr2  1 4.311681

flist1 <- alist(
    y ~ dnorm(mu, sigma),
    mu <- a + b*x + gamma*d + zeta*DX,
    c(a, b, gamma, zeta) ~ dnorm(0, 10), 
    sigma ~ dnorm(0, 5)
)

fit1 <- quap(
  flist1, 
  data = list(y=d$y, x=d$x, d=d$gr, DX=d$DX), 
  start = list(a=0, b=0, gamma=0, zeta=0, sigma=0.5)
  )

precis(fit1)
#>            mean        sd       5.5%     94.5%
#> a      5.202783 0.8167093   3.897524  6.508043
#> b      4.967164 0.2057473   4.638340  5.295988
#> gamma -8.569902 1.2250868 -10.527828 -6.611977
#> zeta  -2.881817 0.2970176  -3.356509 -2.407126
#> sigma  2.069882 0.1034130   1.904608  2.235155

27.6 Regressione multipla

suppressMessages(library("sjPlot"))
suppressMessages(library("sjmisc"))
library("psychTools")
data(epi.bfi)
glimpse(epi.bfi)
#> Rows: 231
#> Columns: 13
#> $ epiE     <int> 18, 16, 6, 12, 14, 6, 15, 18, 15, 8, 13, 14, 15, 19, 15, 11, 16, 17, 7, 13, 1…
#> $ epiS     <int> 10, 8, 1, 6, 6, 4, 9, 9, 11, 5, 9, 12, 10, 11, 10, 5, 10, 11, 4, 8, 7, 7, 10,…
#> $ epiImp   <int> 7, 5, 3, 4, 5, 2, 4, 7, 3, 2, 3, 3, 4, 7, 4, 6, 5, 6, 2, 4, 5, 3, 7, 1, 4, 3,…
#> $ epilie   <int> 3, 1, 2, 3, 3, 5, 3, 2, 3, 2, 3, 6, 5, 0, 2, 7, 0, 4, 1, 4, 3, 1, 2, 2, 1, 1,…
#> $ epiNeur  <int> 9, 12, 5, 15, 2, 15, 12, 10, 1, 10, 9, 1, 2, 3, 7, 13, 18, 11, 10, 12, 3, 10,…
#> $ bfagree  <int> 138, 101, 143, 104, 115, 110, 109, 92, 127, 74, 124, 131, 133, 117, 99, 126, …
#> $ bfcon    <int> 96, 99, 118, 106, 102, 113, 58, 57, 108, 100, 114, 107, 114, 126, 107, 78, 90…
#> $ bfext    <int> 141, 107, 38, 64, 103, 61, 99, 94, 108, 61, 100, 99, 114, 139, 124, 112, 102,…
#> $ bfneur   <int> 51, 116, 68, 114, 86, 54, 55, 72, 35, 87, 110, 92, 56, 47, 62, 83, 106, 72, 8…
#> $ bfopen   <int> 138, 132, 90, 101, 118, 149, 110, 114, 86, 89, 129, 121, 131, 128, 139, 132, …
#> $ bdi      <int> 1, 7, 4, 8, 8, 5, 7, 0, 0, 7, 8, 3, 0, 0, 1, 4, 14, 7, 9, 4, 1, 11, 1, 9, 6, …
#> $ traitanx <int> 24, 41, 37, 54, 39, 51, 40, 32, 22, 35, 43, 33, 23, 23, 27, 45, 58, 39, 43, 3…
#> $ stateanx <int> 22, 40, 44, 40, 67, 38, 32, 41, 26, 31, 39, 25, 32, 23, 28, 28, 56, 44, 56, 3…

m <- lm(bdi ~ bfneur + stateanx, data = epi.bfi)

out <- coef(m)
round(out, 3)
#> (Intercept)      bfneur    stateanx 
#>      -8.039       0.054       0.252

m1 <- lm(bdi ~ stateanx, data = epi.bfi)
head(m1$res)
#>          1          2          3          4          5          6 
#> -0.3151358  0.1743948 -4.0501540  1.1743948 -7.0913093 -1.2133308

m2 <- lm(bfneur ~ stateanx, data = epi.bfi)
head(m2$res)
#>         1         2         3         4         5         6 
#> -19.12342  27.87881 -24.12070  25.87881 -29.11785 -32.12144

m3 <- lm(m1$res ~ m2$res)

coef(m3)[2]
#>     m2$res 
#> 0.05441396

out[2]
#>     bfneur 
#> 0.05441396

27.6.2 Interazione tra i regressone

Esaminiamo ora l’ultima possibilità, ovvero quella di un modello di regressione multipla che contiene due variabili indipendenti che “interagiscono” tra loro. Cosa significa il concetto di “interazione” tra due variabili indipendenti?

Per rispondere a questa domanda iniziamo a considerare un modello senza interazione tra \(x_1\) e \(x_2\), ovvero il modello di regressione multipla con due regressori continui che abbiamo descritto in precedenza. Esaminiamo una rappresentazione geometrica delle predizioni di tale modello.

Per esaminare le predizioni del modello

\[\begin{equation} y = \alpha + \beta_1 x_1 + \beta_2 x_2 + \varepsilon. \end{equation}\]

non possiamo procedere come abbiamo fatto in precedenza, quando avevamo due gruppi di osservazioni, ovvero, non possiamo disegnare una diversa retta di regressione per ciascun gruppo (non essendoci dei gruppi separati). Possiamo invece usare una funzione R come plot_model() che calcola la retta di regressione di bfneur su bdi selezionando alcuni valori “fissi” della variabile stateanx – nello specifico, la media di stateanx, la media meno una deviazione standard, e la media più una deviazione standard. Si produce così la rappresentazione di tre rette di regressione.

plot_model(m, type = "pred", terms = c("bfneur", "stateanx"))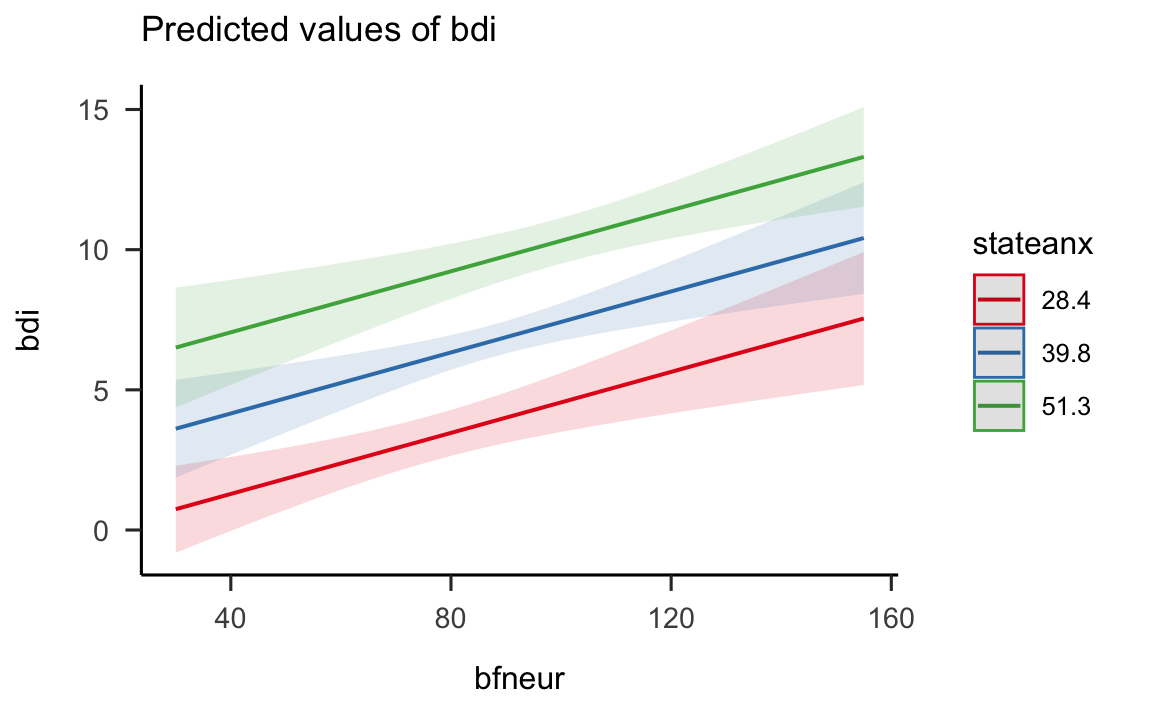

Quello che notiamo dalla figura precedente è che le tre rette sono parallele. Un modello di regressione multipla che non include alcun termine di interazione è infatti un modello additivo: per quale che sia il livello della variabile stateanx, l’effetto di bfneur (ovvero, la pendenza della retta di regressione) non cambia. Quindi, l’effetto di stateanx semplicemente si somma all’effetto di bfneur.

Una situazione ben diversa si ottiene nel caso di un modello con interazione, come il seguente:

\[\begin{equation} y = \alpha + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1 \cdot x_2 + \varepsilon. \end{equation}\]

Adattiamo questo modello ai dati

m4 <- lm(bdi ~ bfneur * stateanx, data = epi.bfi)

e esaminiamo la souluzione ottenuta:

summary(m4)
#> 
#> Call:
#> lm(formula = bdi ~ bfneur * stateanx, data = epi.bfi)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -9.3273 -2.7107 -0.4746  1.9646 14.3104 
#> 
#> Coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)
#> (Intercept)      0.768518   3.763671   0.204   0.8384
#> bfneur          -0.040827   0.040952  -0.997   0.3199
#> stateanx         0.012673   0.100598   0.126   0.8999
#> bfneur:stateanx  0.002501   0.001008   2.483   0.0138
#> 
#> Residual standard error: 4.416 on 227 degrees of freedom
#> Multiple R-squared:  0.4229, Adjusted R-squared:  0.4152 
#> F-statistic: 55.44 on 3 and 227 DF,  p-value: < 2.2e-16

Se rappresentiamo graficamente le predizioni del modello

plot_model(m4, type = "pred", terms = c("bfneur", "stateanx"))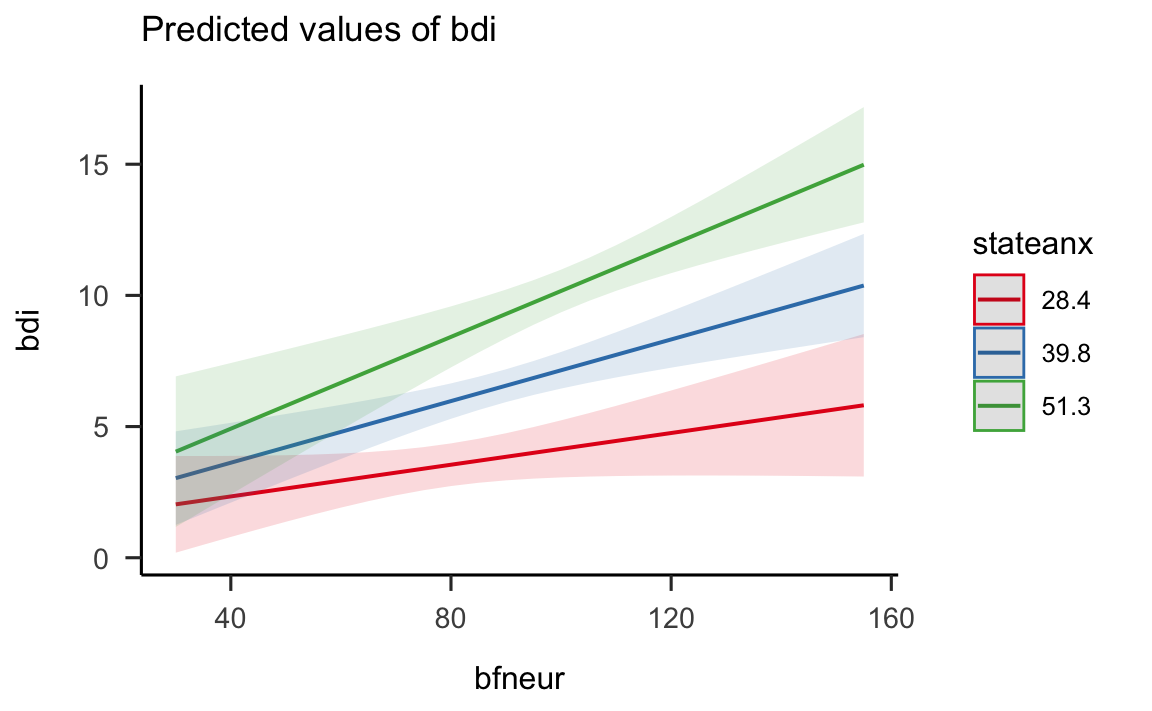

vediamo che, ora, le rette di regressione di bfneur su bdi in corrispondenza dei tre valori prescelti di stateanx non sono più parallele. Questo significa che l’effetto di bfneur su bdi (la pendenza della retta di regressione) dipende dal valore di stateanx. Questo è il significato di “interazione”: bfneur ha un effetto diverso su bdi a seconda del livello di stateanx.

Nel caso presente, vediamo dalla figura che il Neuroticismo ha un effetto più grande sul livello di depressione quando consideriamo coloro che hanno livelli di ansia di stato elevati.

I coefficienti si interpretano come in precedenza. L’intercetta corrisponde al valore atteso di bdi quando bfneur e stateanx hanno il valore di zero. Questo è di poco interesse. Per cui trasformiamo i dati in modo da utilizzare variabili indipendenti “centrate,” ovvero variabili da cui abbiamo sottratto la media.

epi.bfi$neur_c <- epi.bfi$bfneur - mean(epi.bfi$bfneur)
epi.bfi$stateanx_c <- epi.bfi$stateanx - mean(epi.bfi$stateanx)

Riadattiamo il modello con le variabili centrate:

m5 <- lm(bdi ~ neur_c * stateanx_c, data = epi.bfi)
summary(m5)
#> 
#> Call:
#> lm(formula = bdi ~ neur_c * stateanx_c, data = epi.bfi)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -9.3273 -2.7107 -0.4746  1.9646 14.3104 
#> 
#> Coefficients:
#>                   Estimate Std. Error t value Pr(>|t|)
#> (Intercept)       6.450781   0.319275  20.204  < 2e-16
#> neur_c            0.058853   0.014445   4.074 6.38e-05
#> stateanx_c        0.232727   0.030117   7.727 3.51e-13
#> neur_c:stateanx_c 0.002501   0.001008   2.483   0.0138
#> 
#> Residual standard error: 4.416 on 227 degrees of freedom
#> Multiple R-squared:  0.4229, Adjusted R-squared:  0.4152 
#> F-statistic: 55.44 on 3 and 227 DF,  p-value: < 2.2e-16

Si vede che il coefficiente associato al termine di interazione è rimasto immutato. Ma ora è più facile interpretare il coefficiente dell’intercetta. In questo caso, l’intercetta corrisponde al valore atteso di bdi quando bfneur e stateanx assumono il loro valore medio (ovvero zero, per le variabili trasformate). Per quanto riguarda gli effetti separati di bfneur e stateanx, questi non sono interpretabili, in quanto la presenza di un’interazione significa, appunto, che bfneur e stateanx non hanno effetti separati su bdi.