Capitolo 29 Il modello statistico della regressione lineare
Lo scopo della ricerca è trovare le associazioni tra le variabili e fare confronti fra le condizioni sperimentali. Nel caso della psicologia, il ricercatore vuole scoprire le leggi generali che descrivono le relazioni tra i costrutti psicologici e le relazioni che intercorrono tra i fenomeni psicologici e quelli non psicologici (sociali, economici, storici, …). Abbiamo già visto come la correlazione di Pearson sia uno strumento adatto a questo scopo. Infatti, essa ci informa sulla direzione e sull’intensità della relazione lineare tra due variabili. Tuttavia, la correlazione non è sufficiente, in quanto il ricercatore ha a disposizione solo i dati di un campione, mentre vorrebbe descrivere la relazione tra le variabili nella popolazione. A causa della variabilità campionaria, le proprietà dei campioni sono necessariamente diverse da quelle della popolazione: ciò che si può osservare nella popolazione potrebbe non emergere nel campione e, al contrario, il campione manifesta caratteristiche che non sono necessariamente presenti nella popolazione. È dunque necessario chiarire, dal punto di vista statistico, il legame che intercorre tra le proprietà del campione e le proprietà della popolazione da cui esso è stato estratto. Come nel caso della media, anche in questo caso dovrà essere costruita la distribuzione di una statistica; ma però, nel caso presente, la statistica di interesse sarà costruita utilizzando, non i dati di una sola variabile, ma bensì i dati che descrivono l’andamento congiunto di due variabili.
Il modello di regressione utilizza la funzione matematica più semplice per descrivere la relazione fra due variabili, ovvero la funzione lineare. Inizieremo a descrivere le proprietà geometriche della funzione lineare per poi utilizzare questa semplice funzione per costruire il modello statistico della regressione lineare.
29.1 La funzione lineare
Si chiama funzione lineare una funzione del tipo
\[ f(x) = a + b x, \] dove \(a\) e \(b\) sono delle costanti. Il grafico di tale funzione è una retta di cui il parametro \(b\) è detto coefficiente angolare e il parametro \(a\) è detto intercetta con l’asse delle \(y\) (infatti, la retta interseca l’asse \(y\) nel punto \((0,a)\), se \(b \neq 0\)).
Per assegnare un’interpretazione geometrica alle costanti \(a\) e \(b\) si consideri la funzione
\[ y = b x. \] Tale funzione rappresenta un caso particolare, ovvero quello della proporzionalità diretta tra \(x\) e \(y\). Il caso generale della linearità
\[ y = a + b x \] non fa altro che sommare una costante \(a\) a ciascuno dei valori \(y = b x\). Nella funzione lineare \(y = a + b x\), se \(b\) è positivo allora \(y\) aumenta al crescere di \(x\); se \(b\) è negativo allora \(y\) diminuisce al crescere di \(x\); se \(b=0\) la retta è orizzontale, ovvero \(y\) non muta al variare di \(x\).
Consideriamo ora il coefficiente \(b\). Si consideri un punto \(x_0\) e un incremento arbitrario \(\varepsilon\) come indicato nella figura 29.1. Le differenze \(\Delta x = (x_0 + \varepsilon) - x_0\) e \(\Delta y = f(x_0 + \varepsilon) - f(x_0)\) sono detti incrementi di \(x\) e \(y\). Il coefficiente angolare \(b\) è uguale al rapporto
\[ b = \frac{\Delta y}{\Delta x} = \frac{f(x_0 + \varepsilon) - f(x_0)}{(x_0 + \varepsilon) - x_0}, \] indipendentemente dalla grandezza degli incrementi \(\Delta x\) e \(\Delta y\). Il modo più semplice per assegnare un’interpretazione geometrica al coefficiente angolare (o pendenza) della retta è dunque quello di porre \(\Delta x = 1\). In tali circostanze infatti \(b = \Delta y\).
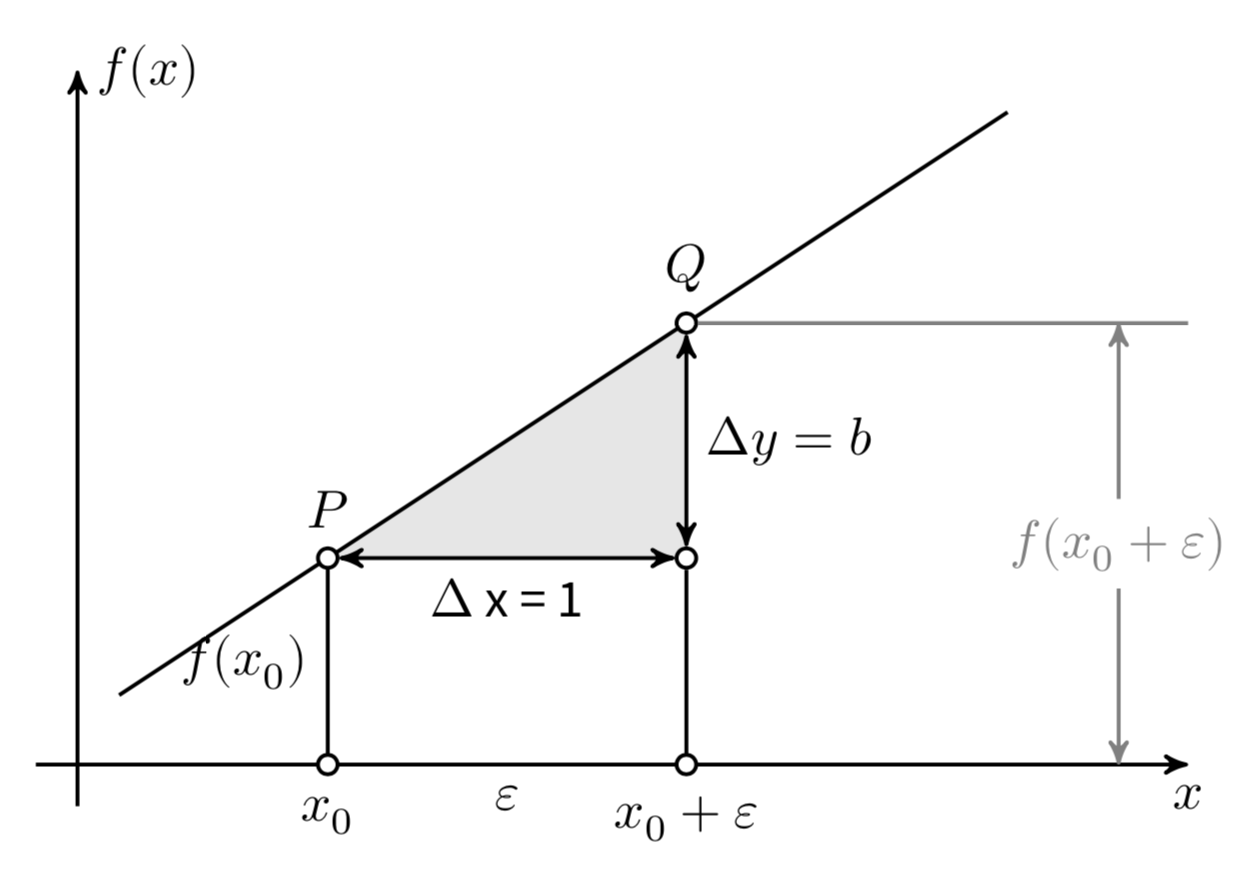
Figura 29.1: La funzione lineare \(y = a + bx\).
29.2 L’errore di misurazione
Per descrivere l’associazione tra due variabili, tuttavia, la funzione lineare non è sufficiente. Nel mondo empirico, infatti, la relazione tra variabili non è mai perfettamente lineare. È dunque necessario includere nel modello di regressione anche una componente d’errore, ovvero una componente della \(y\) che non può essere spiegata dal modello lineare. Nel caso di due sole variabili, questo ci conduce alla seguente formulazione del modello di regressione:
\[\begin{equation} y = \alpha + \beta x + \varepsilon, \tag{29.1} \end{equation}\]
laddove i parametri \(\alpha\) e \(\beta\) descrivono l’associazione tra le variabili aleatorie \(y\) e \(x\) (nella popolazione), e il termine d’errore \(\varepsilon\) specifica quant’è grande la porzione della variabile \(y\) che non può essere predetta nei termini di una relazione lineare con la \(x\).
Si noti che l’eq. (29.1) ci consente di formulare una predizione, nei termini di un modello lineare, del valore atteso della \(y\) conoscendo \(x\), ovvero
\[\begin{equation} \hat{y} = \mathbb{E}(y \mid x) = \alpha + \beta x. \tag{29.2} \end{equation}\]
In altri termini, se i parametri del modello (\(\alpha\) e \(\beta\)) sono noti, allora è possibile predire \(y\) sulla base della nostra conoscenza della \(x\).
Per esempio, se conosciamo la relazione lineare tra quoziente di intelligenza ed aspettativa di vita, allora possiamo prevedere quanto a lungo vivrà una persona sulla base del suo QI. Sì, c’è una relazione lineare tra intelligenza e aspettativa di vita! – per una discussione, si veda, ad esempio, l’articolo di David Z. Hambrick pubblicato su Scientific American il 22 dicembre 2015. Ma quando sarà accurata la nostra previsione? Ciò dipende dal termine d’errore dell’eq. (29.1). L’analisi di regressione ci fornisce un metodo per rispondere a domande di questo tipo.
29.3 Scopi della regressione lineare
Il modello di regressione lineare si pone tre obiettivi:
- descrivere l’associazione tra le variabili \(x\) e \(y\) nel campione esaminato;
- misurare la bontà dell’adattamento dell’associazione tra \(x\) e \(y\);
- fare inferenze sull’associazione tra \(x\) e \(y\) nella popolazione da cui il campione è stato estratto.
Il primo obiettivo intende rispondere alla stessa domanda a cui risponde il coefficiente di correlazione: quali sono l’intensità e il segno della relazione lineare che descrive l’associazione tra due variabili? Vedremo che c’è una precisa relazione tra il coefficiente \(b\) del modello di regressione (che rappresenta la pendenza della retta di regressione) e il coefficiente di correlazione \(r\) di Pearson: il coefficiente di correlazione non è altro che la pendenza della retta di regressione quando i dati sono standardizzati. Vi è però un’importante differenza tra la correlazione ed il modello di regressione. La correlazione è un indicatore simmetrico di associazione tra due caratteri. Il modello di regressione, invece, si chiede come varia una variabile, detta dipendente e solitamente denotata con \(y\), al variare di un’altra variabile, detta indipendente (o predittore), solitamente denotata con \(x\). L’analisi della regressione lineare si pone dunque il problema di studiare la relazione asimmetrica tra due variabili.
Il secondo obiettivo del modello di regressione lineare si chiede se il modello di regressione sia sensato per descrivere l’associazione osservata tra le due variabili. Vogliamo trovare un indice che descriva quanto distanti sono i dati dalla retta di regressione. Se i punti di un diagramma a dispersione sono molto vicini alla retta di regressione, allora il modello di regressione è adeguato per descrivere l’associazione tra le due variabili. In questo caso la bontà di adattamento del modello ai dati è grande. Oppure può succedere che i punti di un diagramma a dispersione siano molto lontani alla retta di regressione e/o che la retta di regressione sia piatta. In questi due ultimi casi non vi è evidenza di una associazione lineare tra le due variabili e l’indice che misura la bontà dell’adattamento dell’associazione tra \(x\) e \(y\) assume un valore basso e prossimo allo zero. Tale indice va sotto il nome di coefficiente di determinazione.
Il terzo obiettivo è quello più ambizioso: ci chiediamo quale potrebbe essere l’associazione tra le variabili \(x\) e \(y\) nella popolazione, alla luce delle informazioni che sono state osservate nel campione. Quello che vorremmo conoscere è \(p(\theta \mid \text{dati})\), laddove \(\theta\) è il parametro sconosciuto che rappresenta la pendenza della retta di regressione nella popolazione. Vedremo come l’approccio Bayesiano può essere usato per rispondere a questa domanda.
Il modello di regressione è, probabilmente, il più importante dei modelli statistici. Noi qui ne esamineremo solo le sue caratteristiche di base. Ma tale modello può essere esteso in modo tale da includere più di un predittore (nel qual caso si parla di modello di regressione multipla), oppure una variabile dipendente qualitativa (il che produce il modello di regressione logistica), oppure molteplici variabili dipendenti continue (il che produce il modello di regressione multivariato). Sviluppi più moderni di questo modello considerano inoltre il caso della violazione dell’assunzione di indipendenza tra le osservazioni, il che conduce alla costruzione dei modelli ad effetti misti (mixed-effects models). Infine, uno sviluppo importante del modello di regressione lineare è l’analisi fattoriale, nel qual caso viene ipotizzata l’esistenza di variabili indipendenti inosservabili (latenti), le quali corrispondono ai costrutti psicologici. Il modello fattoriale, così formulato, costituisce il fondamento della Psicometria, ovvero di quelle tecniche statistiche che stanno alla base della costruzione e della validazione dei reattivi psicologici.
29.4 Quantificare l’associazione fra due caratteri quantitativi
Consideriamo tre variabili aleatorie \(X\), \(Y\) ed \(\varepsilon\) legate dalla relazione lineare
\[ y = \alpha + \beta x + \varepsilon, \]
dove \(\alpha\) e \(\beta\) sono numeri reali e \(\mathbb{E}(\varepsilon) = 0\). Chiameremo modello lineare (semplice) la relazione dell’eq. (29.1) e chiameremo retta di regressione la retta
\[\begin{equation} y = \alpha + \beta x. \tag{29.3} \end{equation}\]
Il parametro \(\alpha\) è l’ordinata all’origine (o intercetta) mentre il parametro \(\beta\) è il coefficiente angolare della retta. Possiamo interpretare l’eq. (29.1) pensando che le variabili aleatorie \(x\) ed \(y\) siano legate tra loro da una relazione lineare perturbata da un errore casuale \(\varepsilon\).
Dato un insieme di realizzazioni campionarie delle variabili aleatorie \(x\) e \(y\), ci poniamo lo scopo di determinare la retta di regressione campionaria
\[\begin{equation} \hat{y}_i = a + b x_i \tag{29.4} \end{equation}\]
che approssima il meglio possibile la distribuzione dei punti \(x_i\), \(y_i\), \(i = 1, \dots, n\). Lo studio di questo problema è detto regressione lineare.
29.5 Stime dei minimi quadrati
Il primo obiettivo dell’analisi di regressione è quello di trovare la retta che meglio descrive l’andamento dei dati osservati in un campione. Iniziamo con il definire i residui \(e_i\) tramite la relazione
\[\begin{equation} e_i = y_i - (a + b x_i). \tag{29.5} \end{equation}\]
In altri termini, il residuo \(i\)-esimo è la differenza fra l’ordinata del punto (\(x_i\), \(y_i\)) e quella del punto di ascissa \(x_i\) sulla retta di regressione campionaria.
Per determinare i coefficienti \(a\) e \(b\) della retta (29.4) non è sufficiente minimizzare la somma dei residui \(\sum_{i=1}^{n}e_i\), in quanto i residui possono essere sia positivi che negativi e la loro somma può essere molto prossima allo zero anche per differenze molto grandi tra i valori osservati e la retta di regressione. Infatti, ciascuna retta passante per il punto (\(\bar{x}, \bar{y}\)) ha \(\sum_{i=1}^{n}e_i=0\).
Dimostrazione. Una retta passante per il punto (\(\bar{x}, \bar{y}\)) soddisfa l’equazione \(\bar{y} = a + b \bar{x}\). Sottraendo tale equazione dall’equazione \(y_i = a + b x_i + e_i\) otteniamo \[ y_i - \bar{y} = b (x_i - \bar{x}) + e_i. \] Sommando su tutte le osservazioni, si ha che
\[ \sum_{i=1}^n e_i = \sum_{i=1}^n (y_i - \bar{y} ) - b \sum_{i=1}^n (x_i - \bar{x}) = 0 - b(0) = 0. \]
Questo problema viene risolto scegliendo i coefficienti \(a\) e \(b\) che minimizzano, non tanto la somma dei residui, ma bensì l’errore quadratico, cioè la somma dei quadrati degli errori:
\[ S(a, b) = \sum_{i=1}^{n} e_i^2 = \sum (y_i - a - b x_i)^2. \]
Il metodo più diretto per determinare quelli che vengono chiamati i coefficienti dei minimi quadrati è quello di trovare le derivate parziali della funzione \(S(a, b)\) rispetto ai coefficienti \(a\) e \(b\):
\[\begin{equation} \begin{aligned} \frac{\partial S(a,b)}{\partial a} &= \sum (-1)(2)(y_i - a - b x_i), \notag \\ \frac{\partial S(a,b)}{\partial b} &= \sum (-x_i)(2)(y_i - a - b x_i). \end{aligned} \tag{29.6} \end{equation}\]
Ponendo le derivate uguali a zero e dividendo entrambi i membri per \(-2\) si ottengono le equazioni normali
\[\begin{equation} \begin{aligned} an + b \sum x_i &= \sum y_i, \notag \\ a \sum x_i + b \sum x_i^2 &= \sum x_i y_i. \end{aligned} \tag{29.7} \end{equation}\]
I coefficienti dei minimi quadrati \(a\) e \(b\) si trovano risolvendo le equazioni (29.7) e sono uguali a:
\[\begin{equation} \begin{aligned} a &= \bar{y} - b \bar{x},\\ b &= \frac{\sum (x_i - \bar{x}) (y_i - \bar{y})}{\sum (x_i - \bar{x})^2}. \end{aligned} \tag{29.8} \end{equation}\]
29.5.1 Un esempio concreto
Consideriamo i dati relativi a 34 coppie di gemelli monozigoti separati alla nascita (Anderson & Finn (2012)). Dei gemelli conosciamo l’ordine della nascita e il quoziente di intelligenza misurato con il Dominoes Intelligence test. Il test è costituito da 48 domande a ciascuna delle quali viene assegnato un punto nel caso di risposta corretta. La media del test nella popolazione è di 28 punti, che corrisponde al punteggiodi 100 sulla scala WAIS. I dati sono:
iq1 <- c(22, 32, 29, 13, 32, 24, 33, 19, 13, 36, 26, 26, 32, 27, 6, 16, 41, 29, 13, 20, 28, 30, 22, 23, 27, 40, 30, 30, 21, 27, 15, 38, 4, 12)
iq2 <- c(12, 28, 35, 4, 18, 33, 26, 9, 22, 34, 17, 20, 33, 28, 10, 28, 40, 30, 10, 24, 22, 34, 23, 21, 25, 38, 25, 26, 27, 24, 9, 27, 2, 9)
df <- data.frame(iq1, iq2)Un diagramma di dispersione per questi dati, insieme alla retta di regressione dei minimi quadrati, è riportato nella figura 29.2.
p <- df %>%
ggplot(aes(x = iq1, y = iq2)) +
geom_smooth(method = "lm", se=FALSE, color="lightgrey", formula = y ~ x) +
geom_point() +
labs(
x = "Qi primo nato",
y = "QI secondo nato",
title = "Gemelli monozigoti separati alla nascita",
caption = "(Fonte: Anderson e Finn, 2012)"
)
p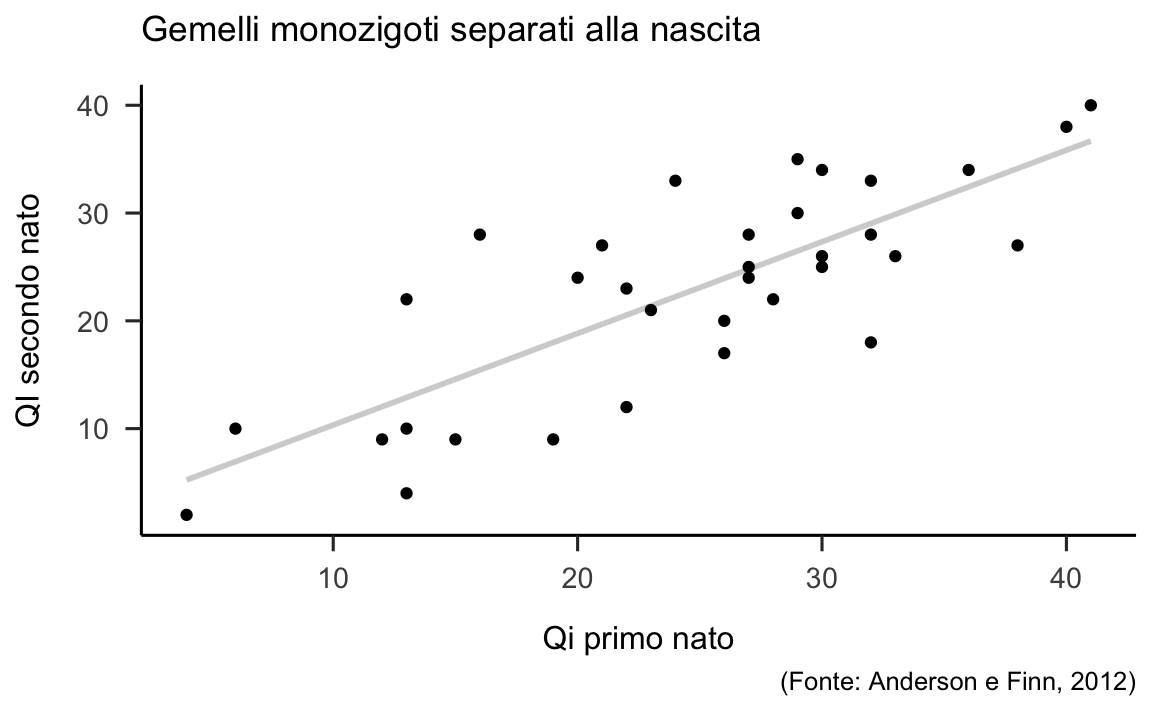
Figura 29.2: Retta di regressione che descrive la relazione lineare tra il quoziente di intelligenza del secondo nato e il quoziente di intelligenza del primo nato.
I coefficienti di regressione si trovano con le formule dei minimi quadrati. Usando R, per \(b\) otteniamo
e per \(a\) otteniamo
Tali risultati corrispondono ai valori trovati dalla funzione lm() con la seguente sintassi:
fm <- lm(iq2 ~ iq1, data = df)L’oggetto creato da {lm() può essere visionato utilizzando coef(fm) o con summary(fm).
summary(fm)
#>
#> Call:
#> lm(formula = iq2 ~ iq1, data = df)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -11.0342 -3.8218 -0.5852 3.4658 12.5635
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.8389 3.0269 0.608 0.548
#> iq1 0.8499 0.1155 7.357 2.29e-08
#>
#> Residual standard error: 6.102 on 32 degrees of freedom
#> Multiple R-squared: 0.6285, Adjusted R-squared: 0.6169
#> F-statistic: 54.13 on 1 and 32 DF, p-value: 2.288e-08I valori predetti dal modello di regressione sono dati da
yhat <- a + b * df$iq1o, in maniera equivalente, possono essere trovati con predict(fm)
predict(fm)
#> 1 2 3 4 5 6 7 8 9
#> 20.535671 29.034216 26.484652 12.886980 29.034216 22.235380 29.884070 17.986107 12.886980
#> 10 11 12 13 14 15 16 17 18
#> 32.433634 23.935089 23.935089 29.034216 24.784943 6.937998 15.436543 36.682907 26.484652
#> 19 20 21 22 23 24 25 26 27
#> 12.886980 18.835962 25.634798 27.334507 20.535671 21.385525 24.784943 35.833052 27.334507
#> 28 29 30 31 32 33 34
#> 27.334507 19.685816 24.784943 14.586689 34.133343 5.238289 12.037125I residui di regressione, ovvero la differenza tra il valore osservato e il valore predetto dal modello, si trovano mediante l’istruzione
e <- df$iq2 - yhato, in maniera equivalente, con residuals(fm)
residuals(fm)
#> 1 2 3 4 5 6 7 8
#> -8.5356706 -1.0342160 8.5153476 -8.8869798 -11.0342160 10.7646203 -3.8840705 -8.9861070
#> 9 10 11 12 13 14 15 16
#> 9.1130202 1.5663659 -6.9350888 -3.9350888 3.9657840 3.2150567 3.0620019 12.5634566
#> 17 18 19 20 21 22 23 24
#> 3.3170932 3.5153476 -2.8869798 5.1640385 -3.6347978 6.6654931 2.4643294 -0.3855252
#> 25 26 27 28 29 30 31 32
#> 0.2150567 2.1669478 -2.3345069 -1.3345069 7.3141839 -0.7849433 -5.5866889 -7.1333432
#> 33 34
#> -3.2382890 -3.0371253I residui possono essere rappresentanti graficamente come riportato nella figura 29.3.
df$predicted <- predict(fm)
df$residuals <- residuals(fm)
p1 <- df %>%
ggplot(aes(x = iq1, y = iq2)) +
geom_smooth(method = "lm", se = FALSE, color = "lightgrey") +
geom_segment(aes(xend = iq1, yend = predicted), alpha = .2) +
geom_point() +
geom_point(aes(y = predicted), shape = 1) +
labs(
x = "Qi primo nato",
y = "QI secondo nato",
title = "Gemelli monozigoti separati alla nascita",
caption = "(Fonte: Anderson e Finn, 2012)"
)
p1
#> `geom_smooth()` using formula 'y ~ x'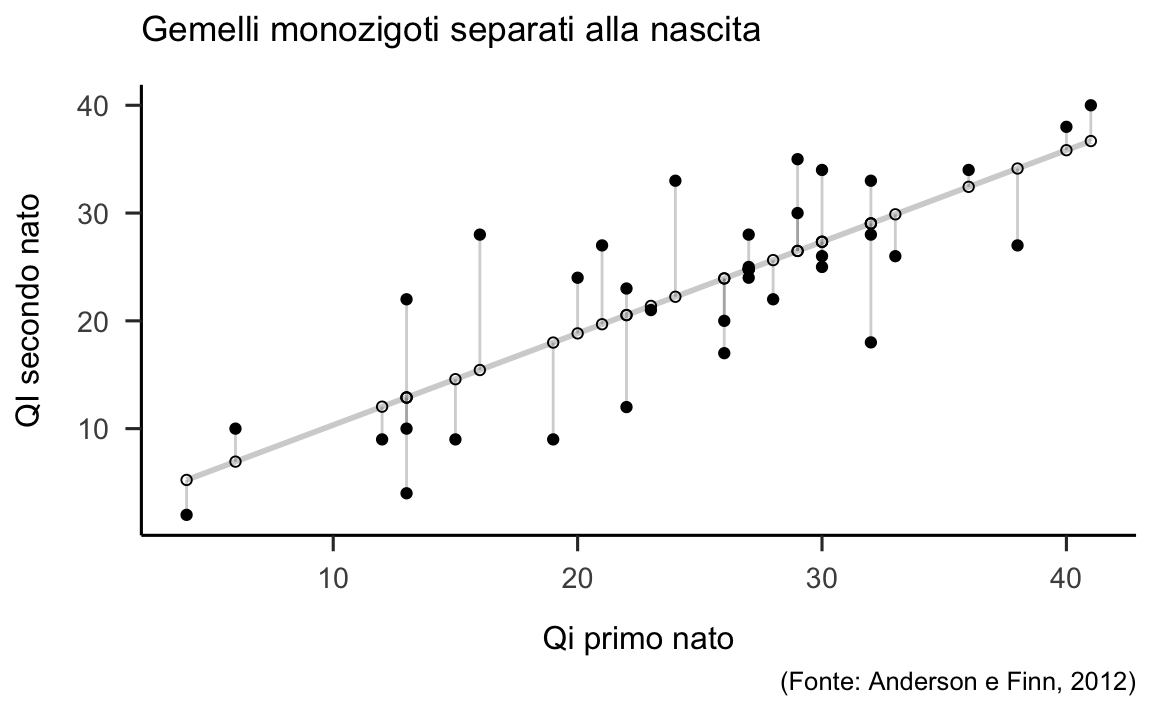
Figura 29.3: Residui del modello di regressione che esprime il quoziente di intelligenza del secondo nato in funzione del quoziente di intelligenza del primo nato.
29.5.2 Coefficiente angolare e correlazione di Pearson
Ricordando che \(r_{xy}=s_{xy} / (s_x s_y)\) è il coefficiente di correlazione lineare e che \(b=s_{xy} /s_x^2\) è la stima dei minimi quadrati del coefficiente angolare della retta di regressione, sostituendo \(r_{xy}s_xs_y\) al numeratore dell’equazione di \(b\) e semplificando, si ottiene \[\begin{equation} b = r_{yx}\frac{s_y}{s_x}. \end{equation}\] Se i dati vengono standardizzati, dunque, l’equazione della retta di regressione campionaria diventa \[\begin{equation} z_{y_i} = r_{xy} z_{x_i} + e_i, \end{equation}\] in quanto \(a = \bar{z}_y - b\bar{z}_x =0\) e \(s_x = s_y = 1\).
Si può dunque assegnare al coefficiente di correlazione di Pearson la seguente interpretazione: \(r_{xy}\) è uguale alla pendenza \(b\) della retta di regressione quando le variabili \(x\) e \(y\) vengono standardizzate (Rodgers & Nicewander, 1988).
Facciamo un esempio calcolando i coefficienti di regressione sui punteggi standardizzati del quoziente di intelligenza dei gemelli monozigoti.
ziq1 <- scale(df$iq1)
ziq2 <- scale(df$iq2)
fm1 <- lm(ziq2 ~ ziq1)
coef(fm1)
#> (Intercept) ziq1
#> 1.818206e-16 7.927594e-01Utilizzando i valori standardizzati del QI l’intercetta diventa pari a zero e la pendenza della retta di regressione diventa uguale alla correlazione tra le due variabili:
cor(df$iq1, df$iq2)
#> [1] 0.792759429.5.3 Regressione verso la media
Il termine regressione fu introdotto da Francis Galton (1822-1911), un
antropologo che fu, tra le altre cose, promotore dell’eugenetica. Nel
1886, nell’ambito dei suoi studi sull’ereditarietà dei caratteri, Galton
raccolse le stature di \(928\) figli adulti e dei loro \(205\) genitori
(padri e madri) – i dati sono disponibili nel data.frame Galton
contenuto nel pacchetto R HistData. Galton esaminò la relazione tra
l’altezza media dei figli e l’altezza media dei genitori, che chiamò
“mid-parent height.” In questi dati, genitori e figli hanno la stessa
altezza media di \(68.2\) pollici. Galton osservò però come l’altezza
media dei figli nati da genitori di una data altezza era più simile al
valore dell’altezza media della popolazione intera di quanto lo fosse la
mid-height dei genitori. Ad esempio, per genitori con una mid-height
compresa tra \(70\) e \(71\) pollici, l’altezza media dei figli risultò
essere di \(69.5\) pollici. Nelle parole di Galton, questo corrispondeva
ad una regression toward mediocrity, un concetto che noi oggi
chiamiamo “regressione verso la media.” Nonostante l’interpretazione
(errata) di Galton, è importante capire come questo sia un fenomeno
statistico, non genetico. Esaminiamo la ragione per cui ciò si verifica.
In precedenza abbiamo visto come, nel caso di dati standardizzati, la retta di regressione campionaria diventa: \[\hat{z}_{y_i} = r_{xy} z_{x_i}.\] Dal momento che \(r_{xy}\) è il coefficiente di regressione, esso assume valori compresi tra \(-1\) e \(1\). Assumiamo che \(r_{xy}\) sia positivo e minore di \(1\) (ovvero, assumiamo che la correlazione tra \(x\) e \(y\) sia positiva ma non perfetta). La formula \(\hat{z}_{y_i} = r_{xy} z_{x_i}\) implica che, se \(z_{x_i}\) è positivo, allora il valore predetto \(\hat{z}_{y_i}\) dovrà essere minore di \(z_{x_i}\). In maniera equivalente, si può dire che la ‘distanza’ tra il valore predetto \(\hat{y}\) della variabile di risposta e la media \(\bar{y}\) tenderà ad essere minore della distanza tra \(x\) e \(\bar{x}\):
\[ \frac{\hat{y} - \bar{y}}{s_y} < \frac{x - \bar{x}}{s_x}. \]
Il termine ‘distanza’ è stato messo tra virgolette in quanto è necessario tenere in considerazione l’unità di misura delle variabili. Per fare questo, la distanza tra le osservazioni e il centro della distribuzione viene misurata solo dopo avere standardizzato le variabili – ovvero, viene misurata in unità di deviazioni standard.
29.5.4 Punti influenti e valori anomali
La soluzione dei minimi quadrati è fortemente influenzata dalla presenza di punti influenti che sono anche delle osservazioni anomale. Un’osservazione anomala è un’osservazione con un residuo elevato (ovvero, avente un valore anomalo di \(y\) rispetto alla previsione). Un punto di leva è un punto con un valore anomalo \(x\). Un punto influente è un’osservazione che influenza in maniera rilevante le stime dei minimi quadrati. Non sempre un punto anomalo è anche un punto influente. Per contro esistono punti non anomali che influiscono notevolmente sulle stime dei minimi quadrati – si veda la Figura 29.4.
Figura 29.4: Osservazioni anomale e osservazioni influenti.
29.6 Bontà dell’adattamento
Il secondo obiettivo dell’analisi della regressione è quello di misurare la bontà di adattamento del modello di regressione ai dati.
29.6.1 Errore standard della stima
Un indice assoluto della bontà di adattamento è fornito dalla deviazione standard dei residui, \(s_e\), chiamata anche errore standard della stima. Uno stimatore non distorto della varianza dei residui nella popolazione è dato da
\[\begin{equation} s^2_e = \frac{\sum e_i^2}{n-2} \tag{29.9} \end{equation}\] e quindi l’errore standard della stima sarà \[\begin{equation} s_e = \sqrt{\frac{\sum e_i^2}{n-2}}. \tag{29.10} \end{equation}\] Dato che \(s_e\) è possiede la stessa unità di misura della variabile \(y\), l’errore standard della stima può essere considerato come una sorta di “residuo medio.”
Consideriamo nuovamente l’esempio dei gemelli monozigoti separati alla nascita. L’errore standard della regressione
è simile, anche se non identico, al valore medio dei residui
In conclusione, se usiamo la retta di regressione per predire il quoziente di intelligenza del gemello nato per secondo a partire dal quoziente di intelligenza del gemello nato per primo compiamo, in media, un errore di circa 6 punti.
29.6.2 Indice di determinazione
Un importante risultato dei minimi quadrati riguarda la cosiddetta scomposizione della devianza di regressione mediante la quale si definisce l’indice di determinazione, il quale fornisce una misura relativa della bontà di adattamento del modello di regressione ai dati del campione. Come indicato nella figura 29.5, per una generica osservazione \(x_i, y_i\), la variazione di \(y_i\) rispetto alla media \(\bar{y}\) può essere descritta come la somma di due componenti: il residuo \(e_i=y_i- \hat{y}_i\) e lo scarto di \(\hat{y}_i\) rispetto alla media \(\bar{y}\): \(y_i - \bar{y} = (y_i- \hat{y}_i) + (\hat{y}_i - \bar{y}) = e_i + (\hat{y}_i - \bar{y})\).
Figura 29.5: Scomposizione della devianza.
Se consideriamo tutte le osservazioni, la devianza delle \(y\) può essere scomposta nel seguente modo:
\[ \begin{aligned} \sum (y_i - \bar{y})^2 &= \sum \left[ e_i + (\hat{y}_i - \bar{y}) \right]^2 = \sum e_i^2 + \sum (\hat{y}_i - \bar{y})^2 + 2 \sum e_i (\hat{y}_i - \bar{y}) \notag\end{aligned} \]
Per i vincoli imposti sui residui dalle equazioni normali, il doppio prodotto si annulla, infatti
\[ \begin{aligned} \sum e_i (\hat{y}_i - \bar{y}) &= \sum e_i \hat{y}_i - \bar{y}\sum e_i = \sum e_i (a + b x_i) \notag \\ &= a \sum e_i + b \sum e_i x_i = 0 \notag\end{aligned} \]
Di conseguenza, possiamo concludere che la devianza totale (\(\dev_T\)) si scompone nella somma della devianza di dispersione (\(dev_E\)) e della devianza di regressione (\(\dev_T\)):
\[ \begin{aligned} \underbrace{\sum_{i=1}^n (y_i - \bar{y})^2}_{\tiny{\text{Devianza totale}}} &= \underbrace{\sum_{i=1}^n e_i^2}_{\tiny{\text{Devianza di dispersione}}} + \underbrace{\sum_{i=1}^n (\hat{y}_i - \bar{y})^2}_{\tiny{\text{Devianza di regressione}}} \notag \end{aligned} \]
La devianza di regressione, \(dev_R \triangleq dev_T - dev_E\), indica dunque la riduzione degli errori al quadrato che è imputabile alla regressione lineare. Il rapporto \(dev_T/dev_T\), detto indice di determinazione, esprime tale riduzione degli errori in termini proporzionali e definisce il coefficiente di correlazione al quadrato:
\[\begin{equation} r^2 \triangleq \frac{dev_R}{dev_T} = 1 - \frac{dev_E}{dev_T}. \tag{29.11} \end{equation}\]
Quando l’insieme di tutte le deviazioni della \(y\) dalla media è spiegato dall’insieme di tutte le deviazioni della variabile teorica \(\hat{y}\) dalla media, si ha che l’adattamento (o accostamento) del modello al campione di dati è perfetto, la devianza residua è nulla ed \(r^2 = 1\); nel caso opposto, la variabilità totale coincide con quella residua, per cui \(r^2 = 0\). Tra questi due estremi, \(r\) indica l’intensità della relazione lineare tra le due variabili e \(r^2\), con \(0 \leq r^2 \leq 1\), esprime la porzione della devianza totale della \(y\) che è spiegata dalla regressione lineare sulla \(x\).
Per i dati dei gemelli monozitoti separati alla nascita, la devianza totale si scompone nelle componenti di “devianza spiegata” e “devianza non spiegata” nel modo seguente:
dev_t <- sum((df$iq2 - mean(df$iq2))^2)
dev_r <- sum((yhat - mean(df$iq2))^2)
dev_e <- sum((df$iq2 - yhat)^2)le quali assumono i valori, rispettivamente, pari a \(3206.618\), \(2015.255\) e \(1191.363\). Ne segue che il coefficiente di determinazione è dev_r / dev_t = 0.628, ovvero 1 - dev_e / dev_t = 0.628. Questo risultato coincide con quello trovato con lm():
summary(fm)$r.squared
#> [1] 0.6284675Possiamo quindi concludere che, nel caso del campione esaminato, i fattori genetici spiegano circa il 63% della varianza del quoziente di intelligenza dei gemelli monozigoti (quando prevediamo il QI dei secondi nati dal QI dei primi nati).
29.7 Inferenza sull’associazione tra \(x\) e \(y\) nella popolazione
Il terzo obiettivo dell’analisi di regressione è quello di fare inferenze sull’associazione tra le due variabili nella popolazione da cui il campione deriva. Ci chiediamo se l’associazione osservata nel campione rifletta le proprietà della popolazione oppure sia imputabile agli errori di campionamento.
Se si segue la scuola frequentista, nella regressione bivariata il problema dell’inferenza statistica è basato sulla stessa logica seguita nel caso di una singola variabile aleatoria. Nell’inferenza su una media, per esempio, viene valutata l’ipotesi nulla \(H_0: \mu=0\) e il parametro di interesse, la media \(\mu\) della popolazione, viene stimato mediante un’opportuna statistica, ovvero la media campionaria \(\bar{y}\). Le inferenze statistiche sono basate sulla conoscenza delle proprietà della distribuzione della statistica campionaria \(\bar{y}\).
È possibile però anche definire degli stimatori che dipendono da due (o più) caratteri. Per esempio, il coefficiente \(b\) della retta di regressione campionaria, che viene usato quale stimatore del coefficiente angolare \(\beta\) della funzione di regressione nella popolazione \(y = \alpha + \beta x + \varepsilon\), è definito rispetto a due caratteri, \(x\) e \(y\). Per ciascun campione casuale di \(n\) osservazioni \(x, y\), lo stimatore \(b\) di \(\beta\) assume un diverso valore (\(b\) è una variabile aleatoria). L’insieme delle stime \(b\) di \(\beta\) nell’universo dei campioni di ampiezza \(n\) costituisce la distribuzione campionaria di \(b\). Analogamente si può dire dello stimatore \(a\) di \(\alpha\). Il problema che ci poniamo ora è appunto quello di descrivere le proprietà delle distribuzioni campionarie dei due stimatori dei minimi quadrati \(a\) e \(b\). Per fare questo, dobbiamo però prima introdurre il modello statistico della regressione lineare.
29.7.1 Modello statistico di regressione lineare
In corrispondenza di a ciascun valore della variabile \(x\), che si ipotizza essere costante da campione a campione, corrisponde nella popolazione una distribuzione di valori \(y\). Ci chiediamo che relazione intercorra tra le medie condizionali \(\bar{y}_i \mid x_i\) e la variabile \(x\). Se disponiamo di un campione di ciascuna distribuzione condizionata \(y_i \mid x_i\), allora possiamo calcolare la media condizionale nel campione per stimare la corrispondente media nella popolazione. Una tale situazione si può verificare in un contesto sperimentale, in cui, mantenendo fissi i valori del carattere \(x\), la ripetizione delle prove produce un campione del carattere \(y\) subordinatamente ad ogni \(x\). Nel caso di dati di tipo osservazionale, invece, vengono osservate coppie di valori (\(x_i, y_i\)), con \(i=1, \dots, n\), e per ogni valore \(x\) si ha a disposizione un unico valore \(y\).
Allo scopo di attenuare le conseguenze derivanti dalle limitazioni di cui soffrono i dati a disposizione, si definisce il modello statistico di regressione lineare introducendo nell’analisi delle ipotesi sulla popolazione. Il modello statistico di regressione è basato sulle quattro seguenti ipotesi a proposito della struttura della popolazione.
La funzione di regressione è lineare (linearità): \[ \mathbb{E}(y_i \mid x_1, \dots, x_n) = \alpha + \beta x_i, \quad i=1, \dots, n, \] ovvero, le medie delle distribuzioni condizionali \(y \mid x_i\) sono linearmente associate alla variabile esplicativa x.
Le varianze delle distribuzioni condizionali \(y \mid x_i\) sono costanti al variare della \(x\) (omoschedasticità): \[ var(y_i \mid x_1, \dots, x_n) = \sigma^2, \quad i=1, \dots, n. \]
Le osservazioni \(y_i\) sono tra loro incorrelate subordinatamente alle \(x_i\) (indipendenza): \[ cov(y_i, y_j \mid x_1, \dots, x_n) = 0, \quad per \hskip.1 in i \neq j, \] ovvero, l’osservazione \(y_i\) è selezionata dalla distribuzione condizionale \(y_i \mid x_i\) tramite un campionamento casuale indipendente.
La distribuzione di \(y_i\) subordinata a \(X=x_i\) segue la distribuzione gaussiana (normalità): \[ (y_i \mid x_i) \sim \mathcal{N}(\alpha+\beta x_i, \sigma^2). \]
29.7.2 Proprietà degli stimatori dei minimi quadrati
Può essere dimostrato (vedi Appendici) che, se le assunzioni del modello lineare sono soddisfatte, allora i coefficienti dei minimi quadrati avranno le seguenti proprietà:
\[\begin{equation} \begin{aligned} b &\sim \mathcal{N}\bigg(\beta, \frac{\sigma^2_{\varepsilon}}{\sum(x_i-\bar{x})^2}\bigg),\\ a &\sim \mathcal{N}\bigg(\alpha, \frac{\sigma^2_{\varepsilon}\textstyle\sum x_i^2}{n \textstyle\sum (x_i-\bar{x})^2} \bigg). \end{aligned} \tag{29.12} \end{equation}\]
29.7.3 Le inferenze sul modello di regressione
L’inferenza statistica sul modello di regressione può essere svolta in modi diversi. Esamineremo qui l’approccio frequentista per affrontare in seguito l’approccio Bayesiano.
L’inferenza statistica frequentista si articola nella formulazione degli intervalli di confidenza per i parametri di interesse e nei test di significatività statistica. Un’ipotesi che viene frequentemente sottoposta a verifica è quella di significatività, cioè l’ipotesi che alla variabile esplicativa sia associato un coefficiente nullo. In tal caso, l’ipotesi nulla è \[ H_0:\beta=0 \] e l’ipotesi alternativa è \[ H_1:\beta \neq 0. \] Sotto l’ipotesi nulla \(H_0: \beta = 0\) la statistica \[ t_{\hat{\beta}} = \frac{\hat{\beta}}{s_{\hat{\beta}}} \] si distribuisce come una variabile aleatoria \(t\) di Student con \(n-2\) gradi di libertà.
Di fronte al problema di decidere se il valore stimato \(\hat{\beta}\) sia sufficientemente ‘distante’ da zero, in modo da respingere l’ipotesi nulla che il vero valore \(\beta\) sia nullo, non è sufficiente basarsi soltanto sul valore numerico assunto da \(\hat{\beta}\), ma occorre tener conto della variabilità campionaria. La statistica ottenuta dividendo \(\hat{\beta}\) per la stima del suo errore standard, \(s_{\hat{\beta}}\), ci permette di utilizzare la distribuzione \(t\) di Student come metrica per stabilire se la stima trovata si debba considerare ‘diversa’ da quanto ipotizzato sotto \(H_0\).
L’ipotesi nulla viene rifiutata quando il valore assoluto del rapporto è esterno alla regione di accettazione, i cui limiti sono definiti dai valori critici della distribuzione \(t\) di Student con \(n - 2\) gradi di libertà per il livello di significatività \(\alpha\) prescelto. Se l’ipotesi nulla viene rifiutata si dice che il coefficiente \(\hat{\beta}\) è “statisticamente significativo” ammettendo così la possibilità di descrivere con un modello lineare la relazione esistente tra le variabili \(x\) e \(y\). Quando non si può rifiutare l’ipotesi nulla nel modello di regressione, si conclude che il coefficiente angolare della retta non risulta significativamente diverso da zero, individuando così nella popolazione una retta parallela all’asse delle ascisse.
Il valore-\(p\) esprime la probabilità di ottenere un valore del test uguale o superiore a quello ottenuto nel campione esaminato, utilizzando la distribuzione campionaria del test sotto l’ipotesi nulla. Se \(t_{\hat{\beta}}\) è il valore osservato del rapporto \(t\) per il coefficiente angolare della retta di regressione, allora il \(p\)-valore è dato da \[p = 2 \times Pr(t \geq |t_{\hat{\beta}}|),\] dove \(t\) è il valore di una variabile aleatoria \(t\) di Student con \((n-2)\) gradi di libertà.
Ogni volta che il \(p\)-valore del test è inferiore al livello di significatività che si è scelto per \(H_0\), il test porta al rifiuto dell’ipotesi nulla. Solitamente si sceglie un livello \(\alpha\) pari a 0.05 o 0.01.
Consideriamo nuovamente la regressione del QI del secondo nato sul QI del primo nato nei gemelli monozigoti esaminati da Anderson & Finn (2012). Dall’output prodotto dalla funzione lm() possiamo ricavare le informazioni per il calcolo della statistica \(t\):
summary(fm)
#>
#> Call:
#> lm(formula = iq2 ~ iq1, data = df)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -11.0342 -3.8218 -0.5852 3.4658 12.5635
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.8389 3.0269 0.608 0.548
#> iq1 0.8499 0.1155 7.357 2.29e-08
#>
#> Residual standard error: 6.102 on 32 degrees of freedom
#> Multiple R-squared: 0.6285, Adjusted R-squared: 0.6169
#> F-statistic: 54.13 on 1 and 32 DF, p-value: 2.288e-08che risulta essere
\[ t = \frac{B}{s_{\hat{\beta}}}=\frac{0.8499}{0.1155} = 7.357. \] Supponendo un’ipotesi alternativa bidirezionale, \(H_1: \beta \neq 0\), la regione critica sarà suddivisa nelle due code della distribuzione \(t\) di Student con \(25\) gradi di libertà. Essendo il valore critico \(t_{n-2, 1-\alpha/2}\) pari a
qt(.975, 32)
#> [1] 2.036933si può rifiutare \(H_0\).
In maniera corrispondente, possiamo considerare il \(p\)-valore. Il \(p\)-valore è l’area sottesa alla funzione di densità \(t\) di Student con \(n-2=32\) gradi di libertà nei due intervalli \([-\infty, -t_{\hat{\beta}}]\) e \([t_{\hat{\beta}}, \infty]\) è
1 - pt(7.357, 32)
#> [1] 1.145083e-08Dato che il \(p\)-valore è minore di \(\alpha = 0.05\), l’approccio frequentista conclude rigettando \(H_0\). Il risultato si può riportare nel modo seguente:
L’analisi della regressione bivariata ha rivelato una relazione lineare positiva tra il QI dei gemelli monozigoti primi nati e il QI dei gemelli secondi nati, \(\hat{\beta} = 0.85\), \(t_{32} = 7.36\), \(p = .0001\).
I test di significatività possono essere eseguiti con R utilizzando la funzione summary() applicata all’oggetto creato dal lm(): Il test statistico sul parametro \(\beta\) del modello di regressione verifica l’ipotesi nulla di indipendenza, ovvero l’ipotesi che, nella popolazione, la pendenza della retta di regressione sia uguale a zero.
Più informativo del test statistico \(H_0: \beta=0\) è l’intervallo di confidenza per il parametro \(\beta\): \[ \hat{\beta} \pm t_{\alpha/2} s_{\hat{\beta}}. \] Nel caso presente, abbiamo
Dato che il limite inferiore dell’intervallo di confidenza è superiore allo zero, possiamo concludere che vi è un’associazione (lineare) positiva tra il QI del primo nato e il QI del secondo nato, nelle coppie di gemelli monozigoti che sono state esaminate da Anderson & Finn (2012).
Considerazioni conclusive
Il modello di regressione lineare semplice viene usato per descrivere la relazione tra due variabili e per determinare il segno e l’intensità di tale relazione. Inoltre, il modello di regressione ci consente di prevedere il valore della variabile dipendente in base ad alcuni nuovi valori della variabile indipendente. Il modello di regressione lineare semplice è in realtà molto limitato, in quanto descrive soltanto la relazione tra la variabile dipendente \(y\) e una sola variabile esplicativa \(x\). Esso diventa molto più utile quando incorpora più variabili indipendenti. In questo secondo caso, però, i calcoli per la stima dei coefficienti del modello diventano più complicati. Abbiamo deciso qui di presentare solo il modello di regressione lineare semplice perché, in quel caso, sia la logica dell’inferenza sia le procedure di calcolo sono facilmente maneggiabili. Nel caso più generale, quello del modello di regressione multipla, la logica dell’inferenza rimarrà identica a quella discussa qui, ma le procedure di calcolo richiedono l’uso dell’algebra matriciale che esula dagli scopi del presente insegnamento. Il modello di regressione multipla può includere sia regressori quantitativi, sia regressori qualitativi, utilizzando un opportuna schema di codifica. È interessante notare come un modello di regressione multipla che include una sola variabile esplicativa quantitativa corrisponde all’analisi della varianza ad una via; un modello di regressione multipla che include più di una variabile esplicativa quantitativa corrisponde all’analisi della varianza più vie. Questi argomenti verranno sviluppati negli insegnamenti di carattere quantitativo più avanzati. Possiamo qui concludere dicendo che il modello di regressione, nelle sue varie forme e varianti, costituisce la tecnica di analisi dei dati maggiormente usata in psicologia.