25.1 Metodi basati su griglie

È possibile stimare l’intera distribuzione a posteriori mediante metodi basati su griglie (grid-based), come abbiamo fatto nel capitolo Modellistica bayesiana. Questo è l’approccio più semplice. Tuttavia, anche se tali metodi possono fornire risultati accuratissimi, a causa della “maledizione della dimensionalità” tali procedure numeriche sono utilizzabili solo nel caso di modelli statistici semplici, con non più di due parametri. Nella pratica concreta tali metodi vengono dunque sostituiti da altre tecniche più efficienti in quanto, anche in comuni modelli utilizzati in psicologia, vengono stimati centinaia se non migliaia di parametri.

25.2 Approssimazione quadratica

L’approssimazione quadratica è uno dei metodi che possono essere usati per superare il problema della “maledizione della dimensionalità.” La motivazione di tale metodo è la seguente. Sappiamo che, in generale, la regione della distribuzione a posteriori che si trova in prossimità del suo massimo può essere ben approssimata dalla forma di una distribuzione Normale. Descrivere la distribuzione a posteriori mediante la distribuzione Normale significa utilizzare un’approssimazione che viene, appunto, chiamata “quadratica” (tale approssimazione si dice quadratica perché il logaritmo di una distribuzione gaussiana forma una parabola e la parabola è una funzione quadratica – dunque, mediante questa approssimazione descriviamo il logaritmo della distribuzione a posteriori mediante una parabola).

L’approssimazione quadratica si pone due obiettivi.

1. Trovare la moda della distribuzione a posteriori. Ci sono varie procedure di ottimizzazione, implementate in R, in grado di trovare il massimo di una distribuzione.

2. Stimare la curvatura della distribuzione in prossimità della moda. Una stima della curvatura è sufficiente per trovare un’approssimazione quadratica dell’intera distribuzione. In alcuni casi, questi calcoli possono essere fatti seguendo una procedura analitica, ma solitamente vengono usate delle tecniche numeriche.

Una descrizione della distribuzione a posteriori ottenuta mediante l’approssimazione quadratica si ottiene mediante la funzione quap() contenuta nel pacchetto rethinking. Tale pacchetto, creato da Richard McElreath per accompagnare il suo testo Statistical Rethinking\(^2\), può essere scaricato utilizzando le istruzioni seguenti:

install.packages(c("coda", "mvtnorm", "devtools", "loo", "dagitty"))
library("devtools")
devtools::install_github("rmcelreath/rethinking")

È possibile che, per i diversi sistemi operativi, sia necessaria l’installazione di componenti ulteriori. Si veda https://github.com/rmcelreath/rethinking.

Le analisi Bayesiane che discuteremo in queste dispense, per la maggior parte, faranno uso della funzione rethinking::quap(). È dunque fondamentale che gli studenti installino sul loro computer il pacchetto rethinking.

Dal nostro punto di vista non è importante capire come si svolgono in pratica i calcoli necessari per la stima della distribuzione a posteriori con il metodo dell’approssimazione quadratica. Quello che è importante capire è il significato della distribuzione a posteriori e questo significato è stato chiarito nell’esempio discusso nel capitolo Modellistica bayesiana. L’approssimazione quadratica fornisce risultati simili (o identici) a quelli ottenuti con il metodo grid-based. Il vantaggio dell’approssimazione quadratica è che disponiamo di una serie di funzioni R che svolgono tutti i calcoli per noi.

In realtà, l’approssimazione quadratica è poco usata in pratica, perché per problemi complessi è più conveniente usare i metodi Monte Carlo basati su Catena di Markov (MCMC) che verranno descritti nella successiva sezione. Per potere utilizzare i metodi MCMC è necessario installare sul proprio computer del software aggiuntivo e tale operazione, talvolta, può risultare complessa. Non è l’obiettivo di questo insegnamento affrontare questo problema. Per questa ragione, per svolgere gli esercizi che discuteremo sarà sufficiente fare ricorso al metodo dell’approssimazione quadratica; ovvero sarà sufficiente usare la funzione rethinking::quap().

25.3 Integrazione con metodo Monte Carlo

Questi algoritmi estraggono campioni da una distribuzione target mediante la seguente procedura (1) facendo una proposta per un nuovo valore casuale del parametro sconosciuto (o dei parametri sconosciuti) e poi (2) accettando o rifiutando tale proposta. Se entrambi questi passaggi vengono eseguiti correttamente, i valori accettati dei parametri costituiranno dei campioni casuali della distribuzione target.

L’idea è semplice: per calcolare le statistiche che ci interessano – solitamente, una qualche misura di tendenza centrale e un qualche intervallo che contiene una data proporzione della massa della distribuzione – non abbiamo bisogno di conoscere l’esatta funzione di densità della distribuzione a posteriori \(p(\theta \mid \mathcal{Y})\). È sufficiente, per la ragione spiegata nella sezione successiva, riuscire a ottenere un grande numero di campioni casuali dalla distribuzione a posteriori. Se i campioni che estraiamo dalla distribuzione a posteriori sono veramente casuali, allora le statistiche che ci interessano, ovvero una qualche misura di tendenza centrale e un qualche intervallo che contiene una data proporzione della massa della distribuzione, saranno stimati con esattezza.

Come facciamo a sapere che i campioni ottenuti sono stati estratti in maniera casuale dalla distribuzione a posteriori \(p(\theta \mid \mathcal{Y})\)? Per ottenere questo risultato, basta che decidiamo, seguendo il secondo passo elencato sopra, di accettare o rifiutare il valore proposto del parametro in base ad una regola che dipende dal valore della densità \(p(\theta \mid \mathcal{Y})\) in corrispondenza della proposta. E un valore che è proporzionale a tale densità è facile da calcolare: non è altro che il prodotto della funzione a priori e della verosimiglianza in corrispondenza del valore della proposta. Questo è in essenza l’algoritmo di Metropolis.

Prima di esaminare in dettaglio i metodi MCMC per la stima della funzione a posteriori, spendiamo qualche parola sul metodo Monte Carlo.

25.4 Legge forte dei grandi numeri

Il termine Monte Carlo si riferisce al fatto che la computazione fa ricorso ad un ripetuto campionamento casuale attraverso la generazione di sequenze di numeri casuali. Una delle sue applicazioni più potenti è il calcolo degli integrali mediante simulazione numerica.

Consideriamo, ad esempio, la formula del valore atteso di una variabile aleatoria continua:

\[ \mathbb{E}(X) = \int_{-\infty}^{+\infty} x f(x) dx. \] Il calcolo del valore atteso richiede la somma dei prodotti \(x f(x)\) per tutti gli infinitesimi “incrementi” \(dx\) dei possibili valori \(x\). Vediamo come si può risolvere questo problema senza dovere calcolare l’integrale esatto per via analitica.

L’integrazione con metodo Monte Carlo trova la sua giustificazione nella Legge forte dei grandi numeri la quale, in termini formali, può essere espressa nel modo seguente. Data una successione di variabili casuali \(Y_{1}, Y_{2},\dots, Y_{n},\dots\) indipendenti e identicamente distribuite con media \(\mu\), ne segue che

\[ P\left( \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{i=1}^n Y_i = \mu \right) = 1. \] Ciò significa che, al crescere di \(n\), la media delle realizzazioni di \(Y_{1}, Y_{2},\dots, Y_{n},\dots\) converge con probabilità 1 al vero valore \(\mu\).

Possiamo fornire un esempio intuitivo della legge forte dei grandi numeri facendo riferimento ad una serie di lanci di una moneta dove \(Y=1\) significa “testa” e \(Y=0\) significa “croce.” Per la legge forte dei grandi numeri, nel caso di una moneta equilibrata la proporzione di eventi “testa” converge alla vera probabilità dell’evento “testa”

\[ \frac{1}{n} \sum_{i=1}^n Y_i \rightarrow \frac{1}{2} \] con probabilità di uno.

Quello che è stato detto sopra non è che un modo sofisticato per dire che, se vogliamo calcolare un’approssimazione del valore atteso di una variabile aleatoria, non dobbiamo fare altro che la media aritmetica di un grande numero di realizzazioni della variabile aleatoria. Come è facile intuire, l’approssimazione migliora al crescere del numero di dati che abbiamo a disposizione. Questa è la giustificazione dell’affermazione precedente secondo la quale una stima del valore atteso di \(p(\theta \mid \mathcal{Y})\) può essere ottenuta mediante un grande numero di campioni casuali della distribuzionea a posteriori.

25.5 Metodi MC basati su Catena di Markov

Ritornando al discorso precedente, diciamo che la costruzione della distribuzione a posteriori, in generale, richiede (al denominsatore) il calcolo di un integrale “intrattabile” per via analitica. Il problema di costruire la distribuzione a posteriori viene dunque affrontato facendo una simulazione numerica che produce un risultato approssimato (ma sufficientemente preciso per tutti gli scopi pratici). A tale scopo vengono usati i cosiddetti metodi Monte Carlo basati su Catena di Markov i quali consentono di costruire sequenze di punti (le “catene”) nello spazio dei parametri le cui densità sono proporzionali alla distribuzione a posteriori – in altre parole, tali “catene” corrispondono a una sequenza di campioni casuali dalla distribuzione a posteriori.

La generazioni di elementi di una catena ha una natura probabilistica e esistono diversi algoritmi per costruire le catene di Markov. Due aspetti da tenere in considerazione sotto questo punto di vista sono il periodo di burn-in e le correlazioni tra i punti. Al crescere degli step della catena si ottiene una migliore approssimazione della distribuzione target mentre, all’inizio del campionamento, la distribuzione può essere molto diversa dalla distribuzione target. Ci vuole un certo numero di iterazioni prima di raggiungere una situazione di equilibrio e tale periodo è detto di burn-in. Perciò i campioni provenienti dalla parte iniziale della catena vengono tipicamente scartati poiché non rappresentano accuratamente la distribuzione target.

Normalmente, un algoritmo MCMC genera catene di Markov nelle quali i campioni non sono indipendenti, ma ognuno è autocorrelato a quelli immediatamente precedenti e successivi. Questa correlazione introduce una distorsione nella soluzione che si ottiene. L’arte dei diversi algoritmi MCMC risiede nel rendere il meccanismo efficiente e capace di produrre un risultato non distorto, il che implica la riduzione al minimo del tempo di burn-in e della correlazione tra i diversi campioni.

Presentiamo ora, in una forma intuitiva, l’algoritmo di Metropolis, ovvero il primo algoritmo MCMC che è stato proposto. Tale algoritmo è stato sviluppato in seguito allo scopo di renderlo via via più efficiente. Il nostro obiettivo qui è solo quello di illustrare la logica soggiacente.

25.6 Il problema del turista viaggiatore

L’algoritmo di Metropolis è stato presentato usando varie metafore: quella di un politico che viaggia tra isole diverse (Kruschke, 2014), o quella di un re che, anche lui, si sposta tra le isole di un arcipelago (McElreath, 2020). Qui mutiamo leggermente la metafora e immaginiamo un turista in vacanza su un’isola che dispone di 10 spiagge di grandezza diversa. Muovendosi in senso orario, la grandezza delle spiagge aumenta: partendo dalla spiaggia più piccola si arriva ad una spiaggia un po’ più grande, via via fino ad arrivare all’ultima spiaggia, la decima, che è la più grande di tutte. Quindi indicheremo con i numeri da 1 a 10 le spiagge dell’isola. Tali numeri rappresentano anche la grandezza (relativa) di ciascuna spiaggia. Dato che l’isola è circolare, la decima spiaggia confina con la prima spiaggia.

Nella nostra metafora, immaginiamo un turista in vacanza sull’isola che abbiamo appena descritto. Per non annoiarsi, il nostro turista vuole passare un po’ di tempo su ogni spiaggia, ma con il vincolo che il tempo passato su ciascuna spiaggia deve essere proporzionale alla grandezza della spiaggia. Infatti, il turista preferisce le spiagge più grandi; nel contempo, però, vuole anche visitare spiagge diverse, quindi il vincolo descritto sopra sembra un buon compromesso tra il desiderio di cambiare spiaggia di tanto in tanto e il desiderio di passare più tempo sulle spiagge più grandi.

Essendo in vacanza, il turista non vuole preparare un calendario che stabilisca in anticipo la spiaggia da visitare ogni giorno, ma vuole decidere in maniera rilassata e un po’ casuale, ogni mattina, restando però fedele al vincolo che si è dato. Al bar incontra un altro turista, l’ingegnere Metropolis, che gli suggerisce come fare per ottenere l’obiettivo che si è prefissato. Seguendo le istruzioni di Metropolis, il nostro turista decide di comportarsi nel modo seguente.

1. Ogni mattina decide tra due alternative: ritornare sulla spiaggia dove era stato il giorno prima (chiamiamola spiaggia corrente) oppure andare in una delle due spiagge contigue.

2. Lancia una moneta. Se esce testa, considera la possibilità di andare nella spiaggia a che confina con la spiaggia corrente muovendosi in senso orario; se esce croce, considera la possibilità di andare nella spiaggia a che confina con la spiaggia corrente muovendosi in senso antiorario. La spiaggia individuata in questo modo viene chiamata spiaggia proposta.

3. Dopo avere trovato la spiaggia proposta, il turista deve decidere se effettivamente andare lì oppure no e, per decidere, procede in questo modo. Prende un numero di conchiglie proporzionale alla grandezza della spiaggia proposta – per esempio, se la spiaggia proposta è la numero 7, allora prenderà 7 conchiglie. Prende un numero di sassolini proporzionale alla grandezza della spiaggia corrente – per esempio, se la spiaggia corrente è la numero 6, allora prenderà 6 sassolini.

4. Se il numero di conchiglie è maggiore del numero di sassolini, il turista si sposta sempre nella spiaggia proposta. Ma se ci sono meno conchiglie che sassolini, scarta un numero di sassolini uguale al numero di conchiglie e mette gli oggetti rimanenti in un sacchetto – per esempio, se la spiaggia proposta è la 5 e la spiaggia corrente è la 6, allora metterà nel sacchetto 5 conchiglie e 1 sassolino. Mescola bene ed estrae dal sacchetto un oggetto: se è una conchiglia si sposta nella spiaggia proposta, se è un sassolino resta nella spiaggia corrente. Di conseguenza, la probabilità che il turista cambi spiaggia (ovvero \(\frac{5}{6}\)) è uguale al numero di conchiglie diviso per il numero originale di sassolini.

Decidere di procedere in questo modo potrebbe sembrare un modo per rovinarsi le vacanze. Invece, questo algoritmo funziona! Seguendo la proposta di Metropolis, il turista passerà su ciascuna spiaggia un numero di giorni proporzionale alla grandezza della spiaggia.

McElreath (2020) ha implementato in R l’algoritmo di Metropolis che abbiamo descritto sopra nel modo seguente:

num_weeks <- 1e5
positions <- rep(0, num_weeks)
current <- 10
for (i in 1:num_weeks) {
  # record current position
  positions[i] <- current
  # flip coin to generate proposal
  proposal <- current + sample(c(-1, 1), size = 1)
  # now make sure he loops around the archipelago
  if (proposal < 1) proposal <- 10
  if (proposal > 10) proposal <- 1
  # move?
  prob_move <- proposal / current
  current <- ifelse(runif(1) < prob_move, proposal, current)
}

Le istruzioni seguenti sono state usate per generare la figura 25.1. Se guardiamo la figura e consideriamo un giorno qualsiasi è difficile capire qual è la spiaggia scelta dal turista.

ggplot(
    data.frame(x = 1:100, y = positions[1:100]),
    aes(x, y)
) +
  geom_point(color = "#8184FC") +
  labs(
    x = "Giorno",
    y = "Isola"
  ) +
  scale_y_continuous(breaks=1:10)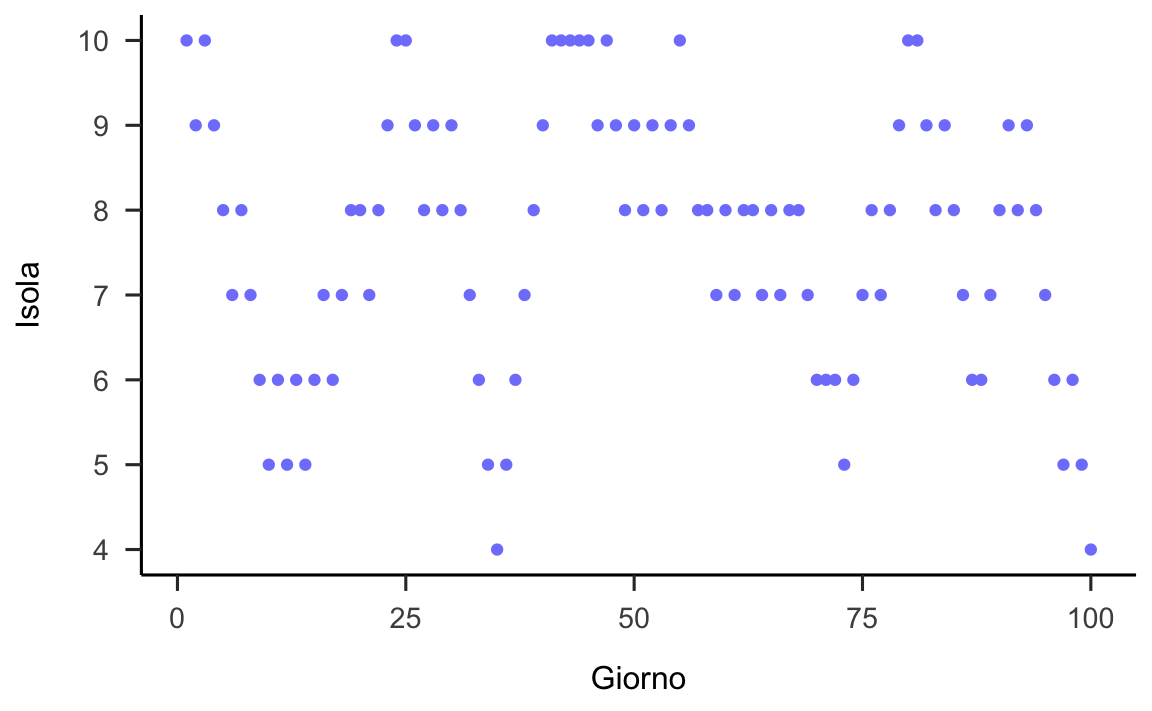

Figura 25.1: Risultati dell’algoritmo di Metropolis utilizzato dal turista viaggiatore. La figura mostra la spiaggia scelta dal turista (asse verticale) in funzione di ciascun giorno della sua vacanza (asse orizzontale).

Tuttavia, se esaminiamo la figura 25.2 che descrive il comportamento a lungo termine dell’algoritmo, ci rendiamo conto che l’algoritmo ha prodotto il risultato che si voleva ottenere: il tempo trascorso dal turista su ciascuna spiaggia è proporzionale alla grandezza della spiaggia.

ggplot(
  data.frame(x = 1:10, y = as.numeric(table(positions))),
  aes(x = x, xend = x, y = 0, yend = y)
  ) +
  geom_segment(color = "#8184FC", size = 1.5) +
  labs(
    x = "Isola",
    y = "Numero di giorni"
  ) +
  scale_x_continuous(breaks=1:10)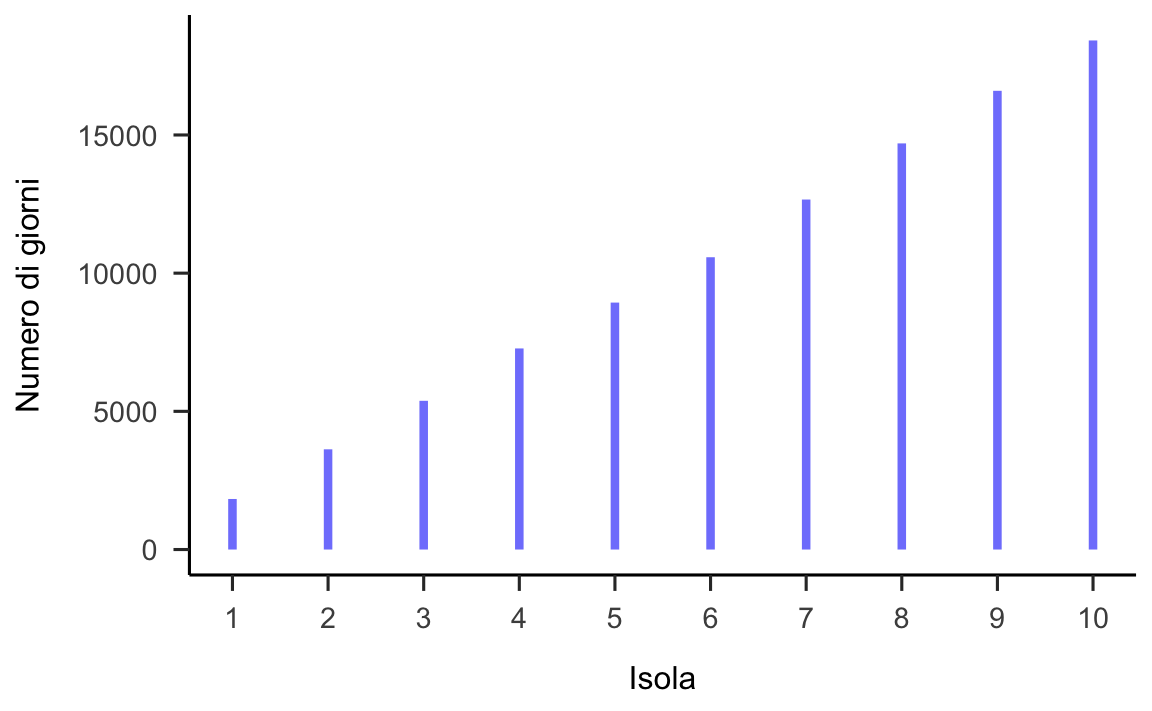

Figura 25.2: Risultati dell’algoritmo di Metropolis utilizzato dal turista viaggiatore. La figura mostra che il numero di volte in cui ciascuna spiaggia è stata visitata è proporzionale alla grandezza della spiaggia.

L’algoritmo di Metropolis funziona anche se il turista decide di spostarsi dalla spiaggia corrente a qualunque altra spiaggia, non solo su quelle confinanti. Inoltre, l’algoritmo funziona per qualunque numero di spiagge e anche se il turista non sa quante spiagge ci sono sull’isola. Affinché l’algoritmo funzioni è solo necessario conoscere la grandezza della spiaggia “corrente” e quella della spiaggia “proposta.”

25.7 L’algoritmo di Metropolis

L’algoritmo descritto nella sezione Il problema del turista viaggiatore è un caso speciale dell’algoritmo di Metropolis e l’algoritmo di Metropolis è un caso speciale dei metodi MCMC. L’algoritmo di Metropolis, al di là dell’uso che ne fa il fortunato turista dell’esempio discusso in precedenza, viene in realtà impiegato per per ottenere una sequenza di campioni casuali da una distribuzione a posteriori la cui forma è, solitamente, sconosciuta. Fuor di metafora:

• i numeri che identificano ciascuna spiaggia corrispondono ai valori del parametro che vogliamo stimare – non è necessario che il parametro assuma solo valori discreti, può anche assumere un insieme continuo di valori;

• la grandezza della spiaggia corrisponde alla densità a posteriori associata a ciascuno dei possibili valori del parametro;

• i giorni di permanenza su una spiaggia corrispondono al numero di campioni estratti dalla distribuzione a posteriori.

L’aspetto cruciale di questa discussione è il fatto che, all’aumentare delle ripetizioni dell’algoritmo di Metropolis, la distribuzione dei valori così ottenuti diventa via via più simile alla distribuzione a posteriori del parametro \(\theta\), anche se questa è sconosciuta. Per un grande numero di passi della catena l’approssimazione è sufficiente. Con questo metodo è dunque possibile generare un grande numero di campioni casuali dalla distribuzione a posteriori per poi poterne calcolare misure di sintesi e potere fare inferenza.

L’esempio precedente ci presenta, in maniera intuitiva, è la logica dell’algoritmo di Metropolis. Una illustrazione visiva di come si svolge questo processo di “esplorazione” di \(p(\theta \mid \mathcal{Y})\) è fornita in questo post.

25.8 Una applicazione concreta

L’algoritmo di Metropolis consente di effettuare quello che viene chiamato un dependent sampling, ovvero ci consente di generare campioni casuali dalla distribuzione a posteriori utilizzando soltanto il numeratore del teorema di Bayes:

\[ P(\theta \mid x) = \frac{P(x \mid \theta)P(\theta)}{P(x)} \] ovvero

\[ P(\theta \mid x) \propto P(x \mid \theta)P(\theta) \] L’algoritmo di Metropolis è la versione più semplice e più conosciuta degli algoritmi MCMC. Guardiamolo ora più da vicino cercando, di nuovo, di sviluppare un intuizione della logica che sta alla base di esso. Abbiamo detto in precedenza che, fondamentalmente, l’algoritmo di Metropolis fa due cose: (1) genera una proposta per un nuovo valore casuale del parametro sconosciuto e (2) accetta o rifiuta tala proposta. Vediamo in concreto come questo viene fatto.

• Per prima cosa troviamo un valore casuale del parametro estraendolo da una distribuzione “proposta”: \(\theta_0 \sim \Pi(\theta)\). La distribuzione proposta può essere qualunque distribuzione, anche se, idealmente, è meglio che sia simile alla distribuzione a posteriori. In pratica la distribuzione a posteriori è sconosciuta e quindi utilizziamo un qualche metodo arbitrario di iniziare la catena di Markov (ovvero utilizziamo un valore iniziale arbitrario).

• In ciascuna iterazione \(t\) viene proposto un nuovo valore del parametro \(\theta'_t\). Il valore \(\theta'_t\) viene estratto in maniera casuale da una qualsiasi distribuzione simmetrica centrata sul valore del parametro dell’interazione precedente, \(t-1\). Ad esempio, possiamo usare la distribuzione Normale con una appropriata deviazione standard: \(\theta_t \sim \mathcal{N}(\theta_{t-1}, \sigma)\). In pratica, questo significa che il valore proposto del parametro sarà un valore nella prossimità di quello attualmente considerato.

• Calcoliamo poi il rapporto \(r\) tra la distribuzione a posteriori non normalizzata determinata dal valore proposto \(\theta'_t\) e la distribuzione a posteriori non normalizzata determinata dal valore del parametro \(\theta'_{t-1}\) dell’iterazione precedente della catena: \(r = \frac{P(x \mid \theta'_t) P(\theta'_t)}{P(x \mid \theta'_{t-1}) P(\theta'_{t-1})}\). Soffermiamoci su tale formula per capire bene cosa significa. La distribuzione a posteriori non normalizzata corrisponde al numeratore del teorema di Bayes, ovvero \(P(x \mid \theta) P(\theta)\), laddove \(P(x \mid \theta)\) è la verosimiglianza di \(x\) dato \(\theta\) e \(P(\theta)\) è la distribuzione a priori di \(\theta\). Abbiamo visto nella sezione Un esempio pratico (versione 2) che il prodotto di due densità si ottiene facendo il prodotto dei valori delle ordinate corrispondenti delle due curve. Il numeratore del teorema di Bayes ci fornisce la distribuzione a posteriori non normalizzata (l’area sottesa alla curva così ottenuta non è unitaria); dato che qui facciamo un rapporto, però, questo è irrilevante. Al numeratore del rapporto \(r\) facciamo il prodotto tra due scalari: la verosimiglianza (l’ordinata) in corrispondenza del valore proposto \(\theta'_t\) e la densità della distribuzione a priori in corrispondenza di \(\theta'_t\). In maniera simile, al denominatore facciamo il prodotto tra la verosimiglianza (l’ordinata) in corrispondenza di \(\theta_{t-1}\) e la densità della distribuzione a priori in corrispondenza di \(\theta_{t-1}\).

• Utilizziamo il valore \(r\) per decidere se dobbiamo effettivamente muoverci nella nuova posizione \(\theta'_t\), oppure se dobbiamo campionare un diverso valore \(\theta'_t\). Il rapporto \(r\) tra le ordinate delle due funzioni a posteriori si pone la seguente domanda: alla luce dei dati, risultano più plausibili i valori proposti del parametro, o quelli del passo precedente della catena? Se il rapporto è maggiore di 1 allora il nuovo valore proposto viene sempre accettato, in quanto la densità a posteriori calcolata con il nuovo valore proposto del parametro è maggiore della densità a posteriori calcolata con il valore del parametro definito nell’interazione precedente della catena. Altrimenti, decidiamo di tenere i valori proposti con una probabilità minore di 1, ovvero non sempre, ma soltanto con una probabilità definita dal rapporto \(r\). Se \(r\) è uguale a 0.10, ad esempio, questo significa che la densità a posteriori calcolata con il nuovo valore proposto del parametro è 10 volte più piccola della densità a posteriori calcolata con il valore del parametro dell’interazione precedente. In queste circostanze, il valore proposto del parametro verrà accettato solo nel 10% dei casi. L’effetto di questo algoritmo è quello di “campionare” la distribuzione a posteriori in modo tale che la probabilità di scegliere i valori “proposti” sia proporzionale alla densità di tali valori nella distribuzione a posteriori. Dal punto di vista algoritmico, questa procedura viene implementata confrontando il valore \(r\) con un valore casuale estratto da una distribuzione uniforme tra zero e uno: \(U(0, 1)\). Se \(r > u \sim U(0, 1)\) allora accettiamo \(\theta'_t\) e la catena si muove in quella nuova posizione, ovvero \(\theta_t = \theta'_t\). Altrimenti \(\theta_t = \theta_{t-1}\) e ripetiamo la procedura descritta sopra campionando un nuovo valore \(\theta'_t\) (questa parte dell’algoritmo di Metropolis corrisponde alla scelta tra conchiglie e sassolini nella metafora del turista viaggiatore).

Per fare un esempio concreto, consideriamo nuovamente i 30 pazienti esaminati da Zetsche et al. (2019) e discussi nella sezione Un esempio pratico. Di essi, 23 hanno manifestato aspettative distorte negativamente sul loro stato d’animo futuro. Utilizzando l’algoritmo di Metropolis, ci poniamo il problema di ottenere la stima a posteriori di \(\theta\) (probabilità di manifestare un’aspettativa distorta negativamente), dati i 23 “successi” in 30 prove. Useremo la stessa distribuzione a priori per \(\theta\) che è stata usata nella sezione Un esempio pratico (versione 2).

25.8.1 Verosimiglianza

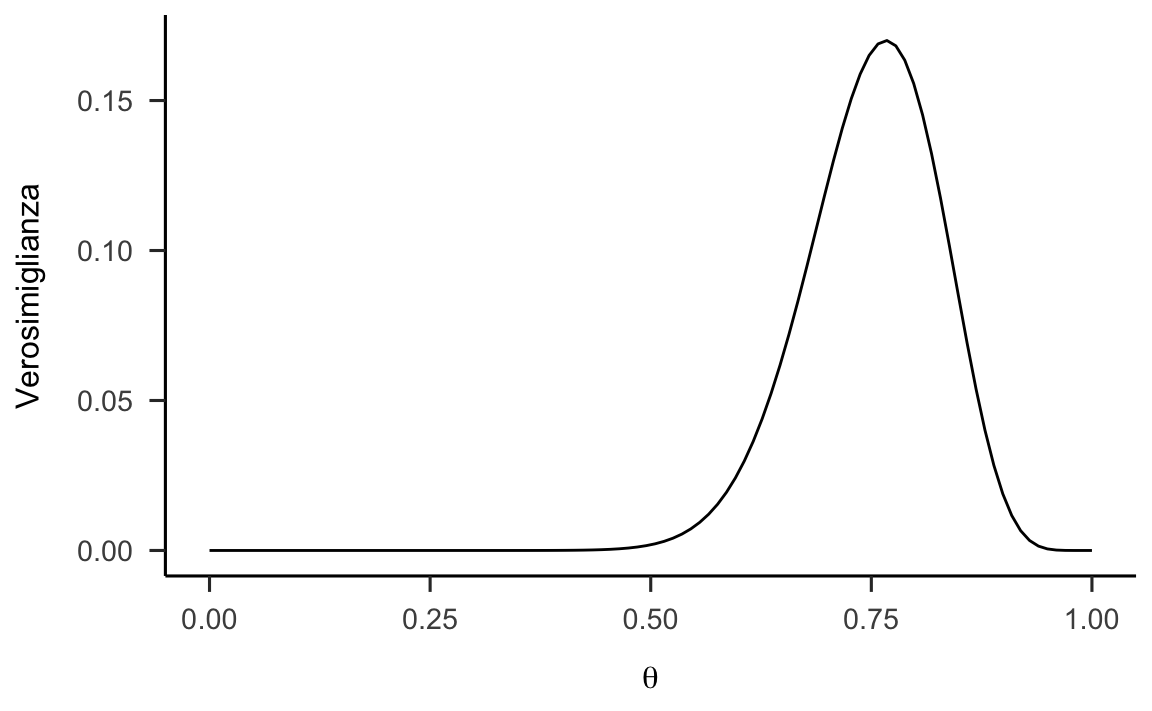
Per trovare la verosimiglianza per i 30 valori di Zetsche et al. (2019) definisco la funzione likelihood() come indicato qui sotto. Tale funzione ritorna l’ordinata della verosimiglianza Binomiale per ciascun valore del vettore param che viene passato alla funzione.

x <- 23
N <- 30
param <- seq(0, 1, length.out = 100)

likelihood <- function(param, x = 23, N = 30) {
  dbinom(x, N, param)
}

data.frame(x = param, y = likelihood(param)) %>% 
  ggplot(aes(x, y)) +
  geom_line() +
  labs(
    x = expression(theta),
    y = "Verosimiglianza"
  )

25.8.2 Distribuzione a priori

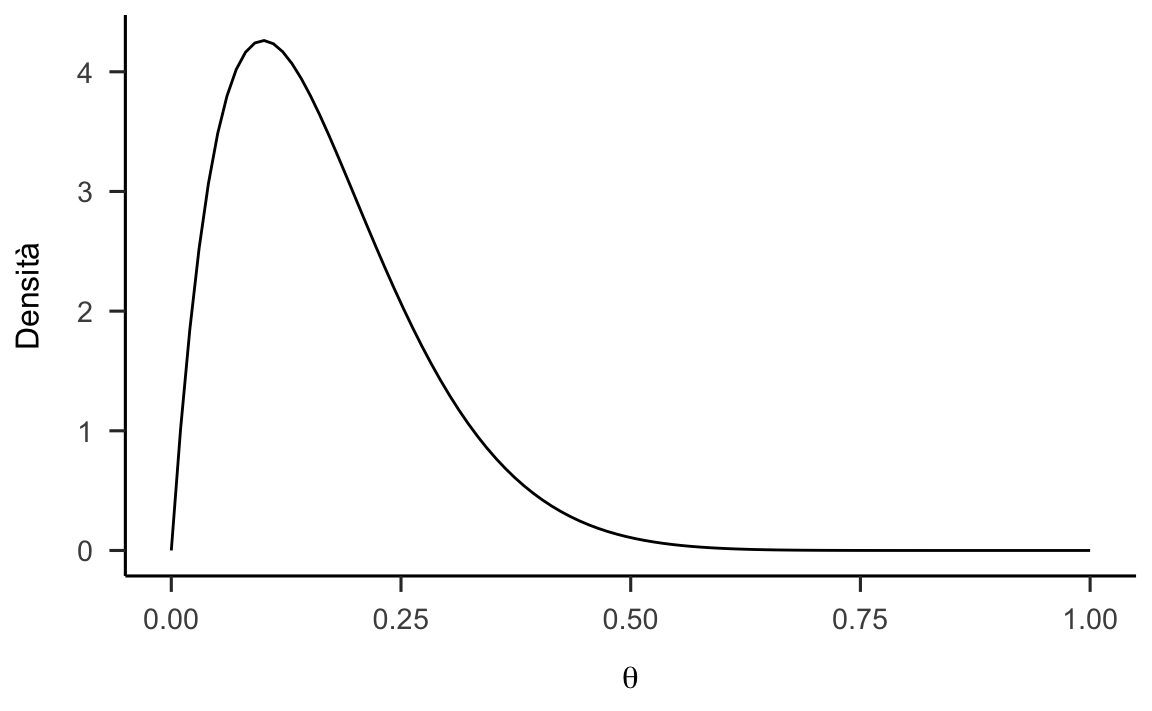
Supponiamo di avere delle credenze forti relativamente ai possibili valori del parametro e utilizziamo la distribuzione a priori informativa discussa nella sezione Un esempio pratico (versione 2).

prior <- function(param, alpha = 2, beta = 10) {
  param_vals <- seq(0, 1, length.out = 100)
  dbeta(param, alpha, beta) # / sum(dbeta(param_vals, alpha, beta))
}

data.frame(x = param, y = prior(param)) %>% 
  ggplot(aes(x, y)) +
  geom_line() +
  labs(
    x = expression(theta),
    y = "Densità"
  )

25.8.3 Distribuzione a posteriori

La funzione a posteriori è data dal prodotto della densità a priori e della verosimiglianza:

posterior <- function(param) {
  likelihood(param) * prior(param)
}

data.frame(x = param, y = posterior(param)) %>% 
  ggplot(aes(x, y)) +
  geom_line() +
  labs(
    x = expression(theta),
    y = "Densità"
  )

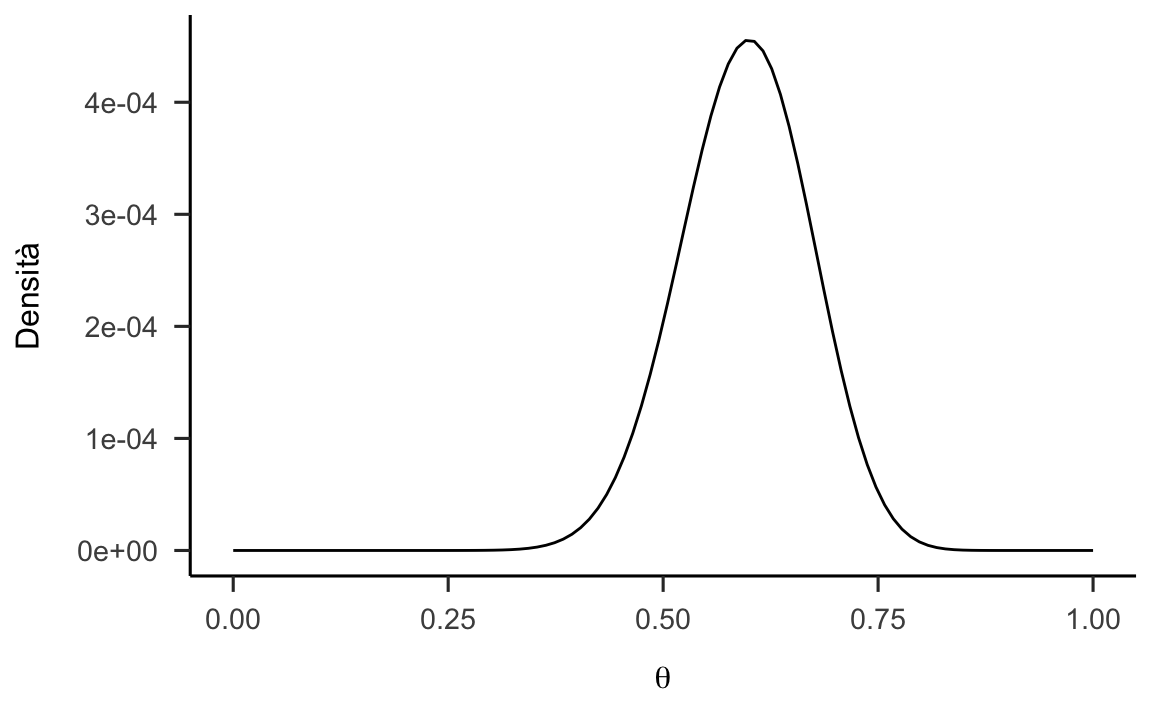
Questo è il risultato che vogliamo ottenere utilizzando l’algoritmo di Metropolis. Dalla figura precedente vediamo che la moda della distribuzione a posteriori è pari a circa 0.6. Questo è il valore più verosimile a posteriori per il parametro \(\theta\), se utilizziamo la distribuzione a priori indicata.

25.8.4 Algoritmo di Metropolis

Implementiamo ora l’algoritmo di Metropolis. Utilizziamo una distribuzione proposta Normale. Il valore proposto da tale distribuzione ausiliaria corrisponde ad un valore selezionato a caso da una distribuzione Normale con media uguale al valore del parametro attualmente considerato nella catena e una deviazione standard adeguata. In questo esempio, la deviazione standard è stata scelta empiricamente in modo tale da ottenere un tasso di accettazione sensato. È stato mostrato che il tasso di accettazione ottimale dovrebbe essere tra il 20% e il 30% (se il tasso di accettazione è troppo grande, l’algoritmo esplora uno spazio troppo ristretto della distribuzione a posteriori). Il tasso di accettazione dipende dalla distribuzione proposta: in generale, tanto più la distribuzione proposta è simile alla distribuzione target, tanto più alto diventa il tasso di accettazione.

proposal_distribution <- function(param) {
  while(1) {
    res = rnorm(1, mean = param, sd = 0.9)
    if (res > 0 & res < 1)
      break
  }
  res
}

In questa implementazione della distribuzione proposta ho inserito dei controlli che fanno in modo che il valore proposto sia incluso nell’intervallo [0, 1] – si possono trovare implementazioni migliori di quella presentata qui. Il unico scopo è quello di spiegare la logica dell’algoritmo di Metropolis, non quello di proporre un’implementazione efficente dell’algoritmo. Tale implementazione “ingenua” funziona, e tanto basta.

L’algoritmo di Metropolis è implementato nella funzione seguente:

run_metropolis_MCMC <- function(startvalue, iterations) {
  chain <- vector(length = iterations + 1)
  chain[1] <- startvalue
  for (i in 1:iterations) {
    proposal <- proposal_distribution(chain[i])
    r <- posterior(proposal) / posterior(chain[i])
    if (runif(1) < r) {
      chain[i + 1] <- proposal
    } else {
      chain[i + 1] <- chain[i]
    }
  }
  chain
}

Generiamo dunqe una catena di valori \(\theta\) con le seguenti istruzioni:

set.seed(123)
startvalue <- runif(1, 0, 1)
niter <- 1e4
chain <- run_metropolis_MCMC(startvalue, niter)

Mediante le istruzioni precedenti otteniamo 4,000 valori della distribuzione a posteriori per il parametro \(\theta\). Di questi valori, 2,000 vengono considerati burn-in e vengono esclusi. Ci restano dunque con 2,000 stime a posteriori di \(\theta\).

Il tasso di accettazione è pari a

burnIn <- niter / 2
acceptance <- 1 - mean(duplicated(chain[-(1:burnIn)]))
acceptance
#> [1] 0.2511498

il che conferma che la deviazione standard che abbiamo scelto per la distribuzione proposta (\(\sigma\) = 0.9) è adeguata.

Una figura che rappresenta la distribuzione a posteriori per \(\theta\), insieme alla rappresentazione dei valori della catena di Markov realizzata dall’algoritmo di Metropolis, può essere prodotta mediante le seguenti istruzioni:

p1 <- data.frame(x = chain[-(1:burnIn)]) %>% 
  ggplot(aes(x)) +
  geom_histogram() +
  labs(
    x = expression(theta),
    y = "Frequenza", 
    title = "Distribuzione a posteriori"
  ) +
  geom_vline(xintercept = mean(chain[-(1:burnIn)]))

p2 <- data.frame(x = 1:length(chain[-(1:burnIn)]), y = chain[-(1:burnIn)]) %>% 
  ggplot(aes(x, y)) +
  geom_line() +
  labs(
    x = "Numero di passi",
    y = expression(theta), 
    title = "Valori della catena"
  ) +
  geom_hline(yintercept = mean(chain[-(1:burnIn)]))

p1 + p2
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.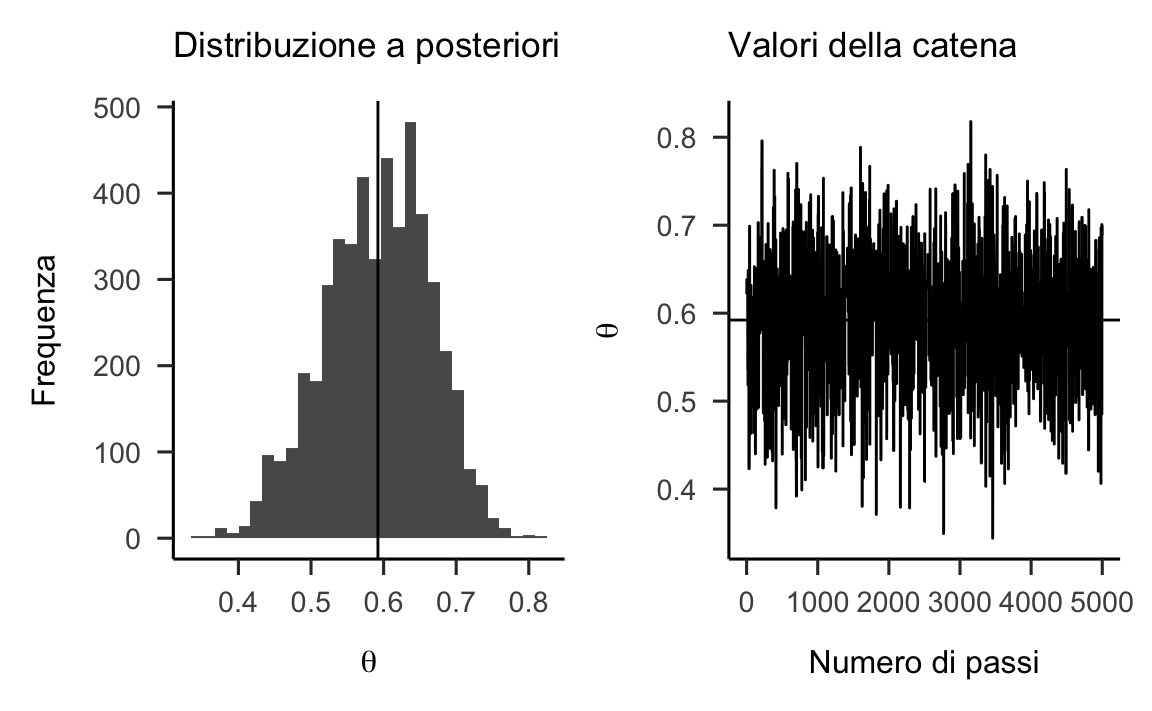

A questo punto è molto facile trovare il massimo a posteriori per il parametro \(\theta\):

mean(chain[-(1:burnIn)])
#> [1] 0.5921799