Capitolo 26 Sintesi a posteriori
La distribuzione a posteriori è un modo per descrivere il nostro grado di incertezza rispetto al parametro incognito (o rispetto ai parametri incogniti) oggetto dell’inferenza. La distribuzione a posteriori contiene tutte le informazioni disponibili sui possibili valori del parametro. Se il parametro esaminato è monodimensionale (o bidimensionale) è possibile fornire un grafico di tutta la distribuzione a posteriori \(p(\theta \mid \mathcal{Y})\). Tuttavia, spesso vogliamo anche giungere ad una sintesi numerica della distribuzione a posteriori, soprattutto se il vettore dei parametri ha più di due dimensioni. A a questo proposito è possibile utilizzare le consuete statistiche descrittive, come media, mediana, moda, varianza, deviazione standard e diversi quantili. In alcuni casi, queste statistiche descrittive sono più facili da presentare e interpretare rispetto alla rappresentazione grafica completa della distribuzione a posteriori.
Di solito, riassumiamo la distribuzione a posteriori nei termini di una stima puntuale e / o di una stima ad intervalli. La stima puntuale fornisce informazioni su quello che può essere considerato il “migliore valore” del parametro, e la stima ad intervalli fornisce un’indicazione di quanto gli altri “valori buoni” del parametro siano sparsi attorno al “miglior valore.” La stima puntuale Bayesiana utilizzata più di frequente è la media della distribuzione a posteriori e la stima dell’intervallo Bayesiano più utilizzata è l’intervallo di credibilità.
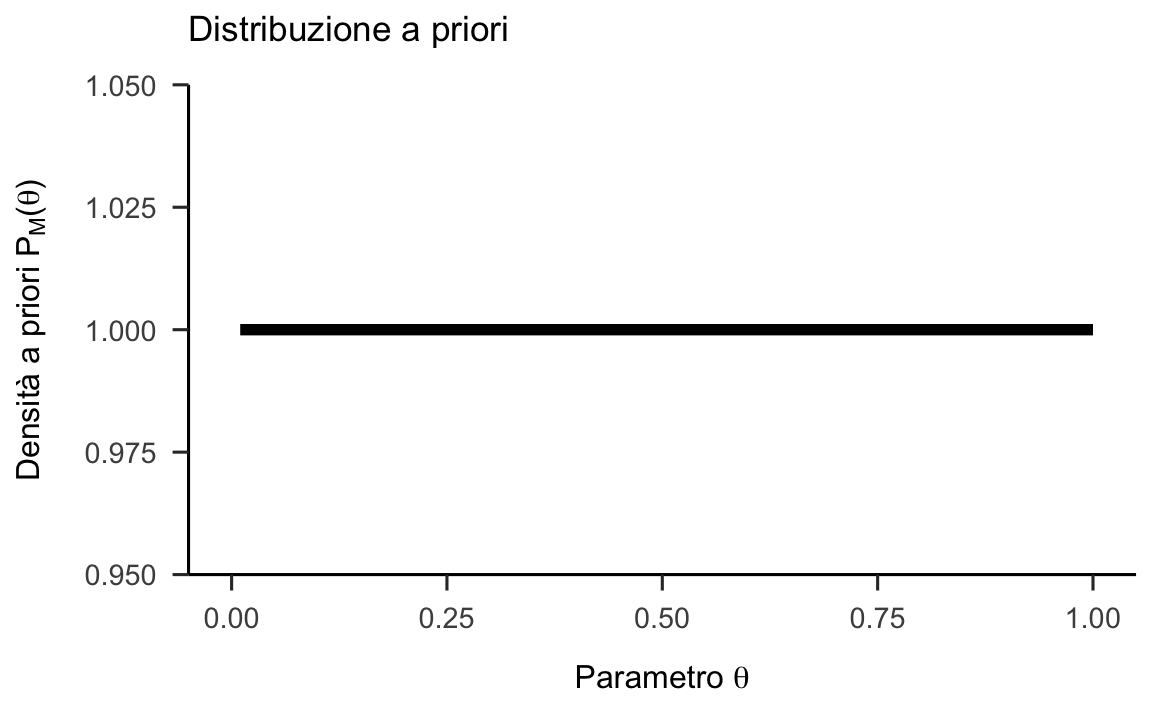
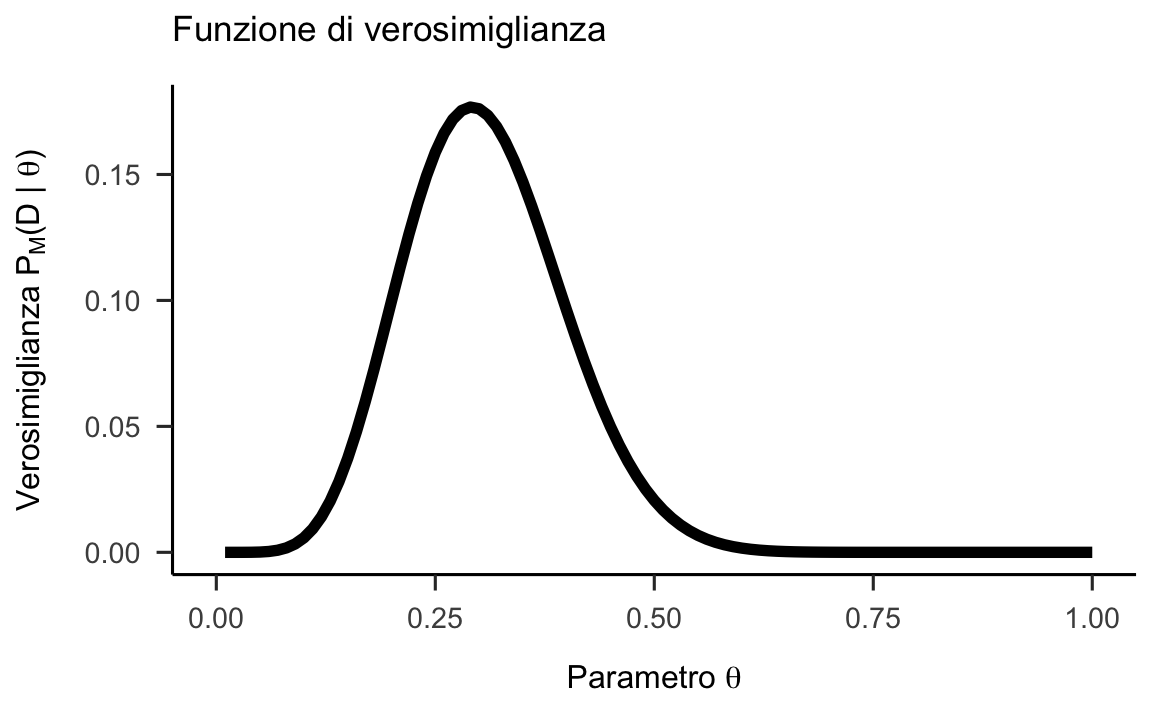
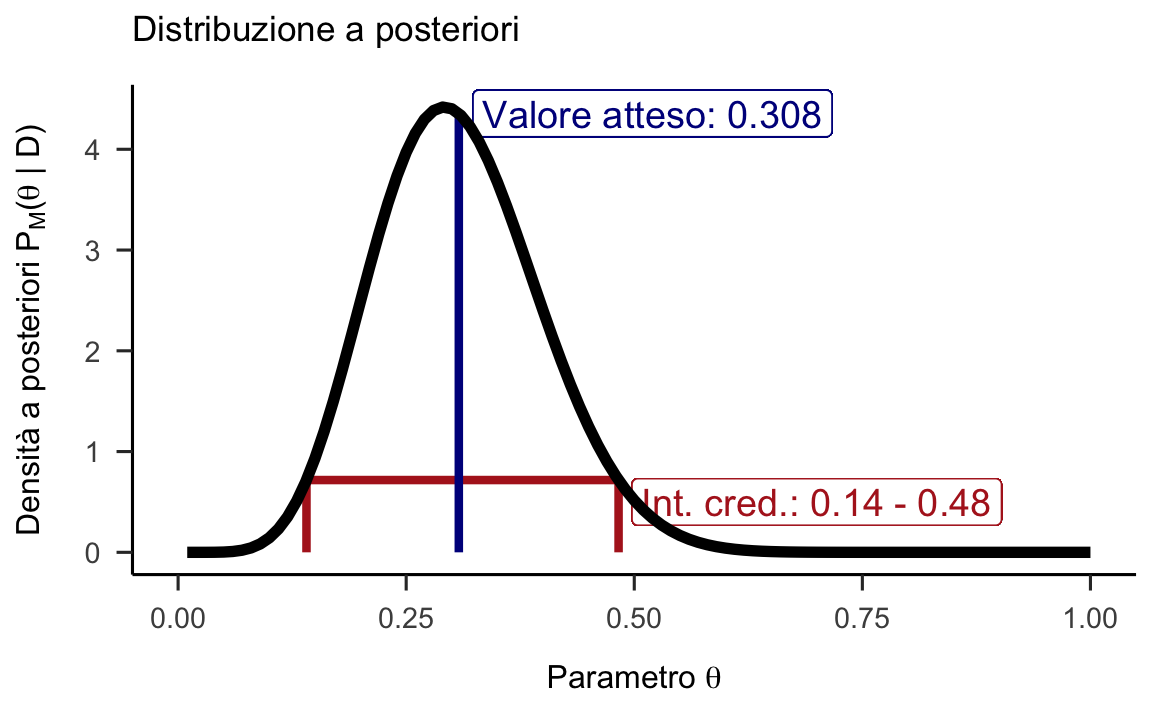
Figura 26.1: Funzione a priori (non informativa), verosimiglianza e distribuzione a posteriori per l’esempio di 7 successi su 24 lanci di una moneta.
26.1 Stima puntuale
Per sintetizzare la distribuzione a posteriori in modo da giungere ad una stima puntuale di \(\theta\) si è soliti scegliere tra moda, mediana o media a seconda del tipo di distribuzione con cui si ha a che fare e della sua forma. Ogni stima puntuale ha una sua interpretazione. La media è il valore atteso a posteriori del parametro. La moda può essere interpretata come il singolo valore più credibile (“più probabile”) del parametro, dati i dati, ovvero il valore per il parametro \(\theta\) che massimizza la distribuzione a posteriori. Per questa ragione la moda viene detta massimo a posteriori, MAP. Il limite della moda quale statistica riassuntiva della distribuzione a posteriori è che, talvolta, tale distribuzione è multimodale e il MAP non è necessariamente il valore “più credibile.” Infine, la mediana è il valore del parametro tale per cui, su entrambi i lati di essa, giace il 50% della massa di probabilità a posteriori.
La misura di variabilità per il parametro è la varianza a posteriori la quale, nel caso di una distribuzione a posteriori ottenuta per via numerica, si calcola con la formula della varianza che conosciamo rispetto alla tendenza centrale data dalla media a posteriori. La radice quadrata della varianza a posteriori è la deviazione standard a posteriori che fornisce l’incertezza a posteriori circa il parametro di interesse il quale, in un’ottica bayesiana, è una variabile aleatoria.
Tutte le procedure bayesiane si basano su sull’uso di metodi MCMC per ottenere le stime a posteriori. Usando un numero finito di campioni, le simulazioni introducono un ulteriore livello di incertezza sull’accuratezza della stima. L’errore standard della stima (in inglese Monte Carlo standard error, MCSE) misura l’accuratezza della simulazione. La deviazione standard a posteriori e l’errore standard della stima sono due concetti molto diversi. La deviazione standard a posteriori descrive l’incertezza circa il parametro ed è una funzione della dimensione del campione; il MCSE descrive invece l’incertezza nella stima del parametro come risultato della simulazione MCMC ed è una funzione del numero di iterazioni nella simulazione.
26.2 Intervallo di credibilità
Molto spesso la stima puntuale è accompagnata da una stima intervallare. Nella statistica bayesiana, se il parametro \(\theta \in \Theta\) è monodimensionale, si dice “intervallo di credibilità” (o intervallo di confidenza bayesiano) un intervallo di valori \(I_{\alpha}\) che contiene la proporzione \(1 - \alpha\) della massa di probabilità della funzione a posteriori: \[\begin{equation} p(\Theta \in I_{\alpha} \mid \mathcal{Y}) = 1 - \alpha. \tag{26.1} \end{equation}\] L’intervallo di credibilità ha lo scopo di esprimere il nostro grado di incertezza riguardo la stima del parametro. Se il parametro \(\theta\) è multidimensionale, si parla invece di “regione di credibilità.”
La condizione (26.1) non determina un unico intervallo di credibilità al \((1 - \alpha) \cdot 100\%\). In realtà esiste un numero infinito di tali intervalli. Ciò significa che dobbiamo definire alcune condizioni aggiuntive per la scelta dell’intervallo di credibilità. Esaminiamo due delle condizioni aggiuntive più comuni.
26.2.1 Intervallo di credibilità a code uguali
Un intervallo di credibilità a code uguali a livello \(\alpha\) è un intervallo \[I_{\alpha} = [q_{\alpha/2}, 1 - q_{\alpha/2}],\] dove \(q_z\) è un quantile \(z\) della distribuzione a posteriori. Per esempio, l’intervallo di credibilità a code uguali al 95% è un intervallo \[I_{0.05} = [q_{0.025}, q_{0.975}]\] che lascia il 2.5% della massa di densità a posteriori in ciascuna coda. Un esempio è fornito nella figura successiva che fornisce una generica rappresentazione di una distribuzione a priori e di una distribuzione a posteriori; l’area evidenziata in grigio rappresenta l’intervallo di credibilità a code uguali al 95%.
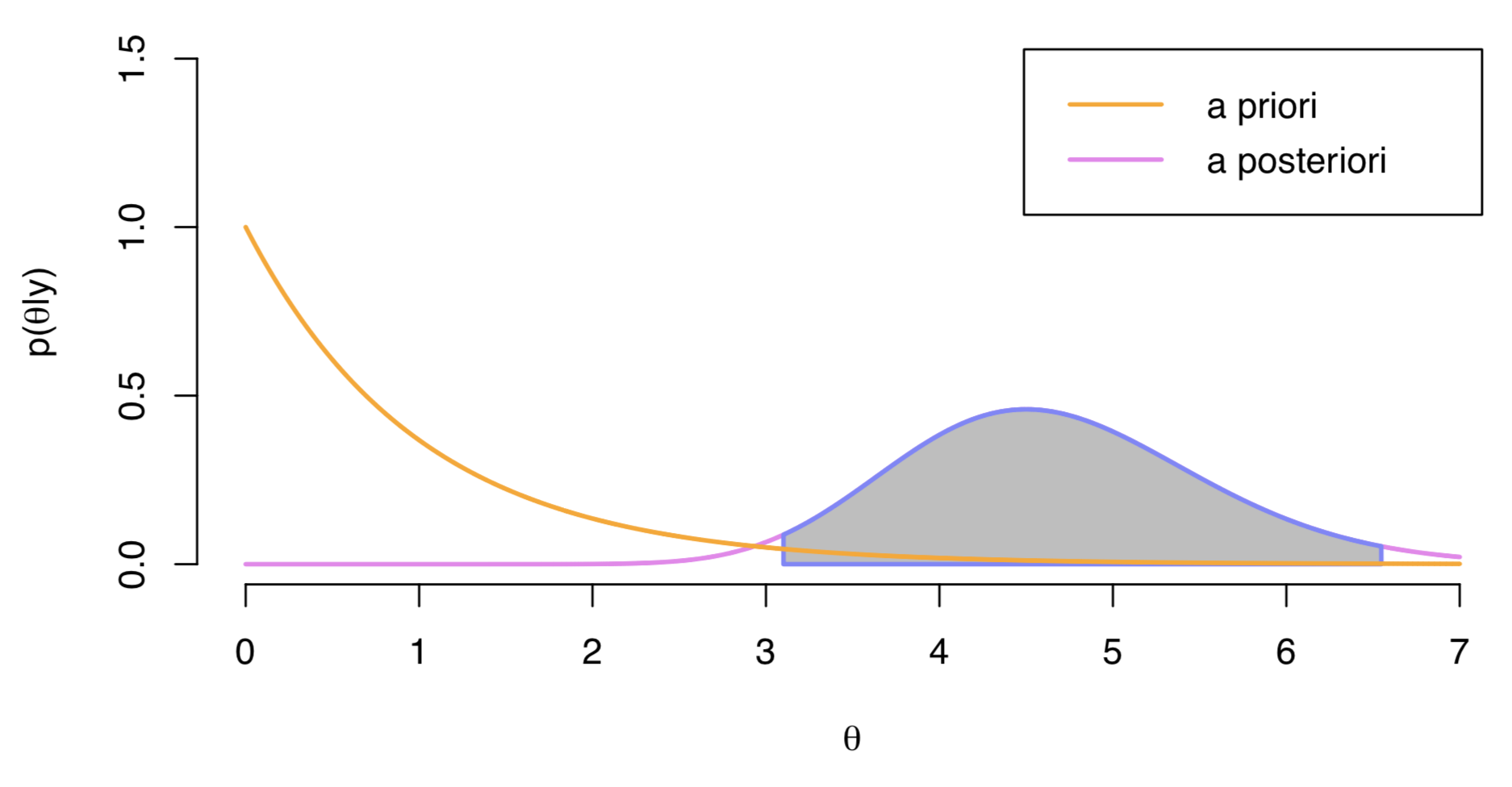
26.2.2 Intervallo di credibilità a densità a posteriori più alta
Nell’intervallo di credibilità a code uguali alcuni valori del parametro che sono inclusi nell’intervallo possono avere una più bassa probabilità a posteriori rispetto a quelli fuori dell’intervallo. L’intrevallo di credibilità a densità a posteriori più alta (in inglese High Posterior Density Interval, HPD) è invece costruito in modo tale da assicurare di avere all’interno dell’intervallo tutti i valori di \(\theta\) che sono a posteriori più plausibili. Graficamente questo intervallo può essere ricavato tracciando una linea orizzontale sulla rappresentazione della distribuzione a posteriori e regolando l’altezza della linea in modo tale che l’area sotto la curva sia pari a \(1 - \alpha\). Questo tipo di intervallo è il meno ampio che si possa determinare e inoltre se la distribuzione a posteriori è simmetrica unimodale l’intervallo di credibilità a densità a posteriori più alta corrisponde all’intervallo di credibilità a code uguali.
26.3 Interpretazione
L’interpretazione dell’intervallo di credibilità è molto intuitiva: l’intervallo di credibilità è un intervallo di valori all’interno del quale cade il valore del parametro incognito con un particolare livello di probabilità soggettiva. Possiamo dire che, dopo aver visto i dati crediamo, con un determinato livello di probabilità soggettiva, che il valore del parametro (ad esempio, la dimensione dell’effetto di un trattamento) abbia un valore compreso all’interno dell’intervallo che è stato calcolato, laddove per probabilità soggettiva intendiamo “il grado di fiducia che lo sperimentatore ripone nel verificarsi di un evento.” Solitamente gli intervalli di credibilità si calcolano con un software.
26.4 Un esempio concreto
Consideriamo nuovamente l’esempio del mappamondo, ovvero il problema di trovare la distribuzione a posteriori della probabilità di “acqua.” Ricordiamo che abbiamo osservato “acqua” 6 volte in 9 lanci. Abbiamo visto come sia possibile, mediante il metodo dell’approssimazione numerica, trovare la distribuzione a posteriori di \(p\) (probabilità di osservare “acqua”) assumendo, ad esempio, una distribuzione uniforme per il parametro di interesse. Le istruzioni R per ottenere tale risultato sono riportate qui sotto.
set.seed(12345)
# Grid
n_points <- 1e4
p_grid <- seq(from = 0, to = 1, length.out = n_points)
# Prior
alpha <- 1
beta <- 1
prior <- dbeta(p_grid, alpha, beta) /
sum(dbeta(p_grid, alpha, beta))
# Likelihood
k <- 6
n <- 9
likelihood <- dbinom(k, size = n, prob = p_grid)
# Unstandardized posterior
unstd_posterior <- likelihood * prior
# Posterior distribution
posterior <- unstd_posterior / sum(unstd_posterior)Chiediamoci ora come sia possibile riassumere la distribuzione a posteriori ottenuta mediante il metodo dell’approssimazione numerica. A tale scopo, estraiamo un campione casuale del parametro \(p\) dalla distribuzione a posteriori, diciamo un campione di ampiezza pari a 10000. Per fare questo, immaginiamo che la distribuzione a posteriori sia un’urna che contiene i valori del parametro \(p\) (ovvero, numeri come 0.107, 0.793, 0.534, 0.908, ecc.). All’interno dell’urna, ciascun valore è presente in proporzione alla sua densità a posteriori: per esempio, valori nell’intorno della moda a posteriori sono molto più comuni di quelli che si trovano nelle code.
Se i valori nell’urna sono ben mescolati, il campione che verrà estratto dall’urna avrà le stesse proporzioni della densità a posteriori. Pertanto, il nostro campione conterrà valori \(p\) che si addenseranno sulla linea dei numeri reali in maniera proporzionale alla densità della distribuzione a posteriori. Questo risultato può essere ottenuto in R con una riga di codice:
samples <- sample(p_grid, prob = posterior, size = 1e4, replace = TRUE)
head(samples)
#> [1] 0.5767577 0.8921892 0.4632463 0.7049705 0.8475848 0.6337634La funzione sample() effettua size = 10000 estrazioni casuali (con rimessa) dall’“urna” p_grid, associando a ciascuno dei valori p_grid una probabilità
di essere estratto che è proporzionale alla densità della distribuzione a
posteriori; questo viene specificato dall’argomento prob = posterior.
Il campione così ottenuto dei 10000 valori a posteriori del parametro \(p\) è rappresentato nella figura seguente la quale illustra la densità della distribuzione a posteriori di \(p\) = probabilità di osservare “acqua” nell’esperimento casuale del lancio del mappamondo.
rethinking::dens(samples) 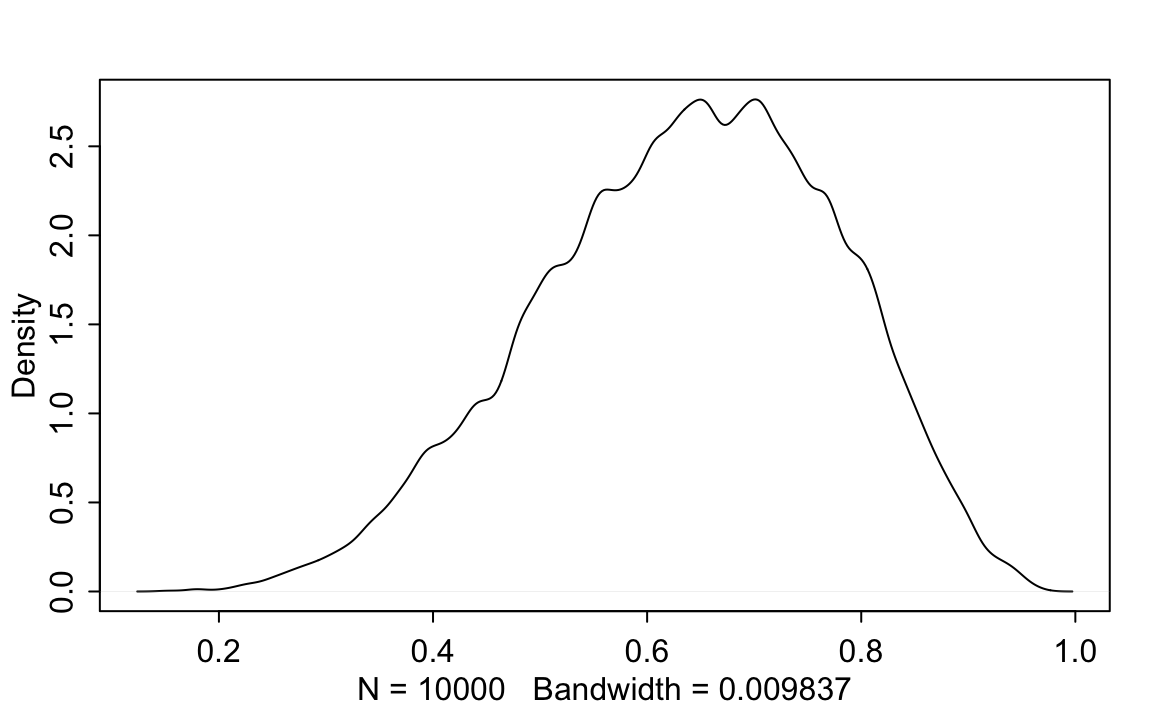
26.4.1 Indici di sintesi della distribuzione a posteriori
Una volta trovata la distribuzione a posteriori prodotta dall’aggiornamento Bayesiano, il lavoro del modello statistico è terminato. Ma il lavoro del ricercatore è appena iniziato. È infatti necessario sintetizzare e interpretare la distribuzione a posteriori. Esattamente quali indici di sintesi usare dipende dallo scopo della ricerca. Ma le domande più comuni includono:
- Qual è la probabilità a posteriori che può essere associata a valori del parametro minori di un certo valore?
- Qual è la probabilità a posteriori che può essere associata ad un intervallo di valori del parametro?
- Quale valore del parametro corrisponde al 5% inferiore della distribuzione a posteriori?
- Quale intervallo di valori del parametro contiene il 90% della distribuzione a posteriori?
- A quale valore del parametro è associata la densità a posteriori maggiore?
26.4.2 Probabilità della distribuzione a posteriori
Supponiamo che si voglia conoscere la probabilità a posteriori che la
proporzione di acqua sia inferiore a 0.5. Supponiamo inoltre di volere
rispondere a questa domanda avendo a disposizione i dati forniti dal
metodo dell’approssimazione numerica, ovvero il vettore samples che costituisce un campione casuale della distribuzione a posteriori. Per rispondere alla domanda che ci siamo posti è sufficiente contare quanti elementi del vettore samples soddisfano la condizione logica che abbiamo enunciato:
sum(samples < 0.5) / n_points
#> [1] 0.1714ovvero 0.17. Questo significa che l’area sottesa alla distribuzione a posteriori del parametro \(p\) nell’intervallo \([-\infty, 0.5]\) è circa uguale a 0.17. Usando lo stesso approccio è possibile trovare, ad esempio, l’area sottesa alla distribuzione a posteriori nell’intervallo compreso tra 0.5 e 0.75:
sum(samples > 0.5 & samples < 0.75) / n_points
#> [1] 0.6038ovvero 0.6. Quindi, possiamo dire che la probabilità a posteriori che il parametro assuma un valore compreso tra 0.5 e 0.75 è circa a 0.6.
R utilizza la funzione sum() per contare quanti elementi del vettore samples soddisfano una data condizione logica. Infatti, R converte internamente un’espressione logica, come samples < 0.5 in un vettore di risultati TRUE e FALSE, uno per ciascun elemento del vettore samples, indicando se tale elemento soddisfa o meno la condizione logica enunciata. Quando il vettore di TRUE e FALSE viene sommato, R valuta ogni TRUE come 1 e ogni FALSE come 0. Facendo così, R conta quanti valori TRUE sono presenti nel vettore, ovvero restituisce il numero di elementi nel vettore samples che soddisfano la condizione logica indicata.
26.4.3 Quantili della distribuzione a posteriori
È più comune sintetizzare la distribuzione a posteriori mediante un intervallo di valori, detto “intervallo di credibilità.” Supponiamo di volere trovare il quantile di ordine 0.8 per la distribuzione a posteriori. Questo risultato, utilizzando il metodo dell’approssimazione numerica, può essere trovato nel modo seguente.
quantile(samples, 0.8)
#> 80%
#> 0.7616962ovvero, 0.76. In maniera simile, l’intervallo che lascia il 2.5% dell’area della distribuzione a posteriori in ciascuna coda è
La funzione rethinking::PI() (percentile intervals) restituisce lo stesso risultato:
rethinking::PI(samples, prob = 0.95)
#> 3% 98%
#> 0.3524327 0.8754925Se la distribuzione a posteriori è asimmetrica, non è sempre una buona
idea utilizzare l’approccio descritto sopra per calcolare gli intervalli
di credibilità. Un approccio alternativo è quello di calcolare
l’intervallo più piccolo che contiene la massa di probabilità specificata –
questo non corrisponde necessariamente con l’intervallo che lascia la
stessa massa di probabilità in ciascuna coda. Tale intervallo può essere
trovato con la funzione rethinking::HPDI():
rethinking::HPDI(samples, prob = 0.95)
#> |0.95 0.95|
#> 0.3658366 0.8851885Nel caso presente, il risultato di HPDI() è molto simile a quello trovato in precedenza, ma questo non è sempre vero.
26.4.4 Stime puntuali della distribuzione a posteriori
Una volta trovata l’intera distribuzione a posteriori, quale valore di sintesi è necessario riportare? Questa sembra una domanda innocente, ma in realtà è una domanda a cui è difficile rispondere. La stima Bayesiana dei parametri è fornita dall’intera distribuzione a posteriori, che non è un singolo numero, ma una funzione che mappa ciascun valore del parametro di interesse ad un valore di plausibilità. Quindi non è necessario scegliere una stima puntuale. In linea di principio, ciò non è quasi mai necessario ed è spesso dannoso in quanto comporta una perdita di informazioni.
Tuttavia ci sono dei casi nei quali tale scelta è necessaria. Diverse risposte sono allora possibili. Una stima del massimo della probabilità a posteriori, o brevemente massimo a posteriori, MAP (da maximum a posteriori probability), è una moda della distribuzione a posteriori. Nel caso del metodo dell’approssimazione numerica, una stima del MAP può essere ottenuta nel modo seguente:
p_grid[which.max(posterior)]
#> [1] 0.6666667e, nel caso presente, corrisponde a 0.67. Lo stesso risultato si ottiene utilizzando i campioni della distribuzione a posteriori:
rethinking::chainmode(samples, adj = 0.01)
#> [1] 0.6107366In alternativa, si possono calcolare la media o la mediana
le quali, nel caso presente, sono entrambe uguali a 0.64.
26.5 Metodo dell’approssimazione quadratica
Usiamo ora il metodo dell’approssimazione quadratica per trovare la distribuzione a posteriori. Usiamo, come dati, quelli dell’esempio del lancio del mappamondo di McElreath. Abbiamo dunque 6 successi in 9 prove Bernoulliane. Carichiamo rethinking:
library("rethinking")Definiamo il modello Bayesiano, ovvero specifichiamo sia la verosimiglianza che la distribuzione a priori. Nella sintassi di rethinking, questo si ottiene passando l’argomento alist() alla funzione quap():
globe_qa <- rethinking::quap(
alist(
W ~ dbinom(W + L, p), # binomial likelihood
p ~ dbeta(1, 1) # uniform prior
),
data = list(W = 6, L = 3)
)Usando la notazione che abbiamo descritto in precedenza, diciamo che la variabile W si distribuisce come una Binomiale avente W + L prove e probabilità di successo p. Questa è la verosimiglianza.
Specifichiamo anche una distribuzione a priori uniforme. Ricordiamo che una Beta di parametri 1, 1 corrisponde ad una distribuzione uniforme:
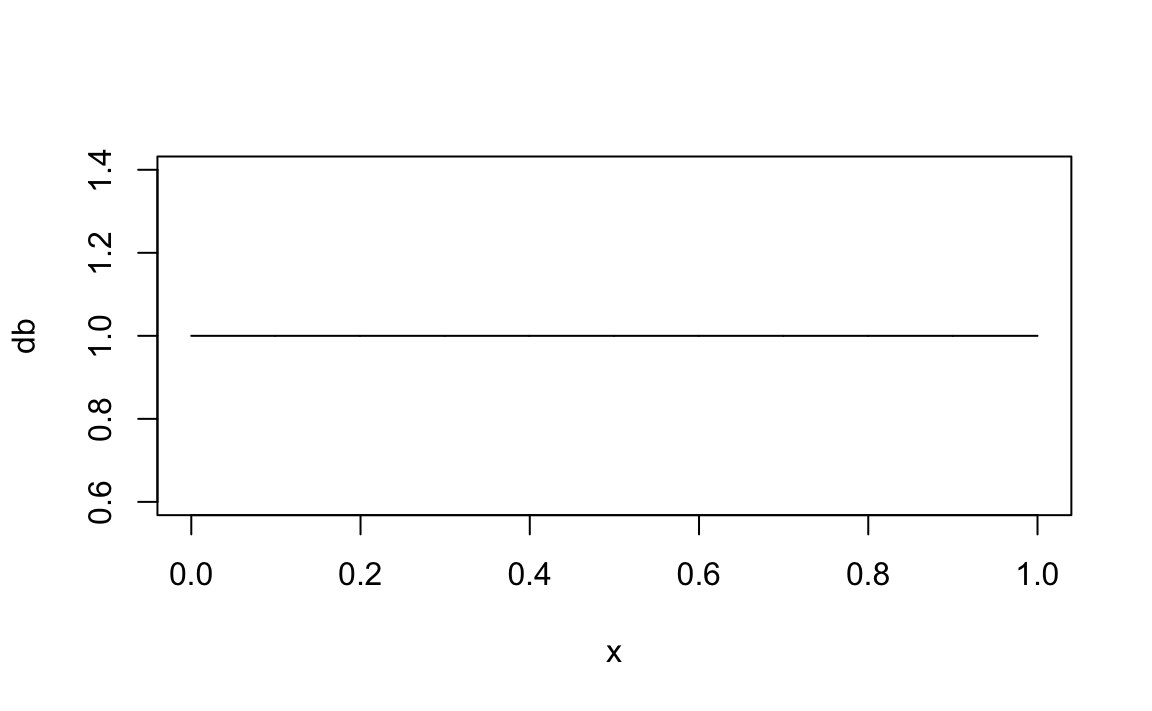
Infine, passiamo a i dati quap(). Avendo definito in questo modo il modello Bayesiano, la funzione quap() calcola la distribuzione a posteriori per il parametro p usando il metodo dell’approssimazione quadratica.
Possiamo esaminare i risultati con rethinking::precis():
rethinking::precis(globe_qa, prob = 0.95)
#> mean sd 2.5% 97.5%
#> p 0.6666666 0.1571338 0.35869 0.9746432Avendo specificato prob = 0.95, otteniamo l’intervallo di credibilità al 95%: [0.36, 0.97]. Si noti che l’intervallo di credibilità al 95% è enorme! Questo dipende dal fatto che abbiamo solo 9 osservazioni. La funzione precis() fornisce anche il valore della media a posteriori, ovvero 0.67.
Consideriamo un’altra distribuzione a priori.
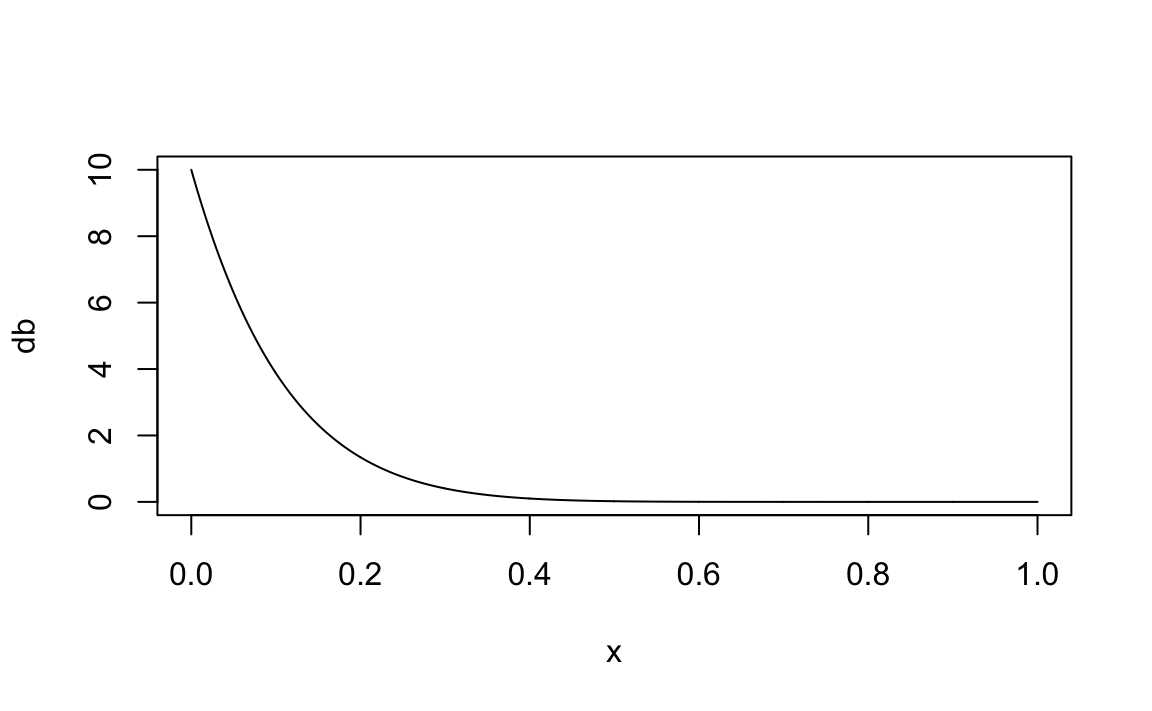
globe2_qa <- rethinking::quap(
alist(
W ~ dbinom(W + L, p), # binomial likelihood
p ~ dbeta(1, 10)
),
data = list(W = 6, L = 3)
)
rethinking::precis(globe2_qa, prob = 0.95)
#> mean sd 2.5% 97.5%
#> p 0.3333336 0.1111104 0.1155612 0.551106Con i dati presenti, una distribuzione a priori informativa ha un enorme effetto sulla distribuzione a posteriori.
Se invece avessimo a disposizione un campione più grande, questo non si verificherebbe:
globe3_qa <- rethinking::quap(
alist(
W ~ dbinom(W + L, p),
p ~ dbeta(1, 10)
),
data = list(W = 600, L = 300)
)
rethinking::precis(globe3_qa, prob = 0.95)
#> mean sd 2.5% 97.5%
#> p 0.660066 0.01571109 0.6292729 0.6908592Si noti che la media a posteriori di 0.66 è quasi identica a quella che avevamo ottenuto con una distribuzione a priori uniforme (ovvero, 0.67). Ancora più importante è il fatto che, con un campione così grande, l’intervallo di credibilità al 95% diventa molto piccolo: [0.63, 0.69]. Questo vuol dire che, avendo a disposizione un campione sufficientemente grande, siamo piuttosto certi di quali sono i valori plausibili del parametro sconosciuto. E la risposta che troviamo non dipende dalle nostre credenze a priori, anche nel caso di credenze a priori molto forti.
Conclusioni
Questo capitolo introduce le procedure di base per la manipolazione
della distribuzione a posteriori. Lo strumento fondamentale che è stato
utilizzato è quello fornito da campioni di valori dei parametri tratti
dalla distribuzione a posteriori. Lavorare con campioni di parametri
tratti dalla distribuzione a posteriori trasforma un problema di calcolo
integrale in un problema di riepilogo dei dati. Abbiamo visto quali sono
le procedure che, mediante R, consentono di utilizzare i campioni a
posteriori per produrre gli indici di sintesi della distribuzione a
posteriori più usati: gli intervalli di credibilità e le stime puntuali.