Capitolo 24 Modellistica Bayesiana

24.1 Modelli statistici

I dati non interpretati non sono informativi. Non possiamo generalizzare, trarre inferenze o tentare di fare previsioni a meno di non fare ipotesi (per quanto minime) sui dati a disposizione: cosa rappresentano, come sono stati generati, quali aspetti sono associati a quali altri aspetti, ecc. I modelli statistici rappresentano un modo per rendere esplicite le nostre assunzioni sui dati.

Definizione 24.1 Un modello statistico è una rappresentazione formale delle ipotesi relative ai dati e al processo che li ha generati.

Nel suo senso naturale più comune, un “modello” è un modello di qualcosa. Intende rappresentare qualcosa d’altro in una forma semplificata, astratta e più maneggevole. Le caratteristiche di un modello dipendono dallo scopo per il quale il modello verrà usato. In generale, un buon modello è in grado di riprodurre alcuni aspetti della realtà mentre ignora, nel contempo, tutte quelle caratteristiche irrilevanti che potrebbero altrimenti offuscare la nostra comprensione di ciò che il modello vuole rappresentare.

Lo scopo più comune di un modello statistico è quello di imparare qualcosa sulla realtà traendo inferenze dai dati - possibilmente con l’ulteriore obiettivo di consentirci di prendere una decisione razionale - o di fare previsioni su eventi sconosciuti (futuri, presenti o passati).

Un modello statistico M è un modello di un processo aleatorio R che potrebbe avere generato i dati che abbiamo osservato. Il modello M descrive in un modo formale le nostre ipotesi sul processo aleatorio R.

Spesso vogliamo spiegare una parte dei nostri dati, ovvero le variabili dipendenti $D_{DV}$, nei termini di altre osservazioni, ovvero le variabili indipendenti $D_{IV}$. Ma è anche possibile che non ci siano delle variabili indipendenti ma solo una o più variabili dipendenti $D_{DV}$.

Un modello M per i dati D necessariamente include una fuzione di verosimiglianza per $D_{DV}$. La funzione di verosimiglianza descrive la plausibilità delle osservazioni $D_{DV}$ alla luce delle corrispondenti osservazioni $D_{IV}$. Molto spesso, la funzione di verosimiglianza ha anche dei parametri liberi, rappresentati da un vettore $\theta$.

La funzione di verosimiglianza del modello M per i dati D con parametri $\theta$ si può scrivere come:

\[ P_M(D_{DV} \mid D_{IV}, \theta). \] Oltre alla verosimiglianza, i modelli Bayesiani includono una componente aggiuntiva, ovvero una distribuzione a priori sui valori dei parametri, comunemente scritta come:

\[ P_M(\theta). \] La distribuzione a priori sui parametri rappresenta qualsiasi ipotesi a priori motivata e giustificabile sui valori che, alla luce delle nostre conoscenze presenti, possiamo attribuire ai parametri.

Esempio 24.1 Supponiamo che il nostro campione di dati sia costituito dagli esiti di una sequenza di lanci di una moneta avente probabilità di successo (testa) $\theta \in [0, 1]$. Abbiamo osservato k successi in N prove. Dunque, conosciamo N e k ma non conosciamo $\theta$. Il parametro $\theta$ è l’unico parametro di questo modello statistico. La variabile dipendente è k. In questo caso, possiamo pensare a N come alla variabile indipendente.

La funzione di verosimiglianza per questo modello statistico è la distribuzione Binomiale:

\[ P_M(k \mid \theta, N) = \text{Binomial}(k, N, \theta) = {N \choose k} \theta^k (1 - \theta)^{N-k}. \]

Per ragioni che diventeranno chiare in seguito, è possibile usare una distribuzione Beta per la distribuzione a priori di $\theta$. Ad esempio, potremmo definire i parametri della distribuzione Beta in modo tale che la distribuzione risultante sia piatta, così da generare una “distribuzione a priori non informativa”:

\[ P_M(\theta) = \text{Beta}(\theta, 1, 1). \]

24.2 Notazione

Per rappresentare in un modo conciso i modelli statistici viene usata una notazione particolare, la quale è molto intuitiva se pensiamo al processo del campionamento. Ad esempio, invece di scrivere

\[ P_M(\theta) = \text{Beta}(\theta, 1, 1), \]

scriviamo:

\[ \theta \sim \text{Beta}(1, 1). \] Il simbolo “$\sim$” viene spesso letto “è distribuito come.” Possiamo anche pensare che significhi che $\theta$ costituisce un campione estratto dalla distribuzione Beta(1, 1). Allo stesso modo, per l’esempio precedente la verosimiglianza può essere scritta nel modo seguente:

\[ k \sim \text{Binomial}(k, N, \theta). \]

24.3 Parametri e distribuzioni a priori

Un modello Bayesiano è costituito da una funzione di verosimiglianza e da una distribuzione a priori dei parametri di interesse:

\[ \begin{aligned} & \text{Verosimiglianza: } & P_M(D \mid \theta) \\ & \text{Distribuzione a priori: } & P_M(\theta) \end{aligned} \]

In questa sezione, esamineremo (nuovamente) il significato di “parametro,” esamineremo il significato di “distribuzione a priori” $P_M(\theta)$ e ci porremo l’obiettivo di usare un modello statistico per fare previsioni a partire dai dati.

L’esempio che considereremo farà uso del modello Binomiale. Come esempio concreto di dati, consideriamo il caso di $N = 24$ lanci di una moneta e di $k = 7$ successi (esito testa).

24.3.1 Cos’è un parametro del modello?

Un parametro del modello è un valore da cui dipende la verosimiglianza dei dati. Ad esempio, il singolo parametro $\theta$ nel modello Binomiale determina la forma della funzione di verosimiglianza Binomiale. Ricordiamo che la funzione di verosimiglianza per il modello Binomiale è:

\[ P_M(k \mid \theta, N) = \text{Binomial}(k, N, \theta) = \binom{N}{k}\theta^k(1-\theta)^{N-k}. \] Per comprendere il ruolo del parametro $\theta$, possiamo generare un grafico della verosimiglianza dei dati (qui: $k = 7$ e $N = 24$) come funzione di $\theta$. La figura mostra, per ogni possibile valore di $\theta \in [0; 1]$ (sull’asse orizzontale), la verosimiglianza dei dati (sull’asse verticale). Dalla figura notiamo che la verosimiglianza dei dati dipende dal valore del parametro $\theta$: i dati risultano più o meno verosimili a seconda dei valori di $\theta$.

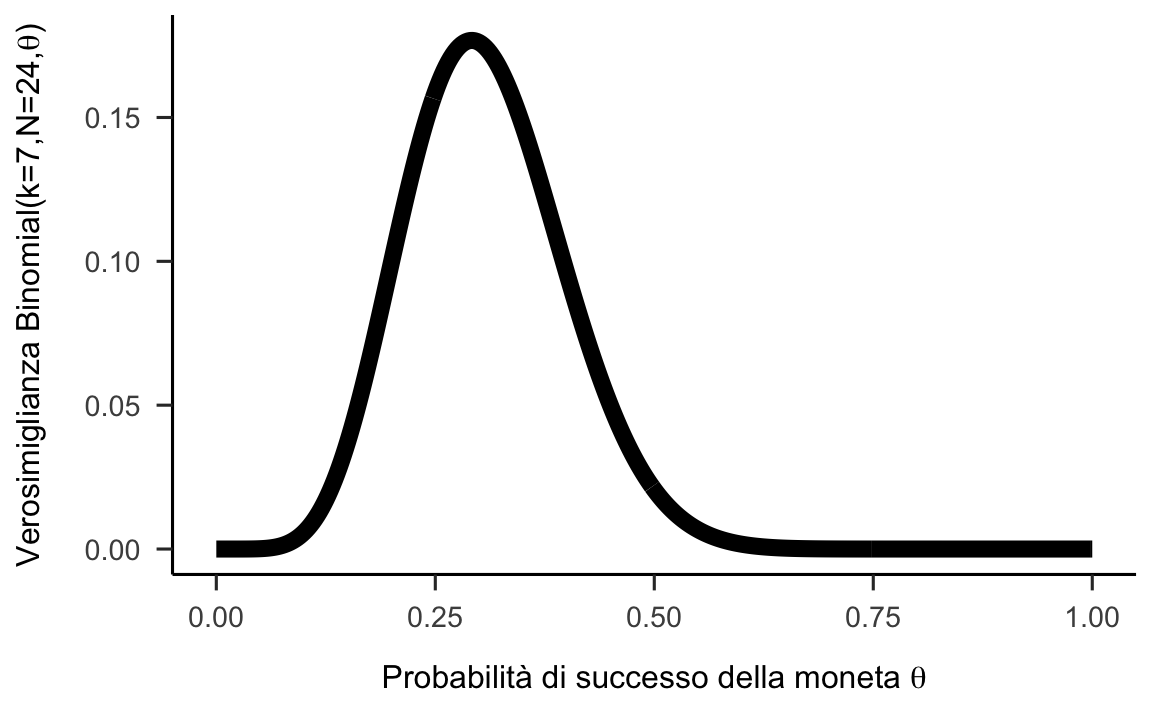
Figura 24.1: Funzione di verosimiglianza per il modello Binomiale con $k=7$ e $N=24$.

24.3.2 Distribuzione a priori sui parametri

Quando adottiamo un approccio Bayesiano all’analisi dei dati, la distribuzione a priori sui valori dei parametri $P_M (\theta)$ è parte integrante del modello statistico. Ciò implica che due modelli (Bayesiani) possono condividere la stessa funzione di verosimiglianza, ma tuttavia devono essere considerati come modelli diversi, se specificano diverse distribuzioni a priori. Ciò significa che, quando diciamo “Modello binomiale,” intendiamo in realtà un’intera classe di modelli, ovvero tutti i possibili modelli che hanno la stessa verosimiglianza ma diverse distribuzioni a priori su $\theta$.

Nell’analisi dei dati Bayesiana, la distribuzione a priori $P_M(\theta)$ codifica le credenze del ricercatore a proposito dei valori dei parametri, prima di avere osservato i dati. Idealmente, le credenze a priori che supportano la specificazione di una distribuzione a priori dovrebbero essere supportate da una qualche motivazione, come ad esempio i risultati di ricerche precedenti, o altre motivazioni giustificabili. Tuttavia, le credenze soggettive sono solo uno dei possibili modi per giustificare le distribuzioni a priori sui parametri.

Possiamo distinguere tre tipi principali di motivazioni per le distribuzioni a priori $P_M (\theta)$.

Le distribuzioni a priori soggettive catturano le credenze del ricercatore nel senso sopra descritto.
Le distribuzioni a priori con finalità pratiche sono distribuzioni a priori che vengono utilizzate pragmaticamente a causa di una loro utilità specifica, ad esempio, perché semplificano un calcolo matematico o una simulazione al computer, o perché aiutano nel ragionamento statistico, come ad esempio quando vengono formulate gli skeptical priors che hanno l’obiettivo di lavorare in senso contrario ad una particolare conclusione.
Le distribuzioni a priori oggettive sono distribuzioni a priori che, come alcuni sostengono, dovrebbero essere adottate per una data funzione di verosimiglianza per evitare conseguenze concettualmente paradossali. Non tratteremo le distribuzioni a priori oggettive in questo corso introduttivo e le menzioniamo qui solo per completezza.

Oltre alla motivazione che giustifica una distribuzione a priori, possiamo distinguere tra distribuzioni a priori in base a quanto fortemente impegnano il ricercatore a ritenere come plausibile un particolare intervallo di valori dei parametri. Il caso più estremo è quello che rivela una totale assenza di conoscenze a priori, il che conduce alle distribuzioni a priori non informative, ovvero quelle che assegnano lo stesso livello di credibilità a tutti i valori dei parametri. Le distribuzioni a priori informative, d’altra parte, possono essere debolmente informative o fortemente informative, a seconda della forza della credenza che esprimono. Il caso più estremo di credenza a priori è quello che riassume il punto di vista del ricercatore nei termini di un unico valore del parametro, il che assegna tutta la probabilità (massa o densità) su di un singolo valore di un parametro. Poiché questa non è più una distribuzione di probabilità, sebbene ne soddisfi la definizione, in questo caso si parla di una distribuzione a priori degenerata.

La figura seguente mostra esempi di distribuzioni a priori non informative, debolmente o fortemente informative, così come una distribuzione a priori espressa nei termini di un valore puntuale per il modello Binomiale. Le distribuzione a priori illustrate di seguito sono le seguenti:

non informativa : $\theta_c \sim \text{Beta}(1,1)$;
debolmente informativa : $\theta_c \sim \text{Beta}(5,2)$;
fortemente informativa : $\theta_c \sim \text{Beta}(50,20)$;
valore puntuale : $\theta_c \sim \text{Beta}(\alpha, \beta)$ con $\alpha, \beta \rightarrow \infty$ e $\frac{\alpha}{\beta} = \frac{5}{2}$.

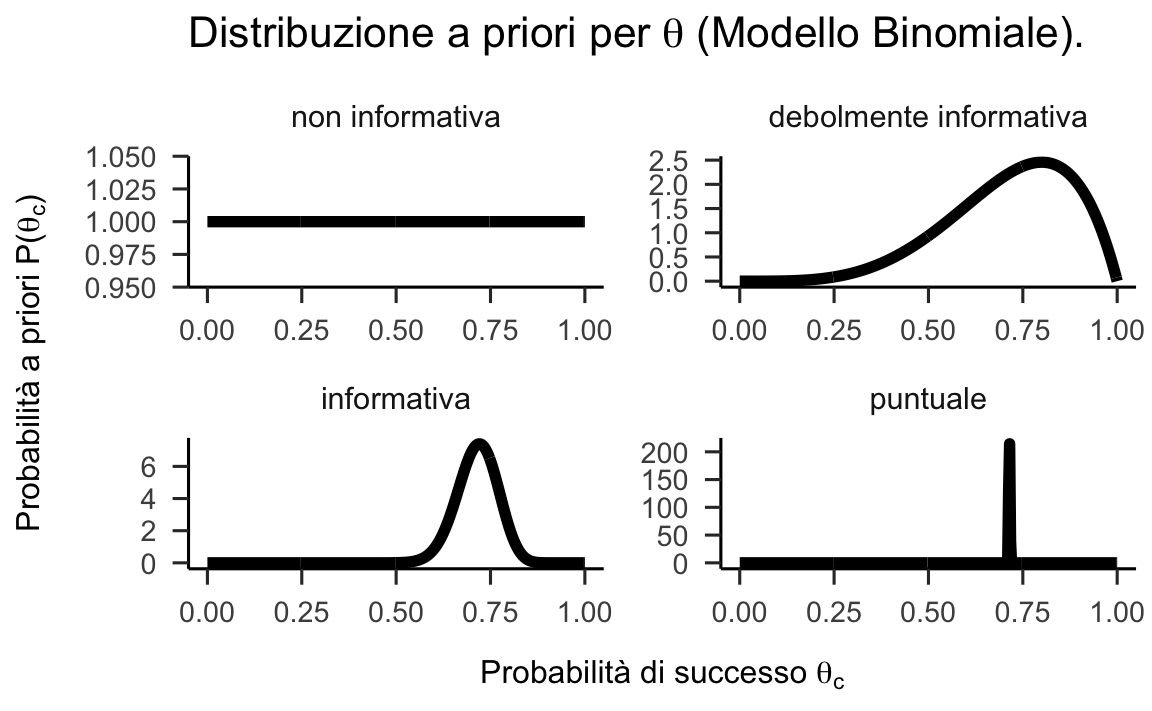
$Esempi di distribuzioni a priori per il parametro $\theta_c$ nel Modello Binomiale.$

Figura 24.2: Esempi di distribuzioni a priori per il parametro $\theta_c$ nel Modello Binomiale.

La selezione delle distribuzioni a priori è stata spesso vista come una delle scelte più importanti che un ricercatore fa quando implementa un modello Bayesiano in quanto può avere un impatto sostanziale sui risultati finali.

La soggettività delle distribuzioni a priori è evidenziata dai critici come un potenziale svantaggio dei metodi Bayesiani. A questa critica, Schoot et al. (2021) rispondono dicendo che, al di là della scelta delle distribuzioni a priori, ci sono molti elementi del processo di inferenza statistica che sono soggettivi, ovvero la scelta del modello statistico e le ipotesi sulla distribuzione degli errori. In secondo luogo, Schoot et al. (2021) notano come le distribuzioni a priori svolgono due ruoli statistici importanti: quello della “regolarizzazione della stima,” ovvero, quel processo che porta ad indebolire l’influenza indebita di osservazioni estreme, e quello del miglioramento dell’efficienza della stima, ovvero, la facilitazione dei processi di calcolo numerico di stima della distribuzione a posteriori.

24.4 Procedura Bayesiana di stima dei parametri

24.4.1 Finalità

Sulla base di un modello statistico $M$ di parametri $\theta$, l’analisi statistica Bayesiana si pone il problema di trovare i valori più plausibili di $\theta$ alla luce dei dati $D$. Il teorema di Bayes viene usato per aggiornare le credenze a priori su $\theta$ (ovvero, la distribuzione a priori) in modo tale da produrre le nuove credenze a posteriori $P_M(\theta \mid D)$ che combinano le informazioni fornite dai dati $D$ con le credenze precedenti. La distribuzione a posteriori riflette dunque l’aggiornamento delle conoscenze del ricercatore alla luce dei dati.

24.4.2 Metodi

Ci sono due diversi metodi per calcolare la distribuzione a posteriori $P_M(\theta \mid D)$:

una precisa derivazione matematica formulata nei termini della distribuzione a priori coniugata alla distribuzione a posteriori; tale procedura però ha un’applicabilità molto limitata;
un metodo approssimato, molto facile da utilizzare in pratica, che dipende da metodi Monte Carlo basati su Catena di Markov (MCMC).

In questo capitolo introdurremo la terminologia e le idee di base che stanno alla base della stima delle funzione a posteriori. In seguito ci porremo il problema di sviluppare un’intuizione dei metodi MCMC.

24.4.3 Terminologia

Consideriamo un modello Bayesiano $M$ avente una verosimiglianza $P(D \mid \theta)$ sui dati osservati $D$ e una distribuzione a priori $P(\theta)$ sui parametri. Applichiamo il teorema di Bayes per produrre la distribuzione a posteriori:

\[ P(\theta \mid D) = \frac{P(D \mid \theta) \ P(\theta)}{P(D)}. \]

L’equazione precedente è costituita dalle seguenti componenti:

la distribuzione a posteriori $P(\theta \mid D)$ - la nuova credenza a posteriori relativamente alla plausibilità di ciascun valore $\theta$ alla luce di $D$;
la funzione di verosimiglianza $P(D \mid \theta)$ - quanto sono verosimili i dati $D$ per ciascun valore fisso $\theta$;
la distribuzione a priori $P(\theta)$ - la credenza iniziale riguardo alla plausibilità di ciascun valore $\theta$;
la verosimiglianza marginale $P(D) = \int P(D \mid \theta) \ P(\theta) \ \text{d}\theta$ - quanto sono verosimili i dati $D$ alla luce della nostra credenza a priori relativamente a $\theta$.

La formula precedente applica il teorema di Bayes per produrre la distribuzione a posteriori dei parametri sconosciuti $\theta$. Tuttavia, molto spesso la probabilità a posteriori è scritta nel modo seguente:

\[ \underbrace{P(\theta \, | \, D)}_{posterior} \propto \underbrace{P(\theta)}_{prior} \ \underbrace{P(D \, | \, \theta)}_{likelihood}, \]

dove il segno di proporzionalità indica che le probabilità a sinistra del simbolo $\propto$ sono definite dai termini a destra di $\propto$ a meno di una costante di normalizzazione. Se $F \colon X \rightarrow \mathbb{R}^+$ è una funzione positiva non normalizzata di probabilità, $P(x) \propto F(x)$ è equivalente a $P(x) = \frac{F(x)}{\sum_{x' \in X} F(x')}$.

24.5 L’effetto della distribuzione a priori sulla distribuzione a posteriori

La notazione $P(\theta \mid D) \propto P(\theta) \ P(D \mid \theta)$ rende particolarmente chiaro che la distribuzione a posteriori è un “miscuglio” della distribuzione a priori e della verosimiglianza. Prima di preoccuparci di come calcolare concretamente la distribuzione a posteriori, cerchiamo di capire cosa significa “mescolare” la distribuzione a priori e la verosimiglianza.

Consideriamo una serie di lanci di una moneta con probabilità di successo (testa) sconosciuta $\theta$. Supponiamo di osservare $k$ successi in $N$ prove. Per descrivere questo esperimento casuale usiamo il modello Binomiale, utilizzando una distribuzione a priori espressa mediante la distribuzione Beta. Ciò produce il seguente modello statistico:

\[ \begin{aligned} k & \sim \text{Binomial}(N, \theta) \\ \theta & \sim \text{Beta}(a, b) \end{aligned} \]

Per studiare l’impatto della distribuzione a priori sulla funzione di verosimiglianza confronteremo due campioni di dati. Nel primo campione, $N = 24$ e $k = 7$; nel secondo campione, $k = 109$ e $N = 311$. Per entrambi i campioni, la funzione di verosimiglianza dei dati è fornita dalla figura seguente.

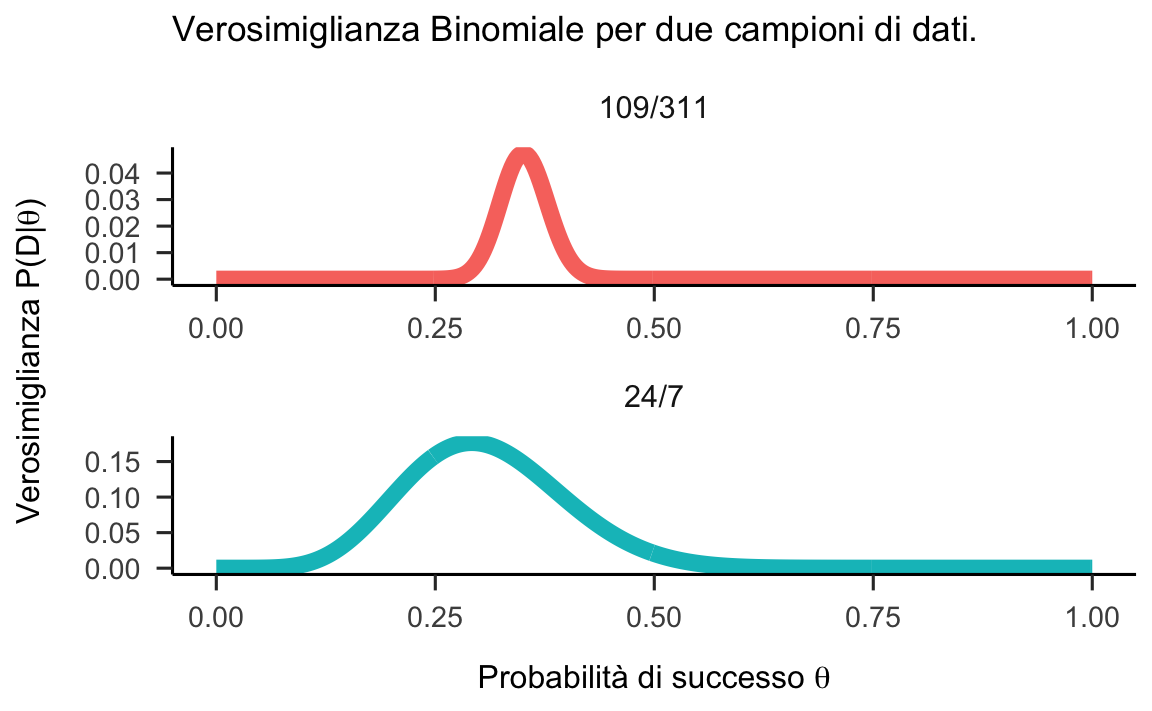
Figura 24.3: Verosimiglianza per due campioni di dati binomiali. Per il primo campione abbiamo $k = 7$ e $N = 24$; per il secondo campione $k = 109$ e $N = 311$.

La cosa più importante da notare è che, maggiore è la quantità di dati ($k = 109$ e $N = 311$), più piccolo diventa l’intervallo di valori dei parametri che rendono plausibili i dati che sono stati osservati. Intuitivamente, questo significa che più dati abbiamo, più piccolo sarà l’intervallo a posteriori dei valori plausibili dei parametri, a parità di tutto il resto.

Consideriamo ora le quattro distribuzioni a priori che abbiamo descrito in precedenza:

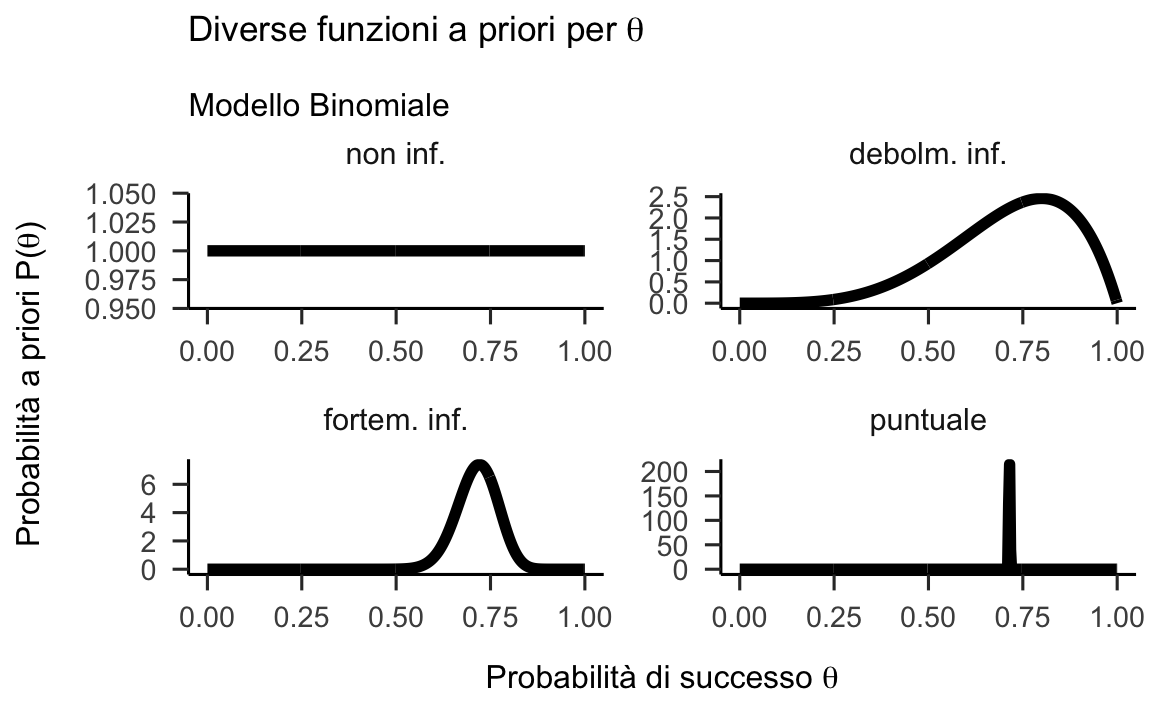
$Esempi di distribuzioni a priori per il parametro $\theta_c$ nel Modello Binomiale.$

Figura 24.4: Esempi di distribuzioni a priori per il parametro $\theta_c$ nel Modello Binomiale.

Combiniamo le quattro distribuzioni a priori con la verosimiglianza dei due campioni di dati. Così facendo notiamo che la distribuzione a posteriori è effettivamente un “miscuglio” della distribuzione a priori e della verosimiglianza.

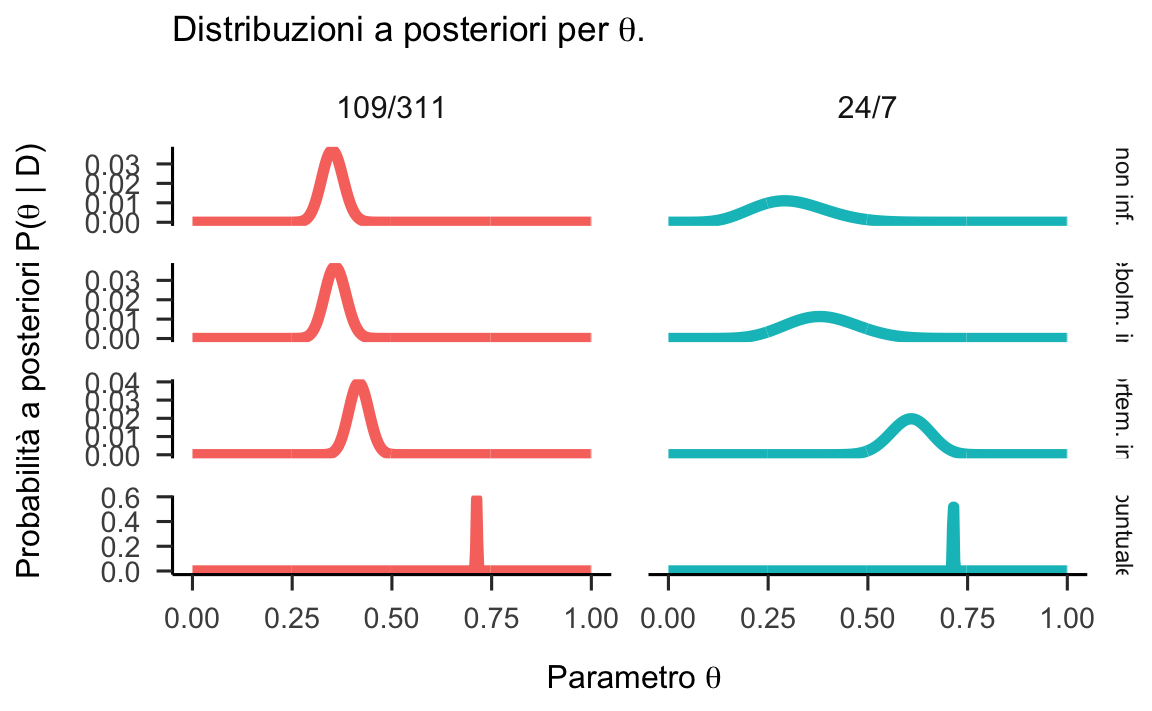
$Distribuzioni a posteriori per il parametro $\theta$ calcolate mediante diverse distribuzioni a priori per due campioni di dati.$

Figura 24.5: Distribuzioni a posteriori per il parametro $\theta$ calcolate mediante diverse distribuzioni a priori per due campioni di dati.

Ciò che è importante notare è che, se il campione è grande, una distribuzioni a priori debolmente informativa ha uno scarso effetto sulla distribuzione a posteriori. Invece, se il campione è piccolo, anche una distribuzioni a priori debolmente informativa ha un grande effetto sulla distribuzione a posteriori, in confronto ad una distribuzione a priori non informativa.

24.6 Le aspettative dei pazienti con disturbo depressivo maggiore

Esaminiamo ora un altro esempio che ha lo scopo di chiarite le relazioni che legano tra loro le tre distribuzioni che abbiamo introdotto sopra: la distribuzione a priori, la verosimiglianza e la distribuzioni a posteriori. Nell’esempio faremo riferimento alla ricerca di Zetsche et al. (2019).

Zetsche et al. (2019) si sono chiesti se gli individui depressi manifestino delle aspettative accurate circa il loro umore futuro, oppure se tali aspettative siano distorte negativamente. Esamineremo qui i 30 partecipanti dello studio di Zetsche et al. (2019) che hanno riportato la presenza di un episodio di depressione maggiore in atto. All’inizio della settimana di test, a questi pazienti è stato chiesto di valutare l’umore che si aspettavano di esperire nei giorni seguenti della settimana. Mediante una app, i partecipanti dovevano poi valutare il proprio umore in cinque momenti diversi di ciascuno dei cinque giorni successivi. Lo studio considera diverse emozioni, ma qui ci concentriamo solo sulla tristezza.

Sulla base dei dati forniti dagli autori, abbiamo calcolato la media dei giudizi relativi al livello di tristezza raccolti da ciascun partecipante tramite la app. Tale media è stata poi sottratta dall’aspettativa del livello di tristezza fornita all’inizio della settimana. Per semplificare l’analisi abbiamo considerato la discrepanza tra aspettative e realtà come un evento dicotomico: valori positivi di tale differenza indicano che le aspettative circa il livello di tristezza sono maggiori del livello di tristezza che in seguito viene effettivamente esperito; ciò significa che le aspettative sono negativamente distorte (evento codificato con “1”). Si può dire il contrario (le aspettative sono positivamente distorte) se tale differenza assume valori negativi (evento codificato con “0”).

Nel campione dei 30 partecipanti clinici esaminati da Zetsche et al. (2019), 23 partecipanti manifestano delle aspettative negativamente distorte e 7 partecipanti manifestano delle aspettative positivamente distorte. Nella seguente discussione, chiameremo $\theta$ la probabilità dell’evento “le aspettative del partecipante sono distorte negativamente.” Il problema che ci poniamo è quello di ottenere la stima a posteriori di $\theta$, avendo osservato 23 “successi” in 30 prove, ovvero $\hat{\theta}$ = 23/30 = 0.77.

Si noti un punto importante qui: un problema di scrivere semplicemente la stima di $\theta$ come 0.77 è che tale valore ignora l’incertezza della nostra stima. Infatti, il valore di 0.77 si può ottenere come 23/30, o come 230/300, o 2300/3000, o 23000/30000. L’incertezza della stima 0.77 è diversa in ciascuno di questi casi e questo è molto importante quando si traggono conclusioni dai dati.

Nell’approccio frequentista, l’unico strumento che abbiamo per caratterizzare la nostra incertezza relativa alla stima di $\theta$ è la distribuzione campionaria della stima di questo parametro nel caso di un ipotetico campionamento ripetuto; non è invece possibile fare riferimento ad un’incertezza relativa al vero valore del parametro stesso. Per una dimensione campionaria pari a 30, la nostra incertezza deriva dalle caratteristiche della distribuzione campionaria e viene calcolata trovando la varianza campionaria – ovvero, $n \cdot \hat{\theta} (1 - \hat{\theta}) = 30 \cdot 0.77 (1 - 0.77) = 5.31$ – e poi l’errore standard, $\sigma / \sqrt{n}$ – qui 0.42. Per la stessa proporzione di successi pari a 0.77, l’aumento della dimensione del campione rende questo errore standard sempre più piccolo. Questa maggiore precisione corrisponde alle proprietà della distribuzione campionaria di $\hat{\theta}$, ma non quantifica l’incertezza relativa al vero valore di $\theta$.

L’approccio Bayesiano procede in modo diverso e ci fornisce invece l’opportunità di quantificare direttamente la nostra incertezza relativa al vero valore del parametro $\theta$, alla luce dei dati – non della distribuzione campionaria di $\hat{\theta}$. Tale quantificazione dell’incertezza si trova costruendo la distribuzione a posteriori di $\theta$ mediante il teorema di Bayes.

Per costruire la distribuzione a posteriori di $\theta$, in questo esempio utilizzeremo l’approccio chiamato grid-based. Il metodo basato su griglia è un metodo di approsimazione numerica basato su una griglia di punti uniformemente spaziati (si veda il capitolo Stima della funzione a posteriori). Anche se la maggior parte dei parametri è continua (ovvero, in linea di principio ciascun parametro può assumere un numero infinito di valori), possiamo ottenere un’eccellente approssimazione della distribuzione a posteriori considerando solo una griglia finita di valori dei parametri. In un tale metodo, la densità di probabilità a posteriori può dunque essere approssimata tramite le densità di probabilità cacolate in ciascuna cella della griglia.

Per calcolare la probabilità a posteriori si procede come indicato di seguito. Per ciascuno specifico valore $\theta'$ (ovvero, per ciascun elemento della griglia) è necessario moltiplicare l’ordinata della distribuzione di probabilità a priori in corrispondenza di $\theta'$ per l’ordinata della funzione di verosimiglianza in corrispondenza di $\theta'$. Tale procedura va ripetuta per ciascun elemento della griglia. C’è ovviamente bisogno di una griglia molto densa per ottenere buone approssimazioni.

Il metodo basato su griglia è, in primo luogo, un utile strumento didattico in quanto rende trasparente la logica del processo dell’aggiornamento Bayesiano. Per ragioni che vedremo in seguito, tale metodo non può essere usato per la stima di modelli complessi che includono un grande numero di parametri – ma non è questo il nostro scopo qui. Ma, al di là di questo limite del metodo basato su griglia, è importante sottolineare che, quale che sia il metodo che si usa per stimare la funzione a posteriori, il significato della funzione a posteriori non cambia ed è ben illustrato dall’esempio qui discusso.

Iniziamo a costruire la griglia di valori del parametro $\theta$. In questo esempio considereremo 50 valori egualmente spaziati nell’intervallo [0, 1]: 0.000, 0.0204, …, 0.978, 1.000. Per ottenere i valori griglia procediamo nel modo seguente:

n_points <- 50
p_grid <- seq(from = 0, to = 1, length.out = n_points)
p_grid
#>  [1] 0.00000000 0.02040816 0.04081633 0.06122449 0.08163265 0.10204082 0.12244898 0.14285714
#>  [9] 0.16326531 0.18367347 0.20408163 0.22448980 0.24489796 0.26530612 0.28571429 0.30612245
#> [17] 0.32653061 0.34693878 0.36734694 0.38775510 0.40816327 0.42857143 0.44897959 0.46938776
#> [25] 0.48979592 0.51020408 0.53061224 0.55102041 0.57142857 0.59183673 0.61224490 0.63265306
#> [33] 0.65306122 0.67346939 0.69387755 0.71428571 0.73469388 0.75510204 0.77551020 0.79591837
#> [41] 0.81632653 0.83673469 0.85714286 0.87755102 0.89795918 0.91836735 0.93877551 0.95918367
#> [49] 0.97959184 1.00000000

24.6.1 Distribuzione a priori

Supponiamo che le nostre credenze a priori sulla tendenza di un individuo clinicamente depresso a manifestare delle aspettative distorte negativamente circa il suo umore futuro siano molto scarse. Assumiamo quindi per $\theta$ una distribuzione a priori non informativa – ovvero, ipotizziamo che la distribuzione a priori sia una distribuzione uniforme nell’intervallo [0, 1]. Dato che consideriamo soltanto $n = 50$ valori possibili per il parametro $\theta$, creiamo un vettore di 50 elementi che conterrà i valori della distribuzione a priori scalando ciascun valore del vettore per $n$ in modo tale che la somma di tutti i valori sia uguale a 1.0 (in questo modo viene definita una funzione di massa di probabilità):

prior1 <- dbeta(p_grid, 1, 1) / sum(dbeta(p_grid, 1, 1))
prior1
#>  [1] 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02
#> [19] 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02
#> [37] 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02

Verifichiamo:

sum(prior1)
#> [1] 1

La distribuzione a priori così costruita è rappresentata nella figura 24.6.

p1 <- data.frame(p_grid, prior1) %>%
  ggplot(aes(x=p_grid, xend=p_grid, y=0, yend=prior1)) +
  geom_line()+
  geom_segment(color = "#8184FC") +
  ylim(0, 0.17) +
  labs(
    x = "Parametro \U03B8",
    y = "Probabilità a priori",
    title = "50 punti"
  )
p1

$Rappresentazione grafica della distribuzione a priori per il parametro $\theta$, ovvero la probabilità di aspettative future distorte negativamente [@zetsche_future_2019].$

Figura 24.6: Rappresentazione grafica della distribuzione a priori per il parametro $\theta$, ovvero la probabilità di aspettative future distorte negativamente (Zetsche et al., 2019).

24.6.2 Funzione di verosimiglianza

Calcoliamo ora la funzione di verosimiglianza utilizzando i 50 valori griglia per $\theta$ che abbiamo definito in precedenza. Per ciascuno dei valori della griglia applichiamo la formula della probabilità binomiale, tendendo sempre costanti i valori dei dati (ovvero 23 “successi” in 30 prove).

Considderiamo, ad esempio, il valore griglia $\theta = 0.816$. Per tale elemento della griglia l’ordinata della funzione di verosimiglianza è pari a

\[ \begin{aligned} \binom{30}{23}& \cdot 0.816^{23} \cdot (1 - 0.816)^{7} = 0.135.\notag \end{aligned} \]

Per fare un secondo esempio, consideriamo il valore griglia $\theta = 0.837$. Per tale elemento della griglia l’ordinata della funzione di verosimiglianza è uguale a

\[ \begin{aligned} \binom{30}{23}& \cdot 0.837^{23} \cdot (1 - 0.837)^{7} = 0.104.\notag \end{aligned} \]

Dobbiamo svolgere questo calcolo per tutti gli elementi della griglia. Usando R il risultato cercato si trova nel modo seguente:

likelihood <- dbinom(x = 23, size = 30, prob = p_grid)
likelihood
#>  [1] 0.000000e+00 2.352564e-33 1.703051e-26 1.644169e-22 1.053708e-19 1.525217e-17 8.602222e-16
#>  [8] 2.528440e-14 4.606907e-13 5.819027e-12 5.499269e-11 4.105534e-10 2.520191e-09 1.311195e-08
#> [15] 5.919348e-08 2.362132e-07 8.456875e-07 2.749336e-06 8.196948e-06 2.259614e-05 5.798673e-05
#> [22] 1.393165e-04 3.148623e-04 6.720574e-04 1.359225e-03 2.611870e-03 4.778973e-03 8.340230e-03
#> [29] 1.390025e-02 2.214199e-02 3.372227e-02 4.909974e-02 6.830377e-02 9.068035e-02 1.146850e-01
#> [36] 1.378206e-01 1.568244e-01 1.681749e-01 1.688979e-01 1.575211e-01 1.348746e-01 1.043545e-01
#> [43] 7.133007e-02 4.165680e-02 1.972669e-02 6.936821e-03 1.535082e-03 1.473375e-04 1.868105e-06
#> [50] 0.000000e+00

Il vettore likelihood è stato ottenuto passando alla funzione dbinom() un vettore di valori, ovvero gli elementi della griglia p_grid. La funzione dbinom(x, size, prob) richiede che vengano specificati tre parametri: il numero di “successi,” il numero di prove e la probabilità di successo. Dato che x (numero di successi) e size (numero di prove bernoulliane) sono degli scalari e prob è un vettore, questo significa che la formula della probabilità binomiale verrà applicata a ciascun elemento di p_grid tenendo costanti i valori di x e size, ovvero i dati. In questo modo otteniamo in output un vettore i cui valori corrispondono all’ordinata della funzione di verosimiglianza per il corrispondente valore griglia di $\theta$. La funzione di verosimiglianza così ottenuta è riportata nella figura 24.7.

p2 <- data.frame(p_grid, likelihood) %>%
  ggplot(aes(x=p_grid, xend=p_grid, y=0, yend=likelihood)) +
  geom_segment(color = "#8184FC") +
  ylim(0, 0.17) +
  labs(
    x = "Parametro \U03B8",
    y = "Verosimiglianza"
  )
p2

$Rappresentazione della funzione di verosimiglianza per il parametro $\theta$, ovvero la probabilità di aspettative future distorte negativamente [@zetsche_future_2019].$

Figura 24.7: Rappresentazione della funzione di verosimiglianza per il parametro $\theta$, ovvero la probabilità di aspettative future distorte negativamente (Zetsche et al., 2019).

24.6.3 La stima della distribuzione a posteriori

La distribuzione a posteriori per il parametro $\theta$ si ottiene facendo prima il prodotto della verosimiglianza e della distribuzione a priori, e poi scalando tale prodotto per una costante di normalizzazione. Quindi, se ci limitiamo a fare il prodotto dei valori della distribuzione a priori e dei valori della funzione di verosimiglianza otteniamo la funzione a posteriori non standardizzata.

Ricordiamo che, usando il metodo basato su griglia, stiamo manipolando funzioni di massa di probabilità. Ovvero, siamo in un “mondo discreto.” In questo contesto, una funzione di massa di probabilità non è altro che un’elenco di valori la cui somma deve essere uguale a 1.0. In un “mondo continuo,” invece, le probabilità sono definite in un modo completamente diverso: corrispondo all’area in un intervallo di valori sotteso alla funzione di densità. Ma nel nostro esempio corrente ci limitiamo al caso discreto in cui, per calcolare le probabilità, è sufficiente fare delle somme, non sono necessari gli integrali.

Nel caso presente abbiamo deciso di usare una distribuzione a priori non informativa, ovvero una distribuzione uniforme. Per ottenere la funzione a posteriori (di massa di probabilità) non standardizzata è dunque sufficiente moltiplicare ciascun valore della funzione di verosimiglianza per 0.02. Per esempio, per il primo valore della funzione di verosimiglianza che abbiamo discusso quale esempio nella sezione precedente, avremo

\[ 0.135 \cdot 0.02; \]

per il secondo valore della funzione di verosimiglianza che abbiamo discusso nell’esempio precedente avremo

\[ 0.104 \cdot 0.02; \]

e così via.

Usando R, possiamo svolgere tutti i calcoli necessari nel modo seguente:

unstd_posterior <- likelihood * prior1
unstd_posterior
#>  [1] 0.000000e+00 4.705127e-35 3.406102e-28 3.288337e-24 2.107415e-21 3.050433e-19 1.720444e-17
#>  [8] 5.056880e-16 9.213813e-15 1.163805e-13 1.099854e-12 8.211068e-12 5.040382e-11 2.622390e-10
#> [15] 1.183870e-09 4.724263e-09 1.691375e-08 5.498671e-08 1.639390e-07 4.519229e-07 1.159735e-06
#> [22] 2.786331e-06 6.297247e-06 1.344115e-05 2.718450e-05 5.223741e-05 9.557946e-05 1.668046e-04
#> [29] 2.780049e-04 4.428398e-04 6.744454e-04 9.819948e-04 1.366075e-03 1.813607e-03 2.293700e-03
#> [36] 2.756411e-03 3.136488e-03 3.363497e-03 3.377958e-03 3.150422e-03 2.697491e-03 2.087091e-03
#> [43] 1.426601e-03 8.331361e-04 3.945339e-04 1.387364e-04 3.070164e-05 2.946751e-06 3.736209e-08
#> [50] 0.000000e+00

Ricordiamo il principio dell’aritmetica vettorializzata: il vettore likelihood è costituito da 50 elementi e il vettore prior1 è anch’esso costituito da 50 elementi. Se facciamo il prodotto tra i due vettori otteniamo un vettore di 50 elementi ciascuno dei quali uguale al prodotto dei corrispondenti elementi di likelihood e prior1.

Avendo calcolato i valori della funzione a posteriori non standardizzata è poi necessario dividere per una costante di normalizzazione. Nel caso discreto, trovare il denominatore del teorema di Bayes è molto facile: esso è dato semplicemente dalla somma di tutti i valori della distribuzione a posteriori non normalizzata. Per i dati presenti, tale costante di normalizzazione è uguale a 0.032:

sum(unstd_posterior)
#> [1] 0.0316129

Per fare un esempio, standardizziamo i due valori che abbiamo discusso negli esempi precedenti: $0.135 \cdot 0.02 / 0.032$ e $0.104 \cdot 0.02 / 0.032$. Così facendo, otteniamo il risultato per cui la somma di tutti e 50 i valori della distribuzione a posteriori normalizzata diventa uguale a 1.0.

Svolgiamo tutti i calcoli in R:

posterior <- unstd_posterior / sum(unstd_posterior)
posterior
#>  [1] 0.000000e+00 1.488357e-33 1.077440e-26 1.040188e-22 6.666313e-20 9.649330e-18 5.442222e-16
#>  [8] 1.599625e-14 2.914574e-13 3.681425e-12 3.479129e-11 2.597379e-10 1.594406e-09 8.295316e-09
#> [15] 3.744893e-08 1.494410e-07 5.350268e-07 1.739376e-06 5.185824e-06 1.429552e-05 3.668548e-05
#> [22] 8.813904e-05 1.991986e-04 4.251792e-04 8.599178e-04 1.652408e-03 3.023432e-03 5.276472e-03
#> [29] 8.794033e-03 1.400820e-02 2.133450e-02 3.106310e-02 4.321259e-02 5.736920e-02 7.255582e-02
#> [36] 8.719259e-02 9.921545e-02 1.063963e-01 1.068538e-01 9.965619e-02 8.532881e-02 6.602021e-02
#> [43] 4.512719e-02 2.635430e-02 1.248015e-02 4.388601e-03 9.711744e-04 9.321354e-05 1.181862e-06
#> [50] 0.000000e+00

Verifichiamo:

sum(posterior)
#> [1] 1

In questo particolare esempio, la distribuzione a posteriori trovata come descritto sopra non è altro che la versione normalizzata della funzione di verosimiglianza: questo avviene perché la distribuzione a priori uniforme non ha aggiunto altre informazioni oltre a quelle che erano già fornite dalla funzione di verosimiglianza.

La funzione a posteriori che abbiamo calcolato con il metodo grid-based è riportata nella figura 24.8.

p3 <- data.frame(p_grid, posterior) %>%
  ggplot(aes(x=p_grid, xend=p_grid, y=0, yend=posterior)) +
  geom_segment(color = "#8184FC") +
  ylim(0, 0.17) +
  labs(
    x = "Parametro \U03B8",
    y = "Probabilità a posteriori"
  )
p3

$Rappresentazione della distribuzione a posteriori per il parametro $\theta$, ovvero la probabilità di aspettative future distorte negativamente [@zetsche_future_2019].$

Figura 24.8: Rappresentazione della distribuzione a posteriori per il parametro $\theta$, ovvero la probabilità di aspettative future distorte negativamente (Zetsche et al., 2019).

Le funzioni rappresentate nelle figure 24.6, 24.7 e 24.8 sono state calcolate utilizzando una griglia di 50 valori equi-spaziati per il parametro $\theta$. I segmenti verticali rappresentano l’intensità della funzione in corrispondenza di ciascuna modalità parametro $\theta$. Nella figura 24.6 e nella figura 24.8 la somma delle lunghezze dei segmenti verticali è pari ad 1.0 (in altri termini, la funzione a priori e la funzione a posteriori sono delle funzioni di massa di probabilità, in questo esempio); ciò non si verifica, invece, nel caso della figura 24.8 (la funzione di verosimiglianza non è mai una funzione di probabilità, né nel caso discreto né in quello continuo).

24.6.4 La stima della distribuzione a posteriori (versione 2)

Continuiamo la discussione dell’esempio precedente ed esaminiamo l’impatto sulla distribuzione a posteriori di una distribuzione a priori informativa. Una distribuzione a priori informativa riflette un alto grado di certezza sui parametri del modello da stimare. Un ricercatore può utilizzare una distribuzione a priori informativa per introdurre nel processo di stima le informazioni esistenti che suggeriscono delle restrizioni sulla possibile gamma di valori di un particolare parametro.

Nel caso presente, supponiamo che la letteratura psicologica fornisca delle informazioni a proposito del valore di $\theta$, ovvero ci fornisca delle informazioni sul valore della probabilità che le aspettative future di un individuo clinicamente depresso siano distorte negativamente – in altri termini, sono già state svolte ricerche precedenti su questo aspetto e risultati empirici sono già stati raccolti: in una serie di ricerche precedenti è stato trovato che $\theta$ assumeva valori compresi in una certa gamma. In tali circostanze, anziché utilizzare una distribuzione a priori non informativa per $p(\theta)$, il ricercatore può decidere di utilizzare una distribuzione a priori informativa che riflette le conoscenze che sono state acquisite in precedenza sul possibile valore del parametro. Nel caso presente, supponiamo (irrealisticamente) che tali conoscenze pregresse si possano esprimere nei termini di una distribuzione che ha la forma di una Beta di parametri $\alpha = 2$ e $\beta = 10$. Tali ipotetiche conoscenze pregresse (ripeto, del tutto irrealistiche) le quali si riflettono in una Beta(2, 10) ritengono molto plausibili valori bassi di $\theta$ e considerano come impossibili i valori $\theta$ superiori a 0.5. Questo è equivalente a dire che ci aspettiamo che le aspettative relative all’umore futuro siano distorte negativamente solo per pochissimi individui clinicamente depressi – in altre parole, ci aspettiamo che la maggioranza degli individui clinicamente depressi sia inguaribilmente ottimista. Questa è, ovviamente, una credenza a priori del tutto irrealistica. La esamino qui, non perché abbia alcun senso nel contesto dei dati di Zetsche et al. (2019), ma soltanto per fare un esempio che illustra come la distribuzione a posteriori fornisca una sorta di “compromesso” tra la distribuzione a priori e la verosimiglianza, ovvero per chiarire l’impatto che la distribuzione a priori ha sulla distribuzione a posteriori.

Con calcoli del tutto simili a quelli descritti sopra si giunge alla distribuzione a posteriori rappresentata nella figura 24.9. Iniziamo a definire una griglia unidimensionale equispaziata di possibili valori del parametro $\theta$. Anche in questo caso usiamo 50 valori possibili del parametro $\theta$:

n_points <- 50
p_grid <- seq(from = 0, to = 1, length.out = n_points)

Per la distribuzione a priori scelgo una Beta(2, 10).

alpha <- 2
beta <- 10
prior2 <- dbeta(p_grid, alpha, beta) / sum(dbeta(p_grid, alpha, beta))
sum(prior2)
#> [1] 1

Tale distribuzione a priori è rappresentata nella figura 24.9.

plot_df <- data.frame(p_grid, prior2)
p4 <- plot_df %>%
  ggplot(aes(x=p_grid, xend=p_grid, y=0, yend=prior2)) +
  geom_segment(color = "#8184FC") +
  ylim(0, 0.17) +
  labs(
    x = "",
    y = "Probabilità a priori",
    title = "50 punti"
  )
p4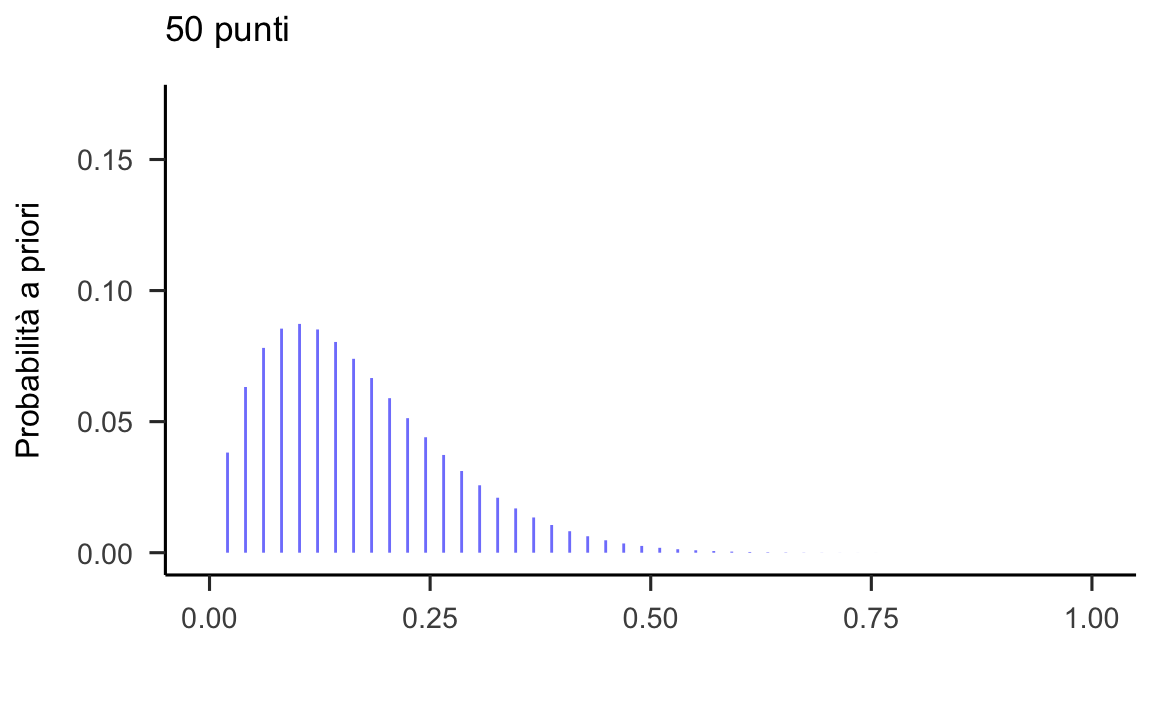

$Rappresentazione di una funzione a priori informativa per il parametro $\theta$.$

Figura 24.9: Rappresentazione di una funzione a priori informativa per il parametro $\theta$.

Calcoliamo il valore della funzione di verosimiglianza in corrispondenza di ciascun punto della griglia. La funzione di verosimiglianza è identica a quella considerata nell’esempio precedente.

likelihood <- dbinom(23, size = 30, prob = p_grid)

Calcolo il prodotto tra la verosimiglianza e la distribuzione a priori, per ciascun punto della griglia:

unstd_posterior2 <- likelihood * prior2

Normalizzo la distribuzione a posteriori in modo tale che la somma sia 1.

posterior2 <- unstd_posterior2 / sum(unstd_posterior2)
sum(posterior2)
#> [1] 1

La nuova funzione a posteriori è rappresentata nella figura 24.10.

plot_df <- data.frame(p_grid, posterior2)
p5 <- plot_df %>%
  ggplot(aes(x = p_grid, xend = p_grid, y = 0, yend = posterior2)) +
  geom_segment(color = "#8184FC") +
  ylim(0, 0.17) +
  labs(
    x = "Parametro \U03B8",
    y = "Probabilità a posteriori"
  )
p5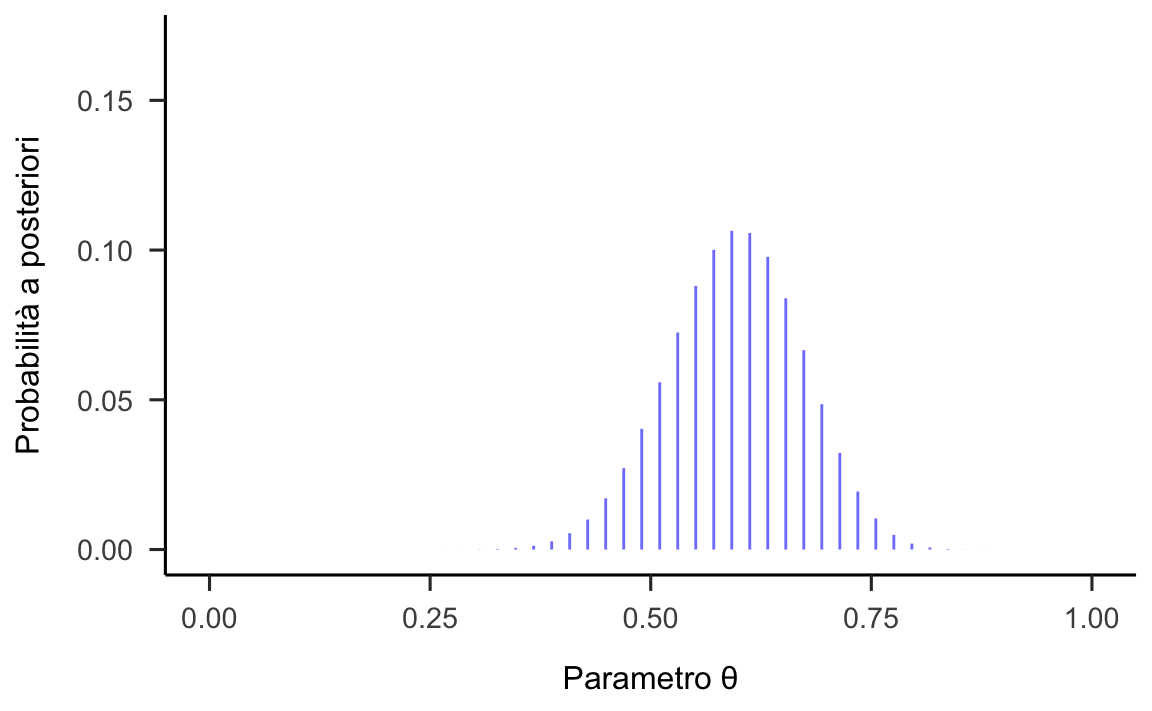

$Rappresentazione della funzione a posteriori per il parametro $\theta$ calcolata utilizzando una distribuzione a priori informativa.$

Figura 24.10: Rappresentazione della funzione a posteriori per il parametro $\theta$ calcolata utilizzando una distribuzione a priori informativa.

Facendo un confronto tra le figure 24.9 e 24.10 si nota come la distribuzione a priori per il parametro $\theta$ e la distribuzione a posteriori per il parametro $\theta$ sono molto diverse. In particolare, si noti che la distribuzione a posteriori rappresentata nella 24.10 risulta spostata verso destra su posizioni più vicine a quelle della verosimiglianza, rappresentata nella figura 24.7. Si noti anche, a causa dell’effetto della distribuzione a priori, le distribuzioni a posteriori riportate nelle figure 24.8 e 24.10 sono molto diverse tra loro. Discuteremo in seguito l’influenza della distribuzione a priori sull’inferenza finale.

24.6.5 Sommario della funzione a posteriori

Una volta calcolata la distribuzione a posteriori dobbiamo riassumerla in qualche modo. Nel caso in cui venga usato un metodo grid-based, il problema del calcolo delle aree sottese alla funzione a posteriori in qualunque intervallo può essere risolto in vari modi. Tuttavia, questo problema trova una soluzione molto più semplice se viene utilizzato un metodo diverso per la stima della distribuzione a posteriori, come vedremo di seguito. Non discuteremo dunque la possibile soluzione di questo problema nel caso presente, in quanto il metodo metodo grid-based per il calcolo della distribuzione a posteriori è solo un esempio didattico.

24.7 Differenza tra intervalli di confidenza e di credibilità

L’approccio frequentista generalmente ipotizza che il mondo abbia certe proprietà (ad esempio, viene assunto che un dato parametro ha un particolare valore vero) e si pone il problema di condurre esperimenti la cui conclusione sarà corretta con almeno un livello minimo di probabilità. Per esprimere l’incertezza della nostra conoscenza dopo un esperimento, l’approccio frequentista utilizza un “intervallo di confidenza” – ovvero, un intervallo di valori progettato per includere il vero valore del parametro con una probabilità minima, diciamo il 95%. Un frequentista progetterà l’esperimento e la procedura di calcolo dell’intervallo di confidenza al 95% in modo tale che su ogni 100 esperimenti eseguiti si prevede che almeno 95 degli intervalli di confidenza risultanti includano il vero valore del parametro; gli altri 5 potrebbero essere leggermente sbagliati, o potrebbero essere del tutto assurdi. Dal punto di vista dell’approccio frequentista, questo è accettabile, purché 95 inferenze su 100 siano corrette (ma ovviamente è preferibile che i 5 risultati sbagliati siano sbagliati di poco, piuttosto che totalmente assurdi).

L’approccio Bayesiano formula il problema in un modo diverso. Invece di dire che il parametro ha un valore vero (ma sconosciuto), il metodo Bayesiano dice che, prima di eseguire l’esperimento, è possibile assegnare una distribuzione di probabilità, che chiamano stato di credenza, a quello che è il vero valore del parametro. Questa distribuzione a priori potrebbe essere nota (per esempio, sappiamo che la distribuzione dei punteggi del QI è normale con media 100 e deviazione standard 15) o potrebbe essere del tutto arbitraria. L’inferenza Bayesiana è semplice: si raccolgono alcuni dati e si calcola la probabilità di diversi valori del parametro dati i dati. Questa nuova distribuzione di probabilità è chiamata “distribuzione a posteriori.” L’approccio Bayesiano riassumere l’incertezza descrivendo un intervallo di valori sulla distribuzione di probabilità a posteriori che include il 95% della probabilità – questo intervallo è chiamato “intervallo di credibilità del 95%.”

Un proponente dell’approccio Bayesiano potrebbe criticare l’intervallo di confidenza frequentista in questo modo: “Perché dovrei dare importanza al fatto che 95 esperimenti su 100 producono un intervallo di confidenza che include il vero valore del parametro sconosciuto? Non mi interessano 95 esperimenti che non ho eseguito; mi interessa l’unico esperimento che ho effettivamente eseguito. La regola decisionale frequentista consente che 5 risultati su 100 siano completamente privi di senso [es., valori negativi, valori impossibili] purché gli altri 95 siano corretti. Ma questo è inaccettabile.”

Un proponente dell’approccio frequentista potrebbe criticare l’intervallo di credibilità Bayesiano in questo modo: “Perché dovrei dare importanza al fatto che il 95% della probabilità a posteriori è incluso in un dato intervallo? La risposta Bayesiana è corretta solo se la distribuzione a priori è corretta. Ma chi mi garantisce che tale distribuzione non sia stata scelta in un modo del tutto inappropriato?”

Vorrei rendere esplicito il fatto che, in questo insegnamento, io mi schiero in maniera chiara a favore dell’approccio Bayesiano. La critica che i Bayesiani rivolgono all’approccio frequentista mi sembra sensata. La critica che i frequentisti rivolgono all’approccio Bayesiano mi sembra, invece, debole e poco convincente. Spero che ciò che verrà detto in seguito chiarirà questo punto.

Conclusioni

Possiamo specificare un modello Bayesiano definendo una distribuzione congiunta su variabili osservate, $\mathcal Y$, e un insieme di parametri sconosciuti, $\theta$.

\[ p(\mathcal Y, \theta). \] Questa distribuzione congiunta si decompone convenientemente in due termini,

\[ p(\mathcal Y, \theta) = p(\theta) p(\mathcal Y \mid \theta). \]

Il primo termine, $p(\theta)$, è la densità a priori e codifica l’insieme di valori plausibili dei parametri, con i valori più plausibili aventi una densità maggiore. È chiamato “a priori” perché racchiude la nostra conoscenza - e la sua mancanza - sui parametri da stimare prima di osservare i dati. Il secondo termine, $p(\mathcal Y \mid \theta)$, è la verosimiglianza. Dati i parametri del modello $\theta$, $p(\mathcal Y \mid \theta)$ definisce il processo di generazione per $\mathcal Y$.

L’inferenza esegue il reverse engineering del processo di generazione dei dati e si chiede:

dato un modello e un campione di osservazioni, $\mathcal Y$, quali sono i valori più plausibili dei parametri che potrebbero aver generato le osservazioni?

In un contesto Bayesiano, l’insieme dei valori plausibili dei parametri condizionati ai dati è caratterizzato dalla distribuzione a posteriori, $p(\theta \mid \mathcal Y)$. La regola di Bayes stabilisce che

\[ p(\theta \mid \mathcal Y) \propto p(\theta) p(\mathcal Y \mid \theta), \]

dove $\propto$ sta per “proporzionale a” e indica che la distribuzione a posteriori combina le informazioni fornite dai dati e la nostra conoscenza precedente. Un’espressione analitica per $p(\theta \mid \mathcal Y)$ è raramente disponibile e dobbiamo fare affidamento su algoritmi di calcolo numerico per conoscere la distribuzione a posteriori. Una strategia generale che esamineremo in seguito consiste nel prelevare campioni approssimativi dalla distribuzione a posteriori e utilizzarli per costruire stime empiriche della media a posteriori, della varianza, della mediana, dei quantili e di altre quantità di interesse. Qui abbiamo presentato il metodo grid-based per il calcolo della distribuzione a posteriori. I metodi basati su griglia funzionano benissimo quando la distribuzione a posteriori dipende da un numero molto piccolo di parametri sconosciuti, ma non possono essere usati nel caso di modelli statistici più complessi che includono un numero maggiore di parametri.

Introduzione

25 Stima della funzione a posteriori