30.1 Modello Binomiale

Se facciamo nuovamente riferimento all’esempio del mappamondo di McElreath (2020), nel quale abbiamo osservato \(A = 6\) volte “acqua” in \(N = 9\) prove Bernoulliane indipendenti, allora il modello statistico che descrive l’esperimento casuale può essere formulato nei termini seguenti:

\[\begin{equation} \begin{aligned} A &\sim \text{Binom}(N, p) \\ p &\sim \text{Unif}(0, 1) \end{aligned} \tag{30.1} \end{equation}\]

dove la prima riga definisce la funzione di verosimiglianza e la seconda riga definisce la distribuzione a priori. Il segno \(\sim\) (tilde) si può leggere “si distribuisce come.” La prima riga, dunque, ci dice che la variabile aleatoria \(A\) segue la distribuzione Binomiale di parametri \(N\) e \(p\). La seconda riga specifica che, quale distribuzione a priori, assumiamo una distribuzione uniforme in (0 e 1) per il parametro \(p\). Sulla base di queste informazioni, il nostro obiettivo è di costruire la distribuzione a posteriori \(P(p \mid A, N)\). Per ottenere questo risultato utilizzeremo il teorema di Bayes:

\[ \text{distribuzione a posteriori} \propto \text{verosimiglianza} \times \text{distribuzione a priori}. \]

30.2 Il presidente Trump e l’idrossiclorochina

Cito dal Washington Post del 7 aprile 2020:

One of the most bizarre and disturbing aspects of President Trump’s nightly press briefings on the coronavirus pandemic is when he turns into a drug salesman. Like a cable TV pitchman hawking ‘male enhancement’ pills, Trump regularly extols the virtues of taking hydroxychloroquine, a drug used to treat malaria and lupus, as a potential ‘game changer’ that just might cure Covid-19.

Tralasciamo qui il fatto che il presidente Trump non è un esperto in questo campo. Esaminiamo invece le evidenze iniziali a supporto dell’ipotesi che l’idrossiclorochina possa essere utile per la cura del Covid-19, ovvero le evidenze che erano disponibili nel momento in cui il presidente Trump ha fatto le affermazioni riportate sopra (in seguito, quest’idea è stata completamente screditata). Tali evidenze sono state fornite da Gautret et al. (2020).

Il disegno sperimentale di Gautret et al. (2020) comprende, tra le altre cose, il confronto tra una condizione sperimentale e una condizione di controllo. Un articolo pubblicato da Hulme et al. (2020) si è posto il problema di rianalizzare i dati di Gautret et al. (2020) – si veda https://osf.io/5dgmx/. Tra gli autori di questo secondo articolo figura anche Eric-Jan Wagenmakers, uno psicologo molto conosciuto per i suoi contributi metodologici. Hulme et al. (2020) sottolineano il fatto che Gautret et al. (2020) si sono concentrati, nella loro analisi dei dati, soltanto su una parte del loro campione. Se però vengono considerati anche i pazienti che sono stati esclusi dall’analisi dei dati, le conclusioni a cui sono giunti Gautret et al. (2020) risultano fortemente indebolite.

L’analisi dei dati proposta da Hulme et al. (2020) richiede l’uso di alcuni strumenti statistici che, in queste dispense, non verranno discussi. Ma possiamo giungere alle stesse conclusioni di Hulme et al. (2020) anche usando le procedure statistiche che abbiamo descritto finora. Nella ricerca di Gautret et al. (2020) il confronto importante è tra la proporzione di paziente positivi al virus SARS-CoV-2 nel gruppo a cui è stata somministrata l’idrossiclorochina (6 su 14) e nel gruppo di controllo (a cui non è stata somministrata l’idrossiclorochina: 14 positivi su 16). Ciò che faremo sarà di calcolare la distribuzione a posteriori per queste due proporzioni. Rappresenteremo graficamente le due distribuzioni a posteriori per il parametro \(p\) che rappresenta la probabilità di risultare positivo al SARS-CoV-2. Calcoleremo anche, separatamente per i due gruppi, l’intervallo di credibilità al 95%. Quindi concluderemo facendo il confronto tra gli intervalli di credibilità dei due gruppi.

Leggiamo i dati in R  creando i due vettori seguenti. Il vettore ym contiene i dati del gruppo a cui è stata somministrata l’idrossiclorochina e il vettore yc i dati del gruppo di controllo. Il valore \(y = 1\) indica che il paziente è positivo al virus SARS-CoV-2 (l’ordine di 0 e 1 è irrilevante).

ym <- c(rep(1, 6), rep(0, 8))
ym
#>  [1] 1 1 1 1 1 1 0 0 0 0 0 0 0 0
yc <- c(rep(1, 14), rep(0, 2))
yc
#>  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0

Utilizziamo ora la sintassi di rethinking per definire il modello statistico appropriato per una proporzione. Specifichiamo inoltre una distribuzione a priori non informativa:

suppressPackageStartupMessages(library("rethinking"))
options(mc.cores = parallel::detectCores())

flist <- alist(
  y ~ dbinom(1, p),
  p ~ dbeta(1, 1) 
)

La funzione alist crea un oggetto R di tipo lista, ovvero un insieme ordinato di oggetti. Nel nostro caso, il primo oggetto contenuto nella lista è la specificazione della funzione di verosimiglianza y ~ dbinom(1, p), mentre il secondo oggetto è la specificazione della distribuzione a priori per il parametro p p ~ dbeta(1, 1). La funzione di verosimiglianza indica che i dati (nel nostro caso, la frequenza assoluta di casi positivi al virus SARS-CoV-2) si distribuiscono come una variabile aleatoria binomiale di parametro \(p\) (il valore \(N\) è fisso e conosciuto). La distribuzione a priori per il parametro sconosciuto \(p\) è inoltre specificata mediante una Beta(1, 1), ovvero mediante una distribuzione uniforme nell’intervallo unitario [0, 1].

Il calcolo della distribuzione a posteriori per il parametro \(p\) può essere svolto mediante la funzione qmap(). Tale funzione richiede due argomenti: il modello statistico specificato da alist() e i dati. Tale funzione stima la funzione a posteriori mediante il metodo dell’approssimazione quadratica discusso in precedenza. Anche i dati devono essere un oggetto R di tipo lista. Tale oggetto può essere creato mediante l’istruzione list(). Nel caso del gruppo sperimentale abbiamo

m <- quap( 
  flist, 
  data = list(y = ym)
)

La funzione quap() crea un oggetto che abbiamo chiamato m il quale contiene tutte le informazioni che ci servono a proposito della distribuzione a posteriori. Per rappresentare conun grafico la distribuzione a posteriori del parametro \(p\) usiamo le seguenti istruzioni:

post <- extract.samples(m)
plot(
  density(post$p), 
  xlim = c(0, 1),
  ylim = c(0, 5),
  main = "",
  xlab = "Parametro p",
  ylab = "Densità"
)

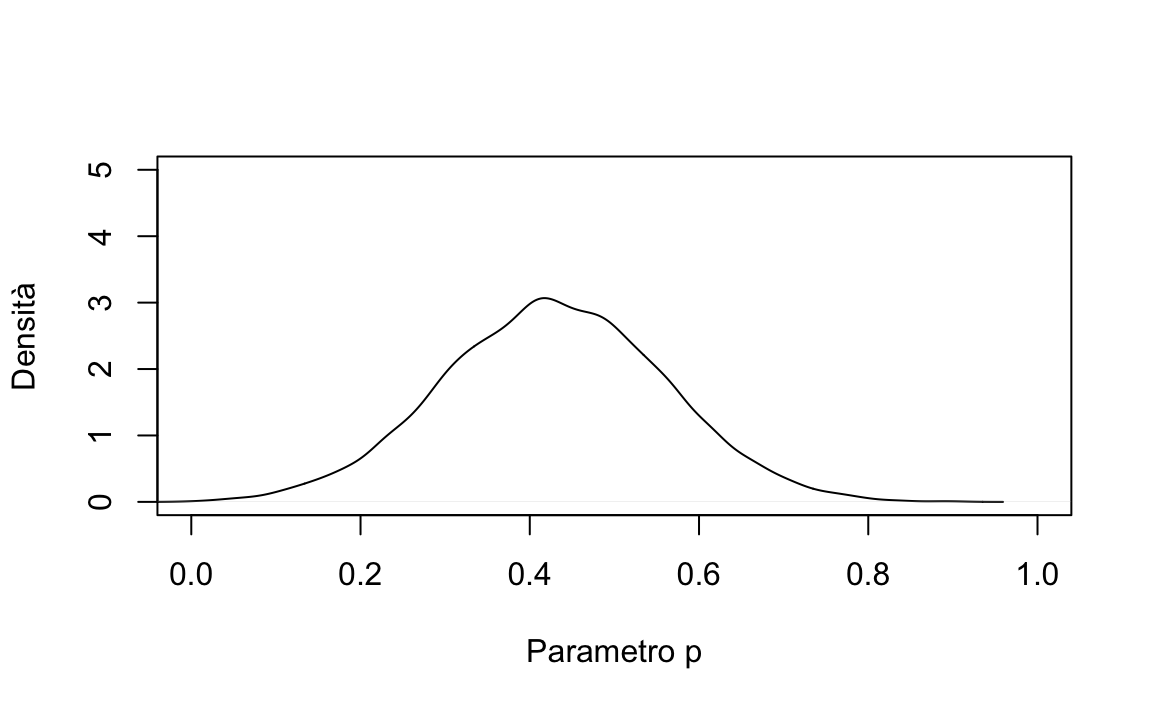Possiamo sintetizzare la distribuzione a posteriori del parametro \(p\) mediante la specificazione dell’intervallo di credibilità al 95%:

precis(m, prob = 0.95)
#>        mean        sd      2.5%     97.5%
#> p 0.4285638 0.1322588 0.1693412 0.6877863

L’intervallo di credibilità al 95% per il parametro \(p\) che abbiamo ottenuto per il gruppo sperimentale ci dice che possiamo essere sicuri al 95% che, nel gruppo sperimentale, la probabilità di risultare positivi al virus SARS-CoV-2 è un valore compreso nell’intervallo [.17, 0.69]. Questo intervallo è piuttosto ampio, il che suggerisce che abbiamo una grande incertezza su quale sia l’effettiva probabilità di risultare positivi al virus SARS-CoV-2 nella popolazione che ha le stesse caratteristiche del gruppo sperimentale, ovvvero in coloro che hanno assunto l’idrossiclorochina.

La nostra domanda riguarda però l’efficacia dell’idrossiclorochina. Dunque vogliamo confrontare la stima della probabilità di risultare positivi al virus SARS-CoV-2 per coloro che hanno assunto l’idrossiclorochina e coloro che non l’hanno assunta. Dobbiamo dunque calcolare l’intervallo di credibilità al 95% per il gruppo di controllo e confrontarlo con quello trovato sopra.

Ripetiamo quindi la stessa procedura appena eseguita, usando però i dati del gruppo di controllo.

mc <- quap( 
  flist, 
  data = list(y = yc)
)

Una rappresentazione grafica della distribuzione a posteriori del parametro \(p\) nella condizione di controllo si ottiene con le istruzioni seguenti:

postc <- extract.samples(mc)
plot(
  density(postc$p), 
  xlim = c(0, 1),
  ylim = c(0, 5),
  main = "",
  xlab = "Parametro p",
  ylab = "Densità"
)
lines(density(postc$p), xlim = c(0, 1))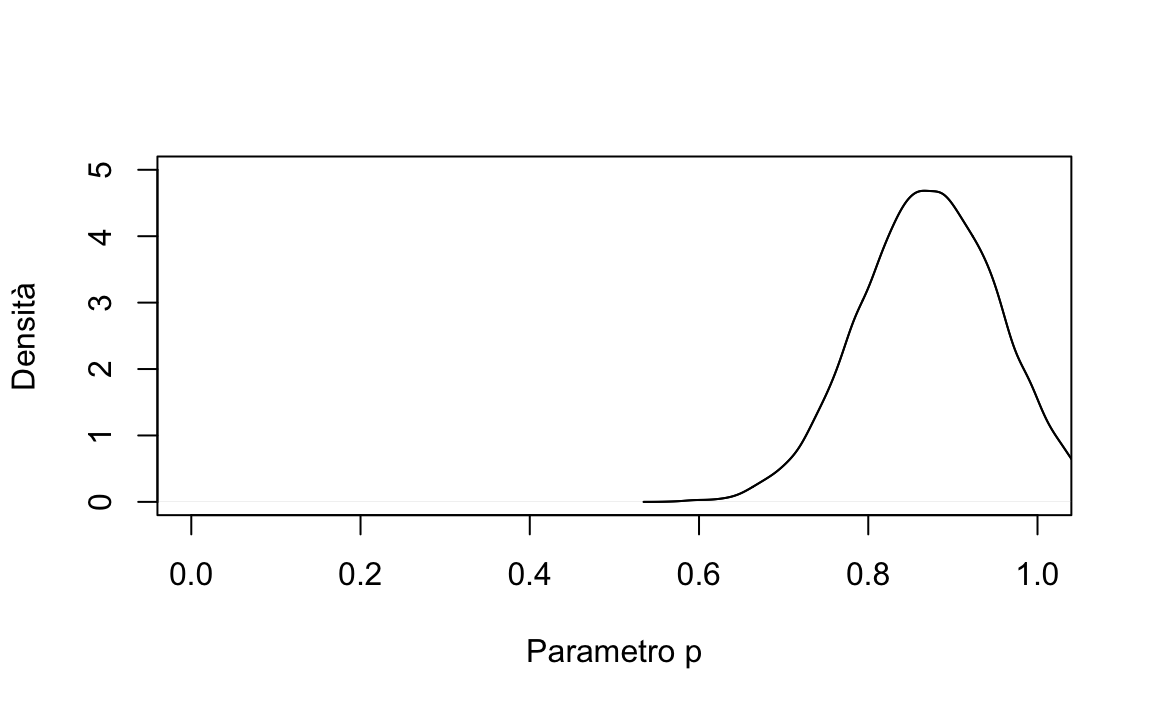

L’intervallo di credibilità al 95% per il gruppo di controllo è

precis(mc, prob = 0.95)
#>        mean         sd      2.5%    97.5%
#> p 0.8749966 0.08267702 0.7129526 1.037041

Le due figure che abbiamo realizzato presentano le distribuzioni a posteriori del parametro \(p\) (cioè la probabilità di risultare positivo al virus SARS-CoV-2) per i due gruppi di pazienti considerati nella ricerca di Gautret et al. (2020). Come si possono interpretare? Le figure ci mostrano che le due distribuzioni a posteriori sono chiaramente separate, il che suggerisce che il parametro \(p\) assume valori diversi nei due gruppi.

Infatti, coerentemente con la conclusioni di Gautret et al. (2020), le stime a posteriori per il parametro \(p\) che abbiamo trovato suggeriscono che i pazienti del gruppo sperimentale (a cui è stata somministrata l’idrossiclorochina) hanno unaprobabilità minore di risultare positivi al SARS-CoV-2 rispetto ai pazienti del gruppo di controllo (a cui non è stata somministrata l’idrossiclorochina). Ciò è indicato dal confronto tra i due intervalli di credibilità al 95% che abbiamo calcolato. Gli intervalli di credibilità dei due gruppi non si sovrappongono. Questo fatto viene interpretato dicendo che il parametro \(p\) è diverso nei due gruppi. Sulla base di queste evidenza, dunque, possiamo concludere, con un grado di certezza soggettiva del 95%, che nel gruppo sperimentale vi è una probabilità più bassa di risultare positivi al SARS-CoV-2 rispetto al gruppo di controllo. In altri termini, la conclusione di questa analisi dei dati suggerisce che l’idrossiclorochina è efficace come terapia per il Covid-19. Svolgendo le analisi precedenti abbiamo dunque replicato le conclusioni a cui sono giunti Gautret et al. (2020), sia pur utilizzando una procedura statistica diversa.

Tuttavia, nella ricerca di Gautret et al. (2020) è presente un aspetto che non abbiamo finora considerato. Hulme et al. (2020) hanno infatti osservato che Gautret et al. (2020), nelle loro analisi statistiche, hanno escluso alcuni dati. Sono stati infatti osservati dei pazienti i quali, nel gruppo sperimentale, sono in realtà peggiorati, anziché essere migliorati. L’analisi di Gautret et al. (2020) non considera questi dati.

Se consideriamo tutti i pazienti – non solo quelli selezionati da Gautret et al. (2020) – la situazione è la seguente. Gruppo sperimentale: 10 positivi su 18; gruppo di controllo: 14 positivi su 16. Ripetiamo dunque l’analisi descritta in precedenza utilizzando, per il gruppo sperimentale, tutti i dati che abbiamo a disposizione. Così facendo otteniamo il seguente intervallo di credibilità al 95%:

ym <- c(rep(1, 10), rep(0, 8))
ym
#>  [1] 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
m <- quap( 
  flist, 
  data = list(y = ym)
)
precis(m, prob = 0.95)
#>        mean        sd      2.5%     97.5%
#> p 0.5555554 0.1171209 0.3260026 0.7851081

Quando utilizziamo tutti i dati – non soltanto i pazienti selezionati da Gautret et al. (2020) – otteniamo il seguente intervallo di credibilità al 95% per il gruppo sperimentale: [0.33, 0.79]. Tale intervallo si sovrappone all’intervallo di credibilità al 95% per il gruppo di controllo, [0.71 1.04]. In base agli standard correnti, un risultato di questo tipo non viene considerato come evidenza sufficiente per potere concludere che il parametro \(p\) assume un valore diverso nei due gruppi. In altri termini, se consideriamo tutti i dati, e non solo quelli selezionati dagli autori, non vi è evidenza alcuna che l’idrossiclorochina sia efficace come terapia per il Covid-19.

Concludiamo questa discussione dicendo che ciò che è stato presentato in questo capitolo è solo un esercizio didattico: la ricerca di Gautret et al. (2020) include tante altre informazioni che qui non sono state qui considerate. Tuttavia, notiamo che la semplice analisi statistica che abbiamo descritto è stata in grado di replicare completamente le conclusioni a cui sono giunti (per altra via) Hulme et al. (2020).

30.3 Modello Normale

Consideriamo ora un altro esempio esaminando, in questo caso, un campione di dati estratto dalla distribuzione Normale:

\[ \begin{aligned} Y_i &\sim \mathcal{N}(\mu, \sigma) \\ \mu &\sim \mathcal{N}(\mu = \bar{X}, \sigma = 100) \\ \sigma &= s_Y \end{aligned} \] Questo modello statistico ci dice che la variabile aleatoria \(Y\) segue la distribuzione Normale di parametri \(\mu\) e \(\sigma\). Il parametro \(\mu\) è sconosciuto e abbiamo deciso di descrivere la nostra incertezza a priori relativa ad esso mediante una distribuzione a priori che segue la legge Normale con media uguale alla media campionaria e con deviazione standard paria a 100. In questo esempio, il parametro \(\sigma\) è fissato ad un valore pari alla deviazione standard del campione, \(s_y\). Prendiamo questa decisione qui per presentare un esempio nelle condizioni più semplici, ovvero quelle nelle quali l’unica incognita è \(\mu\). In generale, però, anche il parametro \(\sigma\) viene considerato ignoto e ad esso viene assegnata una distribuzione a priori; ad esempio, \(\sigma \sim \text{Unif}(0, 100)\).

df <- data.frame(
  x <- c(26, 35, 30, 25, 44, 30, 33, 43, 22, 43, 24, 19, 39, 31, 25, 28, 35, 30, 26, 31, 41, 36, 26, 35, 33, 28, 27, 34, 27, 22)
)

true_sd <- sd(df$x)
true_sd
#> [1] 6.606858

sample_mean <- mean(df$x)
sample_mean
#> [1] 30.93333

flist <- alist(
  x ~ dnorm(mu, sigma), 
  mu ~ a,
  a ~ dnorm(sample_mean, 100),
  sigma ~ true_sd
)

set.seed(123)
m1 <- quap( 
    flist,
    data = df 
)

out <- precis(m1, prob = 0.95)
out
#>       mean       sd     2.5%    97.5%
#> a 30.93333 1.206154 28.56931 33.29735

30.4 Il modello di regressione lineare

I due modelli statistici che abbiamo presentato sopra descrivono il comportamento di una singola variabile aleatoria: una proporzione di “successi” o la media del valore BDI-II in un campione. Se la distribuzione a priori non è informativa, la distribuzione a posteriori risulta centrata sul valore della statistica campionaria (\(p\) o \(\bar{x}\)) utilizzata per la stima del parametro corrispondente (\(\pi\) o \(\mu\)). Quello che “guadagnamo” calcolando la distribuzione a posteriori del parametro sconosciuto è la possibilità di quantificare la nostra incertezza rispetto alla stima del parametro: se l’intervallo di credibilità è molto largo questo significa che i dati del campione sono poco informativi rispetto al valore del parametro; se l’intervallo di credibilità è molto stretto, allora concludiamo che siamo piuttosto certi del valore della nostra stima.

Tuttavia, i modelli di interesse per la psicologia (e per le altre scienze) non si limitano alla stima di un singolo parametro ma descrivono le relazioni tra due o più variabili. Per esempio, nel suo studio Regression towards mediocrity in hereditary stature, Galton (1886) si è chiesto come sia possibile descrivere la relazione tra l’altezza dei figli e l’altezza dei padri. Il modo più semplice per rispondere ad una domanda di questo tipo è quello di formulare la risposta nei termini di un modello di regressione lineare – infatti, la tecnica statistica della regressione lineare fu inventata da Galton proprio per questo scopo.

Il modello di regressione lineare è il più semplice dei modelli statistici che descrivono la relazione tra due (o più) variabili. Abbiamo esaminato il modello statistico della regressione lineare nei capitoli precedenti. Vediamo qui come sia possibile fare inferenza sul modello di regressione usando il metodo Bayesiano.

Usando la notazione che abbiamo introdotto nelle sezioni precedenti di questo capitolo, scriviao il modello statistico di regressione ineare nel modo seguente:

\[ \begin{aligned} Y_i &\sim \mathcal{N}(\mu_i, \sigma) \\ \mu_i &= \alpha + \beta(X_i - \bar{X}) \\ \alpha &\sim \mathcal{N}(0, \sigma_{\alpha}) \\ \beta &\sim \mathcal{N}(0, \sigma_{\beta}) \\ \sigma &\sim \text{Unif}(0, 50) \end{aligned} \] La verosimiglianza indica che ciascun valore \(Y_i\) (la nostra variabile dipendente) segue una distribuzione Normale. Tuttavia, si noti il pedici \(i\). Scrivendo \(Y_i\) con il pedice intendiamo dire che ciascuna \(Y_i\) segue una distribuzione Normale avente una media diversa (\(\mu_i\)). In questa formulazione del modello, tutte le distribuzioni Normali relative alla \(Y\) hanno la stessa deviazione standard (\(\sigma\), il che corrisponde all’assunzione di omoschedasticità). La cosa importante da notare è che non dobbiamo stimare un singolo parametro \(\mu\), come avveniva invece nel caso del modello Normale che abbiamo discusso nel caso dei valori BDI-II. Nel modello statistico della regressione lineare, invece, \(\mu_i\) è espresso nei termini di due due parametri incogniti, \(\alpha\) e \(\beta\), e nei termini di una quantità osservabile chiamata \(X\) (la nostra variabile indipendente). Ciò è indicato nella seconda riga della descrizione del modello statistico.

La seconda riga della specificazione del modello statistico della regressione lineare non descrive una relazione stocastica (non viene usato il simbolo \(\sim\)), ma bensì una relazione deterministica (come indicato dall’uso del simbolo \(=\)). Ciò significa che, una volta fissati i parametri \(\alpha\) e \(\beta\), il valore \(\mu_i\) è determinato in maniera univoca (ovvero, corrisponde alla componente deterministica del modello di regressione lineare che abbiamo descritto in precedenza). Se il modello di regressione lineare è espresso come \(\mu_i = \alpha + \beta(X_i - \bar{X})\), allora possiamo assegnare ai parametri \(\alpha\) e \(\beta\) la seguente interpretazione.

1. Il parametro \(\alpha\) è uguale al valore atteso della \(Y\) in corrispondenza del valore \(X\) medio. Infatti, in precedenza abbiamo notato come, dal punto di vista geometrico, \(\alpha\) corrisponde all’ordinata del punto in cui la retta di regressione interseca l’asse verticale di un sistema di coordinate cartesiane. Nel caso presente abbiamo espresso la \(X\) come scarti (o differenze) dalla media: \(X_i - \bar{X}\). Da ciò segue che la media di \(X\) (espressa in termini di scarti dalla media) avrà valore zero. Di conseguenza, \(\alpha\) corrisponderà a \(\mathbb{E}(Y \mid \bar{X})\).

2. Il parametro \(\beta\) ci dice di quanto varia \(\mathbb{E}(Y \mid X)\) quando \(X\) varia di un’unità.

Nel modello statistico presentato sopra, la nostra incertezza su \(\beta\) è stata quantificata mediante una distribuzione a priori centrata sullo zero e con una deviazione standard pari a \(\sigma_{\beta}\). La nostra incertezza su \(\alpha\) è stata quantificata mediante una distribuzione a priori centrata sullo zero e con una deviazione standard pari a \(\sigma_{\alpha}\). Infine, la nostra incertezza su \(\sigma\) (la deviazione standard della dispersione dei dati attorno alla retta di regressione) è stata quantificata mediante una distribuzione uniforme compresa tra 0 e 50.

Per ora ci siamo limitati a descrivere la formulazione Bayesiana del modello di regressione mediante la sintassi di rethinking, così come fa McElreath (2020). Nelle sezioni seguenti vedremo come sia possibile svolgere l’analisi di regressione in termini Bayesiani. Inizieremo considerando il caso più semplice, ovvero quello nel quale la variabile \(X\) è una variabile dicotomica; considereremo poi il caso in cui \(X\) è una variabile continua.

30.4.2 Un esempio pratico

Esaminiamo un sottoinsieme di dati tratto dal National Longitudinal Survey of Youth i quali sono stati discussi da Gelman et al. (2020). I soggetti sono bambini di 3 e 4 anni. La variabile dipendente, kid_score, è il punteggio totale del Peabody Individual Achievement Test (PIAT) costituito dalla somma dei punteggi di tre sottoscale (Mathematics, Reading comprehension, Reading recognition). La variabile indipendente, mom_hs, è il livello di istruzione della madre, codificato con due livelli: scuola media superiore completata oppure no. La domanda della ricerca è se il QI del figlio (misurato sulla scala PIAT) risulta o meno associato al livello di istruzione della madre.

Codifichiamo il livello di istruzione della madre (\(X\)) con una variabile indicatrice (ovvero, una variabile che assume solo i valori 0 e 1) tale per cui:

• \(X=0\): la madre non ha completato la scuola secondaria di secondo grado (scuola media superiore);

• \(X=1\): la madre ha completato la scuola media superiore.

Supponiamo che i dati siano contenuti nel data.frame df.

library("foreign")
df <- read.dta(here("data", "kidiq.dta"))
head(df)
#>   kid_score mom_hs    mom_iq mom_work mom_age
#> 1        65      1 121.11753        4      27
#> 2        98      1  89.36188        4      25
#> 3        85      1 115.44316        4      27
#> 4        83      1  99.44964        3      25
#> 5       115      1  92.74571        4      27
#> 6        98      0 107.90184        1      18

Calcoliamo le statistiche descrittive per i due gruppi:

df %>% 
  group_by(mom_hs) %>% 
  summarise(
    mean_kid_score = mean(kid_score),
    std = sqrt(var(kid_score))
  )
#> # A tibble: 2 x 3
#>   mom_hs mean_kid_score   std
#>    <dbl>          <dbl> <dbl>
#> 1      0           77.5  22.6
#> 2      1           89.3  19.0

Il punteggio medio PIAT è pari a 77.5 per i bambini la cui madre non ha il diploma di scuola media superiore e pari a 89.3 per i bambini la cui madre ha completato la scuola media superiore. Questa differenza suggerisce un’associazione tra le variabili, ma tale differenza potrebbe essere soltanto la conseguenza della variabilità campionaria, senza riflettere una caratteristica generale della popolazione. Come possiamo usare il modello statistico lineare per fare inferenza sulla differenza osservata tra i due gruppi?

Per rispondere a questa domanda specifichiamo il modello statistico che descrive la differenza tra i punteggi PIAT dei due gruppi mediante un modello di regressione lineare:

flist <- alist(
  kid_score ~ dnorm(mu, sigma),
  mu ~ a + b * mom_hs,
  a ~ dnorm(86.8, 100),
  b ~ dnorm(0, 100),
  sigma ~ dunif(0, 100)
)

Si noti che abbiamo specificato tale modello statistico seguendo la stessa logica descritta in precedenza. Ovvero, abbiamo esplicitato:

• la verosimiglianza dei dati;

• il modello statistico della regressione lineare che esprime il valore atteso della variabile dipendente come una funzione lineare della variabile indipendente;

• la distribuzione a priori di ciascuno dei parametri del modello, ovvero \(a\), \(b\) e \(\sigma\).

Nel caso presente, abbiamo specificato due distribuzioni a priori “debolmente informative” per i parametri \(a\) e \(b\). La distribuzione a priori per il parametro \(a\) è una distribuzione Normale centrata sulla media di tutti i dati (calcolata ignorando la suddivisione in gruppi), con una deviazione standard relativamente grande. Ciò significa che, a priori, per il parametro \(a\) riteniamo plausibili valori che sono inclusi nell’intervallo \(86.8 \pm 2 \times 100\) punti PIAT, anche se riteniamo più probabili i valori prossimi a 86.8. Così facendo esprimiamo una generale incertezza su quello che potrebbe essere il valore della media del gruppo codificato con \(X = 0\).

In maniera simile, caratterizziamo il possibile valore della differenza tra le medie tra i due gruppi (ciò a cui siamo interessati) in maniera molto vaga: affermiamo che potrebbe essere un valore qualsiasi, plausibilmente contenuto nell’intervallo \(0 \pm 2 \times 100\), assegnando una plausibilità a priori maggiore ai valori prossimi allo zero (positivi e negativi). Per il parametro \(b\), specifichiamo dunque una distribuzione a priori Normale centrata sullo zero. Questa scelta ha l’effetto di non favorire a posteriori per \(b\) la cui media è positiva o negativa. In altri termini, specificando una distribuzione a priori per \(b\) centrata sullo zero non favoriamo una soluzione (a posteriori) che indica che vi è un’associazione positiva tra livello di scolarità della madre e intelligenza del bambino, né l’ipotesi opposta (associazione negativa tra le due variabili).

Infine, specifichiamo distribuzione a priori uniforme nell’intervallo (0, 100) per il parametro \(\sigma\) che descrive la distribuzione dei dati attorno al loro valore atteso (la retta di regressione).

Quale distribuzione a priori è corretta?

Un grave problema che è emerso negli anni recenti relativamente all’analisi dei dati psicologici (e non solo) è il cosiddetto “\(p\)-hacking,” ovvero la pratica di adattare il modello e i dati allo scopo di ottenere il risultato desiderato. Il risultato desiderato è generalmente un valore-\(p\) inferiore al 5%. Il problema è che quando il modello statistico viene modificato alla luce dei dati osservati, i valori-\(p\) non mantengono più il loro significato originario: in altre parole, il “\(p\)-hacking” aumenta la probabilità di ottenere dei risultati falsi. L’approccio Bayesiano non prevede i valori-\(p\), ma il rischio rimane se scegliamo le distribuzioni a priori in base alle proprietà del campione allo scopo di ottenere il risultato desiderato. La procedura che invece deve essere seguita è quella di scegliere le distribuzioni a priori sulla base di considerazioni generali, indipendentemente dalle specifiche caratteristiche del campione, come abbiamo fatto sopra utilizzando una distribuzione a priori per \(b\) centrata sullo zero.

30.4.2.1 Inferenza mediante la distribuzione a posteriori

Adattiamo il modello ai dati utilizzando la funzione quap():

m1 <- quap(
  flist,
  data = df
)

Estraiamo alcuni campioni dalla distribuzione a posteriori:

post <- extract.samples(m1)
post[1:5, ]
#>          a         b    sigma
#> 1 80.07328  9.006764 19.73586
#> 2 77.26278 11.935567 19.77395
#> 3 76.66754 11.448966 19.31510
#> 4 77.23189 10.742990 19.97299
#> 5 80.54546  9.255061 19.83349

Esaminiamo la distribuzione a posteriori dei parametri mediante le istruzioni seguenti.

par(mfrow = c(1, 3))

dens(
  post$a, lwd = 2.5, xlab = "",
  ylab = "Densità", main = "p(a | x, y)",
  cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
  cex.sub = 1.5
)
dens(
  post$b, lwd = 2.5, xlab = "",
  ylab = "", main = "p(b | x, y)",
  cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
  cex.sub = 1.5
)
dens(
  post$sigma, lwd = 2.5, xlab = "",
  ylab = "", main = "p(sigma | x, y)",
  cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
  cex.sub = 1.5
)
    
par(mfrow = c(1, 1))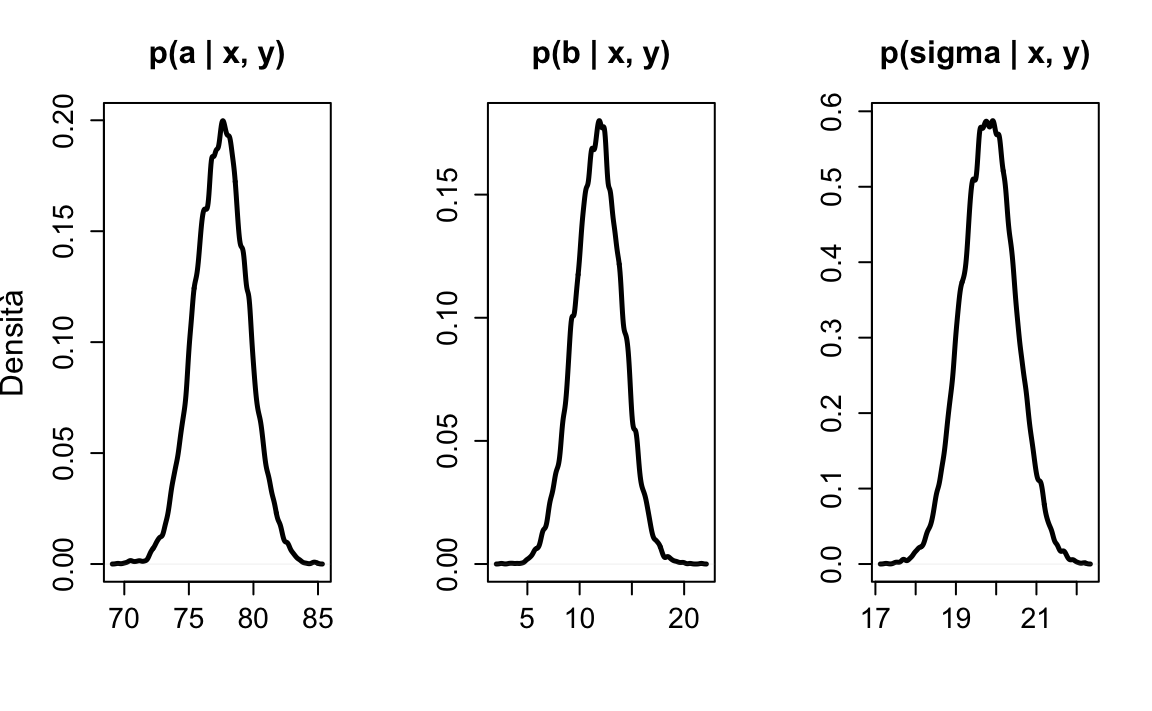

Figura 30.1: Distribuzioni a posteriori dei parametri a, b e \(\sigma\) del modello statistico lineare che descrive i punteggi del Peabody Individual Achievement Test come funzione del gruppo di appartenenza: i bambini la cui madre non ha completato la scuola media superiore e i bambini la cui madre ha completato la scuola media superiore. I dati sono tratti da Gelman et al. (2020).

Come in precedenza, la funzione precis() può essere usata per calcolare la media a posteriori per i parametri del modello:

precis(m1, prob = 0.95)
#>           mean        sd      2.5%    97.5%
#> a     77.55837 2.0528231 73.534910 81.58183
#> b     11.75868 2.3158682  7.219661 16.29770
#> sigma 19.80505 0.6721414 18.487679 21.12243

I risultati confermano ciò che ci aspettavamo: il coefficiente \(a\) corrisponde alla media del gruppo codificato con \(X = 0\), ovvero la media dei punteggi PIAT per i bambini la cui madre non ha completato la scuola media superiore; il coefficiente \(b\) corrisponde alla differenza tra le medie dei due gruppi, ovvero 89.32 - 77.55 = 11.77.

Una rappresentazione grafica dell’interpretazione che abbiamo fornito ai parametri del modello lineare è fornita nella figura 30.2.

Figura 30.2: Distribuzione dei punteggi del Peabody Individual Achievement Test in due gruppi di bambini facenti parte del campione discusso da Gelman et al. (2020): bambini la cui madre non hanno completato la scuola media superiore (\(X\) = 0) e bambini la cui madre ha completato la scuola media superiore (\(X\) = 1).

30.4.2.2 Inferenza

Il coefficiente \(b\) ci dice che i bambini la cui madre ha completato la scuola superiore ottengono in media circa 12 punti in più rispetto ai bambini la cui madre non ha completato la scuola superiore. L’intervallo di credibilità al 95% calcolato mediante la funzione precis() ci dice che possiamo essere sicuri al 95% che tale differenza è di almeno 7 punti e può arrivare fino a ben 16 punti. Possiamo dunque concludere, con un grado di certezza soggettiva del 95%, che c’è un’associazione tra il livello di scolarità della madre e l’intelligenza del bambino: i bambini tendono ad avere un livello di intelligenza più elevato se le madri hanno un più alto livello di istruzione.

30.5 Una variabile indipendente continua

Continuiamo ora con l’esempio relativo al National Longitudinal Survey of Youth discusso da Gelman et al. (2020) ponendoci ora il problema di descrivere l’associazione tra l’intelligenza del bambino, kid_score (ovvero il punteggio totale del Peabody Individual Achievement Test, PIAT), e il quoziente di intelligenza della madre, mom_iq. Si noti che, in questo caso, la variabile indipendente è una variabile continua (e non più dicotomica come nell’esempio precedente).

Iniziamo esaminando i dati, per verificare che un modello lineare sia appropriato per i dati considerati.

df %>% 
  ggplot(aes(x = mom_iq, y = kid_score)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  labs(
    x = "QI della madre",
    y = "Peabody Individual Achievement Test"
  )
#> `geom_smooth()` using formula 'y ~ x'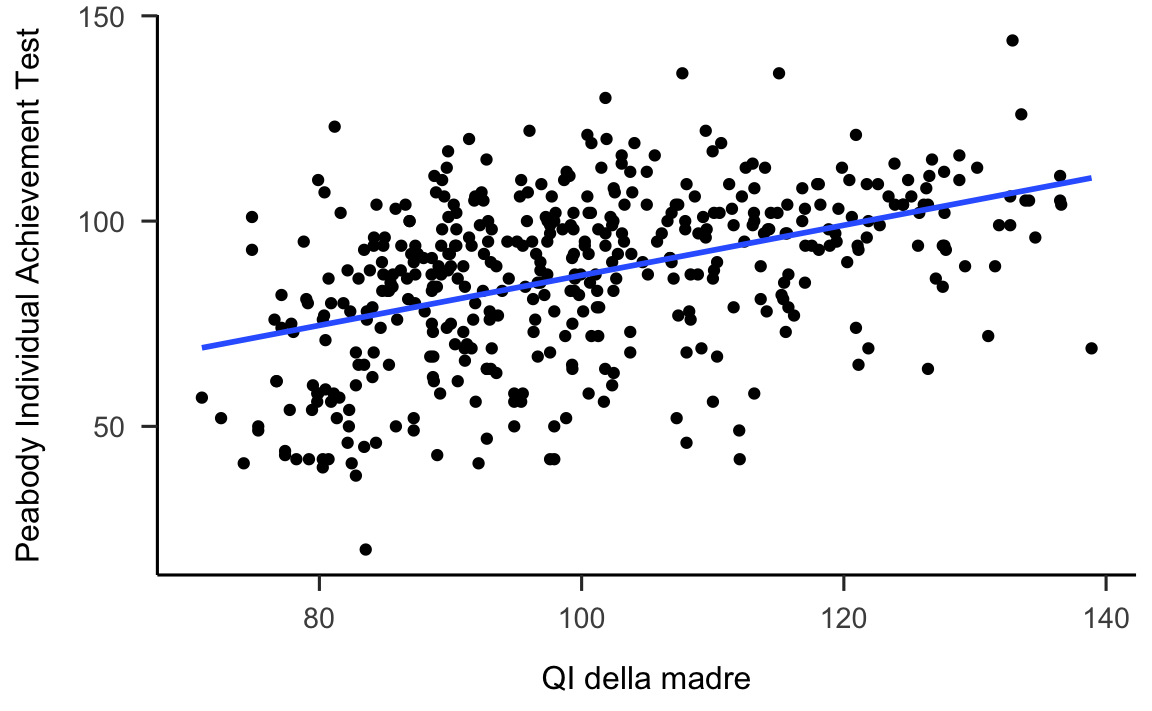

Figura 30.3: Punteggio del test PIAT come funzione del QI materno con sovrapposta la retta di regressione. Ogni punto sulla retta di regressione può essere concepito come un punteggio il punteggio predetto per un bambino la cui madri ha il QI corrispondente o come il punteggio PIAT medio per una sottopopolazione di bambini le cui madri hanno tutte quel particolare valore di QI. I dati sono tratti da Gelman et al. (2020).)

Il diagramma a dispersione suggerisce che un modello lineare è appropriato per questi dati. Descriviamo dunque in termini formali il modello che vogliamo adattare ai dati:

\[ \begin{aligned} Y_i &\sim \mathcal{N}(\mu_i, \sigma) \\ \mu_i &= \alpha + \beta(X_i - \bar{X}) \\ \alpha &\sim \mathcal{N}(0, \sigma_{\alpha}) \\ \beta &\sim \mathcal{N}(0, \sigma_{\beta}) \\ \sigma &\sim \text{Unif}(0, 50) \end{aligned} \]

Si noti che abbiamo descritto \(X\) nei termini degli scostamenti dalla media (\(X_i - \bar{X}\)). Come in precedenza, ciò fa in modo che il coefficiente \(\alpha\) corrisponda al valore atteso della \(Y\) in corrispondenza della media di \(X\) (quoziente di intelligenza della madre) – questa è una conseguenza del fatto che la retta di regressione passa per il punto \((\bar{X}, \bar{Y})\). Infatti, avrebbe poco senso chiederci qual è il valore atteso del punteggio PIAT quando il quoziente d’intelligenza della madre è uguale a zero.

Specifichiamo dunque il modello statistico lineare con la sintassi richiesta da rethinking:

flist <- alist(
  kid_score ~ dnorm(mu, sigma),
  mu ~ a + b * (mom_iq - mean(mom_iq)),
  a ~ dnorm(mean(kid_score), 100),
  b ~ dnorm(0, 100),
  sigma ~ dunif(0, 100)
)

Adattiamo il modello di regressione ai dati

m2 <- quap(
  flist,
  data = df
)

Esaminiamo il risultato ottenuto mediante la funzione precis():

precis(m2, prob = 0.95)
#>             mean         sd       2.5%      97.5%
#> a     86.7973283 0.87475112 85.0828476 88.5118090
#> b      0.6099751 0.05838627  0.4955402  0.7244101
#> sigma 18.2240956 0.61857167 17.0117174 19.4364738

Troviamo così che \[ \mathbb{E}(\text{kid_score}) = 86 + 0.61 \cdot x, \] laddove \(x\) è la variabile kid_score espressa come scostamento rispetto al suo valore medio. Tale retta di regressione stimata è mostrata assieme ai dati nella figura 30.3.

Il coefficiente \(b\) ci dice che, all’aumentare di un punto del quoziente d’intelligenza della madre, la media dei punteggi PIAT cresce di 0.61 unità. Il parametro \(\sigma\) ci dice che la deviazione standard che quantifica la dispersione dei dati attorno alla retta di regressione è pari a 18.22.

L’intervallo di credibilità di questo coefficiente ci dice che, con un livello di certezza del 95%, possiamo essere sicuri che, all’aumentare di un punto del quoziente d’intelligenza della madre, la media dei punteggi PIAT crescerà, come minimo, di 0.50 punti e, come massimo, di 0.72 punti. La differenza 0.72 - 0.50 esprime il nostro grado di incertezza rispetto alla stima del parametro, quando vogliamo che la nostra stima sia “credibile” al livello di 0.95. Ma non c’è niente di “magico” o necessario relativamente al livello di 0.95. Infatti, il default della funzione precis() è 0.89. Ciascuno di questi valori è arbitrario. Sono possibili tantissime soglie per quantificare la nostra incertezza: alcuni ricercatori usano il livello di 0.5. Il nostro obiettivo è quello di descrivere il livello della nostra incertezza relativamente alla stima del parametro. E la nostra incertezza è descritta dall’intera distribuzione a posteriori. Per cui il metodo più semplice, più diretto e più completo per descrivere la nostra incertezza rispetto alla stima dei parametri è quello di riportare graficamente tutta la distribuzione a posteriori, come indicato per esempio nella figura 30.4.

post <- extract.samples(m2)
par(mfrow = c(1, 3))

dens(
  post$a, lwd = 2.5, xlab = "",
  ylab = "Densità", main = "p(a | x, y)",
  cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
  cex.sub = 1.5
)
dens(
  post$b, lwd = 2.5, xlab = "",
  ylab = "", main = "p(b | x, y)",
  cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
  cex.sub = 1.5
)
dens(
  post$sigma, lwd = 2.5, xlab = "",
  ylab = "", main = "p(sigma | x, y)",
  cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
  cex.sub = 1.5
)
    
par(mfrow = c(1, 1))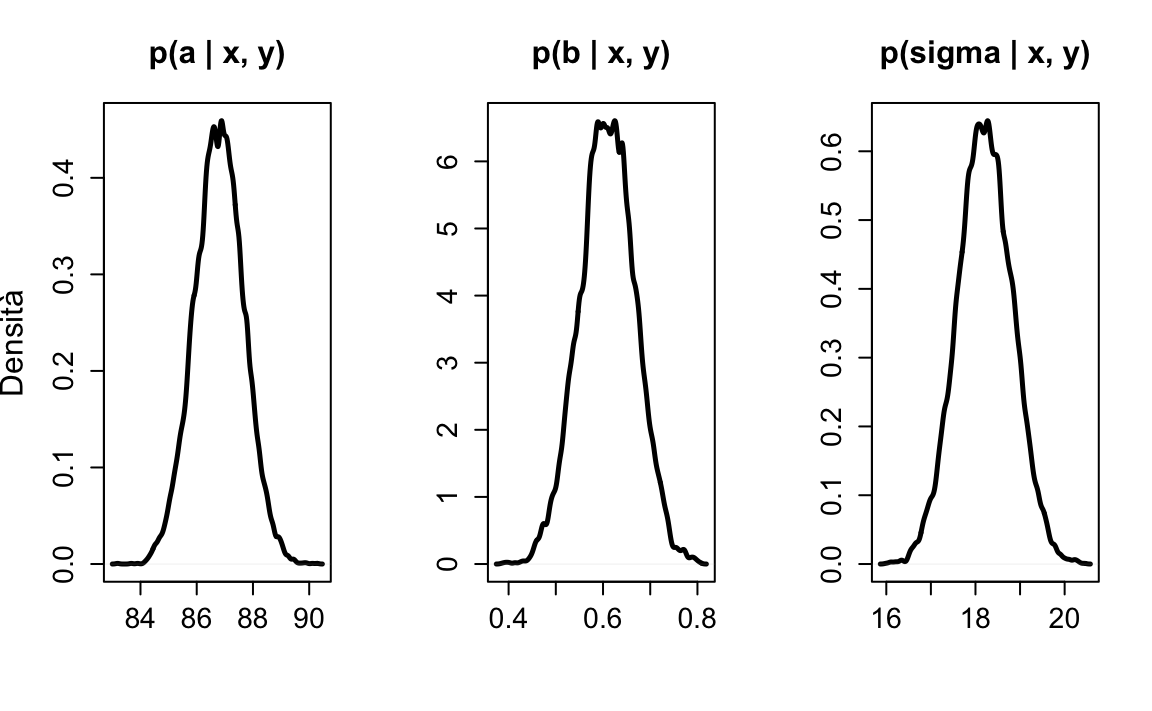

Figura 30.4: Distribuzione a posteriori dei parametri \(a\), \(b\) e \(sigma\) del modello statistico lineare che descrive i punteggi del Peabody Individual Achievement Test come funzione del quoziente d’intelligenza della madre espresso come scostamento rispetto al suo valore medio. I dati sono tratti da Gelman et al. (2020).